Подбор практических задач по математике для спецкурса «производная»

Подбор практических задач по математике для спецкурса «производная»

В статье акцентируется внимание на необходимости обучения решению прикладных задач в обучении математике в профильной школе. Приведенные примеры решения задач экономического, медицинского, химико-биологического и физико-математического профилей обучения по теме «Производная и ее применение». Процесс решения прикладных задач проведения в три этапа, а именно: построение математической модели, исследование модели и интерпретация полученных результатов.

Ключевые слова: методика обучения математике, прикладная задача, производная.

Постановка проблемы. Для современного человека важно быть всесторонне развитым, активным, мобильным, уметь видеть проблему, четко формулировать и всесторонне подходить к ее решению. Владение навыками математической деятельности и умениями их применять к решению различных жизненных ситуации является залогом успешного участия личности в современной общественной жизни.

Целью и задачей образовательной области «Математика» является формирование у учащихся математической компетентности на уровне, достаточном для обеспечения жизнедеятельности в современном мире, успешного овладения знаниями из других образовательных областей в процессе обучения; раскрытие роли и возможностей математики в познании и описании реальных процессов и явлений действительности. Реализовать поставленные цели и задачи можно при условии усиления практической и прикладной направленности школьного курса математики. По нашему мнению, главным средством реализации прикладной направленности курса математики является использование прикладных задач, а формирование умения решать прикладные задачи является составной частью процесса обучения математике.

Анализ исследований и публикаций. Вопрос прикладной направленности школьного курса математики освещали П. Бевз, А.В. Прус. Вопросами принципов отбора системы прикладных задач, требований к их решению занимались исследователи Я. Дутка, Л.А. Соколенко и др. Проблемы применения прикладных задач в процессе обучения производных и интегралов в курсе алгебры и начал анализа исследовали В.В. Ачкан, В.А. Швец. Сущность практической направленности обучения математике исследователи видят в направленности целей, содержания, средств, методов и организационных форм обучения на формирование умений и навыков решения математических задач [7].

Цель работы заключается в исследовании методических особенностей обучения решению прикладных задач в курсе математики профильной школы, в частности при изучении производной и интеграла в курсе алгебры и начал анализа профильного уровня.

Объектом исследования является процесс обучения алгебре и началам анализа в профильной школе, а предметом исследования является методика обучения решению прикладных задач при изучении тем «Производная и ее применение» в курсе алгебры и начал анализа профильной школы.

Изложение основного материала (результатов) исследования.

Под прикладной задачей в школе в основном понимают задачу, которая возникла за курсом математики и решается математическими методами и способами, которые изучаются в школьном курсе.

Также при решении задач практического содержания с применением производной следует обратить внимание учащихся на задачи, в содержании которых говорится о радиоактивном распаде; прирост населения; экономические процессы и тому подобное.

Итак, при изучении темы "Производная и ее применение" ученики не только усваивают технику дифференцирования, изучают связь между производной и свойствами функций, но и совершенствуют навыки работы с приближенными величинами, у них формируется представление об использовании производной в других науках, в реальной жизни.

При решении прикладных задач, уместно выделить две основные группы задач: задачи, не требующие построения математической модели; задачи, решение которых требует построение математической модели. Чаще всего, у учащихся возникают проблемы именно при решении задач, в условии которых нет математической модели, то есть в которых нужно самостоятельно составить математическую модель.

Процессу решения прикладных задач присущи все этапы математического моделирования.

На первом этапе происходит построение математической модели, этот этап требует глубоких знаний учащихся смежных дисциплин или дисциплин в языке которых возникает прикладная задача.

На втором этапе происходит исследование математической модели, то есть решение полученной математической задачи, этот этап позволяет предсказать развитие процесса, рассчитать его характеристики.

На третьем этапе происходит интерпретация полученных на втором этапе результатов, то есть перевод развязку математической задачи с языка математики на язык той области, где она возникла.

Рассмотрим прикладную задачу и ее решение для экономического профиля естественно-математического направления.

Реферат [1]. Капитал в 1000000000 денежных единиц можно положить в банк под 50% годовых или инвестировать в предприятие, при этом эффективность вклада ожидается в размере 100%, а расходы заданные квадратичной зависимости. На прибыль накладывается налог p%  При каких значениях p вклад в предприятие более эффективным, чем размещение капитала в банке?

1. Построение математической модели

Пусть x (млрд. ден. единиц) инвестируется в предприятие, аразмещается под проценты. Размещен капитал через год определяется по формуле сложных процентов а капитал вложен в предприятие, определяется по формуле

Так как по условию задачи расходы задаются квадратичной зависимости, то они будут составлять то есть прибыль от вклада в предприятие  Налоги составляют  то есть чистая прибыль будет равняться

Общая сумма за год составит

Таким образом, экономическая задача сводится к математической задачи нахождения максимального значения функции на промежутке [0,1].

2. Исследование математической модели

Найдем максимума функции на промежутке [0,1].

1) Находим производную

2) Находим критические точки:

3) Находим вторую производную

4)  таким образом х - точка максимума.

Чтобы  необходимо, чтобы выполнялось условие:

 решив неравенство, имеем

 Таким образом, если, то выгоднее ничего не вкладывать в предприятие и разместить весь капитал в банке. Если это можно показать, что при

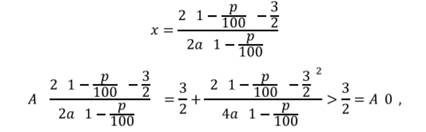
то есть вклад в предприятие выгоднее, чем чистое размещение под проценты.

3. Интерпретация. Переведем результат с математического языка на язык исходной задачи. На прибыль накладывается налог в р%. При  вклад в предприятие является более эффективным, чем размещение капитала в банке. При значениях  выгоднее ничего не вкладывать в предприятие и разместить весь капитал в банке.

При решении этой задачи у учащихся могут возникнуть проблемы на этапе построения математической модели, поскольку нужно обладать экономическими знаниями, знать формулу сложных процентов.

Рассмотрим задачу химико-биологического профиля обучения на применение производной.

Задача [3, с. 80]. Газовая смесь состоит из окиси азота и кислорода .При какой концентрации кислорода реакция окисления происходит с наибольшей скоростью?

1. Построение математической модели.

Построим модель химической реакции окисления: скорость реакции определяется по формуле: где концентрация кислорода в произвольный момент времени в объемных процентах; 100-x - концентрация окиси азота,  k -  константа скорости реакции.

2. Исследование математической модели.

Нужно найти максимум функции скорости реакции, для этого найдем производную:

Приравниваем производную к нулю и находим критические точки:

Исследуем знак производной в окрестностях критических точек

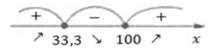
Рисунок 1. Интервал

Итак,

3. Интерпретация. При концентрации кислорода, которая составляет 33,3%, реакция окисления происходит с наибольшей скоростью.

Задача 3 Объем продукции V мастерской, которая изготавливает елочные игрушки, на протяжении дня выражается зависимостью , где . Вычислите продуктивность труда мастерской на протяжении каждого часа работы [1].

Аналогичная работа была проведена с учебниками химии, биологии и другими. Таким образом, в теме «Производная и ее приложение» стало возможным, кроме физического и геометрического, раскрыть химический, биологический, экономический и другой смысл математического понятия производной.

Химический смысл производной. Пусть  – концентрация вещества, которая получается во время химической реакции в момент времени t. Тогда  – скорость реакции в момент .

Задача 4. Известно, что при мономолекулярной реакции за время t образуются молекулы (продукта реакции) . За каким законом можно отобразить скорость образования нового вещества при названной реакции?

Биологический смысл производной. Если  – закон размножения популяций, тогда  – продуктивность популяции в данный момент времени.

Задача 5. Размер популяции бактерий в момент t (время отображено в часах) задается формулой . Найти скорость роста популяций в момент .

В будущем это даст возможность учителю корректно создавать математические модели к разным реальным процессам и рационально решать прикладные задачи, которые касаются разных отраслей науки и человеческой жизнедеятельности.

Чтобы ознакомить учащихся с экономическим, химическим, биологическим содержанием производной нужно найти дополнительное время на уроки или практические занятия, или организовать индивидуальную деятельность учащихся в виде учебных проектов, работы кружка и так далее. На помощь учащихся и преподавателям математического анализа нами подготовлено учебное пособие «Прикладные задачи по математическому анализу» [3], в котором подан минимально необходимый объем сведений о применении методов математического анализа.

Данное учебное пособие разработано в соответствии с Государственным образовательным стандартом высшего образования для бакалавров специальности «Математика». Структура пособия отвечает последовательности изучения соответствующих разделов курса «Математический анализ» для математиков согласно программе по математическому анализу. Каждый параграф содержит отдельные короткие блоки теоретических сведений, наводятся основные определения, главные формулы, которые применяются при решении задач. Этот материал позволит студентам, не отвлекаясь на поиски необходимых формул, больше времени уделить самостоятельному решению задач.

В классическом курсе математического анализа прикладные задачи не выделяются по содержанию (природоведение, физика, химия, биология, экономика), а подаются в соответствии с учебными темами. В то же время есть потребность дополнить курс математического анализа подборками задач, которые касаются определенных направлений науки. Такие задачи помогут студентам лучше понять применение методов математического анализа и более сознательно их использовать в решении прикладных задач. В будущей профессиональной деятельности учителя смогут использовать эти задачи для реализации прикладной направленности школьного курса математики.

Выводы и перспективы дальнейших поисков в направлении исследования. Одним из эффективных путей формирования системы математических компетентностей учащихся является обучение решению прикладных задач. Решения прикладных задач способствует приобретению составляющих математической компетентности. Прикладные задачи достаточно удачно дополняют систему задач школьного курса математики и могут использоваться на различных этапах и реализовывать различные учебные цели: готовить к изучению или начинать изучение новой темы, способствовать углублению знаний в процессе изучения темы.

СПИСОК   ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Ачкан В. В. Использование прикладных задач в процессе изучения производной в курсе алгебры и начал анализа в классах разных профилей / В. В. Ачкан // Научные записки Бердянского государственного педагогического университета. Сер .: Педагогические науки. - 2014. - № 1. - С. 12 - 23.

2. Головань М. С. информатические компетентность: сущность, структура и становления / М. С. Головань // Информатика и информационные технологии в учебных заведениях. - 2007. - № 4. - С. 62 - 69.

3. Личковский Е. И. Высшая математика: учебник / Е. И. Личковский, П. Л. Свердан, В. А. Тиманюк, А. В. Чалый. - Винница: Новая книга, 2014. - 632 с.

4. Прикладные задачи математического анализа: методические указания к самостоятельной работе для студентов / сост. О. Г Ровенская, Н. В. Белых. - Краматорск: ДГМА, 2011. - 152 с. 5. Прус А.В. Общие вопросы прикладной направленности школьного курса математики / А.В. Прус // Вестник Житомирского государственного университета имени Ивана Франко. - 2007. - Вып. 34. - С. 67 - 71.

6. Соколенко Л. А. Система прикладных задач естественного характера как средство формирования эвристической деятельности учащихся / Л. А. Соколенко // Дидактика математики: проблемы и исследования: международный сборник научных работ. - Донецк: ДонНУ, 2009. - № 32. - С. 24 - 28.

7. Швец В. А. Математическое моделирование как содержательная линия школьного курса математики / А. Швец // Дидактика математики: проблемы и исследования: международный сборник научных работ. - Донецк: ДонНУ, 2009. -№ 32. - С. 16 - 23