
 ЗАДАНИЕ 16 Вариант
1
ЗАДАНИЕ 16 Вариант
1
1.Стороны основания правильной четырёхугольной пирамиды равны 14, боковые рёбра равны 25. Найдите площадь поверхности этой пирамиды.
 2. Два ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 8 и 9. Диагональ параллелепипеда равна 17.
Найдите объём параллелепипеда.
2. Два ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 8 и 9. Диагональ параллелепипеда равна 17.
Найдите объём параллелепипеда.
3. Два ребра прямоугольного параллелепипеда равны 7 и 4, а объём параллелепипеда равен 140. Найдите площадь поверхности этого параллелепипеда.
4. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 8. Диагональ параллелепипеда равна 12. Найдите объём параллелепипеда.
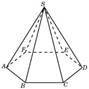 6. Стороны
основания правильной четырёхугольной пирамиды равны 30, боковые рёбра равны 25.
Найдите площадь поверхности этой пирамиды.
6. Стороны
основания правильной четырёхугольной пирамиды равны 30, боковые рёбра равны 25.
Найдите площадь поверхности этой пирамиды.
7. Стороны основания правильной шестиугольной пирамиды равны 14,
боковые рёбра равны 25. Найдите площадь боковой поверхности этой пирамиды.
8. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 7 и 5. Объём параллелепипеда равен 210. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
ЗАДАНИЕ 16 Вариант 2
 1. Найдите объём
правильной четырёхугольной пирамиды, сторона основания которой равна 4, а
боковое ребро равно √17.
1. Найдите объём
правильной четырёхугольной пирамиды, сторона основания которой равна 4, а
боковое ребро равно √17.
2. Стороны основания правильной
шестиугольной пирамиды равна 14, боковые ребра 25. Найдите площадь боковой
поверхности этой пирамиды.
3. Вычислите площадь полной поверхности прямоугольного параллелепипеда, диагональ которого равна 25 см, а диагонали боковых граней равны 15 см и 4√34 см.
4. Высота основания правильной треугольной пирамиды равно 9 а высота боковой грани пирамиды проведенная к ребру основания равна корень из 73. Найдите боковое ребро пирамиды
 5. Стороны основания
правильной шестиугольной пирамиды равны 24, боковые ребра равны 13. Найдите
площадь боковой поверхности этой пирамиды.
5. Стороны основания
правильной шестиугольной пирамиды равны 24, боковые ребра равны 13. Найдите
площадь боковой поверхности этой пирамиды.
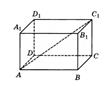
6. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что ВВ1 = 16, А1В1 = 2, A1D1 = 8. Найдите длину диагонали AC1
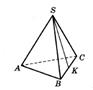
 7. В правильной
треугольной пирамиде SABC медианы основания АВС пересекаются в точке
О. Площадь треугольника АВС равна 2; объём пирамиды равен 4. Найдите длину
отрезка OS.
7. В правильной
треугольной пирамиде SABC медианы основания АВС пересекаются в точке
О. Площадь треугольника АВС равна 2; объём пирамиды равен 4. Найдите длину
отрезка OS.
8. Стороны основания правильной
четырехугольной пирамиды равны 14, боковые ребра равны 25. Найдите площадь
поверхности этой пирамиды.
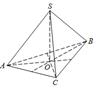
 9.. В правильной треугольной пирамиде
SABC точка K – середина ребра BC, S – вершина. Известно, что
AB = 6, а длина отрезка SK = 7. Найдите площадь боковой поверхности
пирамиды.
9.. В правильной треугольной пирамиде
SABC точка K – середина ребра BC, S – вершина. Известно, что
AB = 6, а длина отрезка SK = 7. Найдите площадь боковой поверхности
пирамиды.
ЗАДАНИЕ 16
Вариант 3
1. В прямоугольном параллелепипеде АВСDA1B1C1D1 AB=5, AD=√3, CC1=2√2. Найдите длину диагонали параллелепипеда АС1.
2. Конус вписан в шар. Объём шара равен 14. Найдите объём конуса, если известно, что радиус основания конуса равен радиусу шара.
 3.
В основании пирамиды SABC лежит правильный треугольник АВС со
стороной 2, а боковое ребро SA перпендикулярно основанию и равно
5√3. Найдите объём пирамиды SABC.
3.
В основании пирамиды SABC лежит правильный треугольник АВС со
стороной 2, а боковое ребро SA перпендикулярно основанию и равно
5√3. Найдите объём пирамиды SABC.
 4. Сторона основания
правильной треугольной призмы АВСА1В1С1 равна 5, а высота этой призмы
равна √3. Найдите объем призмы АВСА1В1С1.
4. Сторона основания
правильной треугольной призмы АВСА1В1С1 равна 5, а высота этой призмы
равна √3. Найдите объем призмы АВСА1В1С1.
 5. Даны два шара с радиусами
6 и 3. Во сколько раз площадь поверхности большего шара больше площади
поверхности меньшего?
5. Даны два шара с радиусами
6 и 3. Во сколько раз площадь поверхности большего шара больше площади
поверхности меньшего?
 6. Даны два шара с
радиусами 6 и 1. Во сколько раз объём большего шара больше объёма меньшего?
6. Даны два шара с
радиусами 6 и 1. Во сколько раз объём большего шара больше объёма меньшего?
7. Даны два конуса. Радиус основания и образующая первого конуса равны, соответственно, 6 и 8, а второго — 4 и 8. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?
 8.
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой
равна 4, а боковое ребро равно √17.
8.
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой
равна 4, а боковое ребро равно √17.
9. Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
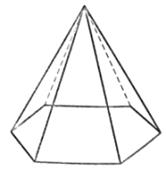 10. Стороны
основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13.
Найдите площадь боковой поверхности пирамиды.
10. Стороны
основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13.
Найдите площадь боковой поверхности пирамиды.
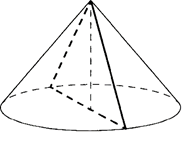 11. Площадь
основания конуса равна 16π, высота — 12. Найдите площадь осевого сечения
конуса.
11. Площадь
основания конуса равна 16π, высота — 12. Найдите площадь осевого сечения
конуса.
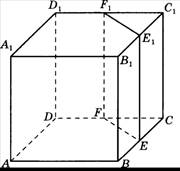
12. В кубе
ABCDA1B1C1D1 точки Е, F, Е1 и F1 являются серединами рёбер ВС,
DC, В1С1 и D1C1 соответственно. Объём треугольной призмы, отсекаемой
от куба плоскостью EFF1, равен 29. Найдите объём куба.
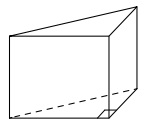
13. В основании прямой призмы лежит правильный треугольник со стороной, равной 6. Высота ее равна √3/24. Найти объем призмы.
 14. В основании
прямой призмы лежит прямоугольный треугольник, один из катетов которого равен
4, а гипотенуза равна 4·√2. Найдите объём призмы, если её высота равна 3.
14. В основании
прямой призмы лежит прямоугольный треугольник, один из катетов которого равен
4, а гипотенуза равна 4·√2. Найдите объём призмы, если её высота равна 3.
15. В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра АB, AD и диагональ AB1равны соответственно 6, 2 и √45. Найдите объём параллелепипеда ABCDA1B1C1D1.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.