Подготовка к ОГЭ

Разберём задачи, которые могут быть на экзамене из курса

 геометрии 7 класса.

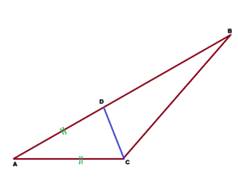
Задача 1.  В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А  треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Решение: Из треугольника ADC видно, что он равнобедренный, поскольку 2 боковые стороны его равны.
А в равнобедренном треугольнике углы при основании равны.
Значит, угол ADC равен углу АСВ.
Но сумма внутренних углов треугольника равна 180°.
Отсюда, сумма двух углов при основании равна 180-16=164°.
Углы, как мы уже сказали, равны. Поэтому, каждый из них равен 164:2 = 82°.
Угол АСВ по условию равен 134°.
А если внутри угла провести луч, то он разделит угол на 2 угла, сумма градусных мер которых будет равна градусной мере первоначального угла.
Т.е. Угол АСВ равен сумме углов АCD и DCB.
Отсюда, угол DCB равен 134 — 82 = 52°.
Ответ: угол DCB равен 52°.

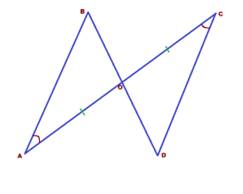Задача 2. Два отрезка АС  и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Доказательство: В искомых треугольниках есть по одной равной стороне и одному равному углу. Значит, согласно признакам равенства треугольников, нам необходимо ещё либо по одной равной стороне, либо по одному равному углу.
Стороны как-то не проглядываются, а вот по равному углу можно ещё найти.
Углы АОВ и DOC  — вертикальные.
А вертикальные углы, как мы знаем, равны.
В каждом из треугольников мы имеем по равной стороне и двум равным углам, прилежащим к ней.
Треугольники равны по 2 признаку.

Скачано с www.znanio.ru