Среди огромного количества самых разнообразных книг по геометрии начиная от школьных учебников и заканчивая олимпиадными сборниками сложно объединить известные или мало известные нам свойства геометрических фигур и их элементов. Поэтому у нас появилось желание поглубже и повнимательней рассмотреть, доказать иногда очевидное, иногда поразительное, а иногда просто фантастические, изумительные свойства привычных нам фигур.

         И мы с надеждой отмечаем, что знание этих свойств, многие из которых составляют содержания известных теорем, а другие еще не попали в школьные учебники, являются вполне достаточным условием для решения задач по планиметрии.

Мы исследовали вписанные четырёхугольники и  хотим вам предложить следующие факты о вписанных четырехугольниках:

1.  Критерии вписанных четырехугольников

2.  Достроение треугольника до вписанного четырехугольника

3. Метрические соотношения для вписанных четырехугольников

4.  Интересные задачи

1. Критерии вписанного четырехугольника.

Первый критерий вписанного четырехугольника связан с серединными перпендикулярами к его сторонам и диагоналям.

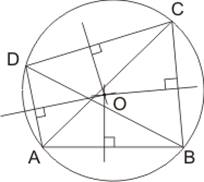Так как центр описанной около четырехугольника окружности равноудален от его вершин, то он принадлежит серединным перпендикулярам к его сторонам и диагоналям. Обратно, если серединные перпендикуляры к трем сторонам четырехугольника пересекаются в одной точке, то эта точка будет равноудалена от его вершин, и поэтому будет являться центром описанной около него окружности.

         Итак, для того чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы серединные перпендикуляры к трем его сторонам пересекались в одной точке.

Второй критерий вписанного четырехугольника связан с его углами

Теорема. Для того чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы сумма его противоположных углов была равна  (т.е. сумы его противоположных углов были равны).

         Необходимость этого условия очевидна: сумма углов А и С вписанного четырехугольника ABCD измеряется полусуммой дуг BCD и BAD, составляющих полную окружность, и потому равна .

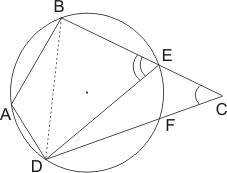
Достаточность. Пусть . Тогда эти углы не могут быть оба острыми или оба тупыми. Для определения будем считать, что . Опишем около треугольника ABD окружность и докажем что точка С ей принадлежит. Для этого необходимо отвергнуть два возможных предположения: 1) точка С находится вне окружности, 2) точка С лежит внутри окружности. При первом предположении и условии  стороны BC и DC пересекают окружность вторично в своих внутренних точках E и F. тогда для вписанного четырехугольника ABED по необходимому условию будет . По теореме о внешнем угле треугольника  и потому , что противоречит условию. Второе предположение аналогично приводит к противоречию . Доказательство закончено.

2. Достроение треугольника до вписанного четырехугольника

Мы знаем, что вокруг любого треугольника можно описать окружность. Рассмотрим несколько условий определяющих точку К, как четвертую точку четырехугольника АВСК, который можно вписать в окружность.

№ 1

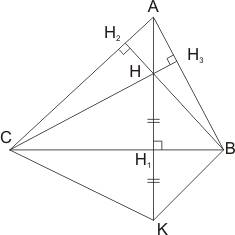
Если К - точка, симметричная ортоцентру Н относительно одной из сторон треугольника АВС, то К лежит на описанной вокруг треугольника АВС окружности, значит вокруг четырехугольника АВКС можно описать окружность.

Доказательство

Пусть высоты  AH₁ , BH₂ , CH₃ пересекаются в точке Н, а К - точка симметричная Н относительно стороны ВС. В четырехугольнике  AH₂HH₃ рассмотрим угол H₂HH₃. Он равняется . Тогда и вертикальный с ним . Легко показать (например, с помощью симметричности), что и . Тогда сумма  и   ровняется . Следовательно, вокруг четырехугольника АВКС можно описать окружность.

№ 2

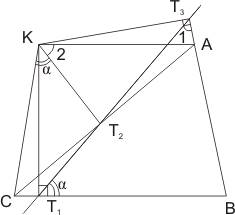Если перпендикуляры,  проведенные из точки К к сторонам , принадлежат одной прямой (задача опирается на прямую Симсона), то К лежит на описанной вокруг треугольника АВС окружности, значит вокруг четырехугольника АВСК можно описать окружность.

Доказательство

Пусть основания данных перпендикуляров – точки Т₁, Т₂, Т₃, и Т₁Т₂Т₃- одна прямая. Точки С, Т₁, Т₂, К лежат на одной окружности с диаметром  КС. Пусть , тогда , а смежный с ним . Вокруг четырехугольника  можно описать окружность и (как вписанные и опирающиеся на одну дугу углы). Но  (из ). Следовательно,  . Тогда . У четырехугольника АВСК сумма противоположных углов равна , следовательно, вокруг него можно описать окружность.

№ 3

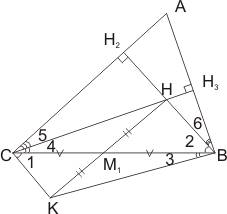Если К – точка, симметричная ортоцентру Н относительно середины какой-либо стороны , то К лежит на описанной вокруг треугольника АВС окружности, значит вокруг четырехугольника АВКС можно описать окружность.

Доказательство

Пусть М – середина стороны ВС, а точка К симметрична ортоцентру Н относительно М.

Четырехугольник ВНСК – параллелограмм (его диагонали точкой пересечения делятся пополам). Тогда  (т.к.  из ), а  ( из ). (из и ). Таким образом,  

. Следовательно, вокруг четырехугольника АВКС можно описать окружность.

№ 4

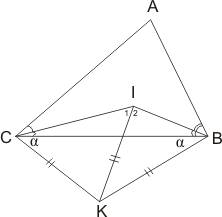Если К – центр окружности описанной около  (I – инцентр, точка пересечения биссектрис ), то К лежит на описанной вокруг треугольника АВС окружности, значит вокруг четырехугольника АВКС можно описать окружность.

Доказательство

Легко показать, что , т.е. он тупой, следовательно точка К находится вне треугольника. Пусть . Пусть также . Тогда , а . Кроме того, . Следовательно, , откуда  и . Найдем сумму углов АСК  и АВК: . Следовательно, вокруг четырехугольника АВКС можно описать окружность.

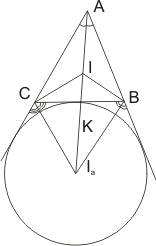№ 5

Если К – середина отрезка который соединяет инцентр с центром какой-нибудь вневписанной окружности , то К лежит на описанной вокруг треугольника АВС окружности, значит вокруг четырехугольника АВКС можно описать окружность.

Доказательство

Пусть одна из вневписанных окружностей с центром  касается ВС и продолжений сторон АС и АВ, а точка К – середина отрезка . Известно что центр вневписанной окружности – точка пересечения 2-х внешних и 1 внутренней биссектрисы. Тогда (углы между биссектрисами смежных углов). Следовательно, точки , В, С, принадлежат одному кругу с диаметром , и с центром в точке К. Задача сводится к задаче 4.

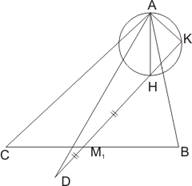№ 6

Если прямая  пересекает окружность, построенную на АН как на диаметре, в точке К, то К лежит на описанной вокруг треугольника АВС окружности, значит вокруг четырехугольника АКВС можно описать окружность.

Доказательство

Продолжим  до точки D , так чтобы . Согласно задаче 3 точки А, В, С, D принадлежат одной окружности диаметром AD. Но  (т.к.– как вписанный угол, упирающийся на диаметр АН маленького круга). Т.к. AD диаметр, описанной вокруг окружности и , то точка К лежит на описанной вокруг  окружности.

№ 7

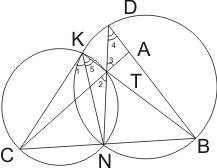Через любую точку N принадлежащую стороне ВС проведем прямую, пересекающую сторону АС в точке Т, а продолжение стороны ВА в точке D. Окружности, описанные около треугольников BDN и CTN, пересекаются в точке К. И эта точка К будет лежать на описанной вокруг треугольника АВС окружности, значит вокруг четырехугольника АВСК можно описать окружность.

Доказательство

Пусть  – как вписанные, опирающиеся на одну дугу углы.  (вертикальные). – как вписанные, опирающиеся на одну дугу углы. Тогда  – внешний угол для . Но и . Следовательно, точки В, А, К, С лежат на одной окружности.

№ 8

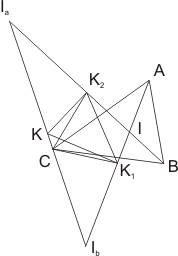Если К – середина отрезка, который соединяет центры 2-х вневписанных окружностей, то К лежит на описанной вокруг треугольника АВС окружности, значит вокруг четырехугольника АВСК можно описать окружность.

Доказательство

Пусть К- середина отрезка  ( касается ВС и продолжений АС и АВ, а  касается АС и продолжений АВ и ВС). Также пусть  и  – середины  и  соответственно. Тогда  и . Кроме того,  (средняя линия ), а  (средняя линия ). Тогда , по 3-м сторонам, и . Следовательно, точки , , , К принадлежат одной окружности. Но точки, ,  принадлежат окружности, описанному около (задача 5). Следовательно, точка К принадлежит описанной вокруг  окружности.

№ 9

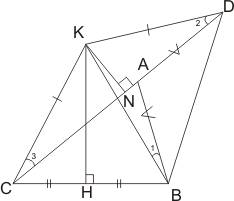
Если серединный перпендикуляр к ВС и перпендикуляр, проходящий через точку N – середину ломаной ВАС – пересекаются в точке К, то К лежит на описанной вокруг треугольника АВС окружности, значит вокруг четырехугольника АВСК можно описать окружность.

Доказательство

Продолжим СА на отрезок AD=AB. Тогда CN=ND ( согласно условию) и CK=DK.

Но СК=ВК ( KM₁ - серединный перпендикуляр к ВС). Имеем: СК=ВК=КD.

Треугольники BAD и BKD – равнобедренные с одинаковой основой BD. Тогда . Но  (- равнобедренный). Тогда , что означает, что точки В, С, К, А принадлежат одной окружности.

№ 10

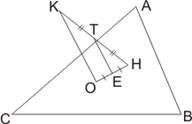Если Т – точка принадлежащая окружности Эйлера треугольника АВС. А К – точка, симметричная ортоцентра Н относительно Т, то К лежит на описанной вокруг треугольника АВС окружности, значит вокруг четырехугольника АВСК можно описать окружность. Утверждение справедливо в обратную сторону: если вокруг четырехугольника АВСК можно описать окружность, то точка К будет симметрична ортоцентру треугольника АВС относительно какой-то точки окружности Эйлера.

Доказательство

Центр окружности Эйлера – середина отрезка ОН, а ее радиус вдвое меньше радиуса описанной около окружности. Пусть Е – середина ОН – центр окружности Эйлера треугольника АВС. Т – любая точка этой окружности и . Т.к. К симметрична Н относительно Т, то НТ=ТК. Тогда ЕТ – средняя линия в треугольнике ОКН и . Следовательно, ОК=R. Т.е. точка К принадлежит окружности описанной вокруг .

№11

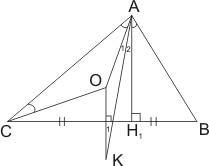Пусть дан произвольный треугольник ABC. Пусть K – точка пересечения биссектрисы угла C и серединного перпендикуляра к стороне AB. Докажем, что четырёхугольник ABCK – вписанный.

Доказательство

Пусть биссектриса  пересекает окружность в точке М. Тогда М-середина дуги АМВ. Значит, серединный перпендикуляр к AB пересекает дугу AMB в точке M, в этой же точке он пересекается и с биссектрисой, то есть точка их пересечения лежит описанной вокруг  окружности  все эти точки лежат на одной окружности.

3. Метрические соотношения для вписанных четырехугольников

1. Выразим углы четырёхугольника через его стороны.

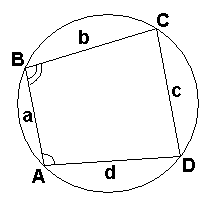Выразим диагональ  по теореме косинусов из  и :

,

, так как .

Выразим :

.

Проведя аналогичные рассуждения для треугольников  и , получим: .

2. Выразим площадь четырехугольника через радиус описанной вокруг него окружности, углы четырёхугольника и угол между диагоналями.

Решение:

По теореме синусов , . Аналогично, . Но площадь ABCD равна , где  - угол между диагоналями. Тогда .

3. Выразим площадь четырёхугольника через его стороны

(т. Брахмагупты).

 Для этого воспользуемся результатами предыдущего пункта. Зная , найдём :

Площадь  можно найти как , а  - как . Тогда площадь  будет равна . Подставив в это выражение , получим .

Но если четырёхугольник не только вписан в окружность, но и описан вокруг другой, это выражение можно упростить:

, откуда

И тогда .

4. Выразим радиус описанной вокруг четырёхугольника окружности через его стороны.

Для произвольного треугольника всегда выполняется равенство , то есть . Заметим, что радиусы окружностей, описанных вокруг треугольников ABC, CDA и четырёхугольника ABCD равны. Тогда  и  откуда .

Выразив AC по теореме косинусов из треугольников ABC и ACD и подставив в данное равенство, получим: .

Когда-то на олимпиаде была задача Игоря Константиновича Жука, она звучала примерно так: « У Васи и у Пети есть по 4 одинаковых наборов отрезков разной длины. Вася составил вписанный четырехугольник, и Петя составил вписанный четырехугольник. Эти  четырехугольники оказались неравными. Доказать, что радиусы описанных вокруг этих четырехугольников окружностей равны ».

С помощью вышеуказанной формулы эту задачу легко решить.

5. Выразим углы вписанного четырёхугольника через углы между продолжениями его сторон.

Пусть , . ABCD – вписанный четырёхугольник, значит , . Далее , как внешние углы для треугольника BQC, , из треугольника PCD.

Решая систему:  

Получаем:

 ,  ,  , .

4.Интересные задачи

1. Теперь рассмотрим биссектрисы углов M и N. Пусть они пересекаются в точке O. Докажем что они перпендикулярны и при пересечении со сторонами четырёхугольника образуют ромб:

. Тогда . , .

. Но тогда и  и биссектрисы перпендикулярны.

Рассмотрим  и :

MO - общая сторона, = (MO - биссектриса)  =

RO=OT.

Аналогично из  и  получаем, что PO=OS.

Значит, в четырехугольнике PRST диагонали пересекаются под прямым углом и делятся точкой пересечения пополам. Следовательно, четырехугольник PRST – ромб.

2. Рассмотрим, за какое наименьшее количество разрезаний по прямым линиям вписанный четырёхугольник можно разделить на части, из которых можно составить прямоугольник. Это задача известна как задача Гольберга.

Возьмём на отрезке точку M на наименьшей стороне AB такую, что отрезок MQ, параллельный CD, имел такую же длину, как и BM. Проведём перпендикуляр QP к CD. Из точки F – середины QD проведём отрезок FT, параллельный BC, где точка T лежит на CD. Тогда из полученных фигур можно будет составить прямоугольник.

Доказательство того, что полученная фигура является четырёхугольником очевидно: находим сумму смежных углов, она действительно будет равна .

Таким образом мы доказали, что любой вписанный четырёхугольник можно не более чем за три разрезания разбить на фигуры, из которых можно составить прямоугольник.

3. Докажем, что если одна из диагоналей четырёхугольника является диаметром описанной окружности, то проекции противоположных сторон на другую диагональ равны.

Пусть BD – диаметр. Тогда . , как опирающиеся на одну и ту же дугу. Тогда треугольники ABK и DBC подобны, .

 Аналогично  из подобия треугольников CDL и BDA имеем: . Заметим, что AK=CL.

4. Рассмотрим две параболы с взаимно перпендикулярными осями. Четыре точки их пересечения будут являться вершинами вписанного четырёхугольника. Докажем это:

Введём систему координат с началом координат в вершине одной из парабол. Тогда уравнение первой параболы будет иметь вид , второй - .

Подставив вместо y  получим ,

 .

Представим это в виде уравнения окружности , тем самым доказав, что все точки лежат на одной окружности.

При , получим

,

 .

То есть все четыре точки лежат на окружности, которая задаётся уравнением

Список используемой литературы:

1. Кокстер Г.С.М., Грейтцер С.Л. Новые встречи с геометрией.

    М.: наука, гл. ред. физ.-мат.лит.,1978.

2. Сивашинский И.Х. Задачник по элементарной математике.

    М.: наука, гл.ред. физ.-мат.лит.,1966.

3. Шарыгин И.Ф. Задачи по геометрии. Планиметрия. 

    М.: наука, гл.ред. физ.-мат.лит.,1986.

4. Прасолов В.В. Задачи по планиметрии.

    М.: наука, гл.ред. физ.-мат.лит.,1995.