
 Подготовка учащихся к ОГЭ по математике.
Подготовка учащихся к ОГЭ по математике.
КРИТЕРИИ ОЦЕНИВАНИЯ И АНАЛИЗ ОШИБОК.
Выполнил: Зилотина О.М.
учитель математики МБОУ СОШ №7 г.Новосибирск, 2022
 НАЗНАЧЕНИЕ ЭКЗАМЕНАЦИОННОЙ РАБОТЫ
НАЗНАЧЕНИЕ ЭКЗАМЕНАЦИОННОЙ РАБОТЫ
❖ ОГЭ представляет собой форму государственной итоговой аттестации
❖ Цель: определить соответствие результатов освоения обучающимися основных образовательных программ основного общего образования соответствующим требованиям федерального государственного образовательного стандарта
❖ ОГЭ проводится в соответствии с законом РФ от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации».
 РЕЗУЛЬТАТОМ ОСВОЕНИЯ ООП ООО ДОЛЖНА
СТАТЬ МАТЕМАТИЧЕСКАЯ КОМПЕТЕНТНОСТЬ ВЫПУСКНИКОВ, Т.Е. ОНИ ДОЛЖНЫ:
РЕЗУЛЬТАТОМ ОСВОЕНИЯ ООП ООО ДОЛЖНА
СТАТЬ МАТЕМАТИЧЕСКАЯ КОМПЕТЕНТНОСТЬ ВЫПУСКНИКОВ, Т.Е. ОНИ ДОЛЖНЫ:
❖ овладеть специфическими для математики знаниями и видами деятельности;
❖ научиться преобразованию знания и его применению в учебных и внеучебных ситуациях;
❖ сформировать качества, присущие математическому мышлению;
❖ овладеть математической терминологией, ключевыми понятиями, методами и приемами.
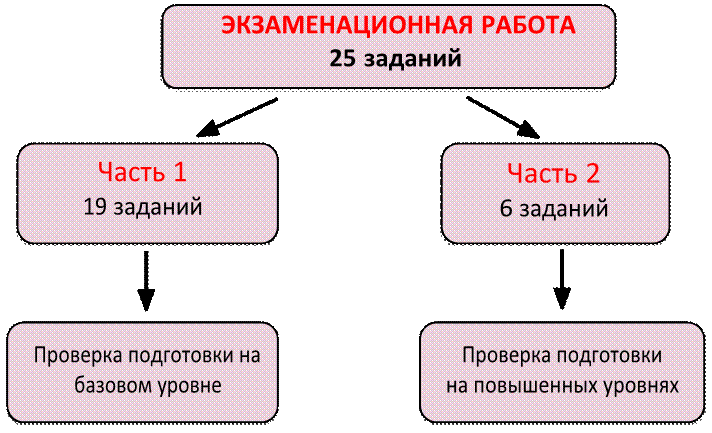
 Характеристика экзаменационной
работы. Часть 1
Характеристика экзаменационной
работы. Часть 1
❖ владение основными алгоритмами;
❖ знание и понимание ключевых элементов содержания (понятий, свойств, приёмов);
❖ умение пользоваться математической записью;
❖ применять знания к решению математических задач, не сводящихся к прямому применению алгоритма;
❖ применять математические знания в простейших практических ситуациях.
 РАСПРЕДЕЛЕНИЕ
ЗАДАНИЙ ЧАСТИ 1
РАСПРЕДЕЛЕНИЕ
ЗАДАНИЙ ЧАСТИ 1 ПО ФОРМЕ ОТВЕТА
❖ 2 задания с кратким ответом в виде одной цифры, которая соответствует номеру правильного ответа;
❖ 17 заданий с кратким ответом в виде числа, последовательности цифр
 Характеристика экзаменационной работы.
Характеристика экзаменационной работы.
Часть 2
Цель: проверка владения материалом на повышенных уровнях.
Основное назначение :
● дифференцировать хорошо успевающих школьников по уровням подготовки;
● выявить наиболее подготовленную часть выпускников, составляющую потенциальный контингент профильных классов.
 Задания части 2 направлены на
проверку таких качеств математической подготовки выпускников, как:
Задания части 2 направлены на
проверку таких качеств математической подготовки выпускников, как:
● уверенное владение формально-оперативным алгебраическим аппаратом;
● умение решить комплексную задачу, включающую в себя знания из разных тем курса алгебры;
● умение решить планиметрическую задачу, применяя различные теоретические знания курса геометрии;
● умение математически грамотно и ясно записать решение, приводя при этом необходимые пояснения и обоснования;
● владение широким спектром приёмов и способов рассуждений.
 Распределение
заданий части 2 по разделам содержания Уравнения и неравенства Функции и графики Геометрия
Распределение
заданий части 2 по разделам содержания Уравнения и неравенства Функции и графики Геометрия
● №20 – упрощение алгебраических выражений, решение уравнений, неравенств и их систем,
●

№21 – решение текстовой задачи:
моделирование реальных ситуаций на языке алгебры; составление выражения,
уравнения и неравенства по условию задачи; исследование построенных моделей с
использованием аппарата алгебры,
● №22 – построение и чтение графика функции,
● №23 – задача на вычисление по геометрии,
● №24 – задача по геометрии на доказательство,
● №25 – геометрическая задача по геометрии высокого уровня сложности.
 ОБЩИЕ
ТРЕБОВАНИЯ К РЕШЕНИЮ И ОФОРМЛЕНИЮ ЗАДАНИЙ ЧАСТИ 2
ОБЩИЕ
ТРЕБОВАНИЯ К РЕШЕНИЮ И ОФОРМЛЕНИЮ ЗАДАНИЙ ЧАСТИ 2 ● Возможны различные способы и записи развёрнутого решения. Главное требование – решение должно быть математически грамотным, из него должен быть понятен ход рассуждений экзаменуемого. В остальном (метод, форма записи) решение может быть произвольным. Полнота и обоснованность рассуждений оцениваются независимо от выбранного метода решения.
● При решении задачи можно использовать без доказательств и ссылок математические факты, содержащиеся в учебниках и учебных пособиях, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ среднего общего образования.
● Каждый этап решения учащегося должен быть аргументирован.
● Утверждения в решении заданий должны иметь однозначную трактовку.
● Критерии не являются эталоном оформления решения задачи, они указывают ключевые моменты решения для эксперта.
● Критерии разработаны применительно к одному из возможных решений, а именно, к тому, которое описано в рекомендациях.
●

При наличии в работах учащихся
других решений критерии вырабатываются предметной комиссией с учетом описанного
общего подхода.
● Решения учащихся могут содержать недочеты, не отраженные в критериях, но которые, тем не менее, позволяют оценить результат выполнения задания положительно (со снятием одного балла). В подобных случаях решение о том, как квалифицировать такой недочет, принимает предметная комиссия.
 ОБЩИЕ
ПОДХОДЫ К ПРОВЕРКЕ И ОЦЕНКЕ ЗАДАНИЙ С РАЗВЕРНУТЫМ ОТВЕТОМ ЧАСТИ 2
ОБЩИЕ
ПОДХОДЫ К ПРОВЕРКЕ И ОЦЕНКЕ ЗАДАНИЙ С РАЗВЕРНУТЫМ ОТВЕТОМ ЧАСТИ 2● Если решение ученика удовлетворяет всем требованиям, то ему выставляется полный балл 2.
● Если в решении допущена ошибка, не принципиального характера (вычислительная, погрешность в терминологии или символике и др.), не влияющая на правильность общего хода решения (даже при неверном ответе) и позволяющая, несмотря на ее наличие, сделать вывод о владении материалом, то учащемуся засчитывается сниженный балл 1.
● В других случаях выставляется 0 баллов.
 ОБЩИЕ
ПОДХОДЫ К ПРОВЕРКЕ И ОЦЕНКЕ ЗАДАНИЙ С РАЗВЕРНУТЫМ ОТВЕТОМ ЧАСТИ 2
ОБЩИЕ
ПОДХОДЫ К ПРОВЕРКЕ И ОЦЕНКЕ ЗАДАНИЙ С РАЗВЕРНУТЫМ ОТВЕТОМ ЧАСТИ 2 ● Ошибка вычислительного характера или вычислительная ошибка – это ошибка, допущенная при выполнении сложения, вычитания, умножения и деления.
● 1 балл допускается ставить в тех случаях, когда единственная вычислительная ошибка стала причиной того, что неверен ответ.
● К вычислительным ошибкам не относятся ошибки в формулах при решении квадратного уравнения, действиях с числами с разными знаками, упрощении выражений со степенями и корнями и т.д.
 ОБЩИЕ
ПОДХОДЫ К ПРОВЕРКЕ И ОЦЕНКЕ ЗАДАНИЙ С РАЗВЕРНУТЫМ ОТВЕТОМ ЧАСТИ 2
ОБЩИЕ
ПОДХОДЫ К ПРОВЕРКЕ И ОЦЕНКЕ ЗАДАНИЙ С РАЗВЕРНУТЫМ ОТВЕТОМ ЧАСТИ 2● Если учащийся при решении задачи использует без пояснений данные, которых нет в условии, то выставляется 0 баллов.
● Лаконичное решение, не содержащее неверных утверждений, все выкладки которого правильны, рассматривается как решение без недочетов.
● При проверке и оценке экзаменационных работ не учитываются особенности почерка и наличие грамматических ошибок в работах учащихся, если они не искажают сути ответа.
 Комментарии к критериям по
заданию № 20
Комментарии к критериям по
заданию № 20● Метод решения может быть любой: используя деление многочлена на многочлен; раскрытие скобок; составление совокупностей и систем и др.
● Ответ может быть записан в виде равенств; перечислением корней; множеством (в фигурных скобках).
● При графическом решении неравенства должна быть записана рассматриваемая функция.
● При использовании метода интервалов точки должны быть найдены (а не просто обозначены на чертеже).
● При решении квадратного уравнения с использованием формул дискриминанта и корней должны присутствовать записи нахождения числового ответа, а не просто ответ.
 Комментарии
к критериям по заданию № 20
Комментарии
к критериям по заданию № 20Балл снижается на 1, если:
● Имеется неточное использование символики при записи ответа (круглые, квадратные скобки);
● ИЛИ - неточное использование символов систем и совокупностей, если это не привело к неверному ответу;
● ИЛИ - только одна вычислительная ошибка или описка.
Решение оценивается 0 баллов, если:
● Нарушен ход решения;
● ИЛИ – найдены не все корни;
● ИЛИ – ошибки в применении формул;
● ИЛИ – более одной вычислительной ошибки или описки и т.д.

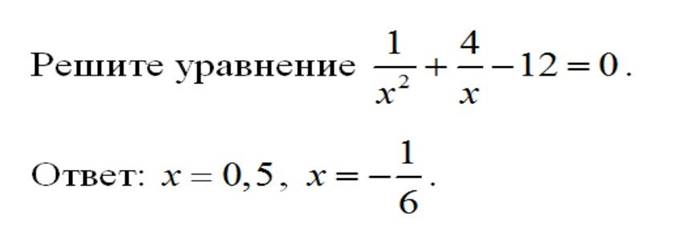



 Комментарии к критериям по
заданию № 21
Комментарии к критериям по
заданию № 21● Должны присутствовать все необходимые действия с данными задачи, записанные в виде нескольких действий с единицами измерения величин, или в виде числового выражения, или уравнения с пояснением к нему (пояснение может быть заменено таблицей или чертежом).
● Переход к уравнению должен быть обоснован, в таблице или на чертеже, в пояснениях должны присутствовать все выражения, используемые при составлении уравнения.
● Графическое решение должно быть обосновано.
● Проверка ОДЗ или проверка корней (оценка величин) обязательна!
Балл снижается на 1, если:
● Уравнение (выражение) составлено правильно, но при его решении допущена одна вычислительная ошибка или описка, с её учётом решение доведено до ответа.
● ИЛИ – Не найдена ОДЗ или нет проверки корней (оценки величин), если это не привело к неверному результату.
● ИЛИ - Нет единиц измерения в некоторых действиях.
● ИЛИ - Графическое решение приведено без достаточного обоснования Решение оценивается 0 баллов, если:
● Нет обоснования к уравнению.
● ИЛИ - Нет нигде указания единиц измерения.
● ИЛИ - Решение не доведено до конца.
● ИЛИ – Имеется более одной вычислительной ошибки или описки.
● ИЛИ - Найдена не та величина и т.п.

|
Баллы |
Критерии |
|
2 |
График построен верно, верно найдены значения параметра |
|
1 |
График построен верно, но искомые значения параметра найдены неверно или не найдены |
|
0 |
Решение не соответствует ни одному из критериев, перечисленных выше |
● Основным условием положительной оценки за решение задания является верное построение графика.
● Верное построение графика включает в себя: масштаб, содержательную таблицу значений (или записи координат точек) или объяснение построения, выколотая точка обозначена в соответствии с ее координатами.
● Функция должна быть названа верно, найдена область определения, объяснено, как выглядит график.
● Точка «склейки» графиков должна быть отражена в таблицах обеих функций.
● Значения параметра могут быть записаны в виде промежутков или неравенств; знак объединения может быть заменен точкой с запятой, но должно быть обоснование ответа (в том числе можно и графически).
Балл снижается на 1, если:
● При нахождении параметра допущена вычислительная ошибка или описка, с ее учетом решение доведено до конца, график построен верно.
● ИЛИ - Нет обоснования нахождения параметра.
● ИЛИ - Допущена вычислительная ошибка или описка при преобразовании выражения, с ее учетом решение доведено до конца.
Решение оценивается 0 баллов, если:
● График построен неверно: неверное направление ветвей или неверно найдены координаты вершины, не найдены координаты точек и не обозначены их координаты на графике и т.п.
● ИЛИ – Имеется более одной вычислительной ошибки или описки.
● Используемые свойства должны быть зафиксированы в явном виде;
●

Все используемые в решении
фигуры (особенно, треугольники) должны быть названы;
● Чертеж – неотъемлемая часть решения.
В качестве объяснения может выступать формула или словесное описание. Балл снижается на 1, если:
● Не обосновано, почему фигура (треугольник) именно такого вида.
● ИЛИ – дано неполное объяснение при использовании теорем.
● ИЛИ - не обоснован переход к алгебраической или арифметической модели.
● ИЛИ – допущена только одна вычислительная ошибка или описка.
Решение оценивается 0 баллов, если:
● Неверно составлено выражение, или какое-либо из действий, или уравнение.
● ИЛИ - Нет никаких обоснований.
● ИЛИ – допущено более одной вычислительной ошибки или описки.
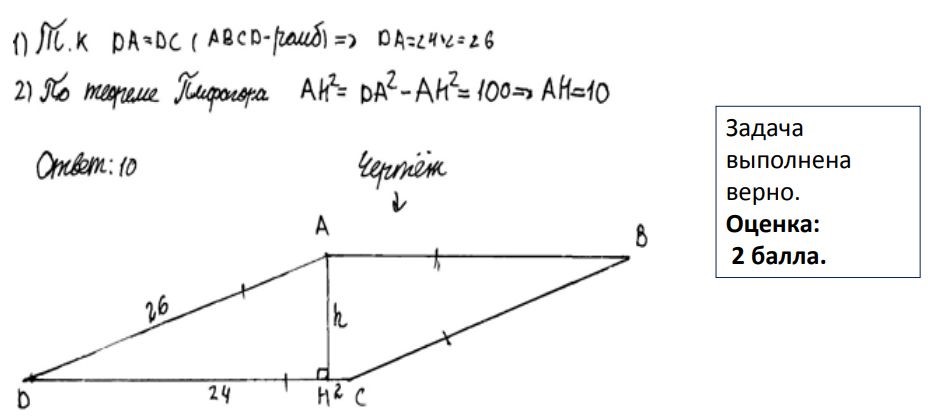
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла.

Вычислите длину высоты ромба.
Ответ: 10.


|
Баллы |
Критерии |
|
2 |
Доказательство верное, все шаги обоснованы |
|
1 |
Доказательство в целом верное, но содержит неточности |
|
0 |
Решение не соответствует ни одному из критериев, перечисленных выше |
На 2 балла:
● Все шаги должны быть обоснованы, получены верные следствия.
Балл снижается на 1, если:
● Имеются неточности в обозначении геометрических фигур (углов, четырехугольников и т.п.).
● ИЛИ – неточности в ссылках на утверждения. Решение оценивается 0 баллов, если:
● Отсутствует хотя бы один шаг в доказательстве.
● ИЛИ - Доказательство содержит хотя бы одно неверное логическое следствие.
|
Баллы |
Критерии |
|
2 |
Ход решения верный, получен верный ответ |
|
1 |
Ход решения верный, все его шаги присутствуют, но допущена описка или ошибка вычислительного характера |
|
0 |
Решение не соответствует ни одному из критериев, перечисленных выше |
На 2 балла:
● Все шаги решения должны быть выполнены правильно. Шаги группируются в две части:
первая часть – доказательная, вторая – вычислительная.
Балл снижается на 1, если:
● Доказательство в целом верное, но содержит неточности (в обозначениях или ссылках на утверждения), при этом получен верный ответ.
● ИЛИ - Доказательная часть не содержит никаких погрешностей: ни в выводах, ни в их обоснованиях, уравнение составлено верно, но есть вычислительная ошибка или описка в решении.
Решение оценивается 0 баллов, если:
● Доказательная часть содержит хотя бы одно неверное логическое следствие.
● ИЛИ – имеются ошибки в преобразованиях выражения.
Общие результаты ОГЭ по математике- 2022
в Новосибирской области
(на 31.08.2022)
|
|
Число участников ОГЭ |
% от общего числа участников |
|
Муниципальные районы |
9701 |
34,87 |
|
Городские округа (г. Бердск, г. Искитим, р.п. Кольцово, г. Обь) |
2304 |
8,28 |
|
г. Новосибирск |
15817 |
56,85 |
|
Новосибирская область |
27822 |
100 |
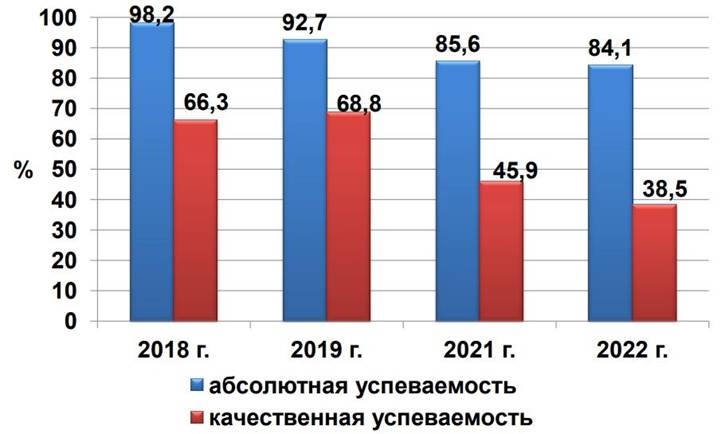
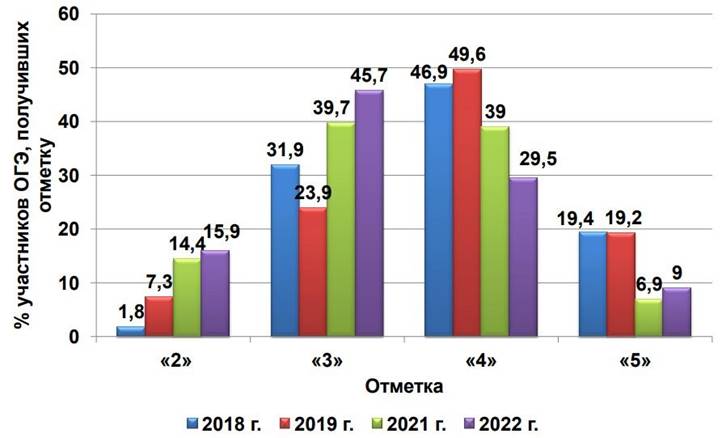
УСПЕВАЕМОСТЬ ПО МАТЕМАТИКЕ ПО ОГЭ В НСО В 2018-2022 ГГ.
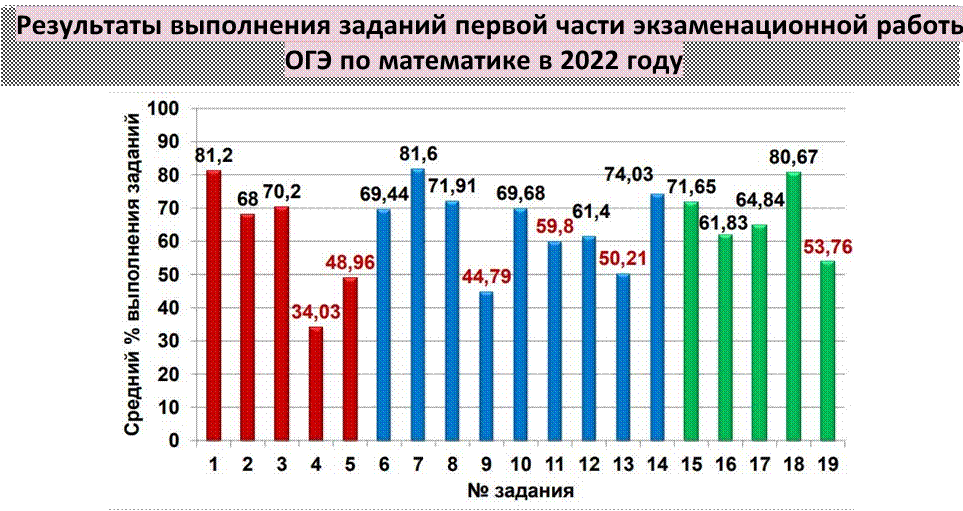

 Решаемость заданий части 1 по разделам содержания
модуля «Геометрия» в сравнении за 3 года
Решаемость заданий части 1 по разделам содержания
модуля «Геометрия» в сравнении за 3 года
|
|
2019 |
2021 |
2022 |
|
|
% |
% |
% |
|
Треугольник |
68,7 |
52,72 |
71,64 |
|
Многоугольники |
56,7 |
77,8 |
64,84 |
|
Окружность и круг |
75,2 |
59,02 |
61,83 |
|
Измерение геометрических величин |
84,3 |
83,07 |
80,67 |
|
Геометрические фигуры и их свойства |
80,6 |
80,6 |
53,76 |
|
По модулю «Геометрия» |
75 |
68,2 |
66,55 |
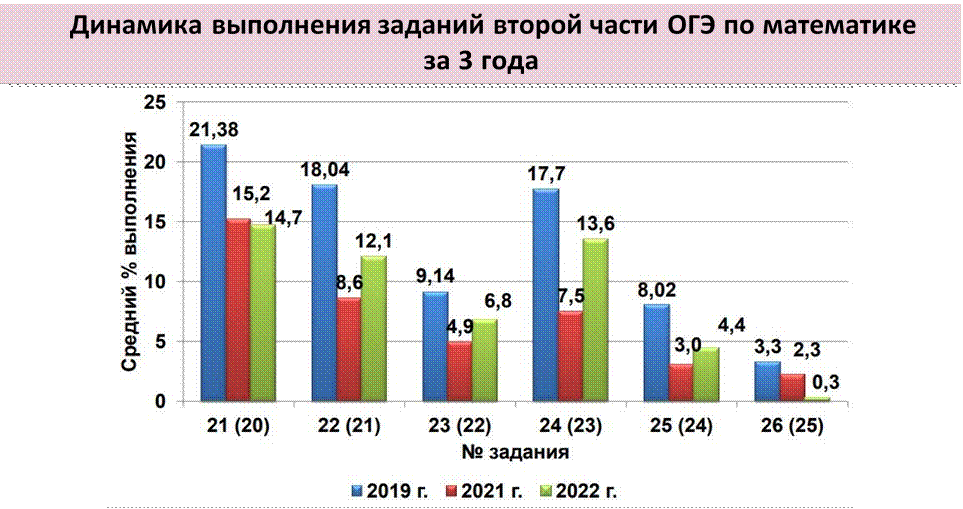
 Решаемость заданий части 1 по разделам содержания
модуля «Геометрия» в сравнении за 3 года
Решаемость заданий части 1 по разделам содержания
модуля «Геометрия» в сравнении за 3 года
|
№ |
АЛГЕБРА |
|
ГЕОМЕТРИЯ |
|||
|
20 |
21 |
22 |
23 |
24 |
25 |
|
|
0 баллов |
85,31 |
87,9 |
93,16 |
86,45 |
95,57 |
99,69 |
|
1 балл |
1,49 |
2,7 |
2,84 |
2,95 |
2,99 |
0,07 |
|
2 балла |
13,2 |
9,4 |
4 |
10,6 |
1,44 |
0,24 |
|
1 или 2 балла |
14,69 |
12,1 |
6,84 |
13,55 |
4,43 |
0,31 |
|
Ожидаемый % выполнения |
30-50 |
15-30 |
3-15 |
30-50 |
15-30 |
3-15 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.