Построение графиков функций

Построение графиков функций.

Табулирование функций и построение их графиков можно выполнить двумя способами.

1 способ.

Задать интервал изменения аргумента в виде

х:=Начальное_Значение,Начальное_Значение + Шаг..Конечное_Значение.

Например,

х:=2,2.1..30.

Если Шаг=1, то Начальное_Значение +Шаг можно не использовать:

х:=2..30.

Двоеточие «..» вводится символом «;» или с помощью панели «Калькулятор». Теперь можно определить функцию этого аргумента, например так:

х:=0,0.01..10             

Чтобы вывести таблицу значений функции, необходимо ввести f(x)=. Чтобы  построить график, воспользуемся панелью «Графика», в которой нужно выбрать Х-У график. В позиции маркера оси х указывается переменная х, в позиции маркера оси y — функция f(x). Можно также явно указать пределы изменения переменной и функции.

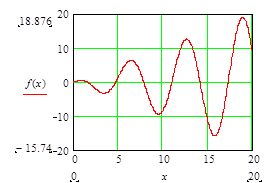
Рис.1

Двойной щелчок по области графика (рис.1) приводит к появлению окна свойств графика Одновременно можно построить много кривых с общим аргументом, указывая функции через запятую. Можно также аргументы указывать через запятую.

2 способ.

Ввести сначала целую переменную, которая пронумерует значения аргумента и функции:

j:=0..1000.

Определить аргумент функции как вектор-столбец

.

Определить значение функции тоже как вектор-столбец

.

Далее  необходимо указать вместо f(x), а  — вместо х при построении графика.

Для построение графика функций двух переменных необходимо сначала сформировать матрицу значений функции, например так:

                                   .

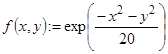
Далее выбрать в панели «Графики» трёхмерный график и в качестве единственного его аргумента указать матрицу M (Рис.2).

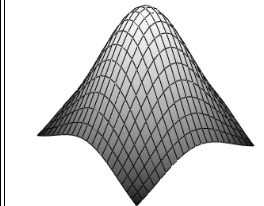
Рис.2

Решение уравнений.  MathCad 2000 обладает несколькими способами приближённого решения уравнений. Простейший способ найти корень уравнения с одним неизвестным  обеспечивает функция root. Например, необходимо найти корень трансцендентного уравнения . Зададим начальное значение , решение дается функцией , . При наличии нескольких корней будет найден корень, наиболее близкий к начальному приближению.

Точность вычислений задаётся системной переменной TOL, равной по умолчанию  и определённой в меню Математика\Опции.

Поиск корней системы уравнений возможен с помощью блока Given … Find(…):

Given

          .

Аналогичный вид имеет блок Given … Minerr(…). Его отличие состоит в том, что решение будет найдено в любом случае, даже при его отсутствии. Дело в том, что здесь ищется не решение системы, а минимальная невязка уравнений.

Некоторые уравнения Mathcad может разрешить в символьном виде. Для этого существуют три возможности:

1. Использование меню Символика. Например, запишем квадратный трёхчлен , выделим переменную x и выберем в меню пункт  Символика\Переменные\Разрешить. Получим решение в символьном виде.

2. Использование оператора solve из панели «Символика:.

®.

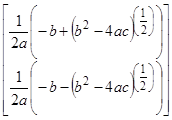При использовании оператора solve необходимо иметь в виду, что переменные, относительно которых решается уравнения, не должны быть определены заранее.

3. Использование блока Given … Find(…)®.

Given

®.

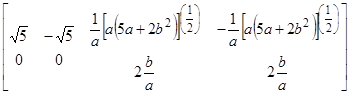Вычисление пределов, производных, интегралов  доступно в панели «Калькулус». Например, вычислим замечательные пределы:

,                     .

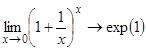Для вычисления производной достаточно поставить функцию под знак :

                  .

Дифференцирование выражения осуществляется также через меню Символика\Переменные\Дифференцировать.  Предварительно необходимо выделить переменную дифференцирования в выражении.

Для вычисления неопределённого интеграла нужно поставить функцию под знак определённого или неопределённого интеграла, либо использовать пункт меню Символика\Переменные\интегрировать.

Комплексные числа. Комплексные числа вводятся в обычной алгебраической записи, в качестве мнимой единицы используется символ i или  j, причём  нельзя просто вводить i, нужно написать 1i. Комплексное сопряжение, выводится символом двойной кавычки после набора имени переменной ".

Функции для работы с комплексными числами: Re(z) — действительная часть числа, Im(z) — мнимая часть числа, arg(z)—  аргумент (угол в комплексной плоскости между вещественной осью и z) модуль .