
Ьлоолоцъ ИКОЛЬНОЫПУ УЧИТЛЗЛД
А.в. АФОНИНА, Е,Е. ИПАТОВА

![]() ПОУРОЧНЫЕ
ПОУРОЧНЫЕ
РАЗРАБОТКИ
ПО МАТЕМАТИКЕ
В ПОМОЩЬ ШКОЛЬНОМУ УЧИТЕЛЮ
А. В. АФОНИНА
Е. Е. ИПАТОВА
ПО МАТЕМАТИКЕ
(М. : Академкнига/Учебник)
Перспективная начальная школа
класс
МОСКВА • «ВАКО» • 2011
удк 372.851
БЖ 74.262.21
А94
Афонина А.В., Ипатова Е.Е.
А94 Поурочные разработки по математике: 4 класс. ![]() М.: ВАКО, 2011. - 352 с. — (В помощь
школьному учителю).
М.: ВАКО, 2011. - 352 с. — (В помощь
школьному учителю).
ISBN 978-5-408-00501-7
Пособие содержит подробные поурочные разработки по математике для 4 класса к УМК А.Л. Чекина, разработанному в соответствии с концепцией «Перспективная начальная школа». Сценарии уроков написаны в занимательной форме, помимо методических указаний к выполнению основных заданий включают обширный игровой материал, загадки, конкурсы, вопроса на развитие смекалки и логики. В издании также представлены тексты самостоятельных и контрольных работ.
Адресовано учителям начальных классов, студентам педагоги-
ческих вузов и колледжей.
удк 372.851
БЖ 74.262.21
ввтч 978-5-408-00501-7 ©
000 «ВАКО»,![]()
От авторов
Методическое пособие предназначено для учителей начальНЫХ классов, работающих по учебнику А.Л. Чекина, разработанному в соответствии с концепцией «Перспективная начальная школа» и новыми требованиями образовательных стандартов.
Учебно-методический комплект (У МК) состоит из учебника в двух частях и рабочих тетрадей № l, 2, 3 (М.: Академкнига / Учебник).
Основная идея УМК — оптимальное развитие каждого ребенка на основе педагогической поддержки его индивидуальности (возраста, способностей, интересов, сюлонностей, развития) в условиях специально организованной учебной деятельности, где ученик выступает то в роли обучаемого, то в роли обучающего, то в роли организатора учебной ситуации.
В пособии представлены примерное тематическое планирование учебного материала, подробные конспекты уроков, примерные самостоятельные работы. Сценарий каждого урока содержит методические указания к выполнению заданий учебника и рабочей тетради, обширный игровой материал, задания на развитие логики и для проверки навыков устного счета.
Особенностью данного издания является возможность применения личностно ориентированного подхода к школьнику с опорой на его жизненный опыт. Дифференцированный подход реализуется как при объяснении нового материала, так и при контроле знаний.
Педагогическая поддержка индивидуальности ребенка при обучении выводит на первый план проблему соотношения обучения и развития. Система заданий разного уровня сложности, сочетание индивидуальной учебной деятельности ребенка с его работой в малых группах позволяют обеспечить условия, при которых об-
по
![]()
учение идет впереди развития, т. е. в зоне ближайшего развития КиДОГО ученика на основе учета уровня его актуального развития и личных интересов. То, что ученик не может выполнить индивидуально, он может сделать с помощью соседа по парте или в малой группе. А то, что представляет сложность для конкретной малой группы, становится доступным пониманию в процессе коллективноЙ деятельности. Высокая степень дифференцированности вопросов и заданий и создает возможности для индивидуального продвижения каждого ученика.
|
|
Тема урока |
Содержание, формируемые понятия |
|
1 |
2 |
З |
|
1, 2, З |
Сначала займемся повторением |
Шестизначные числа. Умножение столбИКОМ многозначных чисел на однозначное и двузначное числа. Вычисление периметра и площади 1рометрической фигуры. Геометрические фигуры. Формулирование и решение задач |
|
4, 5, 6 |
Когда известен результат разностного сравнения |
Задачи на сумму и разность |
Материалы данного пособия педагог может заимствовать полностью или использовать частично для создания собственного сценария урока. Задания, предлагаемые в книге, не обязательно должны быть выполнены в полном объеме. Авторы рекомендуют учителю опираться на психофизиологические возможности учащихся, так как на этапе начального обучения главное — это развитие личности школьника, его творческих способностей, интереса к обучению, формирование желания и умения учиться. Благодаря возможности выбора заданий расширяется воспитательное направление в развитии нравственных и эстетических чувств, ЭМОЦИОНаЛЬНО-ЦеННОСТНОГО позитивного отношения к себе и окружающим.
Выпускник общеобразовательной школы с целостной системой универсальных знаний, умений и навыков самостоятельной деятельности, гражданской ответственности и правового самосознания, духовности и культуры, инициативный, толерантный, способный к успешной социализации в обществе — таков ориентир в работе учителя.
Тематическое планирование
![]()
|
1 |
2 |
з |
|
7, 8 |
Когда известен результат кратного сравнения |
Задачи на сумму и частное |
|
9, 10 |
Учимся решать задачи |
Задачи на сумму и разность, на сумму и частное |
|
ll |
Алгоритм умножения столбиком |
Алгоритмы умножения столбиком: многозначного числа на однозначное, многозначного числа на двузначное, многозначного числа на многозначное |
|
12 |
Поупражняемся в вычислениях столбиком |
Сложение, вычитание и умножение многозначных чисел столбиком |
|
13 |
Тысяча тысяч, или миллион |
Новая разрядная единица — миллион. Миллион — наименьшее семизначное исло |
|
14 |
Разряд единиц миллионов и класс миллионов |
Разряд миллионов. Третий класс — класс миллионов |
|
15 |
Когда трех классов для записи числа недостаточно |
Миллиард. Класс миллиардов |
|
16 |
Поупражняемся в сравнении чисел и повторим пройденное |
Поразрядное сравнение многозначных чисел. Формулирование и решение задач |
|
17 |
Может ли величина изменяться? |
Постоянные и переменные величины |
|
18 |
Всегда ли математическое выражение является числовым? |
Буквенные выражения |
|
19 |
Зависимость между величинами |
Величины, зависимые друг от друга и независимые. Однозначная и неоднозначная зависимость |
|
20 |
Поупражняемся в нахождении значениЙ зависимой величины |
Зависимость величин |
|
21 |
Контрольная работа |
Проверка знаний, умений и навыков учащихся |
|
22, 23 |
Стоимость единицы товара, или цена |
Цена. Задачи на куплю-продажу |
|
24 |
Когда цена постоянна |
Зависимость между количеством купленного товара и его стоимостью при постоянной цене |
по
![]()
|
1 |
2 |
|
|
25 |
Учимся решать задачи |
Задачи на нахождение четвертого пропорционального, на сумму и разность и на сумму и частное |
|
26, 27 |
Деление нацело и деление с остатком |
Случаи деления нацело и случаи деления с остатком |
|
28 |
Неполное частное и остаток |
Названия компонентов действия при делении с остатком |
|
29 |
Остаток и делитель |
Взаимозависимость остатка и делителя при делении с остатком |
|
30 |
Когда остаток равен 0 |
Случаи деления, в которых остаток равен 0 (деление нацело) |
|
31 |
Когда делимое меньше делителя |
Случаи деления с остатком, в которых делимое меньше делителя |
|
32 |
Деление с остатком и вычитание |
Взаимосвязь деления с остатком и вычитания |
|
33, 34 |
Какой остаток может получиться при делении на 2 |
Четные и нечетные числа, их свойства |
|
35 |
Поупражняемся в вычислениях и повторим пройденное |
Деление с остатком. Задачи на сумму и разность, на сумму и частное, на разность и частное |
|
36 |
Запись деления с остатком столбиком |
Основной принцип записи деления с остатком столбиком |
|
37 |
Способ поразрядного нахождения результата деления |
Способ поразрядного нахождения неполного частного |
|
38 |
Поупражняемся в делении столбиком |
Запись деления столбиком |
|
39 |
Вычисления с помощью калькулятора |
Калькулятор, его функции. Правила работы с калькулятором |
|
40 |
Контрольная работа |
Проверка знаний, умений и навыков уча- ЩИХСЯ |
|
41 |
Час, минута и секунда |
Единицы измерения времени: час, минута, секунда. Соотношения между единицами времени |
|
42 |
Кто или что движется быстрее? |
Понятия «быстрее», «медленнее» |
|
43 |
Длина пути в единицу времени, или скорость |
Скорость движения. Единицы скорости, их соотношения |
![]()
|
1 |
2 |
З |
|
44, 45 |
Учимся решать задачи |
Задачи на движение |
|
46 |
Какой сосуд вмещает больше? |
Вместимость сосуда |
|
47 |
Литр. Сколько литров? |
Единица вместимости — литр. Измерения в литрах |
|
48, 49 |
Вместимость и объем |
Объем. Взаимосвязь объема жидких (или сыпучих) тел и вместимости сосудов, которые они занимают |
|
50 |
Кубический сантиметр и измерение объема |
Единица объема — кубический сантиметр. Измерение объема |
|
51 |
Кубический дециметр и кубический сантиметр |
Единица объема — кубический дециметр. Соотношение между кубическим дециметром и кубическим сантиметром |
|
52 |
Кубический дециметр и литр |
Равенство единиц измерения объема —
|
|
53 |
Литр и килограмм |
Литр и килограмм. Задачи на сравнительный анализ |
|
54, 55 |
Разные задачи |
Задачи комбинаторного характера |
|
56 |
Поупражняемся в измерении объема |
Измерение объема различных фигур |
|
57 |
Контрольная работа МЗ |
Проверка знаний, умений и навыков учащихся |
|
58 |
Кто выполнил большую работу? |
Задачи на определение разницы в объеме выполненной работы |
|
59, 60 |
Производительность — это скорость выполнения работы |
Производительность, единицы производительности. Прямая пропорциональная зависимость между производительностью и объемом выполненной работы при постоянном времени |
|
61 |
Учимся решать задачи |
Задачи на вычисление производительности и объема выполненной работы |
|
62 |
Отрезки, соединяющие вершины многоугольника |
Диагональ многоугольника |
|
63 |
Разбиение многоугольника на треугольники |
Разбиение многоугольника на треугольники с помощью диагоналей и без них |
|
64 |
Площадь прямоугольного треугольника |
Способ вычисления площади прямоугольного треугольника по известной площади соответствующего прямоугольника |
по
![]()
|
1 |
2 |
з |
|
|
65 |
Вычисление ПЛОЩади треугольника |
Способ вычисления гшощади треугольника путем разбиения его на прямоугольные треугольники |
|
|
66, 67 |
Закрепление прой денного |
Единицы объема. Соотношения между ю;бическим метром и кубическим дециметром, кубическим метром и кубическим сантиметром |
|
|
68 |
Контрольная работа |
Проверка знаний, умений и НаВЫКОВ учащихся |
|
|
69, 70 |
Деление на однозначное число столбиком |
Запись деления на однозначное число столбиком |
|
|
71 |
Число цифр в записи неполного частного |
Способ определения числа цифр в записи неполного частного до выполнения деления с остатком |
|
|
72 |
Деление на двузначное число столбиком |
Запись деления на двузначное число столбиком |
|
|
73, 74 |
Алгоритм деления столбиком |
Алгоритм деления столбиком |
|
|
75 |
Сокращенная форма записи деления столбиком |
Использование сокращенной формы записи деления столбиком |
|
|
76 |
Поупражняемся в делении столбиком |
Деление столбиком. Решение задач |
|
|
77 |
Сложение и вычитание величин |
Однородные и неоднородные величины. Правила сложения и вычитания ОДНОРОДных величин |
|
|
78 |
Умножение величины на число и числа на величину |
Правила умножения величины на число и числа на величину |
|
|
79 |
Деление величины на число |
Правило деления величины на число |
|
|
80 |
Нахождение доли от величины и величины по ее доле |
Правила нахождения доли от величины и величины по ее доле |
|
|
81 |
Нахождение части от величины |
Правило нахождения доли от величины |
|
|
82 |
Нахождение величины по ее части |
Правило нахождения величины по ее части |
|
|
83 |
Деление величины на величину |
Случаи деления однородной и разнородной величин на величину |
![]()
|
1 |
2 |
з |
|
84 |
Когда время движения одинаковое |
Прямая зависимость пройденного расстояния от скорости при одинаковом времени движения |
|
85 |
Когда длина пройденного пии одинаковая |
Взаимосвязь времени и скорости движения при одинаковой длине пройденного пути |
|
86 |
Движение в одном и том же направле- НИИ |
Задачи на движение в одном и том же направлении. Скорость изменения расстояния |
|
87 |
Движение в противоположных направлениях |
Задачи на движение в противоположных направлениях. Скорость изменения расстояния |
|
88 |
Учимся решать задачи |
Задачи на движение |
|
89 |
Поупражняемся в вычислениях и повторим пройденное |
Деление столбиком. Задачи на движение |
|
90 |
Контрольная работа |
Проверка знаний, умений и навыков учашихся |
|
91 |
Когда время работы одинаковое |
Прямая зависимость объема выполненной работы от производительности при одинаковом времени |
|
92 |
Когда объем выполненной работы одинаковый |
Взаимосвязь времени и производительности при одинаковом объеме выполненной работы |
|
93 |
Производительность при совместной работе |
Задачи на вычисление производительности при совместной работе |
|
94 |
Время совместной работы |
Задачи на вычисление времени совместной работы |
|
95 |
Учимся реплать задачи и повторяем пройденное |
Деление столбиком. Задачи разных типов |
|
96 |
Когда количество одинаковое |
Прямая зависимость стоимости товара от его цены при одинаковом количестве |
|
97 |
Когда стоимость одинаковая |
Взаимосвязь цены и количества товара при одинаковой стоимости |
|
98 |
Цена набора товаров |
Задачи на вычисление цены набора товаров |
|
99 |
Учимся решать задачи |
Задачи на куплю-продажу |
|
100 |
Поупражняемся в вычислениях и повторим пройденное |
Деление столбиком. Задачи разных типов |
|
1 |
2 |
З |
|
lOl |
Вычисления с помощью калькулятора |
Калькулятор, его функции. Правила работы с калькулятором |
|
102 |
Контрольная работа |
Проверка знаний, умений и навыков учащихся |
|
103 |
Как в математике применяют союз «и» и союз «или» |
Математический смысл союзов «и» и «или». Задания на логику |
|
104 |
Когда выполнение одного условия обеспечивает выполнение другого |
Логические конструкции, в которых выполнение одного условия обеспечивает выполнение другого |
|
105 |
Не только одно, но и другое |
Логические конструкции с союзом «не только... но и» |
|
106 |
Учимся решать логшеские задачи |
Логические задачи |
|
107, |
Поупражняемся в вычислениях и повторим пройденное |
Площадь и периметр прямоугольника. Действия над числами |
|
109 |
Квадрат и куб |
Плоские (квадрат) и объемные (куб) фигуры. Поверхность куба. Площадь квадрата и объем куба |
|
ПО |
Круг и шар |
Геометрические фигуры — круг и шар, их свойства |
|
l l l |
Площадь и объем |
Геометричесше фигуры, имеющие шлощадь, и геометрические фигуры, имеющие объем. Многогранники. Фигуры (тела) вращения |
|
|
Измерение площади с помощью палетки |
Способ измерения площадей произвольных фигур с помощью палетки |
|
из, |
Поупражняемся в нахождении площади и объема |
Площадь и объем. Измерение площади фигур с помощью палетки. Вычисление площади фигур и объема тел |
|
15, 1 16 |
Поупражняемся в вычислениях и повторим пройденное |
Действия над числами. Задачи разных типов |
|
1 17 |
Уравнение. Корень уравнения |
Уравнение. Корень уравнения. Решение уравнений способом увеличения (уменьшения) каждой его части на одно и то же число |
|
1 18 |
Учимся решать задачи с помощью уравнений |
Составление уравнений к задачам. Решение задач с помощью уравнений |
по
![]()
|
1 |
2 |
З |
|
119 |
Поупражняемся в вычислениях и повторим пройденное |
Вычисления столбиком. Уравнения. Задачи разных типов |
|
|
Контрольная работа |
Проверка знаний, умений и навыков учащихся |
|
т, 122 |
Разные задачи |
Вероятность. Основные идеи вероятного (стохастического) описания (моделирования) реальных ситуаций |
|
123, 124 |
Натуральные числа и число 0 (повторение) |
Основные свойства целых неотрицательных чисел |
|
125, 126 |
Алгоритмы вычисления столбиком (повторение) |
Алгоритмы сложения, вычитания, умножения и деления столбиком |
|
127, 128 |
Действия с величинами (повторение) |
Правила выполнения действий с величинами |
|
129, ВО |
Как мы научились решать задачи |
Арифметические сюжетные задачи разных типов |
|
131 |
Контрольная работа |
Проверка знаний, умений и навыков учаЩИХСЯ |
|
132, 133 |
Геометрические фигуры и их свойства (повторение) |
Прямоугольник. Площадь прямоугольника. Окружность. Радиус окружности. Треугольник. Виды треугольников. Площадь треугольника |
|
134, 135 |
Буквенные выражения и уравнения |
Буквенные выражения. Формулы. Запись свойств математических действий с помощью буквенных выражений. Уравнение. Корень уравнения |
|
136 |
Закрепление пройденного |
Занимательные вопросы и задания для повторения |
Урок 1 , Сначала займемся повторением
Цель: повторить материал, изученный в 3 классе (шестизначные числа, умножение столбиком многозначных чисел на однозначное и двузначное числа, вычисление периметра и площади геометрической фигуры).
![]() 1. Организационный момент. Сообщение темы и цели урока
1. Организационный момент. Сообщение темы и цели урока
Знакомство с учебником
Интересная работа ждет нас, друзья!
Значит, лениться нам никак нельзя.
Замечательный учебник на партах у вас, Будем знакомиться с ним мы сейчас.
![]() Кто трудился, создавая
учебник математики, по которому мы продолжим работу в 4 классе? (Ответы детей.)
Кто трудился, создавая
учебник математики, по которому мы продолжим работу в 4 классе? (Ответы детей.)
Правильно. Художник, оформитель обложки, корректор, технический редактор и другие помощники.
— Кто автор учебника? ( Чекин Александр ЛеониДович.) ![]() Кто
редактировал учебник? (Роза Пиьфановна Чуракова.)
Кто
редактировал учебник? (Роза Пиьфановна Чуракова.)
![]() Сколько частей в учебнике? (Две.)
Сколько частей в учебнике? (Две.)
![]() Какие условные обозначения
имеются в учебнике? («Работа в парах», «повтори пройденное», «выскажи
преположение», «толковый словарь», «трудное задание», «загляни в словарь»,
«запомни слово», «правило», «смотри ”Математика в вопросах и заданиях ” —
тетраДь для самостоятельной работы». )
Какие условные обозначения
имеются в учебнике? («Работа в парах», «повтори пройденное», «выскажи
преположение», «толковый словарь», «трудное задание», «загляни в словарь»,
«запомни слово», «правило», «смотри ”Математика в вопросах и заданиях ” —
тетраДь для самостоятельной работы». )
![]() Где можно узнать, что
нам предстоит изучать в течение года? (В соДержании учебника на с. 4—6.)
Где можно узнать, что
нам предстоит изучать в течение года? (В соДержании учебника на с. 4—6.)
— Вспомнилр правила обращения с учебниками. (Ответы детей.)
1.
![]()
Мы познакомились с новым учебником математики (с его первой частью). Он будет вам верным помощником. Берегите его, оберните и примите на память открытку-закладку от ваших родителей с правилами обращения с учебниками.
(Учитель раздает открытки-закладки.)
ll. Актуализация знаний
1. Закономерность
— Установите закономерность и вставьте пропущенное число.
![]()
(Закономерность: • 2, — 1; пропущенное число — 7.)
2. Цифровой квадрат
(Квадрат начерчен на доске.)
![]() Рядом с квадратом приведены суммы чисел в каждом ряду и каждом столбце.
Какие числа надо вставить в пустые клетки для того, чтобы получить нужную
сумму?
Рядом с квадратом приведены суммы чисел в каждом ряду и каждом столбце.
Какие числа надо вставить в пустые клетки для того, чтобы получить нужную
сумму?
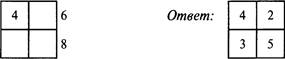
7 7
З. Родственные ряды
(На доске начерчена таблица.)
|
2 |
5 |
|
|
12 |
|
7 |
10 |
В |
15 |
|
![]() Найдите логическую
взаимосвязь между числами первого и второго рядов и в соответствии с этим
определите, какие числа пропущены. (Числа нижнего ряда на 5 больше
соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 8, в нижнем
ряду — 17.)
Найдите логическую
взаимосвязь между числами первого и второго рядов и в соответствии с этим
определите, какие числа пропущены. (Числа нижнего ряда на 5 больше
соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 8, в нижнем
ряду — 17.)
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Как с помощью двух бидонов вместимостью 8 л и 5 л отлить из молочной цистерны 7 л молока? (Примерный ответ. Два раза наполнить молоком пятилитровый бидон и вылить в восьмилитровый бидон. В пятилитровом бидоне останется 5 л + 5 л — 8 л — = 2 л молока. В цистерну с молоком вылить молоко из восьмилитрового бидона, в пустой бидон перелить оставшиеся 2 л молока
![]()
из пятилитрового бидона и добавить туда еще 5 л, получится 7 л молока: 5 л +2 л = 7 л.) l|l. Работа по теме урока Работа по учебнику
![]()
![]() Выполните задание.
Выполните задание.
![]() Прочитайте, какое число получилось. ( 765 432.)
Прочитайте, какое число получилось. ( 765 432.)
![]() — Сколько разрядов в
одном классе? (Три разряда: еДиницы, Десятки и сотни.)
— Сколько разрядов в
одном классе? (Три разряда: еДиницы, Десятки и сотни.)
![]() Подчеркните цифру
разряда десятков тысяч в записи этого числа. (6.)
Подчеркните цифру
разряда десятков тысяч в записи этого числа. (6.)
![]() Какой по счету справа налево является эта цифра? (Пятой.)
Какой по счету справа налево является эта цифра? (Пятой.) ![]() Назовите
цифру, которая в записи этого числа стоит четвертой при счете справа налево.
(5.)
Назовите
цифру, которая в записи этого числа стоит четвертой при счете справа налево.
(5.)
— К какому разряду она относится? (К еДиницам тысяч.) ![]() Назовите
цифру, которая стоит шестой при счете справа налево в записи данного числа.
(7.)
Назовите
цифру, которая стоит шестой при счете справа налево в записи данного числа.
(7.)
![]() К какому разряду она относится? (К сотням тысяч.)
К какому разряду она относится? (К сотням тысяч.)
![]() Сколько сотен тысяч в составе записанного числа? ( 7 сотен тысяч.)
Сколько сотен тысяч в составе записанного числа? ( 7 сотен тысяч.)
— Каким по счету является разряд сотен тысяч? (Шестым.)
![]()
— Как можно получить наибольшее число? (Наибольшее число получится только тогДа, когда, начиная со старшего разряда, все разряды заполняются самыми большими возможными числами.)
![]() Какая цифра может быть в первых трех
старших разрядах? (9.) — Какая цифра может быть в оставшихся трех разрядах?
(1.)
Какая цифра может быть в первых трех
старших разрядах? (9.) — Какая цифра может быть в оставшихся трех разрядах?
(1.)
— Почему? (Другой возможности
использовать три раза цифру ![]() нет.)
нет.)
![]() Почему нельзя записать
цифру в трех высших разрядах? (Если цифру записать ранее, то полученное
шестизначное число будет меньше, чем то, запись которого начинается с трех
Девяток.)
Почему нельзя записать
цифру в трех высших разрядах? (Если цифру записать ранее, то полученное
шестизначное число будет меньше, чем то, запись которого начинается с трех
Девяток.)
![]() Чему равно искомое число? (999 111.)
Чему равно искомое число? (999 111.)
![]()
![]() С чего можно начать
конструирование искомых пар? (Срассмотрения наименьшего шестизначного числа или
наибольшего пятизначного числа.)
С чего можно начать
конструирование искомых пар? (Срассмотрения наименьшего шестизначного числа или
наибольшего пятизначного числа.)
— Назовите наименьшее шестизначное число. (100 000.) ![]() Вычтите
из данного шестизначного числа число 5. Какое число получилось? (99 995.)
Вычтите
из данного шестизначного числа число 5. Какое число получилось? (99 995.)
1.
Какое это число? (Пятизначное.)
Выполните разностное сравнение наименьшего шестизначного числа и полученного пятизначного числа. Что получилось? (5.)
— Назовите следующие пары чисел,
каждая из которых состоит из шестизначного числа и пятизначного числа, а
результат разностного сравнения между ними равен 5. ( Таких пар всего пять: ![]() 99995,
и 99 996, 100002 и 99997, 100 003 и 99 998, 100004 и 99 999.)
99995,
и 99 996, 100002 и 99997, 100 003 и 99 998, 100004 и 99 999.)
— Сколько натуральных чисел располагается между числами в каждой из пар? ( Четыре.)
![]() Перечислите эти
натуральные числа в паре 100 000 и 99 995. (99 996, 99 997, 99 998, 99 999.)
Перечислите эти
натуральные числа в паре 100 000 и 99 995. (99 996, 99 997, 99 998, 99 999.)
М. Физкультминутка
V. Закрепление изученного материала
Работа по учебнику
![]()
![]() Вспомните правило деления на «круглые» числа.
Вспомните правило деления на «круглые» числа.
![]() Чему равен результат кратного сравнения между разрядными единицами 1000
и 10? (100.)
Чему равен результат кратного сравнения между разрядными единицами 1000
и 10? (100.)
— Что нужно сделать, чтобы результат деления не изменился и можно было бы записать еще четыре пары разрядных единиц с таким же результатом кратного сравнения? (Нужно увеличивать или уменьшать Делимое и Делитель в одно и то же число раз. Так как речь идет о разрядных еДиницах, то уменьшить Данные числа можно только в 10 раз, а увеличить — в 10, 100, 1000и т. д. раз.)
![]() Назовите пары разрядных единиц. (100 и 1, 10 ООО и 100, lOOOOOu 1000,
ООООООИ 10000.)
Назовите пары разрядных единиц. (100 и 1, 10 ООО и 100, lOOOOOu 1000,
ООООООИ 10000.)
![]()
(Устное выполнение.)
— Каковы значения выражений, записанных в первых двух скобках? (Одинаковые: 1211 844.)
— Какое свойство использовано в данных выражениях?
(Переместительное свойство сложения.) ![]() Чему равен результат деления? ( 1.)
Чему равен результат деления? ( 1.)
— Чему равно значение выражения в третьих скобках? (4.) — Что получится в итоге? (4.)
![]()
![]() Вспомните, как можно умножить многозначное число на
однозначное. (Письменное умножение многозначного числа на однозначное число
выполняется так же, как умножение
Вспомните, как можно умножить многозначное число на
однозначное. (Письменное умножение многозначного числа на однозначное число
выполняется так же, как умножение
![]()
трехзначного числа на однозначное число: сначала умножают еДиницы, потом Десятки, сотни и т. д.)
Чтобы умножить многозначное число на однозначное, надо единицы каждого разряда множимого умножить на множитель и полученные произведения соединить в одно число.
Рассмотрим на примере: второй множитель 2 подписываем под единицами первого множителя — 20 863.
Сначала умножаем на второй множитель единицы: 2 • 3 = 6; подписываем 6 под единицами.
Умножаем десятки: 2 • 6= 12 (это сотня и 2 десятка); подписываем 2 под десятками, а сотню надо запомнить.
Умножаем сотни: 2 • 8 = 16, прибавляем I сотню, которую запомнили, получаем 17 (это тысяча и 7 сотен); подписываем 7 под сотнями, а тысячу надо запомнить.
Умножаем единицы тысяч: 2 • 0 = 0, прибавляем тысячу, которую запомнили, получаем I единицу тысяч; подписываем под единицами тысяч.
Умножаем десятки тысяч: 2 • 2 = 4, подписываем 4 под десятками тысяч.
![]() Какое число получили? (41 726.)
Какое число получили? (41 726.)
При записи в строчку поразрядное умножение начинают, как правило, со старшего разряда, а при записи столбиком, наоборот, начинают с разряда единиц.
Чтобы выполнить умножение многозначного числа на двузначное столбиком, необходимо правильно записать промежуточные результаты, которые далее нужно будет сложить. Разряд располагается под соответствующим разрядом, и запись приобретает ступенчатый вид.
Рассмотрим на втором примере: умножаем 2 на З, получаем 6, пишем 6 под единицами.
Умножаем на 2 число десятков — 6, получаем 12; это 2 десятка и сотня, пишем 2 под десятками.
Умножаем на 2 число сотен — 8, получаем 16, прибавляем еще
1 сотню, получаем 1 7; это 7 сотен и тысяча, пишем 7 под сотнями. Умножаем на 2 единицы тысяч, получаем 0, прибавляем тысячу, получаем 1 единицу тысяч, пишем под единицами тысяч.
Умножаем на 2 десятки тысяч, получаем 4, пишем 4 под десятками тысяч.
Мы получили первое неполное произведение — 41 726.
Первый множитель — 20 863 умножаем на число десятков — 2. Получаем второе неполное произведение — 41 726.
Начнем подписывать второе неполное произведение под десятками.
2.
![]()
Сложим неполные произведения: 41726
41726
458986
Читаем ответ: четыреста пятьдесят восемь тысяч девятьсот восемьдесят шесть. Это произведение чисел 20 863 и 22.
— В чем преимущество записи умножения столбиком по сравнению с записью в строчку? (В Данной форме записи полученные значения произведений записываются друг под Другом с соблюДением всех требований записи сложения столбиком, что позволяет сразу выполнять сложение именно этим способом.)
Правильно. При записи умножения в строчку выполнить сложение полученных значений произведений может оказаться трудно, а при записи столбиком сложение выполнить легко.
![]()
![]() Прочитайте задание. Нужно ли выражать длины сторон в миллиметрах? (Нет.)
Прочитайте задание. Нужно ли выражать длины сторон в миллиметрах? (Нет.)
— Почему? (Можно сгруппировать слагаемые.)
![]() Как это сделать? ((5 см 5 мм + 5 см 5 мм) + (З см + З см)
Как это сделать? ((5 см 5 мм + 5 см 5 мм) + (З см + З см) ![]() = 11 см +
беи = 17 см.)
= 11 см +
беи = 17 см.)
— Что необходимо сделать для вычисления площади прямоугольника? (Сначала выразить его длину и ширину в миллиметрах: 55 мм и 30 мм.)
— А что нужно сделать потом? (Умножить длину на ширину:
55 мм • 30 мм = 1650 кв. мм.) Ш. Подведение итогов урока
![]() Какие
основные понятия мы повторили на уроке?
Какие
основные понятия мы повторили на уроке?
Домашнее задание
Тетрадь для самостоятельной работы: № 1, 2 (с. 3).
Урок 2, Сначала займемся повторением
Цель: повторить геометрический материал (распознавание геометршеских фигур, их изображение в тетради).
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Волшебные квадраты
(Квадраты начерчены на доске.)
Цифровой квадрат, в котором цифры в горизонтальных, верТИКш1ЬНых и диагональных рядах имеют одинаковую сумму, мы
![]()
называем волшебным. Вот пример такого квадрата. Волшебная сумма равна 15.
|
|
|
|
|
|
|
|
|
5 3 7 |
||
![]() Заполните пустые
клетки соответствующими цифрами от 1 до 9, причем в каждом из квадратов ни одна
цифра не должна повторяться. Волшебная сумма также равна 15.
Заполните пустые
клетки соответствующими цифрами от 1 до 9, причем в каждом из квадратов ни одна
цифра не должна повторяться. Волшебная сумма также равна 15.
|
пап |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Ответы:

2. Родственные ряды
|
|
12 |
4 |
16 |
|
|
5 |
6 |
|
8 |
4 |
( Числа нижнего ряда в 2 раза меньше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 8, в нижнем ряду — 2.) З. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Старший брат идет от дома до школы 30 мин, а младший — 40 мин. Через сколько минут старший брат догонит младшего, если тот вышел на 5 мин раньше? (Примерный ответ. Если бы младший брат вышел на 10 мин раньше старшего, то старший брат догнал бы младшего у школы через 40 мин — 30 мин = 10 мин. Так как младший брат вышел на 5 мин раньше старшего, старший брат догонит младшего в середине пути и пройдет это расстояние за 30 мин : 15 мин.)
Ш. Работа по теме урока Работа по учебнику М 11 (с. 9).
— Что мы знаем о квадрате? (УкваДрата все стороны равны.)
2.
Как найти длину стороны данного квадрата? (32 дм : 4 = 8 дм.) — На сколько дециметров нужно увеличить сторону квадрата, чтобы его периметр увеличился на 12 дм? (Так как все четыре стороны кваДрата имеют оДинаковую длину, то искомая Длина 12 дм : 4 = З дм.)
— Чему будет равна сторона нового квадрата? (8 дм + З дм — — 11 дм.)
![]() Можно ли теперь найти площадь? (Да: 11 дм • 11 дм — =
121 кв. дм.)
Можно ли теперь найти площадь? (Да: 11 дм • 11 дм — =
121 кв. дм.)
— Что необходимо сделать, чтобы выполнить разностное сравнение? (Вычислить мощаДь старого кваДрата: 8 дм • 8 дм — = 64 кв. дм.)
![]() Каков результат разностного сравнения? (121 кв. дм — — 64 кв. дм = 57
кв. дм.) М 12 (с. 9).
Каков результат разностного сравнения? (121 кв. дм — — 64 кв. дм = 57
кв. дм.) М 12 (с. 9).
(Самостоятельное выполнение. Проверка.) lV. Физкультминутка
V, Закрепление изученного материала
1. Работа по учебнику
![]()
(Самостоятельное выполнение. Коллективная проверка.) ![]() Сколько
делений должна пройти минутная стрелка, чтобы получился поворот на прямой угол?
( 15.)
Сколько
делений должна пройти минутная стрелка, чтобы получился поворот на прямой угол?
( 15.)
![]() Какой
угол образуется при повороте минутной стрелки на 15 мин? (Прямой.)
Какой
угол образуется при повороте минутной стрелки на 15 мин? (Прямой.)
![]() Какую часть от 1 5 мин составляют 5 мин?
( Третью часть.)
Какую часть от 1 5 мин составляют 5 мин?
( Третью часть.)
— Какую часть от прямого угла составляет угол поворота минутной стрелки на 5 мин? (Третью часть.) ле 15 (с. 9).
![]() Представьте
число 20 в виде произведения двух множителей. (5, 4,
Представьте
число 20 в виде произведения двух множителей. (5, 4, ![]() 1, 02.)
1, 02.)
![]() Что
нужно знать для построения треугольника площадью 10 кв. см? (Нужно построить
прямоугольник площадью 20 кв. см, его стороны могут быть равны 5 см и 4 см, 10
см и 2 см, Тсм и см. Затем при помощи Диагонали разДелить его на два равных
прямоугольных треугольника. Площадь одного такого треугольника и будет равна 10
кв. см.)
Что
нужно знать для построения треугольника площадью 10 кв. см? (Нужно построить
прямоугольник площадью 20 кв. см, его стороны могут быть равны 5 см и 4 см, 10
см и 2 см, Тсм и см. Затем при помощи Диагонали разДелить его на два равных
прямоугольных треугольника. Площадь одного такого треугольника и будет равна 10
кв. см.) ![]()
2. Выполнение упражнений в тетради для самостоятельной рабсгы
![]()
![]() Что такое сотка? (Это
еДиница тощаДи, равная 100 кв. м. Такую мощаДь имеет кваДрат со стороной 10 м.
Другое название этой еДИНИЦЫ — ар.)
Что такое сотка? (Это
еДиница тощаДи, равная 100 кв. м. Такую мощаДь имеет кваДрат со стороной 10 м.
Другое название этой еДИНИЦЫ — ар.)
Чему будет равна площадь садового участка? (8 сот. = 800 кв. м.)
Чему равна площадь дачного участка? (2400 кв. м.)
— Что такое кратное сравнение? (Сравнение чисел, позволяющее узнать, сколько раз Делитель соДержится в Делимом, во сколько раз Делимое больше Делителя (ми Делитель меньше Делимого). Выполняется Действием Деления.)
![]() Что
такое разностное сравнение? (Способ сравнения чисел Действием вычитания
меньшего числа из большего.)
Что
такое разностное сравнение? (Способ сравнения чисел Действием вычитания
меньшего числа из большего.)
![]() Выполните
кратное и разностное сравнение площадей этих участков. (2400 : 800 = З (раза);
2400 — 800 = 1600 (кв. м).)
Выполните
кратное и разностное сравнение площадей этих участков. (2400 : 800 = З (раза);
2400 — 800 = 1600 (кв. м).)
![]()
— Прочитайте задание. Чему равна площадь участка? (З • 4 =
— 120 (кв. м).)
— Сколько граммов семян потребовалось, если на 10 кв. м участка использовали 15 г семян? (120: 10 • 15 = 12 • 15 = 180(г).)
И. Подведение итогов урока
— Что мы повторили в течение урока?
Домашнее задание
1. Учебник: № 14 (с. 9).
2. Тетрадь для самостоятельной работы: № 3 (с. 3).
Урок З. Сначала займемся повторением
Цель: повторить материал, связанный с формулированием и решением задач.
1. Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Цифровой квадрат
|
з |
9 |
|
|
|
|
|
9 |
|
|
|
12 Ответ:
13
2. Волшебная звезда
В изображении звезды все цифровые линии в сумме дают одно и то же число. В каждом примере ни одна цифра не повторяется. — Заполните пустые окружности таким образом, чтобы волшебная сумма соответствовала той, которая указана рядом.
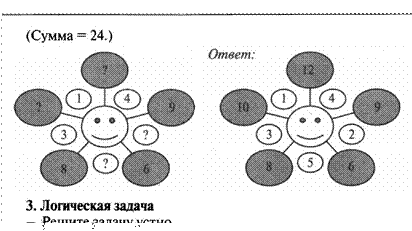
Как на чашечных весах уравновесить кусок олова массой 47 г с помощью набора из пяти гирь: г, 3 г, 9 г, 27 г, 81 г? Гири разрешается класть на обе чаши весов. (На одну чашу весов положить гири массой З г и 81 г, на Другую — кусок олова массой 47 г и гири массой 1 г, 9г и 27 г.)
Ш. Работа по теме урока Работа по учебнику М 16 (с. 10).
(Коллективное выполнение с комментированием у доски.)
— О чем говорят два вопросительных знака в таблице? (Эта задача Должна быть составной.)
— Из каких задач она будет состоять? (Из простой заДачи на уменьшение на НсКОЛЖО еДиниц в косвенной фрме и простой заДачи на уменьшение на несколько еДиниц в прямой форме.)
— Сформулируйте задачу. (Например: Свете 14 лет, и она на З года старше Иры. Сколько лет Марине, если она на год моложе Иры .7)
— Что можно сказать о возрасте Иры? (Ира на З года младше Светы: 14 — З = 11 (лет).)
![]() Что можно сказать о возрасте Марины?
(Марина на 1 год моложе Иры: 11 — 1 — 10 (лет).) № 17(с. 10).
Что можно сказать о возрасте Марины?
(Марина на 1 год моложе Иры: 11 — 1 — 10 (лет).) № 17(с. 10).
![]() Прочитайте задачу. Отличается ли она от
предыдущей? (Да.) — В чем состоит отличие? (В этой задаче речь идет
обувеличении (в косвенной форме) на несколько еДиниц и обуменьшении (в прямой
форме) в несколько раз.)
Прочитайте задачу. Отличается ли она от
предыдущей? (Да.) — В чем состоит отличие? (В этой задаче речь идет
обувеличении (в косвенной форме) на несколько еДиниц и обуменьшении (в прямой
форме) в несколько раз.)
![]() Что можно сказать о
возрасте Андрея? (Он старше Сережи на 4 года: 10 + 4 = 14 (лет).)
Что можно сказать о
возрасте Андрея? (Он старше Сережи на 4 года: 10 + 4 = 14 (лет).)
— Что можно сказать о возрасте Бориса? (Он моложе Андрея в 2 раза: 14 : 2 = 7 (лет).)
![]()
ЛФ 18 (с. 10).
Вариант заДачи. Для участия в спартакиаде школьников прибыли 10 команд по 12 спортсменов и 8 команд по 15 спортсменов в каждой. Сколько всего спортсменов прибыло для участия в спартакиаде?
![]() Вспомните правшо о порядке выполнения
действий в выражении без скобок. (В первую очередь выполняются Действия
умножения (или Деления), во вторую очереДь — Действия сложения (вычитания)
слева направо.) — Вычислите и запишите ответ задачи.
Вспомните правшо о порядке выполнения
действий в выражении без скобок. (В первую очередь выполняются Действия
умножения (или Деления), во вторую очереДь — Действия сложения (вычитания)
слева направо.) — Вычислите и запишите ответ задачи.
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 19 (с. 10).
19 (с. 10).
— Прочитайте задание. Какие числа указаны в диаграмме?
(90u 15.)
— Сформулируйте задачу. (Например: у Юры 90 орехов, а у
Саши — 15. Во сколько раз у Саши меньше орехов, чем у Юры ? Во сколько раз у
Юры больше орехов, чем у Саши ![]()
![]() Устно выполните деление двузначного числа
на двузначное число (90: 15 = 6 (раз).) № 20 (с. 11).
Устно выполните деление двузначного числа
на двузначное число (90: 15 = 6 (раз).) № 20 (с. 11).
— Прочитайте задачу. Что можно вычислить сначала? ( Число
оставшихся упаковок с яблочным соком: 40 — 18 = 22 (уп.).) ![]() Что можно
найти далее?.( Число оставшихся упаковок с апельСИНОВЫМ соком: 18 + З = 21
(уп.); 35 — 21 = 14 (уп.).)
Что можно
найти далее?.( Число оставшихся упаковок с апельСИНОВЫМ соком: 18 + З = 21
(уп.); 35 — 21 = 14 (уп.).)
— Что нужно сделать дальше? (Выполнить разностное сравнение полученных чисел: 22 — 14 = 8 (уп.).)
![]() Существует ли
рациональный путь решения данной задачи? (Да.)
Существует ли
рациональный путь решения данной задачи? (Да.)
— Что мы выясним сначала? (На сколько больше было на склаДе упаковок с яблочным соком, чем с апельсиновым: 40 — 35 = = 5 (уп.).)
— Что сделаем потом? (Выясним, как ИЗЛРНШЮСЬ это
число, если упаковок с апельсиновым соком увезли на З больше, чем с яблочным: 5
+ З = 8 ![]() № 21 (с. 11).
№ 21 (с. 11).
— Посмотрите на диаграмму. Какие числа можно определить? (20 и 5.)
![]() Найдите результат кратного сравнения данных величин.
(20 : 5 = 4.)
Найдите результат кратного сравнения данных величин.
(20 : 5 = 4.)
— Сформулируйте задачу на разностное сравнение, в условии которой одно из данных является результатом кратного
4.
![]()
сравнения, т. е. числом 4. (Например: в одно овощехранилище
привезли 50 ц картофеля, а в Другое — в 4 раза больше. На сколько центнеров
картофеля во второе храншшще привезш больше, чем в первое![]()
— Решите задачу. Вычислите и запишите ответ. м 22 (с. 11).
Вариант заДачи. В одно овощехранилище привезли 5 т картофеля, а в другое — на 15 т больше. Во сколько раз больше тонн картофеля привезли во второе хранилище, чем в первое? Во сколько раз меньше тонн картофеля привезли в первое хранилище, чем во второе?
2. Выполнение упражнения в тетрадщ для самостоятельной работы
![]()
(Самостоятельное выполнение. Коллективная проверка.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 9 (с. 6—7).
Урок 4. Когда известен результат разностного сравнения
Цель: познакомить с задачами на сумму и разность и задачами на две разности.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Арифметический диктант ![]() Решите примеры устно.
Решите примеры устно.
|
81 :9 |
56 : 7 |
|
|
63 : 7 |
6-9 |
48 : 8 |
![]() Решите задачи устно.
Решите задачи устно.
![]() В книге 54 страницы. В первый день мальчик прочитал 20 страниц, а во
второй день дочитал книгу до конца. Сколько страниц мальчик прочитал во второй
день? (34.)
В книге 54 страницы. В первый день мальчик прочитал 20 страниц, а во
второй день дочитал книгу до конца. Сколько страниц мальчик прочитал во второй
день? (34.)
![]() В школьной столовой 12 столов, а стульев в 4 раза больше, чем столов.
Сколько стульев в школьной столовой? (48.)
В школьной столовой 12 столов, а стульев в 4 раза больше, чем столов.
Сколько стульев в школьной столовой? (48.)
![]() Тетрадь стоит 10 руб.
Сколько тетрадей можно купить на ЗОО руб.? (30.)
Тетрадь стоит 10 руб.
Сколько тетрадей можно купить на ЗОО руб.? (30.)
2. Устный счет
(Примеры записаны на доске.)

Работа по учебнику
М 23 (с. 12).
(Коллективное выполнение.)
![]() Прочитайте задание. Ответьте на вопрос. (Удвоенную длину меньшеи части
полоски можно вычислить с помощью выражения 10— 2.)
Прочитайте задание. Ответьте на вопрос. (Удвоенную длину меньшеи части
полоски можно вычислить с помощью выражения 10— 2.)
![]() Чему равно значение этого выражения? (8.)
Чему равно значение этого выражения? (8.)
![]()
![]() Как вычислить длину меньшей части
полоски? (8 : 2 = 4 (см).)
Как вычислить длину меньшей части
полоски? (8 : 2 = 4 (см).) ![]() Как вычислить длину большей части
полоски? (С помощью сложения: 4 + 2 = 6 (см) — или вычитания: 10— 4 = 6 (см). )
Как вычислить длину большей части
полоски? (С помощью сложения: 4 + 2 = 6 (см) — или вычитания: 10— 4 = 6 (см). )
![]() Что
мы нашли? (Длину кажДой части полоски: 4 см и 6 см.)
Что
мы нашли? (Длину кажДой части полоски: 4 см и 6 см.)
![]() Как найти длину большей части полоски? (10 + 2 = 12 (см);
Как найти длину большей части полоски? (10 + 2 = 12 (см); ![]() (см).)
(см).)
![]() Как найти длину меньшей части? (6 — 2 = 4
(см) шти 10— 6 =
Как найти длину меньшей части? (6 — 2 = 4
(см) шти 10— 6 =
— 4 (см). )
![]() Какова длина каждой части полоски? (6 см и 4 см.)
Какова длина каждой части полоски? (6 см и 4 см.)
Таким образом, мы познакомились с двумя
вариантами решения задач на сумму и разность. ![]() 24 (с. 12-13).
24 (с. 12-13).
(Коллективное выполнение.)
— Опишите процесс отгибания части ленточки длиной 20 см.
(1 м - 20 см — ]О0см — 20см = 80см.)
![]() Что сделала Маша с оставшейся частью ленточки после отгибания?
(Разрезала пополам.)
Что сделала Маша с оставшейся частью ленточки после отгибания?
(Разрезала пополам.)
— Как это записать? (80 : 2 40 (см).)
![]() Какую длину мы получили? (Дину меньшей части ленточки.)
Какую длину мы получили? (Дину меньшей части ленточки.)
Если теперь распрямить часть ленточки с ранее отогнутыми 20 см, то получится большая часть ленточки.
— Как вычислить длину большей части ленточки? (С помощью сложения: 40 см + 20 см 60 см — ми вычитания: 100 см — — 40см = 60см.)
![]() Что мы узнали? (Шину кажДой части
ленточки: 40см и 60 см.) — Как Маше удалось сделать так, чтобы одна часть
ленточки была на 20 см длиннее другой? (Вначале она отогнула 20 см ленточки.)
Что мы узнали? (Шину кажДой части
ленточки: 40см и 60 см.) — Как Маше удалось сделать так, чтобы одна часть
ленточки была на 20 см длиннее другой? (Вначале она отогнула 20 см ленточки.) ![]() 13).
13).
![]() Прочитайте задание.
Ответьте на вопрос. (Решением Данной заДачи будет второй вариант.)
Прочитайте задание.
Ответьте на вопрос. (Решением Данной заДачи будет второй вариант.)
5.
![]()
Физкультминутка
М. Закрепление изученного материала
1. Работа по учебнику М 26 (с. 14). (Самостоятельное выполнение. Проверка.) М27(с. 14).
Вариант заДачи. В двух бригадах работают 47 человек. Сколько человек работает в каждой бригаде, если во второй бригаде работает на 7 человек больше, чем в первой?
2. Выполнение упражнения в тетради для самостоятельной рабшы ЛГУ 10 (С. 8-9).
(Вариант — а; вариант 2 — б. Проверка. Задание в выполняется у доски.)
Ш. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 1 (с. 9).
(Рекомендуется предварительно объяснить учащимся, как выполнять задания такого типа.)
Урок 5. Когда известен результат разностного сравнения
Цель: продолжать обучать решению задач на сумму и разность и на две разности.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Цифровой квадрат
|
5 |
4 |
|
|
|
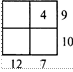 Ответ:
Ответ:
2. Родственные ряды
|
14 |
12 |
|
15 |
|
|
7 |
5 |
|
8 |
|
( Числа нижнего ряда на 7меньше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 8, в нижнем ряду — З.)
пасс
![]()
По вертикальному столбу высотой 6 м движется улитка. За день она поднимается на 4 м, за ночь опускается на 3 м. Сколько дней ей потребуется, чтобы добраться до вершины? (За первые сутки улитка поднялась на высоту 1 м. В конце вторых суток она будет на высоте 2 м: 1 м + 4 м — Зм = 2 м. В конце третьего дня улитка Достигнет вершины: 2 м + 4 м = 6 м.) Ш. Работа по теме урока Работа по учебнику ле 28 (с. 14).
(Коллективное выполнение с комментированием у доски.)
Решение: найти одно слагаемое, которое больше другого на 70, можно двумя способами: с помощью сложения и вычитания.
Первый способ (вычитанием):
1) 550 - 70 = 480;
2) 480 : 2 = 48 дес. : 2 = 24 дес. = 240 - первое слагаемое; 3) 240 + 70 = 310 — второе слагаемое.
Проверка: 240 + 310 = 550.
Второй способ (сложением):
1) 550 + 70 = 620;
2) 620 : 62 дес. : 2 = 31 дес. = 310 — первое слагаемое; 3) 310 — 70 = 240 — второе слагаемое.
![]() Проверьте правильность вычислений. (310 +
240 = 550.)
Проверьте правильность вычислений. (310 +
240 = 550.)
М 29 (с. 14).
— Прочитайте задание. Что это? (Задача.)
— Какого типа эта задача? (Задача нового типа на сумму и разность.)
![]() Выполните разностное
сравнение данных чисел. (235 — - 135=100.)
Выполните разностное
сравнение данных чисел. (235 — - 135=100.)
![]() Что нужно сделать далее? (Значение выражения разДелить пополам: 100 : 2
= 50.)
Что нужно сделать далее? (Значение выражения разДелить пополам: 100 : 2
= 50.)
![]() Что мы установили? (Наименьшее число — 50.)
Что мы установили? (Наименьшее число — 50.)
— Что можно найти следующим действием? (Значение наибольшего числа: 50 + 135 = 185.)
![]() Какие два числа мы нашли? (50 и 185.)
Какие два числа мы нашли? (50 и 185.)
![]() Как можно удостовериться в правильности
нашего решения? (Если к 185 прибавить 50, получится 235; если из 185 вычесть
50, получится 135.)
Как можно удостовериться в правильности
нашего решения? (Если к 185 прибавить 50, получится 235; если из 185 вычесть
50, получится 135.)
М. Физкультминутка
6.
![]()
Закрепление изученного материала
Выпојшекше упражнения в тетради для самостоятельной работы № 12 (с. 10).
— Прочитайте условие задачи. На сколько больше мешков лука собрали с первой грядки? (На 4 мешка больше.)
— На сколько килограммов лука собрали больше с первой грядки? (На 200 кг больше.)
— Сколько килограммов лука в одном мешке? (200 : 4 = = 50(кг).)
![]() Прочитайте условие задачи б. На сколько
больше досок истратил первый столяр, чем второй? (На 21 доску больше.)
Прочитайте условие задачи б. На сколько
больше досок истратил первый столяр, чем второй? (На 21 доску больше.) ![]() Почему?
(Первый столяр сделал больше скамеек.)
Почему?
(Первый столяр сделал больше скамеек.)
![]() На сколько больше? (На 7— 4 = З (с.). )
На сколько больше? (На 7— 4 = З (с.). )
![]() Сколько досок уходит на изготовление одной скамейки?
(21 : з = 7@.).)
Сколько досок уходит на изготовление одной скамейки?
(21 : з = 7@.).)
— Сколько досок истратил первый столяр? (7 • 7= 49 (ДЭ.)
— Сколько досок истратил второй столяр? (7 • 4 = 28 (ДЭ.) (Самостоятельное решение задачи в. Проверка в парах.) Решение:
1) 48 — 39 = 9 (м) — во втором мотке меньше, чем в первом; 2) : 9 = 20 (руб.).
Ответ: м провода стоит 20 руб.
И. Подведение итогов урока
Домашнее задание
Учебник: № 30 (с. 14).
Урок 6. Когда известен результат разностного сравнения
Цель: развивать навыки решения задач на сумму и разность и на две разности.
1. Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Закономерность
(Закономерность: • 2, + 2; пропущенное число — 18.)
![]()
2. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Является ли 0 натуральным числом? (Нет.)
• Существует ли наименьшее натуральное число? (Натуральный ряд начинается с наименьшего числа 1.)
• Существует ли наибольшее натуральное число? Докажите это. (Не существует, так как натуральный ряд можно проДолжать бесконечно.)
• На какое число отличаются два соседних натуральных чис-
![]()
• Как называются знаки, с помощью которых записывают натуральные числа? (Цифры.)
• Сколько всего различных цифр используется для записи натуральных чисел? (9: 1, 2, З, 4, 5, 6, 7, 8, 9.) З. Устный счет
(Примеры записаны на доске.)
• При решении примеров называйте слагаемые, значение суммы, уменьшаемое, вычитаемое, значение разности.
|
20+ 8 |
50 + З |
70 + 5 |
6+ 80 |
|
74+ 10 |
56 + зо |
Ш + 89 |
30 + 61 |
|
90 - 20 |
30 -8 |
40 — 6 |
70-3 |
Ш. Работа по теме урока Работа по учебнику МЛ (с. 14).
![]() Прочитайте задание.
Что нужно сделать, чтобы получилась задача на сумму и разность, в которой
требуется найти большее из двух слагаемых? (К Данному условию присоеДинить
первое требование.)
Прочитайте задание.
Что нужно сделать, чтобы получилась задача на сумму и разность, в которой
требуется найти большее из двух слагаемых? (К Данному условию присоеДинить
первое требование.)
• Что вы найдете первым действием? (Удвоенную стоимость альбома: 52 + 4 = 56 (руб.). )
— Что нужно сделать дальше? (Полученную сумму разДелить пополам: 56 : 2 = 28 (руб.). )
• Как найти стоимость тетради? (28 — 4 = 24 (руб.).)
— Сколько стоят 3 таких альбома? (28 • З = 84 (руб.).)
— Сколько стоят 10 таких тетрадей? (24 • 10 = 240
(руб.). ) ![]() 32 (с. 15).
32 (с. 15).
![]() Прочитайте условие
задачи. Посмотрите на решение, приведенное в учебнике. Сформулируйте к условию
задачи требование, на которое можно ответить с помощью данного решения.
(Сколько граммов мааины в одном лукошке Э
Прочитайте условие
задачи. Посмотрите на решение, приведенное в учебнике. Сформулируйте к условию
задачи требование, на которое можно ответить с помощью данного решения.
(Сколько граммов мааины в одном лукошке Э
— Сколько граммов малины собрал Миша? (Ог • 2 = 10![]()
— Сколько граммов малины собрала Маша? (Ог • З = 2700(г).) lV. Физкультминутка
7. кратного сравнения
![]()
Закрепление изученного материала Работа по учебнику МВ (с. 15).
![]() Прочитайте задание. Как можно вычислить удвоенную длину большей
(красной) части карандаша? (15 + З = 18 (см).) — Как можно вычислить удвоенную
длину меньшей (синей) части карандаша? (15— З = 12 (см).)
Прочитайте задание. Как можно вычислить удвоенную длину большей
(красной) части карандаша? (15 + З = 18 (см).) — Как можно вычислить удвоенную
длину меньшей (синей) части карандаша? (15— З = 12 (см).)
![]() Как найти длину каждой части карандаша? (Полученные величины разДелить
пополам: 18 : 2 = 9 (см); 12 : 2 = 6 (см).)
Как найти длину каждой части карандаша? (Полученные величины разДелить
пополам: 18 : 2 = 9 (см); 12 : 2 = 6 (см).)
Ш. Подведение итогов урока
![]() Чему мы учились на
уроке? (Составлять и решать заДачи, размыииять.)
Чему мы учились на
уроке? (Составлять и решать заДачи, размыииять.)
Решить задачу (текст дан на отдельном листочке).
В одном хранилище было 2 одинаковых мешка с мукой, а в другом — 7 таких же мешков с мукой. Сколько килограммов муки было в каждом хранилище, если во втором было на 250 кг больше, чем в первом?
Урок 7. Когда известен результат кратного сравнения
Цель: познакомить с задачами на сумму и частное.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Блицтурнир
— Устно закончите предложения и ответьте на вопрос.
• Чтобы найти неизвестное слагаемое, нужно...
• Чтобы найти неизвестный множитель, нужно...
• Чтобы найти неизвестное уменьшаемое, нужно...
• Чтобы найти неизвестное вычитаемое, нужно...
• Назовите табличный случай деления с самым большим деЛИМЫМ. (81 : 9 = 9.)
2. Цифровой квадрат
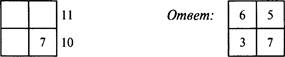
зо
![]()
З. Родственные ряды
|
2 |
4 |
6 |
З |
|
|
20 |
40 |
|
|
|
( Числа нижнего ряда в 10 раз больше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 1, в нижнем ряду — 60.)
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
На одной чаше весов 5 одинаковых яблок и 3 одинаковые груши, на другой чаше — 4 таких же яблока и 4 такие же груши. Весы находятся в равновесии. Что легче: яблоко или груша? (Масса 1 яблока равна массе 1 груши. Если с кажДой чаши весов убрать по 4 яблока и З груши, то на весах останутся 1 яблоко и 1 груша.) Ш. Работа по теме урока Работа по учебнику м 34 (с. 16).
— Рассмотрите рисунок. На сколько частей разрезан торт? (На восемь.)
![]() Во сколько раз одна часть торта меньше, чем все оставшиеся части? (В 8:
1 = 8 (раз).)
Во сколько раз одна часть торта меньше, чем все оставшиеся части? (В 8:
1 = 8 (раз).)
![]() Сколько граммов весит одна часть, если весь торт имеет массу 800 г?
(800: 100
Сколько граммов весит одна часть, если весь торт имеет массу 800 г?
(800: 100![]()
— Сколько частей положили на лопатку? (Одну.)
![]() Сколько граммов будут
весить все оставшиеся части, кроме одной? (800— 100 = 700 (г).)
Сколько граммов будут
весить все оставшиеся части, кроме одной? (800— 100 = 700 (г).)
— Как вы нашли искомое число? (С помощью вычитания уже наиДенной меньшей величины из всей суммы.) мм (с. 16-17).
![]() Прочитайте задание. На
сколько частей разделена вся полоска? (На + 5 = 6 (ч.).)
Прочитайте задание. На
сколько частей разделена вся полоска? (На + 5 = 6 (ч.).)
— Сколько метров в одной части? (30 : 6 = 5 (м).)
— Сколько метров в пяти частях? (30— 5 = 25 (м).)
![]() Какой вариант решения подходит для данной задам? (Первый.) lV.
Физкультминутка
Какой вариант решения подходит для данной задам? (Первый.) lV.
Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику МЗ6 (с. 17).
![]() Прочитайте условие задачи. Сколько учащихся занимается в двух кружках?
(45.)
Прочитайте условие задачи. Сколько учащихся занимается в двух кружках?
(45.)
— На сколько частей разделен чертеж к задаче? (На 4 + 1 =
![]()
8. кратного сравнения

Вариант заДачи. В двух бригадах работают 48 человек. Сколько человек работало в каждой бригаде, если во второй бригаде работало в 3 раза больше людей, чем в первой?
— Какого типа эта задача? (Задача на сумму и частное.) — Решите задачу. Вычислите ответ.
2. Выполнеш«е упражнения в тетради деля самостоятельной работы ЛГ2 13 (с. 11).
![]() Прочитайте условие задачи а. На сколько частей разделен чертеж к задаче?
(На три части.)
Прочитайте условие задачи а. На сколько частей разделен чертеж к задаче?
(На три части.)
![]() Чему равна длина одной части бревна? (81 : З = 27 (Дм). )
Чему равна длина одной части бревна? (81 : З = 27 (Дм). )
— Какова длина второй части бревна? (27 • 2 = 54 (Дм).)
— Прочитайте задачу б. На сколько частей разделен чертеж к задаче? (На 1 + 7= 8 (ч.).)
![]() Сколько граммов в одной части? (800 : 8 =
100 (г).)
Сколько граммов в одной части? (800 : 8 =
100 (г).)
![]() Сколько весит мед без горшка? (100 • 7=
700 (г).)
Сколько весит мед без горшка? (100 • 7=
700 (г).)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 14 (с. 12).
Урок 8. Когда известен результат кратного сравнения
Цель: продолжать обучать решению задач на сумму и частное.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
Арифметический диктант
![]() Запишите только ответы.
Запишите только ответы.
![]() Какое число в 2 раза больше 68? (136.)
Какое число в 2 раза больше 68? (136.)
![]() Во сколько раз 12 меньше 36? (В Зраза.)
Во сколько раз 12 меньше 36? (В Зраза.)
![]() Сложите 86 и 75. (161.)
Сложите 86 и 75. (161.)
![]() Разность чисел 85 и 56 увеличьте в 5 раз. (145.)
Разность чисел 85 и 56 увеличьте в 5 раз. (145.)
![]() Сумму чисел 35 и 60 увеличьте в 10 раз. (950.)
Сумму чисел 35 и 60 увеличьте в 10 раз. (950.)
![]() Из суммы чисел 48 и 36 вычтите разность чисел 100 и 76. (60.)
Из суммы чисел 48 и 36 вычтите разность чисел 100 и 76. (60.)
![]() Частное чисел 54 и 9 увеличьте в 5 раз. (30.)
Частное чисел 54 и 9 увеличьте в 5 раз. (30.)
![]() К произведению чисел 12 и 5 прибавьте 28. (88.)
К произведению чисел 12 и 5 прибавьте 28. (88.)
![]()
![]() На первой полке 27 книг, на второй на 16 книг больше, чем на первой. На
третьей полке столько книг, сколько на первой и второй вместе. Сколько книг на
третьей полке? ( 70.)
На первой полке 27 книг, на второй на 16 книг больше, чем на первой. На
третьей полке столько книг, сколько на первой и второй вместе. Сколько книг на
третьей полке? ( 70.)
![]() Из 9 л молока можно получить 1 л сливок. Сколько литров молока нужно для
получения 3 л сливок? (27 л.) Ш. Работа по теме урока Работа по учебнику ЛФ 38
(с. 18).
Из 9 л молока можно получить 1 л сливок. Сколько литров молока нужно для
получения 3 л сливок? (27 л.) Ш. Работа по теме урока Работа по учебнику ЛФ 38
(с. 18).
— Что представлено на чертеже? (Диаграмма сравнения, иалюстрирующая искомые числа.)
![]() Какого типа эта задача? (На сумму и
частное.)
Какого типа эта задача? (На сумму и
частное.)
— Что нужно сделать для того, чтобы обозначить на схеме величину всей полоски? (СоеДинить Дверазноцветные полоски в одну.)
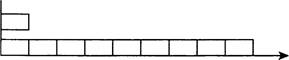
![]() Сколько частей получилось во всей
полоске? (l + 9 = Ю(ч.).)
Сколько частей получилось во всей
полоске? (l + 9 = Ю(ч.).) ![]() Что мы сделаем далее? (350 : 10 = 35 —
это меньшая часть полоски.)
Что мы сделаем далее? (350 : 10 = 35 —
это меньшая часть полоски.)
![]() Как найти большую
часть полоски? (350 — 35 = 315 — это большая часть полоски.)
Как найти большую
часть полоски? (350 — 35 = 315 — это большая часть полоски.)
![]() Какие слагаемые вы получили? (35 и 315; второе слагаемое больше первого
в 9раз: 315 : 9 = 35.)
Какие слагаемые вы получили? (35 и 315; второе слагаемое больше первого
в 9раз: 315 : 9 = 35.)
![]() 40 (с. 18).
40 (с. 18).
![]() Прочитайте задание.
Прочитайте задание.
Примем меньшее искомое число за одну часть, что позволит большее искомое число рассматривать как восемь частей. Это будет означать, что в сумме искомых чисел содержится девять частей.
— Можно ли вычислить величину одной части? (Да.)
— Как вы это сделаете? (МО : 9 = 20.)
![]() Что мы получили? (Меньшее число.)
Что мы получили? (Меньшее число.)
![]() Чему будет равно большее число? ( 180 — 20 = 160.)
Чему будет равно большее число? ( 180 — 20 = 160.)
![]() Чему равны искомые числа? (20 и 160.)
Чему равны искомые числа? (20 и 160.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ЛД 41 (с. 18).
— Прочитайте задачу. Какого она типа? (Задача на сумму и частное.)
9.
Сколько требований в задаче? ( Четыре.)
Если мы рассмотрим только первое требование вместе с условием, то какой тип задачи получится? (Стандартная задача на сумму и частное, в которой требуется найти ЛЕНЬшую из двух искомых величин.)
Примем меньшее число за одну часть (стоимость ручки). Большее искомое число — за пять частей (стоимость фломастеров).
![]() Сколько всего частей в сумме искомых чисел? ( + 5 = 6 (ч.).)
Сколько всего частей в сумме искомых чисел? ( + 5 = 6 (ч.).)
![]() Как найти стоимость ручки? (48 : 6 = 8 (руб.).)
Как найти стоимость ручки? (48 : 6 = 8 (руб.).)
![]() Сколько стоит набор фломастеров? (48 — 8 = 40 (руб.).)
Сколько стоит набор фломастеров? (48 — 8 = 40 (руб.).)
— Можно ли узнать, сколько стоят 10 таких ручек? (8 • 10 =
= 80 (руб.). )
![]() Сколько стоят З набора фломастеров? (40 • З = 120 (руб.).)
Сколько стоят З набора фломастеров? (40 • З = 120 (руб.).)
— На какое требование можно ответить с помощью выражения 48 : (5 + 1) • 5? (Сколько стоят 5 таких ручек?)
2. Выполнение упражнения в тетради для самостотельной рабсгы ЛСР 15(С. 12).
![]() Сколько частей составляют все белые шары? (Одну.)
Сколько частей составляют все белые шары? (Одну.)
— Сколько частей составляют все красные шары? (Четыре.)
![]() Сколько частей составляют все зеленые шары? (Семь.)
Сколько частей составляют все зеленые шары? (Семь.)
![]() Сколько частей в сумме искомых чисел? (1
+ 4 +7= 12 (ч.). )
Сколько частей в сумме искомых чисел? (1
+ 4 +7= 12 (ч.). ) ![]() Сколько шаров в одной части? (60 : 12 = 5
(шар.) — белых.) — Сколько шаров в четырех частях? (5 • 4 = 20(шар.) —
красных.)
Сколько шаров в одной части? (60 : 12 = 5
(шар.) — белых.) — Сколько шаров в четырех частях? (5 • 4 = 20(шар.) —
красных.) ![]() Сколько шаров в семи частях?(5 • 7 = 35
(шар.) — зеленых.)
Сколько шаров в семи частях?(5 • 7 = 35
(шар.) — зеленых.)
![]() Проверьте правильность решения. (5 + 20 + 35 = 60 (шар.).)
Проверьте правильность решения. (5 + 20 + 35 = 60 (шар.).)
Ш. Подведение итогов урока
Домашнее задание
Учебник: № 39 (с. 18).
Урок 9, Учимся решать задачи
Цель: развивать умение формулировать условия задач и решать их.
1. Организационный момент. Сообщение темы и цели урока
11. Актуализация знаний
1. Цифровой квадрат
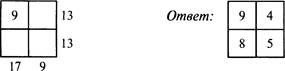
2 Поурочные разработки по математике
![]()
2. Родственные ряды
|
|
8 |
|
12 |
7 |
|
20 |
16 |
|
24 |
|
(Числа нижнего ряда в 2 раза больше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 5, в нижнем ряду — 14.)
З. Устный счет
(Примеры записаны на доске.)
![]() При решении примеров
называйте слагаемые, значение суммы, уменьшаемое, вычитаемое, значение
разности. 36 + 2 54 + З 2 + 67 1 + 78
При решении примеров
называйте слагаемые, значение суммы, уменьшаемое, вычитаемое, значение
разности. 36 + 2 54 + З 2 + 67 1 + 78
41 — 23 74 — 25 52 - 37 66 — 12
42 + 5 + 2 23 + 3+ 3
Ш. Работа по теме урока Работа по учебнику М 42 (с. 19).
![]() Прочитайте задачу.
Какою она типа? (Задача на сумму и разность.)
Прочитайте задачу.
Какою она типа? (Задача на сумму и разность.)
— Заполните таблицу.
— Что означает число 85? (Количество человек в двух
автобусах.) ![]() Что можно определить сначала? (Сначала
можно опреДелить удвоенное число человек в первом автобусе: 85 — 7= 78.)
Что можно определить сначала? (Сначала
можно опреДелить удвоенное число человек в первом автобусе: 85 — 7= 78.)
— Что находим далее? (Делим полученное число пополам, устанавливая количество человек в первом автобусе: 78 : 2 = 39.)
— Как найти число экскурсантов во втором автобусе? (С
помощью вычитания: 85 — 39 = 46 (чел.) — ми сложения: 39 + 7 = = 46 (чел.).) ![]() (с.
19).
(с.
19).
— Прочитайте задание. Как найти число, соответствующее условию «при вычитании — число в 2 раза меньше, чем при сложении»? (240 : 2 = 120.)
![]() Чему равно значение суммы двух чисел?
(120 + 120 = 240.)
Чему равно значение суммы двух чисел?
(120 + 120 = 240.)
![]() А значение их разности? (240 — 120 120.)
А значение их разности? (240 — 120 120.)
![]() Чему равны искомые числа? (120 и 120.)
Чему равны искомые числа? (120 и 120.)
![]() Какого типа эта задача? (Задача на сумму и разность.) Лё 44€. 19).
Какого типа эта задача? (Задача на сумму и разность.) Лё 44€. 19).
![]() Чему равно удвоенное
число меньшего количества денег? (45 руб. 50 коп. — 5 руб. 50 коп. = 40руб.)
Чему равно удвоенное
число меньшего количества денег? (45 руб. 50 коп. — 5 руб. 50 коп. = 40руб.)
— Что делаем далее? (Находим стоимость линейки, устанавливая меньшую стоимость.)
9.
— Как это сделать? (40руб. : 2 = Труб.)
Сколько стоит ручка? (Труб. + 5руб. 50 коп. = 25руб. 50коп.) Сколько стоят 5 линеек? (20 руб. • 5 = 100руб.)
Покажите на рисунке, какая часть полоски изображает стоимость двух линеек.
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику
М 45 (с. 20).
— Прочитайте задание. Сделайте чертеж к задаче.
![]() На сколько частей надо разбить полоску? (На четыре равные части.)
На сколько частей надо разбить полоску? (На четыре равные части.)
— Сколько частей полоски будет соответствовать числу занимающихся в первой секции? (Одна.)
— Чему будут соответствовать
оставшиеся три части? (Числу занимающихся во второй секции.) ![]()
— Сколько всего учащихся занимается в двух секциях? (80.)
![]() Чему равна сумма равных частей? (1 + З = 4 (ч.).)
Чему равна сумма равных частей? (1 + З = 4 (ч.).)
![]() Сколько учащихся занимается в первой секции? (80 : 4 = = 20
Сколько учащихся занимается в первой секции? (80 : 4 = = 20![]()
— Сколько учащихся занимается во
второй секции? (20 • З = = 60![]()
![]() Запишите решение в тетрадь.
Запишите решение в тетрадь.
М 46 (с. 20).
— Прочитайте задачу. Какого она типа? (Задача на сумму и разность.)
— Что можно найти сначала? (Удвоенную длину меньшей части:
![]()
![]() Чему равна меньшая часть? (10 : 2 = 5
(см).)
Чему равна меньшая часть? (10 : 2 = 5
(см).) ![]() Чему равна большая часть? (5 + 2 = 7
(см). )
Чему равна большая часть? (5 + 2 = 7
(см). ) ![]() 47 (с. 20).
47 (с. 20).
![]() Прочитайте задачу.
Какою она типа? (Задача на сумму и разность.)
Прочитайте задачу.
Какою она типа? (Задача на сумму и разность.)
![]() Чему равен периметр? (24 см.)
Чему равен периметр? (24 см.)
— Что можно вычислить, зная, чему равен периметр прямоугольника? (Сумму длин двух его сторон: 24 : 2= 12 (см).)
— Что можно сказать о сторонах прямоугольника? (Стороны прямоугольника будут равны, как и в преДыДущей задаче, 5 см и 7 см.)
2. Вьтолюше упражнения в тетрад для самостоятельной
работы ![]() 18 (с. 13).
18 (с. 13).
— Прочитайте задание а. Что это за задание? (Это задача.)
Какого типа эта задача? (Задача на сумму и разность.) Выполните разностное сравнение данных чисел. ( 135 — 49 = = 86.)
— Что нужно делать далее? (Значение выражения разделить пополам: 86 : 2 = 43.)
![]() Что вы установили? (Меньшее число — 43.)
Что вы установили? (Меньшее число — 43.)
— Что можно найти следующим действием? (Большее число: 135-43 = 92.)
![]() Какие два числа мы нашли? (43 и 92.)
Какие два числа мы нашли? (43 и 92.)
![]() Как можно
удостовериться в правильности решения? (Если к 43 прибавить 92, получится 135;
если из 92 вычесть 43, получится 49.)
Как можно
удостовериться в правильности решения? (Если к 43 прибавить 92, получится 135;
если из 92 вычесть 43, получится 49.)
![]() Прочитайте задание б.
С чего вы начнете решать задачу? (Примем меньшее число за одну часть, а большее
число — за восемь частей. Это будет означать, что в сумме искомых чисел
соДержится Девять частей.)
Прочитайте задание б.
С чего вы начнете решать задачу? (Примем меньшее число за одну часть, а большее
число — за восемь частей. Это будет означать, что в сумме искомых чисел
соДержится Девять частей.)
![]() Можно ли вычислить величину одной части?
(Да.)
Можно ли вычислить величину одной части?
(Да.)
— Как вы это сделаете? (63 : 9 = 7.)
— Что мы получили? (Меньшее число.)
![]() Чему будет равно большее число? (63 —
7=56.)
Чему будет равно большее число? (63 —
7=56.)
— Чему равны искомые числа? (7 и 56.)
— Проверьте правильность решения: (56 + 7= 63; 56: 7= 8)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 20 (с. 14—15).
Урок 1 О. Учимся решать задачи
Цель: развивать умение формулировать и решать задачи.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
1. Волшебные квадраты
— Заполните пустые клетки цифрами от 0 до 8. Волшебная сумма равна 12.
|
|
|
|
|
пап |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
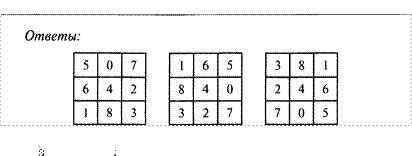
![]() Решите задачу устно.
Решите задачу устно.
В квартирах № 1, 2, З жили три котенка: белый, черный и рыжий. В квартирах № 1 и 2 жил не черный котенок. Белый котенок жил не в квартире № 1. В какой квартире жил каждый котенок? ( ЧерныЙ котенок жил в квартире М З, белый — в квартире М 2, а рыжий — в квартире № 1.) З. Устный счет
(Примеры записаны на доске.)
![]() При
решении примеров называйте слагаемые, значение суммы, уменьшаемое, вычитаемое,
значение разности. 23 74 + 25 52 + 37 12 + 66 47 — 6 38-5 59 — 7 58 - зо
При
решении примеров называйте слагаемые, значение суммы, уменьшаемое, вычитаемое,
значение разности. 23 74 + 25 52 + 37 12 + 66 47 — 6 38-5 59 — 7 58 - зо ![]()
61 + 5+3 7 + 22 + ![]()
Ш. Работа по теме урока Работа по учебнику ЛГ2 48 (с. 20).
![]() Прочитайте задание. Какого типа эта
задача? (Задача на сумму и частное.)
Прочитайте задание. Какого типа эта
задача? (Задача на сумму и частное.)
![]() Как вы будете решать
задачу? (Разделим полоску на три равные части. Пусть одна часть — это меньшая
сторона, а две части — большая сторона.)
Как вы будете решать
задачу? (Разделим полоску на три равные части. Пусть одна часть — это меньшая
сторона, а две части — большая сторона.)
![]() Чему
равна вся полоска? (Длине двух сторон, ши 12 см.)
Чему
равна вся полоска? (Длине двух сторон, ши 12 см.)
![]() Сколько частей в полоске? (1 + 2 = З
(ч.).)
Сколько частей в полоске? (1 + 2 = З
(ч.).)
![]() Найдите
меньшую сторону. (12 : З = 4 (см).)
Найдите
меньшую сторону. (12 : З = 4 (см).)
— Чему равна большая сторона прямоугольника? (4 • 2 — = 8 (см).)
![]() Чему
равны длины сторон прямоугольника? (8 см и 4 см.) М 49 (с. 21).
Чему
равны длины сторон прямоугольника? (8 см и 4 см.) М 49 (с. 21).
— Прочитайте задание. Чему равен периметр прямоугольника? (24 см.)
— Что можно найти? (Сумму длин двух противоположных сторон прямоугольника: 24 см : 2 = 12 (см).)
— Чему равны стороны прямоугольника? (4 см и 8 см, как и в преДыДущей задаче.)
![]() Проверьте
правильность решения. ((4 + 8) • 2 = 24 (см). )
Проверьте
правильность решения. ((4 + 8) • 2 = 24 (см). )
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() (с. 21).
(с. 21).
![]() Прочитайте условие задачи. Выполните разностное сравнение двух множеств
тетрадей по числу элементов. (10 — 7 = = З (тет.).)
Прочитайте условие задачи. Выполните разностное сравнение двух множеств
тетрадей по числу элементов. (10 — 7 = = З (тет.).)
![]() Как узнать стоимость одной тетради? ( 75
: 3= 25 (руб.).)
Как узнать стоимость одной тетради? ( 75
: 3= 25 (руб.).)
![]() Можно ли узнать стоимость 5 тетрадей?
(Да: 25 • 5 = 125 (руб.).) м 51 (с. 21).
Можно ли узнать стоимость 5 тетрадей?
(Да: 25 • 5 = 125 (руб.).) м 51 (с. 21).
Вариант заДачи. Пять мешков картофеля весят на 50 кг больше, чем три таких же мешка с луком. Сколько килограммов овощей в одном мешке? Сколько килограммов овощей в трех таких мешках? Сколько всего килограммов овощей во всех мешках?
Решение:
Первый способ:
1) 5 — 3 = 2 (меш.) — с картофелем больше, чем с луком;
2)
50 : 2 = 25 (кг) — в одном мешке; ![]()
З) 25 • З = 75 (кг) — в 3 мешках;
4) 25 • 5 = 125 (кг) — в 5 мешках;
5) 75 + 125 = 200 (кг) — во всех мешках.
1) 5 — 3 = 2 (меш.) — с картофелем больше, чем с луком;
2) 50 : 2 = 25 (кг) — в одном мешке;
3) 25 • 3 = 75 (кг) — в 3 мешках;
4) 25 • (5 + 3) = 200 (кг) — во всех мешках.
Ответ: в одном мешке 25 кг овощей, в 3
таких мешках 75 кг овощей, во всех мешках 200 кг овощей. ![]() 52 (с. 21).
52 (с. 21).
— Прочитайте задание. Рассмотрите фигуры.
![]() Чему равен результат разностного сравнения площадей двух фигур? (З кв.
см.)
Чему равен результат разностного сравнения площадей двух фигур? (З кв.
см.)
— Сколько квадратов в первой фигуре? ( 7.)
![]() Сколько квадратов во второй фигуре? (10.)
Сколько квадратов во второй фигуре? (10.)
— Чему равен результат разностного сравнения этих чисел?
— Что означает полученное число 3? (Это плОщДь З кв. см,
т. е. один кваДрат tuteem площаДь 1 кв. см.)
— Чему равна площадь первой фигуры? (1 • 7= 7 (кв. см).)
— Чему равна площадь второй фигуры? (1 • 10 = 10 (кв. см).) 2. Выполнение утрахмеюш в тетради для самостоягельной рабшы М 21 (с. 15-16).
(Самостоятельное выполнение. Вариант 1 — а, б; вариант 2 — в, г.)
1 1 . Алгоритм умножения столбиком
![]()
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 19 (с. l4).
Урок 1 1 . Алгоритм умножения столбиком
Цель: познакомить с алгоритмом умножения столбиком.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: — З, • 2; пропущенное число — 10.)
2. Цифровой квадрат
|
6 |
4 |
|
|
|
|
|
4 |
|
|
|
10 Ответ:
П В
З. Родственные ряды
|
З |
12 |
27 |
21 |
|
|
|
4 |
|
7 |
5 |
( числа нижнего ряда в З раза меньше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 15, в нижнем ряду — 9.)
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Кузнецу принесли пять обрывков цепи по три звена в каждом и попросили соединить в одну цепь. Кузнец выполнил заказ, раскрыв только три звена. Как он это сделал? (Кузнец раскрьи три звена одного обрывка цепи и шии соединил оставшиеся четыре обрывка.) Ш. Работа по теме урока Работа по учебнику
ЛГ9 53-55 (с. 22-24).
(Коллективное выполнение с комментированием. Знакомство с алгоритмом умножения столбиком по словарику учебника (с. 116).)
![]()
lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 56 (с. 24).
(Работа в парах.)
2. Выполнение упражнений в тетради для самостоятельной работы
ЛГУ 25 (С. 18).
(Самостоятельное выполнение.) Решение: 207 57 = 11 799 (мин).
Ответ: на пошив 207 наволочек потребуется 1 1 799 мин. м 26 (с. 18).
(Коллективное выполнение с комментированием у доски.)
Вариант заДачи. С первого участка собрали 42 огурца, со второго участка — в 1 раз больше, чем с первого участка, а с третьего — в 65 раз больше, чем со второго. Сколько всего огурцов собрали с трех участков?
Решение:
1) 42 • 11 = 462 (ог.) — на втором участке; 2) 462 • 65 = 30 030 (ог.) — на третьем участке; 3) 42 + 462 + зо озо = зо 534 (ог.).
Ответ: всего собрали 30 534 огурца. З. Работа по учебнику М 57 (с. 24).
— Прочитайте задание. Что нужно сделать? (Установить соответствие между примерами и результатами вычислениЙ.)
![]() Можно ли установить это соответствие, не выполняя вычислений? (Можно.)
Можно ли установить это соответствие, не выполняя вычислений? (Можно.)
![]() Как вы будете рассуждать? (Примерный ответ. Число 540 в 10 раз больше
числа 54, значит, и результат умножения числа 467 на число 540 должен быть в 10
раз больше, чем результат умножения числа 467 на число 54. Из предложенных
результатов число 252 180 в 10 раз больше числа 25 218. Следовательно, число 25
218 — результат умножения числа 467 на число 54, число 252 180 — результат
умножения числа 467 на число 540, а число 235 368 — результат умножения числа
467 на число 504.) Ш. Подведение итогов урока
Как вы будете рассуждать? (Примерный ответ. Число 540 в 10 раз больше
числа 54, значит, и результат умножения числа 467 на число 540 должен быть в 10
раз больше, чем результат умножения числа 467 на число 54. Из предложенных
результатов число 252 180 в 10 раз больше числа 25 218. Следовательно, число 25
218 — результат умножения числа 467 на число 54, число 252 180 — результат
умножения числа 467 на число 540, а число 235 368 — результат умножения числа
467 на число 504.) Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 22—24 (с. 17).
Поупражняемся в вычислениях столбиком
![]()
Урок 1 2, Поупражняемся в вычислениях столбиком
Цель: развивать умение вычитать и умножать столбиком.
1. Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Какие натуральные числа называются однозначными? (Числа, запись которых состоит из одного знака — одной цифры. Например: 1, 2, З, 4, 5, 6, 7, 8, 9).
•
Какие натуральные числа называются многозначными? ( Числа, запись
которых состоит из двух (и более) знаков ![]() цифр. Например: 10,
234, 6547, 78 956 и др.)
цифр. Например: 10,
234, 6547, 78 956 и др.)
2. Устный счет
(Примеры записаны на доске.)
![]() При решении примеров называйте слагаемые, значение
При решении примеров называйте слагаемые, значение
суммы, уменьшаемое, вычитаемое, значение разности. 74+ 16 52 + 28 34 + 36 18 + 32
33-5 46 — 9 42 -6 24 -7
79 — 5—3 68 — 30 —4
Ш. Работа по теме урока Работа по учебнику № 58 (с. 25).
(Самостоятельное выполнение. Проверка.) ![]() 59
(с. 25).
59
(с. 25).
![]() Прочитайте задание.
Что необходимо сделать сначала? (Проверить правильность умножения числа 2052 на
кажДое разрядное слагаемое второго множителя — 423.)
Прочитайте задание.
Что необходимо сделать сначала? (Проверить правильность умножения числа 2052 на
кажДое разрядное слагаемое второго множителя — 423.)
![]() Обязательно ли записывать нули в конце
записи результатов умножения на 2 десятка и 4 сотни? (Не обязательно.)
Обязательно ли записывать нули в конце
записи результатов умножения на 2 десятка и 4 сотни? (Не обязательно.) ![]() Почему?
(При записи столбиком четко определяется местоположение кажДого разряда, и
отсутствие цифры в Данной позиции означает, что эту позицию занимает цифра 0,
хотя она и не написана.)
Почему?
(При записи столбиком четко определяется местоположение кажДого разряда, и
отсутствие цифры в Данной позиции означает, что эту позицию занимает цифра 0,
хотя она и не написана.)
![]() На что нужно обратить
внимание на этапе сложения полученных промежуточных результатов? (На то, что в
четвертом примере из заДания № 58 как раз и записаны те же самые слагаемые,
только все нули в той записи присутствуют.)
На что нужно обратить
внимание на этапе сложения полученных промежуточных результатов? (На то, что в
четвертом примере из заДания № 58 как раз и записаны те же самые слагаемые,
только все нули в той записи присутствуют.)
ЛФ 60 (с. 25).
(Работа в парах. Взаимопроверка. Ответы записаны на доске: ll 740, 99 790, 686 790.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 61 (с. 25).
61 (с. 25).
— Вспомните правило о порядке выполнения действий. 2. Выполнею«е упражнений в тетради для самостотельной работы №27, 29 (с. 19).
(Самостоятельное выполнение. Взаимопроверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 28 (с. 19).
Урок 1 З. Тысяча тысяч, или миллион
Цель: познакомить с новой разрядной единицей — миллионом.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
|
5 |
|
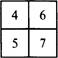 10 Ответ:
10 Ответ:
12 9![]()
2. Родственные ряды
|
|
23 |
15 |
|
19 |
|
2 |
|
6 |
12 |
|
( Числа нижнего ряда на 9 меньше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 21, в нижнем ряду — 10.) З. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Квадрат со стороной м разрезали на
квадраты со стороной ![]() см и выстроили их в один ряд в виде
полосы шириной см. Полоса какой длины получилась? (Разрежем кваДрат на полосы
см и выстроили их в один ряд в виде
полосы шириной см. Полоса какой длины получилась? (Разрежем кваДрат на полосы
ШИРИНОЙ 1 см. Таких полос длиной 1 м будет всего 100. Значит, Длина всей полосы ТОм.)
lll. Работа по теме урока
1. Работа по учебнику М 62 (с. 26).
— Из какого числа маленьких кубиков состоит кубик, изображенный на рисунке? (Из 1000.)
![]() Как вы это посчитали? (10 • 10 • 10 =1000
(ед.).)
Как вы это посчитали? (10 • 10 • 10 =1000
(ед.).)
Если из 1000 таких кубиков построить новый куб, то в нем будет содержаться 1000 • 1000 маленьких кубиков.
![]() Как называется число,
которое получается в результате увеличения числа 1000 в 1000 раз? (Мииион.)
Как называется число,
которое получается в результате увеличения числа 1000 в 1000 раз? (Мииион.)
— Сколько раз нужно сложить число 1000 с самим собой, чтобы получить число 000 000? (1000раз.) Миллион записывают так: 1 000 000. — Сколько знаков в этом числе? (Семь.)
— Какое это число? (Многозначное.)
Миллион — это наименьшее семизначное число.
№ 63, 64 (с. 27).
(Коллективное выполнение с комментированием у доски.)
(Коллективное выполнение.)
Какое число предшествует числу миллион в натуральном ряду чисел? (999 999.)
— А какое число следует за числом миллион? (1 ООО 001.) ![]() Чему
равен результат разностного сравнения соседних натуральных чисел? (Всегда числу
1: 1 ООО ООО — 999 999 = 1,
Чему
равен результат разностного сравнения соседних натуральных чисел? (Всегда числу
1: 1 ООО ООО — 999 999 = 1,
![]()
2. Выполнекме упражнения в тетради для самостоятельной работы м зо (с. 20).
(Выполнение в соответствии с заданиями.) З. Работа по учебнику
Л) 67(с. 27).
![]() Что такое кратное
сравнение? (Сравнение чисел с помощью Деления одного числа на Другое.
ОпреДеление того, сколько раз Делитель содержится в Делимом, во сколько раз
Делимое больше Делителя иаи Делитель меньше Делимого.)
Что такое кратное
сравнение? (Сравнение чисел с помощью Деления одного числа на Другое.
ОпреДеление того, сколько раз Делитель содержится в Делимом, во сколько раз
Делимое больше Делителя иаи Делитель меньше Делимого.)
![]() Используя какое правило, можно выполнить это сравнение? (Правило Деления
на число 10.)
Используя какое правило, можно выполнить это сравнение? (Правило Деления
на число 10.)
1.
Работа по
учебнику ![]() 68 (с. 27).
68 (с. 27).
(Устное выполнение.) ![]() 69 (с. 27).
69 (с. 27).
Вариант заДачи. В хозяйстве собрали 100 т картофеля, а свеклы — в 10 раз больше. Сколько килограммов свеклы собрали в этом хозяйстве?
2. Выполекме упражнения в тирам для самосттељной —гы лгу 33 (с. 21).
а) Решение: 27 500 000 • 2 = 55 000 000 (л).
ОТВеТ.• за два года сердце перекачает 55 000 000 л крови.
6) Решение: 000 000 - 8 000 000 = 92 000 000 (от.).
Ответ: в природе 92 000 000 оттенков других цветов.
И. Подведение итогов урока
— С какой разрядной единицей вы сегодня познакомились?
Домашнее задание
Тетрадь для самостоятельной работы: № 31, 32 (с. 20—21).
Цель: познакомить с разрядом единиц мюлионов и классом миллионов.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
Арифметический диктант
![]() Запишите только ответы.
Запишите только ответы.
• Запишите число, в котором 32 десятка. (320.)
• Какое число стоит между числами 1398 и 1400? (1399.)
• 200 увеличьте в 3 раза, полученное произведение уменьшите на 600, полученное число увеличьте в 6 раз, прибавьте 75. ( 75.)
• Число 48 увеличьте на 72. (120.)
• 500 без 59. (441.)
•
На сколько разность чисел 900 и 150 меньше суммы чисел ![]() и 280? (На
540.)
и 280? (На
540.)
• Найдите периметр квадрата со стороной 5 дм. (20 дм.)
• Магазин работает с 11 ч утра до 8 ч вечера. Сколько часов открыт магазин? (9 ч.)
Разряд единиц миллионов и класс миллионов
![]()
• Продолжительность жизни ели 300 лет, что на 270 лет меньше продолжительности жизни сосны. Сколько может жить сосна? (570лет.)
• Дуб на 16 м ниже березы. А береза на 12 м ниже сосны. Какой высоты дуб и береза, если высота сосны 36 м? (Дуб— 8 м, береза — 24 м.)
Ш. Работа по теме урока Работа по учебнику № т (с. 28).
1 000 000 — это наименьшее семизначное число, единица третьего масса — класса миллионов. В массе миллионов три разряда: единицы миллионов, десятки миллионов и сотни МШШИОНОВ.
Миллионы читают так же, как простые единицы:
10 тысяч — это десяток тысяч.
10 десятков тысяч — это сотня тысяч.
10 сотен тысяч — это I тысяча тысяч, или миллион.
Единицы, десятки, сотни составляют класс единиц (первый класс).
Единицы тысяч, десятки тысяч, сотни тысяч — класс тысяч (второй класс).
Единицы миллионов, десятки миллионов, сотни миллионов — класс миллионов (третий класс).
Три нуля в записи какого-либо класса показывают отсутствие единиц данного класса.
Чтобы прочитать многозначное число:
1) его разбивают на классы, отсчитывая справа по три цифры;
2) считают, сколько в числе единиц каждого класса, начиная с высшего (название класса единиц не произносят). м 71 (с. 28).
— Сколько разрядов в каждом классе? (Три.)
— Как называются эти разряды? (ЕДиницы миллионов — сеДьиой разряд, Десятки МИлОНОВ — восьмой разряд, сотни МИЛЛИОнов — Девятый разряд.)
![]() Представьте число 1 1 11 1 1 1 в виде суммы разрядных слагаемых. (1
000000 + 100000 + 10000 + + + 10 + 1.)
Представьте число 1 1 11 1 1 1 в виде суммы разрядных слагаемых. (1
000000 + 100000 + 10000 + + + 10 + 1.) ![]() Какое из этих слагаемых самое большое? (1
ООО 000.)
Какое из этих слагаемых самое большое? (1
ООО 000.)
![]() К какому классу оно относится? (К третьему классу — классу МИИИОНОВ.)
К какому классу оно относится? (К третьему классу — классу МИИИОНОВ.) ![]() 72
(с. 28).
72
(с. 28).
![]() Прочитайте задание.
Какие разрядные слагаемые относятся к разряду единиц миллионов? (1 ООО ООО, 2
ООО ООО, 3000000, 4000000, 5000000, 6000000, 7000000, 8000000, 9000000.)
Прочитайте задание.
Какие разрядные слагаемые относятся к разряду единиц миллионов? (1 ООО ООО, 2
ООО ООО, 3000000, 4000000, 5000000, 6000000, 7000000, 8000000, 9000000.)
![]()
Работа по учебнику м 73 (с. 29).
— Выполните задание. Сколько знаков в данном числе? (Девять знаков, это Девятизначное число, в состав которого входят разрядные слагаемые всех Девяти разрядов.) М 74 (с. 29).
(Коллективное выполнение с записью на доске.)
![]() Как нужно проводить
разбиение на классы? (Разбиение на классы нужно произвоДить, отсчитывая по три
разряда справа налево.)
Как нужно проводить
разбиение на классы? (Разбиение на классы нужно произвоДить, отсчитывая по три
разряда справа налево.)
— Как правильно читать число? (Нужно
разбить его запись на классы, отсчитывая по три разряда справа налево, после
чего называть кажДое из полученных трехзначных чисел ![]() с Добавлением
названия соответствующего класса. Начинать называть нужно со старшего класса,
название масса еДиниц произносить не нужно.)
с Добавлением
названия соответствующего класса. Начинать называть нужно со старшего класса,
название масса еДиниц произносить не нужно.)
![]() Прочитайте числа,
данные на доске. 125 603 250, 36 008 012, 5 005 005.
Прочитайте числа,
данные на доске. 125 603 250, 36 008 012, 5 005 005.
Ш. Подведение итогов урока
![]() С каким разрядом вы познакомились?
(ЕДиниц миллионов.)
С каким разрядом вы познакомились?
(ЕДиниц миллионов.)
Домашнее задание
Тетрадь для самостоятельной работы: № 35, 36 (с. 22).
Урок 15. Когда трех классов для записи числа недостаточно
Цели: познакомить с числами, для записи которых трех классов (девяти разрядов) недостаточно; ввести число «миллиард».
1. Организационный момент. Сообщение темы и целей урока ll. Актуализация знаний
1. Цифровой квадрат
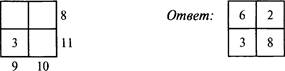
Когда трех классов для записи числа недостаточно
![]()
2. Родственные ряды
|
2 |
8 |
|
20 |
|
|
8 |
|
|
26 |
7 |
( Числа нижнего ряда на 6 больше соответствующих чисел нижнего ряда. В верхнем ряду пропущено число 1, в нижнем ряду —
З. Логическая задача
— Решите задачу устно.
Винни-Пуху в день рождения подарили бочонок с медом массой 7 кг. Когда Винни-Пух съел половину меда, то бочонок с оставшимся медом стал весить 4 кг. Сколько килограммов меда было первоначально в бочонке? (Оставшаяся половина меда в 60чонке имеет массу 7 кг — 4 кг = Зкг. Значит, весь мед в бочонке имеет массу З кг • 2 = 6 кг.)
Ш. Работа по теме урока Работа по учебнику М 76 (с. 30).
![]() Можно ли это число
записать в таблицу разрядов и классов, которое состоит из трех классов? (Нет.)
Можно ли это число
записать в таблицу разрядов и классов, которое состоит из трех классов? (Нет.)
Миллиард — единица четвертого класса. Для записи числа 1 000 000 000 требуется дополнить уже имеющуюся таблицу четвертым классом — классом миллиардов.
(Знакомство с понятием «класс миллиардов» по словарику учебника (с. 117).)
![]() Сколько разрядов в
классе миллиардов? (В юаассе мшииардов тоже три разряда.)
Сколько разрядов в
классе миллиардов? (В юаассе мшииардов тоже три разряда.)
Есть числа, которые состоят из единиц пятого, шестого и т. д. классов, но они используются редко.
М 77 (с. 30).
(Письменное выполнение с записью на доске. Учащиеся обращаются к словарику учебника (с. 119).)
— В какой стране число жителей превышает 1 млрд человек?
(В Китае.)
— Как называют самых богатых людей в мире? (МшииарДеры.) ![]() Каково
расстояние от Земли до Солнца? (150лин км.)
Каково
расстояние от Земли до Солнца? (150лин км.)
![]() Преобразуйте это расстояние в метры.
(1 км = 1000 м; 150млн км = 150 000 • 1000 = 150 000 000 ОООМ =
Преобразуйте это расстояние в метры.
(1 км = 1000 м; 150млн км = 150 000 • 1000 = 150 000 000 ОООМ =
— 150 МЛРД М.)
![]()
1.
Работа по учебнику ![]() 78 (с. 30). (Коллективное выполнение с
комментированием.) ЛГ2 79 (с. 30).
78 (с. 30). (Коллективное выполнение с
комментированием.) ЛГ2 79 (с. 30).
(Устное выполнение.)
2. Выполнение упражнений в тетради для самостоятельной работы
.№37, 39 (с. 23).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
Ш. Подведение итогов урока
![]() С какими числами вы
познакомились на уроке? (Ответы детей.)
С какими числами вы
познакомились на уроке? (Ответы детей.)
Домашнее задание
Тетрадь для самостоятельной работы: № 38 (с. 23).
Урок 16. Поупражняемся в сравнении чисел и повторим пройденное
Цели: развивать навыки поразрядного сравнения многозначных чисел; повторить пройденный материал.
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
1. Закономерность
(Закономерность: — 1, • 2; пропущенное число — 12.)
2. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
В деревне Простоквашино на скамейке перед домом сидят дядя Федор, кот Матроскин, пес Шарик и почтальон Печкин. Если Шарик, сидящий крайним слева, сядет между Матроскиным и дядей Федором, то дядя Федор окажется крайним слева. Кто где сидит?
(Слева направо сиДят: Шарик, дядя ФеДор, Матроскин, Печкин.)
Поупражняемся в сравнении чисел и повторим пройденное
![]()
З. Устный счет
(Примеры записаны на доске.)
![]() При решении примеров
называйте слагаемые, значение суммы, уменьшаемое, вычитаемое, значение
разности.
При решении примеров
называйте слагаемые, значение суммы, уменьшаемое, вычитаемое, значение
разности.
28 + 5 37 + 9
8 + 36 7 + 16
76-7 66 _ 9
38-8 77 — 7
49— — 20 86 - 50 36
Ш. Работа по теме урока Работа по учебнику м 80, 81 (с. 31).
— Запишите числа данной группы в один столбик, соблюдая поразрядный принцип.
— После этого проставьте (карандашом) порядковые номера
над каждым числом, а потом запишите эти числа в строчку, соблюдая установленную
нумерацию. ![]() 82 (с. 31).
82 (с. 31).
(Самостоятельное выполнение.) ![]() 83 (с. 31).
83 (с. 31).
(Выполнение с комментированием у доски.)
— Что нужно сделать сначала? (Выполнить разностное сравнение Данных величин и установить удвоенную длину меньшей части: 587 см — 37 см = 550 см.)
![]() Как найти меньшую
часть ленты? (РазДелить полученное число пополам: 550 см : 2 = (500 см + 50 см)
: 2 = 500 см : 2 +
Как найти меньшую
часть ленты? (РазДелить полученное число пополам: 550 см : 2 = (500 см + 50 см)
: 2 = 500 см : 2 + ![]() +25см = 275см.)
+25см = 275см.)
— Чему равна большая часть ленты? (275см + 37 см = 312 см.)
— Назовите длины частей ленты. (275 см и 312 см.)
![]() Какого типа эта задача? (Задача на сумму и разность.)
Какого типа эта задача? (Задача на сумму и разность.) ![]() 84 (с. 31).
84 (с. 31).
(Выполнение с комментированием у доски.)
![]() С чего вы начнете решать задачу? (Примем меньшую часть массы за одну
часть, а большую — за пять частей.)
С чего вы начнете решать задачу? (Примем меньшую часть массы за одну
часть, а большую — за пять частей.) ![]() Сколько всего частей? (1 + 5 = 6 (ч.).)
Сколько всего частей? (1 + 5 = 6 (ч.).)
![]() Как найти меньшую часть массы? (1 ц 80 кг : 6 = 180 кг : 6 =
Как найти меньшую часть массы? (1 ц 80 кг : 6 = 180 кг : 6 =
![]() Найдите большую часть массы. (30 кг • 5 =
150 кг.)
Найдите большую часть массы. (30 кг • 5 =
150 кг.)
![]() Назовите найденные величины массы. (30 кг
и 150 кг, т. е.
Назовите найденные величины массы. (30 кг
и 150 кг, т. е.
1 ц 50 кг.)
М. Физкультминутка
![]()
V. Закрепление изученного материала Работа по учебнику М 86, 87 (с. ЗЭ.
— Прочитайте задания. Какие числа нужно записать?
(1 111 10000111.) м 88 (с. 32).
![]() Выполните разностное сравнение двух множеств пакетов молока по числу
элементов. (8 — 5 = З (пак.).)
Выполните разностное сравнение двух множеств пакетов молока по числу
элементов. (8 — 5 = З (пак.).)
![]() Как найти стоимость
одного пакета молока? (45 : З — — 15 (руб.).)
Как найти стоимость
одного пакета молока? (45 : З — — 15 (руб.).)
![]() Как узнать стоимость 4 пакетов молока? (15 • 4 = 60 (руб.).)
Как узнать стоимость 4 пакетов молока? (15 • 4 = 60 (руб.).)
М 89 (с. 32).
Вариант заДачи на сумму и разность. Две разные ручки стоят 24 руб. Одна из них на 4 руб. дороже, чем другая. Сколько стоит та ручка, которая дешевле?
Вариант заДачи на сумму и частное. В двух корзинах лежат 72 яблока, причем в одной в 5 раз больше, чем в другой. Сколько яблок лежит в той корзине, где их больше?
№ 90 (с. 32).
— Прочитайте задачу. Какого она типа? (Эта задача двух типов: на сумму и разность и на сумму и частное.)
— Как будете решать задачу? (Примем меньшую часть тощаДи за одну часть, а большую часть площади — за четыре части.)
— Сколько всего частей? (1 + 4 = 5 (ч.).)
![]() Как
найти меньшую часть? (1000 кв. м : 5 = 200 кв. м.)
Как
найти меньшую часть? (1000 кв. м : 5 = 200 кв. м.)
![]() Как найти большую часть? (Н кв. м + о кв.
м = 800 кв. м.)
Как найти большую часть? (Н кв. м + о кв.
м = 800 кв. м.) ![]() Какую площадь имеет меньшая из двух
частей? (200 кв. м.)
Какую площадь имеет меньшая из двух
частей? (200 кв. м.)
— Проверьте правильность решения. (200 кв. м • 4 = 800 кв. м; 200 кв. м + 800 кв. м = 1000 кв. м.)
— Какими еще способами можно решить задачу?
Второй способ:
1) 1000 кв. м — 600 кв. м = 400 кв. м — удвоенная площадь меньшей части;
2) 400 кв. м : 2 = 200 кв. м — площадь меньшей части;
3) 600 кв. м + 200 кв. м = 800 кв. м — площадь большей части.
Третий способ:
1) 4 — = 3 (ч.) — разностное сравнение частей;
2) 600 кв. м : 3 = 200 кв. м — площадь меньшей части;
3) 600 кв. м + 200 кв. м = 800 кв. м. — площадь большей части.
![]() Какого типа эта задача? (Задача на
разность и частное.)
Какого типа эта задача? (Задача на
разность и частное.)
И. Подведение итогов урока
Домашнее задание
Учебник: № 85 (с. 31).
Может ли величина изменяться?
![]()
Урок 17. Может ли величина изменяться?
Цель: познакомить с существованием постоянных и переменных величин.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
15 Ответ: 15 |
7 |
8 |
|
|
|
|
|
16 14
2. Родственные ряды
|
|
5 |
|
25 |
45 |
|
6 |
|
З |
5 |
|
( числа нижнего ряда в 5 раз меньше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 15, в нижнем ряду — 9.)
З. Устный счет
(Примеры записаны на доске.) ![]() Выразите.
Выразите.
16 м 50 см — ... см 2 км 567 м = ... м
![]() 86 ц = ... .
кг
86 ц = ... .
кг
3 т 482 кг = ... кг
6 ц 08 кг = кг
Ш. Работа по теме урока Работа по учебнику ЛФ 91 (с. 33-34).
(Устное выполнение.)
![]() Рассмотрите прямоугольники.
Рассмотрите прямоугольники.
![]() Какова ширина прямоугольников? (Она оДинаковая: 2 см.)
Какова ширина прямоугольников? (Она оДинаковая: 2 см.) ![]() Какова длина
всех прямоугольников? (Она разная: 1 — 5 см, 2— 4 см, З— 6 см, 4— З см.)
Какова длина
всех прямоугольников? (Она разная: 1 — 5 см, 2— 4 см, З— 6 см, 4— З см.)
![]() Какая величина у данных фигур не
изменяется? (Ширина.)
Какая величина у данных фигур не
изменяется? (Ширина.)
Такую величину называют постоянной.
![]() Какая величина изменяется? (Шина.)
Какая величина изменяется? (Шина.)
Такая величина называется переменной. Длина переходит в разряд переменных величин.
Что можно сказать о площади этих прямоугольников? (Площадь прямоугольников разная.)
— Как это можно проверить? (Вычислить ппощаДь прямоугольников.)
![]() Какой величиной
является площадь в данном случае? (Переменной.)
Какой величиной
является площадь в данном случае? (Переменной.)
Площадь будет изменяться при изменении только одной стороны прямоутльника. Если же изменять обе стороны, то площадь может остаться постоянной. Например, прямоугольник со сторонами 6 см и 4 см и прямоугольник со сторонами 8 см и З см имеют одну и ту же площадь (они равновеликие).
Положение фигуры на плоскости никак не
влияет на ее площадь. В этом отношении площадь является постоянной величиной. ![]() 92-94
(с. 34).
92-94
(с. 34).
(Устное выполнение.) lV, Физкультминутка
V. Закрепление изученного материала
1.
Работа по
учебнику ![]() 95 (с. 35).
95 (с. 35).
(Самостоятельное
выполнение.) ![]()
2. Практическая работа М 96 (с. 35).
— Прочитайте задание. Как его выполнить? (Увеличивать длину звеньев при переходе от одной ломаной к Другой. Например, Длина ломаной 10 см. Она состоит из пяти звеньев: З см + + 2см + 1 см + Зсм + 1 см. ПреДставим число 106 виде суммы четырех слагаемых: 4 см + З см + 2см + 1 см, трех слагаемых: 5 см +4см + 1 см.) М 97 (с. 35).
![]() Какой радиус может быть у окружностей? (Например: см, 2 см, З см.)
Какой радиус может быть у окружностей? (Например: см, 2 см, З см.) ![]() 98
(с. 35).
98
(с. 35).
— Выполните задание.
![]() Назовите длины звеньев. (Например: З см, З см и З см; 2 см, 2 сми 2 см;
1 см, 1 СМИ Км.)
Назовите длины звеньев. (Например: З см, З см и З см; 2 см, 2 сми 2 см;
1 см, 1 СМИ Км.)
![]() Может ли одновременно число звеньев ломаной линии увеличиваться, а длина
уменьшаться? (Может. Например, ломаная линия, состоящая из двух звеньев: 5 см и
5 см, шиеет большую длину, чем ломаная линия, состоящая из четырех звеньев по 2
см, а число звеньев в первои ломаной меньше, чем во второй.)
Может ли одновременно число звеньев ломаной линии увеличиваться, а длина
уменьшаться? (Может. Например, ломаная линия, состоящая из двух звеньев: 5 см и
5 см, шиеет большую длину, чем ломаная линия, состоящая из четырех звеньев по 2
см, а число звеньев в первои ломаной меньше, чем во второй.)
Всегда ли математическое выражение является числовым?
![]()
З. Выполнение упражнения в тетради для самостоятельной работы
![]() 43 (с. 26).
43 (с. 26).
(Самостоятельное выполнение.) Ш. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 42 (с. 25).
Урок 18. Всегда ли математическое выражение является числовым?
Цель: познакомить с новым типом математического выражения — буквенным.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Волшебные квадраты
(Волшебная сумма равна 27.)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
апт |
пап |
||||||
|
|
|
|
|
|
|
|
|
|
||
Ответы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
12 |
5 |
|
|
|
|
2. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Сколько разрядов содержится в трехзначном числе? Запишите их. ( Три: разряд сотен, разряд Десятков, разряд еДиниц.) • Сколько разрядов и сколько классов в шестизначном числе? Запишите их. (Шесть разрядов и два класса, кажДыЙ класс содержит по три разряда: класс тысяч состоит из разряда сотен, разряда Десятков и разряДа еДиниц; юаасс еДИНИЦ состоит из разряда сотен, разряда Десятков и разряда еДиниц.)
![]()
• Сколько разрядов в каждом классе? (Три.)
• Как называются первые три класса? (Класс миллионов, класс тысяч, класс еДиниц.)
• Как построить название числа, в записи которого используется больше трех разрядов? (Дм построения названия числа нужно разбить его запись на классы, отсчитывая по три разряда справа налево, после чего называть кажДое из полученных трехзначных чисел, Добавляя названия соответствующих классов. Начинать называть нужно со старшего класса, а класс еДиниц называть не нужно.) Ш. Работа по теме урока Работа по учебнику лэ 99 (с. 36).
(Коллективное выполнение с комментированием. Знакомство с понятием «буквенное выражение» по словарику учебника (с. 116).)
![]() 100 (с. 36).
100 (с. 36).
![]() Прочитайте задание. Запишите буквенное выражение.
Прочитайте задание. Запишите буквенное выражение.
![]()
— ВЫЧИСЛИТЕ значение этого выражения при а = 25 см. (Р =
25 • 4, Р- тосм.) ![]() 101 (с. 36).
101 (с. 36).
— Прочитайте задание. Составьте выражение. (S= а • а.) ![]() Вычислите
значение выражения при а = 25 см. (S = 25 • 25, S = 625 кв. см.) № 102 (с. 37).
Вычислите
значение выражения при а = 25 см. (S = 25 • 25, S = 625 кв. см.) № 102 (с. 37).
— Запишите буквенные выражения. ((а + Ь) • 2, или а • 2 + Ь • 2, или а + а + Ь + Ь.)
![]() Какой из этих вариантов рациональнее? ((а
+ Ь) • 2.)
Какой из этих вариантов рациональнее? ((а
+ Ь) • 2.) ![]() Вычислите значение указанного выражения
при заданных значениях переменных.
Вычислите значение указанного выражения
при заданных значениях переменных.
№ 103 (с. 37).
— Какое свойство сложения использовано в задании? (Переместительное.) м 104 (с. 37).
![]() Запишите равенство, в котором выражается
переместительное свойство умножения. (а • Ь = Ь • а.) М 105€.37).
Запишите равенство, в котором выражается
переместительное свойство умножения. (а • Ь = Ь • а.) М 105€.37).
— Какие буквы используются в данных выражениях? (а, Ь, с.)
— Назовите искомое равенство. (ф + (Ь + с).) ![]() 106 (с. 38).
106 (с. 38).
(Самостоятельное выполнение.)
Зависимость между величинами
![]()
— Какие правила применяются в данных равенствах? (Правшо умножения суммы на число: (а + Ь) • с = а • с + Ь • с. Правшо умножения разности на число (распределительное свойство:
![]()
Мы получили распределительный закон умножения относительно сложения и относительно вычитания.
М. Физкультминутка
V. Закрепление изученного материала
1.
Работа по
учебнику ![]() 108 (с. 38).
108 (с. 38).
![]() Какое правило выражает данное равенство?
(В Данном равенстве выражен правый распределительный закон Деления относительно
сложения, ши правшо Деления суммы на число.)
Какое правило выражает данное равенство?
(В Данном равенстве выражен правый распределительный закон Деления относительно
сложения, ши правшо Деления суммы на число.) ![]() 109 (с. 38).
109 (с. 38).
— Запишите равенства, используя буквенные выражения.
![]()
Эти равенства отражают правило умножения числа на сумму (левый распределительный закон умножения относительно сложения) и правило умножения числа на разность (левый распределительный закон умножения относительно вычитания).
2.
Вьтшшекме
упражнений в тетрадщ для самостоятельной рабшы ![]() 48, 49 (с. 28).
48, 49 (с. 28).
(Самостоятельное выполнение.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 46, 47 (с. 27).
Урок 19. Зависимость между величинами
Цель: познакомить с зависимостью между величинами.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
1. Цифровой квадрат
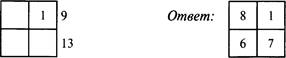
14 8
![]()
2. Родственные ряды
|
12 |
15 |
22 |
33 |
|
|
|
4 |
|
22 |
6 |
( Числа нижнего ряда на 11 меньше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 17, в нижнем ряду — ll.)
З. Устный счет
(Примеры записаны на доске.) ![]() Выразите.
Выразите.
З м 35 см —![]() ... см 3 т 482 кг = .
кг
... см 3 т 482 кг = .
кг
2 м 05 см —![]() . см 1026 см = дм
. см 1026 см = дм
4 км 702 м = ... м 375 дм м
Ш. Работа по теме урока Работа по учебнику ЛЕ 110 (с. 39).
(Коллективное выполнение.)
— Может ли периметр квадрата не измениться, если изменится длина его стороны? (Нет.)
![]() Может ли периметр
квадрата измениться, если длина его стороны не изменилась? (Нет.)
Может ли периметр
квадрата измениться, если длина его стороны не изменилась? (Нет.)
![]() Что это значит? (Каждому значению длины стороны кваДрата соответствует
одно значение периметра кваДрата. При изменении длины стороны кваДрата
обязательно изменится его периметр, т. е. периметр кваДрата однозначно зависит
от длины стороны кваДрата.) ЛГ2 111 (с. 39).
Что это значит? (Каждому значению длины стороны кваДрата соответствует
одно значение периметра кваДрата. При изменении длины стороны кваДрата
обязательно изменится его периметр, т. е. периметр кваДрата однозначно зависит
от длины стороны кваДрата.) ЛГ2 111 (с. 39).
![]() Прочитайте задание. В
каких парах одна величина зависит от другой? (В парах «а», «в», «г». )
Прочитайте задание. В
каких парах одна величина зависит от другой? (В парах «а», «в», «г». )
![]() В каких случаях зависимость будет однозначной? (В парах
В каких случаях зависимость будет однозначной? (В парах
![]()
![]() Почему? (Каждому значению стороны
кваДрата соответствует одно значение площаДи. У кажДоЙ квартиры свой номер,
поэтому увеличение (уменьшение) числа квартир однозначно привеДет к увеличению
(уменьшению) числа номеров квартир.)
Почему? (Каждому значению стороны
кваДрата соответствует одно значение площаДи. У кажДоЙ квартиры свой номер,
поэтому увеличение (уменьшение) числа квартир однозначно привеДет к увеличению
(уменьшению) числа номеров квартир.)
![]() 112 (с. 40).
112 (с. 40).
![]() Приведите примеры
зависимых величин. (Периметр кваДрата зависит от длины его стороны, шющаДь
кваДрата зависит от длины его стороны, стоимость 5 кг яблок зависит от их цены
и т. Д.)
Приведите примеры
зависимых величин. (Периметр кваДрата зависит от длины его стороны, шющаДь
кваДрата зависит от длины его стороны, стоимость 5 кг яблок зависит от их цены
и т. Д.)
— Приведите примеры двух величин, не зависящих друг от друга. (ПроДолжительность урока не зависит от числа
Зависимость между величинами
![]()
учащихся в классе, Длина ломаной линии не зависит от числа ее звеньев, паощаДь спортивной площаДки не зависит от ЧИСЈШ учащихся, тренирующихся на ней.) № 113 (с. 40).
![]() Выполните задание.
Выполните задание.
![]() Является ли зависимость в этом случае
однозначной? (Да.) ЛФ 114 (с. 40).
Является ли зависимость в этом случае
однозначной? (Да.) ЛФ 114 (с. 40).
— Можно ли по известному периметру квадрата установить его площадь? Как это сделать? (Сначала по известному периметру вычислить сторону кваДрата, а потом вычислить площаДь кваДрата по найденной стороне.) lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику № 115 (с. 40).
![]() Можно ли по периметру
прямоугольника однозначно установить его площадь? (ПлощаДь прямоугольника не
будет однозначно зависеть от его периметра.)
Можно ли по периметру
прямоугольника однозначно установить его площадь? (ПлощаДь прямоугольника не
будет однозначно зависеть от его периметра.)
![]() Объясните почему.
(Примерный ответ. Длины сторон прямоугольников, имеющих одинаковый периметр,
могут быть разными, тогда и площади их могут иметь разные значения. Например,
периметр прямоугольника со сторонами 6 см и 4 см равен 20 см. Периметр
прямоугольника со сторонами 8 см и 2 см также равен 20 см. При этом площадь
первого прямоугольника равна 24 кв. см, а второго — 16 кв. см.)
Объясните почему.
(Примерный ответ. Длины сторон прямоугольников, имеющих одинаковый периметр,
могут быть разными, тогда и площади их могут иметь разные значения. Например,
периметр прямоугольника со сторонами 6 см и 4 см равен 20 см. Периметр
прямоугольника со сторонами 8 см и 2 см также равен 20 см. При этом площадь
первого прямоугольника равна 24 кв. см, а второго — 16 кв. см.)
— А существует ли зависимость между периметром и площадью квадрата? (Да. Например, у кваДрата со стороной 4 см периметр равен 16 см и площаДь равна 16 кв. см.) ЛЕ 116 (с. 41).
— Будут ли периметр и площадь равностороннего треугольника однозначно зависеть от длины его стороны? (Да, такая зависимость существует. ) Лё 117(с. 41).
— Что нам известно о диаметре окружности? (Диаметр окружности всегда в два раза больше раДиуса этой же окружности.)
— Какой вывод мы можем сделать? (Диаметр окружности однозначно зависит от ее радиуса.) ЛФ 118€. 41).
![]() Прочитайте задание.
Можем ли мы однозначно ответить, каким будет второе слагаемое? (Нет, так как мы
не знаем, какое слагаемое больше, а какое меньше.)
Прочитайте задание.
Можем ли мы однозначно ответить, каким будет второе слагаемое? (Нет, так как мы
не знаем, какое слагаемое больше, а какое меньше.)
![]()
— Как изменить условие, чтобы второе слагаемое однозначно зависело от первого? (Указать, больше или меньше второе слагаемое, чем первое.)
2. Выполнею«е упражнений в тетради для самосгоятељной работы ЛФ 53 (с. 30).
![]() В какой таблице одна
величина однозначно зависит от другой? (Во второй.)
В какой таблице одна
величина однозначно зависит от другой? (Во второй.)
— Заполните эту таблицу.
ЛСР 51 (С. 29).
(Самостоятельное выполнение. Работа в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 54 (с. 30).
Урок 20. Поупражняемся в нахождении значений зависимой величины
Цель: развивать умение находить значение зависимой величины.
1. Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Закономерность
![]()
(Закономерность: + З, : З; пропущенные числа — 12 и 4.)
2. Цифровой квадрат
|
|
|
Ответ: |
7 |
З |
|
|
|
2 |
8 |
9![]()
З. Родственные ряды
|
2 |
4 |
|
з |
10 |
|
5 |
9 |
15 |
7 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 2 и прибавления еДИНИЦЫ. В верхнем ряду пропущено число 7, в нижнем ряду — 21.)
Поупражняемся в нахождении значений зависимой величины
![]()
4. Устный счет
(Примеры записаны на доске.)
— Выполните действия. Объясните приемы вычислений.
|
35 + 28 |
46 + 27 |
28 + 36 |
56 + 25 |
|
62 -38 |
74 — 55 |
33 - 18 |
54 - 36 |
|
49 + 38 |
64 + 29 |
94 — 59 |
72 - 39 |
Ш. Работа по теме урока Работа по учебнику № 119 (с. 42).
— Какие равенства нуто выписать? (Ь = а • 2, Ь = а + а.)
![]() Как можно в виде произведения записать
сумму а + а?
Как можно в виде произведения записать
сумму а + а? ![]() Выполните вычисление, используя любую из
этих двух формул.
Выполните вычисление, используя любую из
этих двух формул.
м 120, 121 (с. 42).
(Выполнение в соответствии с заданиями.) lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 122 (с. 43).
(Выполнение в соответствии с заданием.) м 123 (с. 43).
122 (с. 43).
(Выполнение в соответствии с заданием.) м 123 (с. 43).
— Найдите значение числового выражения. Как это сделать? (Каждую букву в правой части равенства заменить соответствующим числом.) ле 124 (с. 43).
— Что нужно сделать, чтобы выполнить вычисления? (Составить буквенное соотношение.)
— Как можно обозначить число коробок? (Буквой «о.)
— Как можно обозначить число карандашей в этих коробках? (Буквой «Ь.)
![]() Как будут связаны данные величины?
(Соотношением:
Как будут связаны данные величины?
(Соотношением:
Ь = 12 • а.)
— Заполните таблицу. м 125€. 43).
— Как вычислить периметр равностороннего треугольника, если известна длина его стороны? (С помощью сложения или умножения.)
![]() Назовите
формулу для вычисления периметра равностороннего треугольника. (Р = а • З.)
Назовите
формулу для вычисления периметра равностороннего треугольника. (Р = а • З.)
— Чему равен периметр треугольника, если его сторона равна
25 мм? (Р =25мм +25“
+25“ = ши Р![]()
= 75мм.)
![]()
— Что можно сказать о стороне и о периметре равностороннего треугольника? (Сторона равностороннего треугольника в З раза меньше периметра.)
![]() Сравните
два выражения: 25 мм + 25 мм + 25 мм и (25 мм + + 25 ММ + 25 мм) + (25 ММ + 25
ММ + 25 мм) + (25 мм + + 25 мм + 25 мм).
Сравните
два выражения: 25 мм + 25 мм + 25 мм и (25 мм + + 25 ММ + 25 мм) + (25 ММ + 25
ММ + 25 мм) + (25 мм + + 25 мм + 25 мм).
— Что можно сказать о первом выражении? (С помощью этого выражения можно вычислить периметр Данного равностороннего треугольника.)
— Что можно сказать о втором выражении? (С помощью этого выражения можно найти периметр равностороннего треугольника, у которого сторона увеличена в З раза.)
Значение выражения (25 мм + 25 мм + 25 мм) + (25 мм + + 25 мм + 25 мм) + (25 мм + 25 мм + 25 мм) в 3 раза больше значения выражения 25 + 25 + 25.
Увеличение стороны равностороннего треугольника в 3 раза приведет к увеличению периметра в 3 раза.
Аналогичная картина будет иметь место и при увеличении в любое число раз.
2. Выполнение упражнения в тетради для самостоятельной
работы ![]() 57 (с. 32).
57 (с. 32).
![]() (Самостоятельное выполнение. Проверка в парах.)
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 56 (с. 32).
Цели: проверить знания и умения учащихся; развивать навыки самостоятельной работы.
(Текст контрольной работы выдается каждому ученику на отдельном листочке.) Вариант 1
1. Вычисли.
(708 - 388) : 80
340 - 80 + 70
(620 - 120) 2
2. Построй фигуру, площадь которой на 2 кв. см больше площади данного прямоугольника. Вычисли и запиши площадь построенной фигуры.
72 : х = 9
4. Реши задачу. Вычисли и запиши ответ.
С первой грядки собрали 320 кг моркови, со второй — в 10 раз меньше, чем с первой, с третьей грядки — на 154 кг больше, чем со второй. Сколько килограммов моркови собрали с третьей грядки? Вариант 2
1. Вычисли.
(647 - 287) : 40 ![]()
(73 — 44) • 2
2. Построй фигуру, площадь которой на 4 кв. см больше площади данного прямоугольника. Вычисли и запиши площадь построенной фигуры.

3. Реши уравнения. х • 16 = 48
45 + х 64
54 : х = 6
4. Реши задачу. Вычисли и запиши ответ.
С первого участка собрали 46 кг капусты,
а со второго ![]() на 274 кг больше, чем с первого, с
третьего участка — в 10 раз меньше, чем со второго. Сколько килограммов капусты
собрали с третьего участка?
на 274 кг больше, чем с первого, с
третьего участка — в 10 раз меньше, чем со второго. Сколько килограммов капусты
собрали с третьего участка?
![]()
Урок 22. Стоимость единицы товара, или цена
Цели: познакомить с математической величиной «цена»; научить использовать наименования и терминологию при решении задач на куплю-продажу.
l. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
Арифметический диктант
— Запишите только ответы.
• Напишите число, в котором 306 единиц второго масса и 7 единиц первого масса. (306 007.)
• Запишите число, в котором 7 единиц шестого разряда и 2 единицы второго разряда. ( 700 020.)
• Запишите число 39 тысяч пять. (39 005.)
• Запишите число, в котором 8 единиц второго класса. (8000.)
• 90 м выразите в миллиметрах. (90 ОООММ.)
• 7 умножить на 6, разделить на 2 и увеличить на 160. (181.)
• 2000 г — сколько это кг? (2 кг.)
• Найдите произведение чисел 7 и 400. (2800.)
• Какое число больше 14 в 30 раз? (420.)
• Спортсмен пробежал 500 м за 2 мин. Сколько метров при такой же скорости он пробежит за 7 мин? (1750 м.)
Ш. Работа по теме урока
— Приведите примеры ситуаций, когда вам приходилось
приобретать товар, который исчисляется в разных единицах. Работа по учебнику ![]() 126
(с. 44). (Устное выполнение с комментированием учителя.) Л) 127 (с. 44).
126
(с. 44). (Устное выполнение с комментированием учителя.) Л) 127 (с. 44).
(Коллективное выполнение.)
— В каких единицах выражается цена? (В рублях.)
• Как найти цену? (Делением.)
Запомните правило: чтобы найти цену товара, надо стоимость товара разделить на его количество. Л) 128 (с. 45).
![]() Как записать цену билета в театр?
(90py6./6LQ.)
Как записать цену билета в театр?
(90py6./6LQ.)
• Как вычислить стоимость двух таких билетов? (90 • 2 = — 180 (руб.).)
![]() Как вычислить
стоимость десяти таких билетов? (90 • 10 = = 900 (руб.).)
Как вычислить
стоимость десяти таких билетов? (90 • 10 = = 900 (руб.).)
Стоимость единицы товара, или цена
![]()
IV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 129 (с. 45).
Вариант заДачи. Цена яблок на 10 руб./кг меньше, чем цена груш. Сколько стоят 2 кг груш, если 3 кг яблок стоят 60 руб.?
— Что можно найти сначала? (Цену яблок.)
![]() Как это сделать? (60 : З = 20 (руб./кг).)
Как это сделать? (60 : З = 20 (руб./кг).)
![]() Можно ли теперь установить цену груш?
(Да: 20 + 10 =
Можно ли теперь установить цену груш?
(Да: 20 + 10 =
= 30 (руб./кг). )
— Сколько стоят 2 кг груш? (30 • 2 = 60 (руб.).)
2. Выполнение упражнения в тетради для самостоятельной ра-
М 58 (с. 33).
(Задание а выполняется самостоятельно, остальные — с комментированием.)
а) Решение: 90 : 3 5= 150 (руб.).
Ответ: букет из пяти роз стоит 150 руб.
б) Решение:
1) 66 + 9 = 75 (руб.) — стоимость трех хризантем; 2) 75 : 3 = 25 (руб./шт.) — цена хризантемы; З) 25 — 9 = 16 (руб./шт.) — цена лилии.
Проверка: 25 • 2 + 16 = 66 (руб.).
Ответ: цена хризантемы 25 руб./шт., цена лилии 16 руб./шт. в) Решение: пусть одна часть — цена нарцисса, а две части — цена тюльпана.
1) 2 • 2+ = 5 (ч.) — всего частей;
2) 40 : 5 = 8 (руб./шт.) — цена нарцисса; 3) 8 • 2 = 16 (руб./шт.) — цена тюльпана.
Проверка: 16 • 2 + 8 = 40 (руб.).
Ответ: цена тюльпана 16 руб./шт., цена нарцисса 8 руб./шт.
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 59 (а) (с. 34).
Урок 23. Стоимость единицы товара, или цена
Цель: продолжать обучать решению задач на куплю-продажу.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
![]()
П. Актуализация знаний
1. Цифровой квадрат
|
|
|
|
1 1 |
|
|
9 |
10 |
|
|
|
19 Ответ:
19
20 18
2. Волшебная звезда (Сумма = 28.)
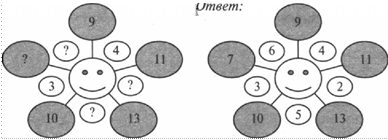
З. Родственные ряды
|
12 |
10 |
8 |
20 |
|
|
22 |
18 |
|
38 |
28 |
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 2 и вычитания числа 2. В верхнем ряду пропущено число 15, в нижнем ряду — 14.)
4. Устный счет
(Примеры записаны на доске.)
— Выполните действия. Объясните приемы вычислений.
|
60 - 24 |
90 - 38 |
50 -3 |
90 _ 9 |
|
83 — 45 |
93 — 47 |
59 + 35 |
77 + 17 |
|
32 + 18 |
36 + 34 |
25 + 74 |
70+5 |
Ш. Работа по теме урока Работа по
учебнику М 130 (с. 45). (Коллективное выполнение.) ![]() 131 (с. 46).
131 (с. 46). ![]() Прочитайте
задачу. Какого она типа? (Задача на сумму и частное.)
Прочитайте
задачу. Какого она типа? (Задача на сумму и частное.)
![]() Что можно сказать о
цене блокнота? (Примем цену блокнота за одну часть.)
Что можно сказать о
цене блокнота? (Примем цену блокнота за одну часть.)
Стоимость единицы товара, или цена
![]()
— Что можно сказать о цене книги? (Цена книги в 5 раз больше цены блокнота. Примем цену книги за пять частей.)
— Сколько всего частей? (1 + 5 = 6 (ч.).)
![]() Найдите меньшую цену. (120 : 6 = 20
(руб./шт.).)
Найдите меньшую цену. (120 : 6 = 20
(руб./шт.).)
![]() Найдите большую цену. ( 120 — 20 = 100
(руб./шт.).)
Найдите большую цену. ( 120 — 20 = 100
(руб./шт.).)
![]() Что означает меньшая цена? (Цену
блокнота.)
Что означает меньшая цена? (Цену
блокнота.) ![]() Что означает большая цена? (Цену книги.)
Что означает большая цена? (Цену книги.) ![]() 132
(с. 46).
132
(с. 46).
Вариант заДачи. Цена фломастера 16 руб./шт., а цена ручки 8 руб./шт. Во сколько раз стоимость 6 фломастеров больше, чем стоимость 4 ручек?
lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику
Л) 133 (с. 46).
![]() Прочитайте задачу.
Какого она типа? (Задача на частное и разность.)
Прочитайте задачу.
Какого она типа? (Задача на частное и разность.)
![]() Рассмотрите чертеж к
задаче. Что вы можете сказать? (Стоимость кг картофеля — это одна часть
полоски, а стоимость 1 кг помиДороз — это три части.)
Рассмотрите чертеж к
задаче. Что вы можете сказать? (Стоимость кг картофеля — это одна часть
полоски, а стоимость 1 кг помиДороз — это три части.)
— Каков результат разностного сравнения частей? (З— 1 = 2.)
![]() Чему равна меньшая цена? (30 : 2 = 15 (руб./кг).)
Чему равна меньшая цена? (30 : 2 = 15 (руб./кг).)
![]() Чему равна большая цена? (30 + 15 = 45
(руб./кг).)
Чему равна большая цена? (30 + 15 = 45
(руб./кг).)
— Что обозначает меньшая цена? (Цену картофеля.)
![]() Что обозначает большая цена? (Цену
помиДоров.)
Что обозначает большая цена? (Цену
помиДоров.)
![]() Какая часть полоски изображает 30 руб.? (Две части полоски.)
Какая часть полоски изображает 30 руб.? (Две части полоски.)
2.
Выполнею•е
упрахшения в тетрац для самостоятельной работы ![]() 59 (в, г) (с. 35).
59 (в, г) (с. 35).
в) Решение:
1) 50 : 5 = 10 (руб./шт.) — цена пачки печенья; 2) 10 • 2 = 20 (руб./шт.) — цена пачки вафель;
З) 5 + 5 = 10 (шт.) — количество пачек вафель;
4) 20 • 10 = 200 (руб.) — стоимость 10 пачек вафель.
Ответ: стоимость 10 пачек вафель 200 руб.; стоимость 10 пачек вафель больше, чем стоимость 5 пачек печенья.
г) Решение:
1) 12 • 13 = 156 (руб.) — стоимость 13 яблок;
2) 12 • 2 = 24 (руб./шт.) — цена груши;
З) 13 — 7 = 6 (шт.) — количество груш;
4) 24 • 6 = 144 (руб.) — стоимость 6 груш.
Ответ: стоимость З яблок 156 руб., стоимость 6 груш l44 руб.; стоимость 3 яблок больше, чем стоимость 6 груш.
З Поурочные разработки по математике
![]()
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 59 (б) (с. 34).
Урок 24, Когда цена постоянна
Цель: познакомить с характером зависимости между количеством купленного товара и его стоимостью при постоянной цене.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
Тест
(Выдается на отдельных листочках.)
1. В каком числе отсутствует разряд десятков?
1) 894 604 321 3) 8 056 233
2) 44377512 зоз 4) 99 990 990 990
2. Что показывает цифра 7 в числе 635 789 000?
1) число сотен тысяч
2) число единиц тысяч
3) число единиц миллионов 4) число сотен
3. Что отсутствует в числе 3 000 000 241 ?
1) класс миллиардов и класс миллионов
2) разряд единиц тысяч и разряд сотен тысяч
З) класс миллионов и класс тысяч
4) разряд единиц миллионов и класс тысяч
4. Укажи число пять миллиардов семьсот четыре тысячи двести.
1) 5 704 то 3) 5 704 000 200 2) 5 704 200 4) 5 704 200 000
5. Назови соседей числа 9 057 759 879.
1) 9 057 759 878 и 9 057 759 890
2) 9 057 759 870 и 9 057 759 880
3)
9057 ![]() 759880
759880
4) 9 057 700 000 и 9 057 800 000
6. Какие из этих неравенств верные?
а) 40 376 609 > 41 265 009; 6) 546 231 750 > 456 231 750; в) 663 725 478 < 667 325 478;
г) 2 000 000 < зоо 000
Когда цена постоянна
![]()
7. Представь число 33 656 054 800 в виде суммы разрядных
слагаемых.
2) 33 000 000 000 + 656 000 000 + 54 000 + 800
3) з 000 000 + з 000 + 6 000 000 + 5 000 000 +
+ 6 000 000 + 5000 + 4000 + 800
4)
зо 000 + з 000 000 000 + ![]() + 50 000 + + 6 000 000 + 50 000 + 4000 +
800
+ 50 000 + + 6 000 000 + 50 000 + 4000 +
800
8. В каком числе 55 тысяч?
|
1) 7 854 766 330 000 |
3) 806 402 333 245 |
|
2) 8911308055511 |
4) 978 зоз зоз зоз |
Ш. Работа по теме урока Работа по учебнику № 134 (с. 47). Решение:
1)
24 : 2 = 12 (руб./шт.) — цена тетради в ПРОИШОМ месяце; ![]() 12
(руб./шт.) — цена тетради сегодня.
12
(руб./шт.) — цена тетради сегодня.
Ответ: цена тетрадей не изменилась. ЛФ 135(с. 47).
![]() Прочитайте задачу и рассмотрите два
варианта решения.
Прочитайте задачу и рассмотрите два
варианта решения.
![]() Что можно сказать о
первом варианте решения? (В первом Действии нахоДят цену картофеля, во втором
Действии узнают, сколько нужно заплатить за 12 кг картофеля, в третьем — во
СКОЛЬКО раз стоимость 12 кг картофеля больше, чем стоимость З кг.)
Что можно сказать о
первом варианте решения? (В первом Действии нахоДят цену картофеля, во втором
Действии узнают, сколько нужно заплатить за 12 кг картофеля, в третьем — во
СКОЛЬКО раз стоимость 12 кг картофеля больше, чем стоимость З кг.)
— С чего начинают решение во втором варианте? (С того, что узнают, во сколько раз 12 кг больше, чем З кг.)
![]() Какой получился
ответ? Сравните его с ответом, полученным в третьем действии первого варианта.
(В 4 раза. Ответ такой же, как в третьем Действии первого варианта.)
Какой получился
ответ? Сравните его с ответом, полученным в третьем действии первого варианта.
(В 4 раза. Ответ такой же, как в третьем Действии первого варианта.)
— Что делают далее? (Во втором Действии узнают стоимость 12 кг, в третьем Действии проверяют, во сколько раз стоимость 12 кг больше стоимости З кг.)
— Какой вывод можно сделать? (Для ответа на требование заДачи Достаточно было узнать, во сколько раз новое количество больше, чем старое.)
![]() О чем это говорит?
(При постоянной цене увеличение количества товара в несколько раз привоДит к
увеличению его стоимости в это же число раз.)
О чем это говорит?
(При постоянной цене увеличение количества товара в несколько раз привоДит к
увеличению его стоимости в это же число раз.)
Правильно, это также означает, что мя вычисления стоимости нового количества товара по той же цене не обязательно узнавать цену, достаточно вычислить, во сколько раз новое количество за
масс
![]()
больше (меньше), чем старое, и умножить старую стоимость на это число раз.
Но использовать такой способ решения можно не всегда, только при условии, что новое количество делится на старое без остатка. Довольно часто это условие не выполняется, поэтому первый способ решения (с вычислением цены) используется чаще. м 136 (с. 47).
![]() Что происходит при увеличении количества в некоторое число раз, например
в 2 раза? (Стоимость также увеличивается в это же число раз. При этом цена
Должна быть постоянной.) № 137(с. 47).
Что происходит при увеличении количества в некоторое число раз, например
в 2 раза? (Стоимость также увеличивается в это же число раз. При этом цена
Должна быть постоянной.) № 137(с. 47).
![]() Прочитайте задание. Что нужно сделать, чтобы узнать, во сколько раз изменилась
стоимость? (Нужно установить, во сколько раз изменилось количество: 9 : З = З
(раза).)
Прочитайте задание. Что нужно сделать, чтобы узнать, во сколько раз изменилась
стоимость? (Нужно установить, во сколько раз изменилось количество: 9 : З = З
(раза).) ![]() 138 (с. 47).
138 (с. 47).
![]() Прочитайте задание. Что нужно узнать сначала? (Нужно вычислить цену
ткани: 840 : 4 = 210 (руб./м).)
Прочитайте задание. Что нужно узнать сначала? (Нужно вычислить цену
ткани: 840 : 4 = 210 (руб./м).)
— Что можно узнать далее? (Стоимость 12 м ткани: 210 • 12 = = 2520 (руб.).)
![]() Можно ли решить эту задачу по-другому? (Да, сначала надо узнать, во
сколько раз увеличилось количество ткани: 12 : 4 = = З (раза), потом вычислить
новую стоимость, увеличив старую стоимость в это число раз: 840 • З = 2520
(руб.).)
Можно ли решить эту задачу по-другому? (Да, сначала надо узнать, во
сколько раз увеличилось количество ткани: 12 : 4 = = З (раза), потом вычислить
новую стоимость, увеличив старую стоимость в это число раз: 840 • З = 2520
(руб.).)
М. Физкультминутка
V. Закрепление изученного материала
1.
Работа по учебнику ![]() М 139 (с. 48).
М 139 (с. 48).
![]() Сформулируйте задачу.
Сформулируйте задачу.
— Решите задачу, используя вариант решения с вычислением цены (применить принцип пропорционального увеличения не позволяют имеющиеся числовые данные: число 20 не делится на 9).
![]() Как
можно рациональнее решить эту задачу, если число 20 заменить на число 27?
(Сначала вычислить, во сколько раз количество товара, купленного вторым
покупателем, больше, чем количество товара, купленного первым покупателем: 27 :
9 = З (раза). А затем узнать стоимость этого количества товара: 99 • З = 297
(руб.). )
Как
можно рациональнее решить эту задачу, если число 20 заменить на число 27?
(Сначала вычислить, во сколько раз количество товара, купленного вторым
покупателем, больше, чем количество товара, купленного первым покупателем: 27 :
9 = З (раза). А затем узнать стоимость этого количества товара: 99 • З = 297
(руб.). ) ![]() 140 (с. 48).
140 (с. 48).
![]() Прочитайте
задание. Вычислите стоимость по известному количеству при постоянной цене. Что
для этого надо сделать? (Умножить цену на количество.)
Прочитайте
задание. Вычислите стоимость по известному количеству при постоянной цене. Что
для этого надо сделать? (Умножить цену на количество.)
Когда цена постоянна
![]()
№ 141 (с. 48).
— Прочитайте задание. Вычислите количество по известной стоимости при постоянной цене. Что для этого надо сделать? (РазДелить стоимость на цену.)
![]() Какой
это случай деления? (Случай Деления на число 10.)
Какой
это случай деления? (Случай Деления на число 10.)
2. Выполнение упражнений в тетради для самостоятельной работы
![]() 61 (с. 36).
61 (с. 36).
— Что означает выражение «по той же цене»? (Цена одинаковая.)
а) Решение:
1) 2 + 3 = 5 (тет.) — количество тетрадей; 2) 95 : 19 (руб./шт.).
Ответ: цена тетради 19 руб./шт.
б) Решение: 56 : 4 7 = 98 (руб.).
Ответ: за 7 пирожных надо заплатить 98 руб.
в) Решение: 27 • 6 = 162 (руб.).
Ответ: Костя заплатил за свои тетради 162 руб. М 63 (с. 38).
— Рассмотрите таблицу а. Как найти стоимость конвертов? (40 + 20 = 60 (руб.).)
— Назовите количество купленных конвертов. (15 шт.)
![]() Можно
ли найти церу конверта? (Да: 60: 15 = 4 (руб./шт.).)
Можно
ли найти церу конверта? (Да: 60: 15 = 4 (руб./шт.).)
— Назовите цену открытки. (5 руб./шт.)
![]() Сколько
открыток куплено? (15 + 1 = 16
Сколько
открыток куплено? (15 + 1 = 16![]()
![]() Что
можно найти при известных цене и количестве открыток? (Стоимость открыток: 16 •
5 = 80 (руб.).)
Что
можно найти при известных цене и количестве открыток? (Стоимость открыток: 16 •
5 = 80 (руб.).)
— Сколько загшатрши за альбомы? (40руб.)
![]() Можно ли найти цену
альбома? (Цена альбома в 2 раза больше, чем цена открытки: 5 • 2 = 10
(руб./шт.).)
Можно ли найти цену
альбома? (Цена альбома в 2 раза больше, чем цена открытки: 5 • 2 = 10
(руб./шт.).)
— Если известны стоимость и цена альбома, что можно найти? (Количество альбомов: 40 : 10 = 4 (шт.). ) — Заполните таблицу б.
Решение:
1) 24 — З = 21 (руб.) — стоимость маленьких стаканов сока;
2) 21 : З = 7 (шт.) — количество маленьких стаканов сока;
3) 3 + 4 = 7 (руб./шт.) — цена среднего стакана сока;
4) 7 • 6 = 42 (руб.) — стоимость средних стаканов сока;
5) 6 : 3 = 2 (шт.) — количество больших стаканов сока;
6) 24 : 2 = 12 (руб./шт.) — цена большого стакана сока. М. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 62 (с. 37). ![]()
![]()
Урок 25. Учимся решать задачи
Цели: развивать умение решать задачи на нахождение четвертого пропорционального; продолжать работу над задачами на сумму и разность и на сумму и частное.
1. Организационный момент. Сообщение темы и целей урока
|
ll. Актуализация знаний 1. Примеры на карточках — Запишите только ответы. |
|
|
|
Вариант 1 |
Вариант 2 |
|
|
25 + 37 40 — 13 |
70 - 32 |
46 + 28 |
|
30 - 24 72-
|
27 + 44 |
58 + |
|
37 +25 49 — 17 |
43— 15 |
83 - 35 |
|
36 + 26 71 +29 |
96 + З |
50 - 32 |
|
41 - 13 42 - 32 2. Цифровой квадрат |
42 + 28 |
34— 17 |
|
4 |
3 |
|
|
|
![]() 7 Ответ:
7 Ответ:
4
5 6
З. Родственные ряды
|
з |
5 |
|
2 |
7 |
|
|
16 |
25 |
7 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на З и прибавления еДИНИЦЫ. В верхнем ряду пропущено число 8, в нижнем ряду — 22.)
4. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Что означает цифра 0 в записи числа? (Если в числе отсутствуют еДИНИЦЫ какого-либо разряда, то на месте этого разряда в записи числа ставят цифру О, например: 290 млн 340 тыс. 201 записывают так — 290340201.)
• Может ли запись натурального числа начинаться с цифры
0? (Нет.)
• Как сравнивают натуральные числа? Приведи пример. (Примерный ответ. Числа можно сравнивать: так:
Учимся решать задачи
![]()
а) по месту, которое они занимают при счете, например:
9 < 10, так как 9 встречается при счете раньше, чем 10;
б) поразрядно, начиная сравнение с высших разрядов, например: 3827 < 5986, так как 3 тыс. < 5 тыс.; 4761 > 4598, так как 7 сот. > 5 сот.; 1235 > 987, так как высший разряд в числе 1235 — тысячи, а в числе 987 — сотни.)
llla Работа по теме урока Работа
по учебнику ![]() 142 (с. 49).
142 (с. 49).
![]() Прочитайте задание. Какого типа эта задача? (Задача на нахожДение
четвертого пропорционального.)
Прочитайте задание. Какого типа эта задача? (Задача на нахожДение
четвертого пропорционального.) ![]() Что такое 160 руб.? (Стоимость.)
Что такое 160 руб.? (Стоимость.)
![]() Что такое 20 м? (Количество.)
Что такое 20 м? (Количество.)
— Что можно найти при известных стоимости и количестве? (Цену.)
![]() Сколько стоит м провода? (160 : 20 =8
(руб.).)
Сколько стоит м провода? (160 : 20 =8
(руб.).)
![]() Сколько нужно заплатить
за 100 м такого же провода? (8, = 800(ру6.).)
Сколько нужно заплатить
за 100 м такого же провода? (8, = 800(ру6.).)
![]() Как можно по-другому решить эту задачу? (Не вычисляя цену: то: 20 = 5
(раз); 160 • 800 (руб.).)
Как можно по-другому решить эту задачу? (Не вычисляя цену: то: 20 = 5
(раз); 160 • 800 (руб.).)
Если количество увеличивается в некоторое число раз (в данном случае в 5 раз), то и стоимость увеличивается в это же число раз.
ЛГ2 143 (с. 49).
Решение:
Первый способ:
1) 75 : 3 = 25 (руб./кг) — цена сахарного песка; 2) 25 руб./кг • 12 кг = 300 (руб.).
Второй способ:
1) 12 : 3 = 4 (раза) — увеличилось количество сахарного песка; 2) 75 • 4 = ЗОО (руб.).
Ответ: за 12 кг сахарного песка нужно заплатить 300 руб.
— Что общего в решениях? (ОДинаковые Действия: Деление и
умножение.) ![]() 144 (с. 49).
144 (с. 49).
Вариант заДачи. За 5 кг картофеля заплатили 60 руб. Сколько килограммов моркови можно купить на 120 руб., если цена картофеля и моркови одинаковая?
— Решите задачу двумя способами.
![]() Какой способ решения
подойдет, если 120 руб. заменить на 96 руб.? (Способ, при котором нужно
вычислять цену.)
Какой способ решения
подойдет, если 120 руб. заменить на 96 руб.? (Способ, при котором нужно
вычислять цену.)
— Почему не подойдет второй способ? (Потому что 96 не делится на 60 нацело, значит, в Данном случае нельзя выполнить кратное сравнение стоимостей. )
![]()
lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ЛГУ 145 (С. 50).
Вариант задачи. Какова стоимость 3 блокнотов по цене 30 руб./шт., 4 альбомов по цене 90 руб./шт., 2 учебников по цене 180 руб./шт.?
м 146 (с. 50).
Вариант заДачи. За кроссовки и футболку заплатили 420 руб. Кроссовки в 6 раз дороже футболки. Сколько нужно заплатить за З такие футболки и 2 пары таких кроссовок?
М 147(с. 50).
![]() Прочитайте задачу.
Какою она типа? (Задача на сумму и разность.)
Прочитайте задачу.
Какою она типа? (Задача на сумму и разность.)
![]() Что можно найти
сначала? (Количество пассажирских мест в двух плацкартных вагонах: 90 + 18 =
108 (м.).)
Что можно найти
сначала? (Количество пассажирских мест в двух плацкартных вагонах: 90 + 18 =
108 (м.).)
— Как найти, сколько мест в одном вагоне? (РазДелить полученное число пополам и получить большее количество мест в вагоне: 108 : 2 = 54 (м.).)
![]() Найдите количество мест в купейном
вагоне. (54 — 18 =
Найдите количество мест в купейном
вагоне. (54 — 18 =
— 36 (м.).)
![]() Проверьте правильность решения. (54 + 36
= 90 (м.).) 2. Вьшшшеише упражнения в тетрам для самостоятельной работы ЛФ 64
(с. 39-40).
Проверьте правильность решения. (54 + 36
= 90 (м.).) 2. Вьшшшеише упражнения в тетрам для самостоятельной работы ЛФ 64
(с. 39-40).
(Самостоятельное выполнение. Взаимопроверка.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 66 (с. 41 ).
Урок 26. Деление нацело и деление с остатком
Цель: познакомить со случаями деления нацело и с остатком.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: • З, — 1; пропущенные числа — 15 и 14.)
Деление нацело деление с остатком
![]()
2. Волшебные квадраты
(Волшебная сумма равна 33.)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пап |
|
|
|
||||
|
апп |
|
|
|
|
|
|
||||
Ответы:
|
14 |
7 |
12 |
|
8 |
В |
12 |
|
|
15 |
8 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
З. Устный счет
(Примеры записаны на доске.) ![]() Сравните величины.
Сравните величины.
2 т 4 ц ... 2 т 400 кг
![]() 7 дм 6 см ... 7 дм 80 мм
7 дм 6 см ... 7 дм 80 мм
Зм 5 дм ... Зм 50 см Ш. Работа по теме урока Работа по учебнику
М 148 (с. 51).
(Коллективное выполнение.)
— Разделите 15 палочек на 6 равных частей. (В кажДоЙ такой части будет по 2 палочки, и еще З палочки останутся в остатке, так как этого количества палочек неДостаточно для того, чтобы разделить на б частей.)
![]() Что показывает число 2? ( Число 2 показывает, какое максимальное число
раз Делитель (число 6) соДержится в Делимом (числе 15). )
Что показывает число 2? ( Число 2 показывает, какое максимальное число
раз Делитель (число 6) соДержится в Делимом (числе 15). )
![]() Что показывает число 3? (Число З показывает, какое еще число остается от
Делимого после того, как из него вычли Делитель максимальное число раз.)
Что показывает число 3? (Число З показывает, какое еще число остается от
Делимого после того, как из него вычли Делитель максимальное число раз.) ![]() 149
(с. 51).
149
(с. 51).
Решение: 3 • 4 14 (с.).
Ответ: мама сварила 14 сосисок.
![]() Как выполнить деление числа 14 на число
4? (14 4
Как выполнить деление числа 14 на число
4? (14 4![]()
(ост. 2).) lV. Физкультминутка
![]()
М. Закрепление изученного материала
1. Работа по учебнику ЛГ2 150 (с. 52).
![]() Рассмотрите приведенные случаи деления.
Рассмотрите приведенные случаи деления.
![]() Что можно сказать о примерах,
записанных в верхней строчке? (Это табличные случаи Деления.)
Что можно сказать о примерах,
записанных в верхней строчке? (Это табличные случаи Деления.)
![]() Какие примеры
записаны в нижней строчке? (Это случаи Деления с остатком.)
Какие примеры
записаны в нижней строчке? (Это случаи Деления с остатком.)
![]() Как вы будете
выполнять деление с остатком? (Используя соответствующие табличные случаи
Деления.)
Как вы будете
выполнять деление с остатком? (Используя соответствующие табличные случаи
Деления.)
![]() Почему для деления с
остатком числа 27 на число 6 предлагается использовать табличный случай деления
24 : 6? ( Число 24 — это самое большое число, которое Делится на 6 без остатка
и не превосхоДит 27.)
Почему для деления с
остатком числа 27 на число 6 предлагается использовать табличный случай деления
24 : 6? ( Число 24 — это самое большое число, которое Делится на 6 без остатка
и не превосхоДит 27.)
— Выполните деление с остатком. (27: 6 = 4 (ост. 3).)
![]() Какое число нужно
вычесть из числа 27, чтобы получить табличный случай деления? (З.)
Какое число нужно
вычесть из числа 27, чтобы получить табличный случай деления? (З.)
— Что представляет собой число 3 в данном случае? (Это остаток.)
![]() Решите остальные примеры самостоятельно.
Решите остальные примеры самостоятельно.
ЛГ2 151 (с. 52).
— Прочитайте задание. Объясните. (При вычитании остатка (З) из Делимого (45) получается число 42, которое Делится нацело на Делитель (7). )
Аналогичным образом всегда можно получить по результатам деления с остатком соответствующий случай деления нацело.
2. Выполнение упражнения в тетради для самостоятельной работы
ЛГ2 67€. 42).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 72, 73 (с. 43).
Урок 27. Деление нацело и деление с остатком
Цель: продолжать рассмотрение случаев деления нацело и с остатком.
1. Организационный момент. Сообщение темы и цели урока
Деление нацело деление с остатком
![]()
11. Актуализация знаний
1. Цифровой квадрат
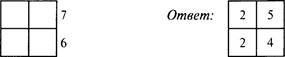
4 9
2. Родственные ряды
|
4 |
8 |
6 |
|
|
|
9 |
21 |
|
27 |
42 |
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на З и вычитания числа З. В верхнем ряду пропущено число 15, в нижнем ряду — 15.) З. Устный счет
(Примеры записаны на доске.)
![]() Вставьте пропущенные числа.
Вставьте пропущенные числа.
150 кг = ... ц ... . кг
38 кг = ... . кг ... г = 7007 г
... ц ... кг = 586 кг
Ш. Работа по теме урока Работа по учебнику ЛГ2 152 (с. 52-53).
![]() Прочитайте задание. Какую запись вы выберете? (67— 4.)
Прочитайте задание. Какую запись вы выберете? (67— 4.) ![]() Почему? (В
результате вычитания получается число 63, которое Делится на 9 нацело.)
Почему? (В
результате вычитания получается число 63, которое Делится на 9 нацело.)
![]() Найдите значение частного. ((67— 4) : 9 = 7.)
Найдите значение частного. ((67— 4) : 9 = 7.)
— Как будет выглядеть запись деления с остатком числа 67 на число 9? (67: 9 = 7 (ост. 4). ) ЛФ 153 (с. 53).
(Коллективное выполнение.) lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику
М 154 (с. 53). (Самостоятельное выполнение.) ЛФ 155 (с. 53).
![]() Прочитайте задание. Какое число делится
на 7 нацело? (56.) — Назовите табличный случай деления. (56 : 7=8.)
Прочитайте задание. Какое число делится
на 7 нацело? (56.) — Назовите табличный случай деления. (56 : 7=8.) ![]() Выполните
деление с остатком.
Выполните
деление с остатком.
— Какой табличный случай деления поможет разделить с остатком на 7 числа 55, 54
— Выполните деление с остатком.
2. Выполнение упражнений в тетради для самостоятельной работы
М 71 (с. 42).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]() 77 (с. 44).
77 (с. 44).
(Самостоятельное выполнение. Взаимопроверка.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 74, 75 (с. 43—44).
Урок 28. Неполное частное и остаток
Цели: познакомить с терминами «неполное частное» и «остаток»; закреплять вычислительные навыки.
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
1. Таблица
умножения и деления ![]()
(Один ученик отвечает у доски, учащиеся предлагат ему решить 6—7 примеров. Таким образом можно опросить 8—9 учеников.)
2. Устный счет
(Примеры записаны на доске.)
![]() Вставьте пропущенные числа.
Вставьте пропущенные числа.
![]() кг 2000
г = ... кг
кг 2000
г = ... кг
8 ц 8 кг = 60 ц =![]()
43 кг = ... г . кг г = 24 350 г З. Логические задачи
— Решите задачу устно.
В магазине СТОИТ очередь. Один и тот же человек оказался пятым с конца и третьим с начала. Сколько всего человек в очереди? ( 7.)
Ш. Работа по теме урока Работа по учебнику ![]() 156 (с. 54).
156 (с. 54).
(Знакомство с терминами по словарику учебника (с. 118—119).
Выполнение в соответствии с заданиями.)
Неполное частное остаток
![]()
М 157€.54).
— Вспомните правило, согласно которому можно получить делимое, используя значение частного и делитель. (Если Делитель умножить на значение частного, то получится делимое.)
— Сформулируйте правило для действия деления с остатком. (Делшиое можно получить, если Делитель умножить на неполное частное и к полученному результату прибавить остаток.) М 158 (с. 54-55).
— Выполните задание. Запишите правило, которым вы пользовались, с помощью буквенного выражения. (а = Ь • с + d.) м 159 (с. 55).
При умножении однозначного числа на двузначное можно воспользоваться переместительным свойством умножения или применить алгоритм умножения столбиком.
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 160 (с. 55).
160 (с. 55).
— Какую запись вы составили? (131 : 12 = 10 (ост. 11).)
— Можно ли в качестве делителя использовать число 10? (Нет, так как число 10 самое маленькое из Данных чисел, а остаток всегда Должен быть меньше Делителя.) М 161 (с. 55).
— Справедливо ли приведенное равенство? (Да.)
— Используя это равенство, составьте верную запись деления с остатком. (224 : 15 = 14 (ост. 14).) № 162 (с. 55).
Решение: в качестве неполного частного можно выбрать числа , 2, 3. Для этих чисел можно вычислить соответствующие делимые:
![]()
Таким образом, получаются следующие случаи деления с остатком:
12 : (ост. 5)
![]() (ост. 5)
(ост. 5)
26 : (ост. 5)
2. Выполнение упражнений в тетради для самостоятельной работы М 81 (с. 46).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]()
а) Решение: 47 : Ш = 4 (ост. 7). Ответ: нужно заказать 4 автобуса.
б) Решение: 80 : 8 (ост. 8).
Ответ: мама сможет купить 8 кг муки, и у нее останется 8 руб.
в) Решение:
2) 39 : 4 = 6 (ост. 3).
№ 78, 79€. 45).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
домашнее задание
Тетрадь для самостоятельной работы: № 80 (с. 45).
Цель: познакомить с взаимозависимостью остатка и делителя при делении с остатком.
1. Организационный момента Сообщение темы и цели урока ll. Актуализация знаний
1. Цифровой квадрат
|
З |
5 |
|
|
|
![]() 8 Ответ:
8 Ответ:
8
7 9
2. Родственные ряды
|
2 |
5 |
|
з |
6 |
|
18 |
48 |
78 |
28 |
|
(Первая цифра чисел нижнего ряда на меньше первой цифры соответствующего числа верхнего ряда, а вторая цифра чисел нижнего ряда — 8. В верхнем ряду пропущено число 8, 6 нижнем ряду — 58.)
З. Устный счет
(Примеры записаны на доске.)
![]() Выполните действия. Объясните приемы
вычислений.
Выполните действия. Объясните приемы
вычислений.
|
65 + 19 — 15 |
49 + 28 - 29 |
45 + 26 — 47 |
|
59+ 17_8 |
80 - 58 + 22 |
79 + — 58 |
|
47 + 29 —76 |
93 — 36 + 39 |
86 - 50 - 36 |
Остаток и делитель
![]()
4. Логическая задача
— Решите задачу устно.
На двух кустах сидели 25 воробьев. Когда с одного куста перелетели на другой 5 воробьев, а со второго куста 7 воробьев улетели, то на первом кусте осталось птиц в 2 раза больше, чем на втором. Сколько птиц было на каждом кусте первоначально? (На первом кусте — 17, на втором — 8.)
Ш. Работа по теме урока Работа по учебнику М 163 (с. 56).
(Работа над теоретическим материалом.)
![]() Разделите с остатком число 52 на число 7. (Сначала мы должны найти
наибольшее число, которое Делится на 7 и не превосхоДит 52. Это число 49. С
помощью табличного случая Деления 49 : 7= 7можно выполнить Деление с остатком
числа 52 на число 7. В результате получится следующая запись: 52: мост. э.)
Разделите с остатком число 52 на число 7. (Сначала мы должны найти
наибольшее число, которое Делится на 7 и не превосхоДит 52. Это число 49. С
помощью табличного случая Деления 49 : 7= 7можно выполнить Деление с остатком
числа 52 на число 7. В результате получится следующая запись: 52: мост. э.)
![]() Выполняется ли условие о том, что остаток должен быть меньше делителя?
(Да.)
Выполняется ли условие о том, что остаток должен быть меньше делителя?
(Да.)
— Что это значит? (Деление с остатком выполнено
правшљно.) ![]() 164 (с. 56).
164 (с. 56).
![]() Выполните задание. (76 : 9 = 8 (ост. 4).
Деление с остатком выполнено правильно, так как выполнено условие, в котором
говорится, что остаток (4) Должен быть меньше Делителя (9). )
Выполните задание. (76 : 9 = 8 (ост. 4).
Деление с остатком выполнено правильно, так как выполнено условие, в котором
говорится, что остаток (4) Должен быть меньше Делителя (9). ) ![]() 165 (с. 56).
165 (с. 56).
Решение:
![]() 57
: 6 (ост. 3)
57
: 6 (ост. 3)
![]() 9
(ост. З)
9
(ост. З)
82 = 9 - 9 + 1 82 : 9-—9 (ост. 1)
![]() 9
(ост. 5)
9
(ост. 5)
95 : 9 = 10 (ост. 5)
![]() Почему равенство 69 =
8 • 7 + 13 нельзя использовать для нахождения неполного частного и остатка?
(Остаток больше неполного Делителя.)
Почему равенство 69 =
8 • 7 + 13 нельзя использовать для нахождения неполного частного и остатка?
(Остаток больше неполного Делителя.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ЛФ 166 (с. 57).
![]() Прочитайте задание. Какую запись вы
составили? (58 : 10 =
Прочитайте задание. Какую запись вы
составили? (58 : 10 =
= 5 (ост. 8). )
Можно ли с помощью равенства 58 = 5 • 10 + 8 выполнить деление с остатком числа 58 на 5? (Нет, так как в этом случае остаток (8) будет больше Делителя (5). ) М 167(с. 57). (Самостоятельное выполнение. Работа в парах.) № 168 (с. 57).
![]() Какие остатки могут
получаться при делении на 9? (При Делении на 9 в качестве остатка может
получиться только целое неотрицательное число, которое меньше Делителя: О, 1,
Какие остатки могут
получаться при делении на 9? (При Делении на 9 в качестве остатка может
получиться только целое неотрицательное число, которое меньше Делителя: О, 1,
![]()
— Какое из приведенных равенств можно преобразовать в запись деления с остатком? (93 9 • 10 + З: 93 : 9 = 10 (ост. З) пи 93: 10 = 9(ост. З). ) № 169 (с. 57).
— Какие остатки могут получиться при делении на 2? (0, 1.)
![]() Какие остатки могут получиться при
делении на ? ( Только 0.)
Какие остатки могут получиться при
делении на ? ( Только 0.)
![]() Сколько получится остатков при делении на
число 3? ( Три:
Сколько получится остатков при делении на
число 3? ( Три:
![]() Какую закономерность
вы заметњли? ( Число остатков совпаДает с Делителем. )
Какую закономерность
вы заметњли? ( Число остатков совпаДает с Делителем. )
![]() При делении на какое
число получится семь различных остатков? (На 7.)
При делении на какое
число получится семь различных остатков? (На 7.)
2. Выполнение упражнений в тетращ1 для самостоятельной работы М 86 (с. 48).
Решение:
42 : 5 = 8 (ост. 2)
42 : (ост. 7)
42 : 7 = 6 (ост. 0)
— Как вы понимаете действие деления, в результате которого получился остаток, равный 0? (Деление выполнено нацело.) № 82, 83 (с. 47).
(Работа в парах. Взаимопроверка.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 84, 85 (с. 47—48).
Урок 30, Когда остаток равен О
Цель: рассмотреть случаи деления с остатком, равным 0.
1. Организационный момент. Сообщение темы и цели урока
остаток равен 0
![]()
П. Актуализация знаний
1. Волшебная звезда (Сумма = 30.)
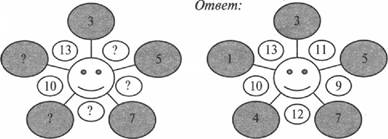
2. Логическая задача
— Решите задачу устно.
Рыболов на вопрос, какова масса пойманной рыбы, ответил: «Масса хвоста кг, масса головы составляет столько, сколько хвост и половина туловища, а масса туловища — столько, сколько голова и хвост вместе». Сколько весит рыба? (8 кг.) З. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Какие числа называются четными?
Приведи пример. (Четные числа — это числа, которые Делятся на 2 нацело. Ряд
таких чисел выглядит так: 2, 4, 6, 8, 10, 12 и т. д. Число Оотносится к четным
числам. Запись любого четного числа заканчивается четной цифрой (О, 2, 4, 6,
8). Например, число 356 7918 четное.) • Какие числа называются нечетными?
Приведи пример. (Нечетные числа — это числа, которые при Делении на 2 Дают ![]() в
остатке 1. Ряд нечетных натуральных чисел выгляДит так: 1, З, 5, 7, 9, 11 и т.
д. Запись любого нечетного числа оканчивается на нечетную цифру (1, З, 5, 7,
9). Например, число
в
остатке 1. Ряд нечетных натуральных чисел выгляДит так: 1, З, 5, 7, 9, 11 и т.
д. Запись любого нечетного числа оканчивается на нечетную цифру (1, З, 5, 7,
9). Например, число
456 829 нечетное.)
lll. Работа по теме урока Работа по учебнику ЛФ 170 (с. 58).
(Коллективное выполнение с объяснением по учебнику.) ![]() Давайте
рассмотрим случаи деления числа на само себя, например: l l • l l = l , 77 : 1,
100 : 100= 1 ит. д.
Давайте
рассмотрим случаи деления числа на само себя, например: l l • l l = l , 77 : 1,
100 : 100= 1 ит. д.
— Что можно сказать про остаток в приведенных примерах? (В этом случае числа Делятся друг на друга без остатка, или нацело.)
![]() Выполнимо ли это
требование, если числа разные? (Для разных чисел требование невыполнимо.)
Выполнимо ли это
требование, если числа разные? (Для разных чисел требование невыполнимо.)
![]() Прочитайте задание. Выполните его.
Прочитайте задание. Выполните его.
— Во всех ли случаях при делении получился остаток? (СреДи этих пар есть такие, которые Делятся нацело: 72 и 9, 45 и 15, 37u 1.)
![]() Чему равен остаток
для этих пар чисел? (Остаток равен 0, что позволяет неполное частное назвать
значением частного.)
Чему равен остаток
для этих пар чисел? (Остаток равен 0, что позволяет неполное частное назвать
значением частного.)
М 172 (с. 58).
— Прочитайте задание. Выполните его.
![]() Какое ближайшее к числу 123 число делится на 8 без остатка? (120.)
Какое ближайшее к числу 123 число делится на 8 без остатка? (120.)
![]() Как можно его
получить? (С помощью вычитания остатка З из Делимого 123.)
Как можно его
получить? (С помощью вычитания остатка З из Делимого 123.)
— Какое следующее за числом 120 число делится на 8 без остатка? (128.)
![]() Как его найти?
(Прибавить к найденному числу 120 число 8, так как сосеДние числа, Делящиеся на
8, отличаются друг от друга также на число 8.) М 173 (с. 59).
Как его найти?
(Прибавить к найденному числу 120 число 8, так как сосеДние числа, Делящиеся на
8, отличаются друг от друга также на число 8.) М 173 (с. 59).
![]() Прочитайте задание. Каме числа вы
записали? (2, 4, 6, 8, 10.)
Прочитайте задание. Каме числа вы
записали? (2, 4, 6, 8, 10.)
![]() 174 (с. 59).
174 (с. 59).
Решение: 93 : 5 = 18 (ост. 3).
Ответ: повар может съесть 3 блина.
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику
М 175 (с. 59).
![]() Какие числа нужно выписать? (7, 14, 21,
28, 35.)
Какие числа нужно выписать? (7, 14, 21,
28, 35.)
— На какое число будет отличаться каждое из выписанных чисел от соседних чисел? (На число 7.) м 176 (с. 59).
![]() Какие числа нужно выписать? (8, 15, 22,
29, 36.)
Какие числа нужно выписать? (8, 15, 22,
29, 36.)
![]() Сравните их с числами
из предыдущего задания. (Они больше на 1.)
Сравните их с числами
из предыдущего задания. (Они больше на 1.)
ЛЕ 177€. 59).
Решение:
1) 25 : 7 = з (ост. 4);
2) 25 — 4 = 21 (конф.).
Ответ: Маша может взять из вазы 21 конфету.
ЛЕ 178 (с. 59).
![]() Прочитайте задание.
Какие числа нужно выписать? (1, 2, З, 4, 6, 8, 12, 24.)
Прочитайте задание.
Какие числа нужно выписать? (1, 2, З, 4, 6, 8, 12, 24.)
делимое меньше делителя
![]() Какое число нужно
прибавить к делимому, чтобы оно делилось на данный делитель без остатка? (
Число, которое равно разности между Делителем и остатком.)
Какое число нужно
прибавить к делимому, чтобы оно делилось на данный делитель без остатка? (
Число, которое равно разности между Делителем и остатком.)
![]() Как найти такое число? (Выполнить Деление
с остатком:
Как найти такое число? (Выполнить Деление
с остатком:
75 : 9 = 8 (ост. З) — и вычесть
остаток из Делителя: 9— З = 6.) ![]() Какое число будет делиться на 9 без
остатка? (81.)
Какое число будет делиться на 9 без
остатка? (81.)
2. Выполнение упражнений в тетрам для самостоятельной рабшн № 87(с. 49). (Самостоятельное выполнение.) ЛФ 89 (с. 50).
а) Решение:
1) 1 1 + 7 = 18 (шт.) — удвоенное количество целых яиц;
2) 18 : 2 = 9 (шт.) — целых яиц;
![]()
Ответ: можно приготовить 3 одинаковые порции омлетов по 3 яйца в каждой.
б) Решение: пусть одна часть — это количество карандашей, а три части — это количество фломастеров.
1) 1 +3=4 (ч.) — всего частей;
2) 28 : 4 = 7 (шт.) — карандашей; 3) 28 — 7 = 21 (шт.) — фломастеров;
4) 7 : I (кар.);
Ответ: можно разложить по карандашу и по 3 фломастера на каждый стол.
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 88 (с. 49).
Урок 31 , Когда делимое меньше делителя
Цель: познакомить со случаями деления меньшего числа на большее.
1. Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Закономерность
![]()
(Закономерность: • 2, + 5; пропущенные числа — 12 и 17.)
2. Цифровой квадрат
|
|
8 |
|
|
|
![]() 9 Ответ:
9 Ответ:
7
З. Родственные ряды
|
36 |
41 |
26 |
61 |
|
|
7 |
8 |
|
12 |
З |
( Числа верхнего ряда получаются в результате умножения соответствующих чисел нижнего ряда на 5 и прибавления еДИНИЦЫ. В верхнем ряду пропущено число 16, в нижнем ряду — 5.)
4. Логические задачи
![]() Решите задачи устно.
Решите задачи устно.
![]() В корзине и в пакете было ровно по 5 яблок. Из корзины в пакет
переложили 2 апельсина. На сколько меньше груш стало в корзине? (ЗаДача не
имеет решения.)
В корзине и в пакете было ровно по 5 яблок. Из корзины в пакет
переложили 2 апельсина. На сколько меньше груш стало в корзине? (ЗаДача не
имеет решения.)
![]() Торт разрезали на 4 одинаковые части, а потом каждую часть разрезали на
2 одинаковые части. На сколько человек хватит торта, если каждому положить на
блюдце по одному куску. (На 8.)
Торт разрезали на 4 одинаковые части, а потом каждую часть разрезали на
2 одинаковые части. На сколько человек хватит торта, если каждому положить на
блюдце по одному куску. (На 8.)
![]() Яйцо варится вкрутую 4 мин. Если бросить 5 яиц в кипящую воду в 9 ч,
когда можно выключить газовую плиту?
Яйцо варится вкрутую 4 мин. Если бросить 5 яиц в кипящую воду в 9 ч,
когда можно выключить газовую плиту?
(В 9 ч 4 МИН.)
Ш. Работа по теме урока Работа по учебнику ле 180 (с. 60).
![]() Прочитайте задание.
Правильный ли случай деления приведен? (Да.)
Прочитайте задание.
Правильный ли случай деления приведен? (Да.)
— Составьте соответствующую запись деления с остатком для следующего равенства. (12 : 15 = О (ост. 12).)
При делении меньшего числа на большее всегда получается 0, а в остатке меньшее число (делимое). ЛФ 181 (с. 60).
![]() Выполните задание.
Выполните задание.
![]() Что общего во всех
этих случаях деления и чем они отличаются? (В остатке всегда получается 8, а
неполное частное равно числу Десятков Делимого.)
Что общего во всех
этих случаях деления и чем они отличаются? (В остатке всегда получается 8, а
неполное частное равно числу Десятков Делимого.)
делимое меньше делителя
![]()
— Какой остаток должен получиться при делении числа 8 на
число 10? Чему будет равно неполное частное? (В остатке должно получиться число
8, а неполное частное будет равно 0.) ![]() Правильно ли в учебнике выполнено деление
с остатком числа 8 на число 10? (Правиьно.) М 182 (с. 60).
Правильно ли в учебнике выполнено деление
с остатком числа 8 на число 10? (Правиьно.) М 182 (с. 60).
— Прочитайте вопрос. О каком условии идет речь? (Делимое должно быть меньше Делителя.)
![]() Приведите примеры таких случаев деления. (10 : 12 = 0 (ост. 10), 6: 8 =
О (ост. 6), 30: 40 = О (ост. 30). ) Лё 183 (с. 60).
Приведите примеры таких случаев деления. (10 : 12 = 0 (ост. 10), 6: 8 =
О (ост. 6), 30: 40 = О (ост. 30). ) Лё 183 (с. 60).
![]() Когда может быть
выполнено данное условие? ( Только когда Делимое меньше Делителя: 10: 15 = О
(ост. 10), 10: 20 = 0 (ост. 10), Пост. 15).)
Когда может быть
выполнено данное условие? ( Только когда Делимое меньше Делителя: 10: 15 = О
(ост. 10), 10: 20 = 0 (ост. 10), Пост. 15).)
М. Физкультминутка
V. Закрепление изученного материала
1.
![]()
![]()
![]() Работа по учебнику М 184 (с. 61).
Работа по учебнику М 184 (с. 61). ![]() (Выполнение в
соответствии с заданиями. Работа с правилом.) ЛЕ 185 (с. 61). — Какие числа при
делении на 56 897 дают в остатке ? (56898, 1.)
(Выполнение в
соответствии с заданиями. Работа с правилом.) ЛЕ 185 (с. 61). — Какие числа при
делении на 56 897 дают в остатке ? (56898, 1.) ![]() 186 (с. 61).
186 (с. 61).
— Прочитайте задание. Какое это число? (4.) — Почему? (Оно меньше всех указанных Делителей.) М 187(с. 61).
![]() — Какое число при делении на любое двузначное число дает в
остатке 9? (9, так как оно меньше любого Двузначного числа. )
— Какое число при делении на любое двузначное число дает в
остатке 9? (9, так как оно меньше любого Двузначного числа. ) ![]() 188(с. 61).
188(с. 61).
— Прочитайте вопрос. Существует ли такое число? (Существует. Так как число 1 меньше любого Другого натурального числа, то при Делении с остатком числа 1 на любое другое натурсаьное число в остатке получается число 1.) м 189 (с. 61).
![]() Прочитайте вопрос. Каким должно быть делимое? (Равно 5.) — Каким
должен быть делитель? (Любым натуральным числом, которое больше 5.) ЛСР
190 (С. 61).
Прочитайте вопрос. Каким должно быть делимое? (Равно 5.) — Каким
должен быть делитель? (Любым натуральным числом, которое больше 5.) ЛСР
190 (С. 61).
— Прочитайте задание. Выполните его.
![]() Какие числа вы выписали? (1, 2, З, 4, 5,
6, 7, 8, 9.)
Какие числа вы выписали? (1, 2, З, 4, 5,
6, 7, 8, 9.)
2.
Выпшшеиме
упражнений в тетрам для самосттельной ра&угы ![]() 92, 93 (с. 51).
92, 93 (с. 51).
(Самостоятельное выполнение. Взаимопроверка.)
![]()
М 94 (с. 52).
Решение:
1) З м 50 см + м 30 см = 4 м 80 см;
2) 4 м 80 см : 2 = 2 м 40 см — ткани первого вида;
З) 2 м 40 см — 1 м 30 см = м 10 см — ткани второго вида; 4) 1 м 10 см < I м 20 см.
Ответ: костюм сшить нельзя.
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 90, 91 (с. 51).
Урок 32, Деление с остатком и вычитание
Цель: показать взаимосвязь двух арифметических действий: деления с остатком и вычитания.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Разминка
— Закончите рассуждения, если это возможно.
• Петя умнее Миши, Коля умнее Пети, следовательно, самый умный — ... (Коля).
• На диване сидели Катя, Женя и Настя. Катя справа от Жени, Женя справа от Насти. Следовательно, посередине была... (Женя).
• Петя не любит ходить в школу, когда там делают прививки. Сегодня он вернулся домой в хорошем настроении. Следовательно... (сегодня в школе прививки не Делали).
• Летучие мыши летают не хуже птиц. Летучие мыши — млекопитающие. Следовательно... (птицы — шекопитающие).
(Это заюаючение ложное.)
|
2. Устный счет (Примеры записаны на доске.) — Решите примеры устно. |
|
|
8 дес. : 2 дес. 9 дес. : 3 дес. |
6 дес. : 3 дес. |
|
10 дес. : 2 дес. 4 дес. : 2 дес. |
10 дес. : 5 дес. |
— Вставьте пропущенные числа.
|
9 кг 370 г = ... г 572 ц = ...
|
... ц=8т4ц 68 кг 170 г = ... г г = I кг 60 г |
Деление с остатком и вычитание
![]()
Ш. Работа по теме урока Работа по учебнику М 191 (с. 62).
• Как с помощью вычитания найти остаток от деления одного числа на другое? (Нужно выполнять вычитание Делителя из Делимого до тех пор, пока это возможно, т. е. до тех пор, пока уменьшаемое будет больше вычитаемого ши равно ему. Получившееся в результате последнего вычитания число и будет равно остатку.)
![]() А как узнать, чему будет равно неполное
частное? (Нужно посчитать число выполненных Деиствии вычитания, это число будет
равно неполному частному.) ле 192 (с. 62).
А как узнать, чему будет равно неполное
частное? (Нужно посчитать число выполненных Деиствии вычитания, это число будет
равно неполному частному.) ле 192 (с. 62).
— Прочитайте задание. Чему будет равно значение разности?
(53— 7 • 7=4.)
— Запишите соответствующий случай деления с остатком. (53: 7(ост. Ф.) ![]() 193 (с. 62).
193 (с. 62).
• Чему будет равно значение разности? (69 — 6 = 63.)
— Как эту разность представить в виде произведения двух множителей, один из которых равен 9? (9 • 7=63.)
— Запишите соответствующие случаи деления с остатком. ![]() 7(ост. 6), 69: 9(ост. о.)
7(ост. 6), 69: 9(ост. о.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику
М 194 (с. 62). Решение:
![]() ц 50 кг = 150 кг;
ц 50 кг = 150 кг;
150 : 35 = 4 (ост. Ш).
Выполнение деления с остатком нужно заменить выполнением кратного вычитания: 150 — 35 — 35 — 35 — 35 = 10.
Ответ: получилось 4 полных мешка, и осталось 10 кг картофеля.
ЛФ 195 (с. 62).
Решение:
387 : 350= (ост. 37); 387 - 350 = 37.
927 : 291 = з (ост. 54);
927 - - 291 - 291 = 54.
1003 : 250 = 4 (ост. 3);
1003 - 250 - 250 - 250 - 250![]()
2. Выполнение упражнений в тетради для самостоятельной рабшы 96, 97€.53).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 98 (с. 53).
Урок 33. Какой остаток может получиться при делении на 2?
Цели: формировать умение разбивать все целые неотрицательные числа на четные и нечетные; рассмотреть свойства четных и нечетных чисел.
1. Организационный момент. Сообщение темы и целей урока
11. Актуализация знаний
1. Цифровой квадрат
|
6 |
|
|
|
|
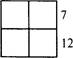 Ответ:
Ответ:
В 6
2. Родственные ряды
|
6 |
5 |
|
|
4 |
|
25 |
21 |
29 |
41 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 4 и прибавления еДиницы. В верхнем ряду пропущено число 7, в нижнем ряду — 17.)
З. Повторение нумерации
(Числа записаны на доске.) ![]() Прочитайте числа.
Прочитайте числа.
38 007, 638 502, 5009, 61 101, 5555, 40 000, 2050, 2409, 3200, 1948. П 002 006, 20 000 305, 008 356, 124 080, 900 999.
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
В шкафу было 7 учебников по математике и 12 учебников по русскому языку. Из шкафа взяли 10 учебников. Остался ли
Какой остаток может получиться при делении на 2?
![]()
в шкафу хотя бы один учебник по
математике? Остался ли в шкафу хотя бы один учебник по русскому языку? (Хотя бы
один учебник по русскому языку останется в любом случае. Учебников по
математике не останется, если взяли З учебника по русскому ЯЗЫКУ и 7 учебников
по математике.) Ш. Работа по теме урока Работа по учебнику ![]() 196 (с.
63).
196 (с.
63).
(Коллективное выполнение. Знакомство с терминами по словарику учебника (с. 1 18—119).)
— Могут ли при делении на 2 в остатке получиться числа, отличные от чисел 0 и 1? (Нет.)
![]() Почему? (Остаток Должен
быть меньше Делителя. Меньше 2 только числа О и 1.) № 197(с. 63).
Почему? (Остаток Должен
быть меньше Делителя. Меньше 2 только числа О и 1.) № 197(с. 63).
![]() Выполните задание.
Выполните задание.
— Что вы можете сказать о расположении четных и нечетных чисел в натуральном ряду чисел? (Они располагаются через одно.)
![]() Как узнать, какое число будет двадцатым в ряду натуральных нечетных
чисел? (Чтобы опреДелить нечетное число по его номеру, нужно уДвоить число,
обозначающее этот номер, и вычесть 1: 20 • 2 — = 39. Двадцатое по поряДку
нечетное число — 39.) № 198 (с. 63).
Как узнать, какое число будет двадцатым в ряду натуральных нечетных
чисел? (Чтобы опреДелить нечетное число по его номеру, нужно уДвоить число,
обозначающее этот номер, и вычесть 1: 20 • 2 — = 39. Двадцатое по поряДку
нечетное число — 39.) № 198 (с. 63).
![]() Назовите самое маленькое нечетное натуральное число. ( 1.) — Можете ли
вы назвать самое большое нечетное натуральное число? (Нет, ряд натуральных
чисел бесконечен, слеДовательно, ряд нечетных (ряд четных) чисел также является
бесконечным. ) № 199 (с. 63).
Назовите самое маленькое нечетное натуральное число. ( 1.) — Можете ли
вы назвать самое большое нечетное натуральное число? (Нет, ряд натуральных
чисел бесконечен, слеДовательно, ряд нечетных (ряд четных) чисел также является
бесконечным. ) № 199 (с. 63).
![]() Назовите самое маленькое четное число. (2.)
Назовите самое маленькое четное число. (2.)
![]() Почему число 0 относят к четным числам? (Четные числа
Почему число 0 относят к четным числам? (Четные числа
Делятся на 2 без остатка: 0 : 2 = 0 (ост. 0). )
![]() Существует ли самое большое четное число?
(Нет.)
Существует ли самое большое четное число?
(Нет.) ![]() 200 (с. 64).
200 (с. 64).
— Прочитайте задание. На какой стороне улицы будет расположен дом № 19? (На нечетной.)
— Как узнать, каким он будет по счету, с помощью сложения? (Увеличить номер на 1, а потом полученное число разДелить пополам: (19 + 1): 10.)
— А как получить ответ на этот вопрос, используя деление с остатком? (19:2 = 9 (ост. 1), 9 + 10.)
![]()
— Как узнать, каким по счету будет дом № 16 (16 : 2 = 8.)
М. Физкультминутка
V. Закрепление изученного материала Работа по учебнику ![]() 201 (с, 64).
201 (с, 64).
![]() Может ли при сложении четных чисел получиться нечетное число (Нет.)
Может ли при сложении четных чисел получиться нечетное число (Нет.)
![]() Приведите примеры сложения четного числа
с четным. (8+2=10, Ю М, 20+8=28ит. д.)
Приведите примеры сложения четного числа
с четным. (8+2=10, Ю М, 20+8=28ит. д.) ![]() 202 (с. 64).
202 (с. 64).
![]() Какое число получится при сложении нечетных чисел? ( Четное.)
Какое число получится при сложении нечетных чисел? ( Четное.)
![]() Приведите
примеры. (З + 3=6, 7+ 7= 14, lll + = 222
Приведите
примеры. (З + 3=6, 7+ 7= 14, lll + = 222
![]() 203 (с. 64).
203 (с. 64).
— Какое число получится при сложении четного числа с нечетным: четное или нечетное? (Может получиться только нечетное число.)
![]() Приведите примеры сложения четного числа с нечетным. (3+4= 7, 7+8=15,
11/+ 1/2=223ит. д.)
Приведите примеры сложения четного числа с нечетным. (3+4= 7, 7+8=15,
11/+ 1/2=223ит. д.)
![]() А если мы будем складывать нечетное число с четным? (Ответ будет тем же
самым, так как мы просто применим переместительное свойство сложения.)
А если мы будем складывать нечетное число с четным? (Ответ будет тем же
самым, так как мы просто применим переместительное свойство сложения.)
№ 204 (с. 64).
![]() Какое получится число при умножении четных чисел друг на друга?
Приведите примеры таких случаев. (Получится четное число: 2 • 2 = 4, 6 • 6 =
36, 20 • 20 = 400 и т. д.)
Какое получится число при умножении четных чисел друг на друга?
Приведите примеры таких случаев. (Получится четное число: 2 • 2 = 4, 6 • 6 =
36, 20 • 20 = 400 и т. д.) ![]() 205 (с. 64).
205 (с. 64).
![]() Какое получится число при умножении нечетных чисел друг на друга?
Подтвердите свой ответ примерами. (Получится нечетное число: З • 9, 5 • 5 = 25,
11 • 11 = 121 и т. д.)
Какое получится число при умножении нечетных чисел друг на друга?
Подтвердите свой ответ примерами. (Получится нечетное число: З • 9, 5 • 5 = 25,
11 • 11 = 121 и т. д.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 99, 100 (с. 54).
Урок 34, Какой остаток может получиться при делении на 2?
Цели: развивать умение разбивать все целые неотрицательные числа на четные и нечетные; продолжать рассмотрение свойств четных и нечетных чисел.
Какой остаток может получиться при делении на 2?
![]()
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
1. Волшебные квадраты
|
|
|
|
|
|
|
|
|
|
|
|
|
ипа |
|
|
|
пот |
||||||
|
|
|
|
|
|
|
|
|
|
||
Ответы:
|
|
|
|
|
|
|
|
|
|
|
|
|
пап пап |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
2. Логические задачи
![]() Решите задачи устно.
Решите задачи устно.
• У меня в сумке 3 кг конфет, ау моего друга 3 кг ваты. У кого груз тяжелее? (ОДинаковый вес.)
• После тренировки по фигурному катанию спортсмены переоделись и оставили в раздевалке 10 коньков. Сколько фигуристов тренировалось на катке? (5.)
З. Устный счет
(Примеры записаны на доске.)
— Выполните действия. Объясните приемы вычислений.
82 - 38 62-48 + 29
56- 19 71 —38 + 19
28 -![]() 84- 29 + 27
84- 29 + 27
27 + 34 72 + -38
76-![]() 49 + 39— l2
49 + 39— l2
Ш. Работа по теме урока Работа по учебнику М (с. 65).
![]() Какое получится число
при умножении четного числа на нечетное? Приведите примеры. (Получится четное
число:
Какое получится число
при умножении четного числа на нечетное? Приведите примеры. (Получится четное
число:
![]()
— Изменится ли ответ, если умножить нечетное число на четное? (Не изменится, так как будет использовано переместительное своиство умножения. )
Какое получится число при вычитании четного числа из четного? Проиллюстрируйте свой ответ примерами.
(Получится четное число: 10— 6 = 4, 100— 40 = 60, 16— 8 =
![]()
м 208 (с. 65).
![]() Какое получится число при вычитании нечетного числа из нечетного?
Приведите примеры таких случаев. (Получится четное число: 21 — 7= 14, 19— 5=
14, 99— 92 и т. Д.) м 209 (с. 65).
Какое получится число при вычитании нечетного числа из нечетного?
Приведите примеры таких случаев. (Получится четное число: 21 — 7= 14, 19— 5=
14, 99— 92 и т. Д.) м 209 (с. 65).
— Какое получится число, если из четного числа вычесть нечетное? Подтвердите свое предположение примерами. (Получится нечетное число: 90 — 5 = 85, 18 — З = 15, — З = = 107и т. д.) № 210 (с. 65).
![]() Какое получится число, если из нечетного числа вычесть четное? Покажите
это на конкретных примерах. (Получится нечетное число: 9— 6=3, 13 — б = 7, 21 —
8= 13 и т. д.) М 211 (с. 65).
Какое получится число, если из нечетного числа вычесть четное? Покажите
это на конкретных примерах. (Получится нечетное число: 9— 6=3, 13 — б = 7, 21 —
8= 13 и т. д.) М 211 (с. 65).
— Какие числа могут получиться при делении четного числа на четное? Приведите примеры. (Могут получиться как четные, так и нечетные числа: 24 : 2 = 12, 24 : 4 = 6, 24 : 8 = З.)
М. Физкультминутка
У. Закрепление изученного материала Работа по учебнику м 212 (с. 66).
— Какое число получится при делении нечетного числа на нечетное? Приведите примеры таких случаев деления. (Получится нечетное число: 21 : 7=3, 45: 5 = 9, 27: 9 = З.) М 213 (с. 66).
![]() Какое получается число при делении четного числа на нечетное? Приведите
примеры. (Получится четное число: •
Какое получается число при делении четного числа на нечетное? Приведите
примеры. (Получится четное число: •
![]()
М 214 (с. 66).
![]() Можно ли нацело разделить нечетное число на четное? Почему? Каким
правилом советуют воспользоваться авторы учебника? (Примерный ответ. Делимое
можно получить, умножив делитель на значение частного. По условию делитель
является четным числом. Если делитель умножить на любое число (четное или
нечетное), то обязательно получится четное число. В нашем случае делимое —
нечетное
Можно ли нацело разделить нечетное число на четное? Почему? Каким
правилом советуют воспользоваться авторы учебника? (Примерный ответ. Делимое
можно получить, умножив делитель на значение частного. По условию делитель
является четным числом. Если делитель умножить на любое число (четное или
нечетное), то обязательно получится четное число. В нашем случае делимое —
нечетное
Поупражняемся в вычислениях и повторим пройденное
![]()
число. Это означает, что никакое
значение частного подобрать в этом случае нельзя.) ![]() (с. 66).
(с. 66).
![]() Прочитайте задание. Выполните его.
Прочитайте задание. Выполните его.
![]() Как узнать, четным
или нечетным числом будет каждое из слагаемых? (Нужно посмотреть на последнюю
цифру в записи числа. Если эта цифра четная (обозначает четное однозначное
число), то и само число четное, если же нечетная (обозначает нечетное
однозначное число), то и само число нечетное.)
Как узнать, четным
или нечетным числом будет каждое из слагаемых? (Нужно посмотреть на последнюю
цифру в записи числа. Если эта цифра четная (обозначает четное однозначное
число), то и само число четное, если же нечетная (обозначает нечетное
однозначное число), то и само число нечетное.)
— Какие цифры относятся к четным? (0, 2, 4, 6, 8.) —
Ак нечетным? (1, З, 5, 7, 9.) м 216 (с. 66). (Самостоятельное выполнение.
Проверка в парах.) ![]() 66).
66).
![]() Прочитайте вопрос. Как найти ответ?
(Всего 90 Двузначных чисел. Самое маленькое Двузначное четное число — 10. А
самое большое нечетное — 99. Четные и нечетные числа чередуются. Поэтому четных
Двузначных чисел столько же, сколько и нечетных, т. е. 90: 2 = 45.) ЛГ2
(с. 66).
Прочитайте вопрос. Как найти ответ?
(Всего 90 Двузначных чисел. Самое маленькое Двузначное четное число — 10. А
самое большое нечетное — 99. Четные и нечетные числа чередуются. Поэтому четных
Двузначных чисел столько же, сколько и нечетных, т. е. 90: 2 = 45.) ЛГ2
(с. 66).
— Запишите самое большое четное шестизначное число.
(999 998.)
— Назовите следующие за ним два числа. (999 999 и 1000 000.) ![]() Что
можно сказать о первом из этих чисел? (Нечетное, шестизначное.)
Что
можно сказать о первом из этих чисел? (Нечетное, шестизначное.)
![]() Сколько знаков во втором числе? (Семь.)
Сколько знаков во втором числе? (Семь.)
![]() Что можно сказать об этом числе? (
Четное, семизначное.)
Что можно сказать об этом числе? (
Четное, семизначное.)
![]() Как называется второе число? (Мшиион.)
Как называется второе число? (Мшиион.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 101 (с. 54).
Урок 35. Поупражняемся в вычислениях и повторим пройденное
Цели: повторить пройденный материал; закрепить полученные умения и навыки.
l. Организационный момент. Сообщение темы и целей урока
![]()
ll. Актуализация знаний
1. Цифровой квадрат
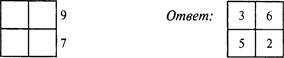
8 8
2. Родственные ряды
|
2 |
4 |
З |
5 |
|
|
4 |
16 |
|
25 |
64 |
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на самих себя. В верхнем ряду пропущено число 8, в нижнем ряду — 9.)
З. Устный счет
(Примеры записаны на доске.)
![]() Выполните действия. Объясните приемы
вычислений.
Выполните действия. Объясните приемы
вычислений.
76 - 15 84- 29 + 27
32 — 14 71 - 38 + 19
58-![]() 55 — 45 + 39
55 — 45 + 39
28 — 9 98 + 2— 35
4. Логические задачи
— Решите задачи устно.
• У Пети несколько собак. После прогулки в ненастную погоду он помыл 12 лап. Сколько собак у Пети? (З.)
• Батон разрезали на 10 частей. Сколько для этого потребовалось сделать разрезов? (9.)
• С утра температура воздуха была —9 градусов, а затем потеплело на 7 градусов. Положительной ли стала температура воздуха к полудню? (Нет.)
Ш. Работа по теме урока Работа по учебнику м 219 (с. 67).
•
С помощью формул найдите числа и заполните таблицу. ![]() Какие числа
получились во второй колонке? ( Четные.)
Какие числа
получились во второй колонке? ( Четные.)
![]() Какие числа получились в третьей колонке?
(Нечетные.) м 220 (с. 67).
Какие числа получились в третьей колонке?
(Нечетные.) м 220 (с. 67).
![]() Прочитайте условие
задачи. Как найти, на каком этаже находится квартира № 29? (Номер квартиры
разделить с остатком на число квартир на одном этаже: 29: 4 = 7 (ост.
Прочитайте условие
задачи. Как найти, на каком этаже находится квартира № 29? (Номер квартиры
разделить с остатком на число квартир на одном этаже: 29: 4 = 7 (ост.![]()
Поупражняемся в вычислениях и повторим пройденное
![]()
— Что нужно сделать дальше? (К полученному неполному частному прибавить число 1, и мы получим ответ на поставленный вопрос. Квартира М 29 нахоДится восьмом этаже.)
— В каком случае не потребуется прибавлять число 1? (Если номер квартиры будет 28.)
![]() Почему? (Число 28 Делится на 4 без остатка.)
Почему? (Число 28 Делится на 4 без остатка.)
![]() Определите, на каком этаже находится квартира № 32.
Определите, на каком этаже находится квартира № 32.
![]()
Мы видим, что в этом случае число 1 прибавлять к частному не нужно, так как 32 делится на 4 нацело.
№ 221 (с. 68). — Прочитайте задачу. Какого она типа? (Задача на сумму и частное.)
![]() Как вы будете решать задачу? (Примем стоимость одной тетраДи за одну
часть, а стоимость книги — за пять частей.)
Как вы будете решать задачу? (Примем стоимость одной тетраДи за одну
часть, а стоимость книги — за пять частей.) ![]() Сколько всего
получится частей? (1 + 5 = 6 (ч.).)
Сколько всего
получится частей? (1 + 5 = 6 (ч.).)
![]() Что можно найти далее? (Цену тетраДи: 120 : 6 = 20 (руб./шт.).) — Как
найти цену книги? (20 • 5 = 100 (руб.).)
Что можно найти далее? (Цену тетраДи: 120 : 6 = 20 (руб./шт.).) — Как
найти цену книги? (20 • 5 = 100 (руб.).)
— Что можно вычислить далее? (Стоимость набора, состоящего из любого количества таких тетраДей и таких книг: 20 • 4 = 8006.) и 2 = (руб.).)
![]() Сколько всего заплатили? (80 + 200 = 280
(руб.).) м 222 (с. 68).
Сколько всего заплатили? (80 + 200 = 280
(руб.).) м 222 (с. 68).
— Прочитайте задачу. Какого она типа? (Задача на сумму и разность.)
![]() Что можно узнать сначала? (Стоимость 2 тетраДей: 120 — -80=40 (руб.).)
Что можно узнать сначала? (Стоимость 2 тетраДей: 120 — -80=40 (руб.).)
— Что можно узнать далее? (Цену тетраДи: 40: 2 = 20(руб./шт.).)
![]() Как
найти цену книги? (120 — 20 = 100 (руб./шт.).)
Как
найти цену книги? (120 — 20 = 100 (руб./шт.).)
![]() Можно ли теперь найти стоимость набора из 5 таких тетрадей и 3 таких
книг? (Да: 20 • 5 + 100 • З = 400 (руб.).) М 223 (с. 68). — Прочитайте задачу.
Какого она типа? (Задача на разность и частное.)
Можно ли теперь найти стоимость набора из 5 таких тетрадей и 3 таких
книг? (Да: 20 • 5 + 100 • З = 400 (руб.).) М 223 (с. 68). — Прочитайте задачу.
Какого она типа? (Задача на разность и частное.)
— Что приняли за одну часть? (Стоимость тетраДи.)
— Что приняли за пять частей? (Стоимость книги.)
![]() Что можно сделать далее? (Выполнить разностное сравнение частей: 5— 1 =
4 (ч.).)
Что можно сделать далее? (Выполнить разностное сравнение частей: 5— 1 =
4 (ч.).)
— Что обозначают четыре части? (Это 80руб.)
![]() Как найти цену тетради? (80 : 4 = 20 (руб./шт.).)
Как найти цену тетради? (80 : 4 = 20 (руб./шт.).)
![]() Как найти цену книги? (20 • 5 = 100 (руб.).)
Как найти цену книги? (20 • 5 = 100 (руб.).)
— Можно ли вычислить стоимость набора из З таких тетрадей и 2 таких книг? (Да: 20 • З + 100 • 2 = 260 (руб.).)
![]()
lV. Физкультминутка
V. Закрепление изученного материала Работа по учебнику ЛГ2 224 (с. 68).
![]() Прочитайте задание. Кате это мотуг быть числа? (Нечетные.)
Прочитайте задание. Кате это мотуг быть числа? (Нечетные.) ![]() Когда
получаются нечетные числа? (При сложении нечетного числа с четным (2573 + 48
686), при вычитании из нечетного числа четного (6549 — 3582), при умножении
нечетных чисел (357. 985).)
Когда
получаются нечетные числа? (При сложении нечетного числа с четным (2573 + 48
686), при вычитании из нечетного числа четного (6549 — 3582), при умножении
нечетных чисел (357. 985).)
— Почему не нужно выписывать оставшиеся выражения? (Потому
что значение каждого из оставшихся выражений будет четным, а четные числа
Делятся на 2 без остатка.) (Выполнение задания. Взаимопроверка.) ![]() (с. 68).
(с. 68).
![]() Что нужно сделать, чтобы записать самое маленькое нечетное шестизначное
число? (Нужно заполнить все разряды СшиЫМИ малеНЬКИМИ из ВОЗМОЖНЫХ чисел.)
Что нужно сделать, чтобы записать самое маленькое нечетное шестизначное
число? (Нужно заполнить все разряды СшиЫМИ малеНЬКИМИ из ВОЗМОЖНЫХ чисел.)
— Какое число нужно записать в первый разряд? (1, так как число должно быть нечетным.)
![]() Какие числа нужно записать в следующие четыре разряда? ( Четыре О.)
Какие числа нужно записать в следующие четыре разряда? ( Четыре О.)
![]() — А в старший разряд?
(1, так как в старшем разряде число О нахоДиться не может.)
— А в старший разряд?
(1, так как в старшем разряде число О нахоДиться не может.)
![]() Какое число получилось? ( 100 001.)
Какое число получилось? ( 100 001.)
![]() Можно ли проверить
правильность выполнения задания? (Для этого нужно записать два преДшествующих
числа: 99 999, то 000.)
Можно ли проверить
правильность выполнения задания? (Для этого нужно записать два преДшествующих
числа: 99 999, то 000.)
![]() Что можно сказать о
первом из этих чисел? (Нечетное, пятизначное.)
Что можно сказать о
первом из этих чисел? (Нечетное, пятизначное.)
— Что можно сказать о втором числе? ( Четное, шестизначное.)
Поэтому число 100 001 действительно является наименьшим нечетным шестизначным числом. Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 103 (с. 55).
Урок 36. Запись деления с остатком столбиком
Цель: научить выполнять деление с остатком столбиком.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
Запись деления с остатком столбиком
![]()
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: + 5, : 10; пропущенные числа — 100 и Ю.)
2. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Что произойдет с числом, если к его записи справа приписать ноль? два нуля? три нуля? (Число увеличится в 10, 100, 1000 раз.)
• Что произойдет с числом, если в его записи, оканчиваюЩеЙСЯ нулями, отбросить один ноль? два нуля? три нуля?
( Число уменьшится в Ю, 100, 1000раз.)
З. Устный счет
(Примеры записаны на доске.)
• Вычислите.
|
40 — 5 |
54 — 4 |
90- 1 |
58- |
|
77 - 70 |
69 - 15 |
61 -2 |
52- 1 |
|
41 _ |
зоо - ПО |
430 — 400 |
800 - 50 |
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Торговка, сидя на рынке, соображала: «Если бы к моим яблокам прибавить половину их, да еще десяток, то у меня была бы целая сотня!» Сколько яблок у нее было? (Примерный ответ. Задачу такого типа надо решать с конца. Отнимем излишек в 10 яблок, тогда останется 90 яблок, в это количество входит З части. Торговка сказала: «Если бы к моим яблокам прибавить их половину...» Следовательно, в числе 90 заключаются две части, да еще та часть (половина яблок), которую торговка желает вновь прибавить. Разделив 90 на 3, мы узнаем, что половина всех яблок равна 30. Значит, у торговки было 30 • 2 = 60 яблок.)
Ш. Работа по теме урока Работа
по учебнику ![]() 226 (с. 69).
226 (с. 69).
(Учащиеся вместе с учителем комментируют выполнение деления с остатком столбиком.)
Делим число 25 на число 8. В частном получается число 3.
Умножаем 3 на 8, получаем 24. Записываем число 24 под числом 25 столбиком: единицы пишем под единицами, десятки — под десятками. Вычитаем из 25 число 24, получаем — столько единиц 4 Поурочные разработки по математике
![]()
осталось разделить. Сравниваем остаток с делителем: единиц (1 ) осталось меньше, чем делитель (8). Деление с остатком выполнено правильно.
![]() Какой основной принцип записи столбиком?
(Разряд записывается под соответствующим разрядом.) М227(с. 69).
Какой основной принцип записи столбиком?
(Разряд записывается под соответствующим разрядом.) М227(с. 69).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
М 228 (с. 69). (Самостоятельное выполнение. Взаимопроверка в парах.) м 229 (с. 70).
(Самостоятельное выполнение с записью решения на доске.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 70).
70).
(Выполнение в соответствии с заданиями.)
![]() Назовите случай деления нацело. (42 : 6 =
7.) — Чему в этом случае равен остаток? (Нулю.) № 231 (с. 70).
Назовите случай деления нацело. (42 : 6 =
7.) — Чему в этом случае равен остаток? (Нулю.) № 231 (с. 70).
![]() Прочитайте задание. Назовите делимое.
(87.)
Прочитайте задание. Назовите делимое.
(87.) ![]() Назовите делитель. (21.) — Чему равно
неполное частное? (4.)
Назовите делитель. (21.) — Чему равно
неполное частное? (4.)
![]() Чему равен остаток? (З.)
Чему равен остаток? (З.)
![]() Значением какого выражения является число
84? (21 • 4.) м 232 (с. 70).
Значением какого выражения является число
84? (21 • 4.) м 232 (с. 70).
![]() Прочитайте задачу. (С
помощью какого действия ее можно решить? (Деления: 50 : 6.)
Прочитайте задачу. (С
помощью какого действия ее можно решить? (Деления: 50 : 6.)
— Вычислите ответ, используя запись столбиком.
![]() Сколько человек окажется в неполной
шеренге? (Два.) М 233 (с. 70).
Сколько человек окажется в неполной
шеренге? (Два.) М 233 (с. 70).
— Прочитайте задание. Вспомните правило деления, когда делимое меньше делителя. (Если при Делении с остатком делимое меньше Делителя, то неполное частное равно 0, а остаток равен Делимому.)
— Выполните вычисления, сделав запись в строчку и столбиком. 2. Выполнение упражнения в тетради для самостягељной работы
М 106 (с. 57).
— Что нужно сделать сначала? (40 : 6 = 6 (ост. 4).)
— Что вы узнали, выполнив деление с остатком? (Количество яблок, которое получит каждый ребенок, и количество оставшихся яблок.)
Способ поразрядного нахождения результата деления
Что нужно сделать дальше? (Вычислить разницу между значешем частного и остатком: 6— 4 = 2.)
Что обозначает эта разница? (Количество яблок, которое необхоДимо Добавить в ящик, чтобы их можно было поДелить поровну между шестью Детьми.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 104, 105 (с. 56—57).
Урок 37. Способ поразрядного нахождения результата деления
Цель: познакомить со способом поразрядного нахождения результата деления, когда этот результат (неполное частное или значение частного) является двузначным числом.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Повторение нумерации
![]() Запишите числа цифрами.
Запишите числа цифрами.
5 тыс., 212 тыс., 12 тыс., 205 тыс., 300 тыс., 5 тыс. ед.
2. Цифровой квадрат
|
|
|
9 Ответ: |
4 |
5 |
|
|
|
6 |
5 |
З. Родственные ряды
|
|
|
|
9 |
|
|
5 |
|
29 |
53 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 6 и вычитания еДиницы. В верхнем ряду пропущено число 5, в нижнем ряду — 35.)
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Ученики пошли в музей. Они построились тройками. Маша, Витя, Коля заметили, что их тройка седьмая спереди и пятая сза-
![]()
ди. Сколько учеников пошло в музей? (Варианты правильных ответов.• 15, 21, 30, 33, 36.)
Ш. Работа по теме урока Работа по
учебнику ![]() 234 (с. 71).
234 (с. 71).
Комментарий для учителя. При знакомстве с новой темой важно обратить внимание на то, что сложение двух полученных результатов деления (20 и 5) в такой записи осуществляется автоматически с помощью совмещения записей двух однозначных чисел (2 и 5) в запись одного двузначного числа (25). Л) 235 (с. 72).
(Выполнение в соответствии с заданием.)
![]() Почему такой способ
называют способом поразрядного нахождения результата деления? (Потому что найти
результат Деления можно не сразу ЦиИКОМ, а отДельно по разРЯДНЫМ слагаемым, из
которых потом легко получается запись ИСКОМОГО результата. )
Почему такой способ
называют способом поразрядного нахождения результата деления? (Потому что найти
результат Деления можно не сразу ЦиИКОМ, а отДельно по разРЯДНЫМ слагаемым, из
которых потом легко получается запись ИСКОМОГО результата. ) ![]() 72).
72).
(Коллективное выполнение с комментированием у доски.)
М. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику м 237(с. 72).
![]() В
чем особенность данного случая деления? (Примерный ответ. Делимое для второго
случая деления (16 : 4) получаем не только с помощью выражения остатка от
первого деления (1 десяток) в единицах соседнего младшего разряда, как это
делалось раньше, но и еще с помощью прибавления к этому числу числа единиц (6)
из соответствующего разряда первоначального делимого: I дес. - ш, 10 + 6 = 16.)
В
чем особенность данного случая деления? (Примерный ответ. Делимое для второго
случая деления (16 : 4) получаем не только с помощью выражения остатка от
первого деления (1 десяток) в единицах соседнего младшего разряда, как это
делалось раньше, но и еще с помощью прибавления к этому числу числа единиц (6)
из соответствующего разряда первоначального делимого: I дес. - ш, 10 + 6 = 16.)
![]() 72). (Самостоятельное выполнение. Проверка
в парах.) ЛГ22З9(с. 72).
72). (Самостоятельное выполнение. Проверка
в парах.) ЛГ22З9(с. 72).
Решение: 95 : 5 19 (б.).
Ответ: получится 1 9 букетов.
![]() Вычислите
ответ этой задачи способом поразрядного НиОждения результата деления, используя
запись столбиком.
Вычислите
ответ этой задачи способом поразрядного НиОждения результата деления, используя
запись столбиком.
2, Выполнение упражнения в тетради для самостоятельной работы
ЛФ 109 (а, 6, г) (с. 58-59).
(Коллективное выполнение с комментированием у доски.)
Поупражняемся в делении столбиком
Прочитайте задачу а. Как будете рассуждать? (Пусть в одной стопке одна часть тетрадей, а в другой стопке две части тетрадей.)
![]() Сколько
всего частей? (1 + 2 = З (ч.).)
Сколько
всего частей? (1 + 2 = З (ч.).)
![]() Сколько тетрадей в меньшей стопке? (54 :
З = 18 (тет.).)
Сколько тетрадей в меньшей стопке? (54 :
З = 18 (тет.).) ![]() Сколько тетрадей в большей стопке? (18 •
2 = 36 (тет.).)
Сколько тетрадей в большей стопке? (18 •
2 = 36 (тет.).)
— Выполните проверку. (18 + 36 = 54 (тет.).)
![]() Прочитайте
задачу б. Что можно сделать сначала? (Выполнить разностное сравнение Данных: 54
— 6 = 48 (тет.). )
Прочитайте
задачу б. Что можно сделать сначала? (Выполнить разностное сравнение Данных: 54
— 6 = 48 (тет.). )
— Как найти меньшее число тетрадей? (48 : 2 = 24 (тет.). )
— Как найти большее число тетрадей? (24 + 6 = 30 (тет.).)
![]() Прочитайте
задачу г. Что можно узнать первым действием? (Цену машинки: 72 : 6 = 12
(руб./шт.).)
Прочитайте
задачу г. Что можно узнать первым действием? (Цену машинки: 72 : 6 = 12
(руб./шт.).)
![]() Какое
действие будет вторым? (96 : 4 = 24 (руб./шт.) — цена куклы.)
Какое
действие будет вторым? (96 : 4 = 24 (руб./шт.) — цена куклы.)
![]() Можем ли мы теперь
узнать разницу в цене? Ща: 24 : 12 — = 2 (раза). )
Можем ли мы теперь
узнать разницу в цене? Ща: 24 : 12 — = 2 (раза). )
Ш. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 107 (с. 58).
Урок 38. Поупражняемся в делении столбиком
Цель: развивать умение выполнять деление столбиком.
1. Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Устный счет
(Примеры записаны на доске.) — Вычислите.
|
81 : 9 |
56 : 7 |
63 : 9 |
45 : 5 |
|
|
|
7 - 4 |
70 • 4 |
|
90 • 7 |
60 |
20 • 6 |
|
|
50 • 5 |
30 • 4 |
|
|
2. Блицтурнир
• Ложка стоит 2 руб. Сколько заплатили за 18 таких ложек?
• На 2 платья идет 8 м материи. Сколько метров материи надо на 10 платьев?
• Если на каждую рубашку идет по 3 м полотна, то из куска полотна выйдет 9 рубашек. Сколько метров ткани в куске?
![]()
• В ларек привезли 4 ящика слив по 9 кг в каждом. До обеда продали 27 кг. Сколько ящиков слив продали?
• Назовите четные числа от 30 до 40.
• Назовите нечетные числа от 45 до 35.
• Сколько и каких разрядных единиц содержится в каждом из данных чисел: 354, 8207, 12 109, 756 023?
• Назовите число, которое содержит 346 единиц масса тысяч, 200 единиц первого класса, 30 единиц второго класса, 6 единиц первого класса.
• Выразите числа в единицах: 67 дес., 48 сот. , 328 сот. , 26 тыс.
• Назовите значения выражений: 99 999 + 1, 1999 + 1, 8899 + 1.
Ш. Работа по теме урока Работа по учебнику
М 240 (с. 73).
(Самостоятельное выполнение.)
![]() В каких случаях
деления в разряде десятков находится цифра (72: 6, 85: 5.)
В каких случаях
деления в разряде десятков находится цифра (72: 6, 85: 5.)
— В каких случаях деления в разряде десятков находится цифра 2? (58: 2, 92: 4.) № 241 (с. 73). (Самостоятельное выполнение. Проверка в парах.) М 242 (с. 73).
(Коллективное выполнение с записью на доске.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 243 (с. 73).
— Выполните задание. Что необычного вы заметили при решении данной задачи? ( Число 45 сначала увеличиш в 2 раза, а потом уменьшшш в это же число раз, И в итоге число не изменипось.)
— Нужно ли было выполнять эти вычисления? (Нет.)
— Какое свойство вы применили при решении этой задачи?
(Если число сначала увеличить в какое-то число раз, а потом уменьшить в это же
число раз, то число в итоге не изменится.) JV2 244 (с. 73). (Коллективное
выполнение с записью на доске.) ![]() 245 (с. 74).
245 (с. 74).
— Сравните данные записи деления и умножения столбиком. Что можно сказать об этом? (Запись умножения связана
Вычисления с помощью калькулятора
![]()
с записью Деления, так как в ней описан процесс умножения Делителя на значение частного из первой записи. Поэтому в результате должно получиться Делимое (76), о чем можно было сказать еще до выполнения самого умножения.)
![]() Какие числа являются
промежуточными результатами? (При умножении Делителя на значение частного (а не
наоборот) в качестве промежуточных результатов получаются именно те числа (36 и
4 дес.), которые фигурируют в записи Деления столбиком.)
Какие числа являются
промежуточными результатами? (При умножении Делителя на значение частного (а не
наоборот) в качестве промежуточных результатов получаются именно те числа (36 и
4 дес.), которые фигурируют в записи Деления столбиком.)
— Как можно объяснить наличие данных промежуточных результатов? (Это не случайно, так как число 4 дес. и число 36 получаются в результате послеДовательного умножения разрядных слагаемых значения частного 19 на Делитель 4: 1 дес. • Дес., 9 • 4=36).) ЛГ2 246 (с. 74).
![]() Прочитайте задание.
Чем оно отличается от задания № 245? (В Данном заДании промежуточное Деление
нужно выполнять трижДы.)
Прочитайте задание.
Чем оно отличается от задания № 245? (В Данном заДании промежуточное Деление
нужно выполнять трижДы.)
2. Выполнение упражнения в тетради для самостоятельной работы
![]() 110 (с. 60).
110 (с. 60).
(Самостоятельное выполнение. Проверка.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 111 (с. 60).
Урок 39, Вычисления с помощью калькулятора
Цель: развивать умение выполнять вычисления с помощью калькулятора.
1. Организационный момент, Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
Ответ: |
|
|
|
|
|
7 |
7 |
8![]()
![]()
2. Волшебная звезда (Сумма = 40.)
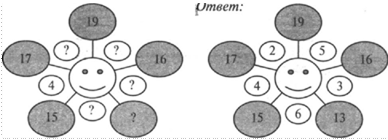
З. Устный счет
(Примеры записаны на доске.)
![]() Вставьте пропущенные числа.
Вставьте пропущенные числа.
![]() кг 4
дм см
кг 4
дм см
2000 г = кг 2 м = ... дм
60 ц = кг 20 см — . дм
4. Родственные ряды
|
2 |
7 |
4 |
8 |
|
|
2 |
47 |
|
62 |
98 |
( Чиста нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на СшиИХ себя и вычитания числа 2. В верхнем ряду пропущено число 10, в нижнем ряду — 14.)
Ш, Работа по теме урока Работа по
учебнику ![]() 75).
75).
(Устное коллективное выполнение.)
![]() Каково назначение калькулятора?
(Калькулятор ускоряет процесс вычислииЙ.) ЛГ2 248 (с. 75).
Каково назначение калькулятора?
(Калькулятор ускоряет процесс вычислииЙ.) ЛГ2 248 (с. 75).
(Коллективное выполнение с комментированием.) lV. Физкультминутка
V. Закрепление изученного материала Работа по учебнику ![]() 249 (с. 76).
249 (с. 76).
![]() Выполните задание.
Выполните задание.
— Что предполагает проверка? (В первом случае сумма оДинаКОВЫХ слагаемых будет заменена соответствующим произведением (47 • 6), а во втором случае полученное число нужно
40. Контрольная работа № 2
![]()
будет последовательно 4 раза разДелить на 9 (в итоге
должно получиться число 9).) ![]() 76).
76).
— Прочитайте задание. С чего нужно начать восстановление?
(С первого промежуточного результата умножения: 867 • 6.) ![]() Что надо
определить далее? ( Число в разряде Десятков второго множителя . )
Что надо
определить далее? ( Число в разряде Десятков второго множителя . )
— Что нужно сделать для этого? ( Число 3468 разделить на 867 и записать полученный результат вместо звезДочки в записи второго множителя: 3468 : 867 = 4).
![]() Что нужно сделать далее? (Выполнить
сложение двух промежуточных результатов умножения и записать это число вместо
пяти звезДочек в последней строке.)
Что нужно сделать далее? (Выполнить
сложение двух промежуточных результатов умножения и записать это число вместо
пяти звезДочек в последней строке.) ![]() 251 (с. 76).
251 (с. 76).
(Самостоятельное выполнение. Проверка в парах.) № 252 (с. 76).
(Самостоятельное выполнение.)
![]() Какое получилось число? (87 045.)
Какое получилось число? (87 045.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 65 (с. 40).
Цели: проверить знания и умения учащихся; развивать навыки самостоятельной работы.
(Текст контрольной работы выдается каждому ученику на отдельном листочке.) Вариант 1
1. Реши задачу. Вычисли и запиши ответ.
В магазине за день продали 53 детских спортивных костюма по цене 60 руб. и 7 одинаковых маек. За все эти вещи получено 6043 руб. Какова цена майки?
Заполни таблицу к данной задаче.
|
Цена |
Количество |
Стоимость |
|
|
|
|
|
|
|
|
2. Выполни деление с остатком:
![]() а) в строчку: 28 : 5, 44 : 8, 32 : З, 27:
5;
а) в строчку: 28 : 5, 44 : 8, 32 : З, 27:
5;
![]()
б) столбиком: 47 : 5, 88 : 9, 36 : 2, 58 : 7.
3. Вычисли значения выражений.
2753 + 48 686 89 232 + 536
4082 • 4 80 200 - 5471
6549 - 3582 1245 : 5
4. Начерти прямоугольник, длина сторон которого 10 см и 2 см. Найди периметр этого прямоугольника.
5. Сравни.
5 м б см ... 420 см
3 т 5 ц ... 460 кг
I ц 6 кг ... 115 кг
Вариант 2
1. Реши задачу. Вычисли и запиши ответ.
За день в магазине продали 32 спортивные шапки по цене 80 руб. и 7 одинаковых шарфов. Всего заплатили 3974 руб. Какова цена шарфа?
Заполни таблицу к данной задаче.
|
Цена |
Количество |
Стоимость |
|
|
|
|
|
|
|
|
2. Выполни деление:
а) в строчку: 28 : 6, 44 : 7, 23 : 3, 27 : 4;
6) столбиком: 58 : 8, 67 : 8, 42 : 2, 66 : 7.
3. Вычисли значения выражений.
6903 + 84 796 30 964 + 5721
2053 • 6 66 174 - 3906
4327 - 1633 1756 •. 2
4. Начерти прямоугольник, длина сторон которого l l см и 3 см. Найди периметр этого прямоугольника.
5. Сравни.
2 км 5 м ... 2015 м
3209 м ... 32 км
2 ц 3 кг ... 203 кг
Урок 41 , Час, минута и секунда
Цели: расширить знания о единицах измерения времени; познакомить с единицей измерения времени — секундой.
1. Организационный момент. Сообщение темы и целей урока
41 . Час, минута и секунда
![]()
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: : 2, + 5; пропущенные числа — 5 и 10.)
2. Цифровой квадрат
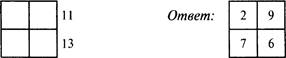
9 15
З. Родственные ряды
|
7 |
|
|
9 |
|
|
З |
6 |
7 |
4 |
|
( Числа верхнего ряда получаются в результате прибавления к соответствующим числам нижнего ряда последующего числа. В верхнем ряду пропущено число 15, в нижнем ряду — 8.)
4. Логическая задача
— Решите задачу устно.
Витя, Саша и Андрей смастерили из бумаги кораблик, змею и аиста. Какую игрушку сделал каждый мальчик, если Витя не делал кораблик и змею, а Саша не делал кораблик? (Саша Делал змею, Витя — аиста, Андрей — кораблик.)
lll. Работа по теме урока
1. Беседа
— Как вы понимаете пословицы: «Делу время, потехе час», «Минута рабочего времени не иголка: потеряешь — не найдешь», «Каждая секунда у нас на строгом учете да в большом почете»? (Ответы детей.)
— Что объединяет понятия «час», «минута», «секунда»? (Это время.)
— Какой предмет позволяет отслеживать время? ( Часы.)
2. Работа по учебнику № 253 (с. 77).
![]() Какая единица
измерения времени является наименьшей? (Секунда.)
Какая единица
измерения времени является наименьшей? (Секунда.)
![]() Сколько
минут в ч? (60 мин.)
Сколько
минут в ч? (60 мин.)
![]()
№ 254 (с. 77).
(Устное выполнение.) ![]() 255 (с. 77).
255 (с. 77).
![]() Сколько секунд в 1 ч? (3600 с.)
Сколько секунд в 1 ч? (3600 с.)
![]() Как
можно получить данное соотношение? (1 ч = 60 мин, 1 мин = 60с, т. е. 1 ч = 60 •
60 = 3600с.) Л) 256 (с. 77).
Как
можно получить данное соотношение? (1 ч = 60 мин, 1 мин = 60с, т. е. 1 ч = 60 •
60 = 3600с.) Л) 256 (с. 77).
![]() Как
выразить в секундах ч 10 мин? (1 ч 10 мин — 3600 С +
Как
выразить в секундах ч 10 мин? (1 ч 10 мин — 3600 С +
![]()
— Остальные временные промежутки выразите в секундах самостоятельно.
![]() 77).
77).
![]() Что
нужно сделать сначала? (Узнать, сколько минут Длятся урок и перемена вместе: 45
мин + 15 мин = 60мин = 1 ч.)
Что
нужно сделать сначала? (Узнать, сколько минут Длятся урок и перемена вместе: 45
мин + 15 мин = 60мин = 1 ч.) ![]() Что нужно сделать дальше? (Перевести ч в
секунДы: ч
Что нужно сделать дальше? (Перевести ч в
секунДы: ч ![]() -3600 с.)
-3600 с.)
![]() Сколько
секунд длится урок вместе с переменой? (3600 с.)
Сколько
секунд длится урок вместе с переменой? (3600 с.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ЛГ2258(с. 78).
![]() Прочитайте задание. Что нужно
сделать сначала? (Перевести все временные промежутки в секунды. Например: 59 мин
59с = 1 ч — = 3600с- 1с =3599с.)
Прочитайте задание. Что нужно
сделать сначала? (Перевести все временные промежутки в секунды. Например: 59 мин
59с = 1 ч — = 3600с- 1с =3599с.)
(Аналогично учащиеся переводят в секунды остальные временные промежутки: ч I мин с - 3661 с, 62 мин = 3720 с, 1 ч мин = 3660 с, 1 ч 10c = 3610 с, 60 мин 60 с = 3660 с.)
![]() Как будут выстроены данные временные
промежутки в порядке возрастания? (59 мин 59с, 1 ч 10 с, ] ч 1 мин = 60 мин
60с, 1 ч 1 мин 1 с, 62 мин.) ЛФ 259 (с. 78).
Как будут выстроены данные временные
промежутки в порядке возрастания? (59 мин 59с, 1 ч 10 с, ] ч 1 мин = 60 мин
60с, 1 ч 1 мин 1 с, 62 мин.) ЛФ 259 (с. 78).
— Прочитайте задание. Что нужно сделать сначала? (Выразить 9 мин в секундах: 60 • 9 = 540 с.)
![]() Как узнать, сколько секунд длится
мультфильм? (Увеличить полученную величину на 20 с: 540 с + Тс = 560 с.) м 260
(с. 78).
Как узнать, сколько секунд длится
мультфильм? (Увеличить полученную величину на 20 с: 540 с + Тс = 560 с.) м 260
(с. 78).
![]() Прочитайте задание.
Что нужно сделать сначала? (Все результаты выразить в одних и тех же еДиницах
измерения.)
Прочитайте задание.
Что нужно сделать сначала? (Все результаты выразить в одних и тех же еДиницах
измерения.)
— Какой спортсмен пробежал быстрее всех? (Спортсмен под номером 4, так как затраченное им время является наименьшим.)
Кто или что движется быстрее?
Прочитайте задание. С чего мы начнем работу? (С выражения
проДолжительности переДачи в секундах: 1 ч 10 мин ![]() = зоос + = 4200с.)
= зоос + = 4200с.)
![]() Можно ли ответить на требование задачи?
(Да: 4200 с
Можно ли ответить на требование задачи?
(Да: 4200 с ![]() - = 3840 с.) М 262 (с. 78).
- = 3840 с.) М 262 (с. 78).
![]() Прочитайте задание. С чего мы начнем
работу? (ПроДолжительность выразим в минутах: ЗОО с : 60 с = 5 мин; 240с : 60с
= 4 мин; 600с : 60с = Юмин.)
Прочитайте задание. С чего мы начнем
работу? (ПроДолжительность выразим в минутах: ЗОО с : 60 с = 5 мин; 240с : 60с
= 4 мин; 600с : 60с = Юмин.)
— Чему равна стоимость телефонных разговоров? (Зруб./мин х х 5мин = 15руб., 4руб./мин • 4мин = 16руб., 2руб.50коп./мин х х 10 мин = 250 коп./мин • 10 мин = 2500 коп. = 25 руб.)
2. Выполнение упражнений в тетрам для самостоятельной работы М 112, 113 (с. 61).
(Самостоятельное выполнение. Коллективная проверка.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 14 (с. 61).
Урок 42. Кто или что движется быстрее?
Цели: развивать умение оперировать понятиями «быстрее» и «медленнее»; подвести к рассмотрению понятия «скорость».
![]() Организационный момент. Сообщение темы и целей урока
Организационный момент. Сообщение темы и целей урока
ll, Актуализация знаний
1. Волшебные квадраты
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
пап |
|
|
|
||||
Ответы:
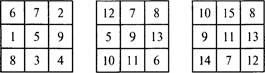
![]()
2. Устный счет
(Примеры записаны на доске.)
![]() Выполните действия и объясните приемы
вычислений.
Выполните действия и объясните приемы
вычислений.
![]() 97
• 40 • 2
97
• 40 • 2 ![]()
60 : 3 : Ш40 • 2 : 20 (25 + 15) • 1
З. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Как называются числа при сложении? (Первое слагаемое, второе слагаемое, сумма.)
• Как называются числа при вычитании? (Уменьшаемое, вычитаемое, разность.)
• Как называются числа при умножении? (Первый множитель, второй множитель, произведение.)
• Как называются числа при делении? (Делимое, Делитель, частное.)
4. Логическая задача
— Решите задачу устно.
Знайка, Кнопочка и Тюбик живут в домах № 14, 17, 19. В каком доме живет КюКДЫЙ из них, если Знайка не живет в домах № 19 и 17, а Кнопочка не живет в доме № 19? (Знайка живет в Доме М 14, Кнопочка — в доме М 17, Тюбик — в доме М 19.)
lll. Работа по теме урока
Работа по учебнику ![]() м 263 (с. 79).
м 263 (с. 79).
— Каким образом судьи соревнований
решают вопрос о том, кто какое место должен занять? (Примерный ответ. Судьи
учитывают то, что спортсмены должны пробежать одинаковую дистанцию, т. е. длина
пройденного пути остается постоянной. Чем меньше спортсмен затратил времени на
ее прохождение, тем быстрее он бежал и тем выше его результат. Таким образом,
первое место занимает тот, кто показывает самыи меньший по времени результат.) ![]() 79).
79).
![]() Прочитайте условие задачи. Каким является затраченное время?
(Постоянным: ч.)
Прочитайте условие задачи. Каким является затраченное время?
(Постоянным: ч.)
![]() Что изменяется? (Длина
пройденного пути.)
Что изменяется? (Длина
пройденного пути.)
![]() Когда туристы двигались быстрее? (В
первый час пути, так как за второй час пути они ПРОШЛИ меньшее расстояние.)
Когда туристы двигались быстрее? (В
первый час пути, так как за второй час пути они ПРОШЛИ меньшее расстояние.) ![]() 79).
79).
— Прочитайте условие задачи. Что нужно выполнить сначала? (Сравнить расстояния, для этого их надо выразить в одних и тех же еДиницах измерения: 2 км = 2000 м.)
Кто или что движется быстрее?
Что вы можете сказать о полученных величинах? (2000м >
> 1500м, значит, 2 км > 1500м.)
— Что движется быстрее?
(Автомобиль.) ![]() Что движется медленнее? (Поезд.) lV.
Физкультминутка
Что движется медленнее? (Поезд.) lV.
Физкультминутка
М. Закрепление изученного материала Работа по учебнику ![]() 266 (с. 79).
266 (с. 79).
— Прочитайте условие задачи. Что можно определить сначала? (Какое максимальное расстояние Миша может преоДолеть за 1 ч 30мин.)
— Как это сделать? (Если за 1 ч Миша может преоДолеть З км, то за 30 мин (половина часа) он может преодолеть
3000 м : 2 = 1500 м, а за 1 ч 30 мин он сможет преоДолеть З км + 1 км 500м = 4 км 500 м.)
![]() Что это значит? (Расстояние 5 км за 1 ч
ЗОмин Миша преоДолеть не сможет.) ж 267(с. 79).
Что это значит? (Расстояние 5 км за 1 ч
ЗОмин Миша преоДолеть не сможет.) ж 267(с. 79).
(Устное выполнение.)
— Какое из перечисленных средств двигается быстрее всех остальных? (Ракета.)
— Выполните задание. (Ракета, самолет, вертолет, автомобипь, велосипед, лоДка без мотора.) ЛФ 268 (с. 80).
(Устное выполнение.)
Самым быстрым зверем на Земле считают гепарда, хотя антилопа его опережает.
Многие крупные животные могут развивать большую скорость, но только на короткое время (на 3—5 мин).
— Приведите данные к общим единицам измерения. Гепард — 30 м/с; зебра — КМ/МИН', страус — 500 м/мин; лев — 80 км/ч; антилопа 25 м/с; жираф — 750 м/мин.
— Знаете ли вы, с какой скоростью летают птицы?
Считается что стрижи, живущие в Индии, развивают скорость до 272 км/ч, это больше по сравнению со стрижами из Месопотамии, которые развивают скорость всего лишь 160 км/ч, и стрижами, живущими в Европе, летающими со скоростью
95— 104 км/ч.
Сокол — 264—288 км/ч; колибри — 90—96 км/ч; голубь — 150 км/ч; скворец — 70—80 км/ч; утки, гуси — 104—120 км/ч; ласточка — от 40 до 75—80 км/ч.
![]()
ЛФ 269 (с. 80).
(Устное выполнение.)
![]() Какое животное можно назвать медлительным? (Коалу, ши сумчатого меДвеДя:
он лениво перебирается с места на место, за что его еще прозвали ленивцем.)
Какое животное можно назвать медлительным? (Коалу, ши сумчатого меДвеДя:
он лениво перебирается с места на место, за что его еще прозвали ленивцем.)
![]() Кто еще относится к самым медлительным
животным? ( Черепаха, улитка.) М 270 (с. 80).
Кто еще относится к самым медлительным
животным? ( Черепаха, улитка.) М 270 (с. 80).
![]() Прочитайте условие задачи. Как двигается автомобиль? (Равномерно.)
Прочитайте условие задачи. Как двигается автомобиль? (Равномерно.)
![]() Сколько километров преодолеет автомобиль за 120 мин? (Так как 120 мин в
2 раза больше, чем 1 ч, то пройденное расстояние будет в 2 раза больше Данного,
т. е. 80 км • 2 — = l60kM.)
Сколько километров преодолеет автомобиль за 120 мин? (Так как 120 мин в
2 раза больше, чем 1 ч, то пройденное расстояние будет в 2 раза больше Данного,
т. е. 80 км • 2 — = l60kM.)
![]() Сколько километров преодолеет автомобиль
за 30 мин? ( Так как ЗОмин в 2 раза меньше, чем ч, то пройденное расстояние
будет в 2 раза меньше Данного, т. е. 80 км : 2 = 40 км.)
Сколько километров преодолеет автомобиль
за 30 мин? ( Так как ЗОмин в 2 раза меньше, чем ч, то пройденное расстояние
будет в 2 раза меньше Данного, т. е. 80 км : 2 = 40 км.) ![]() Сколько километров
преодолеет автомобиль за 15 мин? (За 15 мин можно преодолеть расстояние еще в 2
раза меньшее, чем за 30 мин, т. е. 40 км : 2 = 20 км.)
Сколько километров
преодолеет автомобиль за 15 мин? (За 15 мин можно преодолеть расстояние еще в 2
раза меньшее, чем за 30 мин, т. е. 40 км : 2 = 20 км.)
![]() Какой можем сделать вывод? (Во сколько раз отличаются временные
промежутки, во столько раз отличаются пройДенные расстояния.)
Какой можем сделать вывод? (Во сколько раз отличаются временные
промежутки, во столько раз отличаются пройДенные расстояния.)
![]() На каком виде транспорта можно добраться до места быстрее? (На
скоростном, т. е. на том, который быстрее, поэтому за 1 ч преоДолеть расстояние
1000 км можно на самолете.) И. Подведение итогов урока
На каком виде транспорта можно добраться до места быстрее? (На
скоростном, т. е. на том, который быстрее, поэтому за 1 ч преоДолеть расстояние
1000 км можно на самолете.) И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № I l5 (с. 62).
Урок 43. Длина пути в единицу времени, или скорость
Цель: познакомить с понятием «скорость».
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Разминка
![]() Закончите рассуждения, если это возможно.
Закончите рассуждения, если это возможно.
![]() А = В, В = С. Следовательно... (А = С).
А = В, В = С. Следовательно... (А = С).
Длина пути в единицу времени, или скорость
![]()
![]() Если ученик получит оценку «5», его похвалят. Сетдня ученика не
похвалили. Следовательно... (он не получи оценку «5»).
Если ученик получит оценку «5», его похвалят. Сетдня ученика не
похвалили. Следовательно... (он не получи оценку «5»).
![]() Кит плавает не хуже ската. Скат — рыба. Следовательно...
Кит плавает не хуже ската. Скат — рыба. Следовательно...
(кит — рыба). (Это ложное заюаючение.)
2. Цифровой квадрат
|
5 |
7 |
|
|
7 |
![]() 12 Ответ:
12 Ответ:
17
15 14
З. Родственные ряды
|
54 |
46 |
38 |
|
|
|
46 |
38 |
|
22 |
|
( Числа нижнего ряда на 8 меньше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 22, в нижнем ряду — 30.)
4. Устный счет
(Примеры записаны на доске.) ![]() Вычислите.
Вычислите.
|
24 3 |
48 • 2 |
12 - 8 |
19 • 3 |
|
|
34 • 2 |
27 • з |
14 4 |
|
54 : 2 |
48 : 3 |
96 : 8 |
84 6 |
|
26 • з |
46 : 2 |
96 . 8 |
75 : 25 |
Ш. Работа по теме урока Работа по учебнику М 271 (с. 81).
(Работа над теоретическим материалом. Знакомство с поня-
ТИеМ «скорость» по словарику учебника (с. 119). ) м 272 (с. 81).
![]() Как можно вычислить среднюю скорость
самолета при условии, что она была постоянна? (1800 км : 2 ч = 900 км/ч.)
Как можно вычислить среднюю скорость
самолета при условии, что она была постоянна? (1800 км : 2 ч = 900 км/ч.) ![]() 273
(с. 81).
273
(с. 81).
![]() Как узнать, какое расстояние
преодолевает спортсмен за с? (Так как скорость спортсмена на всей Дистанции
одинакова, то за 1 с он пробежит расстояние в 10 раз меньшее, чем за Тс: ТОм :
10 = Юм.)
Как узнать, какое расстояние
преодолевает спортсмен за с? (Так как скорость спортсмена на всей Дистанции
одинакова, то за 1 с он пробежит расстояние в 10 раз меньшее, чем за Тс: ТОм :
10 = Юм.)
![]() Как
узнать, сколько метров он пробегает за I мин? (За 1 мин он пробегает в браз
больше, т. е. 600 м.)
Как
узнать, сколько метров он пробегает за I мин? (За 1 мин он пробегает в браз
больше, т. е. 600 м.)
![]() Может
ли спортсмен пробежать за мин 600 м? (Нет.) М 274 (с. 81).
Может
ли спортсмен пробежать за мин 600 м? (Нет.) М 274 (с. 81).
(Устное выполнение.)
![]() Решение: из предыдущего задания известно, что
Решение: из предыдущего задания известно, что
— 3600 м/ч, следовательно, 10 м/с = 36 000 м/ч = 36 км/ч. Таким образом, получаем соотношение: 10 м/с = 36 км/ч.
20 м/с = 72 км/ч 30 м/с = 108 км/ч 5 м/с = 18 км/ч 15 м/с = 54 км/ч lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 276 (с. 82).
![]() Прочитайте задание.
Как нужно выразить данные скорости в метрах в секунду, если они даны в метрах в
минуту? (Нужно использовать соотношение 1 м/с = 60м/мин.)
Прочитайте задание.
Как нужно выразить данные скорости в метрах в секунду, если они даны в метрах в
минуту? (Нужно использовать соотношение 1 м/с = 60м/мин.)
![]() Выразите. (120м/мин : 60М/МИН = 2м/с,
240м/мин : 60м/мин =
Выразите. (120м/мин : 60М/МИН = 2м/с,
240м/мин : 60м/мин =
= 4м/с, 600м/мин : 60м/мин = 10м/с, ЗООМ/МИН : 60м/мин — = 5 МД.)
М 277€. 82).
![]() Прочитайте задание.
Что нужно сделать, чтобы расположить данные скорости в порядке возрастания?
(Перевести в одинаковые еДИНИЦЫ измерения.)
Прочитайте задание.
Что нужно сделать, чтобы расположить данные скорости в порядке возрастания?
(Перевести в одинаковые еДИНИЦЫ измерения.)
![]() Какие соотношения потребуются? (1
м/с = 60 М/МИН, 10м/с = 36 км/ч, 1 м/с = 3600м/ч.)
Какие соотношения потребуются? (1
м/с = 60 М/МИН, 10м/с = 36 км/ч, 1 м/с = 3600м/ч.)
— Какой единицей измерения можно воспользоваться? (Километры в час: 100м/мин = 6000м/ч = 6 км/ч.)
— Расставьте скорости в порядке возрастания. (100 м/мин
(6 км/ч), 10м/с (36 км/ч), 90 км/ч, 900 км/ч.)
— Сформулируйте задачу на кратное сравнение, используя данные из таблицы.
(Например: скорость автомобиля 90 км/ч, а скорость самолета 900 км/ч. Во
сколько раз скорость самолета больше скорости автомобиля Э ![]() Решите задачу. (900км/ч : 90 км/ч =
10раз.) М 278 (с. 82).
Решите задачу. (900км/ч : 90 км/ч =
10раз.) М 278 (с. 82).
— Прочитайте задание. Выразите скорость в метрах в час.
(30 = 108 000 (м/ч).)
— Выразите полученную скорость в километрах в час. (108000: 1000 = 108(км/ч).)
![]() Как можно получить соотношение 10
м/с 36 км/ч?
Как можно получить соотношение 10
м/с 36 км/ч?
(10м/с 3600с = 36 ооом/ч, 36 ооом/ч : 1000м = 36 км/ч.) м 279 (с. 82).
— Прочитайте задание. Что нужно сделать? (Сравнить скорость ветра и скорость велосипедиста, для этого их нужно выразить в юиометрах в час.)
Длина пути в единицу времени или скорость
Как это сделать? (Можно воспользоваться соотношением, установленным в преДыДущем заДании. Если 10м/с = 36 км/ч, то 5м/с = 36 км/ч : 2 = 18 км/ч.)
![]() Что можно сказать о скоростях? (Они
равны.)
Что можно сказать о скоростях? (Они
равны.)
![]() Что это значит? (Ветер
не помогает велосипеДисту Двигаться вперед.)
Что это значит? (Ветер
не помогает велосипеДисту Двигаться вперед.)
![]() 280 (с. 82).
280 (с. 82).
![]() Прочитайте условие задачи. Что нужно сделать, чтобы ответить на
требование задачи? (ОпреДелить скорость.)
Прочитайте условие задачи. Что нужно сделать, чтобы ответить на
требование задачи? (ОпреДелить скорость.) ![]() Как это сделать? (
180 км : З ч = 60 км/ч.)
Как это сделать? (
180 км : З ч = 60 км/ч.)
![]() Какое транспортное
средство может развивать такую скорость? (Автомобиль, поезд, мотоциюа.)
Какое транспортное
средство может развивать такую скорость? (Автомобиль, поезд, мотоциюа.)
2. Выполнение упражнения в тетради для самостоятельной работы ЛГ2 117(с. 64-65).
а) Решение:
![]() ч = 3600 с;
ч = 3600 с;
30 км/с 3600 с = 108 000 км.
Ответ: Земля пролетает в час 108 000 км.
б) Решение:
4 ч = 60 мин • 4 = 240 мин;
1 КМ/МИН • 240 мин = 240 км.
Ответ: за 4 ч мотоциклист преодолеет 240 км.
в) Решение: 28 км/ч • 7 ч = 196 км — пройдет катер за 7 ч. Ответ: катер не успеет пройти 200 км за 7 ч.
г) Решение:
1200 м/мин = 72 км/ч;
72 км/ч — 60 км/ч = 12 км/ч.
Ответ: страус движется быстрее, чем мотоциклист, на 1 2 юи/ч.
д) Решение: одна треть минуты составляет 20 с.
15 м/с • 20 = зоо м.
Ответ: за одну треть минуты заяц пробежал 300 м.
е) Решение:
1) 70 км : 2 ч = 35 км/ч — скорость теплохода; 2) 210 км : З ч = 70 км/ч — скорость поезда; З) 70 км/ч : 35 км/ч = 2 (раза).
Ответ: скорость теплохода в 2 раза меньше скорости поезда.
ж) Решение:
1) 16 км/ч • З ч = 48 км — расстояние от поселка до города;
2) 48 км : 4 ч = 12 км/ч — скорость велосипедиста на обратном пути;
З) 16 км/ч — 12 км/ч = 4 км/ч.
Ответ: скорость велосипедиста на обратном пути была на 4 км/ч меньше.
оасс
![]()
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 1 16 (с. 63).
Урок 44. Учимся решать задачи
Цель: научить решать задачи на движение.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
Арифметический диктант
![]() Запишите только ответы.
Запишите только ответы.
15 • 2 56 : 2 78 : 3 30 • 7 18 • 7 640 : 8 80 . з ![]() Решите
задачи устно и запишите ответы.
Решите
задачи устно и запишите ответы.
• До Нового года осталось 4 недели и З дня. Сколько дней осталось до Нового года?
• Сердце здорового человека делает 75 ударов в минуту. Сколько ударов сделает сердце за 2 мин?
• Заяц, когда ему угрожает опасность, пробегает в секунду 12 м, а еж двигается в 6 раз медленнее. Сколько метров в секунду пробегает еж?
• В городском парке 120 берез, а кленов на 89 больше. Сколько кленов в городском парке?
• Юннаты разложили 350 г семян огурцов в 7 пакетов поровну. Сколько граммов семян в 1 пакете?
• Сколько орехов получит каждый из 6 мальчиков, если они разделят поровну 90 орехов?
• За год в деревне построили 6 домов по 4 квартиры в каждом. Сколько квартир получат деревенские жители?
• Масса тыквы 12 кг, а масса дыни на 8 кг меньше. Чему равна масса дыни? Во сколько раз масса тыквы больше массы дыни?
• В массе 16 девочек и 19 мальчиков. На сколько мальчиков больше, чем девочек?
Ш. Работа по теме урока Работа по учебнику ЛФ 281 (с. 83).
![]() Прочитайте задачи.
Прочитайте задачи.
• Что общего в их формулировках? (Предложенные заДачи аналогичны по своей математической сути. Аналогия устанавли-
Учимся решать задачи
![]()
вается не только в тане решения, но и в тане существующей зависимости между величинами.)
![]() Чем задачи отличаются? (В первой
задаче искомой величиной является путь, а во второй — стоимость,
соответственно, различаются и наименования. Величине «скорость» аналогична
величина «цена», что нахоДит отражение и в соответствующих наименованиях этих
величин.)
Чем задачи отличаются? (В первой
задаче искомой величиной является путь, а во второй — стоимость,
соответственно, различаются и наименования. Величине «скорость» аналогична
величина «цена», что нахоДит отражение и в соответствующих наименованиях этих
величин.)
![]() Чем похожи решения?
(Решения аналогичны, ансаогична и существующая зависимость между величинами.)
Чем похожи решения?
(Решения аналогичны, ансаогична и существующая зависимость между величинами.)
— Чем отличаются решения? (В первой задаче надо найти путь, а во второй — стоимость.) ЛГ2 282 (с. 83).
![]() Прочитайте данную задачу.
Прочитайте данную задачу.
![]() Составьте аналогичную задачу на куплю-продажу. (Например: за З ч катания
на лоДке нужно заплатить 270руб. Какова цена (тариф) проката лодки
Составьте аналогичную задачу на куплю-продажу. (Например: за З ч катания
на лоДке нужно заплатить 270руб. Какова цена (тариф) проката лодки![]()
![]() Решите обе задачи. Вычислите и запишите ответы.
Решите обе задачи. Вычислите и запишите ответы.
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику
JV2 283 (С. 83-84).
(Самостоятельное выполнение. Работа в парах.) JV2 284 (с. 84).
Вариант заДачи. Первая группа туристов за 2 ч преодолела 12 км. Сколько километров за 3 ч преодолеет вторая группа туристов, если будет двигаться с такой же скоростью?
![]() Что нужно найти
сначала? (Вычислить скорость переДвижения первой группы туристов: 12 км : 2 ч =
6 км/ч.)
Что нужно найти
сначала? (Вычислить скорость переДвижения первой группы туристов: 12 км : 2 ч =
6 км/ч.)
— С какой скоростью двигалась вторая группа туристов? (С такой же — 6 км/ч.)
![]() Сколько километров
преодолела вторая группа туристов за З ч? (бкм/ч • З ч = 18 км.)
Сколько километров
преодолела вторая группа туристов за З ч? (бкм/ч • З ч = 18 км.)
![]() Можно ли решить
задачу рациональнее? (С теми ДаННЬШИ, которые указаны в таблице, нет, но если в
графе «Время» вместо З ч записать 4 ч, тогДа можно использовать более легкий
путь решения.)
Можно ли решить
задачу рациональнее? (С теми ДаННЬШИ, которые указаны в таблице, нет, но если в
графе «Время» вместо З ч записать 4 ч, тогДа можно использовать более легкий
путь решения.)
— Каким тогда будет решение? (Достаточно выяснить, во
сколько раз отличается одно время от Другого: 4 : 2 = 2 (раза). ) ![]() Что надо
делать далее? (Увеличить в это число раз Данное расстояние: 12 км • 2 = 24 км.)
Что надо
делать далее? (Увеличить в это число раз Данное расстояние: 12 км • 2 = 24 км.)
![]() 285
(с. 84).
285
(с. 84).
— Прочитайте задание. Как изменится пройденный путь? (Путь увеличится в З раза.)
класс
![]()
— Объясните свой ответ. (При постоянном времени Движения существует прямая пропорциональная зависимость между расстоянием и скоростью, т. е. если скорость Движения увеличить во сколько-то раз, во столько же раз увеличится расстояние.)
![]() Приведите примеры самостоятельно.
Приведите примеры самостоятельно.
JV2 286 (с. 84).
![]() Прочитайте задание. Что вы можете
сказать? (Уменьшение цены в 2 раза привеДет к уменьшению стоимости также в 2
раза, если количество остается постоянным. Здесь речь идет о прямой
пропорциональной зависимости между стоимостью и ценой при постоянном
количестве.)
Прочитайте задание. Что вы можете
сказать? (Уменьшение цены в 2 раза привеДет к уменьшению стоимости также в 2
раза, если количество остается постоянным. Здесь речь идет о прямой
пропорциональной зависимости между стоимостью и ценой при постоянном
количестве.) ![]() Приведите примеры самостоятельно.
Приведите примеры самостоятельно.
2. Выполнение упражнения в тетради для самостоятельной
работы ![]() 119 (а) (с. 66).
119 (а) (с. 66).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 18 (с. 66).
Урок 45. Учимся решать задачи
Цель: развивать умение решать задачи на движение.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
З |
12 |
|
|
|
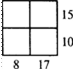 Ответ:
Ответ:
2. Родственные ряды
|
з |
|
|
2 |
7 |
|
п |
4 |
20 |
8 |
|
(Числа нижнего ряда в 4 раза больше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 5, в нижнем ряду — 28.)
Учимся решать задачи
![]()
• Чему равно произведение чисел 18 и 4? (72.)
• Делимое — 70, делитель — 5. Найдите частное. (14.)
• Число 99 уменьшите в 9 раз. (П.)
• Во сколько раз 64 больше 2? (В 32 раза.)
• Разность чисел 38 и 27 умножьте на 8. (88.)
• Разность чисел 38 и 28 умножьте на 8. (80.)
• Сумму чисел 63 и 15 разделите на 6. (В.)
Ш. Работа по теме урока Работа
по учебнику ![]() 287 (с. 85).
287 (с. 85).
![]() Прочитайте задачу.
Запишите буквенное выражение для решения этой задачи. (15 • t.)
Прочитайте задачу.
Запишите буквенное выражение для решения этой задачи. (15 • t.)
• Что выражает первый множитель? (Скорость.)
• Что выражает второй множитель? (Время.)
— Вычислите значение выражения при данных значениях переменной t.
![]() 288 (с. 85).
288 (с. 85).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
М. Физкультминутка
М. Закрепление изученного материала
1.
Работа по учебнику ![]() 289 (с. 85).
289 (с. 85).
(Коллективное выполнение с комментированием.) ![]() 290
(с. 85).
290
(с. 85).
![]() Прочитайте задачу. Как найти расстояние при постоянной скорости
движения? (Скорость умножить на время.)
Прочитайте задачу. Как найти расстояние при постоянной скорости
движения? (Скорость умножить на время.) ![]() Можем ли мы сразу
выполнить умножение? (Нет, так как скорость выражена в юиометрах в час, а время
— в минутах.)
Можем ли мы сразу
выполнить умножение? (Нет, так как скорость выражена в юиометрах в час, а время
— в минутах.) ![]() Что нужно сделать? (В первом случае нужно
выразить 120мин в часах: 120 мин = 2 ч. Теперь можно выполнить умножение и
вычислить расстояние: 80 км/ч • 2 ч = 160 км.)
Что нужно сделать? (В первом случае нужно
выразить 120мин в часах: 120 мин = 2 ч. Теперь можно выполнить умножение и
вычислить расстояние: 80 км/ч • 2 ч = 160 км.)
![]() Как вы будете действовать в двух других случаях? (Так как за ч автомобшљ
преодолевает 80 км, то за ЗОмин (половина 1 ч) он преоДолеет расстояние в 2
раза меньшее: 80 км : 2 — = 40 км, а за 15 мин (половина от 30 мин): 40км : 2 =
20 км.)
Как вы будете действовать в двух других случаях? (Так как за ч автомобшљ
преодолевает 80 км, то за ЗОмин (половина 1 ч) он преоДолеет расстояние в 2
раза меньшее: 80 км : 2 — = 40 км, а за 15 мин (половина от 30 мин): 40км : 2 =
20 км.) ![]() Сможет ли автомобиль преодолеть 20 м за I
с? (Так как 10м/с = 36 км/ч, то 20м/с (10м/с • 2) = 36 км/ч • 2 = 72 км/ч.
Чтобы преоДолеть 20 м за 11 с, автомобшљ Должен Двигаться
Сможет ли автомобиль преодолеть 20 м за I
с? (Так как 10м/с = 36 км/ч, то 20м/с (10м/с • 2) = 36 км/ч • 2 = 72 км/ч.
Чтобы преоДолеть 20 м за 11 с, автомобшљ Должен Двигаться
класс
![]()
с минимальной скоростью 72 км/ч, а он Движется с большей скоростью, значит, аиожет выполнить указанное треЬание.)
2.
Выполнение
упражнения в тира,ди для самосготељной работ ![]() 119 (б) (с. 67).
119 (б) (с. 67).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 120 (с. 67).
Урок 46. Какой сосуд вмещает больше?
Цель: познакомить с понятием «вместимость».
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
Тест
(Выдается на отдельных листочках.)
1. Сколько цифр потребуется для записи числа девятьсот шесть тысяч семьсот пятнадцать?
2. Найди предшествующее число для числа 70 900 000.
1) 70 999 999 3) 70899 999 2) 70 900 ОШ 4) 70 900 009 З. Найди правильный ответ: 800 000 : 1000.
1) 8000 3) 800
2) 80 4) 80 000
5. Катя выехала на тренировку в 1 1 ч. Дорога до спортзала и обратно заняла I ч 25 мин. В спортзале Катя провела 2 ч 15 мин.
В какое время Катя была дома?
1) в 13 ч 40 мин З) в 14 ч 50 мин
2) в 14 ч 40МИН 4) в 15 ч
6. В первой деревне 26 дворов, во второй 35 дворов, в третьей 47 дворов и в четвертой 40 дворов. Узнай среднее количество дво-
ров в четырех деревнях.
1) 34 3) 37
2) 35 4) 38
7. В одном пакете 5 кг конфет, а в другом 12 кг тех же конфет. Второй пакет стоит на 700 руб. дороже. Сколько стоит каждый пакет?
Какой сосуд вмещает больше?
![]()
1) 250 руб. и 950 руб. 3) 700 руб. и 1400 руб.
2) 50Оруб. и 1200руб. 4) 1000 руб. и 1700 руб.
8. В деревне 24 деревянных дома, а кирпичных домов — три четверти от числа деревянных. Сколько всего домов в деревне?
1) 40 3) 30
2) 56 4) 42
9. Вставь пропущенное число: см — . мм.
1) 10 3) 1000
10. Вставь пропущенное число: I км м.
2) 500 4) 10 000
11. Вставь пропущенные числа: 6 852 1 10 кв. м —... кв. км ... кв. м.
1) 6 кв. км 852 110 кв. м 3) 685 кв. км 21 10 кв. м 2) 68 кв. км 52 110 кв. м 4) 6852 кв. км 110 кв. м
12. Вставь пропущенное число: 1 а — . кв. м.
3) то
2) 50 4) 1000
13. Вставь пропущенные числа: 6544 кв. м — а ... кв. м.
![]() 1) 65 а 44 кв. м 3)
654 а 4 кв. м
1) 65 а 44 кв. м 3)
654 а 4 кв. м
![]() 2) 6 а 544 кв. м 4) 32 а
144 кв. м
2) 6 а 544 кв. м 4) 32 а
144 кв. м
14. Вставь пропущенное число: 56 000 000 г = ... кг.
1) 56 3) 5600
2) 560 000 4) 560
15.
Вставь пропущенное число: 3 сут. 13 ч — ![]() 1) 83 3) 73
1) 83 3) 73
2) 85 4) 91
16. Как соотносятся между собой диагонали прямоугольника?
1) ) всегда есть большая диагональ и меньшая диагональ 2) они всегда равны
3) они равны в большинстве случаев
4) у каждого прямоугольника по-своему
17. Вставь пропущенное число: I век ... лет.
2) 50
18. Как можно проверить выражение 283 800 : 6? Запиши ответ.
(Умножением. 47 300.)
19.
Допиши формулу: (а • Ь) • с![]()
20. Запиши решение задачи и ответ.
От одного места одновременно в противоположных направлениях побежали две собаки. Через 7 с расстояние между ними было 147 м. Скорость первой собаки 12 м/с. Найди скорость второй собаки.
пасс
![]()
Решение:
1) 12 • 7 = 84 (м) — пробежала первая собака; 2) 147 — 84 = 63 (м) — пробежала вторая собака; 3) 63 : 7 = 9 (м/с).
Ответ: скорость второй собаки 9 м/с.
Ш. Работа по теме урока Работа по учебнику № 291 (с. 86).
(Коллективное выполнение. Знакомство с понятием «вместимость» по словарику учебника (с. 117). )
![]() Прочитайте условие задачи. Кому бабушка налила молока больше? (Ответы
детей.)
Прочитайте условие задачи. Кому бабушка налила молока больше? (Ответы
детей.)
![]() Вместимость какого сосуда больше: пакета,
стакана, чашки или блюдца? (Молоком, содержащимся в пакете, можно наполнить
сразу и чашку, и стакан, и блюдце. Значит, вместимость пакета больше, чем
вместимость кажДого из данНЫХ сосуДов в отДельности, и Даже больше, чем
вместимость стакана и чашки вместе.)
Вместимость какого сосуда больше: пакета,
стакана, чашки или блюдца? (Молоком, содержащимся в пакете, можно наполнить
сразу и чашку, и стакан, и блюдце. Значит, вместимость пакета больше, чем
вместимость кажДого из данНЫХ сосуДов в отДельности, и Даже больше, чем
вместимость стакана и чашки вместе.) ![]() 292 (с. 86).
292 (с. 86).
(Устное выполнение.)
![]() Прочитайте условие задачи. Вместимость какого сосуда больше: таза или
банки? (Таза.)
Прочитайте условие задачи. Вместимость какого сосуда больше: таза или
банки? (Таза.)
![]() Объясните. (Содержимое таза разами в три банки, значит, вместимость таза
в З раза больше вместимости банки.) № 293 (с. 86).
Объясните. (Содержимое таза разами в три банки, значит, вместимость таза
в З раза больше вместимости банки.) № 293 (с. 86).
— Прочитайте условие задачи. На основании чего сравнивают вместимости бочки и ванны? (На основании измерения этих вместимостей с помощью ведра.)
![]() Вместимость чего меньше: бочки или ванны? (Вместимость инны составляет
15 ведер, а вместимость бочки — 20 ведер, поэтому вместимость ванны меньше.) ЛЕ
294 (с. 87).
Вместимость чего меньше: бочки или ванны? (Вместимость инны составляет
15 ведер, а вместимость бочки — 20 ведер, поэтому вместимость ванны меньше.) ЛЕ
294 (с. 87).
— Прочитайте условие задачи. Что мы примем за единицу измерения: ведро ши бидон? (Бидон.)
— Выразите вместимость детского бассейна в новых единицах, если известны результат измерения в старых единицах и соотношение между этими единицами. Как это сделать? (С помощью Деления.)
![]() Какие числа будут задействованы в данном делении? (32 и З.) — Можно ли выполнить
деление нацело? (Нет.)
Какие числа будут задействованы в данном делении? (32 и З.) — Можно ли выполнить
деление нацело? (Нет.)
![]() Как выполнить деление? (Деление надо выполнить с остат
Как выполнить деление? (Деление надо выполнить с остат![]() 32:3 = тост.
э.).
32:3 = тост.
э.).
![]() Как проверить правшьность выполнения деления с остатком? (Остаток (2)
Должен быть меньше Делителя (3).).
Как проверить правшьность выполнения деления с остатком? (Остаток (2)
Должен быть меньше Делителя (3).).
Какой сосуд вмещает больше?
Сколько полных ведер помещается в бассейне? (10.) Полностью ли заполнился бассейн? (Нет, еще можно Добавить одно неполное ведро.) lV. Физкультминутка
М. Закрепление изученного материала
1. Работа по учебнику ![]() 295 (с. 87).
295 (с. 87).
![]() Прочитайте условие
задачи. Какова ширина и длина двух бассейнов? (Они совпадают, т. е.
одинаковые.)
Прочитайте условие
задачи. Какова ширина и длина двух бассейнов? (Они совпадают, т. е.
одинаковые.)
— Что еще известно про бассейны? (Убассейнов есть
глубина.) ![]() Какова глубина бассейнов? (2 м и 1 м.)
Какова глубина бассейнов? (2 м и 1 м.)
![]() Что можно сказать про глубину бассейнов?
(Они отличаются.) — Будегли отличаться их вместимость из-за разной глубины?
Ща.)
Что можно сказать про глубину бассейнов?
(Они отличаются.) — Будегли отличаться их вместимость из-за разной глубины?
Ща.) ![]() Какой бассейн более вместительный? ( Чем
больше глубина, тем больше вместимость, поэтому вместимость второго бассейна в
2раза больше вместимости первого бассейна. Такое соотношение имеет место межДу
глубиной одного и Другого бассейна.)
Какой бассейн более вместительный? ( Чем
больше глубина, тем больше вместимость, поэтому вместимость второго бассейна в
2раза больше вместимости первого бассейна. Такое соотношение имеет место межДу
глубиной одного и Другого бассейна.)
ЛЕ (с. 87).
![]() Прочитайте условие
задачи. Что нужно сделать для сравнения вместимости? (Перевести результат
измерения, сделанный в одних еДиницах, например в чашках, в другие еДиницы — в
стаканы.)
Прочитайте условие
задачи. Что нужно сделать для сравнения вместимости? (Перевести результат
измерения, сделанный в одних еДиницах, например в чашках, в другие еДиницы — в
стаканы.)
— Сколько чашек помещается в первую кастрюлю? (12.)
— Сколько раз нуто взять по 2 чашки, чтобы получить 12 чашек? (12 : 2 = 6 (раз).)
![]() Как узнать, сколько понадобится стаканов,
чтобы заполнить кастрюлю, в которой помещается 12 чашек воды? (З • 6=18. 12
чашек вмещают столько же, сколько в 18 стаканов.)
Как узнать, сколько понадобится стаканов,
чтобы заполнить кастрюлю, в которой помещается 12 чашек воды? (З • 6=18. 12
чашек вмещают столько же, сколько в 18 стаканов.) ![]() Можем мы теперь
сравнить вместимость кастрюль? (Да: в первой кастрюле помещается 18 стаканов, а
во второй — 20 таких же стаканов, поэтому вторая кастрюля имеет большую
вместимость.)
Можем мы теперь
сравнить вместимость кастрюль? (Да: в первой кастрюле помещается 18 стаканов, а
во второй — 20 таких же стаканов, поэтому вторая кастрюля имеет большую
вместимость.) ![]() 87). (Самостоятельное выполнение.
Взаимопроверка.) м 298 (с. 87).
87). (Самостоятельное выполнение.
Взаимопроверка.) м 298 (с. 87).
— Прочитайте условие задачи. Сколько раз по 5 стаканов вмеищется в кастрюле? (15 : 5 = З (раза).)
— Сколько чашек воды вмещает кастрюля? (4 • З = 12 (чаш.).) № 299 (с. 87).
![]() Что мы знаем про куб?
(Примерный ответ. Это геометрическая фигура, поверхность которой состоит из 6
одинако-
Что мы знаем про куб?
(Примерный ответ. Это геометрическая фигура, поверхность которой состоит из 6
одинако-
![]()
вых квадратов, которые называются гранями. Стороны этих квадратов называются ребрами, а вершины квадратов — вершинами куба. У куба 12 ребер, 8 вершин. Из каждой вершины выходит по 3 ребра, из каждого ребра — по 2 грани.)
— Сколько сантиметров составляет половина ребра? (60см : 2= =зосм.)
![]() До какой высоты нужно
наполнить аквариум водой, чтобы заполнить его наполовину? (До 30 см.)
До какой высоты нужно
наполнить аквариум водой, чтобы заполнить его наполовину? (До 30 см.)
![]() Сколько
сантиметров составляет треть ребра? (60 см : З = = 20 см.)
Сколько
сантиметров составляет треть ребра? (60 см : З = = 20 см.)
— До какой высоты нужно наполнить аквариум водой, чтобы заполнить его на треть? (До 20 см.)
![]() Сколько
сантиметров составляет четверть ребра? (60см : 4 = — 15 см.)
Сколько
сантиметров составляет четверть ребра? (60см : 4 = — 15 см.)
![]() До
какой высоты нужно наполнить аквариум водой, чтобы заполнить его на четверть?
(До 15 см.)
До
какой высоты нужно наполнить аквариум водой, чтобы заполнить его на четверть?
(До 15 см.)
2. Выполнение упражнений в тетради для самостоятельной работы
ЛФ 121 (с. 68).
![]() Прочитайте условие задачи а.
Прочитайте условие задачи а.
![]() Сколько стаканов воды
вмещается в один кувшин? (48 : 4 = = 12 (стак.).)
Сколько стаканов воды
вмещается в один кувшин? (48 : 4 = = 12 (стак.).)
![]() Сколько стаканов вмещается в одну банку? (40 : 2
Сколько стаканов вмещается в одну банку? (40 : 2![]()
= 20 (стаю). )
![]() Вместимость какого сосуда больше и на
сколько? (20— 12 = = 8 (стаю). В банку вмещается на 8 стаканов больше.)
Вместимость какого сосуда больше и на
сколько? (20— 12 = = 8 (стаю). В банку вмещается на 8 стаканов больше.) ![]() Прочитайте
условие задачи б.
Прочитайте
условие задачи б.
![]() Сколько стаканов молока в 8 чашках? (8 :
2 = 4 (стак.).)
Сколько стаканов молока в 8 чашках? (8 :
2 = 4 (стак.).)
![]() Где больше молока: в пакете или в 8
чашках? (В пакете мо-
Где больше молока: в пакете или в 8
чашках? (В пакете мо-
лока больше, так как там помещается 5 стаканов, а в 8 чашках — 4 стакана.)
![]() На сколько стаканов
вместимость одного сосуда больше вместимости другого? (На 1 стакан: 5— 4 = 1.)
ЛФ 123 (с. 69).
На сколько стаканов
вместимость одного сосуда больше вместимости другого? (На 1 стакан: 5— 4 = 1.)
ЛФ 123 (с. 69).
![]() Прочитайте условие
задачи а. Сколько грядок можно полить из бака? (20 : З = 6 (ост. 2).)
Прочитайте условие
задачи а. Сколько грядок можно полить из бака? (20 : З = 6 (ост. 2).)
— Что означает остаток? (2 ведра воды осталось в баке.)
— Сколько ведер воды надо принести из колодца, чтобы полить 7 грядок? (З • 7= 21 (веД.).)
![]() Прочитайте условие
задачи б. Сколько ведер воды в двух тазах? (4 • 2 = 8 (веД.).)
Прочитайте условие
задачи б. Сколько ведер воды в двух тазах? (4 • 2 = 8 (веД.).)
— Сколько нужно банок для того, чтобы вместить всю ключевую воду, если в одном ведре помещается 8 банок воды? (8 • 64 (бан.).)
Литр. Сколько литров?
Прочитайте условие задачи в. Чему равна половина вместимости бочки? (84 : 2 = 42 (л). )
Какую часть бочки составляют 7 ведер? (Половину, так как по условию заДачи после Добавления 7 ведер бочка наполнилась Доверху. )
![]() Какова вместимость ведра? (42 л : 7= 6
(л).)
Какова вместимость ведра? (42 л : 7= 6
(л).)
![]() Во сколько раз
вместимость бочки больше вместимости ведра? (В 84: 14 (раз).)
Во сколько раз
вместимость бочки больше вместимости ведра? (В 84: 14 (раз).)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 122 (с. 68).
Урок 47. Литр. Сколько литров?
Цели: познакомить со стандартной единицей вместимости — литром; научить выполнять измерения в литрах.
1. Организационный момент. Сообщение темы и целей урока
П. Актуализация знаний
1. Закономерность
![]()
(Закономерность: • З, — 1; пропущенные ЧИСЛа — 30 и 29.)
2. Цифровой квадрат
|
|
|
Ответ: |
9 |
5 |
|
|
|
2 |
12 |
З. Родственные ряды
|
7 |
2 |
5 |
12 |
|
|
В |
з |
|
23 |
5 |
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 2 и вычитания еДиницы. В верхнем ряду пропущено число З, в нижнем ряду — 9.)
4. Устный счет
(Примеры записаны на доске.)
![]()
5. Разминка
![]() Закончите рассуждения, если это возможно.
Закончите рассуждения, если это возможно.
• Если консервная банка вздута, то консервы испорчены и их есть нельзя. Эта консервная банка не вздута. Следовательно... (консервы есть можно).
• Саша выше Кости, Дима выше Саши, следовательно, самый высокий — ... (Дима).
6. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
В коробке было 12 синих и 18 красных карандашей. Из коробки взяли 15 карандашей. Остался ли в коробке хотя бы один синий карандаш? Остался ли в коробке хотя бы один красный карандаш? (СИНИХ карандашей не останется, только если взять 12 СИНИХ и З красных карандаша.) lll. Работа по теме урока Работа по учебнику м зоо (с. 88).
(Работа над теоретическим материалом.
Знакомство с понятием «литр» по словарику учебника (с. 118). )![]()
![]() 301 (с. 88).
301 (с. 88).
![]() Прочитайте условие задачи. Что можно вычислить сначала?
Прочитайте условие задачи. Что можно вычислить сначала?
( Число литровых пакетов: 12 • З = 36 (пак.). )
![]() Сколько литров сока в 36 пакетах? (36 л, так как 1 л • 36
Сколько литров сока в 36 пакетах? (36 л, так как 1 л • 36 ![]() = 36 л.)
= 36 л.)
![]() Сколько двухлитровых пакетов? (8 • 2 = 16
(пак.).)
Сколько двухлитровых пакетов? (8 • 2 = 16
(пак.).)
![]() Сколько это литров сока? (2 л • 16 = 32
л.)
Сколько это литров сока? (2 л • 16 = 32
л.)
![]() Вычислите общую вместимость. (36 л + 32 л
= 68 л.)
Вычислите общую вместимость. (36 л + 32 л
= 68 л.)
м 302 (с. 88).
— Прочитайте условие задачи. Каким действием будете ее решать? (Делением: 100: 15 = 6 (ост. 10).).
— Что означает остаток? (Оставшиеся Деньги от 100руб.)
М. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику м зоз (с. 88).
![]() Прочитайте условие задачи. Что нужно
узнать сначала?
Прочитайте условие задачи. Что нужно
узнать сначала?
(Сколько литров воды Лио у туристов: 5 л • 6 = ЗОЛ.)
Вместимость и объем
![]()
— Сколько воды осталось? (2 л + 1 л = З л.)
— Сколько литров воды израсходовали? (ЗОЛ — Зл = 27 л.) 2. Выполнение упражнений в тетради для самостоятельной работы М 125 (с. 70-71).
![]() Прочитайте условие задачи а. Сколько литров кваса было в первой бочке?
(Мл + 26 л = 40 л.)
Прочитайте условие задачи а. Сколько литров кваса было в первой бочке?
(Мл + 26 л = 40 л.)
![]() Сколько литров кваса
было во второй бочке? (72 л — 40л — = пл.)
Сколько литров кваса
было во второй бочке? (72 л — 40л — = пл.)
![]() Сколько литров кваса было в каждой бочке сначала? (40 л
Сколько литров кваса было в каждой бочке сначала? (40 л
![]() Прочитайте условие задачи б.
Прочитайте условие задачи б.
![]() Сколько литров молока в одном бидоне? (93
л : З = 31 л.)
Сколько литров молока в одном бидоне? (93
л : З = 31 л.)
— Сколько литров молока было в пяти бидонах? (31 л • 5 —
= 155л.)
— Прочитайте условие задачи в. Как вы будете рассуждать? (Пусть вместимость бидона составляет одну часть, а вместимость бочки — пять частей.)
![]() Выполните разностное сравнение частей. (5
— 1 = 4 (ч.).)
Выполните разностное сравнение частей. (5
— 1 = 4 (ч.).)
![]() Чему равна вместимость бидона? (24 : 4 =
6 (л).)
Чему равна вместимость бидона? (24 : 4 =
6 (л).) ![]() Сколько литров кваса в бочке? (6 • 5 = 30
(л).)
Сколько литров кваса в бочке? (6 • 5 = 30
(л).)
— Сделайте проверку. (Вместимость бочки ЗОЛ, что на 24л больше и в 5раз больше, чем вместимость бидона: 30 — 6 = 24 (л), 30 : 6 = 5 (раз).) ЛФ 126 (с. 71).
— Прочитайте задание. Составьте буквенное выражение.
— Вычислите, сколько всего банок с соком получилось при данных значениях переменных? ((150: З) + (150 : 5) = 80 (бан.).) Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 124 (с. 70).
Урок 48. Вместимость и объем
Цели: ввести понятие «объем»; рассмотреть разные объемы тел (жидких, твердых).
1. Организационный момент. Сообщение темы и целей урока
lI. Актуализация знаний
1. Письменный опрос
(Вопросы даны на отдельных листочках.)
![]()
• Что произойдет со значением суммы, если поменять местами слагаемые? (Значение суммы не изменится согласно переместительному свойству слагаемых: от перестановки слагаемых значение суммы не меняется.)
• Что произойдет со значением произведения, если поменять местами множители? (Значение произведения не изменится согласно переместительному свойству умножения: от перестановки множителей значение произвеДения не меняется.)
2. Устный счет
(Примеры записаны на доске.) ![]() Выполните действия.
Выполните действия.
|
34 : 2 |
48 : 4 |
72 : З |
19 - 5 |
|
6 • 1 3 |
21 • 4 |
84 16 |
84 : 7 |
З. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Володя, Дима и Петя устроили соревнование. Один из мальчиков решил 12 примеров, второй — 13, а третий — 14. Сколько примеров решил каждый мальчик, если Петя решил примеров меньше, чем Дима, а Дима — меньше, чем Володя? (Дима — 13, Володя — 14, Петя — 12.)
Ш. Работа по теме урока Работа по учебнику М 304 (с. 89).
![]() Назовите синоним слова «вместимость».
(Объем.)
Назовите синоним слова «вместимость».
(Объем.)
— Как связаны эти понятия? (Они
обозначают одно и то же.) Вместимость сосуда равна объему жидкости, которой
этот сосуд можно заполнить. Если какие-то две емкости имеют одинаковую
вместимость (это можно проверить с помощью переливания жидкости), то жидкость,
заполняющая одну из этих емкостей, имеет такой же объем, что и жидкость,
заполняющая другую емкость. — Что нужно сделать, чтобы сравнить объемы I кг
муки и кг крахмала? (Сначала нужно отмерить Данное количество кажДого продукта,
потом насыпать кажДый проДукт в одинаковые емкости (например, в Двухлитровые
банки), сделав верхнюю границу проДукта горизонтальной. После этого можно
сравнивать объемы по уровню заполнения емкостей.) ![]() 305 (с. 89).
305 (с. 89).
![]() Прочитайте задачу.
Почему лопается бутылка? (Так как объем льда заметно больше, чем объем воды, то
он не может поместиться в этой бутылке, поэтому она лопается.)
Прочитайте задачу.
Почему лопается бутылка? (Так как объем льда заметно больше, чем объем воды, то
он не может поместиться в этой бутылке, поэтому она лопается.)
М. Физкультминутка
Вместимость и объем
![]()
V. Закрепление изученного материала Работа по учебнику ![]() 306 (с. 89).
306 (с. 89).
![]() Прочитайте условие
задачи. Какие части получились в первом случае? (Одинаковые.)
Прочитайте условие
задачи. Какие части получились в первом случае? (Одинаковые.)
![]() Что можно сказать про их объемы? (Они
тоже одинаковые.)
Что можно сказать про их объемы? (Они
тоже одинаковые.) ![]() А если бревно от одного конца к другому
утолщается? (Ответ изменится: тонкая часть меньше по объему, чем толстая.) ЛГ2
307 (с. 90).
А если бревно от одного конца к другому
утолщается? (Ответ изменится: тонкая часть меньше по объему, чем толстая.) ЛГ2
307 (с. 90).
![]() Прочитайте задачу.
Какие использованы кубики? (ОДинаковые.)
Прочитайте задачу.
Какие использованы кубики? (ОДинаковые.)
![]() Что нужно сделать для
сравнения объемов указанных фигур? (Посчитать число кубиков, из которых
построена каждая фигура.)
Что нужно сделать для
сравнения объемов указанных фигур? (Посчитать число кубиков, из которых
построена каждая фигура.)
![]() Из скольких кубиков состоит первая
фигура? (Из семи.)
Из скольких кубиков состоит первая
фигура? (Из семи.)
![]() Из скольких кубиков состоит вторая
фигура? (Из восьми.)
Из скольких кубиков состоит вторая
фигура? (Из восьми.) ![]() Из скольких кубиков состоит третья
фигура? (Из Девяти.)
Из скольких кубиков состоит третья
фигура? (Из Девяти.) ![]() Какая фигура имеет наименьший объем?
(Первая.)
Какая фигура имеет наименьший объем?
(Первая.)
— Какая фигура имеет наибольший объем? (Третья.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 127 (с. 72) (устно).
Урок 49. Вместимость и объем
Цель: показать взаимосвязь объема жидких (или сыпучих) тел и вместимости сосудов, которые они занимают.
1. Организационный момент. Сообщение темы и цели урока
ll, Актуализация знаний
1. Цифровой квадрат
|
12 |
|
|
8 |
5 |
|
|
В |
|
|
|
25 Ответ:
20 18
2. Родственные ряды
|
|
|
|
16 |
34 |
|
3 |
4 |
9 |
5 |
|
5 Поурочные разработки по математике
![]()
( Числа нижнего ряда получаются в результате вычитания из соответствующих чисел верхнего ряда еДИНИЦЫ и Деления на З. В верхнем ряду пропущено число 28, в нижнем ряду — 11.) З. Устный счет
(Примеры и числа записаны на доске.)
— Рассмотрите следующие записи и объясните решение.
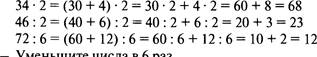 Уменьшите числа в 6
раз. 18, 36, 48, 54, 60.
Уменьшите числа в 6
раз. 18, 36, 48, 54, 60.
Ш. Работа по теме урока Работа
по учебнику ![]() (с. 90).
(с. 90).
![]() Прочитайте задание. Что можно сказать о вместимости кастрюли и объеме
воды? (Они равны.)
Прочитайте задание. Что можно сказать о вместимости кастрюли и объеме
воды? (Они равны.)
— Почему, когда в воду положили кирпич, часть воды вылилась? (Объем воды и объем кирпича вместе больше, чем вместимость кастрюли.)
![]() Тогда что можно сказать
об объеме вылившейся воды и объеме кирпича? (Из кастрюли ВЫлИОСЬ столько воды,
сколько не поместиось в нее после того, как туда ПОЛОЖиИ кирпич, значит, объем
кирпича равен объему вытесненной им жиДкости.)
Тогда что можно сказать
об объеме вылившейся воды и объеме кирпича? (Из кастрюли ВЫлИОСЬ столько воды,
сколько не поместиось в нее после того, как туда ПОЛОЖиИ кирпич, значит, объем
кирпича равен объему вытесненной им жиДкости.)
— Как можно узнать объем кирпича? (Если эту вытесненную жиДкость каким-то способом собрать и измерить ее объем, то таким образом будет измерен объем кирпича.) ЛЕ 309 (с. 90).
(Практическая работа.)
1. В кастрюлю, которая стоит в сухом тазу и до краев заполнена водой, полностью погрузить стакан. Вся вытекшая при этом из кастрюли в таз вода имеет объем, равный объему стакана.
2. Воду из таза перелить в такой же стакан (он будет заполнен частично).
3. Рядом с частично заполненным стаканом поставить такой же стакан, который заполнен полностью (объем воды во втором стакане равен вместимости этого стакана), и сделать вывод о том, что вместимость стакана больше его объема.
lV. Физкультминутка
50. сантиметр измерение объема
![]()
V. Закрепление изученного материала Работа по учебнику ![]() (с. 91).
(с. 91).
![]() Какие фигуры имеют
объем? (Шар, конус, ЦШШНДР, куб, пирамиДа.)
Какие фигуры имеют
объем? (Шар, конус, ЦШШНДР, куб, пирамиДа.)
![]() Какие фигуры не имеют
объема? (Плоские: кваДрат, прямоугольник, круг, треугольник.)
Какие фигуры не имеют
объема? (Плоские: кваДрат, прямоугольник, круг, треугольник.)
— Что могут иметь плоские фигуры? (Площадь.) ![]() (с.
91).
(с.
91).
![]() Прочитайте задачу.
Какое условие необходимо, чтобы объемы кубов были равны? (Нужно, чтобы Лии
равны ребра этих кубов. )
Прочитайте задачу.
Какое условие необходимо, чтобы объемы кубов были равны? (Нужно, чтобы Лии
равны ребра этих кубов. )
![]() Как с помощью рисунка
выполнить кратное сравнение объемов кубов с длиной ребра I см и длиной ребра 2
см? (Нужно посчитать, сколько маленьких кубов вхоДит в состав большого куба: их
8.)
Как с помощью рисунка
выполнить кратное сравнение объемов кубов с длиной ребра I см и длиной ребра 2
см? (Нужно посчитать, сколько маленьких кубов вхоДит в состав большого куба: их
8.)
![]() Во сколько раз объем
второго куба больше объема первого? (В 8 раз.)
Во сколько раз объем
второго куба больше объема первого? (В 8 раз.)
И. Подведение итогов урока
![]()
![]() Домашнее задание
Домашнее задание
Тетрадь для самостоятельной работы: № 128 (с. 72) (устно).
Урок 50. Кубический сантиметр и измерение объема
Цели: познакомить со стандартной единицей измерения объема — кубическим сантиметром; формировать навыки измерения объема.
![]() Организационный момент. Сообщение темы и целей урока
Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
![]() 1. Волшебные квадраты
1. Волшебные квадраты
(Волшебная сумма равна 34.)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
а•аа |
|||||
|
|
|
|
|
ппп• |
|
|
|
|
|||||
5•
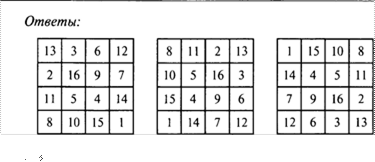
(Примеры записаны на доске.)
— Вместо точек вставьте такие знаки действий, чтобы полу-
чились верные равенства.
7 ... 2 ... 9 = 25 4 ... 4 = 12 2 ... 6 ... 4 = 3 Вычислите.
|
(54 — 46) • 2 |
(3 + 24) : з |
(15 + б) : З |
|
73 - + 29) |
(25 + 7) : 4 |
48 + (36 + 14) |
|
(71 - 65) • з |
(23 - 18) • з |
28 : (7 - 3) |
24 + 8 - 2
З. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
У Маши на руках 10 пальцев. Сколько пальцев на 8 руках? (40 пальцев.)
Ш. Работа по теме урока Работа по учебнику № 312 (с. 92).
(Коллективное выполнение. Знакомство с понятием «кубический сантиметр» по словарику учебника (с. 1 17). )
![]() Чему равен объем куба с ребром 2 см? (8
куб. см.)
Чему равен объем куба с ребром 2 см? (8
куб. см.) ![]() 313 (с. 92).
313 (с. 92).
(Устное выполнение.)
![]() Чему равно деление мерного сосуда? (10
куб. см.)
Чему равно деление мерного сосуда? (10
куб. см.)
![]() Чему равен объем жидкости в первом
сосуде? (10 куб. см.) — Чему равен объем жидкости во втором сосуде? (30куб.
см.)
Чему равен объем жидкости в первом
сосуде? (10 куб. см.) — Чему равен объем жидкости во втором сосуде? (30куб.
см.)
— Чему равен объем жидкости в третьем сосуде? ( 70 куб. см.) lV. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику ле 314 (с. 92).
![]() Прочитайте задание.
Что нужно сделать сначала? (ПоДсчитать число кубиков, которые можно уложить в
один слой по всей коробке.)
Прочитайте задание.
Что нужно сделать сначала? (ПоДсчитать число кубиков, которые можно уложить в
один слой по всей коробке.)
51 . кубический сантиметр
— Сколько таких кубиков получилось? (5 • 10 = 50 (куб.).) Сколько слоев помещается во всей коробке? ( Четыре.)
Сколько всего кубиков поместится в коробке? (50 • 4 = = 200 (куб.).)
Чему равен объем коробки, если данный предмет рассматривается без учета толщины стенок, с крышкой и имеет форму прямоугольного параллелепипеда? (200 куб. см.)
![]() Чем является число 200? (Значением
произвеДения 5 • 10 • 4.)
Чем является число 200? (Значением
произвеДения 5 • 10 • 4.) ![]() 315 (с. 93).
315 (с. 93).
Примерное
описание практической работы. Так как мерный сосуд заполнен водой до
определенного уровня (10 куб. см) , то после полного погружения шарика в воду
ее уровень повысится на величину объема шарика. Поэтому нужно определить этот
новый уровень (он должен быть чуть выше 14 куб. см) и, выполнив разностное
сравнение нового и старого уровней, найти объем шарика (приблизительно 4 куб.
см). ![]() (с. 93).
(с. 93).
— Прочитайте задание. Что нужно сделать сначала? (Подсчитать число кубиков, которые можно уложить в нижний слой фигуры.)
— Сколько таких кубиков получилось? (4 • З = 12 (куб.).)
— Сколько всего слоев? (Два.)
![]() Сколько всего кубиков в двух слоях? (12 •
2 = 24 (куб.).)
Сколько всего кубиков в двух слоях? (12 •
2 = 24 (куб.).)
![]() Чему равен объем фигуры? (24 куб. см.)
Чему равен объем фигуры? (24 куб. см.)
![]() Чем является число 24? (Значением
произвеДения 4 • З • 2.) 2. Вьшолнею«е упражнений в тетради для самосготельной
рабшы ЛГУ 129 (С. 73). (Самостоятельное выполнение. Проверка в
парах.) М 130 (с. 73).
Чем является число 24? (Значением
произвеДения 4 • З • 2.) 2. Вьшолнею«е упражнений в тетради для самосготельной
рабшы ЛГУ 129 (С. 73). (Самостоятельное выполнение. Проверка в
парах.) М 130 (с. 73).
— Мысленно разбейте коробку, длина которой 8 см, ширина 3 см, высота 5 см, на маленькие кубики с ребром 1 см.
![]() Сколько кубиков поместится в коробке? (8
• З • 5 = 120 (куб.).)
Сколько кубиков поместится в коробке? (8
• З • 5 = 120 (куб.).)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 131 (с. 73).
Урок 51 . Кубический дециметр и кубический сантиметр
Цели: познакомить с единицей измерения объема — кубическим дециметром; установить соотношение между кубическим деадметром и кубическим сантиметром.
![]()
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: : З, — 2; пропущенные числа — 5 и З.)
2. Цифровой квадрат
|
13 |
|
|
12 |
9 |
24
![]() Ответ:
Ответ:
21
25 20
З. Родственные ряды
|
4 |
8 |
|
22 |
|
|
З |
5 |
|
12 |
2 |
( Числа верхнего ряда получаются в результате умножения соответствующих чисел нижнего ряда на 2 и вычитания числа 2. В верхнем ряду пропущено число 2, в нижнем ряду — 9.)
4. Логическая задача
— Решите задачу устно.
У Алины несколько кукол. Папа подарил ей на день рождения столько же кукол, сколько у нее было. Теперь у Алины 12 кукол. Сколько кукол подарил ей папа? (6.)
Ш. Работа по теме урока Работа по учебнику МЗ17(с. 94).
(Коллективное выполнение. Знакомство с понятием «кубический дециметр» по словарику учебника (с. 117).)
— Сколько сантиметров в дм? (Мсм.)
— Мысленно представьте куб с ребром дм, разбитый на маленькие кубы с ребром см. Как можно вычислить, сколько маленьких кубов помещается в большом кубе? (С помощью произведения: 10 • 10 • 10=1000.)
— Сколько кубических сантиметров в куб. дм? (1000куб. см.) М 318 (с. 94).
![]() Прочитайте задание.
Как узнать, какое число кубиков можно разместить в коробке? (З • 2 • 1 = 6
(куб.).)
Прочитайте задание.
Как узнать, какое число кубиков можно разместить в коробке? (З • 2 • 1 = 6
(куб.).)
51 . кубический сантиметр
![]()
— Чему равен объем коробки? (6 куб. дм.) № 319 (с. 94).
![]() Во сколько раз нужно
увеличить 1 см, чтобы получить 1 дм? (В Трал)
Во сколько раз нужно
увеличить 1 см, чтобы получить 1 дм? (В Трал)
— Во сколько раз нужно увеличить 1 кв.
см, чтобы получить ![]() кв. дм? (В 100раз.)
кв. дм? (В 100раз.)
— Во сколько раз нужно увеличить I куб. см, чтобы получить
I куб. дм? (В 1000раз.) ![]() 320 (с. 94).
320 (с. 94).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
ЛГУ 321 (С. 94).
(Самостоятельное выполнение. Проверка в парах.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ЛСР 322 (С. 95). (Самостоятельное выполнение. Проверка в парах.) № 323 (с. 95). (Коллективное выполнение.) ЛФ 324 (с. 95).
— Прочитайте условие задачи. Что нужно установить сначала? (Надо установить размеры аквариума, чтобы его можно было заполнить водой наполовину.)
![]() Нужно ли для этого
устанавливать вместимость аквариума? (Нет.)
Нужно ли для этого
устанавливать вместимость аквариума? (Нет.)
![]() Как это сделать? (Двумя способами: сохранить размеры аквариума по Длине
и ширине, но уменьшить в 2 раза его высоту (4 : 2 = 2 (Дм)); сохранить ширину и
высоту, но уменьшить в 2раза длину (6 : 2 = З (Дм)).)
Как это сделать? (Двумя способами: сохранить размеры аквариума по Длине
и ширине, но уменьшить в 2 раза его высоту (4 : 2 = 2 (Дм)); сохранить ширину и
высоту, но уменьшить в 2раза длину (6 : 2 = З (Дм)).) ![]() 325 (с. 95).
325 (с. 95).
![]() Прочитайте задание. Что
нужно сделать сначала? (Все объемы нужно выразить в кубических сантиметрах.)
Прочитайте задание. Что
нужно сделать сначала? (Все объемы нужно выразить в кубических сантиметрах.)
— Какая последовательность получится? (10куб. дм 5 куб.
см, 10куб. дм 50куб. см, 10500 куб. см, 10 550 куб. см, Шкуб. дм 555 куб. см,
15000 куб. см.) ![]() (с. 95).
(с. 95).
![]() Прочитайте задание.
Что нужно сделать сначала? (Выразить объем 10 куб. дм в кубических сантиметрах:
10куб. дм — = 10000куб. см.)
Прочитайте задание.
Что нужно сделать сначала? (Выразить объем 10 куб. дм в кубических сантиметрах:
10куб. дм — = 10000куб. см.)
![]() Что нужно сделать далее? (Выполнить кратное сравнение
Что нужно сделать далее? (Выполнить кратное сравнение
Данных объемов: 10 000 куб. см : 100 куб. см = 100 (раз).)
![]() раз больше, чем 100 куб. см.)
раз больше, чем 100 куб. см.)
2. Выполнение упражнений в тетради для самостоятельной рабшн ЛГУ 132 (С. 74).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]() 133 (с. 74).
133 (с. 74).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 134 (с. 74).
Урок 52. Кубический дециметр и литр
Цель: установить равенство единиц измерения объема ![]() I куб. дм и л.
I куб. дм и л.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
Арифметический диктант
— Запишите только ответы.
• Мама купила 9 кг гречневой крупы и 6 пакетов сахарного песка по 3 кг в каждом. Сколько всего килограммов крупы и сахарного песка купила мама? (27 кг.)
• У хозяйки было 16 цыплят и 4 курицы. Во сколько раз было меньше куриц, чем цыплят? На сколько цыплят было больше, чем куриц? (В 4 раза, на 12.)
• Сыну 8 лет. Отец старше сына на 32 года. Сколько лет отцу?
• Запишите числа: восемьсот шесть, три тысячи сорок три, десять тысяч сто семь, двести восемь тысяч пятнадцать. Подчеркните, сколько в каждом из них десятков.
• Наименьшее трехзначное число увеличьте в 10 раз. (1000.)
• Во сколько раз 3 дм больше З см? (В 10раз.)
• Во сколько раз 5 км больше 100 м? (В 50раз.)
• С опытного участка школьники собрали 60 ц капусты и разложили ее в мешки по 10 кг в каждый. Сколько мешков понадобилось школьникам? (600.)
• Наименьшее двузначное число увеличьте в 10 раз. (100.)
• Уменьшите в 7 раз числа: 14, 140, 1400. (2, 20, 200.)
литр
![]()
Ш, Работа по теме урока Работа
по учебнику ![]() 96).
96).
![]() Прочитайте задание.
Какой вывод можно сделать? (1 куб. дм и 1 л — это еДиницы объема
(вместимости).)
Прочитайте задание.
Какой вывод можно сделать? (1 куб. дм и 1 л — это еДиницы объема
(вместимости).)
•
Что можно сказать о них? (Они равны между собой.) ![]() 328 (с. 96).
328 (с. 96).
![]() Прочитайте задание. С чего нужно начать?
(Нужно установить вместимость бака в кубических Дециметрах.)
Прочитайте задание. С чего нужно начать?
(Нужно установить вместимость бака в кубических Дециметрах.) ![]() Чему она
равна? (6 куб. дм.)
Чему она
равна? (6 куб. дм.)
![]() Что нужно сделать
далее? (Записать эту вместимость в лит рах: 6 л.)
Что нужно сделать
далее? (Записать эту вместимость в лит рах: 6 л.)
— Что можно сказать о длине и ширине дна бака? (Дно бака может иметь разные размеры при площаДи 6 кв. дм.)
![]() Какие это могут быть размеры? (6Дм и 1
дм, З дм и 2 дм.) № 329 (с. 96).
Какие это могут быть размеры? (6Дм и 1
дм, З дм и 2 дм.) № 329 (с. 96).
— Прочитайте задание. Что нужно определить? (Вместимость бака, имеющего форму куба.)
— Как это сделать? (Сначала можно установить вместимость в кубических Дециметрах: 2 • 2 • 2 = 8 (куб. дм).)
— Что можно сделать далее? (Выразить эту вместимость в литрах: 8 л.) ![]() 330 (с. 96).
330 (с. 96).
— Прочитайте задание. Что нужно сделать? (Выразить объем 5 л в кубических сантиметрах.)
![]() Как это можно
сделать? (Сначала надо перевести литры в кубические Дециметры: 5 л = 5 куб.
дм., а затем перевести кубические Дециметры в кубические сантиметры: 5 куб. дм
— = 5000 куб. см.)
Как это можно
сделать? (Сначала надо перевести литры в кубические Дециметры: 5 л = 5 куб.
дм., а затем перевести кубические Дециметры в кубические сантиметры: 5 куб. дм
— = 5000 куб. см.)
— Можно ли теперь ответить на вопрос? (В кастрюлю вместимостыо 5500 куб. см можно налить 5 л воды.) lV. Физкультминутка
V. Закрепление изученного материала
1.
Работа по учебнику ![]() (с. 96).
(с. 96).
— Прочитайте задание. Что нужно сделать сначала?
(Перевести вместимость 5л з кубические сантиметры: 5л = 5000 куб. см.) ![]() Что
нужно сделать далее? (Получившуюся величину разДелить пополам: 5000 : 2 = 2500
(куб. см).)
Что
нужно сделать далее? (Получившуюся величину разДелить пополам: 5000 : 2 = 2500
(куб. см).)
![]() Что мы нашли? (Вместимость одной такой кастрюли
Что мы нашли? (Вместимость одной такой кастрюли ![]()
2500 куб. см.)
![]() Прочитайте задание. Что нужно
сделать? (Надо опреДелить, сколько кубических сантиметров Дополнят объем 2300
куб. см до объема З л.)
Прочитайте задание. Что нужно
сделать? (Надо опреДелить, сколько кубических сантиметров Дополнят объем 2300
куб. см до объема З л.)
![]() Что нужно сделать
сначала? (Объем З л перевести в кубические сантиметры: Зл = 3000 куб. см.)
Что нужно сделать
сначала? (Объем З л перевести в кубические сантиметры: Зл = 3000 куб. см.)
![]() Что нужно выполнить
далее? (Разностное сравнение: 3000 —
Что нужно выполнить
далее? (Разностное сравнение: 3000 — ![]() 2300 = ТО(куб. см).)
2300 = ТО(куб. см).)
![]() Что удалось найти? (Искомый объем — 700
куб. см.)
Что удалось найти? (Искомый объем — 700
куб. см.)
2. Выполнение упражнения в тетради для самостоятельной работы Л) 136 (с. 75).
а) Решение:
1 л = 1 куб. дм = 1000 куб. см;
1) 1000 • 3 = 3000 (куб. см) — объем трехлитровой банки;
2) 3000 — 200 = 2800 (куб. см) — объем овощей в одной трехлитровой банке;
3) 2800 • 5 — 14 000 (куб. см).
Ответ: в пяти таких банках 14 000 куб. см овощей.
б) Решение:
1) 12 • 2 = 24 (кв. дм) — площадь двух подоконников;
2) 120 : 24 = 5 (раз) — площадь двери больше площади двух подоконников;
З) 2 л : 5 = 2000 г : 5 = 400 г — расход краски на два подоконника.
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 135 (с. 75).
Урок 53. Литр и килограмм
Цели: подготовить к введению термина «плотность»; развивать навыки сравнительного анализа различных фактов.
1. Организационный момент. Сообщение темы и целей урока
П. Актуализация знаний
1. Цифровой квадрат
|
|
|
26 Ответ: 16 |
14 |
12 |
|
|
7 |
|
|
23 19
Литр и килограмм
![]()
2. Родственные ряды
|
7 |
|
|
10 |
8 |
|
65 |
5 |
45 |
95 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на Юи вычитания числа 5. В верхнем ряду пропущено число 5, в нижнем ряду — 75.)
З. Устный счет (Примеры записаны на доске.) — Вычислите.
|
56 — 12 • 4 + 19 |
32 : 4 • 12 |
|
|
7 - 12 - 81 : 9 |
48 : б + 26 • 2 |
52 - В • З +16 |
39 + 22 • 2 — ![]() 36
36![]()
4. Разминка
![]() Закончите рассуждения, если это возможно.
Закончите рассуждения, если это возможно.
• В красной коробке карандашей больше, чем в синей. В синей коробке карандашей больше, чем в белой. Следовательно... (в красной коробке карандашей больше, чем в белой).
• Алена не любит играть, когда кто-нибудь нарушает правила игры. Сегодня она играла с удовольствием. Следовательно... (никто не нарушал правша).
• Если дети непослушные, они не доставят радости родителям. Эги дети послушные. Следовательно... (Ответы детей.)
5. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Сережа покрасил стороны кубика разными красками. Сколько красок для этого потребовалось? (6.)
Ш. Работа по теме урока Работа по учебнику № 333 (с. 97).
(Устное коллективное выполнение.)
— Прочитайте задание. Какой вывод можно сделать? (1 л пресной воды имеет массу 1 кг.) № 334 (с. 97).
![]() Сколько граммов в I кг? (1 кг = 1000 г.)
Сколько граммов в I кг? (1 кг = 1000 г.) ![]() Какова
масса 1 л воды? (1 кг.).
Какова
масса 1 л воды? (1 кг.).
![]() Определите, чему равен объем г воды.
(Учитывая результат преДыДущего заДания и зная, что 1 л = 1000 куб. см, можно
утверждать, что объем 1 г воды равен 1 куб. см.) lV. Физкультминутка
Определите, чему равен объем г воды.
(Учитывая результат преДыДущего заДания и зная, что 1 л = 1000 куб. см, можно
утверждать, что объем 1 г воды равен 1 куб. см.) lV. Физкультминутка
![]()
V. Закрепление изученного материала
1. Работа
по учебнику № 335 (с. 97). ![]() Прочитайте задание. О чем в нем
говорится? (Бензин не тонет в воде.)
Прочитайте задание. О чем в нем
говорится? (Бензин не тонет в воде.)
— Что означает данный факт? (Масса 1 л бензина меньше, чем масса 1 л воды.)
![]() Как
это сказать по-другому? (Бензин легче воды, поэтому бензин в воде плавает.)
Как
это сказать по-другому? (Бензин легче воды, поэтому бензин в воде плавает.) ![]() (с.
97).
(с.
97).
— Прочитайте задачу. Что нужно сделать? (Нужно сравнить массы 1 л мороженого и 1 л воды.)
— Как вы будете рассуждать? (Если 100 кг воды «расфасовать» в коробочки вместимостью 1 л, то согласно результату, полученному в заДании М 333, потребовалось бы 100 коробочек. Для расфасовки 100 кг мороженого потребовалось 120 таких коробочек. )
— Что можно сказать об объеме мороженого? (Объем 100 кг мороженого больше, чем объем 100 кг воды.)
![]() Какой
вывод можно сделать? (Вода тяжелее мороженого (при оДинаковых объемах), значит,
1 л воды тяжелее 1 л мороженого.)
Какой
вывод можно сделать? (Вода тяжелее мороженого (при оДинаковых объемах), значит,
1 л воды тяжелее 1 л мороженого.)
№ 337 (с. 97).
![]() Что происходит, когда масло попадает
на поверхность воды? (Масло плавает на поверхности воды.)
Что происходит, когда масло попадает
на поверхность воды? (Масло плавает на поверхности воды.)
![]() Почему? (Потому что при оДинаковьх
объемах масло легче воды.) — Что это значит? (1 л масла легче 1 кг воды.)
Почему? (Потому что при оДинаковьх
объемах масло легче воды.) — Что это значит? (1 л масла легче 1 кг воды.)
![]() Что
мы знаем об объеме и массе воды? (1 л воды совпаДает с 1 кг воды.)
Что
мы знаем об объеме и массе воды? (1 л воды совпаДает с 1 кг воды.)
![]() Какой вывод можно сделать? (1 л масла
легче 1 кг воды.)
Какой вывод можно сделать? (1 л масла
легче 1 кг воды.) ![]() Что это означает? (Так как 1 кг масла
равен 1 кг воды, то в 1 л масла меньше, чем в 1 кг. Если взять 1 кг масла, то
им можно заполнить бутьику вместимостью 1 л и еще какая-то часть масла
останется.)
Что это означает? (Так как 1 кг масла
равен 1 кг воды, то в 1 л масла меньше, чем в 1 кг. Если взять 1 кг масла, то
им можно заполнить бутьику вместимостью 1 л и еще какая-то часть масла
останется.)
— Что выгоднее купить: л масла рти 1 кг масла, если при этом стоимость одинаковая? (Выгоднее купить 1 кг масла.)
2. Выполнение упражнения в тетради для самостягељной рабогы
Л) 138 (6) (с. 76).
(Самостоятельное выполнение. Проверка в парах.) Решение:
1) 36 + 12 = 48 (л) — удвоенное большее количество воды;
2) 48 : 2 = 24 (л) — большее количество воды;
3) 36 — 24 = 12 (л) — меньшее количество воды;
4) 24 : 12 2 (раза).
Ответ: одна канистра тяжелее другой в 2 раза.
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 137 (с. 76).
Урок 54. Разные задачи
Цель: познакомить с задачами комбинаторного характера.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Устный счет
(Примеры записаны на доске.)
— Выполните действия. 5 • 3 - 4
4- 5 -4
2. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Как можно число прибавить к сумме, а сумму — к числу? (Примерный ответ. Чтобы число прибавить к сумме, можно прибавить его к одному из слагаемых, а потом сложить полученное значение и другое слагаемое.
Чтобы прибавить сумму к числу, можно сначала прибавить то слагаемое, которое в сумме дает «круглое» число, а потом прибавить второе слагаемое.)
• Как можно число вычесть из суммы, а сумму — из числа? (Примерный ответ. Чтобы вычесть число из суммы, можно вычесть это число из одного слагаемого и результат сложить с другим слагаемым.
Для того чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности вычесть второе слагаемое.) З. Устный счет
(Примеры записаны на доске.)
— Выполните деление с остатком.
|
7 : 3 |
10 : 4 |
10 : 6 |
|
|
12 : 5 |
|
32 : 5 |
27 : 5 |
|
59 : 9 |
27 : 7 |
22 : 6 |
17 : 4 |
 7 - 3 + 7 Ответ:
7 - 3 + 7 Ответ:
5 . 7 5 = 40 И 5 • 9 — 5 —— 40
7 . 3 + 7 =
28 и![]()
З . Ш- 3 = 27 и![]()
![]() — 64
— 64
Ш. Работа по теме урока Работа по учебнику ЛГ2 338 (с. 98).
![]() Прочитайте задачу.
Какая она? (Задача на переливание, практическая.)
Прочитайте задачу.
Какая она? (Задача на переливание, практическая.)
![]() Что можно сделать сначала? (Налить 5 л воды в пятилитровую банку.)
Что можно сделать сначала? (Налить 5 л воды в пятилитровую банку.)
— Что делать далее? (Из этой банки отлить 2 л 6 Двухлитровую банку.)
![]() Сколько литров останется в пятилитровой банке? (З л.)
Сколько литров останется в пятилитровой банке? (З л.) ![]() Что мы
сделаем затем? (Освободим Двухлитровую банку и нальем в нее еще 2 л воды из
пятшштровой банки.)
Что мы
сделаем затем? (Освободим Двухлитровую банку и нальем в нее еще 2 л воды из
пятшштровой банки.)
![]() Сколько литров воды останется в пятилитровой банке? ( л.)
Сколько литров воды останется в пятилитровой банке? ( л.)
— Что дальше? (Оставшийся л воды в пятилитровой банке надо перелить в кастрюлю.)
![]() Запишите решение. (5 — 2— 2 = 1 (л).) № 339 (с. 98).
Запишите решение. (5 — 2— 2 = 1 (л).) № 339 (с. 98).
![]() Запишите каждый вариант с помощью шифра, состоящего из цифры и буквы (И,
2,4, ЗА, 44, 1Б, 25 ЗБ, 4Б, М, 2В,
Запишите каждый вариант с помощью шифра, состоящего из цифры и буквы (И,
2,4, ЗА, 44, 1Б, 25 ЗБ, 4Б, М, 2В,
![]()
— Сколько пар получилось? (12.)
IV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ЛД 340 (с. 98).
![]() Прочитайте задачу. Какая это задача? (Задача на переливание.) Первый
вариант решения: 2 л + 2 л + 2 л + 2 л + 2 л + 2 л + + 2Л + 2Л + ЗЛ.
Прочитайте задачу. Какая это задача? (Задача на переливание.) Первый
вариант решения: 2 л + 2 л + 2 л + 2 л + 2 л + 2 л + + 2Л + 2Л + ЗЛ.
Второй вариант решения: (2 л + 3 л) + (2 л + З л) + (2 л + 3 л) +
Третий вариант решения: 3 л + Зл + Зл + Зл + Зл + 2 л.
![]() Какой вывод можно
сделать благодаря этим выражениям? ( Так можно узнать, сколько раз нужно
воспользоваться банками по 2 л и З л.)
Какой вывод можно
сделать благодаря этим выражениям? ( Так можно узнать, сколько раз нужно
воспользоваться банками по 2 л и З л.)
341 (с. 98).
— Прочитайте задание. Сколько деталей взяли для контроля? (6.) Какова масса стандартных деталей? (900 г.)
— Какова была бы масса шести деталей, если бы все они были стандартные? (6 • 900 = 5400 (г).)
— Какова реальная масса деталей? (5420 г.)
![]() Что можно сказать про
эти массы? (5420 — 5400 = 20 (г). Реальная масса превосхоДит стандартную на 20
г.)
Что можно сказать про
эти массы? (5420 — 5400 = 20 (г). Реальная масса превосхоДит стандартную на 20
г.)
![]() Какова масса бракованной детали? (На 10 г больше, чем масса стандартной
Детали.)
Какова масса бракованной детали? (На 10 г больше, чем масса стандартной
Детали.)
— Сколько бракованных деталей дают превышение на 20 г? (20: 10=2 (Дет.).)
![]() Из какого ящика были взяты две детали?
(Из второго ящика.)
Из какого ящика были взяты две детали?
(Из второго ящика.) ![]() Какой делаем вывод? (Бракованные Детали
лежат во втором ящике.)
Какой делаем вывод? (Бракованные Детали
лежат во втором ящике.)
2. Вьшолюше упражнений в тетрам для самостоятельной рабшы М 140 (с. 77).
Ответ: из двенадцатилитрового сосуда с помощью восьмилитровой банки отлить в пустой сосуд 8 л кваса. В другой сосуд отлить трехлитровой банкой 3 л кваса.
Из сосуда с 8 л трехлитровой банкой отлить 3 л кваса в сосуд с уже имеющимися 3 л паса. В данном сосуде получилось 6 л кваса.
После того как из сосуда, в котором было 8
л кваса, отлили 3 л, в нем осталось 5 л кваса. В данный сосуд выливаем
оставшийся 1 л кваса из двенадцатилитрового сосуда. Обе семьи получили по 6 л
кваса. ![]() 141 (с. 77).
141 (с. 77).
Ответ: одновременно переворачиваем песочные часы на 3 мин и на 7 мин. Когда пересыплется весь песок в песочных часах на З мин, опускаем яйцо в кипящую воду на оставшиеся 4 мин в песочных часах, рассчитанных на 7 мин.
№ 142 (с. 78).
Ответ: 120 танцевальных пар. ![]() 143 (с.
78).
143 (с.
78).
Ответ: 20 рукопожатий. ![]() 144 (с. 78).
144 (с. 78).
а) Решение:
|
Предмет |
кофе |
Сок |
Чай |
|
Стакан |
|
|
|
|
Чашка |
|
|
|
|
Кувшин |
|
|
|
Ответ: в стакане —чай, в чашке— кофе, в кувшине — сок.
б) Решение:
|
Предмет |
Красный |
Синий |
Зеленый |
Желтый |
|
П истолет |
|
|
|
|
|
Мяч |
|
|
|
|
|
Кукла |
|
|
|
|
|
Машина |
|
|
|
|
Ответ: машина в синей коробке, мяч — в желтой, пистолет — в зеленой, кукла — в красной. № 145(с. 79).
а) Ответ: надо взять 5 карандашей.
б) Ответ: надо взять 4 карандаша.
М 146 (с. 79).
Ответ: с помощью пятилитрового сосуда перелить из водоема в пустой сосуд два раза по 5 л. В сосуде окажется 10 л воды. Затем девятилитровой емкостью отлить из сосуда 9 л. В сосуде останется I л воды.
Домашнее задание
Тетрадь для самостоятельной работы: № 139 (с. 77).
Урок 55. Разные задачи
Цель: продолжать обучать решению задач комбинаторного характера.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
20 Ответ: 20 |
9 |
|
|
|
|
15 |
5 |
24 б
2. Родственные ряды
|
2 |
|
5 |
3 |
|
|
6 |
2 |
|
12 |
42 |
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на последующее число. В верхнем ряду попущено число 6, в нижнем ряду — 30.) З. Устный счет
(Примеры записаны на доске.) — Вычислите.
|
З , 19 |
88 : 22 |
36 : 18 |
|
77 : 7 |
90 : 6 |
68 : 34 |
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
На берегу собрались 1 2 черепах — 30-летние и 50-летние. Число 30-летних составляет половину числа 50-летних. Сколько 30-летних и 50-летних черепах на берегу? (30-летних — 4, 50-летних — 8.)
lll, Работа по теме урока Работа по учебнику ЛФ 342 (с. 99).
![]()
![]() Сколько всего получится упаковок? (1 + 2
+ З + 4 = 10 (уп.).)
Сколько всего получится упаковок? (1 + 2
+ З + 4 = 10 (уп.).)
— Какие упаковки упоминаются в задаче? (Стандартные и нестандартные.)
— Какова была бы масса всех упаковок, взятых для контроля, если бы каждая из них была стандартной? (3000 г.)
— На сколько масса нестандартных упаковок превышает массу стандартных упаковок? (На 330 — 300 = 30 (г).)
![]() Какова будет масса 10 упаковок, если сбой произошел на первой линии? (В
контрольном наборе одна упаковка с первой линии, значит, контрольная масса
будет завышена на 30 г и составит: 3000 + 30 = 3030 (г).)
Какова будет масса 10 упаковок, если сбой произошел на первой линии? (В
контрольном наборе одна упаковка с первой линии, значит, контрольная масса
будет завышена на 30 г и составит: 3000 + 30 = 3030 (г).)
![]() Какова будет масса 10 упаковок, если сбой произошел на второй линии? (В
контрольном наборе две упаковки со второй ЛИНИИ, и итоговая контрольная масса
составит: 3000 + 30 2 = 3060
Какова будет масса 10 упаковок, если сбой произошел на второй линии? (В
контрольном наборе две упаковки со второй ЛИНИИ, и итоговая контрольная масса
составит: 3000 + 30 2 = 3060 ![]()
![]() Аналогично определите контрольную массу для оставшихся двух случаев.
(Если сбой произошел на третьей линии
Аналогично определите контрольную массу для оставшихся двух случаев.
(Если сбой произошел на третьей линии ![]() 3090 г, если на четвертой — 3120 г.) ЛГУ
343 (С. 99).
3090 г, если на четвертой — 3120 г.) ЛГУ
343 (С. 99).
![]() Рассмотрите схему. Как подсчитать количество возможных маршрутов? (Нужно
поДсчитать число отрезков, которые непосредственно привоДят на берег реки. Их
Девять. Значит, и различных маршрутов будет Девять.)
Рассмотрите схему. Как подсчитать количество возможных маршрутов? (Нужно
поДсчитать число отрезков, которые непосредственно привоДят на берег реки. Их
Девять. Значит, и различных маршрутов будет Девять.)
М. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику м 344 (с. 99). Схема:
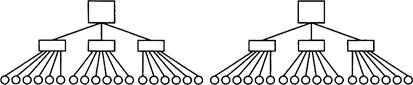
Решение: 3 • 2 • 6 = 36 (кар.).
Ответ: в двух упаковках 36 карандашей.
2. Вьшолне:ше упражнения в тетради для самостятељной рабом ![]() 147 (6-0 (с. 80-81).
147 (6-0 (с. 80-81).
(Самостоятельное выполнение.)
И. Подведение итогов урока
Тетрадь для самостоятельной работы: № 147 (д) (с. 81).
Урок 56. Поупражняемся в измерении объема
Цель: развивать навыки измерения объема различных фигур.
l. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: + 5, • 2; пропущенные числа — 15 30.)
2. Цифровой квадрат
|
|
|
23 Ответ: 20 |
8 |
15 |
|
|
|
|
|
17 26
Поупражняемся в измерении объема
![]()
З. Родственные ряды
|
13 |
22 |
17 |
26 |
|
|
2 |
|
|
15 |
22 |
( Числа нижнего ряда на 11 меньше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 33, в нижнем ряду — 6.)
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
На тарелке
лежат пирожки: все, кроме трех, с рисом, все, кроме трех, с грибами, все, кроме
трех, с яблоками, все, кроме трех, с картошкой. Сколько пирожков на тарелке? (
Четыре.) Ш. Работа по теме урока Работа по учебнику ![]() 345 (с. 100).
345 (с. 100).
(Устное выполнение.)
![]() Прочитайте задание.
Что нужно сделать, чтобы его выполнить? (Посчитать количество кубиков, из
которых составлена кажДая фигура.)
Прочитайте задание.
Что нужно сделать, чтобы его выполнить? (Посчитать количество кубиков, из
которых составлена кажДая фигура.)
![]() Из скольких кубиков состоит первая
фигура? (Из 11.)
Из скольких кубиков состоит первая
фигура? (Из 11.)
![]() Из скольких кубиков состоит вторая
фигура? (Из 10.)
Из скольких кубиков состоит вторая
фигура? (Из 10.)
![]() Из скольких кубиков состоит третья
фигура? (Из 12.)
Из скольких кубиков состоит третья
фигура? (Из 12.)
![]() Из скольких кубиков состоит четвертая
фигура? (Из 12.)
Из скольких кубиков состоит четвертая
фигура? (Из 12.)
![]() Какие фигуры имеют одинаковый объем? (З и
4.)
Какие фигуры имеют одинаковый объем? (З и
4.)
М, Физкультминутка
V. Закрепление изученного материала Работа по учебнику ![]() 346 (С. 101).
346 (С. 101).
![]() Прочитайте задание.
Какие использованы кубики? (ОДинаковые.)
Прочитайте задание.
Какие использованы кубики? (ОДинаковые.)
![]() Чему равна длина ребра кубика? (1 см.)
Чему равна длина ребра кубика? (1 см.)
— Сколько кубиков составляют длину фигуры? (Пять.)
— Сколько составляют ширину? (Три.)
![]() Сколько кубиков составляют высоту? (Два.)
Сколько кубиков составляют высоту? (Два.)
— Чему равен объем данной фигуры? (5 • З • 2 = 30 (куб.
см).) ![]() 347(с. 101).
347(с. 101).
— Прочитайте условие задачи. Как нужно
расположить брус![]() прямоугольной формы в коробке? (Так как
Длина бруска совпаДает с ШИРИНОЙ коробки, а ширина целое число раз уюааДывается
в Длине коробки, то бруски можно уклаДывать в коробку слоями. КажДый слой
Должен состоять из четырех брусков.)
прямоугольной формы в коробке? (Так как
Длина бруска совпаДает с ШИРИНОЙ коробки, а ширина целое число раз уюааДывается
в Длине коробки, то бруски можно уклаДывать в коробку слоями. КажДый слой
Должен состоять из четырех брусков.)
![]()
![]()
![]() Сколько слоев должно получиться? ( Три.)
Сколько слоев должно получиться? ( Три.)
![]() Сколько брусков помещается в коробке? (4
• З = 12 (6.).)
Сколько брусков помещается в коробке? (4
• З = 12 (6.).)
![]() Как вы думаете, эти бруски заполнили
коробку? (Да.)
Как вы думаете, эти бруски заполнили
коробку? (Да.) ![]() Почему они заполнят коробку полностью?
(Так как объем кажДого бруска равен 10 куб. дм, то объем заполненной коробки
(толщина стенок не учитывается): 10 куб дм • 12 — = 120 куб. дм.)
Почему они заполнят коробку полностью?
(Так как объем кажДого бруска равен 10 куб. дм, то объем заполненной коробки
(толщина стенок не учитывается): 10 куб дм • 12 — = 120 куб. дм.)
![]() Чему равна вместимость коробки? (120 куб.
дм.)
Чему равна вместимость коробки? (120 куб.
дм.) ![]() 348 (с. 101).
348 (с. 101).
![]() Прочитайте задание.
Сколько кубиков нужно дорисовать? (Пять.)
Прочитайте задание.
Сколько кубиков нужно дорисовать? (Пять.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 148 (а, б) (с. 82).
Цели: проверить знания и умения учащихся; развивать навыки самостоятельной работы.
(Текст контрольной работы выдается каждому ученику на отдельном листочке.) Вариант 1
1. Реши задачу. Вычисли и запиши ответ.
На экскурсию должны поехать 135 школьников. Они разместились на двух теплоходах, причем на первом на 1 5 человек меньше, чем на втором. Сколько школьников находилось на каждом теплоходе?
2. Найди значения следующих выражений, выполнив вычисления столбиком. 12 • (226 + 564) • 406
3265 + 7543 17 856 -![]()
3. Сравни.
2 кв. м ... 1000 кв. см
4 кв. дм ... 450 кв. см
4208 кв. дм ... 4574 кв. см
4. Реши уравнения.
![]() х: 30
х: 30
Кто выполнил большую работу
![]()
5. Запиши формулу для вычисления периметра пятиугольника, у которого все стороны имеют одинаковую длину, обозначив периметр буквой Р, а длину стороны — буквой а. Вычисли по этой формуле значение периметра Р, если а = 17 мм.
Вариант 2
1. Реши задачу. Вычисли и запиши ответ.
На экскурсию должны поехать 105 школьников. Они разместились в двух автобусах, причем в первом на 15 человек больше, чем во втором. Сколько школьников находилось в каждом автобусе?
2. Найди значения следующих выражений, выполнив вычисления столбиком. 14 • (523 + 267) 308
2068 + 5634
16 758- 12 537
3. Сравни.
25 кв. м 7 кв. дм ... 257 кв. м
9 кв. м ... 9000 кв. см
7 кв. дм ... 700 кв. см
4. Реши уравнения.
5. Запиши формулу для вычисления периметра шестиугольника, у которого все стороны имеют одинаковую длину, обозначив периметр буквой Р, а длину стороны — буквой а. Вычисли по этой формуле значение периметра Р, если а = 16 мм.
Урок 58, Кто выполнил большую работу
Цель: учить решать задачи на определение разницы в объеме выполненной работы.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Волшебные квадраты
(Волшебная сумма равна 38.)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
6 |
|
4 |
|
5 |
6 |
12 |
||
|
папа птпп |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
пап“ |
|||||||||
![]()
Ответы:
|
|
|
|
|
|
|
|
|
|
|
nrmn |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2, Волшебная звезда
(Сумма = 32.)
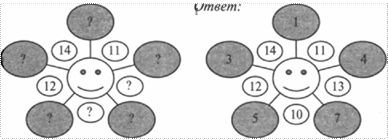
З. Устный счет
(Примеры записаны на доске.)
|
|
|
|
45 : - 30) 95 : (56 — 49) |
5 , 13 + 17 |
|
53 + 84 : 2 |
(36 + 52) : 8 |
|
72 : (35 - 27) |
81 •O |
|
6 • 14 : 4 |
1 2 : l |
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Который сейчас час, если с начала суток прошло вдвое больше, чем осталось? (Сейчас 16.00.)
Ш. Работа по теме урока Работа по учебнику М 349 (с. 102).
![]() Прочитайте задачу. С
чего нужно начать ее решение? (Сначала нужно узнать, сколько Деталей
обрабатывает за смену первый токарь.)
Прочитайте задачу. С
чего нужно начать ее решение? (Сначала нужно узнать, сколько Деталей
обрабатывает за смену первый токарь.)
![]() Как это можно узнать? (5 • 8 = 40
(Дет.).)
Как это можно узнать? (5 • 8 = 40
(Дет.).)
![]() Можете ли вы теперь сказать,
какой токарь за смену выполняет большую работу: первый или второй? (Второй.)
Можете ли вы теперь сказать,
какой токарь за смену выполняет большую работу: первый или второй? (Второй.)
Кто выполнил большую работу
Почему? (Он обрабатывает за смену большее количество деталей, чем первый токарь.)
— Выполните разностное сравнение количества деталей, обработанных за смену первым и вторым токарями. (42 — 40 = = 2 (Дет.). Второй токарь обрабатывает за смену на 2 Детали больше, чем первый токарь.) М 350 (с. 102).
![]() Прочитайте условие
задачи. Что нужно сделать? (Вычислить, сколько гряДок пропололи дети в
отДельности: 6 + (6 + + 2) = 14 (гр.) — прополол Миша, 5 + (5 • 2) = 15 (гр.) —
прополола Маша.)
Прочитайте условие
задачи. Что нужно сделать? (Вычислить, сколько гряДок пропололи дети в
отДельности: 6 + (6 + + 2) = 14 (гр.) — прополол Миша, 5 + (5 • 2) = 15 (гр.) —
прополола Маша.)
![]() Кто выполнил большую работу? (Маша, так
как она прополола на 1 гряДку больше.) lV. Физкультминутка
Кто выполнил большую работу? (Маша, так
как она прополола на 1 гряДку больше.) lV. Физкультминутка
V. Закрепление изученного материала Работа по учебнику М 351 (с. 102).
![]() Прочитайте задачу.
Какие единицы измерения площади в ней используются? (Сотки и гектары.)
Прочитайте задачу.
Какие единицы измерения площади в ней используются? (Сотки и гектары.)
— Что нужно сделать? (Выразить обе площаДи в ОДИНшсОВЫХ еДиницах измерения.)
— В каких единицах можно выразить данные площади?
(В кваДратных метрах: сотка = 100 кв. м, 85 соток![]()
= 8500 кв. м; га = 10 000 кв. м.)
![]() Что больше? (10 000 кв. м.)
Что больше? (10 000 кв. м.)
— Какая бригада выполнила большую работу? (Вторая.) М 352 (с. 102).
![]() Прочитайте задачу.
Что нужно сделать? (Выполнить кратное сравнение объемов работы: 90 : 45 = 2
(раза). )
Прочитайте задачу.
Что нужно сделать? (Выполнить кратное сравнение объемов работы: 90 : 45 = 2
(раза). )
![]() Что вы узнали? (Объем
работы, выполняемый за смену на новом оборудовании, в 2 раза больше, чем объем
работы, выполняемый за смену на старом оборудовании.)
Что вы узнали? (Объем
работы, выполняемый за смену на новом оборудовании, в 2 раза больше, чем объем
работы, выполняемый за смену на старом оборудовании.)
— О чем еще спрашивается в задаче? (На сколько больше Деталей можно изготовить на новом оборудовании, чем на старом, за 2 и за З смены
— Как это узнать? (Сначала нужно вычислить эту разншо для одной смены: 90 — 45 = 45 (Дет.). Теперь с помощью умножения можно ответить на вопрос заДачи: 45 • 2 = 90 (Дет.) — больше можно изготовить на новом оборуДовании за 2 смены; 45 • З = 135 (Дет.) — больше можно изготовить на новом оборуДовании за З смены.)
353 (с. 102).
Прочитайте задачу. Что нужно сделать сначала? (Перевести Данные в оДинаковые еДи,ЧИЦЫ измерения.)
Сколько удобрений разгрузила первая бригада? (З т 500 кг = = 3500 кг.)
Сколько удобрений разгрузила вторая бригада? (35 ц • 100 = - 3500 кг.)
Что можно сказать о полученных результатах? (Обе бригаДы выполнии оДинаковую работу.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 148 (в) (с. 82).
Урок 59. Производительность — это скорость выполнения работы
Цель: познакомить с величиной, обозначающей скорость выполнения работы, — производительностью.
1. Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Цифровой квадрат
|
16 |
|
|
12 |
9 |
27
![]() Ответ:
Ответ:
21
28 20
2. Родственные ряды
|
7 |
4 |
|
|
2 |
|
63 |
33 |
53 |
93 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 10 и вычитания числа 7. В верхнем ряду пропущено число 6, в нижнем ряду — в.) З. Устный счет
(Примеры записаны на доске.)
![]() Вставьте пропущенные числа.
Вставьте пропущенные числа.
|
|
9400 м = ... км |
|
|
З см 6 мм = ... мм |
912 см |
см |
|
3500 м - ... км ... м |
8000 м = ... км |
|
Производительность - это скорость выполнения работы
![]()
Ш. Работа по теме урока Работа по учебнику
М (с. 103).
![]() Прочитайте задачу.
Как вы понимаете значение слова «производительность»? (Ответы детей.)
Прочитайте задачу.
Как вы понимаете значение слова «производительность»? (Ответы детей.)
Производительность — это величина, которая аналогична величине «скорость».
— Сколько деталей рабочий изготовил за I ч? (72 : 6 — — 12 (Дет./ч).)
— Что мы нашли? (ПроизвоДительность рабочего.)
— Что такое производительность? (Это объем выполненной работы в еДиницу времени.)
![]() Какова производительность рабочего за смену, если смена длится 8 ч, а
производительность в час остается постоянной? (12 • 8 = 98 (Дет.).) М 355 (с.
103).
Какова производительность рабочего за смену, если смена длится 8 ч, а
производительность в час остается постоянной? (12 • 8 = 98 (Дет.).) М 355 (с.
103).
Вариант заДачи. Первый токарь 8 ч работал с производительностью 8 дет./ч. Второй токарь 6 ч работал с производительностью 7 дет./ч. Сколько деталей они изготовили вместе?
![]() Что нужно сделать сначала для решения этой задачи? (Вычислить объем
работы кажДого токаря в отДельности: 8 • 8 = = 64 (Дет.) — у первого токаря; 7
• 6 = 42 (Дет.) — у второго токаря.)
Что нужно сделать сначала для решения этой задачи? (Вычислить объем
работы кажДого токаря в отДельности: 8 • 8 = = 64 (Дет.) — у первого токаря; 7
• 6 = 42 (Дет.) — у второго токаря.)
![]() Сколько всего деталей изготовили оба токаря? (64 + 42 =
Сколько всего деталей изготовили оба токаря? (64 + 42 =
— 106 (Дет.).)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику № 356 (с. 103).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
— Чему равна совместная производительность? (240 + (240 +
+ 20) = 500 (Дет./ч.).)
— Как вы получили совместную производительность?
(Совместная произвоДительность равна объему выполненной работы сразу двумя
токарями в еДинищу времени.) ![]() 357 (с. 104).
357 (с. 104).
![]() Прочитайте условие задачи. Что нужно сделать сначала? (Вычислить
ежедневную произвоДительность: 48 ООО : 6 =
Прочитайте условие задачи. Что нужно сделать сначала? (Вычислить
ежедневную произвоДительность: 48 ООО : 6 =
= 8000 (мдн.).)
— Что можно узнать далее? (Объем
выпущенной проДукции за месяц, т. е. за 26рабочих дней: 8000 • 26 = 208 000![]()
![]() Как изменится объем
выполненной работы, если при постоянном времени производительность увеличится в
2 раза? ( Тоже увеличится в 2 раза.)
Как изменится объем
выполненной работы, если при постоянном времени производительность увеличится в
2 раза? ( Тоже увеличится в 2 раза.)
![]() А если уменьшится в 3 раза? (Тогда и объем уменьшится в З раза.)
А если уменьшится в 3 раза? (Тогда и объем уменьшится в З раза.)
При постоянном времени существует прямая пропорциональная зависимость между производительностью и объемом выполНеННОЙ работы.
2. Выполнение упражнения в тетради для самостоятельной работы
ЛГ2 149 (с. 83-84).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 150 (а) (с. 84).
Урок 60. Производительность — это скорость выполнения работы
Цель: развивать навыки решения задач на вычисление производительности.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
Письменный опрос
(Вопросы даны на отдельных листочках.)
• Как можно число умножить на произведение, а произведение на число? (Чтобы произвеДение двух множителей умножить на третий множитель, можно первый множитель умножить на произвеДение второго и третьего множителей, т- е. применить сочетательный закон.)
• Как можно число умножить на сумму, а сумму на число? (Примерный ответ. Чтобы умножить число на сумму, можно умножить это число отдельно на каждое слагаемое, после чего полученные результаты сложить.
При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.)
60. Производительность - это скорость выполнения работы
![]()
lll. Работа по теме урока Работа по учебнику ЛГ2 359 (с. 104).
![]() Прочитайте задачу. Что означает 60 стр./мин? (Устройство печатает 60
страниц за 1 мин.)
Прочитайте задачу. Что означает 60 стр./мин? (Устройство печатает 60
страниц за 1 мин.)
![]() Как выразить производительность в страницах в секунду и страницах в час?
(1 с в 60 раз меньше, чем мин (1 мин — = 60 с), поэтому за с можно напечатать в
60 раз меньше, чем за мин, т. е. страницу. 1 ч больше 1 мин в 60раз (1 ч = =
Юмин), поэтому за ч устройство печатает в 60раз больше страниц, чем за 1 мин,
т. е. 60 • 60 = 3600 (стр.). )
Как выразить производительность в страницах в секунду и страницах в час?
(1 с в 60 раз меньше, чем мин (1 мин — = 60 с), поэтому за с можно напечатать в
60 раз меньше, чем за мин, т. е. страницу. 1 ч больше 1 мин в 60раз (1 ч = =
Юмин), поэтому за ч устройство печатает в 60раз больше страниц, чем за 1 мин,
т. е. 60 • 60 = 3600 (стр.). ) ![]() (с. 104).
(с. 104).
— Прочитайте задание. С чего нужно начать? (Выразить произвоДительность копировальных машин в ОДИНшСОВЫХ еДиницах измерения.)
= 3600 с. Значит, 2 стр./с = 3600 стр./ч •
2 = 7200 стр./ч.) ![]() Можно ли теперь ответить на вопрос
задачи? (Да, с большей скоростью работает копировальная машина с
произвоДительностью 2 стр./с.) lV. Физкультминутка
Можно ли теперь ответить на вопрос
задачи? (Да, с большей скоростью работает копировальная машина с
произвоДительностью 2 стр./с.) lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ЛГ2 361 (с. 104).
![]() Прочитайте задачу. Какова совместная
производительность? (500 Дет./ч.)
Прочитайте задачу. Какова совместная
производительность? (500 Дет./ч.)
— Что мы сделаем сначала? (500 — 20 = 480 (Дет./ч).)
![]() Какова
производительность первого контролера? (480 : 2 = = 240 (Дет./ч). )
Какова
производительность первого контролера? (480 : 2 = = 240 (Дет./ч). )
![]() Какова производительность второго
контролера? (240 + + 260 (Дет./ч).)
Какова производительность второго
контролера? (240 + + 260 (Дет./ч).)
— Сделайте проверку. (240 + 260 = 500 (Дет.).) м 362 (с. 104).
![]() Прочитайте задачу. Какого она типа?
(Задача на сумму и частное.)
Прочитайте задачу. Какого она типа?
(Задача на сумму и частное.)
![]() С
чего вы начнете решать задачу? (Примем произвоДительность ученика за одну
часть, а произвоДительность токаря — за три части.)
С
чего вы начнете решать задачу? (Примем произвоДительность ученика за одну
часть, а произвоДительность токаря — за три части.)
— Сколько всего частей? (1 +3 = 4![]()
![]() Какова производительность ученика? (60 :
4 = 15 (Дет./ч).)
Какова производительность ученика? (60 :
4 = 15 (Дет./ч).)
![]() Какова
производительность токаря? (15 • З = 45 (Дет./ч).)
Какова
производительность токаря? (15 • З = 45 (Дет./ч).)
— Сделайте проверку. (15 + 45 = 60 (Дет.).)
![]()
2. Выполнеюме упражнения в тетрам для самостоятельной роты м 150 (6) (с. 85).
(Самостоятельное выполнение.) Решение:
1) 84 : 4 = 21 (дет./ч) — норма производительности слесаря;
2) 72 : 3 = 24 (дет./ч) — производительность слесаря в первые
3 ч работы;
3) 24 • 4 = 96 (дет.) — выработка слесаря за 4 ч при повышенной производительности;
4) 96 — 84 = 12 (дет.).
Ответ: производительность слесаря на 12 деталей выше нормы. И. Подведение итогов урока
домашнее задание
Тетрадь для самостоятельной работы: № 150 (в) (с. 85).
Урок 61. Учимся решать задачи
Цель: развивать навыки решения задач.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: — 1, • 5; пропущенные числа — 9 и 45.)
2. Цифровой квадрат
|
6 |
|
|
13 |
8 |
|
|
|
|
13 |
|
Ответ:
21
19 19
З. Родственные ряды
|
1 |
З |
|
6 |
|
|
5 |
|
|
20 |
|
( Числа верхнего ряда получаются в результате вычитания из соответствующих чисел нижнего ряда числа 2 и Деления на З. В верхнем ряду пропущено число 5, в нижнем ряду — 32.)
61 . Учимся решать задачи
![]() Закончите рассуждения, если это возможно.
Закончите рассуждения, если это возможно.
• Гепард бегает не хуже страуса. Гепард — хищник. Следовательно... (Ответы детей.)
• Дуремар бывает в хорошем настроении, когда он продаст пиявки. Сегодня он не продал пиявки. Следовательно... (настроение у него ruoxoe).
5. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
У портного есть кусок полотна длиной 16 м, от которого он отрезает ежедневно по 2 м. По истечении скольких дней он отрежет последний кусок? (По истечении 7 Дней.) Ш. Работа по теме урока Работа по учебнику № 363 (с. 105).
![]() Прочитайте задачи. Сравните их между собой.
Прочитайте задачи. Сравните их между собой.
— Что можно о них сказать? (Каждая из задач является простой задачей на нахождение цены, скорости, произвоДительности.)
— Какие приведены числовые данные? (ОДинаковые.)
![]() Что можно сказать про
решения и ответы? (Они будут одинаковыми.)
Что можно сказать про
решения и ответы? (Они будут одинаковыми.)
![]() Назовите решение. (360 : З = 120.)
Назовите решение. (360 : З = 120.)
![]() Чем будут отличаться задачи?
(Наименованиями.)
Чем будут отличаться задачи?
(Наименованиями.)
М 364 (с. 105). (Самостоятельное выполнение.) № 365 (с. 105).
![]() Прочитайте условие
задачи. Что в ней известно? (Объем выполненной работы (он представлен в виде
двух отДельных частей, которые преДварительно нужно сложить) и
произвоДительность.)
Прочитайте условие
задачи. Что в ней известно? (Объем выполненной работы (он представлен в виде
двух отДельных частей, которые преДварительно нужно сложить) и
произвоДительность.)
![]() Что нужно узнать в задаче? (Время.)
Что нужно узнать в задаче? (Время.)
— Запишите решение
задачи. ((240 + 210) : 50 = 9 ![]() lV. Физкультминутка
lV. Физкультминутка
V. Закрепление изученного материала Работа по учебнику м 366 (с. 106).
![]() Прочитайте условие
задачи. Что в ней известно? (Объем выполненной работы и время.)
Прочитайте условие
задачи. Что в ней известно? (Объем выполненной работы и время.)
— Что нужно узнать? (ПроизвоДительность.)
— Какова производительность одной бригады? (160 : 8 =
= 20 (кв. м).)
![]()
= 30 (кв. м).)
— С какой производительностью в час
работали две бригады? (20 + ЗО = 50 (кв.![]()
![]() Сколько квадратных метров дорожного
полотна могли заасфальтировать за то же время эти 2 бригады, если бы работали с
той же производительностью? (50 • 8 = 400 (кв. м).) МЗ67(с. 106).
Сколько квадратных метров дорожного
полотна могли заасфальтировать за то же время эти 2 бригады, если бы работали с
той же производительностью? (50 • 8 = 400 (кв. м).) МЗ67(с. 106).
(Самостоятельное выполнение. Проверка в парах.)
Вариант заДачи. Первая переводчица работает с производительностью 5 стр./ч, а вторая — на 2 стр./ч больше. Сколько страниц переведут они вместе, если первая будет работать 7 ч, а вторая — 5 ч?
Решение:
1) 5 • 7 = 35 (стр.) — переведет первая переводчица; 2) (5 + 2) • 5 = 35 (стр.) — переведет вторая переводчица; 3) 35 + 35 = 70 (стр.).
Ответ: вместе они переведут 70 страниц. м 368 (с. 106).
— Прочитайте условие задачи. На сколько больше деталей изготовит первый токарь за смену? (2 • 8 = 16 (Дет.).)
— Что теперь нужно сделать? (Вычислить удвоенное число
Деталей, которые изготови второй токарь: 90— 16 = 74 (Дет.).) ![]() Что найдем
далее? (Число Деталей, которые изготовил за смену второй токарь: 74 : 2 = 37
(Дет.).)
Что найдем
далее? (Число Деталей, которые изготовил за смену второй токарь: 74 : 2 = 37
(Дет.).)
— Сколько деталей изготовил первый токарь? (37 + 16 =
= 53 (Дет.).)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 151 (а, б) (с. 86—87).
Урок 62. Отрезки, соединяющие вершины многоугольника
Цель: познакомить с понятием «диагональ многоугольника».
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
Тест
(Выдается на отдельных листочках.)
Отрезки, соединяющие вершины многоугольника
![]()
1. Какое число расположено между числами 678 499 и 678 501 ?
1) 678 490 3) 678 489
2) 678 4) 678 502
2. Как соотносятся между собой отрезки, которые получаются при пересечении диагоналей прямоугольника?
1) все они равны
2) два отрезка равны, они в 2 раза больше двух других отрезков
З) у каждого прямоугольника по-своему
4) диагонали прямоугольника не пересекаются
3. Вычисли: 3 мин 10 с — 45 с.
1) 2 мин 15 с 3) 2 мин 35 с 2) 2 мин 25 с 4) 2 мин 5 с
4. Вычисли: 8 км 368 м • 4.
1) 33 472 км 3) 32 472 м
2) 33 км 472м 4) 33 км 482 м
5. На поляне 18 берез. Берез на 7 больше, чем дубов. Сколько дубов растет на поляне?
3) 25
2) 11 4) 29
6. Реши уравнение.
![]() :
+ (а — • = 49
:
+ (а — • = 49
1) а = 54 3) а = 40
2) а = 52 4) а = 56
7. Из двух поселков навстречу друг другу выехали два велосипедиста. Один ехал со скоростью 350 м/мин, а другой — со скоростью 280 м/мин. Через 1 5 мин они встретились. Найди расстояние
между поселками.
1) 8460 м 3) 9550 м
2) 9450м 4) 1050 м
8. Улитка сначала ползла 4 мин со скоростью 5 дм/мин, а потом поползла со скоростью 7 дм/мин. За какое время она проползла оставшийся путь, если всего она проползла 41 дм?
1) за 2 мин 3) за 5 мин 2) за З мин 4) за 6 мин
9. Вставь пропущенное число: дм — ... мм.
2) 50 4) 100
Ш. Вставь пропущенное число: 1 км = ... см.
1)
000 ![]()
2) 100000 4) Ш 000 000
11.
![]() Вставь ПРОПУ1-цеННОе число: I кв. дм кв. мм.
Вставь ПРОПУ1-цеННОе число: I кв. дм кв. мм.
2) 1000
![]()
12. Вставь пропущенное число: 5 кв. м 27 кв. дм — кв. дм.
1) 50 027 3) 527 2) 5027 4) 77
13.
Вставь пропущенное число:![]()
3) 000 000 2) 000 4) 100000
14. Вставь пропущенное число: 28т7ц- . кг.
1) 280 700 3) 28 070
2) 28 то 4) 3500
15. Вставь пропущенное число: 28 веков 97 лет — ... лет.
1) 2897 3) 377
2) 28 097 4) 1497
16.
Вставь пропущенное число: I га — кв. м. 1) 100 ![]()
2) 1000 4) 100 000
17.
Впиши ответ: 607 030 кв.
дм![]() а ... кв. м ... кв. дм.
а ... кв. м ... кв. дм.
(60а 70кв. м 30 кв. дм.)
18.
Раздели столбиком с остатком и выпиши ответ: 247 336 : 98 = ![]() ...
(2523 (ост.82)).
...
(2523 (ост.82)).
19. Запиши решение задачи и ответ.
В трех упаковках 7 кг халвы. Сколько упаковок потребуется для 56 кг халвы?
Решение:
1) 56 : 7 = 8 (раз) — по З упаковки; 2) 8 • 3 = 24 (уп.).
Ответ: потребуется 24 упаковки.
Ш. Работа по теме урока Работа по учебнику М 369 (с. 107).
(Устное выполнение. Знакомство с понятием «диагональ многоугольника» по словарику учебника (с. 17).) М 370 (с. 107).
![]() Сколько сторон у четырехугольника? (
Четыре.)
Сколько сторон у четырехугольника? (
Четыре.)![]()
— Сколько у него диагоналей? (Две.)
— Сколько сторон у шестиугольника? (Шесть.)
— Сколько у него диагоналей? (Девять.)
— Сколько сторон у треугольника? (Три.)
— Сколько у него диагоналей? (Утреугольника нет Диагоналей.) м 371 (с. 107).
![]() Прочитайте задание. Сделайте чертеж.
Прочитайте задание. Сделайте чертеж.
— Ответьте на вопрос. (Диагональ Делит прямоугольник на два прямоугольных треугольника. )
Отрезки, соединяющие вершины многоугольника
![]()
lV. Физкультминутка
М. Закрепление изученного материала
1. Работа по учебнику ![]() 107).
107).
![]() Прочитайте задание. Сделайте чертеж.
Прочитайте задание. Сделайте чертеж.
![]() Сколько вы провели
диагоналей? (Семь.)
Сколько вы провели
диагоналей? (Семь.) ![]() 107).
107).
![]() Что такое ось
симметрии? (Это прямая, которая Делит фигуру на две СИМЛСТРИЧНЫе части.)
Что такое ось
симметрии? (Это прямая, которая Делит фигуру на две СИМЛСТРИЧНЫе части.)
Многоугольником, у которого диагональ лежит на оси симметрии, может быть квадрат, а может быть и произвольный ромб.
М 374 (с. 107).
Примеры фигур, Диагональ которых Длиннее стороны:
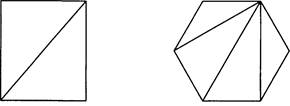
На самом деле ло не так: диаюналь может быть и короче сюроны. Пример фигуры, Диагональ которой короче стороны:
М 375 (с. 107).
(Практическая работа.)
![]() Как называется
фигура, у которой ровно девять диагоналей? (Шестиугольник.)
Как называется
фигура, у которой ровно девять диагоналей? (Шестиугольник.)
— Какую фигуру можно начертить? (Любой выпуюаый шестиугольник.)
2. Выполнение упражнения в тетрам для самостоятельной работы ЛФ 153 (с. 88).
(Самостоятельное выполнение.)
Ш. Подведение итогов урока
Домашнее задание ![]()
Тетрадь для самостоятельной работы: № 152 (с. 88).
6 Поурочные разработки по математике
![]()
Цель: научить разбивать многоугольник на треугольники с помощью диагоналей и без них.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
|
В |
|
|
|
|
|
|
|
15 |
9 |
24 Ответ:
24
26 22
2. Родственные ряды
|
8 |
|
|
Ш |
2 |
|
5 |
8 |
п |
6 |
|
( Числа нижнего ряда получаются в результате Деления соответствующих чисел верхнего ряда на 2 и прибавления еДиницы. В верхнем ряду пропущено число 22, в нижнем ряду — 2.) З. Устный счет
(Примеры записаны на доске.) — Вычислите.
• Разность чисел 11 и 9 умножить на 0.
• Сумму чисел 35 и 36 умножить на разность чисел 20 и 19.
• Сумму чисел 38 и 52 разделить на 1.
• Число 32 умножить на разность чисел 18 и 7.
• Число 99 уменьшить в 9 раз.
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
У Бабы-яги собрались 15 внуков и внучек. Количество внучек составляет половину количества внуков. Сколько внуков и внучек у Бабы-яги? (5 внучек и 10 внуков.)
Ш. Работа по теме урока Работа по учебнику № 376 (с. 108).
![]() Выполните
задание. Какие фигуры получились? (ТреугольНИКИ.)
Выполните
задание. Какие фигуры получились? (ТреугольНИКИ.)
— Сколько треугольников? ( Четыре.)
Разбиение многоугольника на треугольники
![]()
ЛФ 377(с. 108). (Самостоятельная практическая работа.) м 378 (с. 108).
— Прочитайте задание. Как его выполнить? (Провести Диагонали.)
Для того чтобы разбить этот восьмиугольник на восемь треугольников, нужно выбрать некоторую внутреннюю точку и из нее провести отрезки в каждую вершину многоугольника.
М. Физкультминутка
V. Закрепление изученного материала Работа по учебнику М 379 (с. 108).
![]() Прочитайте задание.
Как его выполнить? (Провести из вершины остроугольного треугольника два отрезка
к противоположной стороне.)
Прочитайте задание.
Как его выполнить? (Провести из вершины остроугольного треугольника два отрезка
к противоположной стороне.)

![]() 380 (с. 108).
380 (с. 108).
(Самостоятельная практическая работа.)

![]() 381 (с. 109).
381 (с. 109).
(Самостоятельная практическая работа. Проверка в парах.) № 382 (с. 109).
![]() Начертите треугольники. Выполните
задание.
Начертите треугольники. Выполните
задание.
— Как называется отрезок, с помощью которого вы смогли из каждого треугольника получить два прямоугольных треугольника? (Высота.)
![]()
JV2 383 (С. 109).
6(Самостоятельная 0практическая 0работа. хПроверка 1в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 154, 155 (с. 89).
Урок 64. Площадь прямоугольного треугольника
Цель: подвести к пониманию способа вычисления площади прямоугольного треугольника с опорой на площадь соответствующего прямоугольника.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
Арифметический диктант
— Запишите только ответы.
![]() • Вычислите площадь квадрата со стороной
6 мм. (36 кв. мм.)
• Вычислите площадь квадрата со стороной
6 мм. (36 кв. мм.)
• Прямоугольник имеет стороны 10 см и 15 см. Найдите периметр. (50 см.)
• Длина стороны треугольника равна длине стороны квадрата. Периметр треугольника равен 24 см. Каков периметр квадрата? (32 см.)
• Как называется фигура, у которой 6 граней, 8 вершин, 12 ребер? (Куб.)
• Сколько ребер выходит у куба из каждой вершины? (З.)
• Сколько граней выходит у куба из каждого ребра? (2.)
• Какую форму имеет верхняя часть транспортира? (Полукруга.) Для чего применяется транспортир? (Для измерения углов в градусах.)
• На сколько равных частей разделена половина окружности на шкале транспортира? (На 90.)
• Если прямой угол разделить на 90 равных частей, то одна такая часть будет иметь величину... (1 градус).
Площадь прямоугольного треугольника
![]()
Ш. Работа по теме урока Работа по учебнику № 384 (с. 110).
— Выполните задание.
![]() Что можно сказать о площади
составленного прямоугольного треугольника? (Она в 2 раза больше площаДи кажДого
треугольника.) № 385 (с. 110).
Что можно сказать о площади
составленного прямоугольного треугольника? (Она в 2 раза больше площаДи кажДого
треугольника.) № 385 (с. 110).
• Прочитайте задание. Как найти площадь прямоугольника? (4 • 12 (кв. см).)
— Чему будет равна площадь прямоугольного треугольника?
(12 : 2 = 6 (кв. см).)
М. Физкультминутка
V. Закрепление изученного материала Работа по учебнику ЛГ2 386 (с. 110).
![]() Прочитайте правила.
Прочитайте правила.
— Какие из них вам помогут вычислить площадь прямоугольного треугольника? («а» и «Ь.) ЛФ 387€. 111). (Самостоятельная практическая работа. Проверка в парах.)
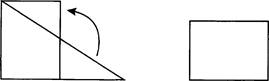
JV2 388 (С. 111).
— Рассмотрите фигуры. Какие даны треугольники? (Прямоугольные.)
— Что нам известно о нахождении площади прямоугольного треугольника? (ПлощаДь треугольника составляет половину от площаДи соответствующего прямоугольника.)
— Что нужно сделать сначала? (Измерить стороны прямоугольников.)
![]() А затем? (Вычислить тощаДи этих
прямоугольников.)
А затем? (Вычислить тощаДи этих
прямоугольников.) ![]() Что потом? (Вычислить площаДи
соответствующих треУГОЛЬНИКОВ.)
Что потом? (Вычислить площаДи
соответствующих треУГОЛЬНИКОВ.)
Ш. Подведение итогов урока Домашнее задание
Учебник: № 393 (с. 114).
Урок 65. Вычисление площади треугольника
Цель: показать, что площадь произвольного треугольника можно узнать, вычислив площадь прямоугольных треугольников, на которые можно разбить любой треугольник.
И. Организационный момент. Сообщение темы и цели урока
II. Актуализация знаний
1. Цифровой квадрат
|
|
13 |
|
|
|
|
15 |
|
|
8 |
16 |
28 Ответ:
24
23 29
2. Родственные ряды
|
2 |
4 |
З |
7 |
|
|
|
|
|
46 |
22 |
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на самих себя и вычитания числа
З. В верхнем ряду пропущено число 5, в нижнем ряду — 6.)
З. Устный счет
(Примеры записаны на доске.) ![]() Вычислите.
Вычислите.
|
(27 - |
(37+ 16) |
|
76 • 56-55 |
о: (29 + 37) |
|
(35 + 28) (34 - 34) |
(25+ 15) • 1 |
|
(44 — 43) (42 — 41) |
|
4. Логическая задача
— Решите задачу устно.
У котят и цыплят 42 ноги и 12 голов. Сколько было котят и цыплят? (9 котят и З цыпленка.)
Ш. Работа по теме урока
Работа по учебнику
№ 389, 390 (с. 112).
(Коллективное выполнение с комментированием.)
— Сформулируйте правило для нахождения площади равнобедренного треугольника. (Площадь равнобедренного треугольника равна половине произведения основания на высоту.)
Вычисление площади треугольника

lV. Физкультминутка
V. Закрепление изученного материала Работа по учебнику № 392 (с. 113).
![]() Чему равна площадь каждого такого треугольника? (Половине площаДи
соответствующего прямоугольника.)
Чему равна площадь каждого такого треугольника? (Половине площаДи
соответствующего прямоугольника.)
![]() Измерьте стороны прямоугольников. (Стороны всех прямоугольников 4 см и 2
см.)
Измерьте стороны прямоугольников. (Стороны всех прямоугольников 4 см и 2
см.)
![]() Что можно сказать об их площади?
(Площади всех прямоугольников также равны и составляют: 4 см • 2 см = 8 кв.
см.)
Что можно сказать об их площади?
(Площади всех прямоугольников также равны и составляют: 4 см • 2 см = 8 кв.
см.) ![]() Чему будет равна площадь закрашенных
треугольников? (8 кв. см: 4 кв. см.) М 395 (с. 115).
Чему будет равна площадь закрашенных
треугольников? (8 кв. см: 4 кв. см.) М 395 (с. 115).
![]() Прочитайте задание.
Что надо сделать сначала? (Найти площаДь листа бумаги: 7 • 7 = 49 (кв. см).)
Прочитайте задание.
Что надо сделать сначала? (Найти площаДь листа бумаги: 7 • 7 = 49 (кв. см).)
— Чему будет равна площадь пятидесяти единичных квадратов? (1 • 50 = 50 (кв. см).)
![]() Ответьте на вопрос задачи. (Так как общая шющаДь кваДратов больше
площаДи листа бумаги, то вырезать это число кваДратов из Данного листа бумаги
нельзя ни при каком способе вырезания.)
Ответьте на вопрос задачи. (Так как общая шющаДь кваДратов больше
площаДи листа бумаги, то вырезать это число кваДратов из Данного листа бумаги
нельзя ни при каком способе вырезания.)
— Как определить, какое число квадратов с длиной стороны 2 см можно вырезать из этого листа бумаги? (Примерный ответ. Квадрат со стороной 2 см имеет площадь 4 кв. см, поэтому максимальное число таких квадратов, которое можно вырезать из данного листа бумаги, если не учитывать возникающие при этом ограничения, можно определить с помощью деления с остатком: 49 : 4 12 (ост. 1). В лучшем случае таких квадратов можно вырезать 2 штук. На самом деле их будет меньше.)
![]() Покажите в тетради, как это сделать. Сколько квадратов реально удается
вырезать? (Девять.)
Покажите в тетради, как это сделать. Сколько квадратов реально удается
вырезать? (Девять.)
![]() Сколько еще таких квадратов можно
составить из оставшихся полосок? (Если разрезать НУЖНЫМ образом оставшиеся
полоски, то из их частей можно было бы сложить еще три таких кваДрата: 12 — 9 =
З.) М 396 (с. 115).
Сколько еще таких квадратов можно
составить из оставшихся полосок? (Если разрезать НУЖНЫМ образом оставшиеся
полоски, то из их частей можно было бы сложить еще три таких кваДрата: 12 — 9 =
З.) М 396 (с. 115).
![]() Прочитайте задание. Что надо сделать сначала? (Вычислить тощаДь листа
бумаги прямоугольной формы: 20 • 10 =
Прочитайте задание. Что надо сделать сначала? (Вычислить тощаДь листа
бумаги прямоугольной формы: 20 • 10 =
= 200 (кв. см). )
Что далее? (Надо ВЫЧиСлитЬ площаДь прямоугольного треугольника, преДварительно установив, что катеты этого треугольника имеют длину 9 см и 12 см.)
— Как найти площадь прямоугольного треугольника? (Умножить длину одного катета на половину Длины Другого катета: 9 • 6= 54 (кв. см).)
![]() Что можно вычислить
далее? (Площадь оставшихся обрезков листа: 200— 54 146 (кв. см).)
Что можно вычислить
далее? (Площадь оставшихся обрезков листа: 200— 54 146 (кв. см).)
![]() Почему сторона длиной 15 см не может выступать в роли катета? (Сторона
длиной 15 см не может выступать в роли
Почему сторона длиной 15 см не может выступать в роли катета? (Сторона
длиной 15 см не может выступать в роли ![]() катета, так как она самая Длинная из
Данных сторон.) Ш. Подведение итогов урока Домашнее задание
катета, так как она самая Длинная из
Данных сторон.) Ш. Подведение итогов урока Домашнее задание
Учебник: № 394 (с. 1 15).
Урок 66. Закрепление пройденного
Цели: развивать навыки работы с различными единицами измерения объема; проанализировать состав термина «миллилитр»; установить соотношение между кубическим метром и кубическим дециметром.
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: + З, : 2; пропущенные числа — Юи 5.)
2. Волшебные квадраты
(Волшебная сумма равна 34.)
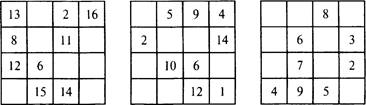
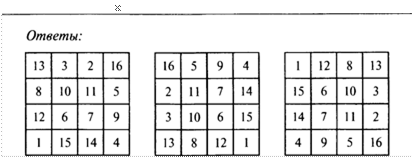
З. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Как можно сумму и разность разделить на число? Запиши соответствующие формулы. ((а + Ь) : с = а : с + Ь : с; (а — Ь) : с —
![]()
• Как можно число разделить на произведение, а произведение на число? Запиши соответствующие формулы. (а : (Ь • с) =
![]()
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Ваня живет выше Пети, но ниже Сени, а Коля живет ниже Пети. На каком этаже четырехэтажного дома живет каждый из них? (Коля — на первом, Петя — на втором, Ваня — на третьем, Сеня — на четвертом.)
Ш. Работа по теме урока Работа по учебнику ![]() 1 (с. 120).
1 (с. 120).
(Коллективное выполнение. Знакомство с понятием «миллиметр» по словарику учебника (с. I 18). )
![]() Что означает слово
«милли»? (Уменьшение исходной еДИНИЦЫ в ТОО раз.)
Что означает слово
«милли»? (Уменьшение исходной еДИНИЦЫ в ТОО раз.)
![]() Сколько миллиметров в I м? (1000 мм.)
Сколько миллиметров в I м? (1000 мм.)
![]() Можно ли, анализируя состав термина
«миллиметр», установить соотношение между метром и миллиметром? (Да.)
Можно ли, анализируя состав термина
«миллиметр», установить соотношение между метром и миллиметром? (Да.) ![]() Что
означает слово «миллилитр»? (Миллилитр — еДиница вместимости (объема), которая
составляет тысячную часть литра (1000 мл 1
Что
означает слово «миллилитр»? (Миллилитр — еДиница вместимости (объема), которая
составляет тысячную часть литра (1000 мл 1 ![]() м 2 (с. 120).
м 2 (с. 120).
![]() Сколько кубических сантиметров в I куб.
дм? ( 1000куб. см.)
Сколько кубических сантиметров в I куб.
дм? ( 1000куб. см.)
— Сколько кубических сантиметров в 1 1 л = 1000куб. см.) ![]() Сколько
миллилитров в л? (1 л =1О00ЛТ.) Значит, куб. см = I мл.
Сколько
миллилитров в л? (1 л =1О00ЛТ.) Значит, куб. см = I мл.
lV. Физкультминутка
![]()
V. изученного материала Работа по учебнику
МЗ (с. 120).
(Коллективное выполнение.)
![]() Прочитайте задание. Что нужно сделать
сначала? (Выразить объемы в кубических сантиметрах.) Решение:
Прочитайте задание. Что нужно сделать
сначала? (Выразить объемы в кубических сантиметрах.) Решение:
250 куб. см = 250 мл
4 куб. дм = 4000 куб. см = 4 мл
7 куб. дм 198 куб. см = 7198 куб. см = 7198 мл ![]() 4
(с. 120).
4
(с. 120).
(Коллективное выполнение.)
![]() Прочитайте задание. Что нужно сделать сначала? (Выразить Данные объемы в
миллилитрах.) Решение:
Прочитайте задание. Что нужно сделать сначала? (Выразить Данные объемы в
миллилитрах.) Решение:
325 мл = 325 куб. см
5 л = 5000 куб. см
7 л 500 мл = 7500 мл = 7500 куб. см 1 л мл = 1001 мл
= 1001 куб. см ![]() 120).
120).
(Коллективное выполнение.)
![]() Прочитайте задачу.
Какого она типа? (Задача на вычисление объема всего разлитого в банки варенья.)
Прочитайте задачу.
Какого она типа? (Задача на вычисление объема всего разлитого в банки варенья.)
![]() Как найти весь объем варенья? (750 • 4 + 500 • 6 = 3000 +
Как найти весь объем варенья? (750 • 4 + 500 • 6 = 3000 +
![]()
JV2 6 (с. 121).
(Коллективное
выполнение. Знакомство с понятием «кубический метр» по словарику учебника (с. 1
17). ) ![]() 7(с. 121).
7(с. 121).
— Можно ли составить куб из восьми кубиков? Покажите на рисунке. (Можно.)
— Чему равен объем куба с ребром 2 м? (2 • 2 • 2 8 (куб.
м).) ![]() 8(с. 121). (Устное выполнение.) ЛГ2
9 (с. 121).
8(с. 121). (Устное выполнение.) ЛГ2
9 (с. 121).
![]() Во сколько раз нужно увеличить 1 дм, чтобы получить м? (В 10 раз, так как
1 м = 10 Дм.)
Во сколько раз нужно увеличить 1 дм, чтобы получить м? (В 10 раз, так как
1 м = 10 Дм.)
— Во сколько раз нужно увеличить 1 кв.
дм, чтобы получить ![]() кв. м? (В 100раз, так как 1 кв. м = 100
кв. дм.)
кв. м? (В 100раз, так как 1 кв. м = 100
кв. дм.)
![]() Во сколько раз нужно увеличить 1 куб. дм, чтобы получить 1 куб. м? (В
1000раз, так как 1 куб. м = 1000 куб. дм.)
Во сколько раз нужно увеличить 1 куб. дм, чтобы получить 1 куб. м? (В
1000раз, так как 1 куб. м = 1000 куб. дм.) ![]() 10, 11 (С. 121).
10, 11 (С. 121).
(Самостоятельное выполнение. Проверка в парах.)
пройденного
![]()
М 12 (с. 122). (Устное выполнение путем подбора.) М 13 (с. 122).
(Коллективное выполнение. Знакомство с понятием «кубометр» по словарику учебника (с. 117).) Решение:
1 куб. м = 1000 куб. дм 20 куб. дм • 10 = 200 куб. дм
20 куб. дм • 5= 100 куб. дм 20 куб. дм • 50 = 1000 куб. дм
Ответ: нужно взять 50 брусков, чтобы их общий объем составил куб. м.
![]() 16 (с. 122).
16 (с. 122). ![]() Прочитайте задачу.
Какого она типа? (Задача на разность и частное.)
Прочитайте задачу.
Какого она типа? (Задача на разность и частное.)
![]() Как будете решать задачу? (Пусть одна часть — это пиломатериалы первого
склаДа, а три части — это пиломатериалы второго склаДа. )
Как будете решать задачу? (Пусть одна часть — это пиломатериалы первого
склаДа, а три части — это пиломатериалы второго склаДа. )
![]() Выполните разностное сравнение частей.
(З — 1 = 2 (ч.).)
Выполните разностное сравнение частей.
(З — 1 = 2 (ч.).)
— Сколько кубометров пиломатериалов на первом складе?
(12 : 2 = 6 (куб. м).)
— Сколько кубометров пиломатериалов на втором складе? (6 + З = 18 (куб. м).)
![]() ВЫПОЛНИТЕ проверку.
(18 : З = 6 (куб. м) шти 6 + 12 = 18(кјб. м) — разница между количеством пиломатериалов
на сюшДах.)
ВЫПОЛНИТЕ проверку.
(18 : З = 6 (куб. м) шти 6 + 12 = 18(кјб. м) — разница между количеством пиломатериалов
на сюшДах.)
Ш. Подведение итогов урока
Домашнее задание
Учебник: М 14, 15 (с. 122).
Урок 67. Закрепление пройденного
Цели: закрепить навыки работы с единицами измерения объема; установить соотношение между кубическим метром и кубическим сантиметром.
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
1. Цифровой квадрат
|
|
П |
23 Ответ: 16 |
12 |
ll |
|
|
|
|
|
19 20
![]()
2. Родственные ряды
|
7 |
2 |
|
98 |
23 |
|
З |
2 |
4 |
|
|
( Числа верхнего ряда получаются в результате умножения соответствующих чисел нижнего ряда на самих себя и вычитания числа 2. В верхнем ряду пропущено число 14, в нижнем ряду — 5.) З. Логическая задача
— Решите задачу устно.
К Айболиту
пришли на прием животные: все, кроме двух, собаки, все, кроме двух, кони, все,
кроме двух, попугаи. Сколько всего животных? ( Три: собака, конь, попугай.) Ш.
Работа по теме урока Работа по учебнику ![]() 17(с. 123).
17(с. 123).
— Прочитайте задание. Какое получилось число? (1 000 000.)
— Во сколько раз увеличилось число 1? (В 1 000 000раз.) ![]() 18(с. 123).
18(с. 123).
— Сколько кубических сантиметров в 1 куб. дм? (100006. см.)
— Во сколько раз нужно увеличить куб.
см, чтобы получить ![]() куб. дм? (В 1000раз.)
куб. дм? (В 1000раз.)
— Сколько кубических дециметров в 1 куб. м? (100006. дм.)
— Во сколько раз нужно увеличить 1 куб. дм, чтобы получить 1 куб. м? (В 1000раз.)
![]() Во сколько раз нужно увеличить 1 куб.
см, чтобы получить 1 куб. м? (В 1 ООО ООО раз, так как куб. м = 1000 • 1000 = =
1 000000 куб. см.) ЛЕ 19(с. 123).
Во сколько раз нужно увеличить 1 куб.
см, чтобы получить 1 куб. м? (В 1 ООО ООО раз, так как куб. м = 1000 • 1000 = =
1 000000 куб. см.) ЛЕ 19(с. 123).
![]() Во сколько раз нужно
увеличить см, чтобы получить м? (В 100раз.)
Во сколько раз нужно
увеличить см, чтобы получить м? (В 100раз.)
![]() Во сколько раз нужно
увеличить 1 кв. см, чтобы получить
Во сколько раз нужно
увеличить 1 кв. см, чтобы получить ![]() кв. м?(В 10 000раз.)
кв. м?(В 10 000раз.)
— Во сколько раз нужно увеличить 1 куб. см, чтобы получить 1 куб. м?(В 1 000 ОООраз.) ЛФ 20-22 (с. 123-124).
(Самостоятельное выполнение. Проверка в парах.)
М. Физкультминутка
V. Закрепление изученного материала Работа по учебнику ![]() 23 (с. 124).
23 (с. 124).
![]() Прочитайте задание. Что нужно сделать сначала? (Выразить все объемы в
кубических сантиметрах: 1 куб. м
Прочитайте задание. Что нужно сделать сначала? (Выразить все объемы в
кубических сантиметрах: 1 куб. м
Контрольная работа № 4
![]()
1 куб. дм 1 куб. см = 1 001 001 куб. см, 1 куб. м 100 куб. см — = 1 000 100куб. см, 100 куб. дм 100 куб. см = 100 100куб. см,
1 куб. м 1 куб. дм 100куб. см = 1 001 100 куб. см.)
— Выполните задание. (1 куб. м 1 куб. дм 100 куб. см,
1 куб. м 1 куб. дм 1 куб. см, 1 куб. м 100куб. см, шкуб. дм 100куб. см.) ![]() 24 (с. 124).
24 (с. 124).
![]() Прочитайте задание. Что нужно сделать сначала? (Выразить 1 кубометр в
кубических сантиметрах: 1 куб. м
Прочитайте задание. Что нужно сделать сначала? (Выразить 1 кубометр в
кубических сантиметрах: 1 куб. м ![]() =
= ![]() см.)
см.)
— Как найти ответ задачи? (С помощью кратного сравнения:
1 000000: = ТОО (куб.).) м 27(с. 124).
— Прочитайте задание. О какой единице объема идет речь? (О кубическом Дециметре: 1 куб. м = 1000 куб. дм, 1 куб. дм =
= 1000куб. см.)
Ш. Подведение итогов урока домашнее задание
Учебник: № 25, 26 (с. 124).
Цели: проверить знания и умения учащихся; развивать навыки самостоятельной работы.
(Текст контрольной работы выдается каждому ученику на отдельном листочке.)
Вариант 1
1. Если самолет летит со скоростью 950 юи/ч, то сможет ли он за 3 ч преодолеть расстояние 2800 км?
2. Реши задачу. Вычисли и запиши ответ.
В одном баке помещается на 24 л воды больше, чем в другом. Сколько литров воды помещается в каждом баке, если для заполнения первого бака требуется 10 ведер воды, а для заполнения второго — 7 таких же ведер?
3. Реши задачу. Вычисли и запиши ответ.
Одна бригада дорожных рабочих отремонтировала 360 кв. м дорожного полотна за З ч, а другая — 440 кв. м такого же дорожного полотна за 4 ч. Какая бригада работала с большей производительностью?
4. Вычисли значение следующего выражения, используя вычисления столбиком.
8 • 236 + : 8
![]()
![]()
5. Начерти многоугольник, из каждой вершины которого выходит пять диагоналей. Сколько всего диагоналей у этого многоугольника?
Вариант 2
![]() . Если самолет летит со скоростью 850
км/ч, то сможет ли он за 3 ч преодолеть расстояние 2600 км?
. Если самолет летит со скоростью 850
км/ч, то сможет ли он за 3 ч преодолеть расстояние 2600 км?
2. Реши задачу. Вычисли и запиши ответ.
В одном баке помещается на 18 л воды больше, чем в другом. Сколько литров воды помещается в каждом баке, если для заполнения первого бака требуется 20 бидонов воды, а для заполнения второго — 14 таких же бидонов?
З. Реши задачу. Вычисли и запиши ответ.
Одна бригада грузчиков разгрузила 390 мешков с удобрениями за 3 ч, а другая — 480 таких же мешков за 4 ч. Какая бригада работала с большей производительностью?
4. Вычисли значение следующего выражения, используя вычисления столбиком.
9 • 234 + : 9
5. Начерти многоугольник, из каждой вершины которого выходит шесть диагоналей. Сколько всего диагоналей у этого многоугольника?
Урок 69, Деление на однозначное число столбиком
Цель: познакомить с делением на однозначное число столбиком.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
12 |
9 |
|
|
|
![]() 21 Ответ:
21 Ответ:
23
25 19
2. Родственные ряды
|
6 |
12 |
18 |
27 |
|
|
З |
5 |
|
|
15 |
Деление на однозначное число столбиком
![]()
( Числа верхнего ряда получаются в результате умножения соот ветствующих чисел нижнего ряда на З и вычитания числа З. В верхнем ряду пропущено число 42, в нижнем ряду — 7.)
З. Устный счет
(Примеры записаны на доске.)
— Выполните действия, сравните приемы вычислений каждой пары выражений.
|
26 • з |
46 : 2 |
|
32 • 2 |
36 : 2 |
|
69 : 3 |
78 : 3 |
|
7 , 12 |
14 - 6 |
4. Разминка
— Закончите рассуждения, если это возможно.
• Число, месяц и год последнего дня ХХ в. . (31 Декабря 200Ог.).
•
Установите правило, по которому составлен ряд чисел, и назовите еще три
числа: 3, 5, 7, 9, 11, 13,![]()
• На столе лежат три карандаша разной длины. Чтобы удалить из середины самый длинный, не трогая его, нужно... (переложить один из тех, что короче).
5. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Приехали 100 туристов. Из них 10 туристов не знают ни немецкого, ни французского. Немецкий знают 75 туристов, французскиЙ — 83 туриста. Сколько туристов знает французский и немецкий? (68.)
Ш. Работа по теме урока Работа по учебнику
ЛГ2
1 (с.![]()
(Коллективное выполнение.)
![]() Прочитайте задание. Как найти неполное
частное? (С помощью соответствующего случая Деления: 56 : 7 = 8.)
Прочитайте задание. Как найти неполное
частное? (С помощью соответствующего случая Деления: 56 : 7 = 8.) ![]() Какой можно
сделать вывод? (Делимое этого табличного случая определяется как наибольшее
число, которое Делится нацело на число 7 и не превосхоДит числа 59.)
Какой можно
сделать вывод? (Делимое этого табличного случая определяется как наибольшее
число, которое Делится нацело на число 7 и не превосхоДит числа 59.)
![]() Что мы узнаем дальше? (Остаток получаем
так: 59 — 56 =
Что мы узнаем дальше? (Остаток получаем
так: 59 — 56 = ![]() Что можно сказать об остатке? (Остаток меньше
Делителя.)
Что можно сказать об остатке? (Остаток меньше
Делителя.)
![]()
(Коллективное выполнение с комментированием.)
![]()
* С этого урока работа ведется по второй части учебника.
Какие числа вы записали? (57, 58, 59, 60, 6], 62.)
— Что можно сказать об остатках? (Остатки изменяются от 1 до 6.)
![]()
![]() Какой наибольший
остаток может получиться при делении на число 7? (6.)
Какой наибольший
остаток может получиться при делении на число 7? (6.)
![]() Как найти наибольшее число, которое при
делении на число 7 дает в неполном частном однозначное число? (63 + 6 =
Как найти наибольшее число, которое при
делении на число 7 дает в неполном частном однозначное число? (63 + 6 = ![]() 69.)
69.)
Это значит, что при делении на 7 всех чисел, которые меньше числа 69, в неполном частном будет получаться однозначное число. Запись в столбик будет состоять из одного шага, и выполняться деление будет, как и при записи в строчку, на основе соответствующего табличного случая деления.
![]()
(Устное выполнение.)
— Для чего нужно уметь определять границы? (Это поможет до выполнения Деления устанавливать число цифр в записи неполного частного.)
![]() Можно ли такой же
подход использовать при делении трехзначных чисел? (Да, при Делении на число 7
эти границы опреДеляются числом 699.)
Можно ли такой же
подход использовать при делении трехзначных чисел? (Да, при Делении на число 7
эти границы опреДеляются числом 699.)
М. Физкультминутка
V. Закрепление изученного материала
1. Выполнение упражнений в тетради для самостоятельной работы
![]()
(Самостоятельное выполнение. Проверка в парах.)
2. Работа
по учебнику ![]() 7-8).
7-8).
(Устное выполнение.)
![]()
(Коллективное выполнение с записью на доске.) ![]() 9-11
(с. 9).
9-11
(с. 9).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № З (с. 4).
![]()
* С этого урока работа ведется по тетради для самостоятельной работы № 2.
70. Деление на однозначное число столбиком
![]()
Урок 70. Деление на однозначное число столбиком
Цель: развивать умение выполнять деление на однозначное число столбиком.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
Арифметический диктант
![]() Запишите только ответы.
Запишите только ответы.
![]() Увеличьте 4 в 8 раз. (32.)
Увеличьте 4 в 8 раз. (32.)
![]() Найдите значение суммы чисел 48 и 36. (84.)
Найдите значение суммы чисел 48 и 36. (84.)
![]() Найдите значение частного чисел 81 и 9. (9.)
Найдите значение частного чисел 81 и 9. (9.)
![]() Значение произведения двух чисел равно 64. Первый множитель — 8. Найдите
второй множитель. (8.)
Значение произведения двух чисел равно 64. Первый множитель — 8. Найдите
второй множитель. (8.)
![]() Делимое — 56, делитель — 7. Чему равно значение частною? (8.)
Делимое — 56, делитель — 7. Чему равно значение частною? (8.)
![]() Значение частного двух чисел равно 9, делитель — 7. Найдите делимое.
(63.)
Значение частного двух чисел равно 9, делитель — 7. Найдите делимое.
(63.)
![]() Найдите значение разности чисел 120 и 19. (101.)
Найдите значение разности чисел 120 и 19. (101.)
![]() Делимое — 54, делитель — 6. Найдите значение частного. (9.)
Делимое — 54, делитель — 6. Найдите значение частного. (9.)
![]() Периметр прямоугольника 20 см, ширина 3 см. Определите длину
прямоугольника. ( 7 см.)
Периметр прямоугольника 20 см, ширина 3 см. Определите длину
прямоугольника. ( 7 см.)
![]() Ширина прямоугольника 9 см, это на 12 см меньше, чем длина. Вычислите
периметр прямоугольника. (60 см.) Ш. Работа по теме урока Работа по учебнику ЛФ
12 (с. 9).
Ширина прямоугольника 9 см, это на 12 см меньше, чем длина. Вычислите
периметр прямоугольника. (60 см.) Ш. Работа по теме урока Работа по учебнику ЛФ
12 (с. 9).
![]() Выполните задание.
Выполните задание.
— Назовите результат деления. (Неполное частное равно 0, а
остаток равен Делимому. ) ![]() 13 (с. 10).
13 (с. 10).
(Устное выполнение.)
![]() Рассмотрите запись.
Рассмотрите запись.
![]() Что можно сказать о
втором промежуточном делимом? (Оно меньше Делителя.)
Что можно сказать о
втором промежуточном делимом? (Оно меньше Делителя.)
![]() Какую цифру в этом случае нужно записать в неполном частном? (0.) ЛЕ 14
(с. 10).
Какую цифру в этом случае нужно записать в неполном частном? (0.) ЛЕ 14
(с. 10).
(Самостоятельное выполнение. Взаимопроверка.)
— Используйте следующие дополнительные пары для отрабожи навыка деления столбиком: 364 : 6, 485 : 8, 756 : 7.
![]()
lV. Физкультминутка
V. Закрепление изученного материала Работа по учебнику ЛФ 15 (с. 10).
![]() Прочитайте задание.
Что означает выражение «что в З раза больше»? (Это уменьшение в несколько раз в
косвенной форме,
Прочитайте задание.
Что означает выражение «что в З раза больше»? (Это уменьшение в несколько раз в
косвенной форме,
т. е. в З раза меньше: 351 : З = 117.) № 16€. 10).
![]() Прочитайте задание.
Как найти длину второй стороны?
Прочитайте задание.
Как найти длину второй стороны? ![]() 73(см).)
73(см).)
![]() Как найти периметр прямоугольника? ((438см + 73 см) • 2 = = = тм 22 см.)
Как найти периметр прямоугольника? ((438см + 73 см) • 2 = = = тм 22 см.)
![]() 17(с. 10).
17(с. 10).
![]() Прочитайте задание. Как найти длину
второй стороны? (455: 7=65 (мм).)
Прочитайте задание. Как найти длину
второй стороны? (455: 7=65 (мм).)
![]() Как найти тоща.дь прямоупуљника? (455 •
65 = 29575 (кв. мм).)
Как найти тоща.дь прямоупуљника? (455 •
65 = 29575 (кв. мм).) ![]() 18 (с. 10).
18 (с. 10).
![]() Вспомните правило вычисления площади квадрата. Как найти площадь
квадрата со стороной 12 см? (12 см • 12 см — — 144 (кв. см).)
Вспомните правило вычисления площади квадрата. Как найти площадь
квадрата со стороной 12 см? (12 см • 12 см — — 144 (кв. см).)
— Как вычислить площадь треугольника, если она меньше в 9 раз, чем площадь квадрата? (144 : 9 = 16 (кв. см).)
Ш. Подведение итогов урока
Тетрадь для самостоятельной работы: № 4 (с. 4).
Урок 71 , Число цифр в записи неполного частного
Цель: научить определять число цифр в записи неполного частного до выполнения деления с остатком.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: : З, • 2; пропущенные числа — 5 и 10.)
71 . Число цифр в записи неполного частного
 Ответ:
Ответ:
З. Родственные ряды
|
2 |
5 |
|
6 |
|
|
15 |
18 |
|
l9 |
23 |
( Числа нижнего ряда на 13 больше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 10, в нижнем ряду — 14.)
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
За три пакета молока и две пачки творога заплатили 38 руб. Сколько стоит пакет молока, если он дороже пачки творога на руб.? (Пакет молока стоит 8руб.) lll. Работа по теме урока 1. Работа по учебнику м 19€. 11). (Устное выполнение.) № 20 (с. 11).
(Коллективное выполнение с комментированием у доски.)
Обозначим первое промежуточное делимое с помощью дуги и посмотрим, сколько цифр осталось за пределами этой дуги.
— Сколько цифр должно остаться за пределами дуги, если первое промежуточное делимое выражает число десятков? (ОДна.)
![]() Какие случаи деления вы выписали? (487 :
8, 254 : б, 83 : 7.)
Какие случаи деления вы выписали? (487 :
8, 254 : б, 83 : 7.) ![]() Сколько цифр будет в записи неполного
частного во всех этих случаях? (Две.)
Сколько цифр будет в записи неполного
частного во всех этих случаях? (Две.)
2. Выполнение упражнений в тетради для самостоятельной ра-
![]()
(Самостоятельное выполнение. Проверка с записью решения на доске.)
З. Работа по учебнику ![]() (с. 11).
(с. 11).
(Коллективное выполнение.)
М. Физкультминутка
![]()
V. Закрепление изученного материала
1. Выпшшение упрахшеюш в тетрам для самостятельной работы М 7€. 5).
(Самостоятельное выполнение.)
2. Работа по учебнику М 22 (с. 12).
— Прочитайте задание. Какую цифру нужно поставить вместо звездочки? (9.)
![]() Объясните свой ответ. (Примерный ответ. Так как неполное частное должно
быть трехзначным, то первое промежуточное делимое должно выражать число сотен.
Учитывая, что само делимое является трехзначным, это возможно лишь в том
случае, когда первое промежуточное делимое яњляется числом из разряда сотен, т.
е. когда это число не меньше делителя. Поскольку делителем является число 9, то
и в разряде сотен делимого должно находиться число 9.) М 23 (с. 12).
Объясните свой ответ. (Примерный ответ. Так как неполное частное должно
быть трехзначным, то первое промежуточное делимое должно выражать число сотен.
Учитывая, что само делимое является трехзначным, это возможно лишь в том
случае, когда первое промежуточное делимое яњляется числом из разряда сотен, т.
е. когда это число не меньше делителя. Поскольку делителем является число 9, то
и в разряде сотен делимого должно находиться число 9.) М 23 (с. 12).
— Прочитайте задание. Как должно
определяться первое неполное делимое? (Первыми двумя цифрами в записи Делимого,
![]() иначе
не получится трехзначное неполное частное.)
иначе
не получится трехзначное неполное частное.)
![]() Какая цифра может стоять на первом месте в записи делимого? ( Так как в
роли Делителя выступает чисто 2, то на первом
Какая цифра может стоять на первом месте в записи делимого? ( Так как в
роли Делителя выступает чисто 2, то на первом ![]() месте в записи
Делимого может стоять только цифра 1.)
месте в записи
Делимого может стоять только цифра 1.)
— Каким получится неполное частное, если будут стоять другие цифры? (Если будут стоять Другие цифры, то неполное частное получится четырехзначным.) — Разделите получившееся число на 2.
![]() 24 (с. 12).
24 (с. 12).
![]() Прочитайте задание. Какие это могут быть числа? (Это могут быть любые
трехзначные числа, запись которых Ношнается с цифр 7, 8 или 9.) № 25 (с. 12).
Прочитайте задание. Какие это могут быть числа? (Это могут быть любые
трехзначные числа, запись которых Ношнается с цифр 7, 8 или 9.) № 25 (с. 12).
![]() Прочитайте задание.
С какой цифры должны начинаться искомые числа? (С любой из цифр от 1 до 6.)
Прочитайте задание.
С какой цифры должны начинаться искомые числа? (С любой из цифр от 1 до 6.)
![]() Как будут определяться первые
промежуточные делимые? (Первыми двумя цифрами, они будут выражать число
Десятков.) М 26 (с. 12).
Как будут определяться первые
промежуточные делимые? (Первыми двумя цифрами, они будут выражать число
Десятков.) М 26 (с. 12).
— Прочитайте вопросы.
![]() Каким может быть
первое промежуточное делимое, если делитель является однозначным числом? (Либо
оДнозначным числом (если оно не меньше Делителя), либо Двузначным числом.)
Каким может быть
первое промежуточное делимое, если делитель является однозначным числом? (Либо
оДнозначным числом (если оно не меньше Делителя), либо Двузначным числом.)
71 . Число цифр в записи неполного частного
![]()
— Что это означает? (Старшим разрядом в неполном частном
будет либо разряд сотен, либо разряд Десятков. Таким образам, однозначное
неполное частное получиться не может.) ![]() Как еще можно это доказать? (Примерный
ответ. Предположим, что неполное частное — самое большое однозначное число и
делитель — самое большое однозначное число. Перемножим их: 9 • 9 = 81. Прибавим
к этому числу самый большой остаток, который может получиться при делении на
однозначное число: 81 + 8 = 89. Число 89 является двузначным числом, значит,
при делении трехзначного числа на однозначное никогда не получится однозначное
неполное частное.)
Как еще можно это доказать? (Примерный
ответ. Предположим, что неполное частное — самое большое однозначное число и
делитель — самое большое однозначное число. Перемножим их: 9 • 9 = 81. Прибавим
к этому числу самый большой остаток, который может получиться при делении на
однозначное число: 81 + 8 = 89. Число 89 является двузначным числом, значит,
при делении трехзначного числа на однозначное никогда не получится однозначное
неполное частное.) ![]() 12).
12).
— Если делимое — четырехзначное число, а в неполном частном должно получиться трехзначное число, как будет определяться первое промежуточное делимое? (Первыми двумя цифрами в записи исходного Делимого.)
![]() Какие это могут быть цифры? ( чтобы первое неполное Делимое бьио не
меньше 23.)
Какие это могут быть цифры? ( чтобы первое неполное Делимое бьио не
меньше 23.)
![]() Какое число будет самым маленьким? (2300, оно при Делении на число 23
дает в результате трехзначное число 100.)
Какое число будет самым маленьким? (2300, оно при Делении на число 23
дает в результате трехзначное число 100.) ![]() 12).
12).
— Как будет определяться первое промежуточное делимое в этом случае? (Первыми тремя цифрами в записи исходного ДИ ИМОГО.)
![]() В каких случаях это возможно? (Когда первые две цифры делимого Дают
число меньше Делителя — числа 23.)
В каких случаях это возможно? (Когда первые две цифры делимого Дают
число меньше Делителя — числа 23.)
![]() Приведите примеры таких чисел. (1234, 1589, 2010, 2157, 2299 И Т. Д.)
Приведите примеры таких чисел. (1234, 1589, 2010, 2157, 2299 И Т. Д.)
![]() Какое число из них является самым большим? (2299. Это число при Делении
на число 23 в неполном частном дает двузначное число 99 (в остатке будет 22).)
Какое число из них является самым большим? (2299. Это число при Делении
на число 23 в неполном частном дает двузначное число 99 (в остатке будет 22).) ![]() 29
(с. 12).
29
(с. 12).
(Устное выполнение.)
З. Выполнеште упражнений в тетрадщ для самостотељной рабом
![]()
(Самостоятельное выполнение. Проверка в парах.) ![]() 11
(с. 6).
11
(с. 6).
Решение:
1) 8 • 23 = 184 (ламп.) — в 23 упаковках; 2) 184 : 7 = 26 (ост. 2).
Ответ: лампочек хватит на 26 люстр.
Хватит ли этого количества лампочек, если для каждой люстры необходимо 7 лампочек? (Не хватит.) Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 9, 10 (с. 6).
Урок 72. Деление на двузначное число столбиком
Цель: развивать умение делить на двузначное число с остатком столбиком.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
1. Устный счет
(Уравнения записаны на доске.)
— Найдите неизвестный множитель.
![]() 36
• х = 0
36
• х = 0
41 • х = 43 27 = 27 • х — Вычислите.
• Произведение чисел: 18 и 4, 9 и П, 47 и 2. (72, 99, 94.)
• Частное чисел: 33 и 3, 95 и 5, 91 и 7. (11, 19, 13.)
• Во сколько раз 64 больше 16, 9 меньше 99? (В 4 раза, в 11 раз.)
• Сумму чисел 63 и 15 разделите на 6. (13.)
• Какое число разделили на 12 и получили 5? (60.)
• Какое число умножили на 3 и получили 69? (23.)
• Назовите число, которое больше: 13 в 6 раз, 25 в 3 раза, 19
“ раза. (78, 75, 76.)
• Назовите число, которое меньше: 84 в 7 раз, 95 в 19 раз, 80 в 5 раз, 70 в 14 раз. (12, 5, 16, 5.)
2. Письменный опрос
(Вопросы даны на отдельных листочках.)
• На какое число деление невозможно? (Деление натурального числа на О невозможно. Деление числа 0 на число О невозможно.) • Какие правила выполнения действий с числом 0 тебе известны? (Примерный ответ. Если одно из двух слагаемых равно 0, то значение суммы равно другому слагаемому. Если из числа вычесть 0, то получится число, из которого вычитали. Если уменьшаемое и вычитаемое равны, то значение
Деление на двузначное число столбиком
![]()
разности равно 0. Если один из множителей равен числу 0, то значение произведения также равно 0. При делении числа 0 на любое натуральное число в результате получается число 0.)
З. Логическая задача
• Решите задачу устно.
Имеется несколько поросят одинаковой массы и несколько ягнят одинаковой массы. Три поросенка и два ягненка весят 22 кг, а два поросенка и три ягненка — 23 кг. Сколько весит один поросенок и один ягненок? (4 кг и 5 кг.)
Ш. Работа по теме урока 1. Работа по учебнику м зо (с. 13).
— Прочитайте задание. Что нужно сделать для того, чтобы найти искомое число? (Последовательно умножать число 23 на числа 1, 2, З, 4, 5... до тех пор, пока не получится число, которое больше, чем число 117.)
![]() Какое число будет искомым? (5.)
Какое число будет искомым? (5.)
— Была ли необходимость умножать на числа 1, 2, 3? (Нет.)
В тех случаях, когда результат будет заведомо меньше числа 1 7, умножение можно не выполнять.
![]() Что вы находили
описанным способом? (Наибольшее число, которое при умножении на 23 дает в
результате число, не превосходящее 117, т. е. неполное частное при Делении
числа 117на 23.)
Что вы находили
описанным способом? (Наибольшее число, которое при умножении на 23 дает в
результате число, не превосходящее 117, т. е. неполное частное при Делении
числа 117на 23.)
![]() С чем мы познакомились в ходе выполнения этот задания? (С одним из
способов подбора однозначного неполного частного, который можно применять при
выполнении Деления столбиком.) М 31 (с. 13).
С чем мы познакомились в ходе выполнения этот задания? (С одним из
способов подбора однозначного неполного частного, который можно применять при
выполнении Деления столбиком.) М 31 (с. 13).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
2. Выполнекше упражнений в тегрщщ для самостоюельной рабшы м 13, 14 (с. 7).
(Самостоятельное выполнение. Проверка в парах.) lV. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику м 32 (с. 13).
— Прочитайте задание. Что нужно сделать? (ПоДобрать однозначное неполное частное.)
— Какие числа предложены? ( четные.)
В чем смысл такого способа подбора? (Примерный ответ. Сначала делитель нужно последовательно умножать только на четные однозначные числа, а не на все однозначные числа, как это предлагалось ранее.)
![]() Сколько таких
случаев умножения нужно рассмотреть? (Умножение нужно выполнять до тех пор,
пока в результате вычислений первый раз не получится число, которое больше
Делителя.)
Сколько таких
случаев умножения нужно рассмотреть? (Умножение нужно выполнять до тех пор,
пока в результате вычислений первый раз не получится число, которое больше
Делителя.)
![]() Какой из предложенных в задании
случаев умножения рассматривать уже не нужно? (На число 8, так как число,
получившееся при умножении числа 17 на предыдущее однозначное Двузначное число,
больше числа 17.)
Какой из предложенных в задании
случаев умножения рассматривать уже не нужно? (На число 8, так как число,
получившееся при умножении числа 17 на предыдущее однозначное Двузначное число,
больше числа 17.)
— Что нужно делать далее? (Умножать уже не на следующее Двузначное число, а на предыдущее однозначное нечетное число, в Данном случае на число 5.)
![]() Выполните умножение. (17 • 5 = 85.)
Выполните умножение. (17 • 5 = 85.)
![]() Будет ли число 5 искомым неполным частным? Ща, так
Будет ли число 5 искомым неполным частным? Ща, так ![]() как в
результате умножения числа [7 на 5 получилось ЧИСлО, которое не превосходит
Делимое (89). )
как в
результате умножения числа [7 на 5 получилось ЧИСлО, которое не превосходит
Делимое (89). )
![]() Нужно ли в этом случае рассматривать число 4 в качестве предполагаемого
неполного частного? (Нет. ПреДшествующее четное однозначное число будет
неполным частным, если при умножении на нечетное однозначное число получится
число, которое больше Делимого.) № 33 (с. 13).
Нужно ли в этом случае рассматривать число 4 в качестве предполагаемого
неполного частного? (Нет. ПреДшествующее четное однозначное число будет
неполным частным, если при умножении на нечетное однозначное число получится
число, которое больше Делимого.) № 33 (с. 13).
(Самостоятельное выполнение. Проверка в парах.) № 34 (с. 14).
(Выполнение в соответствии с заданием.)
![]() Как с помощью таблицы подобрать неполное частное для случая деления
числа 79 на число 16? (При заполнении таблицы слева направо число, которое
больше 79, первый раз встречается как значение произведения чисел 16 и 6: 16 •
6 = 96. Это означает, что искомым неполным частным может быть либо число 4,
либо 5.)
Как с помощью таблицы подобрать неполное частное для случая деления
числа 79 на число 16? (При заполнении таблицы слева направо число, которое
больше 79, первый раз встречается как значение произведения чисел 16 и 6: 16 •
6 = 96. Это означает, что искомым неполным частным может быть либо число 4,
либо 5.)
![]() Как определить,
какое из этих чисел является искомым? (Сделаем проверку для числа 4, вычислим
предполагаемый остаток: 79 — 64 = 15. Так как полученный остаток оказался
меньше Делителя, то число 4 и является искомым неполным частным.)
Как определить,
какое из этих чисел является искомым? (Сделаем проверку для числа 4, вычислим
предполагаемый остаток: 79 — 64 = 15. Так как полученный остаток оказался
меньше Делителя, то число 4 и является искомым неполным частным.)
— Нужно ли выполнять проверку для числа 5? (Нет.) м 35 (с. 14).
(Самостоятельное выполнение.)
Алгоритм деления столбиком
![]()
ЛГ2З6 (с. 14). (Самостоятельное
выполнение. Проверка в парах.) ![]() 14).
14).
Решение: 155 : = 12 (ост. 11).
Ответ: можно составить 12 наборов.
2. Выполнение упражнений в тетради для самостоятељной
работн ![]() 15(с. 8). (Самостоятельное выполнение.
Проверка в парах.) М 17(с. 9).
15(с. 8). (Самостоятельное выполнение.
Проверка в парах.) М 17(с. 9).
![]() Прочитайте задание. Что нужно сделать
сначала? (Привести Данные к общим еДиницам измерения.)
Прочитайте задание. Что нужно сделать
сначала? (Привести Данные к общим еДиницам измерения.) ![]() Решите задачи.
Решите задачи.
М 18 (с. 9).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № l6 (с. 8).
Урок 73, Алгоритм деления столбиком
Цель: познакомить с алгоритмом деления столбиком.
1. Организационный момент. Сообщение темы и цели урока
11. Актуализация знаний
1. Цифровой квадрат
|
|
|
Ответ: 15 |
8 |
1 1 |
|
|
|
10 |
5 |
18 16
2. Родственные ряды
|
|
23 |
|
|
25 |
|
2 |
|
6 |
|
|
( Числа нижнего ряда на 9 меньше соответствующих чисел верхнего ряда. В верхнем ряду пропущено число 15, в нижнем ряду — 16.) З. Устный счет
(Примеры записаны на доске.)

![]() кв. мм = 25 кв. см 2 кв. мм
кв. мм = 25 кв. см 2 кв. мм
![]() . кв. дм ... кв. см = 723 кв. см
. кв. дм ... кв. см = 723 кв. см
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
В трех ящиках 300 кг апельсинов. Масса апельсинов первого ящика составляет половину массы апельсинов второго ящика и треть массы апельсинов третьего ящика. Сколько апельсинов в каждом ящике? (50 кг, 100 кг, 150 кг соответственно.) Ш. Работа по теме урока Работа по учебнику
![]() 38-40 (с. 15-16).
38-40 (с. 15-16).
(Коллективное выполнение с комментированием.)
М. Физкультминутка
V. Закрепление изученного материала
Выполнение упражнений в тетради для самостоятельной работы
![]() 19 (с. 10). (Самостоятельное выполнение.
Проверка.) М 20 (с. 10).
19 (с. 10). (Самостоятельное выполнение.
Проверка.) М 20 (с. 10).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 21 (с. 11).
Урок 74. Алгоритм деления столбиком
Цель: научить применять алгоритм деления столбиком.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
Арифметический диктант
— Запишите только ответы.
• Какое число больше 6 в 8 раз? (48.)
• 6 увеличьте в 9 раз. (54.)
• Во сколько раз 24 больше 6? (В 4 раза.)
• Уменьшите 36 в 9 раз. (4.)
• Найдите произведение чисел 8 и 7. (56.)
Сокращенная форма записи деления столбиком
![]()
• Найдите частное чисел 81 и 9. (9.)
• 9 умножьте на 3. (27.)
• 21 разделите на 7. (З.)
• 6 увеличьте на 9. (15.)
• 12 уменьшите в З раза. (4.)
• 12 уменьшите на 3. (9.)
• Во сколько раз 49 больше 7? (В 7раз.)
• Какое число больше 9 в 2 раза? (18.)
• Найдите частное чисел 18 и 6, 72 и 8. (З, 9.)
• Найдите произведение чисел 9 и 4, 7 и 4. (36, 28.)
• Какое число надо умножить на 7, чтобы получить 56? (8.)
Ш. Работа по теме урока Работа по учебнику Лё 41 (с. 16-17).
(Выполнение с комментированием. Знакомство с алгоритмом деления столбиком по словарику учебника (с. 118).) lV. Физкультминутка
М. Закрепление изученного материала Работа по учебнику № 42 (с. 17). (Самостоятельное выполнение. Взаимопроверка.) М 43 (с. 17).
— Прочитайте задачу. Как вы будете рассуждать? (Пусть одна
часть быаа в одном рулоне, а семь частей — в другом рулоне.) ![]() Сколько
всего частей? (1 + 7= 8 (ч.).)
Сколько
всего частей? (1 + 7= 8 (ч.).)
— Сколько метров пленки в одном рулоне? (864 : 8 = 108
(м).) ![]() Сколько метров пленки в другом рулоне?
(108 • 7= 756 (м).)
Сколько метров пленки в другом рулоне?
(108 • 7= 756 (м).)
— Сделайте проверку. (108 + 765 = 864 (м). )
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 22 (с. 11).
Урок 75. Сокращенная форма записи деления столбиком
Цель: научить пользоваться сокращенной формой записи деления столбиком.
1. Организационный момент. Сообщение темы и цели урока
![]()
ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
19 Ответ: 20 |
9 |
|
|
|
|
13 |
7 |
22 17
2. Родственные ряды
|
2 |
5 |
7 |
4 |
|
|
В |
28 |
|
23 |
8 |
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнегоряДа на 5 и прибавления числа З. В верхнем ряду пропущено число 1, в НИЖНејИ ряду — 38.)
З. Логическая задача
— Решите задачу устно.
Собака и поросенок имеют такую же массу, что и пять ящиков. Масса поросенка равна массе четырех кошек. Две кошки и поросенок имеют такую же массу, что и три ящика. Массе скольких кошек равна масса одной собаки? (Примерный ответ. Поросенок в 4 раза тяжелее кошки. Масса шести кошек равна массе трех ящиков, так как масса одного поросенка равна массе четырех кошек, т. е. масса двух кошек равна массе одного ящика, масса пяти ящиков равна массе десяти кошек, а масса поросенка равна массе четырех кошек, т. е. масса собаки равна массе шести кошек.)
Ш. Работа по теме урока Работа
по учебнику ![]() 44 (с. 18).
44 (с. 18).
(Коллективное выполнение с комментированием.)
![]() Рассмотрите записи. Чем они отличаются? (Во второй записи не привоДится
этап, на котором требуется разДелить меньшее число (27) на большее число
(28).). Лб 45(с. 18).
Рассмотрите записи. Чем они отличаются? (Во второй записи не привоДится
этап, на котором требуется разДелить меньшее число (27) на большее число
(28).). Лб 45(с. 18).
(Самостоятельное выполнение. Проверка.)
— Какие записи можно отнести к сокращенным? (5150 : 17, 5260: 17.)
![]() Можно ли при делении 5320 на 17 использовать сокращенную форму записи?
(Нет.)
Можно ли при делении 5320 на 17 использовать сокращенную форму записи?
(Нет.)
Если ни на одном этапе не требуется делить меньшее число на большее, то сокращенную форму записи применять нельзя.
Поупражняемся в делении столбиком
![]()
(Самостоятельное выполнение. Проверка в парах.)
М. Физкультминутка
V. Закрепление изученного материала Работа по учебнику Л) 48 (с. 19).
(Самостоятельное выполнение. Проверка в парах.) ![]() 49,
50 (с. 19).
49,
50 (с. 19).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
И. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 22—24 (с. 12).
Урок 76. Поупражняемся в делении столбиком
Цель: закрепить навыки деления столбиком.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Закономерность
(Закономерность: : 2, — З; пропущенные числа — 5 и 2.)
2. Повторекше нумерации
![]() Чем похожи и чем отличаются числа каждой
пары?
Чем похожи и чем отличаются числа каждой
пары?
105 и 15, зоо и 30, 803 и 405, 204 и 240.
![]() Прочитайте числа.
Прочитайте числа.
487, 308, 720, 109, 111.
![]() Сколько цифр потребовалось для записи каждого
числа?
Сколько цифр потребовалось для записи каждого
числа? ![]() Прочитайте числа, составьте другие
числа, записанные теми же цифрами.
Прочитайте числа, составьте другие
числа, записанные теми же цифрами.
562, 248, 309, 871, 830.
Ш. Работа по теме урока
1. Выполиение упрахшения в тетрац для самостоятельной работы ЛФ 25 (с. 13).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]()
(Самостоятельное выполнение. Проверка в парах.) lV. Физкультминутка
V. Закрепление изученного
материала Работа по учебнику ![]() 54 (с. 20). (Самостоятельное выполнение.)
ле 55 (с. 20).
54 (с. 20). (Самостоятельное выполнение.)
ле 55 (с. 20).
![]() Прочитайте задание.
Как найти первое промежуточное делимое? (Сначала нужно найти наименьшее
промежуточное Делимое: 4 • 9 = 36. Если взять промежуточное Делимое меньше, чем
36, то первая цифра в записи неполного частного будет меньше 4. Таким образом,
число 36 — это наименьшее первое промежуточное Делимое.)
Прочитайте задание.
Как найти первое промежуточное делимое? (Сначала нужно найти наименьшее
промежуточное Делимое: 4 • 9 = 36. Если взять промежуточное Делимое меньше, чем
36, то первая цифра в записи неполного частного будет меньше 4. Таким образом,
число 36 — это наименьшее первое промежуточное Делимое.)
— Что нужно определить дальше? (Наибольшее первое промежуточное Делимое, т. е. наименьшее число, которое при делении на число 9 дает число 5.)
![]() Какое это будет
число? (5 • 9 = 45. Искомое промежуточное Делимое должно быть меньше этого
числа, т. е. самое большое его ЗНачение — 44.)
Какое это будет
число? (5 • 9 = 45. Искомое промежуточное Делимое должно быть меньше этого
числа, т. е. самое большое его ЗНачение — 44.)
![]() Выполните деление столбиком числа 449 на
число 9.
Выполните деление столбиком числа 449 на
число 9.
М 56, 57 (с. 21).
— Прочитайте вопросы. Какие могут быть варианты? (В первом случае неполное частное может быть либо пятизначным, либо четырехзначным числом, а во втором — либо четырехзначным, либо трехзначным числом.) м 58 (с. 21).
Вариант заДачи. С одного поля собрали 2850 т зерна, а с другого — 3645 т зерна. Все зерно распределили между 1 5 зернохранилищами. По сколько тонн зерна отправлено в зернохранилища?
![]() Какое правило применяется при решении данной задачи?
Какое правило применяется при решении данной задачи?
(Правило Деления суммы на число.)
![]() Решите задачу. ((2850 + 3645) : 15 = 433 (по.)
Решите задачу. ((2850 + 3645) : 15 = 433 (по.) ![]() 59 (с. 21).
59 (с. 21).
— Прочитайте задание. Что нужно сделать сначала? (Умножить
неполное частное на Делитель: 3002 • 17 = 51 034.) ![]() Что вы нашли?
(Неполное Делимое.)
Что вы нашли?
(Неполное Делимое.) ![]() Что нужно сделать далее? (К полученному
результату прибавить остаток: 51 034 + 8 = 51 042.)
Что нужно сделать далее? (К полученному
результату прибавить остаток: 51 034 + 8 = 51 042.)
Таким образом, мы восстановили делимое по известному делителю, неполному частному и остатку.
Сложение и вычитание величин
Прочитайте задачу. Какого она типа? (Это составная задача, в которую входит простая задача на уменьшение в несколько раз в косвенной форме.)
![]() Решите задачу. (2568 : 12 + 2568 = 2782
(Дер.). ) м 61 (с. 21).
Решите задачу. (2568 : 12 + 2568 = 2782
(Дер.). ) м 61 (с. 21).
![]() Прочитайте задачу.
Какого она типа? (Простая задача на деление.)
Прочитайте задачу.
Какого она типа? (Простая задача на деление.)
![]() В чем будет
заключаться ее решение? (В нахожДении неизвестного множителя, который и
является корнем Данного уравнения.)
В чем будет
заключаться ее решение? (В нахожДении неизвестного множителя, который и
является корнем Данного уравнения.)
— Найдите корень уравнения. Запишите ответ задачи.
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 26, 27 (с. 13).
Урок 77. Сложение и вычитание величин
Цель: научить сложению и вычитанию однородных величин.
![]() Организационный момент, Сообщение темы и цели урока ll. Актуализация
знаний
Организационный момент, Сообщение темы и цели урока ll. Актуализация
знаний
1. Цифровой квадрат
|
9 |
9 |
|
|
|
![]() 18 Ответ:
18 Ответ:
20 19 19
2. Родственные ряды
|
|
|
|
|
2 |
|
|
33 |
18 |
36 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на З и прибавления числа З. В верхнем ряду пропущено число 5, в нижнем ряду — 9.) З. Устный счет
(Примеры записаны на доске.) ![]() Вычислите.
Вычислите.
(5843 + 108) - 108 940- (585 -9)
2345 - (345 + 2000)
(6207 - 207) + 207
4. Логическая задача
149 + 563 + 851 + 437
Федя и Костя получили в школе двойку и тройку. Федины родители обычно ругают сына за тройки, а привыкшие к тройкам Костины родители ругают его только за двойки. Кому попадет на этот раз, если известно, что Федя не получил тройку? (ПопаДет Феде, так как он получи Двойку, а Костя — тройку.)
Ш. Работа по теме урока Работа
по учебнику ![]() 62 (с. 22).
62 (с. 22).
— Что нужно сделать сначала? (ОДнороДные величины, выра,ЖеННЫе в разных еДиницах измерения, привести к ОДИНшсОВЫМ еДиницам измерения.)
— Как вы будете составлять пары на сложение? (При составлении всевозможных пар на сложение можно записывать величины в любом порядке.)
![]() Что нужно учитывать при составлении пар
на вычитание? (В роли уменьшаемого Должна быть большая из двух величин.) Л) 63
(с. 22).
Что нужно учитывать при составлении пар
на вычитание? (В роли уменьшаемого Должна быть большая из двух величин.) Л) 63
(с. 22). ![]() Прочитайте задание. Какие величины вы
выберете? ( 7 кв. см, 17 кв. дм.)
Прочитайте задание. Какие величины вы
выберете? ( 7 кв. см, 17 кв. дм.)
![]() Что нужно сделать перед выполнением действия сложения?
Что нужно сделать перед выполнением действия сложения?
(Выразить 5 кв. м в квадратных сантиметрах и квадратных Дециметрах: 5 кв. м = 50 ООО кв. см, 5 кв. м = 500 кв. дм.)
— Выполните сложение.
![]() 64 (с. 22).
64 (с. 22).
![]() Прочитайте задание. Какие величины можно выбрать? (Только те, которые
меньше 250л: 150 куб. дм и 450 куб. см.) — Что нужно сделать для вычитания
величин? (Выразить 250л в кубических Дециметрах и кубических сантиметрах: 250л
= = 250куб. дм, 250л = куб. см.) — Выполните вычитание.
Прочитайте задание. Какие величины можно выбрать? (Только те, которые
меньше 250л: 150 куб. дм и 450 куб. см.) — Что нужно сделать для вычитания
величин? (Выразить 250л в кубических Дециметрах и кубических сантиметрах: 250л
= = 250куб. дм, 250л = куб. см.) — Выполните вычитание.
lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ЛФ 65 (с. 22).
(Самостоятельное выполнение. Проверка с записью решения на доске.) ле 66, 67 (с. 23).
(Самостоятельное выполнение. Проверка.)
Умножение величины на число и числа на величину
ЛФ 68 (с. 23).
Прочитайте задание. Что нужно сделать? (Вычислить искомую величину, уменьшив З ч на 240 с.)
Какая это величина? (З ч — 240 с = 180 мин — 4 мин ![]() — 176 мин.) М 69 (с. 23).
— 176 мин.) М 69 (с. 23).
![]() Прочитайте задание.
Что нужно сделать? (Вычислить искомую величину, увеличив 2 т на 500 кг.)
Прочитайте задание.
Что нужно сделать? (Вычислить искомую величину, увеличив 2 т на 500 кг.)
![]() Какая это величина? (2 т + 500 кг = 2000 кг + 500 кг
Какая это величина? (2 т + 500 кг = 2000 кг + 500 кг![]()
![]()
М т (с. 23).
![]() Прочитайте условие
задачи. В каких единицах выражено количество молока Т первом бидоне? (В
литрах.)
Прочитайте условие
задачи. В каких единицах выражено количество молока Т первом бидоне? (В
литрах.)
— Что это значит? (Указан объем молока в этом бидоне.)
![]() А во втором бидоне? (Указана масса
молока.)
А во втором бидоне? (Указана масса
молока.)
![]() Можно ли складывать указанные величины?
(Нет.)
Можно ли складывать указанные величины?
(Нет.)
![]() Почему? (Нельзя склаДывать разнородные
ВиИЧИНЫ.)
Почему? (Нельзя склаДывать разнородные
ВиИЧИНЫ.)
— Можно ли решить данную задачу, сформулированную в таком виде? (Нельзя.)
2. Выпшшение упражнения в тетради для самостоятельной
работы ![]() 29 (1-3) (с. 14-15).
29 (1-3) (с. 14-15).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 28 (с. 14).
Урок 78, Умножение величины на число и числа на величину
Цель: научить умножать величину на число и число на величину.
1. Организационный момент, Сообщение темы и цели урока
ll. Актуализация знаний
Тест
( Выдается на отдельных листочках.)
1. Найди число, в котором 70 единиц третьего класса, 800 единиц второго класса и 4 единицы первого масса.
1) 70800004 3) 780 040
2)
7 800 004 4) 700 080![]()
7 Поурочные разработки по математике
![]()
2. Представь число 258 090 в виде суммы разрядных слагаемых.
1) 2 000 000 + 500 + 8000 + 90
2) то + 50 + 8000 + 90
3) 20 000 + 5000 + 800 + 90
4) 200 000 + 50 000 + 800 + 9
3. Найди пример, ответом к которому будет число 708 000.
1) 75 800 - 5000 3) 758000- 50000
2) 7 580 000 - 500 000 4) 705 800 — 5000
4.
9 КГ 497 Г 8![]()
1) 75кг 976г 3) 74 кг 976 г 2) 7 кг 5 976 г 4) 75 кг 974 г
5. Реши уравнение: (470 + 430) : 3 — х : 5 = 100.
1) х = 40 3) х = 1000
2) 80 4) Х = 2000
6. Из одного пункта выехали две машины. Одна ехала 3 ч со скоростью 60 км/ч. С какой скоростью должна была ехать другая машина, чтобы преодолеть это расстояние за 2 ч?
1) 90 км/ч 3) 80 км/ч
2) 120 км/ч 4) 100 км/ч
7. Длина коробки 60 см, а ширина на 20 см меньше. Коробку СКЛмЛИ скотчем 7 раз по периметру. Сколько скотча потребовалось?
1) 140 см 3) 1400см
2) 1120 см 4) 700 см
8. Вставь пропущенное число: м — ... дм.
3) 20
4) 100
9. Вырази в сантиметрах: 7 м 9 дм 3 см.
1) 793см 3) 7093 см
2) 703 см 4) 70 903 см
Ш. Вставь пропущенное число: 1 кв. м — ... кв. дм.
4) 10 000
11. Вставь пропущенное число: а кв. дм.
3) 000
2) 10000 4) 000 000
12. Вставь пропущенное число: 1 т
2) 10 4) 1000
13. Вставь пропущенное число: 35 т 26 ц = . кг.
1) 37600 3) 350 260
2) 352 600 4) з 502 600
14. Вставь пропущенные числа: 1 мес. . или ... сут![]()
1) 30 ми 31 3) 32 33
2) 31 или 32 4) 30 или 40
Умножение величины на число и числа на величину
![]()
1) З г. 3 мес. 3) 2 года 5 мес. 2) 2 г. 7 мес. 4) 2 года 9 мес.
l6. Сторона клумбы квадратной формы равна 8 м. Ромашками
засажено — всей площади клумбы, а остальная гшощадь — розами.
16
На какой площади клумбы посажены розы?
1) 28 кв. м 3) 56 кв. м
2) 36 кв. м 4) 64 кв. м
17. Вырази в миллиметрах: 56 м 97 см. (56 970мм.)
18. Реши пример столбиком и напиши ответ: 901 000 — 455 987.
(445 013.)
19. Запиши решение задачи и ответ.
Надо перевезти 144 пассажира. Один автомобиль может сделать это за 12 рейсов, другой — за 36 рейсов. За сколько рейсов они перевезут всех пассажиров, работая вместе? Решение:
1) 144 : 12 = 12 (пасс.) — МОжНО перевезти в одном автомобиле за один рейс;
2) 144 : 36 = 4 (пасс.) — можно перевезти в другом автомобиле за один рейс;
З) 12 + 4 = 16 (пасс.) — перевезут оба автомобиля за один рейс;
4) 144 : 16 = 9![]()
Ответ: всех пассажиров перевезут за 9 рейсов.
Ш. Работа по теме урока Работа по учебнику № 71 (с. 24).
(Самостоятельное выполнение. Проверка с записью решения на доске.) м 72 (с. 24). (Коллективное выполнение с записью на доске.) М 73 (с. 24).
(Коллективное выполнение с комментированием у доски.)
— Прочитайте задание. Как можно переформулировать задачу? (В одной неделе 7 суток, а в одних сутках 24 ч. Сколько часов Длится одна неДеля
![]() Запишите решение
задачи в виде суммы. (24 ч + 24 ч + 24 ч + +24 ч + 24 ч + 24 ч +24 ч = 168 ч.)
Запишите решение
задачи в виде суммы. (24 ч + 24 ч + 24 ч + +24 ч + 24 ч + 24 ч +24 ч = 168 ч.)
![]() Запишите решение
задачи в виде произведения. (24 ч • 7 — = 168ч.)
Запишите решение
задачи в виде произведения. (24 ч • 7 — = 168ч.)
![]() Во сколько раз неделя продолжительнее
суток? (В 7раз.)
Во сколько раз неделя продолжительнее
суток? (В 7раз.)
— Во сколько раз продолжительность суток больше, чем продолжительность часа? (В 24 раза.)
![]()
— Во сколько раз продолжительность недели больше, чем продолжительность часа? (В 168 раз.)
— Каково соотношение между неделей и часом? (1 нед.![]()
= 168ч.)
М 74 (с. 25).
(Самостоятельное выполнение. Проверка в парах.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 75 (с. 25).
(Самостоятельное выполнение. Проверка в парах.)
![]() Выполните задание. Какова длина первого
отрезка? (2 см.)
Выполните задание. Какова длина первого
отрезка? (2 см.) ![]() Какова длина второго отрезка? (6 см.)
Какова длина второго отрезка? (6 см.)
![]() Выполните кратное сравнение этих величин (6 : 2 = З (раза).)
Выполните кратное сравнение этих величин (6 : 2 = З (раза).) ![]() В
чем смысл обозначения За для длины второго отрезка? (Длину первого отрезка
обозначили буквой а. Если число З
В
чем смысл обозначения За для длины второго отрезка? (Длину первого отрезка
обозначили буквой а. Если число З
умножить на длину первого отрезка (2 см), мы получим длину второго отрезка: З • 2 см = 6 см. Значит, второй отрезок в З раза Длиннее первого.)
2. Выполнение упражнений в тетради для самостоятельной работы м 31 (с. 16).
(Выполнение с комментированием у доски.) МЗЗ, 34 (с. 17).
(Самостоятельное выполнение. Проверка в парах.) З.
Работа по учебнику ![]() 76 (с. 25).
76 (с. 25).
![]() Прочитайте задание. Запишите в виде суммы каждое произведение, в котором
число умножается на величину. (Исм • 5 = = 18 см + 18 см + 18 см + 18 см + 18
см, 38 дм 4 = 38 дм +
Прочитайте задание. Запишите в виде суммы каждое произведение, в котором
число умножается на величину. (Исм • 5 = = 18 см + 18 см + 18 см + 18 см + 18
см, 38 дм 4 = 38 дм +
+ 38 Дм + 38 Дм + 38 Дм, 23 мм • З = 23 мм + 23 мм + 23 мм.) — Составьте равенства, воспользовавшись правилом из предьщущего задания. (5 • 18см = 18см • 5, 4 • 38Дм = 38Дм • 4, з • 23мм = 23мм • З.) М 77 (с. 25).
![]() Прочитайте условие
задачи. Какие из предложенных произведений будут являться решением этой задачи?
(2 л • 8 = — 16 ли 8 • 2 л = Мл.)
Прочитайте условие
задачи. Какие из предложенных произведений будут являться решением этой задачи?
(2 л • 8 = — 16 ли 8 • 2 л = Мл.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 30, 32 (с. 16).
Деление величины на число
![]()
Урок 79. Деление величины на число
Цель: научить делить величину на число.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
Ответ: 22 |
2 |
|
|
|
|
14 |
8 |
16 9
2. Родственные ряды
|
2 |
5 |
8 |
10 |
|
|
|
22 |
|
97 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисеа верхнегоряДа на самих себя и вычитания числа З. В верхнем ряду пропущено число З, в нижнем ряду — 61.)
З. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Какие действия относятся к действиям первой ступени?
(Сложение и вычитание.)
• Какие действия относятся к действиям второй ступени?
(Умножение и Деление.)
• Какие правила порядка выполнения действий в выражениях без скобок тебе известны? (Примерный ответ. 1. Если в выражении без скобок встречаются действия сложения и умножения, то сначала выполняется умножение, а потом сложение. 2. Если в выражении без скобок встречаются два действия, одно из которых умножение, а другое вычитание, то сначала выполняется умножение, а рке потом — вычитание. 3. Если в выражении без скобок присутствуют действия первой и второй ступеней, то сначала выполняются по порядку действия второй ступени, а уже потом действия первой ступени.)
• Какие правила порядка выполнения действий в выражениях со скобками тебе известны? (Сначала нахоДят значения выражений в скобках, затем выполняют Действия по поряДку
![]()
слева направо, сначала умножение и Деление, а потом сложение и вычитание.)
4. Устный счет
(Примеры записаны на доске.)
![]() Вычислите.
Вычислите.
![]() 840 : 4- 3
840 : 4- 3 ![]()
|
260 • з - 390 |
70 , 6 . Ш |
|
230 • 4 — 460 |
570 + 204 : 4 |
|
660 : |
4 , 15 — 28 |
Ш. Работа по теме урока Работа по учебнику М 78(с. 26).
— Если величину разделить на несколько равных частей, что можно сказать об одной такой части? (Одна такая часть будет меньше всей величины во столько раз, сколько будет таких частей.)
![]() Выполните задание. (Если отрезок длиной 8 см разДелить на четыре равные части,
то одна такая часть (2 см) будет в 4 раза меньше всего отрезка.) ЛГ2
79 (с. 26).
Выполните задание. (Если отрезок длиной 8 см разДелить на четыре равные части,
то одна такая часть (2 см) будет в 4 раза меньше всего отрезка.) ЛГ2
79 (с. 26).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]() Что означает деление величины на данное число? (Это ОЗНачает уменьшение
этой величины в Данное число раз.)
Что означает деление величины на данное число? (Это ОЗНачает уменьшение
этой величины в Данное число раз.) ![]() 80 (с. 26).
80 (с. 26).
![]() Что означает
выражение «половина вместимости»? (Это значит, что величину надо уменьшить в 2
раза.)
Что означает
выражение «половина вместимости»? (Это значит, что величину надо уменьшить в 2
раза.)
— Что можно сказать о четверти вместимости? (Это уменьшение величины в 4 раза.)
— Выполните уменьшение одной и той же величины в различное число раз.
ЛФ 81 (с. 26).
![]() Прочитайте задачу.
Какого она типа? (Простая задача на деление.)
Прочитайте задачу.
Какого она типа? (Простая задача на деление.)
— О каком делении идет речь? (О Делении величины на число.)
— Что нужно сделать сначала? (Перевести 1 кг в граммы: 1 кг =
- 1ОООг.)
— Чему будет равна масса одной части торта? (1000 г : 8 —
= 125г.)
![]() 82 (с. 26).
82 (с. 26).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]() Деление величины на число lV. Физкультминутка
Деление величины на число lV. Физкультминутка
М. Закрепление изученного материала
1. Работа по учебнику ![]() 83 (с. 27).
83 (с. 27).
(Коллективное выполнение.) ![]() 84 (с. 27).
84 (с. 27).
— Прочитайте задачу. Какого она типа? (Составная задача, в
логическую структуру которой вхоДит простая задача на уменьшение в несколько
раз в косвенной форме.) ![]() Решите задачу. Запишите ответ.
Решите задачу. Запишите ответ.
Решение:
1) 2350 л : 5 = 470 л — дизельного топлива; 2) + 470 л = 2820 л.
Ответ: на автозаправочную станцию привезли 2820 л
горючего. ![]() 85 (с. 27).
85 (с. 27).
![]() Прочитайте задачу.
Как узнать, на сколько равных частей в итоге разрезали торт? (4 • 2 = 8 (ч.).)
Прочитайте задачу.
Как узнать, на сколько равных частей в итоге разрезали торт? (4 • 2 = 8 (ч.).)
— Сколько граммов в одной части? (1 кг 200г : 8 = 1200? : 8= = 150 г.)
ЛФ 86 (с. 27). ![]() Можно ли нацело разделить I м на 8
равных частей? (Ответы детей.)
Можно ли нацело разделить I м на 8
равных частей? (Ответы детей.)
![]() Что можно сделать? (Выразить м в миллиметрах: м — - ТООмм.)
Что можно сделать? (Выразить м в миллиметрах: м — - ТООмм.)
![]() Выполните деление нацело. (1000мм : 8 = 125 мм.)
Выполните деление нацело. (1000мм : 8 = 125 мм.) ![]() 87 (с. 27).
87 (с. 27).
Вариант заДачи. В одном рулоне 2835 м ткани, что в 7 раз больше, чем в другом рулоне. Сколько метров ткани в двух рулонах?
— Какого типа эта задача? (Простая задача на уменьшение в несколько раз в косвенной форме.)
![]() Какое
действие нужно выполнить сначала? (Деление.)
Какое
действие нужно выполнить сначала? (Деление.)
— Как найти искомое число? (Сложением.)
— Решите задачу. Вычислите и запишите ответ.
2. Выполнение упражнений в те»ади ддя самостоятельной работы ЛГ2З7(с. 19).
1. Решение: (165 + 375) : 15 = 36 (кг).
Ответ: в каждый магазин отвезли 36 кг фруктов.
2. Решение:
1) 58 - 28 = 30 (м) — удвоенное количество ткани во втором куске;
2) 30 : 2 = 15 (м) — во втором куске;
3) 15 + 23 = 43 (м) — в первом куске.
Ответ: в первом куске 43 м ткани, во втором 15 м ткани.
![]()
3. Решение:
l) 860 : 15 = 4 (км/ч) — скорость пешехода;
2) 8 : 4 = 2 (ч) — время, за которое пешеход проходит 8 км; 3) 860 : 2 = 430 (км).
Ответ: за то время, за которое пешеход пройдет 8 км, самолет пролетит 430 км. М 36 (с. 18).
Решение:
1) 160 мм : 10 = 16 мм — второй катет прямоугольного треугольника;
2) 160 мм • 16 мм = 2560 кв. мм — площадь прямоугольника; З) 2560 кв. мм : 2= 1280 кв. мм.
Ответ: площадь прямоугольного треугольника 1280 кв. мм.
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 35 (с. 18).
Урок 80. Нахождение доли от величины и величины по ее доле
Цель: научить находить долю от величины и величину по ее доле.
![]() Организационный момент. Сообщение
темы и цели урока ll. Актуализация знаний
Организационный момент. Сообщение
темы и цели урока ll. Актуализация знаний
Арифметический диктант
— Запишите только ответы.
• Сумма двух чисел равна 570. Одно из слагаемых — 180. Найдите второе слагаемое. (390.)
• Первое слагаемое — 345, второе — 103. Чему равно значение суммы? (448.)
• Какое число на 8 больше, чем 96? (104.)
• Найдите значение разности чисел 810 и 490. (320.)
• Уменьшаемое — 52, значение разности — 17. Чему равно вычитаемое? (35.)
• На сколько сумма чисел 540 и 460 больше разности тех же чисел? (На 920.)
• Найдите сумму чисел 140 и 250. (390.)
• На сколько 400 больше 120? (На 280.)
• На сколько 900 г меньше 1 кг 200 г? (На 300 г.)
• На участке леса росло 1908 берез, что на 75 больше, чем дубов. Сколько дубов росло на участке? (1833.)
80. доли от величины и величины по ее доле
![]()
Ш. Работа по теме урока Работа по учебнику № 88 (с. 28). (Устное выполнение с комментированием учителя.) М 89 (с. 28).
![]() Как можно разделить
квадрат на четыре равные части? (Ответы детей.)
Как можно разделить
квадрат на четыре равные части? (Ответы детей.)
Есть два способа:
1) провести диагонали;
2) провести средние линии, т. е. отрезки, соединяющие середины противоположных сторон.
![]() Как найти площадь одной такой части?
(Нужно выполнить Деление площаДи кваДрата на число 4: 16 кв. см : 4 = 4 кв.
см.)
Как найти площадь одной такой части?
(Нужно выполнить Деление площаДи кваДрата на число 4: 16 кв. см : 4 = 4 кв.
см.) ![]() Как выполнить последнее задание?
(РазДелить кажДую из полученных частей пополам.)
Как выполнить последнее задание?
(РазДелить кажДую из полученных частей пополам.)
![]() Как это сделать? (Провести Диагонали или
среДние линии.)
Как это сделать? (Провести Диагонали или
среДние линии.)
— Как вычислить площадь одной восьмой части квадрата? (РазДелить площадь всего кваДрата на число 8 или разДелить пополам площаДь одной четвертой части, которая была вычислена ранее: 16 кв. см : 8 = 2 кв. см; 4 кв. см : 2 = 2 кв. см.) м 90 (с. 28). (Самостоятельное выполнение. Проверка в парах.) ЛФ 91 (с. 29).
![]() Что можно сказать о
трети величины? (Она в Зраза меньше самой величины. )
Что можно сказать о
трети величины? (Она в Зраза меньше самой величины. )
![]() Как найти всю величину? (Умножить треть
величины на З.)
Как найти всю величину? (Умножить треть
величины на З.)
![]() Вычислите длину отрезка. (5 см • З = 15
см.)
Вычислите длину отрезка. (5 см • З = 15
см.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 92 (с. 29).
92 (с. 29).
![]() Прочитайте задачу. Что известно?
(Масса восьмой доли торта.)
Прочитайте задачу. Что известно?
(Масса восьмой доли торта.)
![]() Как найти массу торта? (125 г • 8 =
1000г = 1 кг.) М 93 (с. 29).
Как найти массу торта? (125 г • 8 =
1000г = 1 кг.) М 93 (с. 29).
![]() Прочитайте задачу.
Какого она типа? (Это составная заДача, в логическую структуру которой вхоДят
как простая задача на нахождение всей величины по ее доле (известна масса
четверти всего собранного картофеля), так и простая задача на нахождение доли
от сЛИЧИНЫ (треть от всего собранного картофеля).)
Прочитайте задачу.
Какого она типа? (Это составная заДача, в логическую структуру которой вхоДят
как простая задача на нахождение всей величины по ее доле (известна масса
четверти всего собранного картофеля), так и простая задача на нахождение доли
от сЛИЧИНЫ (треть от всего собранного картофеля).)
— Решите задачу. Запишите ответ.
![]()
Решение:
1) 300 т • 4 = 1200 т — собранный урожай картофеля, 2) 1200 т : з = 400 т.
Ответ: во второе хранилище привезли 400 т картофеля.
ЛЕ 94 (с. 29).
![]() Прочитайте задачу. Какого она типа? (Это
составная задача, в состав которой, кроме простых задач на нахожДение ВиИЧИНЫ
по ее доле и доли от величины, включены заДачи на сложение и вычитание
площадей.) — Решите задачу. Решение:
Прочитайте задачу. Какого она типа? (Это
составная задача, в состав которой, кроме простых задач на нахожДение ВиИЧИНЫ
по ее доле и доли от величины, включены заДачи на сложение и вычитание
площадей.) — Решите задачу. Решение:
1) 200 кв. м • 1000 кв. м — вся запланированная работа на неделю;
2) 1000 кв. м : 4 = 250 кв. м — отремонтировали за второй день; 3) 1000 кв. м — (200 кв. м + 250 кв. м) = 550 кв. м.
Ответ: осталось отремонтировать 550 кв. м.
ЛСР 95 (с. 29).
(Самостоятельное выполнение. Проверка в парах.) Решение: 32 • 5 = 160 (руб.).
Ответ: батон колбасы стоит 160 руб.
![]() 96 (с. 29).
96 (с. 29).
![]() Прочитайте задание.
Что нужно сделать предварительно? (Узнать, сколько минут составляют треть часа
и четверть часа.)
Прочитайте задание.
Что нужно сделать предварительно? (Узнать, сколько минут составляют треть часа
и четверть часа.)
![]() Как это можно узнать? (60 : З = 20
(мин) — треть часа; 60 : 4 = 15 (мин) — четверть часа.)
Как это можно узнать? (60 : З = 20
(мин) — треть часа; 60 : 4 = 15 (мин) — четверть часа.)
![]() Выполните разностное
сравнение этих величин. (20— 15 = — 5 (мин). )
Выполните разностное
сравнение этих величин. (20— 15 = — 5 (мин). )
![]() Как узнать, во
сколько раз половина часа больше, чем четверть часа? ( Так как половина часа —
это ЗОмин, то 30 : 15 = — 2 (раза). )
Как узнать, во
сколько раз половина часа больше, чем четверть часа? ( Так как половина часа —
это ЗОмин, то 30 : 15 = — 2 (раза). )
2. Выполнение упражнения в тетради для самосттельной
работы ![]() 40 (с. 21).
40 (с. 21).
1. Решение: 567 : 7 — 480 : 6= (стр.).
Ответ: отец прочитал на страницу больше, чем мама.
2. Решение: 36 : З : 2 = 6 (пасс.).
Ответ: в автобусе осталось 6 пассажиров. З. Решение: 128 • З : 4 = 96 (т).
Ответ: четвертая часть всего урожая составляет 96 т.
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 38, 39 (с. 20).
81 . части от величины
![]()
Урок 81 . Нахождение части от величины
Цель: научить находить часть от величины.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Закономерность
(Закономерность: — 4, • 4; пропущенные числа — 6 и 24.)
2. Цифровой квадрат
|
|
5 |
|
|
|
 Ответ:
Ответ:
20 22
З. Родственные ряды
|
з |
5 |
|
6 |
4 |
|
19 |
35 |
|
46 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на СтиИХ себя и прибавления числа 10. В верхнем ряду пропущено число 2, в нижнем ряду — 26.)
4. Логическая задача
— Решите задачу устно.
В школьном буфете Наташа, Яна и Алена покупали пирожные — бисквитное с вареньем, бисквитное с кремом и трубочку с кремом. Кто что купил, если каждая девочка съела по одному пирожному, Яна и Алена любят пирожные с кремом, а Наташа и Алена купили себе по бисквитному пирожному? (Жена — бисквитное пирожное с кремом, Яна — трубочку с кремом, Наташа — бисквитное с вареньем.)
Ш. Работа по теме урока
1. Работа по учебнику ![]() 97(с. 30).
97(с. 30).
Из диалога Маши и Миши мы узнали правило нахождения части от величины, которое основано на увеличении в нужное число раз соответствующей доли.
Как найти две трети от 60 кг? Что находим сначала? (Одну треть от 60 кг: 60 кг : З = 20 кг.)
— Что нужно сделать потом? (УДвоить
полученное число: ![]() = 40 кг.)
= 40 кг.)
Эго же правило можно применить для нахождения трех четвертей от 60.
— Что находим сначала? (Одну четвертую от 60кг: 60кг : 4 = = 15 кг.)
![]() Что потом? (Найденную
долю надо утроить: 15 кг • З = 45 кг.) М 98 (с. 30).
Что потом? (Найденную
долю надо утроить: 15 кг • З = 45 кг.) М 98 (с. 30).
— Рассмотрите чертеж. На сколько долей разделен круг? (На восемь.)
— Сколько частей закрашено? (Две.)
![]() Какую часть от площади всего круга составляет площадь закрашенной части?
(Две восьмых.)
Какую часть от площади всего круга составляет площадь закрашенной части?
(Две восьмых.)
— Вычислите площадь закрашенной части круга. (16 кв. см : 8 х х 2 = 4 кв. см.) М 99 (с. 30).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
2. Выполнение упражнения в тетради для самосттельной рабшн
![]() 41 (с. 22).
41 (с. 22).
(Работа в парах. Взаимопроверка.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику
М 100 (с. 30).
(Самостоятельное выполнение. Проверка в парах.)
![]() Как вы будете выполнять
задание? (Сначала с помощью деления величины на число 7 найдем, чему равна одна
седьмая часть от Данной величины, затем с помощью умножения увеличим найденную
долю в нужное число раз.)
Как вы будете выполнять
задание? (Сначала с помощью деления величины на число 7 найдем, чему равна одна
седьмая часть от Данной величины, затем с помощью умножения увеличим найденную
долю в нужное число раз.)
ЛЕ 101 (с. 31),
![]() Прочитайте задачу. Какого она типа? (Составная задача, в логическую
структуру которой вхоДит задача на нахожДение части от величины.)
Прочитайте задачу. Какого она типа? (Составная задача, в логическую
структуру которой вхоДит задача на нахожДение части от величины.)
— Что мы найдем сначала? (Расстояние, которое туристы проими за день, т. е. три четверти всего пути: 40: 4 • З = 30 (км). )
— Что найдем потом? (Сколько километров ши осталось
пройти.• 40- зо = ш (км).) ![]() 102 (с. 31).
102 (с. 31).
Вариант заДачи. Масса внука составляет две седьмых массы дедушки. Чему равна масса внука, если масса дедушки равна 70 кг?
величины по ее части
![]()
Решение: 70 : 2 = 20 (кг).
Ответ: масса внука равна 20 кг.
№ 103 (с. 31). Решение:
|
|
= 80 (кг) |
120 : 6 • 4 = 80 (кг) |
|
|
= 90 (кг) |
|
120 : 96 (кг)
— Как объяснить, что две третьих и четыре шестых части оказались равны? М 104 (с. 31).
![]() Прочитайте условие
задачи. Сколько километров туристы преодолели за один день? (Если туристы
кажДый день преодолевали одно и то же расстояние и за неделю прошли 175 км, то
за один день они преоДолели 175 км : 7 = 25 км, т. е. одну седьмую всего
расстояния. )
Прочитайте условие
задачи. Сколько километров туристы преодолели за один день? (Если туристы
кажДый день преодолевали одно и то же расстояние и за неделю прошли 175 км, то
за один день они преоДолели 175 км : 7 = 25 км, т. е. одну седьмую всего
расстояния. )
![]() Сколько километров туристы преодолели за
3 дня? (25 юи х х З = 75 км, что составляет три СеДЫМЫХ всего
расстояния.) 2. Выполнение упражнения в теиради для самостягељной работы М 42
(с. 22).
Сколько километров туристы преодолели за
3 дня? (25 юи х х З = 75 км, что составляет три СеДЫМЫХ всего
расстояния.) 2. Выполнение упражнения в теиради для самостягељной работы М 42
(с. 22).
Решение:
1)
: 5 • 2 = 80 ![]()
2) 200 : 20 = 80 (м).
Ответ: две пятых части от 200 м и восемь двадцатых частей от 200 м равны.
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 43 (с. 23).
Урок 82. Нахождение величины по ее части
Цель: научить находить величину по ее части (доле).
1. Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Волшебные оадраты
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
пшшп пп•п |
|||||
|
|
|
|
|
|
|
|
|
||||||

(Примеры записаны на доске.)
|
— Вычислите. |
|
|
99 999 + |
2999 + |
|
1999 + |
10 ООО- 1 |
![]() 8999 +
8999 + ![]()
7000 - 3000
6540 - 500 ![]()
З. Повторение нумерации
— Запишите числа.
284 689, l l 000 370, 9 004 300, 700 001, 36 480 000, 9 006 600, 8 088 088, 000 lOl.
— Запишите, между какими ближайшими числами находятся числа 80 000, Ш 000, 6000, 565 999.
4. Логическая задача
— Решите задачу устно.
У Вики, Ани и
Лены очень красивые куртки — синяя и красная с капюшонами и синяя без капюшона.
У кого какая куртка, если Аня и Лена ходят с капюшонами, а у Ани и Вики куртки
синего цвета? (У Вики синяя куртка без капюшона, у Ани — синяя с капюШоном, у
Лены — красная.) Ш. Работа по теме урока Работа по учебнику ![]() 105 (с.
32). (Коллективное выполнение с комментированием.) ЛГ2 106 (с. 32).
105 (с.
32). (Коллективное выполнение с комментированием.) ЛГ2 106 (с. 32).
— Как найти длину одной седьмой части, если известно, чему равны четыре седьмых всей длины? (Уменьшить четыре седьмых всей длины в 4 раза.)
![]() Найдите длину одной седьмой части
электропровода.
Найдите длину одной седьмой части
электропровода.
![]()
![]() Во сколько раз вся
длина больше, чем одна седьмая часть этой длины? (В 7раз.)
Во сколько раз вся
длина больше, чем одна седьмая часть этой длины? (В 7раз.)
![]() Найдите
всю длину провода по ее части. (39 м • 7= 273 м.)
Найдите
всю длину провода по ее части. (39 м • 7= 273 м.)
величины по ее части
![]() электропровода, если четыре
седьмых этой длины составляют 176 м. (176 м : 4 • 7= 308 м.) lV.
Физкультминутка
электропровода, если четыре
седьмых этой длины составляют 176 м. (176 м : 4 • 7= 308 м.) lV.
Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику
![]() 107, 108 (с. 33).
107, 108 (с. 33).
(Самостоятельное выполнение. Проверка в парах.) Л) 109 (с. 33).
— Прочитайте задачу. Какого она типа? (Задача на
нахожДение всей величины, если известно значение ее части.) ![]() Решите
задачу. Запишите ответ.
Решите
задачу. Запишите ответ.
Решение:
Первый способ:
1) 6 сот. : 3 = 2 (сот.) — площадь одной пятой всего участка; 2) 2 сот. • 5= 10 (сот.).
Второй способ: 6 сот. : 3 • 5 = 10 (сот.).
Ответ: площадь всего участка 10 соток. ![]() 110
(с. 33).
110
(с. 33).
(Самостоятельное выполнение. Проверка в парах.) Решение:
1) 8 : 2 • 5 = 20 (сот.) — площадь первого участка; 2) 8 : 4 • 10 = 20 (сот.) — площадь второго участка.
20 сот. = 20 сот.
![]() Почему площади оказались равны? (Две
пятых и четыре Десятых всегда совпадают. ) Л) 111 (с. 33).
Почему площади оказались равны? (Две
пятых и четыре Десятых всегда совпадают. ) Л) 111 (с. 33).
![]() Прочитайте задание. Что можно
сказать о двух третьих и трех четвертых частях? (Это разные части.)
Прочитайте задание. Что можно
сказать о двух третьих и трех четвертых частях? (Это разные части.)
![]() В каком случае
возможно равенство этих частей? (Только в том случае, если они взяты не от
одной и той же величины, а от разных.)
В каком случае
возможно равенство этих частей? (Только в том случае, если они взяты не от
одной и той же величины, а от разных.)
— Как найти эти две разные величины? (По известной части кажДой из них.)
— Чему будет равна вместимость первого бака? (54 : 2 • З = 81 (л).)
— Чему будет равна вместимость второго бака? (54 : З • 4 =
72 (л).) ![]() Что нужно сделать далее? (Выполнить
разностное сравнение величин: 81 л — 72л = 9 л.)
Что нужно сделать далее? (Выполнить
разностное сравнение величин: 81 л — 72л = 9 л.)
2. Выполнение упражнений в тетради для самостоятельной работы
![]() 44, 45 (с. 24).
44, 45 (с. 24).
(Устное выполнение.)
![]()
м 46 (с. 25).
(Самостоятельное выполнение. Проверка в парах.)
1. Решение:
1) 1200 : 3 • 5 = 2000 (бул.) — выпекают всего; 2) 2000 - 1200 800 (бул.).
Ответ: во втором цехе выпекают 800 булок.
2. Решение:
1) 1470 : 7 • 12 = 2520 (тел.) — всего; 2) 2520 : 9 2 = 560 (тел.).
Ответ: 560 телевизоров средних размеров.
З. Работа по учебнику .№ 127 (с. 37) (вариант 1). № 128 (с. 37) (вариант 2).
(Самостоятельное выполнение.)
И. Подведение итогов урока
Домашнее задание
Учебник: № 121, 122 (с. 36).
Урок 83. Деление величины на величину
Цель: рассмотреть случаи деления однородной и разнородной величин на величину.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
22 Ответ: |
9 |
|
|
|
|
9 |
|
18 23
2. Родственные ряды
|
25 |
36 |
4 |
9 |
|
|
4 |
5 |
|
2 |
6 |
( Числа верхнего ряда получаются в результате прибавления к соответствующим числам нижнего ряда еДиницы и умножения получившейся суммы на саму себя. В верхнем ряду пропущено число 49, в нижнем ряду — 1.)
Деление величины на величину
![]()
67 дес., 48 сот. , 328 сот. , 26 тыс., 275 тыс. 6 ед.
4. Устный счет
(Примеры записаны на доске.) ![]() Вычислите.
Вычислите.
|
70 • 4 |
90 - 7 |
8 60 |
20 , 6 |
|
14 , 6 |
27 - 3 |
3 - 18 |
23 • 4 |
|
51 : 7 |
51 • l |
24 • |
12 • 8 |
Ш. Работа по теме урока Работа по учебнику м 112 (с. 34).
(Устное выполнение по цепочке.)
![]() В какой паре одна величина отличается от
другой в 25 раз?
В какой паре одна величина отличается от
другой в 25 раз?
![]()
ЛГУ 113 (С. 34).
(Выполнение в соответствии с заданиями.)
— Какую величину вы получили, выполнив деление. (Скорость.)
— Назовите единицу измерения полученной величины. (Километры в час (км/ч). )
![]() Какие еще единицы скорости вам известны?
(Метры в секунду (мд), метры в минуту (м/мин), киаометры в секунДу (км/с).)
Какие еще единицы скорости вам известны?
(Метры в секунду (мд), метры в минуту (м/мин), киаометры в секунДу (км/с).)
— Из единиц каких величин получается любая единица скорости движения? (Из еДИНИЦЫ длины и еДИНИЦЫ времени.) ЛГ2 114 (с. 34).
— Как вычислить цену товара? (Разделить стоимость на количество.)
![]() В чем выражается
стоимость? (В рублях, копейках, в Долларах, в евро.)
В чем выражается
стоимость? (В рублях, копейках, в Долларах, в евро.)
![]() В чем выражается
количество? (Это зависит от вида товара: в штуках, в еДиницах длины, массы,
вместимости, тОщди и т. д.)
В чем выражается
количество? (Это зависит от вида товара: в штуках, в еДиницах длины, массы,
вместимости, тОщди и т. д.)
![]() В каких единицах может быть выражена
цена? (Ответы детей.) Существует множество вариантов единиц цены.
В каких единицах может быть выражена
цена? (Ответы детей.) Существует множество вариантов единиц цены.
![]() цена
каких товаров выражается в руб./кв. м? ( Ткани, обоев, линолеума и т. д.)
цена
каких товаров выражается в руб./кв. м? ( Ткани, обоев, линолеума и т. д.)
![]() Вычислите
цену каждого товара из данной таблицы самостоятельно.
Вычислите
цену каждого товара из данной таблицы самостоятельно.
М. Физкультминутка
![]()
М. Закрепление изученного материала
1. Выполнение упражнений в тетради для самосшжгельной работы м 47, 48(с. 26).
(Выполнение в соответствии с заданиями.)
2. Работа по учебнику М 115 (с. 35).
Решение: 1750 ц : 50 га = 35 ц/га.
Ответ: урожайность пшеницы составляет 35 ц/га.
— Какая величина получилась в результате деления массы собранного урожая на площадь участка, с которого этот урожай собрали? (Урожайность.)
— Какой единицей обозначается эта величина? (ц/га.) М 116 (с. 35).
(Работа в парах. Взаимопроверка.)
![]() В каких единицах в данной задаче
измеряется производительность? (Если объем работы выражен в Деталях (Дет.), а
время работы — в часах (ч), то произвоДительность будет выражена в Дет./ч.) М
117(с. 35).
В каких единицах в данной задаче
измеряется производительность? (Если объем работы выражен в Деталях (Дет.), а
время работы — в часах (ч), то произвоДительность будет выражена в Дет./ч.) М
117(с. 35).
![]() Какую величину на
какую нужно разделить, чтобы получить производительность? (Объем выполненной
работы на время работы.)
Какую величину на
какую нужно разделить, чтобы получить производительность? (Объем выполненной
работы на время работы.)
![]() Приведите примеры единиц объема работы.
(Ответы детей.)
Приведите примеры единиц объема работы.
(Ответы детей.) ![]() Какие можно использовать единицы
времени? (Смена, сутки, неделя, квартал, час, минута, секунда и т. д.)
Какие можно использовать единицы
времени? (Смена, сутки, неделя, квартал, час, минута, секунда и т. д.) ![]() Самостоятельно
приведите примеры единиц производительности.
Самостоятельно
приведите примеры единиц производительности.
(Проверка в парах.) м 118 (с. 35).
— Как получить плотность населения? (Число всех жителей
Данного региона разДелить на площаДь этого региона.) ле 119 (с. 35).
(Устное выполнение.)
![]() Что показывает
величина, полученная путем деления массы на объем? (Массу еДИНИЦЫ объема.)
Что показывает
величина, полученная путем деления массы на объем? (Массу еДИНИЦЫ объема.)
![]() В каких единицах она
может быть выражена? (Килограмм на кубический метр (кг/куб. м), грамм на
кубический сантиметр (г/куб. см) и т. д.)
В каких единицах она
может быть выражена? (Килограмм на кубический метр (кг/куб. м), грамм на
кубический сантиметр (г/куб. см) и т. д.)
Эта величина называется «плотность вещества». С ней вы встретитесь в курсе физики.
М 120 (с. 35).
(Устное выполнение.)
время движения одинаковое
![]()
— Каше объекты могут двигаться со скоростью 8 км/с? (Ракета-носитель, космический корабль, спутник.)
З. Выполнение упрахшитя в тегрщщ мя самостоятельной
ра&пы ![]() 49 (с. 27).
49 (с. 27).
(Самостоятельное выполнение. Проверка в парах.)
4. Работа по учебнику ![]() 125, 126 (с. 36).
125, 126 (с. 36).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока домашнее задание
Учебник: № 123, 124 (с. 36).
Урок 84. Когда время движения одинаковое
Цели: показать прямую зависимость пройденного расстояния от скорости в случае, если время движения одинаковое; развивать навыки решения задач.
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
Письменный опрос
(Вопросы даны на отдельных листочках.)
• Какие величины тебе известны? (Длина, площадь, масса, скорость, время, вместимость (объем), плотность.)
Дополнительная информация. Еще в «Началах» Евклида (III в. до н. э.) были отчетливо сформулированы свойства величин, называемых теперь положительными скалярными величинами. Эго первоначальное понятие величины является непосредственным обобщением более конкретных понятий: длины, площади, объема, массы, времени, скорости и т. п. Каждый конкретный род величины связан с определенным способом сравнения физических тел или других объектов. Например, в геометрии отрезки сравниваются при помощи наложения, и это сравнение приводит к понятию длины: два отрезка имеют одну и ту же длину, если при наложении они совпадают; если же один отрезок накладывается на часть другого, не покрывая его целиком, то длина первого меньше длины второго. Общеизвестны более сложные приемы, необходим ые для сравнения плоских фигур по площади или пространственных тел по объему.
![]()
• Какие единицы длины, площади, вместимости, массы, времени ты знаешь? Напиши известные тебе соотношения между разными единицами каждой из перечисленных величин. (Примерный ответ. Единицы длины: миллиметр (мм), сантиметр (см), метр (м), километр (км); 1 см = 10 мм, 1 дм = 10 см, 1 м = 10 дм, 1 м = 100 см, 1 км = = 1000 м. Единицы площади: ар (а), сотка, квадратный миллиметр (кв. мм), квадратный сантиметр (кв. см), квадратный дециметр (кв. дм), квадратный метр (кв. м), квадратный километр (кв. км); 1 кв. см = 100 кв. мм, кв. дм = = 100 кв. см, кв. м = 100 кв. дм, а = 100 кв. м = сотка,
1 га ![]() — 10 000 кв. м, кв. км = 100 га, кв. дм
— 10 000 кв. м, кв. км = 100 га, кв. дм![]()
= 10 000 кв. мм, кв. м = 10 000 кв. см, а = 10 000 кв. дм,
1 га 10 000 кв. м, 1 кв. м = 10 000 а, кв. км ![]() = 000 000 кв. м. Единицы вместимости
(объема): миллилитр (мл), литр (л), кубический мртлиметр (куб. мм), кубический
сантиметр (куб. см), кубический дециметр (куб. дм), кубический метр (куб. м); 1
л = 1000 мл,
= 000 000 кв. м. Единицы вместимости
(объема): миллилитр (мл), литр (л), кубический мртлиметр (куб. мм), кубический
сантиметр (куб. см), кубический дециметр (куб. дм), кубический метр (куб. м); 1
л = 1000 мл, ![]() л = I куб. дм = 1000 куб. см, 1 куб. см = 1000 куб. мм, 1 куб. м = 1 000
000 куб. см = 1000 куб. дм, 1 куб. дм =
л = I куб. дм = 1000 куб. см, 1 куб. см = 1000 куб. мм, 1 куб. м = 1 000
000 куб. см = 1000 куб. дм, 1 куб. дм =
![]() 1000 куб. см. Единицы массы: грамм (г), килограмм
1000 куб. см. Единицы массы: грамм (г), килограмм
(кг), центнер (ц), тонна (т); 1 кг = 1000 г, 1 ц = 100 кг, 1 т =
= 1000 кг, т = 10 ц. Единицы времени: секунда (с), минута
(мин), час (ч), сутки (сут.), неделя (нед.), месяц (мес.), год
(г.), век (в.); 1 мин = 60 с, 1 ч = 60 мин, 1 сут. = 24 ч, 1 год =
= 12 мес., 1 век = 100 лет.)
• Какие действия над величинами можно выполнять? (Сложение, вычитание, умножение, Деление.)
Ш, Работа по теме урока Работа по учебнику ![]() 135 (с. 39).
135 (с. 39).
— Как вы думаете, какое соревнование называется «суточный бег»? (Участники такого соревнования должны бежать 6 течеше суток с небольшими перерывами на отдых.)
![]() Кто из спортсменов
становится победителем такого соревнования? (Тот, который за это время
преодолеет самое большое расстояние.)
Кто из спортсменов
становится победителем такого соревнования? (Тот, который за это время
преодолеет самое большое расстояние.)
— Как определить среднюю скорость участника соревнования
по суточному бегу? (129 км : 24 ч = 5 км/ч.) ![]() 136 (с. 39).
136 (с. 39).
![]() Прочитайте задание. Вычислите время, потраченное на преодоление первой части
пути. (160 км : 80 км/ч = 2 (ч).)
Прочитайте задание. Вычислите время, потраченное на преодоление первой части
пути. (160 км : 80 км/ч = 2 (ч).)
время движения одинаковое
— Вычислите время, потраченное на преодоление второй части пути. (150км : 75 км/ч = 2
![]() Что можно сказать о найденном времени? (Время, за которое автобус
преодолел кажДую часть пути, не изменилось.) М 137 (с. 39-40).
Что можно сказать о найденном времени? (Время, за которое автобус
преодолел кажДую часть пути, не изменилось.) М 137 (с. 39-40).
(Коллективное выполнение с комментированием.)
— Существует ли зависимость длины пройденного пути от скорости при постоянном времени? (Да. Если время постоянно, то с увеличением или уменьшением скорости в некоторое число раз во столько же раз увеличивается шти уменьшается пройденный путь.)
М. Физкультминутка
V. Закрепление изученного материала
1.
Вьто.мекте
упражнения в тетрадщ для самостоятельной работы ![]() 54 (с. 29).
54 (с. 29).
(Устное выполнение.)
2.
Работа по учебнику ![]() 138 (с. 40). (Выполнение в соответствии с
заданием. Учащиеся формулируют правило.) ЛЕ 139 (с. 40).
138 (с. 40). (Выполнение в соответствии с
заданием. Учащиеся формулируют правило.) ЛЕ 139 (с. 40).
![]() Прочитайте задание. Какова средняя скорость автобуса? (В 15 раз больше,
чем средняя скорость пешехода.)
Прочитайте задание. Какова средняя скорость автобуса? (В 15 раз больше,
чем средняя скорость пешехода.)
— Что можно сказать о расстоянии, которое дачник проходит пешком? ( Так как время, которое Дачник идет пешком, равно времени, которое он едет на автобусе, а скорость автобуса в 15 раз больше скорости Дачника, то расстояние, которое Дачник проезжает на автобусе, в 15 раз больше расстояния, которое он прохоДит пешком.)
![]() Какое расстояние дачник преодолеет на автобусе? (З км х х 15=45 км.)
Какое расстояние дачник преодолеет на автобусе? (З км х х 15=45 км.)
![]() Какое расстояние дачнику нужно
преодолеть всего? (45 юи + + З км = 48 км.) М 140 (с. 40).
Какое расстояние дачнику нужно
преодолеть всего? (45 юи + + З км = 48 км.) М 140 (с. 40).
(Коллективное выполнение с комментированием.)
— Как выразить пройденный путь через скорость и время?
(Ответы детей.)
Это можно записать с помощью соответствующей формулы:
З. Выполнение упражнения в тетрам для самостягельной работы ЛЕ 55 (с. 30).
(Самостоятельное выполнение. Проверка в парах.)
![]()
Ш. Подведение итогов урока
Домашнее задание
Учебник: № 129, 130 (с. 37).
Урок 85. Когда мина пройденного пути одинаковая
Цель: показать взаимосвязь времени и скорости движения при одинаковой длине пройденного пути.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат

8 25
2. Родствекшые ряды
|
2 |
4 |
|
|
|
|
7 |
|
|
23 |
|
( Числа НИЖНиО ряда получаются в результате умножения соответствующих чисел верхнего ряда на 2 и прибавления числа З. В верхнем ряду пропущено число 7, в нижнем ряду — 25.)
З. Устный счет
(Примеры записаны на доске.)
![]() Вставьте пропущенные числа и докажите.
Вставьте пропущенные числа и докажите.
|
1 мин 16с= ... с 2 сут. 7 ч = ... ч 240 мин — 12 ч 33 мин — ... мин 10 мин 25 с = ...с |
420 мин — З сут. 7 ч = ... ч 36 мес. ... лет 6 тыс. 90 лет веков . . лет 720 лет — ... веков ... лет |
4. Разминка
• Сколько будет 6 + 6 : 6? (7, так как первое Действие Деление.)
• Если колесо имеет 10 спиц, то сколько между ними промежутков? (10.)
• Назовите лишнее слово, объяснив свой выбор: каша, папа, небо, земля. (Ответы детей.)
длина пройденного пути одинаковая
![]()
Ш. Работа по теме урока Работа по учебнику М 141 (с. 41).
(Коллективное выполнение с комментированием.)
![]() Какова зависимость между скоростью и
временем при одинаковой длине пройденного пути? (При постоянной Длине
пройденного пути увеличение скорости в некоторое число раз привоДит к
уменьшению времени в это же число раз.)
Какова зависимость между скоростью и
временем при одинаковой длине пройденного пути? (При постоянной Длине
пройденного пути увеличение скорости в некоторое число раз привоДит к
уменьшению времени в это же число раз.) ![]() 142 (с. 41).
142 (с. 41).
(Коллективное выполнение с комментированием.)
![]() Прочитайте условие
задачи. Что можно сказать о длине пройденного пути? (Она постоянна.)
Прочитайте условие
задачи. Что можно сказать о длине пройденного пути? (Она постоянна.)
![]() А время? (Время
меняется: для велосипеДиста — 2 ч, для автомобиля — 30 мин.)
А время? (Время
меняется: для велосипеДиста — 2 ч, для автомобиля — 30 мин.)
— Что нужно сделать, чтобы ответить на вопрос задачи? (Узнать, во сколько раз время, которое Должен затратить автомобиль, меньше времени, которое Должен затратить велосипеДист.)
![]() Как это узнать?
(Перевести 2 ч в минуты и выполнить кратное сравнение двух временных
промежутков: 2 ч : 30 мин
Как это узнать?
(Перевести 2 ч в минуты и выполнить кратное сравнение двух временных
промежутков: 2 ч : 30 мин ![]() — 120мин : ЗОмин = 4 (раза).)
— 120мин : ЗОмин = 4 (раза).)
![]() Что можно сказать о скоростях объектов?
(Скорость авто-
Что можно сказать о скоростях объектов?
(Скорость авто-
МОбШИ больше скорости велосипеДиста в 4 раза.) lV. Физкультминутка
V. Закрепление изученного материала
1. Выполнение упражнения в тетрајщ для самостоятељной работы
ЛГ2 58 (1-3) (с. 31).
(Выполнение в соответствии с заданиями.)
2. Работа по учебнику № из (с. 42).
(Коллективное выполнение с комментированием.)
![]() Прочитайте задачу. Во сколько раз
увеличилось время на втором километре дистанции? (40мин : Тмин = 2 (раза).) —
Что можно сказать о скорости пловца на втором километре дистанции? (Она
уменьшиась в 2 раза.)
Прочитайте задачу. Во сколько раз
увеличилось время на втором километре дистанции? (40мин : Тмин = 2 (раза).) —
Что можно сказать о скорости пловца на втором километре дистанции? (Она
уменьшиась в 2 раза.)
![]() Какая зависимость существует между
скоростью и временем при постоянной длине пути? (При постоянной Длине
пройденного пути увеличение времени в некоторое число раз привоДит к уменьшению
скорости в это же число раз.) ЛД 144 (с. 42).
Какая зависимость существует между
скоростью и временем при постоянной длине пути? (При постоянной Длине
пройденного пути увеличение времени в некоторое число раз привоДит к уменьшению
скорости в это же число раз.) ЛД 144 (с. 42).
![]() Как будет выглядеть
формула, в которой скорость выражается через пройденный путь и время? (Ответы
детей.)
Как будет выглядеть
формула, в которой скорость выражается через пройденный путь и время? (Ответы
детей.)
![]()
ЛФ 145(с. 42).
— Что можно сказать о времени движения автобуса? (Примерный ответ. Так как и автомобиль, и автобус преодолели одинаковое расстояние, а скорость автобуса в 2 раза меньше, чем скорость автомобиля, то время движения автобуса в 2 раза больше, чем время движения автомобиля. Следовательно, время движения автобуса на 2 ч и в 2 раза больше, чем время движения автомобиля.)
![]() Как найти время
движения автобуса? (Пусть время автомобиая — одна часть, а время автобуса — две
части. Так как время автобуса на 2 ч больше, то на одну часть прихоДятся 2 ч.
Следовательно, время автомобиая (одна часть) равно 2 ч, а время автобуса (Две
части) равно 4 ч.)
Как найти время
движения автобуса? (Пусть время автомобиая — одна часть, а время автобуса — две
части. Так как время автобуса на 2 ч больше, то на одну часть прихоДятся 2 ч.
Следовательно, время автомобиая (одна часть) равно 2 ч, а время автобуса (Две
части) равно 4 ч.)
![]() Как вычислить
среднюю скорость автобуса? (160 км : 4 ч — = 40 км/ч.)
Как вычислить
среднюю скорость автобуса? (160 км : 4 ч — = 40 км/ч.)
З. Вьшолнение упражнения в тетради для самостте.љной рабтн ![]() 59 (с. 32).
59 (с. 32).
(Коллективное выполнение с комментированием.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 32 (с. 60).
Урок 86. Движение в одном и том же направлении
Цель: рассмотреть случаи решения задач на движение в одном и том же направлении.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: — 2, : З; пропущенные числа — 9 и З.)
2. Разминка
• Прочитайте слова и подумайте, по какому признаку можно их сгруппировать.
одном и том же направлении
![]()
Чашка, стол, диван, сапоги, кастрюля, стул, босоножки, тапочки, вилка. (Ответы детей.)
• Какая вода по воде плавает? (Лед.)
• Верно ли, что 64 + 53 - 127? (Нет.)
• Кто под проливным дождем, не имея зонтика, не замочит волосы? (Лысый человек.) З. Устный счет
(Пример записан на доске.)
![]() Вычислите удобным способом.
Вычислите удобным способом.
270 + 280 + 290 + зоо + З] + 279 + 320 + 330 (2100)
Ш. Работа по теме урока Работа
по учебнику ![]() 146 (с. 43). (Коллективное выполнение с
комментированием.) ЛФ 147 (с. 44).
146 (с. 43). (Коллективное выполнение с
комментированием.) ЛФ 147 (с. 44).
— Прочитайте задачу. Как начинается движение? (ОДновременно, но из разных пунктов.)
![]() Чему равно расстояние между этими
пунктами? (ТОм.)
Чему равно расстояние между этими
пунктами? (ТОм.)
![]() Какова скорость передвижения у Маши и
у Миши? (У Маши — 200м/мин, у Миши — 250м/мин.)
Какова скорость передвижения у Маши и
у Миши? (У Маши — 200м/мин, у Миши — 250м/мин.)
![]() Что
будет происходить с расстоянием, когда Миша начнет догонять Машу? (Так как
скорость Миши больше, чем скорость Маши, то сначала расстояние между объектами
начнет уменьшаться . )
Что
будет происходить с расстоянием, когда Миша начнет догонять Машу? (Так как
скорость Миши больше, чем скорость Маши, то сначала расстояние между объектами
начнет уменьшаться . )
— Сколько времени потребуется Мише для устранения
преимущества в расстоянии? ( Так как скорость изменения расстояния 250М/МИН —
200М/МИН = 50м/мин, то для устранения преимущества в ТОм Мише потребуется ТОм :
50м/мин = 4 мин.) ![]() Какую дистанцию за это время преодолеет
Миша? (250м/мин • 4 мин = 1000 м = 1 км).)
Какую дистанцию за это время преодолеет
Миша? (250м/мин • 4 мин = 1000 м = 1 км).)
![]() Догонит ли Миша Nidi11J? (Миша Догонит
Машу на самом финише, т. е. к финишу они приеДут одновременно.)
Догонит ли Миша Nidi11J? (Миша Догонит
Машу на самом финише, т. е. к финишу они приеДут одновременно.) ![]() 148 (с.
44).
148 (с.
44).
![]() Прочитайте задачу.
Как начинается движение? (Из одного пункта, но с некоторым временным
интервалом.)
Прочитайте задачу.
Как начинается движение? (Из одного пункта, но с некоторым временным
интервалом.)
— Какое расстояние проедет автобус за 1 ч? (60 км.) ![]() Выполните
разностное сравнение скоростей. (80 км/ч
Выполните
разностное сравнение скоростей. (80 км/ч ![]() — 60 км/ч = 20 км/ч.)
— 60 км/ч = 20 км/ч.)
— Через сколько часов такси дотнит автобус? (60км : 20юи/ч —
![]() 149 (с. 44).
149 (с. 44).
— Прочитайте задание. Выполните разностное сравнение скоростей. (бм/с — 5м/с = 1 мд.)
![]()
= 15 с.)
— За какое время участник из команды 4 «А» класса преодолеет всю дистанцию? (90м : бм/с = 15 с.)
— Какая команда станет победителем? (Команды приДут к финишу одновременно.)
![]() Как могло бы повлиять на данную
ситуацию изменение длины дистанции? (Если бы Длина последнего этапа была меньше
90 м, то победила бы команда 4 «Б» класса, а если бы эта Длина была больше 90
м, то побеДила бы команда 4 «А» класса.)
Как могло бы повлиять на данную
ситуацию изменение длины дистанции? (Если бы Длина последнего этапа была меньше
90 м, то победила бы команда 4 «Б» класса, а если бы эта Длина была больше 90
м, то побеДила бы команда 4 «А» класса.)
М. Физкультминутка
М. Закрепление изученного материала
1. Работа по учебнику М 150 (с. 44-45).
(Чтение правила. Самостоятельное
выполнение упражнения. Проверка с записью решения на доске.) ![]() 151 (с.
45).
151 (с.
45).
![]() Прочитайте задание.
Как найти расстояние между катером и плотом? (20 км/ч • 2 ч = 40 км.)
Прочитайте задание.
Как найти расстояние между катером и плотом? (20 км/ч • 2 ч = 40 км.)
![]()
![]() Почему для
ответа на требование задачи не нужно знать скорость движения плота? (Скорость
Движения тота совпаДает со скоростью Движения реки. Значит, если скорость
катера на 20 км/ч больше скорости течения реки, то она также на 20 км/ч больше
скорости Движения тота.)
Почему для
ответа на требование задачи не нужно знать скорость движения плота? (Скорость
Движения тота совпаДает со скоростью Движения реки. Значит, если скорость
катера на 20 км/ч больше скорости течения реки, то она также на 20 км/ч больше
скорости Движения тота.)
![]() Можно ли, располагая
теми же данными, узнать расстояние, пройденное катером? (Нет.)
Можно ли, располагая
теми же данными, узнать расстояние, пройденное катером? (Нет.)
— Что нужно узнать сначала? (Скорость Движения катера вниз по течению реки.)
![]() Как узнать, с какой скоростью двигался
катер вниз по течению реки? (К скорости катера в стоячей воде прибавить
скорость течения реки: 2 км/ч + 20 км/ч = 22 км/ч.)
Как узнать, с какой скоростью двигался
катер вниз по течению реки? (К скорости катера в стоячей воде прибавить
скорость течения реки: 2 км/ч + 20 км/ч = 22 км/ч.) ![]() Чему равно
расстояние? (22 км/ч • 2 ч = 44 км.) ЛГ2 152 (с. 45).
Чему равно
расстояние? (22 км/ч • 2 ч = 44 км.) ЛГ2 152 (с. 45).
Вариант заДачи. От одной автостанции одновременно в одном и том же направлении отправились автобус и маршрутное такси. Средняя скорость автобуса равна 50 км/ч, а такси — 70 юл/ч. Через сколько часов расстояние между автобусом и такси будет 40 км?
2. Выполнение упражнения в тетради для самостоятельной ра-
![]() 63 (с. 34).
63 (с. 34).
(Самостоятельное выполнение. Взаимопроверка.)
противоположных направлениях
![]()
1. Решение:
1) 50 • 3 = 150 (м/мин) — скорость велосипедиста;
2) 150 м/мин • 120 мин — 50 м/мин • 120 мин = 18 000 м — - 6000 м = 12 000 м = 12 км.
Ответ: велосипедист обгонит пешехода на 12 км.
2. Решение: 40 : 2 = 20 (км/ч).
Ответ: скорость надо увеличить на 20 км/ч.
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 62 (с. 33—34).
Урок 87. Движение в противоположных направлениях
Цель: рассмотреть случаи решения задач на движение в противоположньж направлениях.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
12 |
3 |
|
6 |
18 |
![]() 15 Ответ:
15 Ответ:
24
18 21
2. Родственные ряды
|
10 |
20 |
|
12 |
|
|
10 |
15 |
|
П |
8 |
( Числа нижнего ряда получаются в результате прибавления к соответствующим числам верхнего ряда числа 10 и Деления на 2. В верхнем ряду пропущено число 6, в нижнем ряду — 20.) З. Устный счет
— Выберите все правильные ответы.
(Варианты ответов даны на доске. )
1. Какие числа больше числа 65 439?
|
а) 65 349 |
г) 63 954 |
|
6) 93 465 |
д) 95 643 |
|
в) 69 435 |
е) 49 653 |
![]() а) 32 000 и 800 г)
3280u 6) 328 и д) 32 800 и о
а) 32 000 и 800 г)
3280u 6) 328 и д) 32 800 и о
в) 1 и 32 800 е) 32 799 и 1
3. Если число 574 100 уменьшить на 100, то получится:
а) 574 000 6) 5741
в) 573![]()
г) сумма чисел 570 000 и 4000
д) частное от деления 573 100 и ![]()
е) число, в котором 4 еДИНИЦЫ четвертого разряда
4. Чему равно первое слагаемое, если второе слагаемое равно 1, а сумма — 49 999?
а) 50 000 6) 49 998
в) 39 999
г) числу, в котором 49 единиц первого класса
д) числу, которое на единицу меньше 50 001
е) разности чисел 49 999 и ![]()
5. Чему равна сумма чисел 75 300 и 20?
а) 75 500 6) 75 280
в) 75 320
г) произведению чисел 7532 и 10
д) разности чисел 75 390 и 10
е) числу, которое называют при счете сразу после числа
75 499
4. Логическая задача
— Решите задачу устно.
Вите, Пете и Андрею подарили по видеокассете: одну — с комедией, другую — с веселыми мультфильмами, а третью — с фантастическим фильмом. Кто что получил в подарок, если известно, что Петя и Витя не любят смотреть мультфильмы и в процессе просмотра Петя хохотал до упаду? (Вите — фантастический фильм, Пете — комеДию, Андрею — мультфильмы.)
Ш. Работа по теме урока Работа по учебнику М 153 (с. 46).
![]() Прочитайте условие
задачи. Как двигались поезда? (В противоположных направлениях.)
Прочитайте условие
задачи. Как двигались поезда? (В противоположных направлениях.)
![]() Чему равна скорость
увеличения расстояния между поездами? (Скорость увеличения расстояния между
поезДами равна сумме скоростей этих поезДов: 80км/ч + 70 юи/ч = 150 км/ч.)
Чему равна скорость
увеличения расстояния между поездами? (Скорость увеличения расстояния между
поезДами равна сумме скоростей этих поезДов: 80км/ч + 70 юи/ч = 150 км/ч.)
противоположных направлениях
![]()
— Какое будет расстояние между поездами через ч после их встречи? (150км/ч • 1 ч = 150 км.)
— Какое будет расстояние между поездами через 2 ч после их
встречи? (150 км/ч • 2 ч = ЗОО км.) ![]() 154 (с. 46).
154 (с. 46).
(Коллективное выполнение. Чтение правила.)
![]() Прочитайте условие задачи. Чему равна скорость изменения расстояния
между поездами? (Сумме скоростей этих поезДов: 80 км/ч + 70 км/ч = 150 км/ч.)
Прочитайте условие задачи. Чему равна скорость изменения расстояния
между поездами? (Сумме скоростей этих поезДов: 80 км/ч + 70 км/ч = 150 км/ч.)
— Как будет изменяться расстояние до встречи поездов? (Сокращаться.)
— Через сколько часов произойдет встреча этих поездов? (ЗОО КМ : 150км/ч = 2 ч.)
![]() Как будет изменяться расстояние после встречи поездов? (Увеличиваться.)
Как будет изменяться расстояние после встречи поездов? (Увеличиваться.)
![]() Какое расстояние будет между поездами через 3 ч после встречи? (150 км/ч
• З ч = 450 км.) № 155 (с. 46—47).
Какое расстояние будет между поездами через 3 ч после встречи? (150 км/ч
• З ч = 450 км.) № 155 (с. 46—47).
Вариант заДачи. Из двух населенных пунктов, расстояние между которыми 280 км, по одному маршруту одновременно отправились навстречу друг другу автобус и легковая машина. Через сколько часов они встретятся, если скорости их движения постоянны и равны соответственно 60 км/ч и 80 км/ч?
lV. Физкультминутка
V. Закрепление изученного материала
1. Вьшолнение упражнения в тетради ддя самостте.љной работы ле 64 (с. зэ.
(Самостоятельное выполнение. Проверка в парах.) 2. Работа по учебнику ле 156 (с. 47).
![]() Прочитайте условие задачи и первое требование.
Прочитайте условие задачи и первое требование.
![]() Нужно ли для ответа на это требование знать скорость течения реки?
(Нет.)
Нужно ли для ответа на это требование знать скорость течения реки?
(Нет.)
— Как узнать расстояние между катером и плотом? (20км/ч х х 2 ч = 40км.)
![]() Что еще требуется узнать в задаче? (Какое расстояние преодолел катер за
2 ч.)
Что еще требуется узнать в задаче? (Какое расстояние преодолел катер за
2 ч.)
![]() Можно ли вычислить
это расстояние, зная только скорость катера в стоячей воде? (Нет, чтобы
вычислить расстояние, нужно знать скорость катера против течения реки.)
Можно ли вычислить
это расстояние, зная только скорость катера в стоячей воде? (Нет, чтобы
вычислить расстояние, нужно знать скорость катера против течения реки.)
— Как найти эту скорость, если скорость течения реки 2 км/ч? (20 км/ч — 2 км/ч = 18 км/ч.)
![]()
= 36 км.)
М 157(с. 47).
Вариант заДачи. От одной станции одновременно в противоположных направлениях отправились два поезда. Первый поезд двигался со скоростью 50 км/ч, а второй — со скоростью 70 км/ч. Какое расстояние будет между поездами через 2 ч после отправления?
![]() Как найти расстояние
межщ поездами? ((50км/ч + 70км/ч) х х 2 = 240 км.)
Как найти расстояние
межщ поездами? ((50км/ч + 70км/ч) х х 2 = 240 км.)
— А если бы первый поезд отправился на час раньше второго,
то каким бы было расстояние между ними через 2 ч после того, как выехал второй
поезд? (50 км + 240км = 290 км.) ![]() Как вы рассуждали? (На момент
отправления второго поезда первый поезД уже проехап 50 км, так как его скорость
50 км/ч. К этому расстоянию прибавиш 240 км, на которые увеличшюсь расстояние
между поезДами за 2 ч совместного Движения.)
Как вы рассуждали? (На момент
отправления второго поезда первый поезД уже проехап 50 км, так как его скорость
50 км/ч. К этому расстоянию прибавиш 240 км, на которые увеличшюсь расстояние
между поезДами за 2 ч совместного Движения.)
З. Выполнение упражнений в тетради для самосттељной ра&угы М 65 (с. 35).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]() 66 (с. 36).
66 (с. 36).
1. Решение: l700 м : (50 м/мин + 35 м/мин) = 20 мин.
Ответ: после выхода из дома соседи встретятся через 20 мин.
2. Решение: (50 м/мин + 35 м/мин) • 20 мин = 1700 м. Ответ: расстояние между домами 1700 м.
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 67 (с. 36).
Урок 88. Учимся решать задачи
Цель: развивать навыки решения задач на движение.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
Ариф метический диктант
— Я буду зачитывать вам утверждения, а вы отвечайте «да» или «нет».
Учимся решать задачи
![]()
• Если первый множитель равен 800, а второй — 10, то произведение равно 8000. (Да.)
•
В числе 7600 содержится 6 единиц первого класса. (Нет.) ![]() Если число
2300 увеличить на 50, то получится 2350. (Да.)
Если число
2300 увеличить на 50, то получится 2350. (Да.)
• Разность чисел 1400 и 800 равна 700. (Нет.)
• В числе 7000 всего 700 десятков. (Да.)
• Частное от деления чисел 9000 и 100 равно 9. (Нет.)
• Если число 8000 увеличить в 10 раз, то получится 8010. (нет.)
• Число 5600 больше 600 на 5000. (Да.)
• В ЗЧ 300 мин. (Нет.) Ш. Работа по теме урока Работа по учебнику № 158 (с. 48-49).
— Рассмотрите схемы. Чем они отличаются? (Примерный отват. На схеме а представлено движение в одном направлении из одного пункта, скорость первого объекта больше скорости второго объекта. Первый объект постоянно будет удаляться от второго. На схеме б представлено движение из разных пунктов, скорость второго объекта (догоняющего) больше, чем скорость первого объекта (убегающего). При таком движении расстояние между объектами сначала будет сокращаться (до тех пор, пока второй объект не догонит первый), а потом будет увеличиваться (второй объект начнет удаляться от первого). На схеме в представлено движение из разных пунктов, причем скорость второго объекта меньше скорости первого объекта. В этом случае первый объект в течение всего процесса движения будет удаляться от второго.)
— Прочитайте задачу. Какой схемой нужно воспользоваться для ее решения? (Схемой «Ь.)
— Почему? (По условию заДачи нужно узнать время, за которое пассажирский поезД Догонит товарный.)
— Что нужно узнать сначала? (Скорость изменения расстояния
между поезДами: 80 км/ч — 60 км/ч = 20 км/ч.) ![]() Что можно узнать
теперь? (Время, за которое пассажирский поезД Догонит товарный: 80 км : 20 км/ч
= 4 ч.)
Что можно узнать
теперь? (Время, за которое пассажирский поезД Догонит товарный: 80 км : 20 км/ч
= 4 ч.)
— Какое расстояние будет между поездами через 2 ч после момента обгона, если движение продолжится с теми же скоростями? (20км/ч • 2 ч = 40 км.)
— Какая схема иллюстрирует данное дополнительное требование? (Схема «а». )
 Какие из них похожи
и почему? (Схемы «а» и «в» похожи, так как описывают процесс Движения, при
котором происхоДит постоянное удаление одного объекта от Другого.)
Какие из них похожи
и почему? (Схемы «а» и «в» похожи, так как описывают процесс Движения, при
котором происхоДит постоянное удаление одного объекта от Другого.)
— Что иллюстрирует схема б? (Движение, при котором объекты сначала сближаются (До момента встречи), а потом начинают удаляться друг от Друга.)
![]() Прочитайте задачу. Какая схема к ней подходит? (Схема «а».)
Прочитайте задачу. Какая схема к ней подходит? (Схема «а».) ![]() Что
надо найти сначала? (Скорость изменения расстояния между поезДами: 60 км/ч + 80
км/ч = 140 км/ч.)
Что
надо найти сначала? (Скорость изменения расстояния между поезДами: 60 км/ч + 80
км/ч = 140 км/ч.)
![]() Какое расстояние
будет межщ поездами через 3 ч? ( 140км/ч х х зч = 42004.)
Какое расстояние
будет межщ поездами через 3 ч? ( 140км/ч х х зч = 42004.)
![]() Запишите решение задачи.
Запишите решение задачи.
— Самостоятельно вычислите, через какое время расстояние между поездами будет 280 км, если они будут двигаться с теми же скоростями.
(Проверка с записью решения на доске.)
М. Физкультминутка
У. Закрепление изученного материала
1. Работа по учебнику М 161 (с. 50).
![]() Прочитайте условие
задачи. Как узнать, с какой скоростью должно двигаться другое транспортное
средство при движении в одном и том же направлении? (При ДВИЖИИИ в одном и том
же направлении 60 км/ч Должна составлять разность скоростей. Значит, другое
транспортное среДство должно Двигаться со скоростью 100 км/ч: 100 км/ч — 40
км/ч
Прочитайте условие
задачи. Как узнать, с какой скоростью должно двигаться другое транспортное
средство при движении в одном и том же направлении? (При ДВИЖИИИ в одном и том
же направлении 60 км/ч Должна составлять разность скоростей. Значит, другое
транспортное среДство должно Двигаться со скоростью 100 км/ч: 100 км/ч — 40
км/ч ![]() = 60 км/ч.)
= 60 км/ч.)
— А если объекты движутся в
противоположных направлениях? ( ТогДа 60 км/ч Должна равняться сумма скоростей.
СлеДовательно, скорость Другого объекта 20 км/ч: 40 км/ч + 20 км/ч ![]() =
60 км/ч.)
=
60 км/ч.)
2. Выполнение упражнения в тетради для самостоятельной работы
М 68 (1-3) (с. 37-38).
1. Решение:
1) (50 + 60) • 3 = 330 (км) — расстояние между поездами через 3 ч; 2) 600 : 50 = 12 (ч) — время в пути поезда, идущего со скоростью 50 км/ч;
3) 600 : 60 = 10 (ч) — время в пути поезда, идущего со скоростыо 60 км/ч;
Поупражняемся в вычислениях и повторим пройденное
![]()
Ответ: поезд, идущий со скоростью 60 км/ч, прибудет на станцию раньше поезда, идущего со скоростью 50 км/ч, на 2 ч. 2. Решение:
1) (90 + 60) • 2 = 300 (км) — расстояние между ними через 2 ч;
2) 450
: = з![]()
Ответ: через 3 ч расстояние между поездами будет 450 км.
3. Решение:
1) 660 : (70 + 40) = 6 (ч) — время, через которое поезда встретятся;
2) (70 - 40) • (км).
Ответ: встреча произойдет на расстоянии 180 км от каждой из станций отправления.
И. Подведение итогов урока
Домашнее задание
Учебник: М 162 (с. 50).
Урок 89. Поупражняемся в вычислениях и повторим пройденное
Цели: повторить пройденный материал; развивать вычислительные навыки.
1. Организационный момент. Сообщение темы и целей урока ll. Актуализация знаний 1. Эстафета по рядам
Первый ряд
1 ООО - 200
880 - 80
710- Ш
660 — 60
820 - 800
1 ООО - ЗОО
2. Цифровой квадрат
![]() 23
23
15
16 22
8 Поурочные по математике
|
Второй ряд |
Третий ряд |
|
650 - 50 |
430 — 400 |
|
|
980 — 900 |
|
290 - |
- 700 |
|
1000 - 600 |
950 - 50 |
|
370 - 70 |
1000 - |
|
170- 10 |
440 — 40 |
|
12 |
|
|
4 |
|
Ответ:
![]()
З. Волшебные квадраты
|
папа |
|
п•пп |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
пап |
|
|
|
|
|||||
Ответы:

4. Родственные ряды
|
9 |
15 |
|
|
36 |
|
2 |
4 |
9 |
|
|
( числа нижнего ряда получаются в результате Деления соответствующих чисел верхнего ряда на З и вычитания еДиницы. В верхнем ряду пропущено число 6, в нижнем ряду — 11.)
5. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Три девочки — Таня, Катя и Марина — занимаются в трех различных кружках — вышивки, танцев и хорового пения. Катя не знакома с девочкой, занимающейся танцами. Таня часто ходит в гости к девочке, занимающейся вышивкой. Подружка Кати — Марина хочет в следующем году добавить к своим увлечениям занятия пением. Кто из девочек чем занимается? (Катя — пением, Таня — танцами, Марина — вышивкой.)
Ш. Работа по теме урока Работа по учебнику Л) 163 (с. 51). (Самостоятельное выполнение. Проверка в парах.) ЛФ 164 (с. 51).
(Проверка с записью решения на доске.)
Решение: пусть одна часть — деньги, истраченные на рынке, а четыре части — деньги, истраченные в магазине.
1) 4— 1 = З (ч.) — разностное сравнение частей денег;
Поупражняемся в вычислениях и повторим пройденное
![]()
2) 1563 : 3 = 521 (руб.) — истрачено на рынке; 3) 521 • 4 = 2084 (руб.) — истрачено в магазине; 4) 2084 + 521 = 2605 (руб.).
Ответ: всего покупатель истратил 2605 руб. ![]() 165
(с. 51).
165
(с. 51).
Вариант заДачи. Из двух населенных пунктов одновременно в одном и том же направлении отправились грузовой автомобиль со скоростью 70 юи/ч и легковой — со скоростью 80 юи/ч. Грузовой автомобиль двигался вслед за легковым. Какое расстояние будет между автомобшшми через 2 ч движения?
Решение:
Первый способ:
1) 70 • 2 = 140 (км) — проедет грузовик;
2) 80 • 2 = 160 (км) — проедет легковой автомобиль; 3) - = 20 (км).
ВтороЙ способ:
1) 80 — 70 = 10 (км/ч) — скорость изменения расстояния между автомобилями;
2)
![]() 10 • 20 (км). Ответ: через 2 ч расстояние между автомобшшми будет 20
км.
10 • 20 (км). Ответ: через 2 ч расстояние между автомобшшми будет 20
км.
lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ЛФ 166 (с. 51).
Вариант заДачи. От двух станций одновременно навстречу друг другу отправились два поезда: товарный и пассажирский. Скорость товарного поезда 50 юи/ч, а скорость пассажирского 60 км/ч. Через сколько часов расстояние между поездами будет 1 10 км?
Решение:
1) 60 + 50 = 1 10 (км/ч) — скорость изменения расстояния между поездами;
Ответ: через ч расстояние между поездами будет км.
2.
Выполнение
упражнения в тетради для самостоятельной рабшы ![]() 70 (с. 39).
70 (с. 39).
(Самостоятельное выполнение. Проверка в парах.) Решение:
1) 144 : 48 = З (ч) — время автобуса в пути;
2) 3 ч + 10 мин • 2 = 3 ч 20 мин = 200 мин — время в пути автобуса с остановками;
З) 135 : 54 = 2 ч 30 мин = 150 мин — время в пути электрички;
![]()
4) 150 мин + 5 мин • 5 — 175 (мин) — время в пути электрички с остановками;
5) 200 мин — 175 мин = 25 мин.
Ответ: на электричке добираться до города быстрее на 25 мин. И. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 69 (с. 39).
Цели: проверить знания и умения учащихся; развивать навыки самостоятельной работы.
(Текст контрольной работы выдается каждому ученику на отдельном листочке. )
Вариант 1
1. Найди два числа, значение суммы которых равно 21, а значение разности — 3.
2. Используя буквенные выражения, запиши решение следующей задачи.
Для поздравления с Новым годом Маша купила а открыток по цене 12 руб. и конверты, стоимость которых 25 руб. Найди стоимость покупки Маши.
Вычисли значение составленного выражения, если а = 11.
3. Вычисли и запиши значение выражения. 34 : (91 : 7-9).
4. Реши задачи. Вычисли и запиши ответ каждой из них.
• Скорость гоночного автомобиля 240 км/ч. Какое расстояние пройдет автомобиль за 4 ч?
• Слесарь за 2 смены вытачивает 6 деталей. Сколько смен потребуется слесарю, чтобы выточить 30 деталей?
Вариант 2
1. Найди два числа, значение суммы которых равно 20, а значение частного — 3.
2. Используя буквенные выражения, запиши решение следукощей задачи.
К Новому году Миша купил Ь синих шаров по цене 14 руб. и мишуру, стоимость которой 28 руб. Найди стоимость всей покупки Миши.
Вычисли значение составленного выражения, если Ь = 11.
3. Вычисли и запиши значение выражения.
52 : (85 : 5-9)
91 время работы одинаковое
![]()
4. Реши задачи. Вычисли и запиши ответ каждой из них.
• Скорость пешехода 65 м/мин. Какое расстояние пройдет пешеход за 3 мин?
• Швея за 3 ч может сшить 9 наволочек. Сколько часов потребуется швее, чтобы сшить 27 наволочек?
Урок 91 Когда время работы одинаковое
Цели: показать прямую зависимость объема выполненной работы от производительности в случае, если время работы одинаковое; развивать навыки решения задач.
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: • 2, : З; пропущенные числа — 30 и 10.)
2. Цифровой квадрат
|
|
|
23 Ответ: 15 |
17 |
6 |
|
|
|
|
|
25 В
З. Родственные ряды
|
2 |
|
5 |
6 |
8 |
|
8 |
9 |
5 |
4 |
|
(Сумма соответствующих чисел верхнего и нижнего рядов равна 10. Пропущено число 2.)
4. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Какие геометрические фигуры тебе известны? (Точка, линия (кривая, прямая, ломаная), луч, отрезок, угол (прямой, тупой, острый), круг, многоугольники (треугольник, четырех-, пяти-, шестиугольник и т. д.), многогранники (пирамиДа, призма, куб), фигуры (тела) вращения (конус, ЦШШНДр, шар). )
![]()
• Какая линия является границей многоугольника? (Замкнутая ломаная.)
• Какая фигура называется прямоугольником? ( Четырехугольник, у которого все углы прямые, а противоположные стороны равны.)
• Какая фигура называется квадратом? (Прямоугольник, у которого все стороны равны.)
• Какие виды треугольников тебе известны? Как их распознать? (Прямоугольный (есть прямой угол), остроугольный (все углы острые), тупоугольный (есть тупой угол); разносторонний (все стороны разной длины), равносторонний (Длины всех трех сторон равны), равнобеДренный (длины хотя бы двух сторон равны). )
5. Устный счет
(Примеры записаны на доске.)
|
|
|
|
|
67 дес. ... ед.
|
38 сот. |
ед. |
|
2 т 9 кг — . кг |
8Т8 Ц |
|
Ш. Работа по теме урока Работа по учебнику ![]() 167 (с. 52).
167 (с. 52).
![]() Прочитайте задачи. Чем они
отличаются? (Одна задача на Движение, а Другая задача на работу.)
Прочитайте задачи. Чем они
отличаются? (Одна задача на Движение, а Другая задача на работу.)
— Чем они похожи? (Математическая суть рассматриваемых зависимостей одна и та же.)
![]() Решите задачи. Вычислите и запишите
ответы.
Решите задачи. Вычислите и запишите
ответы.
М 168 (с. 52).
![]() Прочитайте вопрос.
От чего зависит объем произведенной продукции, если время работы останется тем
же? (Ответы детей.)
Прочитайте вопрос.
От чего зависит объем произведенной продукции, если время работы останется тем
же? (Ответы детей.)
Если время работы одинаковое, то увеличение (уменьшение) производительности в некоторое число раз приводит к увеличению (уменьшению) объема выполненной работы в это же число раз.
Давайте проверим это правило на примере, который предлагают авторы учебника.
— Что нужно сделать сначала? (Вычислить, при какой произвоДительности за восьмичасовой рабочий день изготавливают 120 Деталей: 120 : 8 = 15 (Дет./ч).)
![]() Как можно увеличить
число деталей, изготавливаемых за такой же рабочий день? (Увеличить
произвоДительность Деталей за 1 ч, например, в З раза: 15 • З = 45 (Дет./ч).)
Как можно увеличить
число деталей, изготавливаемых за такой же рабочий день? (Увеличить
произвоДительность Деталей за 1 ч, например, в З раза: 15 • З = 45 (Дет./ч).)
объем выполненной работы одинаковый
Как изменится объем произведенной продукции? (45 • 8 =
= 360 (Дет.). )
Как проверить правило? (360 дет. : 120 Дет. = З (раза). )
— Что мы выяснили? (При оДинаковом
времени работы увеличение произвоДительности в некоторое число раз привоДит к
увеличению объема выполненной работы в это же число раз. ) lV. Физкультминутка ![]()
М. Закрепление изученного материала
1. Работа по учебнику Лё 169 (с. 52).
(Коллективное выполнение с комментированием.)
2. Вьшшшение упражнения в тетра№ для самосттельной ра&уты ле 72 (с. 40-41).
(Задача I — коллективное выполнение с комментированием, задача 2 — самостоятельное выполнение с проверкой в парах.) Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 71 (с. 40).
Урок 92. Когда объем выполненной работы одинаковый
Цели: показать взаимосвязь времени и производительности при одинаковом объеме выполненной работы; развивать навыки решения задач.
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний тест
(Выдается на отдельных листочках.)
1. Найди число, в котором 7 единиц девятого разряда, 5 единиц седьмого разряда, 3 единицы шестого разряда, 9 единиц четвертого разряда, 2 единицы второго разряда, I единица первого разряда.
1)
750 390 3) 705 390![]()
2) 705 039 021 4) 705 309 021
2. Сколько в числе 627 980 единиц тысяч? 1) 62
2) 6279 4) 627
![]() 296 3)
406 100 • 372
296 3)
406 100 • 372
2) 418 • 392 4) 408 то • 382
5. Посчитай: с • 7, где с = 236 663.
![]() 22 175 3)
086 475
22 175 3)
086 475
2) 1 656641 4) 108 275
6. Из одного пункта в противоположных направлениях одновременно выехали два скутериста. Через 3 ч расстояние между ними было 300 км. Скорость первого скутериста 40 км/ч. С какой скоростью ехал второй скутерист?
1) 50 км/ч З) 70 км/ч 2) 60 км/ч 4) 80 км/ч
7. Раздели с остатком: 89 070 : 100.
1) 89 (ост. 70) 3) 890(ост. 70)
2) 89 (ост. 7) 4) 8 (ост. 907)
8. В четырех пакетах умещается 15 кг крупы. Сколько нужно пакетов, чтобы разместить 75 кг крупы? 1) 15 3) 20
4) 25
9. Из одной норы одновременно в разных направлениях побежали две мыши. Когда одна из них пробежала 4 м со скоростью 20 см/с, расстояние между ними стало 7 м. Найди скорость второй мыши.
1) 10 см/с 3) 25 см/с
2) 15см/с 4) 30 см/с
10. Площадь участка 84 кв. м, его ширина 7 м. Найди периметр участка.
1) 36 м 3) 19м 2) 17 м 4) 38 м
11. Вставь пропущенное число: м — ... см.
3) 100
2) 50 4) 1000
1 1. Вырази в сантиметрах 37 000 мм.
1) 37 см 3) зтосм
2) 370 см 4) 370 000 см
12. Вставь пропущенные числа.• 278с = ... мин . . с.
1) 2 мин 78 с 3) 4 мин 18 с
2) 5 мин 28 с 4) 4 мин 38 с
13. Вставь пропущенное число: кв м кв. см.
3) 10000
2) 1000 4) 100 000
14. Вставь пропущенное число: сут![]()
1) 24 3) 18
2) 20 4) 26
объем ВЫПОЛНеННОЙ работы одинаковый

16. Запиши ответ: 46 кв. м — . (46 ООО ООО) кв. мм.
17. Запиши, как называется год, в котором 366 суток. (ВИСОкосный.)
18. Запиши решение задачи и ответ.
Участок земли имеет форму прямоугольника, длина которого 80 м, а ширина на 50 м меньше. Он обнесен проволокой в 9 рядов. Сколько метров проволоки потребовалось?
Решение:
1) 80 — 50 = 30 (м) — ширина участка земли;
2) (80 + 30) • 2 = 220 (м) — периметр прямоугольного участка земли;
3)
220 • 1980![]()
Ответ: потребовалось 1980 м проволоки.
Ш. Работа по теме урока Работа по учебнику ![]() (с. 53).
(с. 53).
(Коллективное выполнение с комментированием.) ![]() 171
(с. 53).
171
(с. 53).
Решение:
360 мин = 6 ч;
12 ч : 6 ч = 2 (раза).
Ответ: производительность пекарни должна увеличиться в 2 раза.
ЛГ2 172 (с. 54).
(Коллективное выполнение с комментированием. Чтение правила.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ЛЕ 173 (с. 54).
(Самостоятельное выполнение. Проверка в парах.) ![]() 174 (с. 54).
174 (с. 54).
(Выполнение в соответствии с заданиями.)
![]() Сформулируйте правило. (При
оДшшковом объеме роты увеличеше (уменьшение) произвоДителычости в нескапжораз
приОит к уменьшению (увеличению) времени в это же число раз.)
Сформулируйте правило. (При
оДшшковом объеме роты увеличеше (уменьшение) произвоДителычости в нескапжораз
приОит к уменьшению (увеличению) времени в это же число раз.)
— Чем это правило отличается от правила, сформулированного в № 172? (Меняется направление зависимости между величинами, в Данном мучае время зависит от производительности.)
![]()
2, Выполнение упражнения в тетрам для самосттельной рабсгы М 73 (с. 42).
(Самостоятельное выполнение.)
Ш. Подведение итогов урока
Домашнее задание ![]()
Тетрадь для самостоятельной работы: № 74 (с. 42).
Урок 93, Производительность при совместной работе
Цель: познакомить с решением задач на вычисление производительности при совместной работе.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
П |
12 |
|
4 |
15 |
![]() 23 Ответ:
23 Ответ:
19
15 27
2. Волшебная звезда
(Сумма = 26.)
 Ответ:
Ответ:
З. Родственные ряды
|
6 |
2 |
|
8 |
|
|
|
2 |
4 |
|
|
Производительность при совместной работе
![]()
( Числа нижнего ряда получаются в результате умножения соответстзующих чисел верхнего ряда на 2 и вычитания числа 2. В верхнем ряду пропущено число З, в нижнем ряду — 20.)
4. Логическая задача
— Решите задачу устно.
Миша, Коля и Настя решили помочь маме собрать смородину, крыжовник и вишню. КаЖДЫЙ из них собирал что-то одно. Кто что собирал, если известно, что больше всего было собрано смородины, Миша не собирал крыжовник, а Миша и Коля вдвоем набрали ягод меньше, чем Настя? (Миша собирал вишню, Коля — крыжовник, Настя — смородину.) Ш. Работа по теме урока Работа по учебнику м 175 (с. 55).
(Коллективное выполнение.)
![]() Прочитайте задачу.
Какого она типа? (На произвоДительность при совместной работе. )
Прочитайте задачу.
Какого она типа? (На произвоДительность при совместной работе. )
![]() Как находится производительность при
совместной работе? (Сложением исходных производительностей.)
Как находится производительность при
совместной работе? (Сложением исходных производительностей.) ![]() 176 (с.
55).
176 (с.
55).
— Прочитайте задание. Установите взаимосвязь общей производительности и индивидуальных производительностей при совместном выполнении одинаковой работы. Запишите решение задачи и ответ.
Решение:
1) 96 : 8 = 12 (дет./ч) — производительность первою контролера; 2) 12 + 10 = 22 (дет./ч).
Ответ: оба контролера за ч проверят 22 детали.
№ 177(с. 55).
![]() Прочитайте
условие задачи. Что ну,ю-ю определить сначала? (Сколько магнитофонов привозят
на склаД за день: 20 • 8 =
Прочитайте
условие задачи. Что ну,ю-ю определить сначала? (Сколько магнитофонов привозят
на склаД за день: 20 • 8 =
— 160![]()
— С помощью какого действия можно установить скорость заполнения склада готовой продукцией? (Вычитания.) — Найдите эту скорость. (160— 150 = 10 (шт.).)
— Можно ли теперь ответить на основное требование задачи?
ща: 1000: = то ![]() М 178 (с. 56).
М 178 (с. 56).
![]() Прочитайте
задачу. Чему равны исходные производительности за сутки? (80 куб. м/сут. и 24 •
З куб. м/ч = 72 куб. м/сут.) — Чему равна итоговая производительность? (80 куб.
м/сут.
Прочитайте
задачу. Чему равны исходные производительности за сутки? (80 куб. м/сут. и 24 •
З куб. м/ч = 72 куб. м/сут.) — Чему равна итоговая производительность? (80 куб.
м/сут. ![]()
— 72 куб. м/сут. = 8 куб. м/сут.)
Чему равна половина вместимости бассейна? (32006. м : 2 = = 160 куб. м.)
Чему равно искомое время? (160 куб. м : 8 куб. м/сут.![]()
= 20 суп.)
IV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 179 (с. 56).
Вариант заДачи. Первая бригада за 5 ч работы обрабатывает 135 деталей. Если эту же работу вместе с первой бригадой будет выполнять и вторая бригада, то они за 3 ч смогут обработать 150 деталей. С какой производительностью в этом случае будет работать вторая бригада, если производительность первой бригады не будет меняться?
Решение:
1) 135 дет. : 5 ч = 27 дет./ч — производительность первой бригады;
2) 150 дет. : 3 ч = 50 дет./ч — производительность при совместной работе;
3) 50 дет./ч — 27 дет./ч = 23 дет./ч.
Ответ: вторая бригада будет работать с производительностью 23 детали в час.
М 180 (с. 56).
(Самостоятельное выполнение. Проверка в парах.) Решение: 20 000 : 4 - 3000 = 2000 (экз.дн.).
Ответ: вторая типография работает с производительностью 2000 экземпляров в день.
2. Выполнение упражнения в тетради для самостоятельной работы
М 75 (с. 42-43).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 76 (с. 44).
Урок 94. Время совместной работы
Цель: научить определять время совместной работы.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
Время совместной работы
![]()
ll. Актуализация знаний
Арифметический диктант
— Запишите только ответы.
• Если все собранные яблоки разложить в ведра по 10 кг в каждое, то понадобится 5 ведер. Сколько килограммов яблок собрали? (50 кг.)
• Каждую минуту автомат закрывает 180 банок. Сколько банок закрывает автомат за 4 мин? ( 720.)
• В булочной до обеда продали 220 батонов, а после обеда —
360 батонов. Сколько всего батонов продали за день? (580.) • На товарной станции разгрузили 70 вагонов с овощами, а с фруктами — в 2 раза меньше. Сколько вагонов с фруктами разгрузили? (35.)
• В математической олимпиаде участвовали 120 школьников. Они сидели поровну в шести комнатах. Сколько школьников было в одной комнате? (20.)
• В магазин привезли 240 букетов роз и 120 букетов гвоздик. На сколько больше привезли букетов роз, чем букетов гвоздик? (На 120.)
• Сколько яиц в ящике, если они лежат в 10 рядов по 90 штук в каждом? (900.)
• В школе собрали 400 кг макулатуры. Две восьмых всей бумаги собрал 1 класс. Сколько килограммов макулатуры собрали остальные классы? (300 кг.)
• В типографии после рабочей смены находилось 60 книг. Одна третья часть всех книг в переплете. Сколько книг без переплета? (40.)
• В двух пакетах по 62 ореха. Из одного пакета взяли 19 орехов, а из другого — столько, сколько осталось в первом. Сколько орехов осталось в двух пакетах? (62.)
Ш. Работа по теме урока Работа по учебнику
М 181 (с. 57).
(Коллективное выполнение.)
— Рассмотрите таблицу. Прочитайте задание.
![]() Какие бригады нужно пригласить? (Первую,
вторую и третью. )
Какие бригады нужно пригласить? (Первую,
вторую и третью. ) ![]() Как вы определили? (4 + 6 + 2 = 12
(зД./гоД).)
Как вы определили? (4 + 6 + 2 = 12
(зД./гоД).)
— Сколько месяцев потребуется каждой бригаде для строительства одного здания, если их производительность не изменится? (Первой — 12 : 4 = З (мес.), второй — 12 : 6 = 2 (мес.), третьей — 12 : 2 = 6 (мес.), четвертой — 12 : З = 4 (мес.).)
— Сколько времени потребуется каждой бригаде, чтобы построить 12 зданий? (Первой — З • 12 = (36 мес.), второй —
![]()
2 • 12 = 24 (мес.), третьей — 6 • 12 = 72 (мес.), четвертой — 4 , 12 = 48(мес.).)
При выполнении одного и того же объема работы время совместной работы меньше, чем время любой индивидуальной работы.
м 182 (с. 57).
Решение:
1) 48 сот. : 6 дн. + 48 сот. : 3 дн. 24 сот./дн. — производительность при совместной работе;
2) 48 сот. : 24 сот./дн. = 2 дн.
Ответ: обе бригады при совместной работе собрали бы весь урожай за 2 дня.
![]() Изменится ли ответ задачи, если
изменится площадь участка? (Примерный ответ. Нет, так как в данном случае время
связано не с объемом выполненной работы, а с индивидуальной производительностью
каждой бригады. С уменьшением (увеличением) площади участка в несколько раз
производительность уменьшится (увеличится) в это же число раз, а время останется
тем же.) № 183 (с. 57).
Изменится ли ответ задачи, если
изменится площадь участка? (Примерный ответ. Нет, так как в данном случае время
связано не с объемом выполненной работы, а с индивидуальной производительностью
каждой бригады. С уменьшением (увеличением) площади участка в несколько раз
производительность уменьшится (увеличится) в это же число раз, а время останется
тем же.) № 183 (с. 57).
— Прочитайте задачу. Как вы будете рассуждать? (Примерный ответ. Так как все коровы поедают корма с одинаковой скоростью, то две коровы съедят весь запас кормов за то же время, за которое одна корова съест половину этого запаса: 6 : 2 = 3 (дн.). Три коровы съедят весь запас кормов за то же время, за которое одна корова съест третью часть всех кормов: 6 : 3 = 2 (дн.). Шесть коров съедят весь запас кормов за то же время, за которое одна корова съест шестую часть всех кормов: 6 : (дн.).)
М. Физкультминутка
V, Закрепление изученного материала 1. Работа по учебнику м 184 (с. 58).
— Прочитайте задание. Как найти совместную производительность? (Разделить объем работы на время: 48 : 8 = 6 (ап./ч).)
— Что можно найти далее? (ПроизвоДительность первого контролера: 48: 12 = 4 (ап./ч).)
— Найдите разницу между индивидуальными производительностями. (6 — 4 = 2 (ап./ч).)
![]() Сколько времени
потребуется второму контролеру на всю эту работу, если он будет работать один и
с той же производительностью? (48 : 2 = 24 (ч).)
Сколько времени
потребуется второму контролеру на всю эту работу, если он будет работать один и
с той же производительностью? (48 : 2 = 24 (ч).)
Учимся решать задачи и повторяем пройденное
![]()
М 185 (с. 58).
Вариант заДачи. Первая бригада за 9 дней работы может выпустить 36 т продукции. Вторая бригада этот же объем продукции может выпустить за 1 8 дней. Сколько дней потребуется бригадам для выпуска этой же продукции, если они будут работать совместно и с той же производительностью?
![]() Решите задачу самостоятельно. Вычислите
и запишите ответ. м 186 (с. 58).
Решите задачу самостоятельно. Вычислите
и запишите ответ. м 186 (с. 58).
— Прочитайте задание. Как вы будете рассуждать? (Пршиерный ответ. Если две бригады работают с одинаковой производительностью, то для выполнения всей работы им нуто столько же времени, сколько и для выполнения всей рабом одной бригадой, так как вторую половину работы выполняет вторая бригада. Одной бригаде на выполнение половины работы нужно в 2 раза меньше времени, чем на выполнение всей работы. Значит, время совместной работы двух бригад будет также в 2 раза меньше, чем время работы одной бригады.) № 187 (с. 58).
(Устное выполнение.)
2. Вьшолнекме упражнения в тетрад для самостятељной работы № 78 (1, 2) (с. 46).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 77 (1, 2) (с. 45).
Урок 95. Учимся решать задачи и повторяем пройденное
Цели: повторить пройденный материал; развивать навыки решения задач.
1, Организационный момент. Сообщение темы и целей урока ll. Актуализация знаний
1. Устный счет
— Выберите все правильные ответы.
(Варианты ответов даны на доске.)
1.
Чему равно делимое, если делитель равен 100, а частное![]()
а) 10 6) 1000
![]()
в) 110
г) произведению чисел 0 и 1000
д) разности чисел 70 ООО и 69 ООО
2. Число 12 000 — это:
а) сумма чисел 10 ООО и 2000
б) произведение чисел 1000 и 12 000
в) разность чисел 20 000 и 8000
г) частное от деления чисел 120 000 и 100
д) сумма чисел 9000 и 3000
3. Как можно вычислить площадь прямоугольника со сторонами 4 см и 6 см?
![]() 4+4
4+4
2. Цифровой квадрат
|
|
|
l9 Ответ: 19 |
8 |
|
|
|
|
|
12 |
15 23
З. Родственные ряды
|
З |
5 |
|
6 |
8 |
|
|
|
6 |
|
69 |
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на СшиИХ себя и прибавления числа 5. Попущено число 41.) 4. Логическая задача
— Решите задачу устно.
Трое друзей — Игорь, Андрей и Владимир — имеют собак — овчарку, пуделя и добермана. Игорь живет в одном подъезде с владельцем пуделя. Доберман, выходя вечером гулять со своим хозяином, всегда очень радуется, встречая Владимира с его собакой, но не любит пуделя и всегда злобно облаивает его при встрече. У кого из мальчиков какая собака? (У Игоря — Доберман, у ВлаДимира — овчарка, у Андрея — пуДель.)
lll. Работа по теме урока
1. Работа по учебнику
М 188 (с. 59).
(Перед решением задачи учащиеся чертят схему.)
Учимся решать задачи и повторяем пройденное
![]()
Решение:
1) 2 м/день + 3 м/день = 5 м/день — совместная производительность;
2) 1000 м : 5 м/день = 200 дн.
Ответ: бригады встретятся через 200 дней.
2.
Выполнение
упражнения в тетрац для самосоягељной работы ![]() 81 (с. 47).
81 (с. 47).
(Самостоятельное выполнение. Работа в парах.) З. Работа по учебнику ЛЕ 189 (с. 59).
Вариант заДачи. За 8 ч работы в первом цехе выпустили 2568 м ткани. Сколько метров ткани за это же время выпустили во втором цехе, если производительность во втором цехе на 10 м/ч больше, чем в первом?
Решение:
Первый способ:
1) 2568 м : 8 ч = 321 м/ч — производительность в первом цехе; 2) 321 м/ч + 10 м/ч = 331 м/ч — производительность во втором цехе;
3. 331 м/ч • 2648 м.
Второй способ:
1) 10 м/ч • 8 ч = 80 м — выпустят больше во втором цехе за 8 ч; 2) 2658 м + 80 м = 2648 м.
Ответ: во втором цехе за 8 ч выпустят 2648 м ткани.
ЛГ2 190 (с. 59).
(Самостоятельное выполнение.)
М. Физкультминутка
V. Закрепление изученного материала Работа по учебнику
М 191 (с. 60). (Самостоятельное выполнение.) № 192 (с. 60).
— Прочитайте задачу. Какого она типа? (На совместную работу, в которой вычисление произвоДительности ученика представляет собой задачу на сумму и частное.)
— Что нужно сделать сначала? (Вычислить совместную произвоДительность: 24 : 2 = 12 (Дет./ч).)
![]() Как найти
производительность ученика? (Нужно ВОСПОЛЬЗОваться предложенной схемой, в
которой вся полоска изображает произвоДительность мастера и ученика, за одну
часть примем произвоДительность ученика, а за три части — произвоДительность
мастера. )
Как найти
производительность ученика? (Нужно ВОСПОЛЬЗОваться предложенной схемой, в
которой вся полоска изображает произвоДительность мастера и ученика, за одну
часть примем произвоДительность ученика, а за три части — произвоДительность
мастера. )
Сколько всего частей? (1 + З = 4 (ч.).)
Как найти производительность ученика? ( 12 : 4 = З (Дет./ч).) Как найти производительность мастера? (З • З = 9 (Дет./ч).)
— За какое время сможет обработать 24 детали ученик?
193 (с. 61).
Прочитайте задачу. Какого она типа? (На совместную работу, в которой вычисление произвоДительности ученика представляет собой задачу на сумму и разность.)
![]() Как найти
производительность ученика? (Нужно воспользоваться предложенной схемой, в
которой вся полоска изображает производительность мастера и ученика.)
Как найти
производительность ученика? (Нужно воспользоваться предложенной схемой, в
которой вся полоска изображает производительность мастера и ученика.)
![]() Как найти совместную
производительность? (24 : 2 —
Как найти совместную
производительность? (24 : 2 — ![]() 12 (Дет./ч).)
12 (Дет./ч).)
— Как найти производительность ученика? ((12 — 6) : 2 = — З (Дет./ч).)
— Найдите производительность мастера. (З + 6 = 9 (Дет./ч).) — Выполните проверку. (З Дет./ч + 9 Дет./ч = 12 Дет./ч.) № 194 (с. 61).
(Самостоятельное выполнение.) № 195 (с. 61).
(Самостоятельное выполнение. Вариант 1 —
а; вариант 2 — б.) ![]() Вспомните правило порядка выполнения
действий в выражениях со скобками.
Вспомните правило порядка выполнения
действий в выражениях со скобками.
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 80 (с. 47).
Урок 96. Когда количество одинаковое
Цели: показать взаимосвязь цены и стоимости; развивать навыки решения задач.
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: • З, : 2; пропущенные числа — ЗОИ 15.)
Когда количество одинаковое
![]()
2. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Что такое периметр многоугольника? (Сумма длин всех его сторон.)
• Как вычислить периметр многоугольника? квадрата? (Периметр прямоугольника вычисляется так: а • 2 + Ь • 2, или (а + Ь) • 2, или а + Ь + а + Ь. Периметр кваДрата вычисляется так: а 4 или а + а + а + а.)
• Как вычислить площадь прямоугольника? квадрата? (Площадь прямоугольника вычисляется так: а • Ь. ПлощаДь кваДрата вычисляется так: а • а.) З. Логическая задача
• Решите задачу устно.
У паука 4 пары ног, а у козленка 2 пары ног. На сколько ног меньше у козленка, чем у паука? (На 4.)
lll. Работа по теме урока Работа по учебнику М 196 (с. 62).
(Коллективное выполнение.)
![]() Можно ли записать
решение всех трех задач с помощью одного числового выражения? (Да: (40 • 2 • 4)
: (40 • 4)
Можно ли записать
решение всех трех задач с помощью одного числового выражения? (Да: (40 • 2 • 4)
: (40 • 4) ![]() = 2 (раза). )
= 2 (раза). )
![]() Во сколько раз стоимость
второй покупки больше, чем стоимость первой? (В 2 раза.)
Во сколько раз стоимость
второй покупки больше, чем стоимость первой? (В 2 раза.)
![]() Какой можем сделать вывод? (При увеличении цены в несколько раз
стоимость увеличивается в это же число раз.) lV. Физкультминутка
Какой можем сделать вывод? (При увеличении цены в несколько раз
стоимость увеличивается в это же число раз.) lV. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику м 197, 198€. 62).
(Устное выполнение.)
2. Выполнекме упражнений в тетради для самосгоягељной
работы ЛЕ 82 (с. 48). (Устное выполнение.) ![]() 83 (с. 48).
83 (с. 48).
Решение:
1) 45 • 2 = 90 (руб.) — цена помидоров;
2)
45 : 3 = 15 (руб.) — цена огурцов; З) 15 : 5 = 3 (руб.) — цена моркови;
4) 45 + 90 + ![]() 153 (руб.).
153 (руб.).
Ответ: стоимость всех овощей 153 руб.
![]()
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 87 (с. 50).
Урок 97 в Когда стоимость одинаковая
Цели: показать взаимосвязь цены и количества товара при одинаковой стоимости; развивать навыки решения задач.
![]() Организационный момент. Сообщение темы и целей урока ll. Актуализация
знаний
Организационный момент. Сообщение темы и целей урока ll. Актуализация
знаний
1. Устный счет
(Примеры записаны на доске. Учащиеся по цепочке называют только ответы. )
|
930 - зоо |
750 + 50 |
|
340 + 60 |
340 + 500 |
|
560 + 70 |
270 - 50 |
|
980 - 80 |
180 - 90 |
|
360 - 70 |
720 — 40 |
|
620 - 40 |
100 - 100 |
|
1000 - 900 2. Цифровой квадрат |
|
|
21 |
19 |
|
22 |
8 |
|
21 |
|
|
|
|
40 Ответ:
43 27
З. Родственные ряды
|
2 |
4 |
6 |
8 |
|
|
2 |
8 |
18 |
32 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 1, 2, З, 4, 5. Пропущено число 50.)
4. Логическая задача
— Решите задачу устно.
У Пети, Саши и Вовы было два ранца и один портфель. Какой предмет был у каждого из мальчиков, если известно, что у Пети
Когда стоимость одинаковая
![]()
и Саши были одинаковые предметы? (У Пети и у Саши — ранцы, у Вовы — портфель.)
lll. Работа по теме урока
Работа по учебнику ![]() 199 (с. 63).
199 (с. 63).
(Коллективное выполнение.)
— Какую зависимость вы заметили? (При увеличении цены в 2 раза количество купленного товара уменьшается в 2раза, если стоимость покупки остается одной и той же.) М 200 (с. 63). (Устное выполнение. Чтение правила.) М 201 (с. 64).
(Самостоятельное выполнение. Проверка в парах.)
М. Физкультминутка
V. Закрепление изученного материала
1.
Работа по учебнику ![]() ЛФ 202 (с. 64).
ЛФ 202 (с. 64).
(Самостоятельное выполнение. Проверка в парах.) Решение:
Первый способ:
1)15 • 20 = 300 (руб.) — стоимость огурцов; 2) зоо : 30 = (кг).
Второй способ:
1) 30 : 15 = 2 (раза) — кратное сравнение цен; 2) 20 : 2 = Ш (кг).
Ответ: на эти же деньги можно было бы купить 10 кг помидоров.
![]() 203 (с. 64).
203 (с. 64).
Вариант заДачи. За 4 кг курицы заплатили 300 руб. Купленная рыба по цене оказалась в 2 раза дороже, чем курица. Сколько килограммов рыбы купили, если за нее заплатили 600 руб. ?
№ 204 (с. 64).
(Устное выполнение.)
2. Выполнение упражнения в тетради для самостоятельной работы
М 85 (с. 49).
(Выполнение в соответствии с заданиями.) Ш. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 86 (1, 2) (с. 50).
![]()
Урок 98. Цена наборов товаров
Цель: познакомить с решением задач на определение цены наборов товаров.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Волшебные квадраты
— Заполните пустые клетки цифрами от 0 до 8. Волшебная сумма равна 12.
|
пап |
|
|
|
|
|
апп апа |
||||
|
|
|
|
поа ваа |
|||||||
|
|
|
|
|
|
|
|||||
Ответы:

2. Устный счет
(Величины записаны на доске.) — Сравните.
|
1 ч ... 60 мин 1 м ... 1 дм Ш мм ... см |
4 м 5 дм ... 5 м 4 дм 600 мин ... 6 ч 8 м 7 дм ... 7 м 8 дм |
![]() Каждую длину выразите в миллиметрах. 5 дм, 9 дм, 12 дм, 45 дм.
Каждую длину выразите в миллиметрах. 5 дм, 9 дм, 12 дм, 45 дм.
З. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
У великана на куртке 585 карманов. В каждом кармане живет по 3 мышки, а у каждой мышки по 5 мышат. Сколько мышат обитает в куртке великана? (585 • З • 5 = 8775 (мышат).)
lll. Работа по теме урока Работа по учебнику м 205 (с. 65).
(Коллективное выполнение с комментированием.)
Учимся решать задачи
![]()
(Самостоятельное выполнение. Проверка с записью решения на доске.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 207 (с. 65).
![]() Прочитайте условие
задачи. Что нужно определить сначала? (Цену набора: 800руб. : 5 наб. = 160
руб./наб.)
Прочитайте условие
задачи. Что нужно определить сначала? (Цену набора: 800руб. : 5 наб. = 160
руб./наб.)
![]() Какое условие нужно
соблюдать, составляя наборы? (Стоимость набора не Должна превышать 160руб.)
Какое условие нужно
соблюдать, составляя наборы? (Стоимость набора не Должна превышать 160руб.)
![]() Составьте самостоятельно возможные
наборы.
Составьте самостоятельно возможные
наборы.
2. Выполнение упражнения в тетради для самосгоягељной ра&лы
Л) 88 (1-3) (с. 51-52).
(Выполнение в соответствии с заданиями.) Ш. Подведение итогов урока
Тетрадь для самостоятельной работы: № 89 (с. 52).
Урок 99. Учимся решать задачи
Цель: развивать навыки решения задач.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
1. Устный счет
(Примеры записаны на доске.)
![]() Выразите.
Выразите.
3 кг 25 г = ![]()
![]() ц ... кг =
586 кг
ц ... кг =
586 кг
60 т 20 кг = ... ц ... кг
... т ... ц = 82 ц
3 т 400 кг =![]()
2. Цифровой квадрат
|
|
|
|
13 |
|
![]() 40
40
38 32
... ц. кг = 1073 кг
91 ц = ... т... кг
... кг ... г = 4090 г
|
25 |
15 |
|
13 |
17 |
Ответ:
![]()
З. Родственные ряды
|
6 |
8 |
|
4 |
25 |
|
15 |
19 |
5 |
|
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 2 и прибавления числа З. В верхнем ряду пропущено число 1, в нижнем ряду — 53.)
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Масса дыни и еще половины такой же дыни равна 9 кг. Найдите массу целой дыни. (Целая дыня — это две половинки. Мы знаем, что масса двух половинок да еще одной половинки (трех половинок) равна 9 кг. Значит, масса одной половинки равна З кг. Тогда целая дыня весит З кг • 2 = 6 кг.)
Ш. Работа по теме урока Работа
ло учебнику ![]() 208 (с. 66).
208 (с. 66).
![]() Вспомните правило, связывающее стоимость покупки и количество купленного
товара при постоянной цене. (Увеличение кутиенного товара в несколько раз привоДит
к увеличению стоимости покупки в это же число раз.)
Вспомните правило, связывающее стоимость покупки и количество купленного
товара при постоянной цене. (Увеличение кутиенного товара в несколько раз привоДит
к увеличению стоимости покупки в это же число раз.)
![]() Как нужно изменить данные в формулировке задачи? (Изменить количество
коробок конфет так, чтобы одно число ДеЛИЛОСЬ на другое без остатка: 15 и 30,
10 и 20, 15 и 45, 15 и 5 ит. Д.) ЛЕ 209 (с. 66).
Как нужно изменить данные в формулировке задачи? (Изменить количество
коробок конфет так, чтобы одно число ДеЛИЛОСЬ на другое без остатка: 15 и 30,
10 и 20, 15 и 45, 15 и 5 ит. Д.) ЛЕ 209 (с. 66).
![]() Прочитайте условие задачи. Как можно определить стоимость I кг черешни?
(330руб. — 200руб. = 130руб.)
Прочитайте условие задачи. Как можно определить стоимость I кг черешни?
(330руб. — 200руб. = 130руб.)
![]() Как определить стоимость кг клубники? (330 руб.
Как определить стоимость кг клубники? (330 руб. ![]()
— 210руб. = 120 руб.)
—
Определите стоимость кг абрикосов. (210руб. — 130руб.![]()
— 80руб. 200 руб. — 1Труб. 80руб.)
![]() Выполните разностное
сравнение цены черешни и цены ютубники. (130руб. — 120руб. = Труб.)
Выполните разностное
сравнение цены черешни и цены ютубники. (130руб. — 120руб. = Труб.)
![]() Можно ли получить этот
результат, не вычисляя цены клубники и черешни? (Для этого надо обратить
внимание на то, что стоимость 1 кг черешни и 1 кг абрикосов 210py6., а
стоимость 1 кг клубники и 1 кг абрикосов отличается от первой стоимости на 10
руб.: 210 руб. — 200 руб.
Можно ли получить этот
результат, не вычисляя цены клубники и черешни? (Для этого надо обратить
внимание на то, что стоимость 1 кг черешни и 1 кг абрикосов 210py6., а
стоимость 1 кг клубники и 1 кг абрикосов отличается от первой стоимости на 10
руб.: 210 руб. — 200 руб.![]()
= Труб.) lV. Физкультминутка
100. Поупражняемся в вычислениях и повторим пройденное
![]()
V. Закрепление изученного материала
1. Работа по учебнику М 210 (с. 66).
![]() Прочитайте задачу.
Какого она типа? (Задача на нахождение стоимости по известной цене и
количеству.)
Прочитайте задачу.
Какого она типа? (Задача на нахождение стоимости по известной цене и
количеству.)
![]() Сколько
метров ткани закуплено? (Зм • 12 = 36 м.)
Сколько
метров ткани закуплено? (Зм • 12 = 36 м.)
![]() Сколько стоила вся покупка? (350руб./м •
Мм = 12 600руб.) М 211 (с. 66).
Сколько стоила вся покупка? (350руб./м •
Мм = 12 600руб.) М 211 (с. 66).
(Самостоятельное выполнение. Проверка в парах.)
2. Выполнение упражнений в тетради для самостоятельной работы
![]() 90 (1-3) (с. 53).
90 (1-3) (с. 53).
(Выполнение с комментированием у доски.) Л) 91 (1, 2) (с. 54).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 92 (с. 54).
Урок 100, Поупражняемся в вычислениях и повторим пройденное
Цели: повторить пройденный материал; развивать вычислительные навыки.
1. Организационный момент. Сообщение темы и целей урока
П. Актуализация знаний
Арифметический диктант
• Число 38 600 уменьшите в l00 раз. (386.)
• Сколько всего десятков в числс 203 751? (20 375.)
• Назовите пять первых и пять последних чисел в ряду шестизначных. (100000, 100001, 100002, 100003, 100004; 199995, 199996, 199997, 199998, 199999.)
• Если к числу 380 справа приписать 0, то во сколько раз и на сколько единиц оно увеличится? (В 10раз, на 3420.)
• Произведение чисел 30 и 50 уменьшите на второе число. (1450.)
• Во сколько раз 60 кв. м больше 60 кв. дм? (В 100раз.)
• Число 37 680 округлите до тысяч. (37 ООО.)
![]()
• В среднем по величине муравейнике живет до 3000 муравьев, а в термитнике — 600 000 термитов. Во сколько раз больше термитов, чем муравьев? (В Трал)
• Сердце мыши за 2 мин делает 2600 ударов. Сколько ударов сделает ее сердце за 6 мин? ( 7800.)
Ш. Работа по теме урока Работа по учебнику м 212 (с. 67). (Самостоятельное выполнение. Проверка в парах.) м 213 (с. 67).
• Прочитайте задачу. Какого она типа? (Задача на Движение в противоположных направлениях, основной структурной составляющей которой является задача на сулшу и разность.)
— Что нужно сделать сначала? (ОпреДелить сумму скоростей поезДов: 280 : 2 = 140 (км/ч).)
— Чему равна удвоенная меньшая скорость поездов? (140 —
• 20 = 120 (км/ч).)
— Определите скорость одного поезда (меньшую). (120 : 2 =
= 60 (км/ч).)
— Определите скорость другого поезда. (60 + 20 = 80
(км/ч).) ![]() 214 (с. 67).
214 (с. 67).
• Прочитайте задачу. Какого она типа? (Задача на Движение в одном направлении, в которой требуется найти скорость более медленного транспортного среДства по известной скорости Другого транспортного средства и по вычисляемой скорости изменения расстояния между этими транспортными средствами.)
— Что нужно найти сначала? (Скорость изменения расстояния между катером и тешюхоДом: 75 км : З ч = 25 км/ч.)
— Найдите среднюю скорость теплохода. (45 км/ч — 25 км/ч — = 20 км/ч.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 67).
67).
(Практическая работа.)
— Прочитайте задание. Чему равна разность длин соседних сторон? (4 см сии 40 мм.)
![]() Как найти сумму длин
сторон прямоугольника? ( 180мм : 2 = = 90 ММ.)
Как найти сумму длин
сторон прямоугольника? ( 180мм : 2 = = 90 ММ.)
— Найдите удвоенную длину меньшей стороны. (90 мм — — 40 мм = 50 ММ.)
101 . Вычисления с помощью калькулятора
![]()
— Найдите одну длину меньшей стороны. (50ММ : 2 = 25 мм.)
— Найдите длину другой стороны прямоугольника. (90 мм — — 25мм = 65 мм.)
![]() Каковы длины сторон прямоугольника? (25
мм и 65 мм.) — Начертите прямоугольник. м 216 (с. 67).
Каковы длины сторон прямоугольника? (25
мм и 65 мм.) — Начертите прямоугольник. м 216 (с. 67).
(Практическая работа.)
— Прочитайте задание. Как найти сумму длин сторон прямоугольника? (200 мм : 2 = 100 мм.)
— Что нужно сделать дальше? (Меньшую сторону прямоугольника принять за одну часть, а большую — за три части.)
— Сколько всего частей? (1 +3 = 4 (ч.).)
![]() Найдите меньшую
сторону прямоугольника. (100 мм : 4 = = 25 ми.)
Найдите меньшую
сторону прямоугольника. (100 мм : 4 = = 25 ми.)
![]() Найдите большую сторону прямоугольника. (25 мм • З — = 75мм.)
Найдите большую сторону прямоугольника. (25 мм • З — = 75мм.)
— Каковы длины сторон прямоугольника? (25 мм и 75 мм.) Л) 217(с. 67).
![]() Прочитайте задачу. Назовите стоимость букета. (100руб.)
Прочитайте задачу. Назовите стоимость букета. (100руб.) ![]() Как найти
стоимость букета из пяти гвоздик? (100 — 25 = - 75 (руб.).)
Как найти
стоимость букета из пяти гвоздик? (100 — 25 = - 75 (руб.).)
![]() Найдите цену гвоздики. (75 : 5 = 15 (руб./шт.).)
Найдите цену гвоздики. (75 : 5 = 15 (руб./шт.).)
2. Выполнение упражнения в тетрам для самостоятельной работы ЛГ2 93 (с. 55).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 94 (с. 55).
Урок 101. Вычисления с помощью калькулятора
Цель: закрепить навыки вычислений с помощью калькулятора.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Закономерность
![]()
(Закономерность: • 2, • З; пропущенные числа — 10 и 30.)
 Ответ:
Ответ:
З. Родственные ряды
|
6 |
12 |
20 |
2 |
|
|
8 |
П |
15 |
6 |
|
( Числа нижнего ряда получаются в результате прибавления к соответствующим числам верхнего ряда числа 10 и Деления на 2. Пропущено число 20.)
4. Разминка
• Кролики прыгали: один среди двух и три в ряд, один впереди и два позади, один позади и два впереди. Сколько же было всех кроликов? (Три.)
• Сколько времени показывают часы, если обе стрелки направлены своими концами в противоположные стороны и показывают целое число часов? (6 ч.)
• Ветер, при котором образуется пена на гребнях волн, моряки называют свежим. Средняя скорость свежего ветра равна 9 м/с. Определите скорость свежего ветра в минуту. (540 м/мин.)
Ш, Работа по теме урока Работа
по учебнику ![]() 68).
68).
(Устное выполнение.) № 219, 220 (с. 68).
(Коллективное выполнение.) № 221 (с. 68-69).
(Самостоятельное выполнение. Проверка в парах.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику
№ 222 (с. 69). (Самостоятельное выполнение. Проверка в парах.) м 223 (с. 69).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
Контрольная работа № 6
Прочитайте задание. Что нужно сделать? (РазДелить 387921 на 95 с остатком. Полученный остаток и будет тем числом, которое нужно вычесть из числа 387 921, чтобы оно Делилось на 95 нацело.)
— Выполните деление. (387 921 : 95 = 4083 (ост. 36). )
— Как найти еще два варианта ответа? (К числу 36 прибавить
95: 36 + 95 = 131 (второй вариант ответа) и еще раз прибавить 95: 131 +
95=226.) ![]() 225 (с. 69).
225 (с. 69).
— Прочитайте задание. Что нужно сделать? (Найти значение разности между Делителем и остатком. Полученный результат и будет тем числом, на которое нужно увеличить число 258 317, чтобы оно ДеЛИОСЬ на 85 нацело.)
![]() Найдите остаток. (258 317: 85 = 3039
(ост. 2).)
Найдите остаток. (258 317: 85 = 3039
(ост. 2).)
![]() Чему равно значение
разности между делителем и остатком? (85-2=83.)
Чему равно значение
разности между делителем и остатком? (85-2=83.)
— Как найти еще два варианта ответа на это задание? (Два раза увеличить число 83 на величину Делителя: 83 + 85 = 168, 168 +
+ 85 = 253.) м 226 (с. 69).
(Самостоятельное выполнение. Проверка в парах.)
2. Выполнение упражнений в тетради для самостоятельной работы
ЛГУ 95, 96 (С. 56).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 97 (с. 56).
Цели: проверить знания и умения учащихся; развивать навыки самостоятельной работы.
(Текст контрольной работы выдается каждому ученику на отдельном листочке.) Вариант 1
1. Вычисли значение выражения.
422 715 : 15 + 918 936 : 36
![]()
2. Найди всю величину, если три восьмых этой величины равны 51 243 кг.
3. Реши задачу. Вычисли и запиши ответ.
От двух пристаней, находящихся на расстоянии 120 км друг от друга, отправляются одновременно навстречу друг другу два теплохода, скорость которых в стоячей воде одинаковая и равна 20 км/ч. Скорость течения реки 2 км/ч. Через сколько часов теплоходы встретятся?
4. Реши задачу. Вычисли и запиши ответ.
Папа и сын должны покрасить забор длиной 36 м. Папа может покрасить этот забор за 6 ч, а сын — за 12 ч. За сколько часов они покрасят этот забор, если будут работать совместно, не мешая друг другу?
5. Вырази в оадратных дециметрах и квадратных сантиметрах:
386 кв. см, 2056 кв. см.
Вариант 2
1. Вычисли значение выражения.
899 Вб : 36 + 272 : 15
2. Найди всю величину, если три восьмых этой величины равны 45 213 м.
З. Реши задачу. Вычисли и запиши ответ.
От двух пристаней, находящихся на расстоянии 160 км друг от друга, отправляются одновременно навстречу друг другу два катера, скорость которых в стоячей воде одинаковая и равна 40 км/ч. Скорость течения реки I км/ч. Через сколько часов они встретятся?
4. Реши задачу. Вычисли и запиши ответ.
Мама и дочь должны прополоть грядку длиной 60 м. Мама может прополоть эту грядку за 3 ч, а дочь — за 6 ч. За сколько часов они смогут прополоть эту грядку, если будут работать совместно, не мешая друг другу?
5. Вырази в квадратных дециметрах и квадратных сантиметрах: 845 кв. см, 4023 кв. см.
Урок 1 ОЗ. Как в математике применяют союз «и» и союз «или»
Цель: познакомить с заданиями логического характера, в которых используются союзы «и» и «или».
1. Организационный момент. Сообщение темы и цели урока
Как в математике применяют союз «и» и союз «или»
![]()
ll. Актуализация знаний
1. Цифровой квадрат
|
24 |
21 |
|
27 |
28 |
|
|
21 |
|
|
|
45 Ответ:
55
51 49
2. Волшебная звезда
(Сумма = 31.)
 Ответ:
Ответ:
З. Родственные ряды
|
3 |
12 |
|
45 |
15 |
|
0 |
3 |
8 |
|
|
( Числа верхнего ряда получаются в результате умножения соответствующих чисел нижнего ряда на З и прибавления числа З. В верхнем ряду пропущено число 27, в нижнем ряду — 4.)
4. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Как называется отрезок, соединяющий центр окружности с любой ее точкой? (Радиус.)
• Как связаны диаметр и радиус одной и той же окружности? (Отрезок, образованный двумя радиусами, называется диаметром.)
5. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Осел, козел и косолапый мишка за исполнение хорошей музыки получили призы: мед, сено и капусту. Какой приз получил каждый музыкант, если осел выбрал себе не сено и не капусту,
![]()
а козел тоже не взял себе капусту? (Осел взял мед, козел — сено, мишка — капусту.)
Ш. Работа по теме урока Работа по учебнику ![]() 70).
70).
(Коллективное устное
выполнение.) ![]() 70).
70).
![]() Прочитайте задание.
Какие числа нужно выписать в первый столбик? (25698, 54 718, 23 564.)
Прочитайте задание.
Какие числа нужно выписать в первый столбик? (25698, 54 718, 23 564.)
![]() Какие числа нужно
выписать во второй столбик? (25 698, 35471, 8946, 54 718, 23 564.)
Какие числа нужно
выписать во второй столбик? (25 698, 35471, 8946, 54 718, 23 564.) ![]() 70).
70).
(Выполнение в соответствии с заданиями.)
— С помощью какого союза можно соединить эти неравенства? (С помощью союза «и». ) lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 70).
(Самостоятельное выполнение. Проверка в парах.) М 231 (с. 71).
70).
(Самостоятельное выполнение. Проверка в парах.) М 231 (с. 71).
![]() Прочитайте задание.
Прочитайте задание.
(Учащиеся приводят свои примеры.)
Таким образом, мы получили три случая, когда значение произведения двух чисел равно нулю:
1) первый множитель равен нулю, а второй не равен нулю; 2) второй множитель равен нулю, а первый не равен нулю; 3) оба множителя равны нулю.
![]() Сформулируйте
условие с учетом данных случаев. (Значение произвеДения двух чисел равно нулю,
если первый множитель равен нулю ми второй множитель равен О, т. е. если хотя
бы один из множителей равен нулю.)
Сформулируйте
условие с учетом данных случаев. (Значение произвеДения двух чисел равно нулю,
если первый множитель равен нулю ми второй множитель равен О, т. е. если хотя
бы один из множителей равен нулю.)
Таким образом, все три случая можно
объединить в одно условие при помощи союза «или». м 232 (с. 71). (Коллективное
выполнение с комментированием.) ![]() 71).
71).
![]() Прочитайте задание. Какие числа можно
поставить вместо х? (Все натуральные числа от 1 до 12 вюаючительно.)
Прочитайте задание. Какие числа можно
поставить вместо х? (Все натуральные числа от 1 до 12 вюаючительно.) ![]() 234
(с. 71).
234
(с. 71).
![]() Прочитайте задание. Какие пять чисел
можно выписать?
Прочитайте задание. Какие пять чисел
можно выписать?
(12, 13, 14, 15, 16.)
Как выполнение одного условия обеспечивает выполнение...
![]()
— Прочитайте условие задачи. В каком случае дачник успеет на электричку? (Если будет Двигаться с такой скоростью, что окажется на платформе к моменту отправления электропоезДа или с большей скоростью.)
![]() С какой наименьшей скоростью может
двигаться дачник?
С какой наименьшей скоростью может
двигаться дачник?
( Так как за полчаса ему нужно пройти 2 км, то его скорость Должна быть 4 км/ч.)
— ЗаПИШИТЕ полученный ответ с помощью
знака Э. (v ) 4 км/ч.) ![]() 72).
72).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]() 72).
72).
![]() Прочитайте задание.
Какие утверждения являются ответами? (Под буквами «в», «г», «д». )
Прочитайте задание.
Какие утверждения являются ответами? (Под буквами «в», «г», «д». )
2. Выполнение упражнений в тетради для самосттельной рабшы
![]() 98, 99 (с. 57).
98, 99 (с. 57).
(Самостоятельное выполнение. Проверка в парах.) № 100 (с. 57).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
№ 101, 102 (с. 57).
(Самостоятельное выполнение.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 103, 104 (с. 57—58).
Урок 104. Как выполнение одного условия обеспечивает выполнение другого
Цель: рассмотреть логические конструкции, в которых выполнение одного условия обеспечивает выполнение другого.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
Арифметический диктант
— Запишите только ответы.
• Ученица прочитала 18 страниц книги. Это составило одну пятую часть всей книги. Сколько страниц в книге? (90.)
• Чему равны три четверти от 280? (210.)
9 Поурочные разработки по математике
![]()
• На сколько меньше три четверти суток, чем семь восьмых суток? (На З ч.)
• На сколько больше девять десятых часа, чем пять шестых часа? (На 4 мин.)
• К какому числу надо прибавить 3600, чтобы получить 7200?
(к 3600.)
• Длина сарая 8 м, а ширина 4 м. Три четверти площади пола покрашено. Сколько квадратных метров площади пола не покрашено? (8 кв. м.)
• Уменьшаемое равно l40, разность на 90 меньше. Найдите вычитаемое. (90.)
• Брату l2 лет 7 месяцев. Он старше сестры на 3 года 5 месяцев. Определите возраст сестры. (9лет 2 месяца.)
• Юннаты посадили 400 семян гороха. Из каждых 50 семян не взошли 2 семени. Сколько семян не взошло? (16.)
• Задуманное число разделили на 12 и получили 20. Какое число задумали? (240.)
Ш, Работа по теме урока Работа
по учебнику ![]() 238 (с. 73).
238 (с. 73).
(Коллективное устное выполнение с комментированием.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 239 (с. 73).
(Устное выполнение.)
![]() Прочитайте задание. Переформулируйте утверждение. (Если у прямоугольника
все стороны равны, то этот прямоугольник является квадратом.)
Прочитайте задание. Переформулируйте утверждение. (Если у прямоугольника
все стороны равны, то этот прямоугольник является квадратом.) ![]() 240 (с. 73).
240 (с. 73).
(Устное соревнование по рядам.)
2.
Вьшшшение
упражнения в тетради для самосттельной рабшы ![]() 106 (с. 59).
106 (с. 59).
(Самостоятельное выполнение. Взаимопроверка.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 107 (с. 59).
Урок 105. Не только одно, но и другое
Цель: познакомить с логическими конструкциями, в которых используется союз «не только... но и».
Не только одно, но и другое
![]()
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
Ответ: |
25 |
29 |
|
|
|
28 |
19 |
53 48
2. Родственные ряды
|
5 |
12 |
|
20 |
2 |
|
8 |
22 |
Ш |
38 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 2 и вычитания ЧИСЈШ 2. В верхнем ряду пропущено число 6, в нижнем ряду — 2.) З. Логическая задача
— Решите задачу устно.
В одном ряду 8 камешков, лежащих на расстоянии 2 см один от другого. В другом ряду 15 камешков, лежащих на расстоянии I см один от другого. Какой ряд длиннее? (Первый.)
Ш. Работа по теме урока Работа по учебнику ![]() 241 (с. 74).
241 (с. 74).
(Устное выполнение.) ![]() 242 (с. 74).
242 (с. 74).
![]() Прочитайте задание.
Какая логическая связка в нем использована? («Не только по Действиям, но и с
помощью одного выражения». )
Прочитайте задание.
Какая логическая связка в нем использована? («Не только по Действиям, но и с
помощью одного выражения». )
![]() Сколько вариантов решения нужно
записать? (Два.) — Запишите оба варианта решения.
Сколько вариантов решения нужно
записать? (Два.) — Запишите оба варианта решения.
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 243 (с. 74).
— Прочитайте задание. Какие числа нужно выписать? (7583,
53 381, 3333.) ![]() (с. 74).
(с. 74).
(Устное соревнование по рядам.)
![]()
2. Выполните упражнения в тетради для самосгоягељной работы ЛГ2 109 (1, 2) (с. 60).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 108 (с. 60).
Урок 1 Об. Учимся решать логические задачи
Цель: научить решать логические задачи.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Закономерность
![]()
(Закономерность: • 5, : 2; пропущенные числа![]()
2. Волшебные квадраты
![]() Заполните пустые
клетки цифрами от I до 9. Волшебная сумма равна 15.
Заполните пустые
клетки цифрами от I до 9. Волшебная сумма равна 15.
|
|
|
|
|
пап |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Ответы:

З. Логические задачи
![]() Решите задачи устно.
Решите задачи устно.
• У Левы, Гены, Васи, Толи и Миши были три барабана и две трубы. Какой музыкальный инструмент был у каждого мальчика, если у Гены и Васи, а также у Левы и Толи были разные инструменты, а у Гены и Левы был такой же
Учимся решать логические задачи
![]()
инструмент, как у Миши? (УЛевы, Гены, МИШИ были барабаны, у Васи и Толи — трубы.)
• У Лены, Нины, Кати, Маши, Гали и Светы было три книги и три журнала. Что было у каждой девочки, если у Нины и Маши были разные предметы, у Нины и Светы одинаковые предметы, у Лены — журнал, у Светы и Лены одинаковые предметы? (У Лены, Нины, Светы были журналы, у Кати, Маши, Гали — книги.)
Ш. Работа по теме урока Работа
по учебнику ![]() 75).
75).
![]() Какие условия
перечислены в задании? ( Число должно быть «круглым», в записи числа должно
быть шесть цифр, число должно быть меньше, чем 100 010.)
Какие условия
перечислены в задании? ( Число должно быть «круглым», в записи числа должно
быть шесть цифр, число должно быть меньше, чем 100 010.)
— Каким союзом соединены эти три условия? (Союзом «и».) ![]() Что
это означает? (Искомое число должно отвечать всем этим условиям.)
Что
это означает? (Искомое число должно отвечать всем этим условиям.)
![]() Назовите все шестизначные числа, которые
меньше, чем число 100 ОТО. (100009, 100008, 100007 100001, 100000.)
Назовите все шестизначные числа, которые
меньше, чем число 100 ОТО. (100009, 100008, 100007 100001, 100000.) ![]() Какое
число среди них является «круглым»? ( 100 000.)
Какое
число среди них является «круглым»? ( 100 000.) ![]() 246 (с. 75).
246 (с. 75).
![]() Прочитайте задание.
В чем его принципиальное отличие от предыдущего? (В формулировке заДания вместо
союза «и» употребляется союз
Прочитайте задание.
В чем его принципиальное отличие от предыдущего? (В формулировке заДания вместо
союза «и» употребляется союз![]()
![]() В чем заключается логический смысл союза
«или»? (Искомое число должно удовлетворять хотя бы одному из указанных
требований: быть «круглым» Двузначным ми быть Двузначным и меньше 15.)
В чем заключается логический смысл союза
«или»? (Искомое число должно удовлетворять хотя бы одному из указанных
требований: быть «круглым» Двузначным ми быть Двузначным и меньше 15.) ![]() Какие
числа можно назвать? (10, 20, 30, 40, 50, 60, 70, 80, 90, 14, в, 12, п.)
Какие
числа можно назвать? (10, 20, 30, 40, 50, 60, 70, 80, 90, 14, в, 12, п.)
— Какое число отвечает сразу двум данным требованиям?
( 10: оно «круглое», Двузначное и меньше 15.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 75).
75).
(Коллективная практическая работа.)
![]() Какие фигуры
оказались невыбранными? (Остроугольный и тупоугольный треугольники (в них нет
прямого угла), пятиугольник с прямым углом (он не является ни треугольником, ни
четырехугольником).)
Какие фигуры
оказались невыбранными? (Остроугольный и тупоугольный треугольники (в них нет
прямого угла), пятиугольник с прямым углом (он не является ни треугольником, ни
четырехугольником).)
(Коллективное выполнение с комментированием.) Прочитайте приведенные утверждения.
— Какие из них являются верными и почему? (Примерный ответ.
Утверждение а верное, так как все треугольники делятся на три типа —
остроугольные, прямоугольные и тупоугольные и в каждом таком треугольнике
обязательно есть острый угол. Утверждение б неверное, так как, например, в
остроугольном треугольнике не может быть прямого угла по определению.
Утверждение в верное, так как оно фактически является определением
прямоугольного треугольника. Утверждение г неверное, так как, например, в прямоугольном
треугольнике есть прямой угол, но он не является остроугольным. Утверждение д
неверное, так как, например, в прямоугольнике все углы прямые, а он является
четырехугольником. Утверждение е неверное, так как прямоугольная трапеция
является четырехугольником, имеющим прямой угол, но она не является
прямоугольником. Утверждение ж верное, так как оно фактически является
определением прямоугольника.) ![]() Перепишите верные утверждения в тетрадь.
Перепишите верные утверждения в тетрадь.
![]() 249 (с. 76).
249 (с. 76).
![]() Прочитайте условие
задачи. Могут ли Витя и Сережа оказаться за одной партой? (Нет, так как по
условию один из них Должен сиДеть с Колей.)
Прочитайте условие
задачи. Могут ли Витя и Сережа оказаться за одной партой? (Нет, так как по
условию один из них Должен сиДеть с Колей.)
— В каком случае Витя и Сережа могут сидеть за одной партой? (Когда Коля отсутствует на уроке.)
![]() Может ли Петя сидеть
с Сережей? (Да, если Коля будет сидеть с Витей.) № 250 (с. 76).
Может ли Петя сидеть
с Сережей? (Да, если Коля будет сидеть с Витей.) № 250 (с. 76).
![]() Рассмотрите первый
ребус. С чего надо начать его разгадывать? (С разряда Десятков.)
Рассмотрите первый
ребус. С чего надо начать его разгадывать? (С разряда Десятков.)
![]() Какая буква стоит на этом месте? (Буква
Р.)
Какая буква стоит на этом месте? (Буква
Р.)
![]() Какую цифру она обозначает? (0.)
Какую цифру она обозначает? (0.)
![]() Какую цифру может обозначать буква И?
(Например, цифру 2. )
Какую цифру может обозначать буква И?
(Например, цифру 2. ) ![]() Тогда какую цифру обозначает буква А?
(4.)
Тогда какую цифру обозначает буква А?
(4.)
![]() Какую цифру может обозначать буква Т?
(Например, цифру 8.)
Какую цифру может обозначать буква Т?
(Например, цифру 8.)
![]() Какую цифру обозначает буква Д? (1.)
Какую цифру обозначает буква Д? (1.)
![]() Назовите пример. (802 + 802 = 1604.)
Назовите пример. (802 + 802 = 1604.)
(Аналогично разбираются остальные примеры.)
2. Выполнение упражнения в тетради для самостоятельной работы
М 111 (с. 61).
(Самостоятельное выполнение. Проверка в парах.)
Поупражняемся в вычислениях и повторим пройденное
![]()
И. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 1 10 (с. 61).
Урок 107, Поупражняемся в вычислениях и повторим пройденное
Цели: повторить пройденный материал; развивать вычислительные навыки.
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний![]()
1. Цифровой квадрат
|
29 |
25 |
|
21 |
26 |
 Ответ:
Ответ:
50 51
2. Родственные ряды
|
|
5 |
16 |
12 |
|
|
19 |
15 |
4 |
8 |
|
(Сумма соответствующих чисел верхнего и нижнего рядов равна 20. Пропущено число 10.)
З. Логическая задача
— Решите задачу устно.
На собачью выставку привели 101 далматинца. У 56 из них черное пятно только на левом ухе, у 15 — только на правом, а у 29 — уши белые. У скольких собак пятна на обоих ушах? (101 — 56 — - 15- (Далм.).)
Ш. Работа по теме урока
1. Работа по учебнику № 251 (с. 77).
(Самостоятельное выполнение. Проверка в парах.)
— Вспомните порядок действий в выражениях со скобками. 2. Вьшолнеш«е упражнения в тетради для самостягельной работы ЛГ2 116€. 63).
(Самостоятельное выполнение. Проверка в парах.)
![]()
З. Работа по учебнику № 252 (с. 77).
(Самостоятельное выполнение. Проверка с записью решения на доске.) lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику № 253 (с. 77). — Прочитайте задачу. Какого она типа? (Задача на разность и частное.)
— Как вы будете рассуждать? (Пусть одна часть — это меньшая сторона, а четыре части — это большая сторона.)
![]() Выполните разностное сравнение частей.
(4 — 1 = З (ч.).)
Выполните разностное сравнение частей.
(4 — 1 = З (ч.).)
![]() Найдите меньшую сторону. (75 мм : З = 25 мм.)
Найдите меньшую сторону. (75 мм : З = 25 мм.)
![]() Найдите большую сторону. (25 мм • 4 = 100 мм.)
Найдите большую сторону. (25 мм • 4 = 100 мм.)
![]() Какую длину имеют стороны
прямоугольника? (25 мм и 100 мм, ши 2см 5 мм и Мсм.)
Какую длину имеют стороны
прямоугольника? (25 мм и 100 мм, ши 2см 5 мм и Мсм.)
— Начертите данный
прямоугольник. ![]() 77).
77).
![]() Прочитайте условие
задачи. Как вы ответите на вопрос? (З З = 9 (раз). )
Прочитайте условие
задачи. Как вы ответите на вопрос? (З З = 9 (раз). )
2. Выполнение упражнений в тетради для самостоятельной работы ле 114, 115(с. 63).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 12 (с. 61).
Урок 108. Поупражняемся в вычислениях и повторим пройденное
Цель: развивать вычислительные навыки и навыки решения различных задач.
1. Организационный момент. Сообщение темы и цели урока П. Актуализация знаний тест
(Выдается на отдельных листочках.)
Поупражняемся в вычислениях и повторим пройденное
![]()
1. Найди число, в котором 87 единиц третьего класса, 4 единицы пятого разряда, 9 единиц четвертого разряда, 47 единиц первого класса.
1) 870 409 047 3) 87 490 047
2) 87049 047 4) 807 049 470
2. Найди пример, ответом к которому будет число 706 000.
1) 74 600 - 4000 3) 746000- 40000
2) 7 460 000 - 400 000 4) 746 000 — 400 000 З. Реши пример столбиком: 701 000 — 99 405.
1) 601595 3) 691 595
2) 601 695 4) 601 695
4.
Вставь пропущенное число: 8 лет — 7 мес. —![]() . мес.
. мес.
1) 87 3) 91
2) 89 4) 85
5. Выполни деление: 211 км 72 м : 8.
1) 26 км зим 3) 26 384 см
2) 26 км 46 м 50 см 4) 26 км 484 м
6. Как соотносятся между собой отрезки, которые получаются при пересечении диагоналей квадрата?
1) они все равны
2) два отрезка равны, они в 4 раза больше двух других отрезков
3) у каждого квадрата по-своему
4) диагонали квадрата не пересекаются
7. Реши пример столбиком: 241 402 : 86.
1) 3807 3) 2816
2) 2707 4) 2807
8. Из ворот дома одновременно в противоположных направлениях вышли два пешехода. Скорость первого пешехода 95 м/мин, скорость второго пешехода 78 м/мин. Какое расстояние будет между ними через 12 мин?
1) 286 м 3) 2 км 760 м 2) 2 км 76-и 4) 2 км 86 м
9. В каком случае надо поставить знак >?
Ш. Периметр листа картона 52 см, его ширина 9 см. Чему равна
площадь листа картона?
1) 144 кв. см
2) 162 кв. см
З) 387 кв. см 4) 153 кв. см
![]()
1 1. Вставь пропущенное число: 1 м = мм.
1) 50 3) 1000
2) 100 4) 000
12. За два дня Митя решил 48 примеров. В первый день Митя решил пять восьмых примеров. Сколько примеров Митя решил во второй день?
1) 18 3) 16
2) 28 4) 24
13. Вставь пропущенное число: кв. м — кв. мм.
1) Ш 000 3) 000000
2) ШО 000 4) 000 000
14. Длина стороны квадрата 4 см, а ширина прямоугольника 2 см. Сравни площади прямоугольника и квадрата, если периметр прямоугольника 24 см.
1) 16 кв. см > 12 кв. см 3) 16 кв. см < 20 кв. см 2) 16 кв. см < 24 кв. см 4) 8 кв. см < 12 кв. см
15. Вставь пропущенное число: 4 т 72 ц 25 кг = . кг.
1) 11225 3) 7625
2) 47 225 4) 472 025
16. Вставь пропущенное число: 7 лет 4 мес. мес.
1) 102 3) 86
2) 88 4) 74
17. ПРОШЛИ обычный год и високосный. Сколько прошло суток?
1) 730 3) 732
2) 731 4) 733
18.
Напиши формулу периметра прямоугольника. (Р![]()
![]()
19. Напиши формулу площади квадрата. (SkB = а • а.)
20. Запиши решение задачи и ответ.
Площадь зала 135 кв. м, его ширина 9 м. Чему равен периметр зала?
Решение:
1) 135 : 15 (м) — длина зала;
2) (15
+ 9)![]()
Ответ: периметр зала равен 48 м.
Ш. Работа по теме урока Работа по учебнику № 255€. 77).
Между периметром и площадью нет ни прямой, ни обратной зависимости. При увеличении периметра прямоугольника площадь может как увеличиваться, так и уменьшаться.
![]() Какими могут быть
стороны прямоугольников? (Первого — 9см и 2 см, второго — 6 см и 4 см.)
Какими могут быть
стороны прямоугольников? (Первого — 9см и 2 см, второго — 6 см и 4 см.)
Квадрат и куб
![]()
IV. Физкультминутка
М. Закрепление изученного материала Работа по учебнику ![]() 256 (с. 77).
256 (с. 77).
![]() Прочитайте задание.
Существует ли такой прямоугольник? (Примерный ответ. Если длина прямоугольника
будет достаточно большой, а ширина — очень маленькой, то можно получить какой
угодно большой периметр (он будет приблизительно равен удвоенной длине большей
стороны) и какую угодно маленькую площадь (она может быть близка к 0 за счет
достаточно маленькой длины второй стороны). Искомый прямоугольник должен иметь
приблизительно следующие размеры: длина большей стороны чуть меньше 500 м, а
длина меньшей стороны близка к нулю и отличается от нуля на столько, на сколько
длина большей стороны отличается от 500 м.)
Прочитайте задание.
Существует ли такой прямоугольник? (Примерный ответ. Если длина прямоугольника
будет достаточно большой, а ширина — очень маленькой, то можно получить какой
угодно большой периметр (он будет приблизительно равен удвоенной длине большей
стороны) и какую угодно маленькую площадь (она может быть близка к 0 за счет
достаточно маленькой длины второй стороны). Искомый прямоугольник должен иметь
приблизительно следующие размеры: длина большей стороны чуть меньше 500 м, а
длина меньшей стороны близка к нулю и отличается от нуля на столько, на сколько
длина большей стороны отличается от 500 м.) ![]() 77).
77).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 113 (с. 62).
Цели: рассмотреть плоскую и объемную фигуры на примере квадрата и куба; познакомить с понятием «поверхность куба»; сопоставить площадь квадрата и объем куба.
1. Организационный момент. Сообщение темы и целей урока
ll. Актуализация знаний
1. Цифровой квадрат
|
35 |
25 |
|
15 |
5 |
 Ответ:
Ответ:
50 зо
2. Родственные ряды
|
|
14 |
6 |
п |
2 |
|
50 |
98 |
18 |
72 |
|
![]()
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на самих себя и Деления на 2. Пропущено число 2.)
З. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Из каких частей состоит формулировка задачи? (Из условия и требования.)
• Как формулируется требование задачи на разностное сравнение? (На сколько больше (меньше)... )
• Как формулируется требование задачи на кратное сравнение? (Во сколько раз больше (меньше)... )
• Какие существуют способы записи решения задачи? (По Действиям, по Деиствиям с пояснением, с вопросами, выражением.)
4. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
У продавца были чашечные весы и гири: 1 кг, 2 кг и 4 кг. Какую массу он может измерить с помощью этих гирь, если будет класть их только на одну чашу весов? (Самый маленький вес — 1 кг, самый большой — +2 + 4 = 7 кг.)
— Какие еще массы можно измерить? (2 кг, 4 кг, З кг (1 кг +
+ 2 кг), 5 кг (1 кг + 4 кг), 6 кг (2 кг + 4 кг).)
Ш. Работа по теме урока Работа по учебнику ![]() 78).
78).
(Коллективное выполнение.)
![]() Из скольких
квадратов состоит поверхность куба? (Из шести кваДратов.)
Из скольких
квадратов состоит поверхность куба? (Из шести кваДратов.)
![]() Как
найти объем куба с ребром 2 см? (Разбить этот куб на кубы с ребром 1 см. Таких
еДиничных кубов будет восемь, объем кажДого из них равен 1 куб. см. Поэтому
объем Данного куба равен 8 куб. см.)
Как
найти объем куба с ребром 2 см? (Разбить этот куб на кубы с ребром 1 см. Таких
еДиничных кубов будет восемь, объем кажДого из них равен 1 куб. см. Поэтому
объем Данного куба равен 8 куб. см.) ![]() 78).
78).
![]() Как вычислить
площадь поверхности куба с ребром 50 см? (Сначала вычислить ПЛОщДЬ кваДрата с
длиной стороны 50 см (площаДь одной грани этого куба): 50 см • 50 см — = 2500
кв. см., а затем умножить эту площаДь на КОЛИчество граней куба: 2500 кв. см •
6 = 15 000 кв. см = 1 кв. м 5000 кв. см = 1 кв. м + 5000 кв. см.)
Как вычислить
площадь поверхности куба с ребром 50 см? (Сначала вычислить ПЛОщДЬ кваДрата с
длиной стороны 50 см (площаДь одной грани этого куба): 50 см • 50 см — = 2500
кв. см., а затем умножить эту площаДь на КОЛИчество граней куба: 2500 кв. см •
6 = 15 000 кв. см = 1 кв. м 5000 кв. см = 1 кв. м + 5000 кв. см.)
![]() Что
такое 5000 кв. см? (5000 кв. см составляют половину 1 кв. м, поэтому для
покраски этой площаДи нужна половина той краски, что расходуется на 1 кв. м, т.
е. 100г : 2 = 50 г.)
Что
такое 5000 кв. см? (5000 кв. см составляют половину 1 кв. м, поэтому для
покраски этой площаДи нужна половина той краски, что расходуется на 1 кв. м, т.
е. 100г : 2 = 50 г.)
Квадрат и куб
![]()
— Сколько краски потребуется для покраски модели куба? (50г + тог = мог.)
![]() (с. 78).
(с. 78).
![]() Какую форму будет
иметь аквариум? (Форму куба без верхней грани с длиной ребра 1 м.)
Какую форму будет
иметь аквариум? (Форму куба без верхней грани с длиной ребра 1 м.)
— Чему равна вместимость этого аквариума? (1 куб. м.)
![]() Сколько литров в 1
куб. м? (1 куб. м = 1000куб. дм = 1000л.) IV. Физкультминутка
Сколько литров в 1
куб. м? (1 куб. м = 1000куб. дм = 1000л.) IV. Физкультминутка
М. Закрепление изученного материала 1, Работа по учебнику № 261 (с. 78-79).
(Практическая работа.)
![]() Прочитайте условие
задачи. Сколько граней оказалось раскрашено? (9 • 6 = 54 (гр.).)
Прочитайте условие
задачи. Сколько граней оказалось раскрашено? (9 • 6 = 54 (гр.).)
— Сколько кубиков оказалось нераскрашенными? (Один, тот, который бьи расположен в центре большого кубика.)
— Сколько кубиков с одной раскрашенной гранью? (Шесть, это те кубики, что были расположены в центре кажДой грани большого кубика.)
![]() У скольких кубиков
оказались раскрашены две грани? (У 12 маленьких кубиков, которые были
расположены между угловыми кубиками.)
У скольких кубиков
оказались раскрашены две грани? (У 12 маленьких кубиков, которые были
расположены между угловыми кубиками.)
![]() Сколько кубиков
имеет три раскрашенных грани? (Восемь, те, что были расположены в углах
большого кубика.)
Сколько кубиков
имеет три раскрашенных грани? (Восемь, те, что были расположены в углах
большого кубика.)
— Есть ли кубики, у которых раскрашено более трех граней?
(Нет.)
ЛФ 262 (с. 79).
(Устное выполнение.)
![]() Сколько ребер у куба? (12.)
Сколько ребер у куба? (12.)
![]() Сколько потребуется цветов для
раскрашивания каждого ребра? (12.) № 263 (с. 79).
Сколько потребуется цветов для
раскрашивания каждого ребра? (12.) № 263 (с. 79).
![]() Еще раз посмотрите
на куб из № 261. У каких кубиков
Еще раз посмотрите
на куб из № 261. У каких кубиков ![]() ни одно ребро не раскрашено? Сколько их?
(Это кубики, которые были расположены либо в центре большого кубика (такой
кубик один), либо в центре кажДой грани большого кубика (таких кубиков шесть).
Всего получшюсь семь кубиков, у которых ни одно ребро не раскрашено. )
ни одно ребро не раскрашено? Сколько их?
(Это кубики, которые были расположены либо в центре большого кубика (такой
кубик один), либо в центре кажДой грани большого кубика (таких кубиков шесть).
Всего получшюсь семь кубиков, у которых ни одно ребро не раскрашено. )
![]() У скольких кубиков
раскрашено только одно ребро? Где они были расположены? (У 12 маленьких
кубиков, которые были расположены между угловыми кубиками. )
У скольких кубиков
раскрашено только одно ребро? Где они были расположены? (У 12 маленьких
кубиков, которые были расположены между угловыми кубиками. )
![]()
— Сколько кубиков с тремя раскрашенными ребрами? (Восемь, это кубики, которые бьии расположены в углах большого кубика.)
— Есть ли такие кубики, у которых раскрашено два или более трех ребер? (Нет.)
2. Выполнение упражнений в тетради для самостоятельной ра-
м 117, 118(с. 64).
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 1 19 (с. 64).
Урок 110. Круг и шар
Цели: рассмотреть геометрические фигуры — круг и шар; познакомить со свойствами круга и шара.
![]() Организационный момент. Сообщение темы и целей урока
Организационный момент. Сообщение темы и целей урока
П. Актуализация знаний
Арифметический диктант
— Запишите только ответы.
• Сколько килограммов в трех четвертых тонны? (750 кг.)
• Сколько минут в трех четвертых часа? (45 мин.)
• Увеличьте 36 кг в 4 раза. (144 кг.)
• Найдите частное 8 ци 16 кг. (50 кг.)
• Найдите сумму величин 3 км 850 м и км 150 м. (5 км.)
• Периметр квадрата 24 см. Чему равна площадь? (36 кв. см.)
• Поезд за одну третью часа проходит 18 км. Сколько километров он проходит за 1 ч? (54 км.)
• Москва-река бывает покрыта льдом 12 дней. Сколько дней в году Москва-река свободна ото льда? (253 дня.)
• Ураган несется со скоростью 45 м/с. За сколько секунд он преодолеет 9 км? (За 5 с.)
•
Произведение равно 21 000. Первый множитель — 3. Чему равен другой
множитель? ( 7000.) Ш. Работа по теме урока Работа по учебнику ![]() 264 (с.
80).
264 (с.
80).
(Устное выполнение.)
1 Круг и шар
Рассмотрите глобус. Какие круги (окружности) на нем изображены? Как они называются? (Это мериДианы и параллели.)
Все меридианы — это окружности одного и того же радиуса, совпадающего с радиусом шара.
Все параллели — это окружности, радиусы которых изменяются в пределах от 0 до радиуса шара.
Если параллель имеет радиус, равный радиусу шара, то эта параллель называется экватором.
В сечении шара плоскостью, проходящей через центр, получается круг.
№ 265 (с. 80).
![]() Прочитайте задание.
С какой точки по глобусу начал движение Миша? (Эта точка называется полюсом.)
Прочитайте задание.
С какой точки по глобусу начал движение Миша? (Эта точка называется полюсом.)
— Сколько существует таких точек на глобусе? (Таких точек две: Северный полюс и Южный полюс. )
— На что похоже перемещение Миши по глобусу? ( Траектория описанного перемещения по глобусу напоминает треугольник, только сторонами этого «треугольника» будут не отрезки, а дуги.)
М 266 (с. 80).
— Где оказался медведь? (На Северном полюсе.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 267 (с. 80).
267 (с. 80).
![]() Можно ли сделать емкость для хранения жидкости в форме шара? (Да, так
как это объемная фигура.)
Можно ли сделать емкость для хранения жидкости в форме шара? (Да, так
как это объемная фигура.)
![]() А в форме круга? (Нет, так как это тоская фигура.)
А в форме круга? (Нет, так как это тоская фигура.) ![]() Как
называется отрезок, соединяющий центр круга и точку на границе круга? (Радиус.)
Как
называется отрезок, соединяющий центр круга и точку на границе круга? (Радиус.)
![]() 268 (с. 81).
268 (с. 81).
— Рассмотрите рисунок.
— Из скольких одинаковых кругов можно составить фигуру,
также похожую на треугольник? (Из З, из 10, из 15 и т. д.) ![]() 269 (с.
81).
269 (с.
81).
(Знакомство с понятием «пирамида» по словарику учебника
(с. 119).)
Решение:
![]()
1 + 3 +6 = 10
масс
![]()
2. Выполнение упражнений в тетради для самостоятельной ра-
№ 120 (с. 65).
(Коллективное выполнение.) М 121, 123 (с. 65).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 122 (с. 65).
Цель: научить различать геометрические фигуры, распознавать фигуры, которые имеют объем и площадь.
1. Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Закономерность
![]()
(Закономерность: + 6, — 2; пропущенные числа — 16 и 14.)
2. Волшебная звезда
(Сумма = 40.)
 Ответ:
Ответ:
1 Площадь и объем
![]()
2. Цифровой квадрат
|
31 |
32 |
|
25 |
24 |
|
|
|
|
25 |
|
63 Ответ:
49
56 56
4. Родственные ряды
|
2 |
7 |
6 |
З |
4 |
|
9 |
54 |
|
14 |
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на самих себя и прибавления числа 5. Пропущено число 21.)
5. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
В библиотеке на двух полках было 19 книг. Купили новые книги и на каждую полку поставили еще столько же книг, сколько на них было. Сколько теперь книг стоит на двух полках? ( Число 19 представляет собой сумму двух слагаемых: числа книг на первой полке и числа книг на второй полке. КажДое слагаемое увеличшш вдвое, следовательно, и сумма увеличилась в два раза: 19 • 2 = 38 (КНИГ).)
Ш. Работа по теме урока Работа по учебнику М 270 (с. 82). (Устное выполнение.) М 271 (с. 82).
(Коллективное выполнение с комментированием. Знакомство с терминами по словарику учебника (с. 119—120.)
![]() Относится ли куб к многогранникам? (Да, так как у него шесть граней.)
Относится ли куб к многогранникам? (Да, так как у него шесть граней.)
Наличие шести граней у куба является основанием для другого его названия, которое имеет греческое происхождение — гексаэдр,
т. е. шестигранник.
М. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику м 272 (с. 83).
(Устное выполнение.)
![]() Рассмотрите рисунки.
Рассмотрите рисунки.
![]()
— Какие фигуры имеют форму многогранника? ( Третья (призма), пятая (усеченная пирамиДа).) М 273 (с. 83).
(Коллективное выполнение с комментированием. Знакомство с терминами по словарику учебника (с. 119—120).) № 274 (с. 83).
![]() Прочитайте задание.
Чему равен диаметр шара? даме ребра куба — 4 см.)
Прочитайте задание.
Чему равен диаметр шара? даме ребра куба — 4 см.)
— Чему равен радиус шара? (4 см : 2 = 2 см.)
2. Вьшштекме упражнений в тирам для самостоятельной рабшы № 125 (с. 67).
(Коллективное выполнение.) № 126 (с. 67).
(Коллективное выполнение с комментированием.)
![]() Какие фигуры имеют объем? (Куб, шар,
пирамиДа.)
Какие фигуры имеют объем? (Куб, шар,
пирамиДа.)
— Какие фигуры имеют только площадь? (КваДрат, трапеция, прямоугольник.)
![]() Какие фигуры имеют только длину?
(Отрезок.)
Какие фигуры имеют только длину?
(Отрезок.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 124 (с. 66).
Урок 1 12. Измерение площади с помощью палетки
Цель: познакомить со способом измерения площадей произвольных фигур с помощью палетки.
![]() Организационный момент. Сообщение
темы и цели урока ll. Актуализация знаний
Организационный момент. Сообщение
темы и цели урока ll. Актуализация знаний
1. Устный счет
(Примеры записаны на доске.)
![]() Назовите ответы.
Назовите ответы.
208 4 125 • 4
360 • 2 240 • 2 16 • : 40
![]() :
90 70 40 28 зо
:
90 70 40 28 зо
2. Разминка
![]() Продолжите фразы.
Продолжите фразы.
![]() Чтобы найти неизвестное слагаемое, нужно...
Чтобы найти неизвестное слагаемое, нужно...
![]() Чтобы найти неизвестное уменьшаемое, нужно...
Чтобы найти неизвестное уменьшаемое, нужно...
Измерение площади с помощью палетки
![]()
![]() Чтобы найти неизвестное вычитаемое, нужно...
Чтобы найти неизвестное вычитаемое, нужно...
![]() Чтобы найти неизвестный множитель, нужно...
Чтобы найти неизвестный множитель, нужно...
![]() Чтобы найти неизвестное делимое, нужно...
Чтобы найти неизвестное делимое, нужно...
![]() Чтобы найти неизвестный делитель, нужно...
Чтобы найти неизвестный делитель, нужно...
З. Логическая задача
— Решите задачу устно.
Костя задумал число, прибавил к нему 1, отнял 2, умножил результат на 3 и разделил на 4. Получилось 6. Какое число задумал Костя? (9.)
![]() Выполните проверку. ((9 + 1 — 2) • З : 4 = 6.)
Выполните проверку. ((9 + 1 — 2) • З : 4 = 6.)
Ш. Работа по теме урока Работа по учебнику
![]() 275 (с. 84-85).
275 (с. 84-85).
(Самостоятельное выполнение. Работа в парах.) М 276 (с. 85). (Самостоятельное выполнение. Проверка в парах.) № 277 (с. 85).
(Коллективное выполнение с записью на доске.) — Рассмотрите чертеж.
![]() Из каких фигур состоит верхний ряд? (Из половинок еДиничных кваДратов.)
Из каких фигур состоит верхний ряд? (Из половинок еДиничных кваДратов.)
![]() Можно ли сказать, что квадрат разбит на
половинки? (Без
Можно ли сказать, что квадрат разбит на
половинки? (Без
Дополнительных измерений этого нельзя утзержДать.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику № 278 (с. 86).
![]() Рассмотрите рисунок.
Рассмотрите рисунок.
![]() На что похожа фигура? (На лужу.)
На что похожа фигура? (На лужу.)
![]() С помощью чего можно
измерить фигуру? (С помощью палетки.)
С помощью чего можно
измерить фигуру? (С помощью палетки.)
![]() Какую площадь произвольной фигуры мы можем найти? (Приблизительную.)
Какую площадь произвольной фигуры мы можем найти? (Приблизительную.)
— Чему она равна? (Числу, которое получается в результате сложения числа клеток пааетки, полностью расположенных 6 пределах границы Данной фигуры, и половины числа клеток, которые лишь частично расположены 6 пределах Данной фигуры.)
Так как измеряемая фигура произвольна, то можно говорить о том, что для каждой неполной клеточки существует другая неполная клеточка и вместе они дают такую же площадь, как и одна полная клеточка.
![]()
м 279 (с. 87).
— Чему приблизительно равна площадь данной фигуры? (15 +
+ (12 : 2) = 21 (полная клетка).) м 280 (с. 87).
(Самостоятельное выполнение. Проверка с записью решения на доске.) м 281 (с. 87). (Самостоятельное выполнение. Проверка в парах.) м (с. 87).
(Коллективное выполнение с записью на доске.)
2. Выполнение упражнения в тетради ддя самостоятельной работы
№ 128 (с. 68).
(Выполнение в соответствии с заданиями.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 127 (с. 68).
Урок 1 1 З. Поупражняемся в нахождении площади и объема
Цель: развивать навыки решения задач на нахождение площади и объема фигур.
l. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой квадрат
|
23 |
28 |
|
35 |
39 |
![]() 51 Ответ:
51 Ответ:
74
58 67
2. Родственные ряды
|
4 |
50 |
32 |
46 |
8 |
|
7 |
|
21 |
28 |
|
( Числа нижнего ряда получаются в результате Деления соответствующих чисел верхнего ряда на 2 и прибавления числа 5. Пропущено число 9.)
нахождении площади и объема
![]()
Буратино снял номер в сказочной гостинице. За проживание в нем Буратино должен платить 1 сольдо в день. У Буратино есть купюры в 1 сольдо и в 2 сольдо. Как он сможет расплачиваться за гостиницу на протяжении трех дней, если гшатить надо ежедневно? (В первый день надо отДать 1 сольдо, во второй день отДать 2 сольдо и взять сдачу 1 сольдо, в третий день отДать 1 сольдо.)
Ш. Работа по теме урока Работа по учебнику М 283 (с. 88).
(Практическая работа.)
М. Физкультминутка
V. Закрепление изученного материала Работа по учебнику ![]() 284 (с. 88).
284 (с. 88).
![]() Прочитайте
задание. Мысленно разбейте данный куб на единичные кубы с ребром 1 дм. Сколько
единичных кубов получилось? (Восемь.)
Прочитайте
задание. Мысленно разбейте данный куб на единичные кубы с ребром 1 дм. Сколько
единичных кубов получилось? (Восемь.)
— Чему равна вместимость этого бака? (2 дм • 2 дм • 2 дм — = 8 куб. дм = 8 л.)
![]() Чему
равна площадь боковой стенки бака? (2 дм • 2 дм
Чему
равна площадь боковой стенки бака? (2 дм • 2 дм![]()
= 4 кв. дм.) м 285 (с. 89).
— Рассмотрите рисунок.
— Мысленно разбейте бассейн на единичные кубы с ребром 1 м. Сколько единичных кубов получилось? (5 • З • 1 = = 15 (кубов). )
![]() Какой объем воды поместится в таком
бассейне? ( 15 куб. м.)
Какой объем воды поместится в таком
бассейне? ( 15 куб. м.) ![]() Какую форму имеют дно и стенки бассейна?
( Форму прямоугольника.)
Какую форму имеют дно и стенки бассейна?
( Форму прямоугольника.)
![]() Какую
площадь имеет дно бассейна? (5 м • Зм = 15 кв. м.)
Какую
площадь имеет дно бассейна? (5 м • Зм = 15 кв. м.) ![]() Какую площадь имеет
длинная стенка бассейна? (5 м • м — = 5 кв. м.)
Какую площадь имеет
длинная стенка бассейна? (5 м • м — = 5 кв. м.)
![]() Какую
площадь имеет короткая стенка бассейна? (Зм • 1 м — = З кв. м.)
Какую
площадь имеет короткая стенка бассейна? (Зм • 1 м — = З кв. м.)
— Сколько квадратных метров облицовочной плитки нужно для того, чтобы выложить стенки бассейна? ((5 кв. м + + З кв. м) 16 кв. м.) И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 129 (с. 69).
![]()
Урок 1 14. Поупражняемся в нахождении площади и объема
Цель: развивать навыки решения задач на нахождение площади и объема фигур.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Логическая задача
— Решите задачу устно.
Ване и его отцу вместе 40 лет. Сколько лет будет им вместе через три года? ( Число 40является суммой двух слагаемых: возраста Вани и возраста отца. Через три года кажДое из этих слагаемых увеличится на З года. А сумма возрастов будет больше преДыДущей суммы на З + З = 6 (лет). Значит, она станет 40 + 6 = 46 (лет).)
2. Волшебные квадраты
(Волшебная сумма равна 33.)
|
пап |
|
пп• |
|
пап оас |
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
пап |
|
|
|
||||
Ответы:
|
|
|
|
|
|
13 |
12 |
|
10 |
15 |
8 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
З. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Как найти скорость изменения расстояния между объектами, движущимися в одном и том же направлении? в противоположных направлениях? (При Движении в одном направлении скорость изменения расстояния между Движущимися объектами равна разности скоростей этих объектов, при движении в противоположных направлениях — сумме скоростей этих объектов. )
• Как зависит пройденный путь от времени при постоянной скорости движения? (При постоянной скорости Движения увеличение (уменьшение) времени Движения в некоторое число
раз привоДит к увеличению (уменьшению) длины пройденного пути в это же число раз.)
• Как зависит пройденный путь от скорости при постоянном времени движения? (При постоянном времени ДВИЖИИЯ увеличение (уменьшение) скорости Движения в некоторое число раз привоДит к увеличению (уменьшению) длины пройденного пути в это же число раз.)
• Как связаны между собой скорость и время движения при одинаковом пройденном пути? (При постоянной Длине пройДенного пути увеличение (уменьшение) времени в некоторое число раз привоДит к уменьшению (увеличению) скорости в это же число раз.)
Ш. Работа по теме урока Работа по учебнику
![]() 286 (с. 89).
286 (с. 89).
(Самостоятельная практическая работа.) lV. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 287 (с. 89).
![]() Мысленно разбейте куб на единичные кубы.
Сколько единичных кубов получилось? (5 • 5 • 5 = 125 (кубов).)
Мысленно разбейте куб на единичные кубы.
Сколько единичных кубов получилось? (5 • 5 • 5 = 125 (кубов).) ![]() Каков объем
аквариума? ( 125 куб. дм.)
Каков объем
аквариума? ( 125 куб. дм.)
![]() Какова вместимость аквариума? (125 л.)
Какова вместимость аквариума? (125 л.)
— Сколько пятилитровых банок воды потребуется, чтобы заполнить аквариум до самого верха? (125 : 5 = 25 (бан.).)
2. Выполнение упражнения в тетради для самостятельной работы
№ 130 (с. 69).
(Самостоятельное выполнение. Проверка в парах.) Ш. Подведение итогов урока
Тетрадь для самостоятельной работы: № 132 (с. 70).
Урок 1 15. Поупражняемся в вычислениях и повторим пройденное
Цели: развивать навыки решения задач, вычисления столбиком, вычисления значений выражений со скобками и без скобок; повторить понятие «двойное неравенство»; закрепить навыки работы с геометрическим материалом.
1. Организационный момент. Сообщение темы и целей урока
П. Актуализация знаний
1. Цифровой квадрат
|
|
|
|
25 |
|
|
35 |
55 |
|
25 |
45 |
90 Ответ:
70
60 ШО
2. Родственные ряды
|
2 |
5 |
|
15 |
7 |
|
7 |
в |
63 |
|
|
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 2 и прибавления числа З. Пропущено число 33.)
З. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
![]() Если после каждой
партии проигравший выбывает, сколько будет победителей в этих соревнованиях?
(Один, и им станет человек, выигравший все сыгранные им партии.)
Если после каждой
партии проигравший выбывает, сколько будет победителей в этих соревнованиях?
(Один, и им станет человек, выигравший все сыгранные им партии.)
— Если игроков было 15, то сколько человек должно выбыть?
(15- 1 = 14 (чел.).)
— А сколько человек выбывает по итогам одной партии? (Один.)
— Значит, сколько было партий? (14 : 1 = 14 (партий).)
— Найдите ответ на требование задачи.
(14— (5 + 6) = З (партии).) llI. Работа по теме урока Работа по учебнику ![]() 288
(с. 90).
288
(с. 90).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
ЛФ 289 (с. 90).
![]() Прочитайте задачу.
Какого она типа? (Задача на Движение навстречу друг Другу.)
Прочитайте задачу.
Какого она типа? (Задача на Движение навстречу друг Другу.)
— Сколько часов автомобиль был в пути? (4 ч — 2 ч = 2 ч.) Что можно найти далее? (Пройденный автобусом путь: 60 км/ч • 4 ч = 240 км.)
— Что нужно сделать дальше? (Рассчитать путь, пройденный автомобием: 80 км/ч • 2 ч = 160 км.)
— Как вычислить искомое расстояние? (240 км + 160 км![]()
= 400 км.)
![]() 290 (с. 90).
290 (с. 90). ![]() Прочитайте задачу. Какого она типа? (Задача на сумму и частное.)
Прочитайте задачу. Какого она типа? (Задача на сумму и частное.)
— С чего нужно начинать решать задачи такого типа? (Пусть тощаДь меньшего кваДрата составляет одну часть, а мощадь большего кваДрата — Девять частей.)
— Сколько всего частей? (1 + 9 = 10![]()
— Найдите площадь меньшего квадрата. (1000 кв. мм : 10 =
= 100 кв. мм = 1 кв. см.)
— Найдите площадь большего квадрата. (100 кв. мм • 9 —
= 900 кв. мм = 9 кв. см.)
— Назовите длину стороны квадрата, площадь которого равна
I кв. см. (1 см.)
![]() Назовите длину стороны квадрата, площадь
которого равна 9 кв. см. (З см, так как З см • З см = 9 кв. см.)
Назовите длину стороны квадрата, площадь
которого равна 9 кв. см. (З см, так как З см • З см = 9 кв. см.) ![]() Начертите
квадраты.
Начертите
квадраты.
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 291 (с. 90).
![]() Прочитайте задачу. Какого она типа?
(Задача на сумму и разность.)
Прочитайте задачу. Какого она типа?
(Задача на сумму и разность.) ![]() ладану.
ладану.
Решение:
1) 1000 кв. мм — 800 кв. мм = 200 кв. мм — удвоенная площадь меньшего квадрата;
2) 200 кв. мм : 2 = 100 кв. мм = кв. см — плоиладь меньшего квадрата;
3) 100 кв. мм + 800 кв. мм = 900 кв. мм = 9 кв. см — площадь большего квадрата.
— Какова длина стороны меньшего квадрата? (1 см.)
— Какова длина стороны большего квадрата? (З см.)
![]() Можно ли было для
иллюстрации решения данного задания воспользоваться квадратами, полученными при
выполнении предыдущего задания? (Да, так как кваДраты оДинаковые.)
Можно ли было для
иллюстрации решения данного задания воспользоваться квадратами, полученными при
выполнении предыдущего задания? (Да, так как кваДраты оДинаковые.)
— Начертите квадраты. М 292 (с. 91).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
2. Выполнение упражнения в тетрам для самостоятельной рабсгы М 133 (1) (с. 70).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 133 (2) (с. 70).
Урок 1 16. Поупражняемся в вычислениях и повторим пройденное
Цели: развивать умение решать геометрические задачи; закрепить навыки работы с геометрическим материалом.
![]() Организационный момент. Сообщение темы и целей урока
Организационный момент. Сообщение темы и целей урока
1. Закономерность
![]()
(Закономерность: — З, + 5; пропущенные числа — 7и 12.)
2. Цифровой \оадрат
|
24 |
|
59 Ответ: 95 |
24 |
35 |
|
|
|
42 |
53 |
66 88
З. Родственные ряды
|
17 |
В |
2 |
5 |
|
|
32 |
24 |
2 |
8 |
88 |
( Числа нижнего ряда получаются в результате умножения соответствующих чисел верхнего ряда на 2 и вычитания числа 2. Пропущено число 45.)
Ш. Работа по теме урока Работа по учебнику № 293 (с. 91).
![]() Сколько пар противоположных граней у кубика? (Три пары.)
Сколько пар противоположных граней у кубика? (Три пары.)
— Каким цветом они должны быть раскрашены? (Одним цветом.)
— Сколько различных цветов нужно для окрашивания граней?
(Три.) ЛГ2 294 (с. 91).
Решение:
2 ) 210 мм : 2 = 105 мм — сумма длин двух сторон прямоугольника. Пусть одна часть — длина меньшей стороны, а шесть частей — длина большей стороны.
3 1 ч. + 6 ч. = 7 ч. — всего частей;
![]() = 15 мм — длина меньшей стороны;
= 15 мм — длина меньшей стороны;
4) 15 мм • 6 = 90 мм — длина большей стороны;
5) 15 мм • 90 мм = 1350 кв. мм — площадь прямоугольника.
— Чему равна длина сторон искомого прямоугольника? (1 см
5 мм и 9см.)
![]() Начертите этот прямоугольник.
Начертите этот прямоугольник.
М 295 (с. 91).
![]()
— Как найти периметр данного прямоугольника? ((2 см +
— Как найти площадь данного прямоугольника? (2 см • бсм — — 12 кв. см.)
![]() Начертите этот прямоугольник.
Начертите этот прямоугольник.
М. Физкультминутка
М. Закрепление изученного материала Работа по учебнику ![]() 296 (с. 91).
296 (с. 91).
— Прочитайте условие задачи. Как найти длину второй стороны прямоугольника? (Нужно применить правшо нахождения части от величины: 8 см : 4 • З = 6 см.)
![]() Как найти периметр данного
прямоугольника? ((8 см + +6см) 28 см.)
Как найти периметр данного
прямоугольника? ((8 см + +6см) 28 см.)
— Как найти площадь данного прямоугольника? (8см • 6 см ![]() =
48 кв. см.) М 297(с. 91).
=
48 кв. см.) М 297(с. 91).
(Коллективное выполнение.)
КпСС
![]()
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 134 (с. 71 ).
Урок 1 1 7, Уравнение, Корень уравнения
Цели: систематизировать и обобщить знания об алгебраическом понятии «уравнение»; познакомить с понятием «корень уравнения»; развивать навыки нахождения корня уравнения.
1. Организационный момент. Сообщение темы и целей урока ll. Актуализация знаний
1. Устный счет
— Выберите все правильные ответы.
(Ответы записаны на доске.)
1. Если уменьшаемое равно 1 100, а разность — 900, то чему равно вычитаемое?
а) 2000 6) 200
в) 12 000
г) 2 сотням
д) числу, в котором 2 единицы второго ютасса
е) произведению чисел I и 12 000
2. Для решения каких уравнений надо выполнить сложение?
а) 5600 - х = 400 г) х + 3000 = 7000
З. Какие числа делятся одновременно на 10 и на 100?
а) 56 000 г) 800 6) 2000 д) 54 320
в) 78 950 е) 9000
2. Разминка
• По чему ![]() воздуху.)
воздуху.)
• Что становится легче, когда увелитшвается в размерах? (Шарик.)
• Два раза рождается, один раз умирает. Кто это? (Птица.)
• Назовите признак, по которому объединены эти слова: бабочка, самолет, птица, воздушный шар, ракета, пушинка. (Летающие объекты.)
• Самый первый воздушный шар смог подняться над землей всего на 8 м. Зато во время следующего полета — уже
Уравнение. Корень уравнения
![]()
на 56 м. Во сколько раз выше поднялся шар во второй раз? (В паз.)
Ш. Работа по теме урока Работа по учебнику ![]() 298 (с. 92).
298 (с. 92).
(Коллективное выполнение с комментированием.)
![]() Что такое уравнение?
(Это математическое равенство с одной ши НиКОЛЬКИМИ неизвестными величинами.)
Что такое уравнение?
(Это математическое равенство с одной ши НиКОЛЬКИМИ неизвестными величинами.)
— Что такое корень уравнения? (Это искомое число, при
подстановке которого в уравнение получается верное равенство. ) ![]() 299 (с.
92).
299 (с.
92).
![]() Прочитайте задание. Выполните его.
Прочитайте задание. Выполните его.
![]() Какое число будет корнем первого
уравнения? (37 541.)
Какое число будет корнем первого
уравнения? (37 541.) ![]() Каким свойством вы воспользовались для
нахождения данного корня? (Переместительным свойством сложения.)
Каким свойством вы воспользовались для
нахождения данного корня? (Переместительным свойством сложения.)
— Какое число будет корнем второго уравнения? (4173.)
— Каким свойством или правилом можно воспользоваться для
нахождения данного корня? (Сочетательным свойством сложения или правшюм
прибавления суммы к числу.) ![]() Какое число будет корнем третьего
уравнения? (2379.)
Какое число будет корнем третьего
уравнения? (2379.) ![]() Каким свойством вы воспользовались для
нахождения данного корня? (Переместительным свойством умножения.)
Каким свойством вы воспользовались для
нахождения данного корня? (Переместительным свойством умножения.) ![]() Какое число
будет корнем четвертого уравнения? (42.)
Какое число
будет корнем четвертого уравнения? (42.)
— Каким свойством или правилом вы воспользовались для нахождения данного корня? (Сочетательным свойством умножения или правилом умножения числа на произведение.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() (с. 92).
(с. 92).
— Прочитайте задание. Какая пара уравнений имеет одинаковый корень? (х — 356 = 217 и х — 217 = 356.)
![]() Как вы нашли данную пару? (За
неизвестным уменьшаемым скрывается одно и то же число, так как равенство
сохраняется, если вычитаемое и значение разности меняются местами.)
Как вы нашли данную пару? (За
неизвестным уменьшаемым скрывается одно и то же число, так как равенство
сохраняется, если вычитаемое и значение разности меняются местами.) ![]() Есть
еще пары уравнений, которые имеют одинаковый корень? (х - 25 698 = 356 х - 356
= 25 698 (х = 25 342), х +25698 = 356 217=356- 217(x = 356).) ЛФ 301 (с.
92-93).
Есть
еще пары уравнений, которые имеют одинаковый корень? (х - 25 698 = 356 х - 356
= 25 698 (х = 25 342), х +25698 = 356 217=356- 217(x = 356).) ЛФ 301 (с.
92-93).
(Коллективное выполнение с комментированием.)
![]() Прочитайте вопрос.
Верным или неверным будет полученное равенство? (Верным.)
Прочитайте вопрос.
Верным или неверным будет полученное равенство? (Верным.)
![]()
— Подтвердите данный вывод методом подбора на примере равенства 25 + 75 = 100.
— Кашм будет корень уравнения? (25.)
— На какое число нужно уменьшить каждую часть данного уравнения, чтобы в левой части осталось только неизвестное х? (На число 75.)
— Какой можно сделать вывод? (Если в уравнении с неизвестным слагаемым каждую часть уменьшить на известное слагаемое, то получится новое уравнение, в котором в одной части будет нахоДиться неизвестное х, а в другой — разность между значением суммы и известным слагаемым.)
— Какое выражение в этом случае будет находиться в правой части? (100— 75.)
![]() Будет ли значение этого выражения корнем
исходноКО уравнения? (Да. Значение последней разности (25) будет как корнем
нового уравнения, так и корнем исходного уравнения.) М 302 (с. 93).
(Самостоятельное выполнение. Проверка в парах.) М ЗОЗ (с. 93). (Коллективное
выполнение с комментированием.) М 304 (с. 93).
Будет ли значение этого выражения корнем
исходноКО уравнения? (Да. Значение последней разности (25) будет как корнем
нового уравнения, так и корнем исходного уравнения.) М 302 (с. 93).
(Самостоятельное выполнение. Проверка в парах.) М ЗОЗ (с. 93). (Коллективное
выполнение с комментированием.) М 304 (с. 93).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
2. Выполнение упражнений в тетради для самостоятельной работы ЛГ2 137(с. 72). (Коллективное выполнение с записью на доске.) М 136 (с. 72).
(Самостоятельное выполнение. Вариант I — уравнения 1, 3,
5, 7; вариант 2 — уравнения 2, 4, 6, 8.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 135 (с. 71).
Урок 118. Учимся решать задачи с помощью уравнений
Цель: развивать умение решать арифметические сюжетные задачи с помощью уравнений.
1. Организационный момент. Сообщение темы и цели урока
Учимся решать задачи с помощью уравнений
![]()
П. Актуализация знаний
1. Цифровой квадрат
|
44 |
22 |
|
33 |
55 |
|
|
|
|
33 |
|
66 Ответ:
88
77 77
2. Родственные ряды
|
90 |
6 |
30 |
|
33 |
|
29 |
|
9 |
5 |
|
( Числа верхнего ряда получаются в результате умножения соответствующих чисел нижнего ряда на З и прибавления числа З.
Пропущено число 18.)
З. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Мы знаем, что Олег родился с 15 по 18 июля. Сколько вопросов надо задать Олегу, чтобы узнать день его рождения, если на все вопросы он отвечает «да» или «нет»? Какой вопрос может быть первым? (Примерный ответ. Нам нужно определить одно из четырех чисел. Разобьем весь период на две части: с 15 по 16 июля и с 17 по 18 июля. Для этого зададим первый вопрос: «Ты родился с 15 по 16 июля?» После получения любого ответа нам уже надо будет искать ответ среди двух чисел. А это уже можно сделать, задав один вопрос. Значит, чтобы узнать дату рождения Олега, ему нужно задать один вопрос.)
4. Устный счет
(Примеры записаны на доске.)
![]() Вычислите значения выражений.
Вычислите значения выражений.
|
2 км 500 м • 6 10 км 75 м • 2 |
7 руб. 20коп. : 9
|
|
3 ц 2 кг 8 |
36 руб. 50 коп. : 5 |
|
4 руб. 50 коп. • 5 |
60 кг: 8 |
Ш. Работа по теме урока Работа по учебнику ![]() 305 (с. 94).
305 (с. 94).
(Коллективное выполнение с комментированием учителя.) ![]() 306
(с. 94).
306
(с. 94).
— Прочитайте условие задачи. Составьте к ней уравнение. (х + (х- 30) = 350.)
Прочитайте условие задачи. Какое уравнение подходит к данной задаче? (х + (х— 100) = 1000.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику JV2 308 (С. 95).
Вариант задачи. За альбом и книгу заплатили 280 руб. Сколько стоит альбом, если книга на 80 руб. дороже альбома?
![]() Чему равен корень уравнения? (100.) ле
309 (с. 95).
Чему равен корень уравнения? (100.) ле
309 (с. 95).
![]() Как можно получить
стоимость хрестоматий? (Цену хрестоматии умножить на количество экземпляров.)
Как можно получить
стоимость хрестоматий? (Цену хрестоматии умножить на количество экземпляров.)
— Каким будет искомое уравнение? (х • 45 = 2250.)
— Как можно получить количество хрестоматий? (Стоимость
всех экземпляров разделить на цену хрестоматии. ) ![]() Составьте уравнение.
(2250 : х = 45.)
Составьте уравнение.
(2250 : х = 45.)
![]() Чему равен общий корень уравнений? (50.)
Чему равен общий корень уравнений? (50.)
![]() Сформулируйте
две обратные задачи.
Сформулируйте
две обратные задачи.
Варианты задач. 1. для школьной библиотеки закупили одинаковые хрестоматии по цене 50 руб./шт. Сколько хрестоматий было куплено, если за них заплатили 2250 руб.?
2. Для школьной библиотеки закупили 45 одинаковых хрестоматий по цене 50 руб./шт. Какова стоимость всех хрестоматий?
![]() Составьте уравнение
к каждой задаче. Шля первой заДачи: 1 — 2250 : х = 50; для второй задачи: 2 — х
: 45 = 50.)
Составьте уравнение
к каждой задаче. Шля первой заДачи: 1 — 2250 : х = 50; для второй задачи: 2 — х
: 45 = 50.)
2. Выполнение упражнения в тетради для самостотељной работы
![]() 138 (1-3) (с. 73).
138 (1-3) (с. 73).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 139 (с. 74).
Урок 1 1 9, Поупражняемся в вычислениях и повторим пройденное
Цель: развивать навыки решения уравнений, вычислений столбиком, составления уравнений к задачам.
1. Организационный момент. Сообщение темы и цели урока
Поупражняемся в вычислениях и повторим пройденное
![]()
ll. Актуализация знаний
1. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Составьте перевертыш — фразу, которая читается одинаково слева направо и справа налево. Вот ее первая часть, превышающая половину: «Аргентинам...» (Примерный ответ. Если здесь написана первая часть фразы, превышающая половину, нужно узнать, какая буква из написанных может служить центром фразы. Только буква м, так как она не повторяется. Теперь нужно после буквы м написать все буквы в обратном порядке: аргентина м анитнегра. Правильно разбив фразу на слова, получим: «Аргентина манит негра».)
2. Волшебная звезда
(Сумма = 66.)
 Ответ:
Ответ:
З. Устный счет
(Примеры записаны на доске.) — Вычислите.
56 дм — 3 м 7 дм
6 дм 30 см — 6 дм
4 м 40 см — 5 дм
4. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Как зависит объем выполненной работы от времени при постоянной производительности? (При постоянной произвоДительноспш увеличение (уменьшение) времени в несколько раз призоДит к увеличению (уменьшению) объема выполненной работы в это же число раз.)
• Как зависит объем выполненной ра&пы от производительности при постоянном времени работы? (Если время работы одинаковое, то увеличение (уменьшение) произвоДительности в некоторое число раз привоДит к увеличению (уменьшению) объема выполненной работы в это же число раз.)
10 Поурочные разработки по математике
![]()
• Как связаны между собой производительность и время работы при одинаковом объеме работы? (При одинаковом объеме работы увеличение (уменьшение) времени в несколько раз привоДит к уменьшению (увеличению) произвоДительноспш в это же число раз.) Ш. Работа по теме урока Работа по учебнику № 310 (с. 96). (Выполнение в соответствии с заданиями.) М 311 (с. 96).
— Прочитайте задачу. Какого она типа? (Задача на Движение в противоположных направлениях.) Решение:
1) 120 км : 2 ч = 60 км/ч — скорость изменения расстояния между катером и теплоходом.
Пусть одна часть — скорость теплохода, а две части — скорость катера.
2) 1 ч. + 2 ч. = 3 ч. — всего частей; 3) 60 км/ч : 3 = 20 км/ч.
Ответ: скорость теплохода 20 км/ч.
lV. Физкультминутка
![]() Закрепление изученного материала
Закрепление изученного материала
1. Работа по учебнику № 312 (с. 96).
![]() Прочитайте задачу. Составьте уравнение. (х + х + 20 = 190.)
Прочитайте задачу. Составьте уравнение. (х + х + 20 = 190.) ![]() Чему
равен корень данного уравнения? (85.) № 313 (с. 96).
Чему
равен корень данного уравнения? (85.) № 313 (с. 96).
![]() Прочитайте задачу. Какое выражение является решением задачи? ((63 — З) :
З = 20 (руб./л).)
Прочитайте задачу. Какое выражение является решением задачи? ((63 — З) :
З = 20 (руб./л).)
2. Выполнение упражнений в тетради для самостоятельной работы м 141, 142 (с. 75).
(Самостоятельное выполнение. Проверка.) М 143 (с. 76).
(Самостоятельное выполнение. Проверка с записью решения на доске.) ле 144 (с. 76).
(Самостоятельное выполнение. Проверка.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 140 (с. 75).
Контрольная работа № 7
![]()
Цели: проверить знания и умения учащихся; развивать навыт самостоятельной работы.
(Текст контрольной работы выдается каждому ученику на отдельном листочке. )
Вариант 1
1. Из данного набора чисел выбери и запиши в первый столбик все числа, которые являются нечетными и шестизначными, а во второй — все числа, которые являются нечетными или ше-
СТИЗНаЧНЫМИ.
123 456, 654 321, 999 999, П ш, 001, 895 347.
2. Какое минимальное число маленьких кубиков нужно добавить к 50 таким же кубикам, чтобы из них можно было составить один большой кубик? Все маленькие кубики одинаковые.
3. При измерении площади фигуры с помощью палетки получилось 5 полных клеточек и 23 неполные клеточки. Чему приблизительно равна площадь этой фигуры, если площадь одной клеточки палетки равна 1 кв. см?
4. Составь уравнение, с помощью которого можно решить следующую задачу.
Альбом и книга стоят 270 руб. Ютига дороже альбома на 30 руб. Сколько стоит альбом?
5. Какое суммарное число очков имеет больше шансов выпасть при бросании двух игральных кубиков: 4 или 1? Почему?
Вариант 2
1. Из данного набора чисел выбери и запиши в первый столбик все числа, которые являются нечетными и шестизначными, а во второй — все числа, которые являются нечетными или шестизначными.
345 678, 876 543, 555 555, 99 999, 100 001, 195 343.
2. Какое минимальное число маленьких кубиков нужно добавить к 60 таким же кубикам, чтобы из них можно было составить один большой кубик? Все маленькие кубики одинаковые.
З. При измерении площади фигуры с помощью палетки получилось 6 полных клеточек и 25 неполных клеточек. Чему приблизительно равна площадь этой фигуры, если площадь одной клеточки палетки равна 1 кв. см?
4. Составь уравнение, с помощью которого можно решить следующую задачу.
![]()
Журнал и книга стоят 230 руб. Книга дороже журнала на 70 руб. Сколько стоит журнал?
5. Какое суммарное число очков имеет больше шансов выпасть при бросании двух игральных кубиков: З шли 10? Почему?
Урок 121. Разные задачи
Цели: познакомить с некоторыми идеями вероятностного (стохастического) описания (моделирования) реальных ситуаций; довести до понимания учащихся основной смысл понятия «вероятность».
1. Организационный момент. Сообщение темы и целей урока
И. Актуализация знаний
1. Закономерность
![]()
(Закономерность: — 7, + 4; пропущенные числа![]()
2. Цифровой квадрат
|
|
|
40 Ответ: 60 |
|
|
|
|
|
20 |
40 |
зо 70
З. Родственные ряды
|
5 |
12 |
7 |
0 |
8 |
|
|
З |
8 |
|
7 |
(Сумма соответствующих чисел верхнего и нижнего рядов равна 15. Пропущено число 15.)
4. Логическая задача
— Решите задачу устно.
Вася написал все числа от 1 до 1000. Сколько цифр написал Вася? (Примерный ответ. Первые девять однозначных чисел написаны девятью цифрами. Двузначные числа от 10 до 99 требуют по две цифры. А так как этих чисел 99 — 9 = 90, то на их написа-
Разные задачи
![]()
ние ушло 180 цифр. Для записи трехзначных чисел нужно по три цифры. Их 999 — 99 = 900, следовательно, понадобилось 3 • 900 = = 2700 (цифр). И на число 1000 потрачено четыре цифры. Общее число написанных Васей цифр: 9 + 2 • 90 + 3 • 900 + 4 = 2893.)
Ш. Работа по теме урока ![]() по учебнику
по учебнику
№ 314 (с. 97).
(Коллективное выполнение с комментированием.) ![]() Заполните
таблицу.
Заполните
таблицу.
![]() Сколько раз в ней встречается число 12?
(Один.)
Сколько раз в ней встречается число 12?
(Один.)
— Как объяснить подмеченную Мишей и Машей закономерность? ( 7 очков может получиться шестью разными способа-
![]()
а 12 очков только одним способом: 6 + 6 = 12.) № 315 (с. 98).
![]() Сколько раз в таблице из № 314
встречается число 7? (Шесть.)
Сколько раз в таблице из № 314
встречается число 7? (Шесть.)
— Какое число (или какие числа) встречается среди значений этой таблицы наименьшее число раз? (Наименьшее число раз встречаются число 2 и число 12 (по оДному разу).)
![]() Для каждого возможного числа
определите, сколько раз оно встречается среди значений таблицы. (2 (один раз),
З (Два раза), 4 (три раза), 5 (четыре раза), 6 (пять раз), 7 (шесть раз), 8
(пять раз), 9 (четыре раза), 10 (три раза), 11 (Два раза), 12 (один раз).)
Для каждого возможного числа
определите, сколько раз оно встречается среди значений таблицы. (2 (один раз),
З (Два раза), 4 (три раза), 5 (четыре раза), 6 (пять раз), 7 (шесть раз), 8
(пять раз), 9 (четыре раза), 10 (три раза), 11 (Два раза), 12 (один раз).)
— Кто из детей имеет больше шансов выиграть? (Маша, так как 8 очков имеют больше благоприятных вариантов, чем 9 очков (5 > ф.) lV. Физкультминутка
М. Закрепление изученного материала
1. Работа по учебнику № 317 (с. 98-99).
(Работа в парах.)
![]() Кто победит в
соревновании? (Тот, кто выберет для себя число 11, так как для этого числа
количество благоприятных вариантов равно восьми, а для числа 12 — семи.)
Кто победит в
соревновании? (Тот, кто выберет для себя число 11, так как для этого числа
количество благоприятных вариантов равно восьми, а для числа 12 — семи.)
2. Выполнение упражнений в тетради для самостоятельной работы
М 147€. 78).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]()
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
Домашнее задание
Учебник: № 316 (с. 98).
Урок 122. Разные задачи
Цель: продолжать знакомить с некоторыми идеями вероятностного (стохастического) описания (моделирования) реальных ситуаций, с понятием «вероятность».
![]() Организационный момент. Сообщение темы и цели урока ll. Актуализация
знаний
Организационный момент. Сообщение темы и цели урока ll. Актуализация
знаний
1. Разминка
• Как называется самая близкая к Земле звезда? (Солнце.)
• На Луне все предметы весят в 6 раз меньше, чем на Земле, потому что Луна в 6 раз слабее притягивает к себе тела, чем Земля. Сколько будет весить на Луне гиря массой 18 кг? (З кг.)
• Если бы Несмеяна жила на Луне, она весила бы там 10 кг. Каков вес Несмеяны на Земле? (60 кг.)
• По удаленности планет от Солнца Юпитер дальше Земли, Плутон дальше Юпитера. Следовательно, самая удаленная от Солнца гшанета — . (Плутон).
• У многих планет Солнечной системы есть естественные спутники. У Земли естественный спутник один. Какой? (Луна.)
2. Устный счет
(Примеры записаны на доске.)
![]() Решите
примеры и объясните способ вычисления.
Решите
примеры и объясните способ вычисления.
![]() 32
• (8 + 2)
32
• (8 + 2)
1800 : (9 • 2) П - 178
23-7-41 24 • 8 + 16
Ш. Работа по теме урока Работа по учебнику ЛФ 318 (с. 99).
— Прочитайте условие задачи. Что нужно сделать, чтобы ответить на вопрос? (Сравнить число Девочек и число мальчиков.)
— Какой ответ мы получим в результате данного сравнения?
(18 : 9 = 2 (раза).)
Разные задачи
![]()
— Что означает полученное число? (У Девочки в 2 раза больше шансов оказаться у доски, чем у мальчика.)
Так мы сравнили число благоприятных вариантов для одного события с числом благоприятных вариантов для другого события. М 319 (с. 99).
— Прочитайте задачу. Одинаковы ли шансы вынуть шар с четным номером шли с нечетным номером? (СреДи натуральных чисел от 1 до 99 нечетных чисел 55, а четных 54. Так как 55 > 54, шансов вынуть шар с нечетным номером больше, чем с четным.)
М. Физкультминутка
V. Закрепление изученного материала Работа по учебнику м 320 (с. 99).
— Прочитайте задачу. Как ответить на вопрос? (Либо непосреДственно воспользоваться указанной таблицей, либо составить и пересчитать соответствующие варианты. ЧИСЛО 9 встречается восемь раз, а чисао 10 — Девять раз.) м 321 (с. 99). (Самостоятельное выполнение.) м 322 (с. 99).
— Какой результат: четный или нечетный — среди табличных случаев сложения встречается чаще? (В кажДом столбике либо пять четных результатов и четыре нечетных, либо наоборот. При этом столбиков первого типа на один больше, чем столбиков второго типа. Поэтому четных результатов на один больше, чем нечетных (41 четный результат и 40 нечетных). )
— А среди табличных случаев умножения? ( Четных результатов гораздо больше. )
— Как это можно объяснить? (Примерный ответ. Нечетный результат умножения может получиться только тогда, когда оба множителя являются нечетными числами, в остальных случаях (а их гораздо больше) результат будет четным числом. Например, если рассмотреть второй столбик таблицы (умножение числа 2), то в нем результаты будут только четными числами.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 146 (с. 77).
![]()
Урок 123. Натуральные числа и число О (повторение)
Цель: повторить основные свойства целых неотрицательных
чисел.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
Ответ: 80 |
20 |
|
|
|
|
|
50 |
50 60
2. Родственные ряды
|
14 |
6 |
41 |
|
|
|
З |
|
6 |
8 |
5 |
( Числа верхнего ряда получаются в результате умножения соответствующих чисел нижнего ряда на самих себя и прибавления числа 5. Пропущено число 69.)
З. Логическая задача
— Решите задачу устно.
Зайчиха для своих зайчат разложила 42 морковки на семь кучек так, что кучек с одинаковым количеством морковок не было. Причем число морковок в каждой кучке выражено однозначным числом. Сколько морковок в каждой кучке? (Замети, что 42 = З + 4 + 5 + 6 + 7+ 8+ 9, значит, в кучках бьио З, 4, 5, 6, 7, 8,
9 морковок.)
4. Устный счет
(Примеры записаны на доске.) ![]() Вычислите.
Вычислите.
• 560 разделить на 4.
• Во сколько раз 1000 больше 200?
• Три четверти от 800.
• Сумму чисел 280 и 120 уменьшите в 100 раз.
• Число 3600 разделите на частное чисел 180 и 30.
• 920 разделите на произведение чисел 10 и 2.
Натуральные числа и число О (повторение)
![]()
Ш. Работа по теме урока ![]() Работа по учебнику м 323 (с. 100).
Работа по учебнику м 323 (с. 100).
(Устное выполнение.)
![]() Назовите самое маленькое натуральное
число. (1.)
Назовите самое маленькое натуральное
число. (1.)
![]() Является ли число 0 натуральным? (Нет.)
Является ли число 0 натуральным? (Нет.)
— Существует ли самое большое натуральное число? (Смого
большого натурального числа нет. Если к Данному натуральному числу прибавить
число 1, то результат будет также натуральным числом, причем этот результат
будет больше Данного числа.) ![]() 324 (с. 100).
324 (с. 100).
![]() Какое пятизначное
натуральное число самое маленькое? (10000.)
Какое пятизначное
натуральное число самое маленькое? (10000.)
— Какое пятизначное натуральное число самое большое?
(99 999.)
![]() Сколько существует
пятизначных чисел? (99 999 — 10 000 = — 89 999. К полученному результату надо
прибавить ЧИСло 1, чтобы учесть и само число 10000. Следовательно, всего 89 999
+ 1 = 90 000 (пятизначных чисел).)
Сколько существует
пятизначных чисел? (99 999 — 10 000 = — 89 999. К полученному результату надо
прибавить ЧИСло 1, чтобы учесть и само число 10000. Следовательно, всего 89 999
+ 1 = 90 000 (пятизначных чисел).)
— Как вы получили результат? (С помощью разностного сравнения.) lV. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику м 325, 326 (с. 100). (Работа в парах.)
— Как
расположить числа в порядке возрастания? (23 654, 68 736, 96542, 142 578,
687369.) ![]() Как расположить числа в порядке убывания? (857 931, 389 621, 125369,
96547, 84 635.)
Как расположить числа в порядке убывания? (857 931, 389 621, 125369,
96547, 84 635.)
![]() Чем вы воспользовались при выполнении
данного задания?
Чем вы воспользовались при выполнении
данного задания?
(Поразрядным способом сравнения натуральных чисел.) м 327 (с. 100).
![]() Какое число будет
расположено между данными числами? (458 962)
Какое число будет
расположено между данными числами? (458 962)
![]() Запишите ответ с помощью двойного
неравенства. (458 961 < 458962< 458 963.)
Запишите ответ с помощью двойного
неравенства. (458 961 < 458962< 458 963.)
![]() Может ли другое число находиться между
данными числа-
Может ли другое число находиться между
данными числа-
ми? (Нет.) м 328 (с. 100).
— Какие числа можно получить, переставив цифры в записи числа 123? (123, 132, 213, 231, 312, 321.)
Сколько таких чисел получилось? (Шесть.)
Какое из этих чисел наибольшее? (321.)
— Каких чисел больше: четных или нечетных? (Нечетных.)
— Чем это можно объяснить? (В записи Данного числа присутствуют две нечетные цифры и только одна четная цифра.)
2. Выполнение упражнений в тетради для самостоятельной работы
![]() 149 (с. 79).
149 (с. 79).
(Самостоятельное выполнение.) № 150 (с. 79).
(Работа в парах.) ![]() 152 (с. 79).
152 (с. 79).
(Самостоятельное выполнение.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 151 (с. 79).
Урок 124. Натуральные числа и число О (повторение)
Цель: продолжать повторение основных свойств целых неотрицательных чисел.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Волшебные квадраты
(Волшебная сумма равна 27.)
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
пап |
|
|
|
||||
Ответы:
|
10 |
П |
6 |
|
|
|
|
|
12 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Натуральные числа и число О (повторение)
![]()
2. Логическая задача
— Решите задачу устно.
Роман и Федор — два брата. У них вместе 100 марок. В день рождения Федора Роман подарил ему 20 марок, и у них стало одинаковое количество марок. Сколько марок было у Романа и Федора до этого? (Примерный ответ. Общее количество марок не изменилось после того, как один брат подарил другому 20 марок, и у каждого из братьев стало марок поровну, т. е. по 100 : 2 = = 50 (марок). Если у Романа стало 50 марок, а он отдал брату 20 марок, то до этого у него было 50 + 20 = 70 (марок). Если у Федора стало 50 марок, а получил он от брата 20 марок, то до этого у него было 50 — 20 = 30 (марок).)
З. Устный счет
(Примеры записаны на доске.)
— Выполните действия удобным
способом. ![]() зоо + (240 : 60)
зоо + (240 : 60)
|
5 , 18 , 20 25 • 4 . 96 |
(20 + б) • 4 7200 : (9 • 4) |
![]() 31
• (3 • 100)
31
• (3 • 100)
90 : (5 • 2)
Ш. Работа по теме урока Работа по учебнику ![]() 329 (с. 101).
329 (с. 101).
— Прочитайте задание. Каким будет значение первой суммы? ( Четным числом.)
![]() Почему?
(Так как склаДываются два нечетных числа.)
Почему?
(Так как склаДываются два нечетных числа.)
— Каким будет значение второй суммы? (Нечетным числом.) ![]() Почему?
( Так как складывается нечетное число с четным.)
Почему?
( Так как складывается нечетное число с четным.)
— Каким будет значение разности? (Нечетным.)
— Докажите. (Так как из четного числа вычитается нечетное ЧИСЛО.)
![]() Что представляет
собой второе выражение? (Произведение двух сумм.)
Что представляет
собой второе выражение? (Произведение двух сумм.)
— Каким будет значение первой суммы? (Нечетным числом.) ![]() Объясните.
( Так как к четному числу прибавляется нечетное число.)
Объясните.
( Так как к четному числу прибавляется нечетное число.)
— Каким будет значение второй суммы? (Нечетным числом.)
— Почему? (Так как к четному числу прибавляется нечетное число.)
![]() Каким будет значение произведения?
(Нечетным числом.)
Каким будет значение произведения?
(Нечетным числом.)
— Докажите. (Перемножаются нечетные числа.)
зоо
![]()
Прочитайте задание. Как найти искомое число? (Надо перемножить числа 2, З и 5.)
— Почему надо выбрать этот способ? (Значение произведения всегда Делится на кажДый множитель.)
— Какое получится число? (30.)
![]() Существуют ли другие натуральные числа,
которые также делятся нацело на числа 2, 3, 5? (Да, любое число, которое кратно
числу 30, т. е. 60, 90, 120 и т. д.) М 331 (с. 101).
Существуют ли другие натуральные числа,
которые также делятся нацело на числа 2, 3, 5? (Да, любое число, которое кратно
числу 30, т. е. 60, 90, 120 и т. д.) М 331 (с. 101).
— Прочитайте задание. Какое число будет
искомым? (31.) ![]() Как вы получили это число? (Увеличили
число 30, полученное в предыдущем заДанш, на число 1.) lV. Физкультминутка
Как вы получили это число? (Увеличили
число 30, полученное в предыдущем заДанш, на число 1.) lV. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику м 332 (с. 101).
— Значение какого из данных выражений нельзя вычислить? (Под буквой «а.)
![]() Почему? (Значение разности, на которую
нужно разДелить значение суммы, равно нулю, а на ноль Делить нельзя.)
Почему? (Значение разности, на которую
нужно разДелить значение суммы, равно нулю, а на ноль Делить нельзя.) ![]() Значение
какого из оставшихся выражений легко вычислить устно? (Под буквой «в».)
Значение
какого из оставшихся выражений легко вычислить устно? (Под буквой «в».)
![]() Как это сделать? (Значение разности, на
которую нужно умножить значение суммы, равно нулю, а при умножении любого числа
на ноль получается ноль.) № 333 (с. 101).
Как это сделать? (Значение разности, на
которую нужно умножить значение суммы, равно нулю, а при умножении любого числа
на ноль получается ноль.) № 333 (с. 101). ![]() Прочитайте задание.
Какую цифру нужно записать в первом разряде? (0.)
Прочитайте задание.
Какую цифру нужно записать в первом разряде? (0.)
![]() Какие цифры запишем
в следующих разрядах? (Во втором — 2, в третьем — 4, в четвертом — 6, в пятом —
8.)
Какие цифры запишем
в следующих разрядах? (Во втором — 2, в третьем — 4, в четвертом — 6, в пятом —
8.)
![]() Какое число получилось? (86 420.)
Какое число получилось? (86 420.)
— Как найти втрое число? (В первом разряде запишем цифру 1, во втором — З, в третьем — 5, в четвертом — 7, в пятом — 9.) — Какое число получилось? (97 531.)
— Могут ли в первом разряде быть записаны другие цифры, кроме 0 и 1? (Нет.)
![]() Почему? (В противном
случае мы не сможем увеличить на 2 число еДиниц в пятом разряде.)
Почему? (В противном
случае мы не сможем увеличить на 2 число еДиниц в пятом разряде.)
— Сколько искомых чисел существует?
(Два: 86 420 и 97 531.) ![]() 101).
101).
(Работа в парах. Взаимопроверка.)
Алгоритмы вычисления столбиком (повторение)
2. Вьто.лнею|е упражнений в тетради для самосттељной ра&лы 153, 154 (с. 79-80).
(Самостоятельное выполнение. Проверка с записью решения на доске.) м 155, 156 (с. 80).
(Самостоятельное выполнение.)
Ш. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 157, 158 (с. 80).
Урок 125. Алгоритмы вычисления столбиком (повторение)
Цель: повторить алгоритмы вычисления столбиком для всех четырех арифметических действий.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
1. Цифровой квадрат
|
50 |
|
|
40 |
|
![]() 80 Ответ:
80 Ответ:
50
90 40
2. Родственные ряды
|
32 |
8 |
2 |
50 |
18 |
|
8 |
4 |
2 |
|
|
( Числа верхнего ряда получаются в результате умножения соответствующих чисел нижнего ряда на 1, 2, З, 4, 5. Пропущено Число 6.) З. Логическая задача
![]() Решите задачу устно.
Решите задачу устно.
Малыш может
съесть 600 г варенья за 6 мин, а Карлсон ![]() в 2 раза быстрее. За
какое время они съедят это варенье вместе? (За минуту Малыш съеДает 600 : 6=100
(г) варенья. Карлсон может съесть все варенье за 6 : 2 = З (мин), значит, за
минуту он съеДает 600 : З = 200 (г) варенья. Вместе Малыш и Карлсон съеДают за
минуту 100 + 200 = ЗОО (г) варенья. Все варенье они сьеДят за 600 : ЗОО = 2
(мин). )
в 2 раза быстрее. За
какое время они съедят это варенье вместе? (За минуту Малыш съеДает 600 : 6=100
(г) варенья. Карлсон может съесть все варенье за 6 : 2 = З (мин), значит, за
минуту он съеДает 600 : З = 200 (г) варенья. Вместе Малыш и Карлсон съеДают за
минуту 100 + 200 = ЗОО (г) варенья. Все варенье они сьеДят за 600 : ЗОО = 2
(мин). )
![]()
Ш. Работа по теме урока Работа по учебнику
М 335, 336 (с. 102).
(Самостоятельное выполнение.)
— Что вы повторили, выполняя данные задания? (Алгоритмы сложения и вычитания столбиком, переместительное СВОЙство сложения, взаимосвязь между сложением и вычитанием.)
М. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику м 337, 338 (с. 102-103).
(Самостоятельное выполнение.)
— Что вы вспомнили при выполнении данных заданий? (Алгоритмы умножения и Деления столбиком, переместительное своЙство умножения, взаимосвязь умножения и Деления.) 2. Вьтшшение упражнений в тетради для самостягељной работы ле 160 (с. 81).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]() 161 (с. 81).
161 (с. 81).
(Самостоятельное выполнение. Проверка в парах.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 159 (с. 81).
Урок 126. Алгоритмы вычисления столбиком (повторение)
Цель: продолжать повторение алгоритма вычисления столбиком для всех четырех арифметических действий.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
Il. Актуализация знаний
1. Закономерность
![]()
(Закономерность: — 5, + 6; пропущенные числа — 1 и 7.)
Алгоритмы вычисления столбиком (повторение) зоз
 Ответ:
Ответ:
З. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Как зависит стоимость от количества купленного товара при постоянной цене? (При постоянной цене увеличение (уменьшение) количества купленного товара привоДит к увеличению (уменьшению) стоимости покупки.)
• Как зависит стоимость от цены купленного товара при постоянном количестве? (При постоянном количестве товара с увеличением (уменьшением) цены в несколько раз стоимость увеличится (уменьшится) в это же число раз.)
• Как связаны между собой цена и количество купленного товара при одинаковой стоимости? (При оДинаковой стоимости увеличение (уменьшение) количества товара в несколько раз привоДит к уменьшению (увеличению) цены в это же число раз.)
Ш. Работа по теме урока Работа по учебнику № 339 (с. 103).
— Назовите правила порядка выполнения действий в
выражениях со скобками и без скобок. ![]() 340 (с. 103).
340 (с. 103).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику
М 341 (с. 103).
(Творческая работа в парах.)
2. Выполнение упражнения в тетрац для самостоятельной работы № 162 (1, 2) (с. 82).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
И. Подведение итогов урока домашнее задание
Тетрадь для самостоятельной работы: № 162 (3) (с. 82).
масс
![]()
Урок 127 а Действия с величинами (повторение)
Цель: повторить основные вопросы, относящиеся к выполнению действий с величинами.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Цифровой квадрат
|
|
40 |
|
20 |
20 |
![]() 50 Ответ:
50 Ответ:
40
30 60
2. Логическая
задача ![]()
![]() Решите задачу устно.
Решите задачу устно.
Количество яблок в корзине выражено двузначным числом. Яблоки можно разделить поровну между 2, 3, 5 детьми, но нельзя разделить поровну между 4 детьми. Сколько яблок в корзине? (30.)
З. Устный счет
(Примеры записаны на доске.)
— Вычислите.
Зм: Ш 45 800 :![]()
![]() 68
•
68
•![]()
6 руб. : 10 810
: 9 з м 20 см :![]()
Ш. Работа по теме урока
Работа по учебнику
ЛФ 342, 343 (с. 104).
(Самостоятельное выполнение с предварительным повторением.)
— В каких случаях возможно сложение и вычитание величин?
(Когда величины оДнороДны.)
— Как выполнять вычисления с величинами? (Как с натуральНЫМИ числами.)
— На что нужно обратить внимание? (На то, что Данные величины нужно выразить в оДинаковых еДиницах.) lV. Физкультминутка
Действия с величинами (повторение)
![]()
V. Закрепление изученного материала
1. Работа по учебнику ![]() 344 (с. 104).
344 (с. 104).
![]() Выполните задание.
Выполните задание.
— Во сколько раз в итоге увеличилась каждая величина?
(В Трал)
— Можно ли заменить эти два действия на увеличение сразу в
10 раз? (Да.) ![]() 345 (с. 104).
345 (с. 104).
— Обязательно ли выполнять уменьшение величин в два этапа?
(Да, для этого нужно кажДую величину уменьшить в такое число раз, которое
получается при умножении чисел, выступающих в роли коэффициента уменьшения на
кажДом этапе, т. е. в 10раз.) ![]() 346, 347 (с. 105).
346, 347 (с. 105).
![]() Прочитайте задание.
Что нужно сделать сначала? (Выразить величины кажДой пары в одних и тех же
еДиницах.)
Прочитайте задание.
Что нужно сделать сначала? (Выразить величины кажДой пары в одних и тех же
еДиницах.)
2. Выполнение упражнения в тетради для самостоятельной работы
![]() 163 (с. 83).
163 (с. 83).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 164 (с. 84).
Урок 128. Действия с величинами (повторение)
Цель: продолжать повторение основных вопросов, относящихся к выполнению действий с величинами.
![]() Организационный момент. Сообщение темы и цели урока
Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
Тест
(Выдается на отдельных листочках.)
1. Найди число, в котором 4 сотни миллионов, сотня тысяч,
3 десятка тысяч, 5 десятков и 4 единицы.
1) 400 во 054 3) 4 054 2) 40 ВО 054 4) 135![]()
2. Найди пример с ответом 71 009.
1 1 Поурочные разработки по математике
![]()
1) 70000+ 1000+9 3) 7000 + +9 2) 700 000 + 10 000 + 90 4) 7000 + + 9
3. Реши пример столбиком: 800 100 — 460 354.
1) 349 746 3) 338 756
2) 349 756 4) 339 746
4. Какой пример соответствует ответу 201 986 421 ?
1) 502 307 407 3) 514 207 • 406
2) 501 207- 403 4) 501 407 • 403
5. В шкафу 150 книг. На каждой полке 10 книг в синих обложках и 15 книг в красных обложках. Сколько всего книг в синих обложках и сколько всего мИГ в красных обложках в шкафу?
1) 50 и 3) 70 и 80
2) 90 4) 40 и 110
6. Найди решение: 50 240 • 3000.
1)
150 720 000 3) 507 200![]()
2) 157 200 000 4) 150 620 000
7. Раздели столбиком с остатком: 15 414 : 48.
1) 321 (ост. 6) 3) 314 (ост. 12)
2) 322 (ост. 4) 4) 331 (ост. 8)
8. Привезли 360 заготовок для деталей. Мастер может изготовить все детали за 6 дней, его ученик — за 12 дней. За сколько дней мастер и ученик могут выполнить все задание, работая вместе?
1) за 2 3) за 4 2) за 3 4) за 5
9. В каком случае надо поставить знак <?
10. В первом саду 27 яблонь, во втором 34 яблони, в третьем 48 яблонь, в четвертом 53 яблони и в пятом 58 яблонь. Узнай среднее количество яблонь в пяти садах.
1) 38 3) 46
2) 42 4) 44
11. Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найди ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
3) зом 2) 14 м
12.
Вставь пропущенное число: 6 мин 39 с — ![]() 1) 399 3) 339
1) 399 3) 339
2) 639 4) 389
Действия с величинами (повторение)
![]()
13. Расстояние между пристанями 150 км теплоход прошел за 6 ч. На обратном пути его скорость увеличилась на 5 юл/ч. За какое время теплоход пройдет весь путь туда и обратно?
1) за 10 ч 3) за 11 ч
2) за 9 ч 4) за 12 ч
14. Хозяйка сварила варенье из 12 кг клубники и 4 кг вишни, расходуя на каждую банку одинаковую массу ягод. Всего у нее получилось 8 банок. Сколько банок каждого варенья она сварила?
3) 5 и з
2) би2
15. В первый магазин привезли 24 мешка картофеля, а во второй — 28 мешков. Во второй магазин привезли на 160 кг больше, чем в первый. Сколько килограммов картофеля привезли в каждый магазин?
1) 1000 кг и 1160 кг З) 1060 кг и 1220 кг
2) 860 кг и 1020 кг 4) 960 кг и 1120кг
16.
Вставь пропущенное число: ч —![]()
1) 1000 3) 3500
2) 2400 4) 3600
17. Вставь пропущенное число: кв. км — ... кв. м.
1) 000 3) 000 000
2) 1 000000 4) 10 000 000
18. Напиши формулу площади прямоугольника. (Яр = а • Ь.)
19. Напиши формулу периметра квадрата. (Ро = а • 4.)
20. Запиши решение задачи и ответ.
Периметр комнаты 28 м, ширина комнаты 6 м. Найди шющадь комнаты.
Решение:
1) 28 : 2 = 14 (м) — сумма ширины и дЛИНЫ комнаты; 2) 14 — 6 = 8 (м) — длина комнаты; 3) 6 • 8 = 48 (кв. м).
Ответ: площадь комнаты 48 кв. м.
Ш. Работа по теме урока Работа по учебнику М 348 (с. 105).
(Самостоятельное выполнение. Проверка с записью решения на доске.) ле 349 (с. 105).
— Прочитайте задание. Что нужно сделать сначала? (Соответствующую величину разДелить на число 11, а потом полученный результат умножить на число З.)
IV. Физкультминутка
![]()
У. Закрепление изученного материала
1. Работа по учебнику М 350 (с. 105).
![]() Прочитайте задание. Что нужно сделать
сначала? (РазДелить Данную часть величины на число 4, а потом полученный
результат умножить на число 7.) М 351 (с. 105).
Прочитайте задание. Что нужно сделать
сначала? (РазДелить Данную часть величины на число 4, а потом полученный
результат умножить на число 7.) М 351 (с. 105).
![]() Прочитайте задание.
Что можно узнать, выполнив деление? (Массу еДиницы длины Данного провоДа, т. е.
массу 1 м провода: 360г : 12 м = 30г/м.)
Прочитайте задание.
Что можно узнать, выполнив деление? (Массу еДиницы длины Данного провоДа, т. е.
массу 1 м провода: 360г : 12 м = 30г/м.)
![]() Как найти массу 20 м провода? (30г/м •
20 м = 600 г.) № 352 (с. 105).
Как найти массу 20 м провода? (30г/м •
20 м = 600 г.) № 352 (с. 105).
![]() Что значит «выполнить кратное
сравнение»? (Узнать, во сколько раз одна величина больше (меньше) Другой.)
Что значит «выполнить кратное
сравнение»? (Узнать, во сколько раз одна величина больше (меньше) Другой.) ![]() Как выполняется кратное сравнение
величин? (С помощью Деления ОДНОРОДНЫХ величин.)
Как выполняется кратное сравнение
величин? (С помощью Деления ОДНОРОДНЫХ величин.)
— Что значит «деление однородных величин»? (Измерение величины, являющейся Делимым, в еДиницах величины, являющейся Делителем.)
— Выполните кратное сравнение самостоятельно.
2. Вьшшшение упражнения в тетради для самосттељной рабтн М 165 (1, 2) (с. 84).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 165 (3) (с. 84).
Урок 129. Как мы научились решать задачи
Цель: развивать навыки решения различных арифметических сюжетных задач.
1. Организационный момент. Сообщение темы и цели урока
11. Актуализация знаний
1. Цифровой квадрат
|
|
|
50 Ответ: |
|
20 |
|
|
|
Ш |
20 |
40 40
Как мы научились решать задачи
![]()
Нильс летит в стае на спине гуся Мартина. Он обратил внимание, что построение стаи напоминает треугольник: впереди вожак, затем — 2 гуся, в третьем ряду 3 гуся и т. д. Стая остановилась на ночлег на льдине. Нильс увидел, что расположение гусей на этот раз напоминает квадрат, состоящий из рядов, в каждом ряду — одинаковое количество гусей, причем число гусей в каждом ряду равно числу рядов. Гусей в стае меньше 50. Сколько гусей в стае? (36.)
З. Устный счет
(Примеры выдаются учащимся на отдельных листочках.)
|
В • 20 |
24 • зо |
16 • 50 |
|
|
60 : 5 |
24 : 2 |
96:3 |
84 : 6 |
|
42 : |
88 : 44 |
64 : 16 |
96 : 32 |
Ш. Работа по теме урока Работа ло учебнику М 353 (с. 106).
— Прочитайте условие задачи. Запишите решение задачи в виде одного выражения. Вычислите и запишите ответ. (240 мин — ч 25 мин — (1 ч 25 мин + 45 мин) = 25 мин.) М 354 (с. 106).
Решение:
1) 220 км : 2 ч = 1 10 км/ч — скорость изменения расстояния между автобусами;
2) 110 км/ч — 60 км/ч = 50 км/ч — средняя скорость второго автобуса;
3) 60 юи/ч • 2 ч = 120 юи — расстояние, которое проехал первый автобус;
4) 50 км/ч • 2 ч = 100 юи — расстояние, которое проехал второй автобус.
Ответ: средняя скорость второго автобуса 50 км/ч, расстояние от первого населенного пункта 120 км, от второго — 100 км. № 355 (с. 106-107).
— Прочитайте условие задачи. Вычислите время полета первого самолета. (1800км : 900км/ч = 2 ч.)
— В какое время приземлился первый самолет? (В 11 ч.)
— В какое время вылетел второй самолет? (В 10 ч, так как он вылетел на 1 ч позже, чем первый самолет.)
— В какое время приземлился второй самолет? (В 11 ч 40МИН, так как он приземшися на 40 мин позже, чем первый самолет.)
Как можно определить время полета второго самолета? (11 ч 40мин — 10 ч 00 мин = 1 ч 40мин = 100 мин.)
Как вычислить скорость второго самолета? ( 18Шкм : тмин — = 18 км/мин = 1080 км/ч.)
М. Физкультминутка
V. Закрепление изученного материала 1. Работа по учебнику м 356 (с. 107).
— Прочитайте задачу. Какого она типа? (Задача на нахождение четвертого пропорционального.)
— Запишите решение задачи и ответ.
Решение:![]()
1) 96 : 16 = 6 (б.) — в одной коробке;
2)
360 : 6 = 60 (кор.) — потребуется для 360 банок; 3) 60 — 16 = 44 (кор.).
![]()
Ответ: потребуется еще 44 коробки.
М 357€. 107).
![]() Прочитайте задачу.
Какого она типа? (ЗаДача на сумму и частное.)
Прочитайте задачу.
Какого она типа? (ЗаДача на сумму и частное.)
(Учащиеся вместе с учителем строят схему, на которой стоимость кг яблок выражена отрезком, принятым за одну часть, а стоимость I кг абрикосов — отрезком в 2 раза длиннее, т. е. отрезком, принятым за две части.)
— Чему будет равна стоимость набора, состоящего из 1 кг яблок и кг абрикосов? (600 : 5 = 120 (руб.).)
— Что отражает эту стоимость на схеме? (Весь отрезок, т. е. З части.)
![]() Как найти стоимость 1 кг яблок? (
120руб. : З = 40руб./кг.)
Как найти стоимость 1 кг яблок? (
120руб. : З = 40руб./кг.)
— Как найти стоимость кг абрикосов? (40 руб./кг • 2 ![]() = 80 руб./кг.)
= 80 руб./кг.)
— Сколько килограммов абрикосов можно купить на 240 руб.?
(240руб. : 80руб./кг = З кг.) м 358 (с. 107).
![]() Прочитайте задачу. Какого она типа?
(Задача на Движение в противоположных направлениях, состазнои частью которой
является задача на сумму и разность.)
Прочитайте задачу. Какого она типа?
(Задача на Движение в противоположных направлениях, состазнои частью которой
является задача на сумму и разность.) ![]() Запишите решение задачи и ответ.
Запишите решение задачи и ответ.
Решение:
1) 140 км : 2 ч = 70 км/ч — скорость изменения расстояния между катерами;
2) 70 км/ч — 10 км/ч = 60 км/ч — удвоенная меньшая скорость катера;
Как мы научились решать задачи
![]()
3) 60 «[ч : 2 = 30 км/ч — меньшая скорость катера;
4) 30 км/ч + 10 км/ч = 40 км/ч — большая скорость катера.
Ответ: скорости катеров 30 км/ч и 40 юи/ч.
М 359 (с. 107).
— Прочитайте задание. Как найти скорость течения реки? (Найти половину разности между скоростью по течению и скоростью против течения: (43 км/ч — 37км/ч) : 2 = З км/ч.)
2. Выполнение упражнения в тетради для самостоятельной работы
М 166 (1-4) (с. 85).
(Самостоятельное выполнение. Решение задачи 1 проверяется у доски.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 166 (5) (с. 86).
Урок 130. Как мы научились решать задачи
Цель: развивать навыки решения различных арифметических сюжетных задач.
1. Организационный момент. Сообщение темы и цели урока
ll. Актуализация знаний
1. Цифровой \оадрат
|
|
|
Ответ: 50 |
|
20 |
|
|
|
|
40 |
20 60
2. Разминка
•
![]() Что общего у автомобиля, арфы, велосипеда и рояля?
(Педали.)
Что общего у автомобиля, арфы, велосипеда и рояля?
(Педали.)
• Какой ванной пользуются, не наполняя ее? (Солнечной.)
• Какую траву и слепой узнает? (Крапиву.)
• Кто это и какого цвета?
|
Я ЦЗА Р МЕО ГНЕС Ц НЕ ЛОС |
ГУ ЛАК ЯШ МИ ПОРОД ДЕДЕВМЬ ВЬЯНИС |
![]()
Ответы: заяц, море, снег, солнце, лягушка, помидор, медведь, свинья.
Ш. Работа по теме урока Работа по учебнику ле 360 (с. 108).
— Прочитайте задачу. Какого она типа? (Задача на вычисление цены по стоимости и количеству.)
— Что нужно найти сначала? (Установить стоимость перечисленных проДуктов на основе вычитания части из целого.)
— Сколько стоят 5 кг картофеля? ( 122 руб. — 72 руб. = 50руб.)
• Сколько стоят 3 кг капусты? (122 руб. — 92 руб. = 30руб.)
— Сколько стоят 3 кг светы? (92 руб. — 50руб. = 42 руб.) ![]() Что
нужно найти далее? (Цену кажйго из указанных продуктов.)
Что
нужно найти далее? (Цену кажйго из указанных продуктов.) ![]() Как это можно
сделать? (Делением.)
Как это можно
сделать? (Делением.)
![]() Выполните деление. (50 руб. : 5 кг 10 руб./кг — цена картофеля; 30 руб.
: 2 кг — 15 руб./кг — цена капусты; 42 руб. : З кг = 14 руб./кг — цена свеклы.)
lV, Физкультминутка
Выполните деление. (50 руб. : 5 кг 10 руб./кг — цена картофеля; 30 руб.
: 2 кг — 15 руб./кг — цена капусты; 42 руб. : З кг = 14 руб./кг — цена свеклы.)
lV, Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 361 (с. 108).
— Прочитайте задачу. Какого она типа? (ЗаДача на ПРОИЗВОДИтельность.)
![]() Сколько способов решения у данной задачи? (Два.)
Сколько способов решения у данной задачи? (Два.) ![]() Запишите оба способа
решения. Вычислите ответ.
Запишите оба способа
решения. Вычислите ответ.
Решение:
Первый способ:
1) 1200 бат. : 8 ч = 150 бат./ч — производительность на старом оборудовании;
2) 150 бат./ч • 2 = 300 бат./ч — производительность на новом оборудовании;
3) 300 бат./ч • 8 ч = 2400 бат.
Второй способ: 1200 • 2 = 2400 (бат.).
Ответ: пекарня стала выпускать 2400 батонов за смену.
![]() На чем основывается второй способ решения задачи? (На существовании
прямой пропорциональной зависимости объема работы от произвоДительности при
постоянном времени работы.)
На чем основывается второй способ решения задачи? (На существовании
прямой пропорциональной зависимости объема работы от произвоДительности при
постоянном времени работы.)
— Какой способ решения является рациональным? (Второй.) ![]() 362
(с. 108).
362
(с. 108).
![]() Прочитайте задачу. Какого она типа? (Задача на совместную работу.)
Прочитайте задачу. Какого она типа? (Задача на совместную работу.)
Контрольная работа № 8
![]()
— Что нужно найти сначала? (ПроизвоДительность при совместной работе: 150 пан. : З ч = 50 пан./ч.)
— Что находим далее? (ПроизвоДительность первого рабочего: 135 пан. .•5ч = 27 пан./ч.)
![]() Чему равна производительность второго рабочего? (50 пан./ч — 27 пан./ч =
23 пан./ч.) № 363 (с. 108).
Чему равна производительность второго рабочего? (50 пан./ч — 27 пан./ч =
23 пан./ч.) № 363 (с. 108).
— Дополните задачи недостающими данными из географического атласа.
![]() Чему равна площадь
озер? (Ладожского — 17 700 кв. км, Онежского — 9690 кв. км.)
Чему равна площадь
озер? (Ладожского — 17 700 кв. км, Онежского — 9690 кв. км.)
![]() Чему равна высота
над уровнем моря горных вершин? (Эльбруса — 5642 м, Казбека — 5033 м.)
Чему равна высота
над уровнем моря горных вершин? (Эльбруса — 5642 м, Казбека — 5033 м.)
— Решите дополненные задачи самостоятельно.
![]() Вычислите и запишите ответ каждой
задачи.
Вычислите и запишите ответ каждой
задачи.
— Для каждой задачи сформулируйте обратную задачу и решите ее.
(Проверка с записью решения на доске.)
2. Выполнение упражнения в тетради для самостоятельной работы ЛФ 166 (7-10) (с. 87-88).
(Самостоятельное выполнение.)
Ш. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 166 (11) (с. 88).
Цели: проверить знания и умения учащихся; развивать навыки самостоятельной работы.
(Текст контрольной работы выдается каждому ученику на отдельном листочке.) Вариант 1
1. Вычисли значение выражения.
26 • (1672 + 1448) : (8713 - 8661)
2. Реши задачу. Вычисли и запиши ответ.
В первой коробке 65 скрепок, а в другой на 35 скрепок больше, чем в первой. В третьей коробке в 5 раз меньше скрепок, чем во второй. Сколько скрепок в трех коробках?
3. Найди три восьмых части от величины, равной 40 кг.
![]()
4. Площадь прямоугольника 28 кв. см, а длина одной из его сторон 7 см. Вычисли периметр прямоугольника.
Вариант 2
1. Вычисли значение выражения.
32 • (1462 + 748) : (7846 - 7781)
2. Реши задачу. Вычисли и запиши ответ.
На первой полке 75 книг, а на второй в 5 раз меньше, чем на первой. На третьей полке на 35 книг больше, чем на второй. Сколько книг на трех полках?
3. Найди четыре седьмых от величины, равной 42 кг.
4. Площадь прямоугольника 36 кв. см, а длина одной из его сторон 9 см. Вычисли периметр этого прямоугольника.
Урок 132. Геометрические фигуры и их свойства (повторение)
Цель: повторить вопросы, связанные с геометрическими фитурами и их свойствами.
![]() Организационный момент- Сообщение темы и цели урока ll. Актуализация
знаний
Организационный момент- Сообщение темы и цели урока ll. Актуализация
знаний
1. Творческое практическое задание
— Дорисуйте недостающие элементы.![]()
(Зарисовки учащиеся получают на отдельных листочках.)

2. Цифровой квадрат
|
5 |
25 |
|
10 |
|
 Ответ:
Ответ:
15 26
З. Устный счет
(Примеры записаны на доске.)
— Вставьте пропущенные числа.
Геометрические фигуры их свойства (повторение)
![]()
1350 см - ... м ... см 1000 кв. см = ... кв. дм
4500 мм = ... дм 6931 кг = ... ц кг
4. Разворачивающиеся фигуры
![]() (Геометрические
фигуры получает каждый ученик.) — Разверните фигуру на 45 градусов. Ответ:
(Геометрические
фигуры получает каждый ученик.) — Разверните фигуру на 45 градусов. Ответ:
![]()
![]() —
Разверните фигуру на 45 градусов. Ответ:
—
Разверните фигуру на 45 градусов. Ответ:
![]() Разверните фигуру на
90 градусов.
Разверните фигуру на
90 градусов.  Ответ:
Ответ: 
Ш. Работа по теме урока Работа по учебнику ![]() 364 (с. 109).
364 (с. 109).
(Практическая работа. Учащиеся строят прямоугольник и проводят диагональ.)
![]() Чему равна диатналь прямоугольника с длиной сторон 8 см и 6 см? (10см.)
Чему равна диатналь прямоугольника с длиной сторон 8 см и 6 см? (10см.)
![]() На какие два треугольника разбит построенный прямоугольник? (На два
прямоугольных треугольника.)
На какие два треугольника разбит построенный прямоугольник? (На два
прямоугольных треугольника.)
— Вычислите периметр любого из треугольников. (8 см +
+6 см + 10см = 24см.)
— Вычислите площадь прямоугольника. (8см • бсм = 48кв. си.) Вычислите площадь одного прямоугольного треугольника. (48 кв. см : 2 = 24 кв. см.)
— Измерьте площадь этого треугольника с помощью палетки. — Сравните результат, полученный с помощью вычислений, с результатом измерения с помощью палетки.
М 365 (с. 109).
(Практическая работа с коллективным комментированием.) IV. Физкультминутка
М. Закрепление изученного материала
1. Работа по учебнику
М 366 (с. 109).
(Учащиеся строят треугольник.)
![]() Как построенный
треугольник разбить на четыре одинаковых равносторонних треугольника? (Попарно
соеДинить отрезками середины сторон Данного треугольника.)
Как построенный
треугольник разбить на четыре одинаковых равносторонних треугольника? (Попарно
соеДинить отрезками середины сторон Данного треугольника.) ![]() 109).
109).
![]() Прочитайте задание. Что нужно сделать сначала? (РазДелить отрезок
пополам с помощью циркуля и линеЙки.)
Прочитайте задание. Что нужно сделать сначала? (РазДелить отрезок
пополам с помощью циркуля и линеЙки.)
![]() Что будете делать
далее? (Каждую половину Данного отрезка разДелим еще пополам.)
Что будете делать
далее? (Каждую половину Данного отрезка разДелим еще пополам.)
![]() Что получится в итоге? (Данный отрезок будет разделен на четыре равные
части.) м 368 (с. 110).
Что получится в итоге? (Данный отрезок будет разделен на четыре равные
части.) м 368 (с. 110).
(Самостоятельное выполнение. Проверка в парах.)
2. Выполнение упражнений в тетради для самостоятельной ра-
М 167(1-3), 169 (с. 89-90).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Тетрадь для самостоятельной работы: № 170 (с. 91).
Урок 133. Геометрические фигуры и их свойства (повторение)
Цель: продолжать повторение вопросов, связанньж с геометрическими фигурами и их свойствами.
1. Организационный момент. Сообщение темы и цели урока
Геометрические фигуры их свойства (повторение)
![]()
ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
35 Ответ: 25 |
10 |
25 |
|
|
|
5 |
20 |
15 45
2. Разворачивающиеся фигуры
(Геометрические фигуры получает каждый ученик.) — Разверните фигуру на 45 градусов.
![]() Ответ:
Ответ: 
![]() Разверните фигуру на 90 градусов.
Разверните фигуру на 90 градусов.
![]() Ответ:
Ответ: 
— Разверните фигуру на 45 градусов.
![]() Ответ:
Ответ: 
Ш. Работа по теме урока Рота по учебнику № 369 (с. 110).
— Прочитайте задание. С чего нужно начать? (С построения острого угла.)
— Что нужно сделать далее? (На одной из сторон построенного угла отложить отрезок длиной 10 см.)
— А потом? (На другой стороне угла выбрать такую точку, чтобы при соеДинении ее с концом отложенного отрезка получится остроугольный треугольник.)
— Как это сделать? (На второй стороне угла отложить отрезок длиной 10 см и взять в качестве искомой точки конец этого отрезка.)
— Какой треугольник получился? (Равнобедренный треугольник с острым углом при вершине, который обязательно является остроугольным.) № 370 (с. 110).
— Прочитайте задание. С чего нужно начать? (С построения тупого угла.)
— Что нужно сделать далее? (На одной из сторон построенного угла нужно опиожить отрезок длиной 10 см.)
![]() А потом? (На другой
стороне угла выбрать такую точку, чтобы при соеДинении ее с концом отложенного
отрезка получился искомый треугольник.)
А потом? (На другой
стороне угла выбрать такую точку, чтобы при соеДинении ее с концом отложенного
отрезка получился искомый треугольник.)
— Какой треугольник получился? (Тупоугольный.) lV. Физкультминутка
V. Закрепление изученного материала
![]() Прочитайте задание. С чего нужно начать? (С построения прямого угла . )
Прочитайте задание. С чего нужно начать? (С построения прямого угла . )
![]() Что нужно сделать
далее? (На одной из сторон построенного угла нужно отложить отрезок длиной 10
см.)
Что нужно сделать
далее? (На одной из сторон построенного угла нужно отложить отрезок длиной 10
см.)
— А потом? (На другой стороне угла выбрать такую точку, чтобы при соеДинении ее с концом отложенного отрезка получися искомый треугольник.)
— Какой треугольник получился? (Прямоугольный.) .№372 (с. 110).
![]() Прочитайте задание. С чего нужно начать? (Построить две прямые, которые
пересекаются под прямым углом.)
Прочитайте задание. С чего нужно начать? (Построить две прямые, которые
пересекаются под прямым углом.)
— Что нужно сделать далее? (На одной из прямых от точки пересечения отложить отрезок длиной 4 см — это высота, а на Другой — отрезок длиной 8 см — это основание треугольника.)
— Как лучше расположить второй отрезок? (Он может располагаться как угодно. Но лучше, когДа точка пересечения прямых лежит внутри этого отрезка.)
— Что дальше? (Для построения треугольника Достаточно соеДинить концы второго отрезка с тем концом первого отрезка, который не совпадает с точкой пересечения прямых.)
Л@З7З (с. 110).
— Рассмотрите рисунок.
— Что общего у этих треугольников? (Это треугольники, вписанные в окружность, одна из сторон которых совпаДает с Диаметром этой окружности. )
![]() К какому виду
относятся эти треугольники? (К прямоугольньш треугольникам.)
К какому виду
относятся эти треугольники? (К прямоугольньш треугольникам.)
— Что нужно сделать, чтобы начертить прямоугольный треугольник, у которого большая сторона имеет длину 4 см? (Сначала нужно начертить окружность с Диаметром 4 см, а потом вписанный треугольник, сторона которого совпадает с Диаметром построенной окружности. Это и будет искомый треугольник.)
2. Выполнение упражнений в тетради для самостоятельной
рабсгы ![]() 171 (1-4), 172 (с. 90-91).
171 (1-4), 172 (с. 90-91).
(Самостоятельное выполнение. Проверка в парах.)
И. Подведение итогов урока
Домашнее задание
Тетрадь для самостоятельной работы: № 173 (с. 91).
Цель: повторить и обобщить изученный алгебраический материал.
1. Организационный момент. Сообщение темы и цели урока
П. Актуализация знаний
1. Цифровой квадрат
|
|
|
Ответ: 16 |
|
20 |
|
|
|
l0 |
6 |
20 26
2. Письменный опрос
(Вопросы даны на отдельных листочках.)
• Что называется корнем уравнения? (Корень уравнения — это искомое число, при поДстановке которого в уравнение получается верное равенство.)
• Как найти неизвестное слагаемое? (Если из известного значения суммы вычесть известное слагаемое, то получится неизвестное слагаемое.)
• Как найти неизвестное вычитаемое? (Если из известного уменьшаемого вычесть известное значение разности, то получится неизвестное вычитаемое.)
• Как найти неизвестное уменьшаемое? (Если к известному вычитаемому прибавить известное значение разности, то получится неизвестное уменьшаемое.)
• Как найти неизвестный множитель? (Если известное значение произвеДения разДелить на известный множитель, то получится неизвестный множитель.)
• Как найти неизвестный делитель? (Если известное Делимое разДелить на известное значение частного, то получится неизвестный Делитель.)
• Как найти неизвестное делимое? (Если известное значение частного умножить на известный Делитель, то получится неизвестное Делимое.) З. Устный счет
Сто солдат шли на парад.
Ладно мундиры на каждом сидят.
Первым ответит кто из ребят,
Сколько пуговиц [шЛО на парад? (800.)
• Было когда-то на свете 25 оловянных солдатиков, которых сделали из старой оловянной ложки массой 123 г. Из них 24 солдатика были одинаковыми, друг от друга не отличалисы А один был не такой, как все. Его отливали последним, олова немного не хватило, и он оказался одноногим. Какова масса последнего солдатика? (З г.)
Ш. Работа по теме урока Работа
по учебнику ![]() 111).
111).
(Самостоятельное выполнение.
Проверка в парах.) ![]() 111).
111).
•
Прочитайте задание. Как называется первая фигура? (Ромб.) ![]() Как будет
выглядеть формула для нахождения периметра ромба? (Р = а • 4.)
Как будет
выглядеть формула для нахождения периметра ромба? (Р = а • 4.)
• Как называется вторая фигура? (Паршиелограмм.)
— Как будет выглядеть формула для нахождения периметра параллелограмма? (Р = (а + Ь) • 2.)
Третья фигура — это равнобедренная трапеция.
— Как будет выглядеть формула для нахождения периметра равнобедренной трапеции? (Р = а + Ь + с • 2.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику М 376 (с. 112).
![]() Прочитайте вопрос. Что получится в результате такого сложения? (Число
а.)
Прочитайте вопрос. Что получится в результате такого сложения? (Число
а.)
![]() Какое равенство можно записать? (а + О = а.) М 377(с. 112).
Какое равенство можно записать? (а + О = а.) М 377(с. 112).
![]() Прочитайте вопрос. Что получится в результате вычитания нуля из некоторого
числа а ? (Число а.)
Прочитайте вопрос. Что получится в результате вычитания нуля из некоторого
числа а ? (Число а.)
— Какое равенство можно записать? (а — О а.)
![]() Что получится в
результате вычитания числа а из некоторого числа а? (Ноль.)
Что получится в
результате вычитания числа а из некоторого числа а? (Ноль.)
— Какое равенство можно записать? (а — а = 0.) м 378 (с. 112).
![]() Что получится в
результате умножения некоторого числа а на ноль? (Ноль.)
Что получится в
результате умножения некоторого числа а на ноль? (Ноль.)
![]() Какое равенство можно записать? (а • 0 =
0.)
Какое равенство можно записать? (а • 0 =
0.)
![]() Какое равенство можно записать? (а • 1 =
а.) ЛГ2З79(с. 112).
Какое равенство можно записать? (а • 1 =
а.) ЛГ2З79(с. 112).
— Что получится, если число 0 разделить на некоторое натуральное число а? (Ноль.)
— Какое равенство можно записать? (О: а = О.) № 380 (с. 112).
![]() Что получится, если некоторое число а разделить на число
Что получится, если некоторое число а разделить на число
![]()
![]() Какое равенство можно записать? (а : 1 = а.)
Какое равенство можно записать? (а : 1 = а.)
— Что получится, если некоторое натуральное число а разделить на это же число? ( число 1.)
— Какое равенство можно записать? (а : а = 1.)
2. Выполнение упражнений в тетради для самостоятельной работы ле 175, 176 (с. 92-93).
(Выполнение в соответствии с заданиями.)
Ш. Подведение итогов урока
Домашнее задание
Составить три уравнения и решить их.
12 Поурочные разработки по математике
Урок 135. Буквенные выражения и уравнения (повторение)
Цель: продолжать повторение и обобщение изученного алгебраического материала.
1. Организационный момент. Сообщение темы и цели урока ll. Актуализация знаний
1. Цифровой квадрат
|
5 |
|
|
15 |
20 |
![]() 35 Ответ:
35 Ответ:
35
20 50
2. Задача в стихах
Над болотцем тихо-тихо
В теплом воздухе парят
Сам комар да комариха, С ними — туча комарят.
Комариха с комаром говорят:
— Сосчитай-ка, комар, комарят.
— Как же счесть, комариха, комарят?
Не поставишь комарят наших в ряд.
Насчитала комариха 40 пар, А продолжил этот счет сам комар.
Комарят комар до вечера считал.
Насчитал 13 000 и устал...
А теперь считайте сами вы, друзья:
Велика ли комариная семья?
(Из стихотворения И. Демьянова «О комарятах»)
Ш. Работа по теме урока Работа по учебнику ЛФ 381 (с. 113).
(Самостоятельное выполнение. Проверка с записью решения на доске.)
М 382 (с. 113).
![]() Прочитайте задание. Выполните его.
Прочитайте задание. Выполните его.
![]() Какое уравнение получилось? ((х + 38) : 25 = 8.)
Какое уравнение получилось? ((х + 38) : 25 = 8.)
М. Физкультминутка
V. Закрепление изученного материала
1. Работа по учебнику ![]() 383 (с. 113).
383 (с. 113).
![]() Посмотрите на уравнение.
Посмотрите на уравнение.
![]() Какое выражение
является делимым в данном уравнении? (х + 38.)
Какое выражение
является делимым в данном уравнении? (х + 38.)
![]() Можно ли найти делимое по данному
уравнению? (Да, нужно значение частного умножить на Делитель: 8 • 25 = 200.)
Можно ли найти делимое по данному
уравнению? (Да, нужно значение частного умножить на Делитель: 8 • 25 = 200.) ![]() Каким
будет новое уравнение? (х + 38 = 200.)
Каким
будет новое уравнение? (х + 38 = 200.)
(Самостоятельное выполнение. Проверка с записью решения на доске.)
![]() 385 (с. 113).
385 (с. 113).
![]() Какие могут быть уравнения? (Например: х
+ 275 = 1000,
Какие могут быть уравнения? (Например: х
+ 275 = 1000,
![]()
2. Вьшо.ме»ше упрахшеюш в тетрам для самостоятельной работы ЗаДание «Проверь себя» (с. 94—95).
|
Название хмвотного |
Средняя продолжительность ховни в природе |
Наибольшая продолжительность жизни в зоопарке |
Количество дополнительных лет жизни |
|
1 |
2 |
з |
4 |
|
Рыбный филин |
30 лет : 2 = = 15 лет |
30 лет |
30 лет — 15 лет = = 15 лет |
|
Фламинго |
20 лет: 5 • 2= 8 лет |
20 лет |
20 лет — 8 лет — = 12 лет |
|
Белорукий гиббон |
30 лет : 3 • = 20 лет |
30 лет |
30 лет — 20 лет — — 10 лет |
|
Панда |
34 ода: 17 • = 20 лет |
34 года |
34 года — 20 лет = = 14 лет |
|
Кондор и гриф |
50 лет |
50 лет — 70 лет |
70 лет — 50 лет = — 20 лет |
|
Орел, коршун, беркут, ястреб |
25 лет |
25 лет = 55 лет |
55 лет — 25 лет = = 30 лет |
|
Леопард |
24 года — 9 лет = — 15 лет |
24 года |
24 года — 15 лет — = 9 лет |
|
лев |
5 лет |
15 лет • 2 = 30 лет |
30 лет — 15 лет = = 15 лет |
|
Снежный барс |
18 лет — З года — 1 5 лет |
8 лет |
18 лет — 15 лет = 3 года |
![]()
|
1 |
2 |
З |
4 |
|
Летучая мышь |
5 лет |
5 лет • 15 лет |
15 лет — 5 лет = 10 лет |
|
Мышьмалютка |
9 мес. |
Около З лет — = 12 мес. • = 36 мес. |
36 мес. — 9 мес. = 27 мес. — = 2 года З мес. |
|
Горный козел |
10 лет |
10 лет • 2 = 20 лет |
20 лет — 10 лет — = 10 лет |
|
Амурский горал |
6 лет |
18 лет 8 мес. |
18 лет 8 мес. — 6 лет = = 12 лет 8 мес. |
![]() Кто из перечисленных
животных является долгожителем по сравнению со своими «дикими» собратьями?
(Кондор и гриф.)
Кто из перечисленных
животных является долгожителем по сравнению со своими «дикими» собратьями?
(Кондор и гриф.)
Ш. Подведение итогов урока
Урок 136. Закрепление пройденного
Цель: повторить теоретический материал по всему курсу математики .
1. Организационный момент. Сообщение темы и цели урока
Ребята, сегодня мы отправляемся в занимательное путешествие по удивительной стране Знаний.
ll. Актуализация знаний
1. Цифровой квадрат
|
|
|
45 Ответ: 25 |
25 |
20 |
|
|
|
15 |
|
40 30
2. Волшебные квадраты
(Волшебная сумма равна 40.)
|
8 |
|
|
|
|
|
12 |
6 |
19 |
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
19 |
6 |
12 |
|

З. Задачи-шутки
• В каком числе букв столько же, сколько и цифр? (100.)
• Две дочери, две матери да бабушка с внучкой. Сколько их?
(Трое.)
• У семерых братьев по одной сестре. Сколько всего сестер?
(Одна.)
• В корзине три яблока. Как разделить их на трех человек, чтобы одно яблоко осталось в корзине? (ОтДать одному яблоко вместе с корзиной.)
Ш. Работа по теме урока
1. Групповая игра «Числовой ряд»
(У каждого ученика на парте лежит карточка-шаблон, на которой с одной стороны изображен кедр, а с другой стороны записаны числа: 6482, 9367, 1, 4538, 7500.)
![]() Посмотрите на обратную сторону карточек, на ней записаны числа. Давайте
их прочитаем.
Посмотрите на обратную сторону карточек, на ней записаны числа. Давайте
их прочитаем.
![]() Какое число самое большое? (9367.)
Какое число самое большое? (9367.)
— Какое число самое маленькое? (1211.)
— Назовите данные числа в порядке возрастания. (1211, 4538,
6482, 7500, 9367.)
(Один ученик выставляет данные числа на доске, остальные учащиеся записывают в тетради.)
2. Игра-соревнование «Цепочка»
(Игра проводится между рядами. Примеры даны на индивидуальных карточках. Каждая пара решает один пример, записывает ответ и передает карточку следующей паре.)
|
Первый ряд |
Результат |
Второй ряд |
Результат |
Третий ряд |
Результат |
|
84 : 6 |
|
|
65 |
630 : зо |
21 |
|
|
98 |
+ 35 |
100 |
|
84 |
|
— 49 |
49 |
+ 180 |
280 |
— 48 |
36 |
|
+ 15 |
64 |
40 |
7 |
• 18 |
2 |
![]()
|
Первый ряд |
Результат |
Второй ряд |
Результат |
Третий ряд |
Результат |
|
• 16 |
4 |
• 60 |
420 |
• 450 |
900 |
|
• 20 |
80 |
|
140 |
|
|
|
+ 23 |
|
-58 |
82 |
|
420 |
|
|
515 |
+718 |
800 |
|
500 |
(Итог подводится по завершении работы. Ответы сверяются с данными на доске. Выигрывает тот ряд, у которого все ответы получились верными.)
З. Игра «Самый смекалистый»
— Расставьте знаки действий и скобки так, чтобы получился верный ответ. 5 5 5 5 = 249999 - 18
![]()
5 5 5 5= 269999- 82
5 5 55 = 10099 99=63 lV. Физкультминутка
V. Закрепление изученного материала
1. Иира-конкурс «Задачи в стихах»
Мы — большущая семья, Самый младший — это я!
Сразу нас не перечесть:
Маня есть, и Ваня есть, Юра, Шура, Юташа, Даша,
И Наташа тоже наша.
Мы по улице идем —
Говорят, что детский дом.
Посчитайте поскорей,
Сколько нас в семье детей. (8.) Мы за чаем не скучаем — По две чашки получаем.
Восемь чашек, восемь пар ![]() Выпиваем самовар.
Выпиваем самовар.
Чашек пьем всего по паре.
Сколько чашек в самоваре? (16.)
2. Игра «Сбор шишек»
(На доске записаны примеры и прикреплены карточки с ответами в виде шишек. Ученики по очереди выходят к доске, решают примеры, находят карточки-шишки с соответствующими
|
ответами.) |
|
|
|
235 + 347 |
Вб + 383 |
531 - |
|
604 + |
501 - 32 |
723 - 365 |
Закрепление пройденного
![]()
З. Игра на внимание «Какая геометрическая фигура исчезла?»
(На полочку классной доски ставятся карточки, на которых изображены геометрические фигуры: треугольник, отрезок, четырехугольник, прямой угол, прямоугольник, квадрат, круг. К доске выходит один из учеников, который внимательно рассматривает все фигуры, стараясь их запомнить. Затем он отворачивается от доски, а в это время другой ученик прячет одну из фигур. Первый ученик вновь поворачивается лицом к доске и пытается вспомнить, какая из геометрических фигур исчезла.)
4. Конкурс «Знаете ли вы?»
![]() Какие хвойные деревья вы знаете? (Ответы детей.)
Какие хвойные деревья вы знаете? (Ответы детей.)
— А вы знаете, что существует около 100 видов сосен?
Я хочу рассказать вам о кедровой сибирской сосне. Это дерево часто зовут сибирским кедром, но прямого отношения к настоящим кедрам оно не имеет. У обыкновенной сосны хвоинки собраны в пучки по две, а у сибирской — по пять.
(Учитель демонстрирует либо живую ветку, либо из гербария.) Кедровая сосна может вырастать до 45 м.
— Среднюю высоту этого дерева в метрах вы узнаете, решив пример.
2750 7 : 2 - 9597 (Им)
Но главное отличие кедровой сосны от обычной — в семенах, ведь семена сибирской сосны — это всем известные кедровые орешки. Ее орехами лакомятся 70 видов зверей и 200 видов птиц. Чтобы вырастить урожай кедровых орехов, дереву приходится немало потрудиться.
![]() Сколько месяцев созревают шишки с семенами? Ответ спрятался в следующем
примере. 23 4- (93 + 1796) (27)
Сколько месяцев созревают шишки с семенами? Ответ спрятался в следующем
примере. 23 4- (93 + 1796) (27)
Да, зреют семена 27 месяцев, причем, из 10 лет только 3 года считаются урожайными.
Но у этой сосны ценны не только орехи, но и древесина. ![]() Знаете
ли вы, как люди раньше ее использовали? (Ответы детей.)
Знаете
ли вы, как люди раньше ее использовали? (Ответы детей.)
![]() Решите уравнения.
Решите уравнения.
(Уравнения написаны на карточках-шишках, с обратной стороны напечатаны слова (мебель, посуда, музыкальные инструменты). По мере решения уравнений карточки-шишки переворачиваются и учитель сообщает интересные сведения об использовании древесины кедровой сосны.)
![]()
4200 : х = 6 х : 50 = 500
![]()
Из древесины кедровой сосны делали мебель: сундуки, шкафы. В сундуках, сделанных из душистой древесины этого дерева, не заводится моль, в них можно долго хранить ценные вещи.
В посуде, сделанной из кедровой древесины, долго не скисает молоко, а ведь раньше холодильников не было.
Из кедровой древесины делали музыкальные инструменты. Звучание этой древесины обнаружили немецкие торговые фирмы, закупавшие в России кедровое масло. Они потребовали поставлять им емкости с маслом в таре из кедровых досок. Разбирая эту тару и продавая ее на заводы музыкальных инструментов, торговцы значительно увеличивали свой доход.
Ш. Подведение итогов урока
ПРИЛОЖЕНИЕ
![]()
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
Повторение
Вариант 1
1. Реши уравнения. х: 72= 3 Р 7=28
2. Стороны треугольника равны 1506 мм, 1506 мм и 4 м. Вычисли периметр этого треугольника.
3. Реши задачу. Вычисли и запиши ответ.
Площадь всей квартиры 63 кв. м. Площадь первой комнаты
![]() 2 кв. м, площадь второй комнаты 9 кв. м.
Во сколько раз площадь квартиры больше площади двух комнат?
2 кв. м, площадь второй комнаты 9 кв. м.
Во сколько раз площадь квартиры больше площади двух комнат?
4* Длина одной стороны прямоугольника 2400 мм, а другой в 12 раз больше. Вычисли площадь прямоугольника.
Вариант 2
1. Реши уравнения. х: 94 = 4
х-6=42
2. Стороны треугольника равны 1048 мм, 1048 мм и З м. Вычисли периметр этого треугольника.
3. Реши задачу. Вычисли и запиши ответ.
Площадь всей квартиры 66 кв. м. Площадь первой комнаты 14 кв. м, площадь второй комнаты 8 кв. м. Во сколько раз площадь квартиры больше площади двух комнат?
4* Длина одной стороны прямоугольника 2200 мм, а другой в 14 раз больше. Вычисли площадь прямоугольника.
![]()
* Здесь и далее — задания повышенной сложности.
![]()
Задачи на разностное и кратное сравнение
Вариант 1
1. Прочитай задачу. Из предложенных схем выбери и отметь ту, с помощью которой ее можно решить. Реши задачу. Вычисли и запиши ответ.
Из 26 оконных стекол, привезенных в магазин, цветных оказалось на 18 штук меньше, чем обычных. Сколько цветных стекол привезли в магазин? 18 18
![]()
26 26
2. Реши задачу с помощью схемы. Вычисли и запиши ответ.
Задумали два числа, одно из которых в 4 раза больше другого. Значение суммы этих чисел равно 35. Найди эти числа.
.3* Вычисли значение следующего выражения.
202 • (12 (341 + 2267) - 30 202)
Вариант 2
1. Прочитай задачу. Из предложенных схем выбери и отметь ту, с помощью которой ее можно решить. Реши задачу. Вычисли и запиши ответ.
Из 29 взрослых человек, пришедших в магазин, женщин на 9 человек больше, чем мужчин. Сколько женщин пришло в магазин?
9 9
![]()
29 29
2. Реши задачу с помощью схемы. Вычисли и запиши ответ.
Задумали два числа, одно из которых в 3 раза меньше другого. Значение суммы этих чисел равно 28. Найди эти числа.
3*. Вычисли значение следующего выражения.
(21 • (1341 + 251) - 974) • 207
Класс миллионов. Буквенные выражения
![]()
Класс миллионов. Буквенные выражения
Вариант 1
I . Запиши следующие числа в порядке возрастания. Вычисли значение произведения самого большого и самого маленького из этих чисел столбиком.
721 163
721 1 630
72
6 262 626
626 262
2. Заполни следующую таблицу такими значениями длин сторон прямоугольников, чтобы площадь прямоугольника была постоянной при переходе от одного прямоугольника к другому.
|
Номер прямоугольника |
1 |
2 |
|
|
Длина одной стороны, см |
1 |
|
|
|
Длина другой стороны, см |
|
|
|
|
Площадь, кв. см |
12 |
|
|
3. В магазин привезли 80 кг моркови в ящиках по а кг в каждом и с ящиков свеклы.
Составь выражение, с помощью которого можно вычислить, сколько всего ящиков овощей привезли. Вычисли значение этого выражения, если а = 16, с = 17.
4*. Прочитай задачи. Выполни задания.
• Собака бежит по окружности, в центре которой стоит будка. Зависит ли расстояние от собаки до ее будки от времени бега? Собака пробегает за каждую минуту одно и то же расстояние.
Заполни данную таблицу, если а — время бега собаки, Ь — расстояние до будки.
|
а |
lc |
|
|
24 С |
62 с |
|
|
|
|
|
|
|
• Собака бежит по прямой. Зависит ли расстояние от собат до ее будки от времени бега? Собака пробегает за каждую минуту одно и то же расстояние. Заполни данную таблищ, если а — время бега собаки по прямой от будки, Ь — расстояние до будки.
а lc 10c 24 с 62 с
![]()
Вариант 2
1. Запиши следующие числа в порядке возрастания. Вычисли значение произведения самого большого и самого маленького из этих чисел столбиком. з 535 353 612 882
61
353 535
6 128 820
2. Заполни следующую таблицу такими значениями длин сторон прямоугольников, чтобы площадь прямоугольника была постоянной при переходе от одного прямоугольника к другому.
|
Номер прямоугольника |
1 |
2 |
з |
|
Длина 1-й стороны, см |
2 |
|
|
|
Длина 2-й стороны, см |
|
|
|
|
Площадь, кв. см |
24 |
|
|
3. На склад отправили 84 кг яблок в ящиках по а кг в каждом и с ящиков груш.
Составь выражение, с помощью которого можно вычислить, сколько всего ящиков фруктов отправили на склад. Вычисли значение этого выражения, если а = 28, с = 25.
4*. Прочитай задачи. Выполни задания.
• Собака бежит по окружности, в центре которой стоит будка. Зависит ли расстояние от собаки до ее будки от времени бега? Собака пробегает за каждую минуту одно и то же рас-
стояние.
Заполни данную таблицу, если а — время бега собаки, Ь — расстояние до будки.
|
а |
|
|
|
24 с |
юс |
|
|
|
|
|
|
|
• Собака бежит по прямой. Зависит ли расстояние от собаки до ее будки от времени бега? Собака пробегает за каждую минуту одно и то же расстояние.
Заполни данную таблицу, если а — время бега собаки по пря-
мой от будки, Ь — расстояние до будки.
а lOc 24 С 62 с
Задачи на куплю-продажу
![]()
Вариант 1
1. Определи цену одной ручки, если за 7 таких ручек заплатили 42 руб.
2. За 6 пирожков заплатили 12 руб. 60 коп. Определи стоимость 5 таких же пирожков.
3. Прочитай задачу. Заполни таблицу. Реши задачу. Вычисли и запиши ответ.
За 4 кг яблок заплатили 36 руб. Сколько килограммов этих же яблок можно купить на 81 руб.?
|
Цена |
Количество |
Стоимость |
|
|
|
|
|
|
|
|
4*. Заполни таблицу.
|
Вид товара |
Цена |
Количество |
Стоимость |
|
|
42 руб./шт. |
|
? , на 40 руб. больше |
|
Б |
? , на 12 руб./шт. меньше |
5 шт. |
|
|
в |
|
? , на 6 шт. больше |
44 руб. |
Вариант 2
1. Определи цену одной тетради, если за 8 таких тетрадей заплатили 40 руб.
2. За 4 коробки спичек заплатили 16 руб. 40 коп. Определи стоимость 5 таких же коробок спичек.
3. Прочитай задачу. Заполни таблицу. Реши задачу. Вычисли и запиши ответ.
За 4 м ленты заплатили 28 руб. Сколько метров этой же ленты можно купить на 56 руб.?
|
Цена |
Количество |
Стоимость |
|
|
|
|
|
|
|
|
4* Заполни таблицу.
|
Вид товара |
Цена |
Количество |
Стоимость |
|
|
13 руб./кг |
|
? , на 57 руб. меньше |
|
|
|
9 в 2 раза больше |
96 руб. |
|
в |
9 на 7 руб./кг больше |
2 кг |
|
Деление с остатком
Вариант 1 1 . Выполни деление:
а) в строчку: 34 : 7, 14 : 21;
б) столбиком: 67 : 5, 42 : 2. Подчеркни случай деления нацело.
2. Найди делимое. ... : 3=4 (ост. 2)
3. Из следующих записей действия деления выбери и подчеркни ту, в которой деление выполнено неправильно. Исправь ошибку.
24 : 7 = з (ост. 3)
45 : 8 = 4 (ост. 21)
4* Может ли значение произведения двух чисел быть нечетным числом? Какими при этом, четными или нечетными, должны быть эти два числа? Приведи примеры таких чисел.
Вариант 2
1. Выполни деление:
а) в строчку: 39 : 6, 34 : 76;
2. Найди делимое.
![]() 2 (ост. 3)
2 (ост. 3)
3. Из следующих записей действия деления выбери и подчеркни ту, в которой деление выполнено неправильно. Исправь ошибку.
45 : 7 = 5 (ост. 10)
34 : 5 = 6 (ост. 4)
4*. Может ли значение суммы двух чисел быть нечетным числом? Какими при этом, четными или нечетными, должны быть эти два числа? Приведи пример таких чисел. Задачи на движение
Вариант 1
1. Определи скорость пешехода, если за 8 мин он прошел 400 м.
2. За 5 ч поезд проехал 155 км. Сколько километров проедет поезд за 12 ч, если будет двигаться с такой же скоростью?
3. Прочитай задачу. Заполни таблицу. Реши задачу. Вычисли и запиши ответ.
Велосипедист проехал 24 км за 2 ч. Сколько часов потребуется велосипедисту, чтобы проехать 60 км, если он будет двигаться с такой же скоростью?
|
Скорость |
Время |
Расстояние |
|
|
|
|
|
|
|
|
4* Реши задачу. Вычисли и запиши ответ.
Велосипедисту необходимо преодолеть путь, состоящий из трех участков: 7 юи подъема, 10 км ровной дороги и 6 км спуска. Причем по ровной дороге велосипедист движется со скоростью 10 км/ч, на подъеме — со скоростью 7 км/ч, на спуске — 12 км/ч. Сколько времени потратит велосипедист на весь путь?
Вариант 2
1. Определи скорость пешехода, если за 4 мин он прошел 160 м.
2. За 7 ч автомобиль проехал 175 км. Сколько километров проедет автомобиль за 12 ч, если будет двигаться с такой же скоростью?
3.
Лодка проплыла 39 км за 3 ч. Сколько часов потребуется лодке, чтобы проплыть 65 км, если она будет плыть с такой же скоростью?
|
Скорость |
Время |
Расстояние |
|
|
|
|
|
|
|
|
4* Реши задачу. Вычисли и запиши ответ.
Автомобилю необходимо проехать путь, состоящий из трех разных участков: первый участок — 65 км, второй — 1 10 км, третий — 18 0,1. При этом на первом участке автомобиль едет со скоростью 65 км/ч, на втором — 10 км/ч, на третьем — 36 км/ч. Сколько времени потребуется автомобилю, чтобы проехать весь путь?
Вместимость и объем
Вариант 1
I . Ответь на вопрос, выполнив необходимые вычисления.
В тарелке отца 40 столовых ложек супа, а в тарелке сына 80 десертных ложек. В одной столовой ложке помещается три чайные ложки, а в одной десертной — две чайные ложки. В чьей тарелке супа больше?
2. В два сосуда с одинаковым количеством воды опустили шар и куб. Используя следующие рисунки, сравни объемы этих геометрических тел. Определи объем каждого из тел, если известно, что в сосудах было по 16 л воды (каждое деление — I л).

3* Реши задачу. Вычисли и запиши ответ.
Бочка вмещает 84 л воды. Когда бочку налили наполовину и добавили еще 7 ведер воды, бочка заполнилась доверху. Во сколько раз вместимость бочки больше вместимости ведра?
Вариант 2
В первую банку налили 12 кружек воды, а во вторую — 23 стакана. В одной кружке помещается 8 чашек воды, а в одном стакане — 4 чашки. Вместимость какой бани больше?
2. В два сосуда с одинаковым количеством воды опустили шар и куб. Используя следующие рисунки, сравни объемы этих геометрических тел. Определи объем каждого из тел, если известно, что в сосудах было по 18 л воды (каждое деление — 1 л).

3* Реши задачу. Вычисли и запиши ответ.
Бак вмещает 24 л воды. Когда бак налили наполовину и добавили еще 3 ведра воды, бак заполнился доверху. Во сколько раз вместимость бака больше вместимости ведра?
производительность
![]()
Задачи на производительность
Вариант 1
![]() . Определи
производительность бригады, если за восьмичасовую рабочую смену она производит
160 т кирпича.
. Определи
производительность бригады, если за восьмичасовую рабочую смену она производит
160 т кирпича.
2. За 4 ч художник оформил 12 страниц. Определи, сколько таких же страниц художник оформит за 6 ч.
3. Прочитай задачу. Заполни таблицу. Реши задачу. Вычисли и запиши ответ.
Экскаватор за 4 ч вырыл 120 м траншеи. Сколько времени ему потребуется, чтобы при той же производительности вырыть 210 м траншеи?
|
Производительность |
Время работы |
Объем работы |
|
|
|
|
|
|
|
|
4* Заполни таблицу.
|
Фасовоч- ная линия |
Время работы |
Объем рабсгы |
Производительность |
|
|
9. » на 2 мин больше |
48 мешков |
|
|
|
10 мин |
|
9, на мешок/мин меньше |
|
в |
|
? , на З мешка меньше |
5 |
Вариант 2
1. Бригада за 6 дней асфальтирует 5400 м дороги. Определи производительность бригады.
2. Мельница перемалывает 24 мешка зерна за 3 дня. Определи, сколько таких же мешков смелет мельница за 7 дней.
З. Прочитай задачу. Заполни таблицу. Реши задачу. Вычисли и запиши ответ.
За 5 ч рабочий собирает 70 деталей. Сколько времени потребуется рабочему, чтобы при той же производительности собрать 120 деталей?
|
Производительность |
Время работы |
Объем работы |
|
|
|
|
|
|
|
|
![]()
![]()
4* Заполни таблицу.
|
Фасовоч- ная линия |
Время работы |
Объем работы |
Производительность |
|
|
|
? , на 4 мин больше |
21 кг |
|
|
|
|
З мин |
|
? , на I кг/мин меньше |
|
|
в |
|
? , на 14 кг больше |
5 |
Деление столбиком
Вариант 1
1. Определи и запиши количество цифр в неполном частном. 821 : 6 2818 : 5
2. Вычисли.
1842 : 6 167 : 62
3* Реши задачу. Вычисли и запиши ответ.
Для подарков купили 126 яблок, а апельсинов — в 3 раза больше. Всего получилось 42 подарка. Сколько яблок и сколько апельсинов положили в каждый подарок?
Вариант 2
1. Определи и запиши количество цифр в неполном частном. 624 : 7 9l63 : 5
2. Вычисли.
249 : 6 1224 : 4 64 : 16 165 : 52
3* Реши задачу. Вычисли и запиши ответ.
для класса купили 108 ручек, а карандашей — в 4 раза больше. Все ручки и карандаши раздали 27 учащимся. Сколько ручек и сколько карандашей досталось каждому ученику? Действия над величинами
Вариант 1
1.Вычисли.
5 м 4дм + 273 см 40 000 кв. см • 6 8 т 4 ц — 23 ц 82 кг
2.Найди пять девятых от 108 л.
3.Чему равна вся величина, если три пятых от этой величины составляют 45 км?
движение
![]()
4.12 наборов ручек стоят 144 руб. Вычисли и запиши цену этого набора.
5*. Реши задачу. Вычисли и запиши ответ.
Первая бригада грузчиков разгружает 1500 кг за 1 мин, а вторая — 315 кг за 3 мин. Какая из бригад работает с большей производительностью?
Вариант 2
1. Вычисли.
зм7дм+ см 70 000 кв. см • 5 6т2 ц— 31 ц 53 кг
2.
Найди четыре седьмых от 168 л. ![]()
3. Чему равна вся величина, если восемь девятых от этой величины составляют 96 км?
4. Вычисли и запиши цену одной коробки клюквы, если 13 коробок стоят 169 руб.
5* Реши задачу. Вычисли и запиши ответ.
Первый дворник подметает 150 кв. м двора за 15 мин, а второй — 48 кв. м за 4 мин. Какой из дворников работает с большей производительностью?
Задачи на движение
Вариант 1
1. Ответь на следующие вопросы.
• Велосипедист проехал 12 км за несколько часов. Уменьшится или увеличится скорость велосипедиста, если за то же время он проедет расстояние 48 км? Во сколько раз изменится скорость велосипедиста?
• Катер проплыл некоторое расстояние за 4 ч. Уменьшится или увеличится скорость катера, если он проплывет то же расстояние за 8 ч? Во сколько раз изменится скорость катера?
2. Реши задачу. Вычисли и запиши ответ.
два автомобиля выехали одновременно с одной стоянки в одном направлении. Первый автомобиль движется со скоростью 35 км/ч, а второй — 65 км/ч. На каком расстоянии друг от друга окажутся автомобили через 3 ч?
З. Реши задачу. Вычисли и запиши ответ.
Два поезда выехали одновременно с одной станции в противоположных направлениях. Скорость первого поезда 70 км/ч, второго — 48 км/ч. Какое расстояние будет между поездами через 5 ч? 4* Реши задачу. Вычисли и запиши ответ.
![]()
Скорость первого бегуна 7 м/с, а второго — 9 м/с. Дистанция составляет 100 м. Второй начал свой бег на 5 с позже, чем первый. Какой бегун выиграет в этих соревнованиях?
Вариант 2
1. Ответь на следующие вопросы.
• Велосипедист проехал l6 км за несколько часов. Уменьшится или увеличится скорость велосипедиста, если за то же время он проедет расстояние 48 км? Во сколько раз изменится скорость велосипедиста?
• Катер поплыл некоторое расстояние за 6 ч. Уменьшится или увеличится скорость катера, если он проплывет то же расстояние за 12 ч? Во сколько раз изменится скорость катера?
2. Реши задачу. Вычисли и запиши ответ.
Два автомобиля выехали одновременно с одной стоянки в одном направлении. Первый автомобиль движется со скоростью 37 км/ч, а второй — 57 км/ч. На каком расстоянии друг от друга окажутся автомобии через 4 ч?
3. Реши задачу. Вычисли и запиши ответ.
Два поезда выехали одновременно с одной станции в противоположных направлениях. Скорость первого поезда 60 км/ч, второго — 52 км/ч. Какое расстояние будет между поездами через 3 ч? 4* Реши задачу. Вычисли и запиши ответ.
Скорость первого бегуна 6 м/с, а второго — 8 м/с. Дистанция составляет 100 м. Второй начал свой бег на 7 с позже, чем первый. Какой бегун выиграет в этих соревнованиях?
Задачи на производительность
Вариант 1
1. Ответь на следующие вопросы.
• За смену завод выпускает 16 000 т трпича. Уменьшится или увеличится производительность завода, если за смену будет выпущено 32 000 т кирпича? Во сколько раз изменится производительность завода?
• Мальчик прочитывает несколько страниц за 40 мин. Уменьшится или увеличится скорость чтения мальчика, если то же количество страниц он прочитает за 20 мин? Во сколько раз изменится скорость его чтения?
2. Производительность первого насоса 150 л/ч, производительность второго насоса 130 л/ч. Сколько воды смогут перекачать два насоса за 3 ч, работая одновременно?
куплю-продажу
![]()
3. Реши задачу. Вычисли и запиши ответ.
На стройке 120 т кирпича. Первый кран может поднять весь кирпич за 60 мин, а второй — за 12 мин. Сколько времени потребуется двум кранам, чтобы поднять весь кирпич, работая одновременно?
4* Реши задачу. Вычисли и запиши ответ.
К началу строительства было затовлено 45 т кирпша. Бригада каменщиков за четырехчасовую смену укладывает 240 т кирпича. Каждый час на эту стройку подвозят 55 т кирпича. Через сколько часов на стройке не останется ни одного кирпича?
Вариант 2
1. Ответь на следующие вопросы.
• За несколько часов на электрической плите можно вскипятить 250 л воды. Уменьшился или увеличился произВOЩПРЛЬность плиты, если за это же время на ней встпртг 750 л воды? Во сколько раз изменится производительность плиты?
• Мальчик прочитывает несколько страниц за 60 мин. Уменьшится или увеличится скорость чтения мальчика, если то же количество страниц он прочитает за 30 мин? Во сколько раз изменится скорость его чтения?
2. Производительность первого станка 75 дет./ч, производительность второго станка 35 дет./ч Сколько деталей смогут выточить два станка за 2 ч, работая одновременно? З. Реши задачу. Вычисли и запиши ответ.
В зале 150 лампочек. Первый электрик может поменять все лампочки за 15 ч, а второй — за 30 ч. Сколько времени потребуется двум электрикам, чтобы поменять все лампочки, работая одновременно?
4* Реши задачу. Вычисли и запиши ответ.
К началу рабочего дня в хлебном магазине было 50 батонов. За 8 ч работы магазина купили 400 батонов. Каждый час в магазин привозят 40 батонов. Через сколько часов в магазине не будет ни одного батона?
Вариант 1
1. Ответь на следующие вопросы.
• За несколько килограммов яблок покупатель заплатил 72 руб. Уменьшится или увеличится цена яблок, если это же количество яблок купить за 36 руб.? Во сколько раз изменится цена яблок?
![]()
• За несколько рублей купили 20 л молока. Уменьшится или увеличится цена молока, если на эту же сумму купить 40 л? Во сколько раз изменится цена молока?
2. Реши задачу. Вычисли и запиши ответ.
Для каждого ученика класса нужно купить одну линейку по цене 5 руб./шт., один карандаш по цене 7 руб./шт. и один ластик по цене 3 руб./шт. За всю покупку заплатили 300 руб. Сколько учеников в этом классе?
3*. Реши задачу. Вычисли и запиши ответ.
Коробка сахара массой 250 г стоит 8 руб./кор., пакет сахара массой 500 г стоит 15 руб./пак. Можно купить развесной сахар по цене 29 руб./кг. Какой сахар покупать выгоднее: в коробках, пакетах или на вес?
Вариант 2
1. Ответь на следующие вопросы.
• За несколько килограммов помидоров покупатель заплатил 84 руб. Уменьшится или увеличится цена помидоров, если это же количество помидоров купить за 42 руб.? Во сколько раз изменится цена помидоров?
• За несколько рублей купили 20 кусков мыла. Уменьшится или увеличится цена мыла, если на эту же сумму купить 60 кусков? Во сколько раз изменится цена мыла?
2. Реши задачу. Вычисли и запиши ответ.
Для каждого рабочего бригады купили одну пару рукавиц по цене 15 руб./пара, один фартук по цене 18 руб./шт. и один берет по цене 27 руб./шт. За всю покупку заплатили 300 руб. Сколько человек в этой бригаде?
3*. Реши задачу. Вычисли и запиши ответ.
Пачка макарон массой 200 г стоит 5 руб./п., коробка макарон массой 500 г стоит 13 руб./кор. Можно купить макароны на вес по цене 23 руб./кг. Какие макароны покупать выгоднее: в пачках, коробках или на вес?
Вариант 1
1. Из чисел 34, 40, 500, 721, 63, 70 выбери и запиши:
а) «круглые» и двузначные;
2) «круглые» или двузначные.
2. Из чисел 5, 8, 12, 14, 16, 18, 20 выбери и запиши те, которые можно поставить вмесгор так, чтобы данная запись оказалась верной.
а)р> 16; б) 8 <р< 16.
Геометрические фигуры и тела
![]()
3. Продолжи утверждения так, чтобы они были верными.
• Если длина стороны квадрата меньше 12 см, то его периметр...
• Число 14 не только четное, но и...
4* Заверши следующее утверждение так, чтобы оно было верным.
Если «круглое» двузначное число 5 < а < 20, то а =![]()
Вариант 2
1. Из чисел 24, 50, 120, 512, 81, 20 выбери и запиши:
а) «круглые» и двузначные;
б) «круглые» или двузначные.
2. Из чисел 2, 6, П, 13, 14, 17, 21 выбери и запиши те, которые можно поставить вместо р так, чтобы данная запись оказалась верной.
а)р> 14; б) 14.
3. Продолжи утверждения так, чтобы они были верными.
• Если мина стороны квадрата меньше 15 см, то его периметр...
• Число 13 не только нечетное, но и...
4*. Заверши следующее утверждение так, чтобы оно было верным.
Если «круглое» двузначное число 2 < с < 20, то с![]()
Геометрические фигуры и тела
Вариант 1
1. Вычисли площадь поверхности куба, длина ребра которого равна 3 см.
2. Измерь и вычисли площадь данного многоугольника, если известно, что площадь одной клетки 25 кв. мм.

![]()
3. Прочитай названия фигур.
Куб, треугольник, шар, пирамида, прямоугольник, цилиндр.
Выпиши:
а) названия фигур, которые имеют объем;
б) названия тел вращения.
4*. Измерь приблизительно площадь данной фигуры. Выбери и подчеркни правильный ответ.

а) около 2 кв. см;
б) около 6 кв. см;
в) около 10 кв. см.
Вариант 2
1. Вычисли площадь поверхности куба, длина ребра которого равна 2 см.
2. Измерь и вычисли площадь данного многоугольника, если известно, что площадь одной клетки 25 кв. мм.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г- |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Прочитай названия фигур.
Куб, прямоугольник, пирамида, треугольник, шар, конус. Выпиши:
а) названия фигур, которые имеют объем;
б) названия тел вращения.
4* Измерь приблизительно площадь данной фигуры. Выбери и подчеркни правильный ответ.
Уравнения
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оао• |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) около 3 кв. см;
б) около 7 кв. см;
в) около кв. см.
Вариант 1
I. Найди корень каждого
уравнения. х + 3412 = 7351 х- 462 =![]()
2. Реши задачу с помощью уравнения.
В вазе стоит 15 гвоздик, причем красных на З больше, чем белых. Сколько белых гвоздик в вазе? 3* Найди корень уравнения.
х . (617 - 598) = (781 + 78) 19
Вариант 2
1 . Найди корень каждого уравнения. х + 4103 = 6261 х- 272 = 681
![]() ЗОО
ЗОО
х . 61 = 39
2. Реши задачу с помощью уравнения.
На столе лежит 1 8 ложек и вилок, причем ложек на 6 больше, чем вилок. Сколько вилок лежит на столе? 3*. Найди корень уравнения. х • (805 -- 788) = (625 + • 17
Список литературы
1. Блинова И.В. Занимательные сказочные материалы к урокам литературного чтения и математики в l—4 классах. Волгоград: Учитель, 2006.
2.
Волина В.В. Праздник числа: Занимательная математика для ![]() детей. М.:
Знание, 1994.
детей. М.:
Знание, 1994.
3. Захарова О.А. Проверочные работы по математике и технология организации коррекции знаний учащихся: 1—4 классы: Методическое пособие. М.: Академкнига/Учебник, 2007.
4. Зеленина Л. М., Хохлова Т.Е. Тесты: Начальная школа. 4 класс: Учеб.-метод. пособие. М.: Дрофа, 2003.
5. Чекин АЛ. Математика: 4 класс: Методическое пособие / Под ред. Р.Г. Чураковой. М.: Академкнига/Учебник, 2010.
6.
ШеверДина Н.А., Сушинскас Л.]. Новые олимпиады для начальной школы.
Ростов н/Д: Феникс, 2007.
Содержание
Ог авторов
![]() Тематическое планирование .
Тематическое планирование .
Урок 1. Сначала займемся повторением![]() 12
12
Урок 2. Сначала займемся повторением![]()
Урок 3. Сначала займемся повторением![]() 20
20
Урок 4. Когда известен результат разностного сравнения
.![]() . 23 Урок 5. Когда известен результат разностного сравнения
. 23 Урок 5. Когда известен результат разностного сравнения![]() . 25 Урок 6. Когда известен результат
разностного сравнения . . . . . . . . . . . 27 Урок 7. Когда известен результат
кратного сравнения .
. 25 Урок 6. Когда известен результат
разностного сравнения . . . . . . . . . . . 27 Урок 7. Когда известен результат
кратного сравнения .![]() . 29 Урок 8. Когда известен результат кратного сравнения
. 29 Урок 8. Когда известен результат кратного сравнения![]() . 31
. 31
Урок 9. Учимся решать задачи![]() . 33 Урок 10. Учимся решать задачи
. 33 Урок 10. Учимся решать задачи![]() . 36
. 36
Урок 1 1. Алгоритм умножения столбиком![]()
Урок 12. Поупражняемся в вычислениях столбиком![]() . 41
. 41
Урок 13. Тысяча тысяч, РТИ МиЛЛИОН![]() . 42
. 42
Урок 14. Разряд единиц миллионов и класс миллионов![]() . 44 Урок 15. Когда трех классов для
записи числа недостаточно
. 44 Урок 15. Когда трех классов для
записи числа недостаточно![]() . 46
. 46
Урок 16. Поупражняемся в сравнении
чисел и повторим пройденное![]() 48
48
Урок 17. Может ли величина изменяться?![]() . 51
. 51
Урок 18. Всегда ли математическое
выражение яшшется числовым?![]() 53
53
Урок 19. Зависимость между величинами![]() 55
55
Урок 20. Поупражняемся в нахождении значений зависимой
величины . .![]() . 58 Урок 21. Контрольная работа № I
. 58 Урок 21. Контрольная работа № I![]() 60
60
Урок 22. Стоимость единицы товара, кли цена .![]() . 62 Урок 23. Стоимость единицы
товара, или цена .
. 62 Урок 23. Стоимость единицы
товара, или цена .![]() 63
63
Урок 24.
Когда цена постоянна .![]() 66 Урок 25. Учимся решать задачи
66 Урок 25. Учимся решать задачи![]() 70
70
Урок 26. Деление нацело и деление с остатком .![]() 72 Урок 27. Деление нацело и деление
с остатком
72 Урок 27. Деление нацело и деление
с остатком![]() 74 Урок 28. Неполное частное и остаток
74 Урок 28. Неполное частное и остаток![]() 76
76
348 Содержание
![]()
Урок 29. Остаток и делитель![]() 78 Урок 30. Когда остаток равен 0
78 Урок 30. Когда остаток равен 0![]() 80
80
Урок 31. Когда делимое меньше делителя![]() 83 Урок 32. Деление с остатком и
вычитание
83 Урок 32. Деление с остатком и
вычитание![]() 86
86
Урок 33. Какой остаток может получиться при делении на 2?![]() 88 Урок 34. Какой остаток может
получиться при делении на 2?
88 Урок 34. Какой остаток может
получиться при делении на 2?![]() 90 Урок 35. Поупражняемся в вычислениях и повторим пройденное
90 Урок 35. Поупражняемся в вычислениях и повторим пройденное![]() . 93
. 93
Урок 36. Запись деления с остатком столбиком![]() 96
96
Урок 37. Способ поразрядного нахождения результата деления . 99
Урок 38. Поупражняемся в делении столбиком
Урок 39. Вычисления с помощью калькулятора Урок 40. Контрольная работа № 2
|
Урок 41. Час, минута и секунда . |
106 |
|
Урок 42. Кто или что движется быстрее? |
109 |
|
Урок 43. Длина пути в единицу времени, шли скорость
. |
112 |
|
Урок 44. Учимся решать задачи |
Пб |
![]() Урок 45. Учимся решать задачи
Урок 45. Учимся решать задачи
Урок 46. Какой сосуд вмещает больше?
|
Урок 47. Литр. Сколько литров? |
125 |
|
Урок 48. Вместимость и объем |
127 |
|
Урок 49. Вместимость и объем |
129 |
|
Урок 50. Кубический сантиметр и измерение объема |
131 |
|
Урок 51. Кубический дециметр и кубический сантиметр |
ВЗ |
|
Урок 52. Кубический дециметр и литр |
136 |
|
Урок 53.Литр и килограмм |
138 |
|
Урок 54. Разные задачи |
141 |
|
Урок 55. Разные задачи |
|
|
Урок 56. Поупражняемся в измерении объема |
|
|
Урок 57. Контрольная работа № 3 |
|
Урок 58. Кто выполнил большую работу![]() 149
149
Урок 59. Производительность — это скорость выполнения работы . 152 Урок 60. Производительность — это скорость выполнения работы . 154
Урок 61. Учимся решать задачи ![]() 156
156
Урок 62. Отрезки, соединяющие вершины многоугольника . 158
Урок 63. Разбиение многоугольника на треугольники . 162
|
Урок 64. Площадь прямоугольного треугольника . |
|
|
Урок 65. Вычисление площади треугольника |
|
|
Урок 66. Закрепление пройденного |
|
|
Урок 67. Закрепление пройденного |
|
|
Урок 68. Контрольная работа № 4 |
|
|
Урок 69. Деление на однозначное число столбиком . |
|
|
Урок 70. Деление на однозначное число столбиком . |
177 |
|
Урок 71.Число цифр в записи неполного частного |
178 |
|
Урок 72.Деление на двузначное число столбиком |
182 |
|
Урок 73. Алгоритм деления столбиком |
185 |
|
Урок 74. Алгоритм деления столбиком |
186 |
|
Урок 75. Сокращенная форма записи деления столбиком |
187 |
|
Урок 76. Поупражняемся в делении столбиком . |
189 |
|
Урок 77. Сложение и вычитание величин |
191 |
Содержание 349
![]()
Урок 78. Умножение величины на число и числа на величину![]() 193
193
Урок 79. Деление величины на число![]() 197
197
Урок 80. Нахождение доли от величины и величины по ее доле![]() 200
200
Урок 81.
Нахождение части от величины![]() 203 Урок 82. Нахождение величины по ее части
203 Урок 82. Нахождение величины по ее части![]() . 205
. 205
Урок 83. Деление величины на величину![]() 208
208
Урок 84. Когда время движения одинаковое![]()
Урок 85. Когда длина пройденного пути одинаковая .![]() . 214 Урок 86. Движение в одном и том
же направлении
. 214 Урок 86. Движение в одном и том
же направлении![]() 216
216
Урок 87. Движение в противоположных направлениях .![]() 219
219
Урок 88. Учимся решать задачи![]() 222
222
Урок 89. Поупражняемся в вычислениях и повторим
пройденное![]() 225
225
Урок 90. Контрольная работа № 5![]() 228
228
Урок 91. Когда время работы одинаковое![]() 229
229
Урок 92. Когда объем выполненной работы одинаковый![]() 231 Урок 93. Производительность при
совместной работе .
231 Урок 93. Производительность при
совместной работе .![]() 234
234
Урок 94. Время совместной работы .![]() 236
236
Урок 95. Учимся решать задачи и повторяем пройденное .![]() 239
239
Урок 96. Когда количество одинаковое![]() 242 Урок 97. Когда стоимость одинаковая
.
242 Урок 97. Когда стоимость одинаковая
.![]() 244 Урок 98. Цена наборов товаров .
244 Урок 98. Цена наборов товаров .![]() 246
246
Урок 99. Учимся решать задачи![]() 247
247
Урок 100. Поупражняемся в вычислениях и повторим
пройденное ![]() 249
249
Урок 101. Вычисления с помощью калькулятора![]() 251
251
Урок 102. Контрольная работа № 6![]() 253 Урок 103. Как в математике
применяют союз «и» и союз «или» . . .
253 Урок 103. Как в математике
применяют союз «и» и союз «или» . . .![]() 254
254
Урок 104. Как выполнение одного условия обеспечивает
выполнение другого![]() 257 Урок 105. Не только одно, но и другое
257 Урок 105. Не только одно, но и другое![]() 258 Урок 106. Учимся решать
логические задачи .
258 Урок 106. Учимся решать
логические задачи .![]() 260
260
Урок 107. Поупражняемся в вычислениях и повторим
пройденное ![]() 263 Урок 108. Поупражняемся в вычислениях и повторим пройденное
263 Урок 108. Поупражняемся в вычислениях и повторим пройденное ![]() 264
264
Урок 109. Квадрат и куб![]() 267 Урок ПО. Круг и шар
267 Урок ПО. Круг и шар![]() 270
270
Урок 1 11. Площадь и объем![]() 272
272
Урок 112. Измерение площади с помощью палетки![]() . 274 Урок В. Поупражняемся в
нахождении площади и объема
. 274 Урок В. Поупражняемся в
нахождении площади и объема![]() 276 Урок 114. Поупражняемся в нахождении площади и объема
276 Урок 114. Поупражняемся в нахождении площади и объема![]() 278 Урок 115. Поупражняемся в
вычислениях и повторим пройденное . 279 Урок 116. Поупражняемся в вычислениях и
повторим пройденное
278 Урок 115. Поупражняемся в
вычислениях и повторим пройденное . 279 Урок 116. Поупражняемся в вычислениях и
повторим пройденное ![]() 282
282
Урок 117. Уравнение. Корень уравнения![]() 284
284
Урок 118. Учимся решать задачи с помощью уравнений .![]() 286
286
Урок 119. Поупражняемся в вычислениях и повторим пройденное . 288
Урок По. Контрольная работа № 7![]() 291 Урок 121. Разные задачи
291 Урок 121. Разные задачи![]() 292
292
Урок 122. Разные задачи![]()
Урок 123. Натуральные числа и число 0 (повторение)![]() 296 Урок 124. Натуральные числа и
число 0 (повторение)
296 Урок 124. Натуральные числа и
число 0 (повторение)![]() 298
298
Урок 125.Алгоритмы вычисления столбиком (повторение)![]() 301
301
350 Содержание
Урок Пб. Алгоритмы вычисления столбиком (повторение)![]() 302 Урок 127. Действия с величинами
(повторение)
302 Урок 127. Действия с величинами
(повторение)![]() 304
304
Урок 128.Действия с величинами (повторение)![]() 305 Урок 129. Как мы научились решать
задачи . . .
305 Урок 129. Как мы научились решать
задачи . . .![]() 308 Урок ВО. Как мы научились решать задачи . . .
308 Урок ВО. Как мы научились решать задачи . . .![]()
Урок 131. Контрольная работа № 8![]() . ЗВ Урок 132. Геометричесие фигуры и
их свойства (повторение)
. ЗВ Урок 132. Геометричесие фигуры и
их свойства (повторение)![]() . 314 Урок 133. Геометрические фигуры и их свойства (повторение)
. 314 Урок 133. Геометрические фигуры и их свойства (повторение)![]()
Урок 134. Буквенные выражения и уравнения (повторение)
.![]() . 319
. 319
Урок 135. Буквенные выражения и уравнения (повторение)![]() 322
322
Урок 136. Закрепление пройденного![]() 324
324
ПРИЛОЖЕНИЕ. Самостоятельные работы
Повторение![]() 329
329
Задачи на разностное и кратное сравнение![]() 330
330
Класс миллионов. Буквенные выражения![]() 331
331
Задачи на куплю-продажу![]() 333 Деление с остатком
333 Деление с остатком![]() . 334 Задачи на движение
. 334 Задачи на движение![]() 334 Вместимость и объем
334 Вместимость и объем![]() 335
335
Задачи на производительность![]() . 337
. 337
Деление столбиком![]() . 338
. 338
Действия над величинами![]() . 338
. 338
Задачи на движение![]() 339
339
Задачи на производительность![]() 340
340
Задачи на куплю-продажу![]() 341
341
Логика![]() 342
342
Геометрические фигуры и тела .![]() 343
343
Уравнения. . .![]() 345 Список литературы .
345 Список литературы .![]() 346
346
Учебно-метоДическое пособие
В ПОМОЩЬ ШКОЛЬНОМУ УЧИТЕЛЮ
Афонина Алла Васильевна
Ипатова Екатерина Евсеевна
ПОУРОЧНЫЕ РАЗРАБОТКИ ПО МАТЕМАТИКЕ
4 класс
Выпускающий редактор Анна Короткова Дизайн обложки Екатерины БеДриной
По вопросам приобретения книг издательства «ВАКО» обращаться в ООО «Образовательный проект» по телефонам: 8 (495) 778-58-27, 746-15-04. Сайт: www.obrazpro.ru
Приглашаем к сотрудничеству авторов.
Телефон: 8 (495) 507-33-42. Сайт: www.vaco.ru
Налоговая льгота —
Общероссийский классификатор продукции ОК 005-93-953000.
Издательство «ВАКО»
Подписано к печати 12.04.2011.
Формат 84 х 108/32. Печать офсетная. Гарнитура Newton. Усл. печ. листов 18.48. Тираж 5000 экз. Заказ № 2015.
Отпечатано в полном соответствии с качеством предоставленных материалов в ОАО «Дом печати — ВЯТКА»
610033, г. Киров, ул. Московская, 122 Факс: (8332) 53-53-80, 62-10-36 http://www.gipp.kirov.ru, e-mail: pto@gipp.kirov.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.