
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТІРЛІГІ
АКАДЕМИК СӘТБАЕВ АТЫНДАҒЫ ЕКІБАСТҰЗ ИНЖЕНЕРЛІК - ТЕХНИКАЛЫҚ ИНСТИТУТЫНЫҢ КОЛЛЕДЖІ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
ЕКИБАСТУЗСКИЙ КОЛЛЕДЖ ИНЖЕНЕРНО - ТЕХНИЧЕСКОГО ИНСТИТУТА ИМЕНИ АКАДЕМИКА САТПАЕВА

по дисциплине
|
ФИЗИКА И АСТРОНОМИЯ |
|
|
для всех специальностей
|
ПОУРОЧНЫЕ ПЛАНЫ-КОНСПЕКТЫ |
|
Раздел 1 -«МЕХАНИКА» |
|
Курс |
1 |
|
|
Курс |
|
|
2017г.
Тема 1.1 Кинематика. Характеристики механического движения. Виды движения.
Тема 1.2 Динамика. Законы классической механики.
Тема 1.3 Силы в природе. Закон всемирного тяготения. Невесомость.
Тема 1.4 Законы сохранения в механике. Закон сохранения импульса. Реактивное движение. Механическая энергия и ее виды. Закон сохранения механической энергии.
Тема 1.5 Статика. Момент силы. Условия равновесия твердого тела.
Демонстрации
1. Движение тел по инерции
2. Невесомость
3. Закон сохранения импульса
Лабораторная работа №1 «Определение ускорения тела при равноускоренном движении»
Практическая работа №1 « Построение ССС»
Практическая работа №2 «Определение положения центра тяжести сложной фигуры»
Кинематика - (от греч. kinematos -
движение), раздел механики, в котором изучаются геометрические свойства
движения тел без учета их массы и действующих на них сил. Напомните,
пожалуйста, основные характеристики движения…
Итак, что изучает кинематика?
Виды движения:
Прямолинейное:
· Равномерное
· Неравномерное (равноускоренное и с переменным ускорением)
Криволинейное:
· Равномерное движение по окружности
· Ускоренное движение по окружности
Вращательное:
· Равномерное вращение
· Вращение с ускорением
Колебательное:
· Гармонические колебания
· Негармонические колебания
Остановимся на уже знакомом вам прямолинейном движении, а именно: равномерном... флеш-анимация «График скорости равномерного движения»
Теперь обратим свои взоры и мысли на неравномерное движение. Кто как себе представляет этот вид движения?.. Приведите примеры…
Внимание на экран: флеш-анимация «Определение пути равнопеременного движения по графику скорости»
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. Механическоедвижениеотносительно: теломожетпокоиться в однойсистемеотсчета и в это же времядвигаться в другой; егоположение (координата) различно в разных системах отсчета. Относительна и траекториядвижениятела. Перемещениетела, пройденныйим путь и егоскоростьтакжеизменяются при переходе от однойсистемыотсчета к другой. Так, водительнеподвиженотносительно корпуса автомобиля, движущегося по шоссе, перемещение, путь и скоростьводителяотносительноавтомобиляравны нулю, но, например, относительнодеревьеввдольшоссеониимеютнекоторыезначения.
Можно ли быть неподвижным и при этом двигаться быстрее автомобиля Формулы 1? Оказывается, можно. Любое движение зависит от выбора системы отсчета, то есть любое движение относительно. Тема сегодняшнего урока: «Относительность движения. Закон сложения перемещений и скоростей». Мы узнаем, как выбрать систему отсчета в том или ином случае, как при этом найти перемещение и скорость тела
Относительность движения
Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени. В этом определении ключевой является фраза «относительно других тел». Каждый из нас относительно какой-либо поверхности неподвижен, но относительно Солнца мы совершаем вместе со всей Землей орбитальное движение со скоростью 30 км/с, то есть движение зависит от системы отсчета.
Система отсчета – совокупность системы координат и часов, связанных с телом, относительно которого изучается движение. Например, описывая движения пассажиров в салоне автомобиля, систему отсчета можно связать с придорожным кафе, а можно с салоном автомобиля или с движущимся встречным автомобилем, если мы оцениваем время обгона (Рис. 1).

Рис. 1. Выбор системы отсчета
Какие же физические величины и понятия зависят от выбора системы отсчета? Это:
1. Положение или координаты тела.
2. Траектория.
3. Перемещение и путь.
4. Скорость.
Зависимость характеристик движения от выбора системы отсчета называется относительностью движения.
В истории человечества были и драматические случаи, связанные как раз с выбором системы отсчета. Казнь Джордано Бруно, отречение Галилео Галилея – все это следствия борьбы между сторонниками геоцентрической системы отсчета и гелиоцентрической системой отсчета. Уж очень сложно было человечеству привыкнуть к мысли о том, что Земля – это вовсе не центр мироздания, а вполне обычная планета. А движение можно рассматривать не только относительно Земли, это движение будет абсолютным и относительно Солнца, звезд или любых других тел. Описывать движение небесных тел в системе отсчета, связанной с Солнцем, намного удобнее и проще, это убедительно показали сначала Кеплер, а потом и Ньютон, который на основании рассмотрения движения Луны вокруг Земли вывел свой знаменитый закон всемирного тяготения.
Закон сложения перемещений и скоростей
Если мы говорим, что траектория, путь, перемещение и скорость являются относительными, то есть зависят от выбора системы отсчета, то про время мы этого не говорим. В рамках классической, или Ньютоновой, механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково. Рассмотрим, как находить перемещение и скорость в одной системе отсчета, если они нам известны в другой системе отсчета.
Человек идет по палубе парохода со скоростью ![]() относительно
парохода. Пароход движется поступательно со скоростью
относительно
парохода. Пароход движется поступательно со скоростью ![]() относительно
берега. Найдем скорость
относительно
берега. Найдем скорость ![]() человека
относительно берега (Рис. 2).
человека
относительно берега (Рис. 2).
Свяжем неподвижную систему отсчета (хОу) с Землей, а подвижную (х’О’у) – с пароходом.
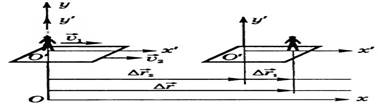
Рис. 2. Пример задачи
Из Рис. 2 видно, что перемещение:
Δ![]() =
Δ
=
Δ![]() +
Δ
+
Δ![]() ⇒ Δ
⇒ Δ![]() ≠
Δ
≠
Δ![]() ,
,
где Δ![]() –
перемещение человека относительно парохода, Δ
–
перемещение человека относительно парохода, Δ![]() –
перемещение парохода относительно берега, Δ
–
перемещение парохода относительно берега, Δ![]() –
перемещение человека относительно берега.
–
перемещение человека относительно берега.
Таким образом, если тело одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею в каждом из движений. В этом состоит установленный экспериментально принцип независимости движений.
Разделив это уравнение на промежуток времени, за который произошли перемещения человека и парохода, получим закон сложения скоростей:
![]() =
= ![]() +
+ ![]()
Скорость ![]() тела
относительно неподвижной системы отсчета равна геометрической сумме
скорости
тела
относительно неподвижной системы отсчета равна геометрической сумме
скорости ![]() тела
относительно подвижной системы отсчета и скорости
тела
относительно подвижной системы отсчета и скорости ![]() самой
подвижной системы отсчета относительно неподвижной.
самой
подвижной системы отсчета относительно неподвижной.
Упражнение 1.Какую систему координат следует выбрать (одномерную, двухмерную или трехмерную) для определения положения следующих тел:
– Трактор в поле.
– Вертолет.
– Поезд.
– Люстра в комнате.
– Лифт.
– Подводная лодка.
– Шахматная фигура.
– Самолет на взлетной полосе.
Задание для групп
Задание 1.В рабочей тетради нарисуйте дорогу, на которой изобразите велосипедиста, мост, автомобиль, дерево, идущего пешехода, светофор.
Проведите в тетради координатную ось параллельно дороге. Примите дерево за тело отсчета.
Выберите масштаб (1 деление - 100 м).
Определите координаты моста, дерева и светофора.
Определите начальные координаты пешехода, велосипедиста и автомобиля.
Покажите вектор перемещения для каждого из этих тел, его проекцию на ось Y и найдите модуль вектора перемещения, а также пройденный путь в следующих случаях:
– автомобиль доехал до светофора;
– пешеход дошел до дерева;
– велосипедист доехал до светофора и вернулся к дереву.
Задание 2.Выполните те же упражнения, что и в задании 1, но за тело отсчета выберите мост.
Сравните пути и перемещения каждого из тел (полученные при выполнении заданий 1 и 2).
– Ответьте устно на вопросы:
1) В чем состоит основная задача механики?
2) Зачем введено понятие материальной точки? Когда тело можно считать материальной точкой?
3) Что такое система отсчета (СО)? Для чего вводится?
4) Какие виды систем координат (СК) вы знаете?
5) Что такое траектория?
6) В чем отличие пути от перемещения?
– Решите кроссворд:
1. Наука о неживой природе. 2. Тысячная доля метра. 3. Прибор для измерения объема жидкостей. 4. Что означает греческое слово цэушы [физис], от которого произошло слово «физика»? 5. Механические, тепловые, электрические, световые явления – это явления… 6. Все, что есть во Вселенной. 7. Древнегреческий ученный. 8. «Отец» русской авиации. 9. Город, в котором в 1954 г. была построена первая в мире атомная электростанция. 10. Величина, характеризующая степень нагретости тела. 11. Русский ученый, усовершенствовавший лампы дневного света. 12. Свертывающаяся в круг металлическая или матерчатая измерительная лампа с делениями. 13. Название транспортного отечественного самолета, грузоподъемностью 150 т, построенного в 1985 году. 14. Единица длины, равная 0,1 м. 15. Русский ученый и организатор, с именем которого связано развитие отечественной автономной энергетики. 16. Физическая величина, характеризующая расстояние. 17. «Он создал первый русский университет. Он, лучше сказать, сам был первым нашим университетом» (А. С. Пушкин). 18. Критерий истины.

Ответы:1. Физика. 2. Миллиметр. 3. Мензурка. 4. Природа. 5.... физические. 6. Материя. 7. Аристотель. 8. Жуковский. 9. Обнинск. 10. Температура. 11. Вавилова. 12. Рулетка. 13. Руслан. 14. Дециметр. 15. Курчатов. 16. Длина. 17. Ломоносов. 18. Опыт.
1. Что называется механическим движением? Примеры.
2. В чем заключается основная задача механики?
3. Что называется телом отсчета? Системой отсчета?
4. Что называется материальной точкой? Примеры.
5. Что называется траекторией? Примеры.
6. Что такое путь? Обозначение, единицы измерения.
7. Что называется перемещением? Примеры.
8. В каком случае модуль перемещения и путь совпадают?
9. От чего зависит знак проекции вектора перемещения?
10. Чем путь отличается от координаты
Виды механического движения можно разделить на прямолинейные и криволинейные по форме траектории. А по закону движения виды механического движения делят на равномерные и неравномерные.
Прямолинейное движение тела определение:
Прямолинейное движение – это вид механического движения, при котором направление скорости не меняется. Но может меняться модуль скорости.
Криволинейное движение тела определение:
Криволинейное движение – это вид механического движения, при котором направление скорости изменяется. Модуль скорости может меняться.
Равномерное движение тела определение:
Если тело за равные промежутки времени проходит равные расстояния, то такое движение называется равномерным движением. При равномерном движении модуль скорости есть постоянная величина. А направление скорости может меняться.
Неравномерное движение тела определение:
Если тело за равные промежутки времени проходит различные расстояния, то такое движение называется неравномерным. При неравномерном движении модуль скорости есть переменная величина. Направление скорости может меняться.
Равнопеременное движение тела определение:
Если за равные промежутки времени модуль скорости изменяется на одну и ту же величину, то такое движение называется равнопеременным движением.
Тангенциальное ускорение есть величина постоянная при равнопеременном движении. Если при этом направление скорости не меняется, то получим прямолинейное равнопеременное движение.
Равноускоренное движение тела определение:
Пусть при равнопеременном движении модуль скорости возрастает, такое движение называется равноускоренным движением.
Равнозамедленное движение тела определение:
Если при равнопеременном движении модуль скорости уменьшается, такое движение называется равнозамедленным движением.
Когда мы говорим о механическом движении тела, то можно рассмотреть понятие поступательного движения тела.
Поступательное движение тела определение:
Если при движении тела любая прямая, проведенная в этом теле, остается параллельной себе, то такое движение называется поступательным.
Вращательное движение тела определение:
При вращательном движении тела все точки этого тела движутся по концентрическим окружностям, при этом центры таких окружностей лежат на оси вращения. Ось вращения является прямой.
Сложное движение тела определение:
Сложное движение тела в одной плоскости можно представить как сумму поступательного и вращательного движений.
|
Тема : Механическое движение. Тело отсчета. Относительность движения. |
||||
|
Задачи изучения этого урока |
Сформировать у учащихся представление об относительности движения и покоя; ввести новые понятия: тело отсчета, система отсчета; систематизировать знания по теме; Развитие речи, мышления; развитие умственной деятельности: умений обобщать, моделировать; формирование эмоциональной сферы личности, развитие творческих способностей; Развитие нравственных и эстетических представлений о нормах поведения в современном обществе. Воспитание установки на самообразование; |
|||
|
Задачи занятия |
Учащиеся покажут: 1. Знание теоретического материала, 2. Умение применять их при работе. 3. Умение работать с учебником и определять ключевые моменты. 4. Ораторские способности. |
|||
|
Языковые задачи |
Предметно-ориентированная лексика и терминология: Механическое движение, тело отсчета, система отсчета, относительность движения. |
|||
|
Прошлый материал |
Масса и плотность вещества, инертность. |
|||
|
План |
|
|||
|
Планируемое время |
Планируемые задания |
Источники |
||
|
2 минуты
3 минуты
2 минуты
3 минуты
2 минуты
2 минуты
1 минута
2 минуты
5 минут
1 минута
5 минут
3 минуты
6 минут (по 3 минуты на каждую группу)
2 минуты
2 минуты
2 минуты
2 минуты
|
Орг момент. «Стартер». Физический диктант Прежде чем приступить к изучению новой темы, давайте-ка повторим домашнее задание. Я предлагаю вам написать физический диктант. Взаимопроверка по ключу.
Дифференцированные задания (по своему усмотрению выбирают уровень заданий) Самопроверка по ключу.
Целеполагание. Через наводящие вопросы привести к понятию движения в окружающем мире. - Мы с вами изучили основные положения о строении вещества. Вспомним, что все вещества состоят из …? (молекул). Каково поведение молекул в веществе? (молекулы в веществе двигаются непрерывно, беспорядочно, хаотично). Но движутся не только молекулы. Движутся люди, животные, небесные тела, словом все то, что существует Во вселенной независимо от нашего сознания, т.е. материя. Основное свойство материи – движение. Движение – есть жизнь.
Более конкретно сформулировать мысли школьников. Для озвучивания темы урока задействовать учеников. Рефлексия «Древо знаний» На начало урока – определение уровня своих знаний о движении Разбивка на группы Каждый ученик вытягивает карточку с фрагментом высказывания о движении. Группируются по целому высказыванию 1. В движении сила растет и набирает мощь. Вергилий 2. Жизнь требует движения. Аристотель
Изучение новой темы Учащиеся работают над теоретическим материалом. Индивидуальное изучение темы.
равила работы в группе. Распределение обязанностей. (оратор, будильник, теоретик, практик, оформитель)
Создание постера «Механическое движение»
Физ.минутка Выполняют Защита постера Соблюдение критериев. -ключевые слова -примеры -рисунок или аппликация с определением тела отсчета и системы отсчета. Оценивание постеров Выставление и комментарии оценок. Обратная связь. Треугольник 3-2-1: -три ключевых слова урока -две характеристики работы группы -один вопрос учителю по данной теме (на следующий урок) Древо знаний - отразите изменения в ваших знаниях о движении, Оценки за урок по шкале баллирования самостоятельный перевод в оценку за урок Домашнее задание. |
Звучит музыка
Карточки Ключ ответов и критерии оценивания ответов на слайде презентации.
Презентация к уроку. На интерактивной доске сетка кроссворда.
Ключ ответов и критерии оценивания ответов на слайде презентации
Древо знаний
Карточку с фрагментом высказывания о движении.
Учебник физики §11.
Правила работы в группе
атман, фломастеры, стикеры, клей, журнал «Непоседа»
презентация
постеры
стикеры
карточка
Древо знаний
Таблица оценивания
Учебник физики §11.
|
||
|
Дополнительная информация |
||||
|
Дифференцирование – Как вы планируете помочь ученикам? Какие задания вы планируете для способных учеников? Физический диктант позволит оценить степень усвоения материала, дифференцированные задания – знаниевый уровень учащихся. Для талантливых учеников – выполнение всех трех уровней заданий (дополнительные баллы), оценивание участия каждого ученика в групповой работе. |
Оценка – Как вы планируете проверять знания учеников? Каждое задание имеет критерии оценивания, итоги урока собираются в таблицу оценивания. Формативное оценивание позволит корректировать знания и умения учеников. |
Здравоохранение и безопасность. Связи ИКТ. Во время урока постоянная смена деятельности, что позволяет ученикам быть постоянно активными. |
||
|
Модули: Лидерство и, ТиО, ДО, ОцО и ОО, КМ, ИКТ, ОТкУ и ВОУ |
||||
|
Отражение.
1. Были ли задачи урока ясны? 2. Чему сегодня научились ученики? 3. Какая была атмосфера в классе? 4. Хорошо ли прошла работа по дифференцированию? 5. Прошло ли все согласно запланированному времени? 6. Какие изменения в плане я сделала бы и почему? |
Место для оценки вашего урока. |
|||
|
1. Задачи урока были ясны и полностью выполнимы, так целеполагание исходило от них. 2. Определять что является телом отсчета и относительность движения. 3. Ученики с большим удовольствием участвовали на всех этапах урока, атмосфера дружелюбия, сотрудничества. 4. Ученики оказывали друг другу помощь, консультировали, спорили, искали способы решения проблемы 5. Немного не хватило времени для обратной связи, пришлось занять время перемены (2 минуты) 6. Дать опережающее задание для талантливых и одаренных. |
||||
|
Общая оценка. |
|
|||
|
1. Какие две вещи понравились больше всего (учитывая как преподавание, так и обучение)? 1. Способность приводить примеры и наглядно демонстрировать их. 2. Перевод баллов в оценку за урок полностью совпал уровнем знаний учащихся 2. Какие идеи могли бы улучшить урок? 1. Использование ИКТ не только для демонстрации презентации, и при работе в группе 3. Что я узнала из этого урока о своем классе в целом и отдельно об учениках, которые будут со мной на следующем уроке? Оценивание групповой работы было завышенным (в основном 5 и 4). |
||||
Тема 1.2 Динамика. Законы классической механики. Законы Ньютона
Дина́мика (греч. δύναμις «сила, мощь») — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, момент импульса, энергия[1].
Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчета).
Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости.
Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Эрнст Мах считал, что основы динамики были заложены Галилеем[2].
Исторически деление на прямую и обратную задачу динамики сложилось следующим образом[3].
· Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.
· Обратная задача динамики: по заданным силам определить характер движения тела
· Законы Ньютона — законы классической механики, позволяющие записать уравнения движения для любой механической системы.
· Первый закон Ньютона
· Инерциальнои называется та система отсчёта, относительно которой любая, изолированная от внешних воздействий, материальная точка либо покоится, либо сохраняет состояние равномерного прямолинейного движения.
· Первый закон Ньютона гласит: существуют такие системы отсчета, относительно которых тела сохраняют свою скорость постоянной, если на них не действуют другие тела и поля (или их действие взаимно скомпенсировано).
· По сути, этот закон постулирует инерцию тел, то есть их свойство сопротивляться изменению их текущего состояния.
· Второй закон Ньютона
· Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как мерило проявления инерции материальной точки в выбранной инерциальной системе отсчёта (ИСО).
· Второй закон Ньютона утверждает, что в инерциальной системе отсчета ускорение, которое получает материальная точка, прямо пропорционально приложенной к ней силе и обратно пропорционально её массе.
· В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:
· В инерциальной системе отсчета скорость изменения импульса материальной точки равна действующей на неё силе.
· Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности.
· Нельзя рассматривать частный случай второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.
· Третий закон Ньютона
· Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой, а второе — на первое с силой. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
· Сам закон: Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению:
· Выводы
· Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U( | rl - r2 | ). Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:
· Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики.
· Комментарии к законам Ньютона Сила инерции
· Законы Ньютона, строго говоря, справедливы только в инерциальных системах отсчета. Если мы честно запишем уравнение движения тела в неинерциальной системе отсчета, то оно будет по виду отличаться от второго закона Ньютона. Однако часто, для упрощения рассмотрения, вводят некую фиктивную «силу инерции», и тогда эти уравнения движения переписываются в виде, очень похожем на второй закон Ньютона. Математически здесь всё корректно (правильно), но с точки зрения физики новую фиктивную силу нельзя рассматривать как нечто реальное, как результат некоторого реального взаимодействия. Ещё раз подчеркнём: «сила инерции» — это лишь удобная параметризация того, как отличаются законы движения в инерциальнои и неинерциальнои системах отсчета.
· Законы Ньютона и Лагранжева механика
· Законы Ньютона — не самый глубокий уровень формулирования классической механики. В рамках Лагранжевой механики имеется одна-единственная формула (запись механического действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), и из этого можно вывести все законы Ньютона. Более того, в рамках Лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима...
|
Дата: |
|||
|
Тема: Классическая механика. Законы классической механики. Закон всемирного тяготения. |
|||
|
Цель урока: Изучить закон всемирного тяготения. Показать его практическую значимость. Шире раскрыть понятие взаимодействия тел на примере этого закона и ознакомить учащихся с областью действия гравитационных сил. ОбразовательныеСформулировать понятие гравитационных сил, добиться усвоения закона всемирного тяготения . познакомиться с опытным определением гравитационной постоянной РазвивающиеРазвить умение строить самостоятельные высказывания в устной и письменной формах .Развить речь , мышление, воображения .логический подход к решению поставленных задач. Заинтересовать учащихся физикой, |
|||
|
|
Деятельность учителя |
Деятельность обучающихся |
Наглядности |
|
3 мин. |
I. Организационный момент. Приветствует учеников. Для создания психологической атмосферы проводит игру «Путаница».
|
Ученики делятся на группы. Осмысливают поставленную цель. |
|
|
10 мин. |
II. Проверка пройденного материала. По таксономии Блума осуществляет проверку домашней работы. А для начала ответим на вопросы кроссворда , повторим основные понятия кинематики и динамики (у всех учеников на столе карточки с кроссвордом)
1- линия,которую описывает материальная точка в процессе своего движение. 2 - в результате взаимодействия тело приобретает _______ 3 - раздел механики изучающий движение тела. 4 - раздел механики изучающийсилы , под действием которых движутся тела. 5 - этот ученный сформулировал основные законы механики. 6- как называется система отсчета. которая движется равномерно и прямолинейно. 7 -это свойство
тела сохранять свою скорость неизменной при 8 - она возникает при взаимодействии тел. 9 - величины бывают скалярные и______ 10- эта сила возникает при деформации тела.
. Вспомним и ответим на следующие вопросы: 1.
Что называется свободным падением тела?
|
Демонстрируют свои знания, умения по домашней работе. |
Кубик Блума |
|
20 мин. |
III. Актуализация знаний Постановка цели урока. Мотивация изучения материала. По методу «Кластер» осуществляет усвоение нового материала. Работая в группах, ученики самостоятельно изучают новый материал.
Получили слово ГРАВИТАЦИЯ (тяжесть,тяготение) Тысячу лет человечество сетовало на эту силу .,которая не давала возможность строить высотные дома ,преодолевать пропасти ,наблюдать за сходом лавин ,движением рек ,водопадов. Но человек не подозревал ,что эта сила удерживает атмосферу Земли ,воду в морях и океанах, Землю на орбите. А сама Вселенная? И ОНА НЕ УСТОЯЛА БЫ БЕЗ СИЛЫ ВСЕМИРНОГО ТЯГОТЕНИЯ .Человек заставил служить себе эту силу. Раскрыть эту силу помогли такие ученные как: 1- Птоломей –знаменитый александрийский астроном предложил геоцентрическую систему мира, т.е, в центре Земля ,а вокруг нее вращаются Луна, Солнце. 2 - 1515г Николай Коперник – опроверг учение о неподвижности Земли .В центре мира находится Солнце, а вокруг вращаются 5 планет . Земля вращается вокруг Солнца за год и движется вокруг своей оси за сутки. 3 - Джордано Бруно-итальянский мыслитель ,бывший монарх. продолжил учение Коперника, он провозгласил бесконечность Вселенной и был сожжен на костре в1600г 4 - Галилей изготовил телескоп и подтвердил справедливость учение Коперника, но труды Галилея были запрещены церквью и он сам в течении 9 лет считался уздником инквизиции. 5 - Датский ученный Тихо Браге в течении20 лет наблюдал за положением неподвижных звезд и перемещением относительно них планет, видимых с Земли. Он открыл три закона движения планет. Его наблюдения были настолько точны ,что ими пользуются до сих пор. Перед смертью он их передал своему ученику Иоганну Кеплеру.6-Кеплер не смог объяснить ,почему планеты обращаются вокруг Солнца по таким законам. На этот вопрос сумел ответить И. Ньютон, используя законы Кеплера и общие законы динамики “Если я видел дальше ,чем другие, то лишь потому ,что стоял на плечах гигантов”(И .Ньютон ) И.Ньютон с гениальной прозорливостью предположил ,что абсолютно все тела во Вселенной притягиваются друг к другу по одному и тому же закону. И силы -это силы всемирного тяготения или гравитационные силы. И так МЕЖДУ ТЕЛОМ И ЗЕМЛЕЙ ,МЕЖДУ ПЛАНЕТАМИ И СОЛНЦЕМ ,МЕЖДУ ЛУНОЙ И ЗЕМЛЕЙ ДЕЙСТВУЮТ СИЛЫ ВСЕМИРНОГО ТЯГОТЕНИЯ ,обобщенные в закон:
*Все тела притягиваются друг к другу с силой , прямо пропорциональной произведениям масс и обратно пропорциональной квадрату расстояния между ними* Это сила направлена вдоль прямой ,соединяющей материальные точки.Gгравитационная постоянная. Физический смысл: Она численно равна силе с которой притягиваются два тела с массой по 1кг каждое ,находящихся на расстоянии 1м друг от друга. Величина этой силы равна
|
||
|
10 мин. |
IV. Итог урока. Групповая работа метод «Ключевые термины» Учитель на доске вывешивает термины: «Классическая механика. Законы классической механики. Закон всемирного тяготения» Методом мозговой атаки группы дают общую трактовку этих терминов. 1-Во сколько раз изменится сила тяготения ,если при неизменном расстоянии массы тел увеличатся в два раза 2-масса одного тела увеличилась в 4раза, а второго—уменьшилась в2 раза .Как изменилась сила тяготения 3—Что произойдет с силой тяготения двух одинаковых тел, если расстояние между ними увеличить в 4 раза 4—Почему мы не замечаем притяжения окружающих тел друг к другу, хотя притяжение этих тел к Земле наблюдать легко Проводит рефлексию. - Понравился ли вам урок? - Что было трудным для вас? - Что вам больше понравилось?
|
Оценивают работу своих одноклассников. На стикерах записывают свое мнение по поводу урока. |
Дерево Блоба
Стикеры |
|
2 мин. |
Объясняет особенности выполнения домашней работы.
|
Записывают домашнюю работу в дневниках. |
|
· Итог урока:_________________________________________________________
· Положительные стороны урока:__________________________________________________
_____________________________________________________________________________
· Отрицательные стороны урока:__________________________________________________
Тема 1.3 Силы в природе. Закон всемирного тяготения. Невесомость
|
Дата: |
|||||||||||||||
|
Тема:Силы в механике. Силы всемирного тяготения. Закон всемирного тяготения.
|
|||||||||||||||
|
Цель урока:Создание условий для изучения, понимания и практического применения изученного материала по теме «Закон всемирного тяготения». Развитие навыков работы в группах и навыков критического мышления, умения сравнивать, анализировать, делать выводы, решать задачи по теме урока.
|
|||||||||||||||
|
|
Деятельность учителя |
Деятельность обучающихся |
наглядности |
||||||||||||
|
3 мин. |
I. Организационный момент. Приветствует учеников, проверяет готовность к уроку, желает успеха. Для создания психологической атмосферы проводит игру «Мне в тебе нравится» |
Ученики осмысливают поставленную цель. Проводят игру «Мне в тебе нравится» |
Мяч |
||||||||||||
|
5 мин. |
Проверка домашней работы. С помощью метода «Ассоциативная карта» осуществляет проверку домашней работы.
1. Если действий со стороны других тел на данное тело нет или они скомпенсированы, то тело может покоиться, двигаться с постоянной скоростью или двигаться с постоянным ускорением. (–) 2. Формулировка 1 закона Ньютона: существуют системы отсчета, называемые инерциальными, относительно которых свободные тела движутся равномерно и прямолинейно. (+) 3. Тело, на которое не оказывают воздействие другие тела, называется свободным. (+) 4. Инертность – это физическое явление, заключающееся в том, что тело стремиться сохранять свою скорость. (–) 5. Масса – это скалярная величина, характеризующая инертность тела. (+) 6. Инерция – это свойство тел сохранять свою скорость. (–) 7. Второй закон Ньютона: произведение массы на ускорение равно сумме действующих на тело сил. (+) 8. 3 закон Ньютона: силы, с которыми тела действуют друг на друга, не одной природы, равны по модулю и направлены по одной прямой в противоположные стороны. (–) 9. Направление силы совпадает с направлением скорости (–) – Предлагаю посмотреть, что нам ответил детектор лжи.
|
Ученики составляют ассоциативную карту. |
Бумага А4 |
||||||||||||
|
20 мин. |
III. Актуализация знаний 1. Почему? При каких условиях тело совершает равномерное движение или находится в покое?.Ответ дает 1-й закон Ньютона. 2. Почему и при каких условиях тело движется равноускоренно? Ответ дает на этот вопрос 2-й закон Ньютона. 3. Как вообще возникает сила? Ответ на этот вопрос дает 3-й закон Ньютона. 4. От единичного факта – падения яблока – Ньютон приходит к грандиозному обобщению. Какому?
Кажда О притяжении планет к Солнцу говорили многие учёные. 1) Тихо Браге – датский астроном, наблюдал за движением планет. 2) Николай Коперник – создал гелиоцентрическую систему. 3) Иоганн Кеплер – установил законы движения планет вокруг Солнца. 4) Исаак Ньютон – выяснил, как планеты обращаются вокруг Солнца. Первые мысли о природе сил, определяющих движение небесных тел, возникла ещё у Ньютона студента. Согласно легенде, мысль о всемирном тяготении осенила Ньютона в тот момент, когда он, отдыхая в саду, увидел падающее яблоко. Было это или нет, никто точно не знает. Первые вычисления не дали правильных результатов, так как имеющиеся в то время данные о расстоянии между Землёй и Луной были неточными. После того как было уточнено это расстояние, Ньютон опубликовал свой закон. Формулировка закона: Два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними. m1 m2 F = G------------------- r2 F – сила гравитационного притяжения; m1, m2 – массы тел; r – расстояние между телами; G – гравитационная постоянная.
G= 6,67 · 10-11 Н · м2 /кг2 Гравитационная постоянная была измерена Кавендишем с помощью крутильных весов. Установка представляла собой деревянное коромысло с прикреплёнными к его концам небольшими свинцовыми шарами радиусом 5 см и массой 775 г. Оно подвешено на нити из посеребрённой меди длиной 1 метр. К шарам подносят шары большего размера радиусом 20 см и массой 49,5 кг, сделанные также из свинца. В результате действия гравитационных сил коромысло закручивается на некий угол. По углу поворота коромысла можно вычислить гравитационную постоянную. Границы применимости закона: 1. Для шара большого радиуса, взаимодействующего с телами, размеры которых значительно меньше размеров шара. 2. Для тел, имеющих форму шара. 3. Для материальных точек. Открытие закона позволило Ньютону создать теорию движения небесных тел. Но почему все тела притягиваются друг к другу? Ответ на этот вопрос Ньютон не дал. «Причину же свойств силы тяготения я до сих пор не мог вывести из явлений, гипотез же я не измышляю. Довольно того, что тяготение на самом деле существует и действует согласно изложенным нами законам и вполне достаточно для объяснения всех движений небесных тел и моря». Скажите, какое явление подразумевал Ньютон, говоря о море? (приливы и отливы). Как они образуются? Практическая значимость закона. 1. Закон объясняет движение планет. 2. Закон объясняет приливы и отливы. 3. Закон объясняет солнечные и лунные затмения. 4. Закон объясняет движение космических кораблей. Одно из блестящих подтверждений закона произошло спустя 120 лет после смерти Ньютона. Это было открытие планеты Нептун. я группа получает индивидуальное задание, представитель группы защищает флипчарт. Задание для группы Задание № 1 а) Прочитать §32 «Силы всемирного тяготения»; б) Построить устное выступление по плану: - опытные факты, послужившие основанием для разработки теории, – основные понятия и положения теории, - математический аппарат теории и явления, объясняемые данной теорией, - явления и свойства тел, предсказанные теорией.
Задание № 2 а) Прочитать § 32 «Закон всемирного тяготения»; б) Подготовить выступление по плану: - связь между какими величинами выражает закон, - формулировка закона и математическая формула, описывающая его |
Ученики отвечают на вопросы учителя. Демонстрируют свои знания. Ученики выполняют упражнения.
|
учебник
карточки
Таблицы по теме «СПП»
|
||||||||||||
|
10 мин. |
Закрепление урока. Работа в парах по методике «КСО» Что вы поняли по данной теме? Расскажите друг другу, что обозначают придаточные уступки, на какие вопросы 1 группа Силы всемирного тяготения – это силы, с которыми все тела ………. друг к другу. Закон всемирного тяготения гласит, что сила всемирного тяготения двух тел прямо пропорциональна ……….. этих тел и обратно пропорциональна …………………….. между ними, и записывается формулой …………….. . Коэффициентом пропорциональности G называется ……….. , он равен …….. , был измерен английским физиком ……….. , с помощью прибора, называемого ………………………. 2 группа Удивительное свойство гравитационных сил состоит в том, что они сообщают всем телам независимо от их масс одинаковое …………. . Ускорение свободного падения, которое сообщает телам сила притяжения к Земле, равно …….. При перемещении тела от полюса к экватору ускорение свободного падения …………, что объясняется изменением расстояния от центра Земли до поверхности Земли. Первая космическая скорость искусственного спутника Земли равна …………………………. (формула и числовое значение)
|
Ученики обсуждают между собой, отвечают на вопросы своих одноклассников. |
|
||||||||||||
|
5 мин. |
V. Итог урока. Этап рефлексии: Стратегия «Телеграмма» - Что тебе понравилось на уроке? - Что не понравилось? - Насколько трудным был урок? Кратко написать самое важное, что уяснил с урока с пожеланиями соседу по парте и отправить. |
Оценивают работу своих одноклассников, пишут телеграммы. |
фишки
стикеры |
||||||||||||
|
2 мин. |
VI. Домашнее задание. Объясняет особенности выполнения домашней работы. |
Записывают домашнюю работу в дневниках. |
|
||||||||||||
Итог урока:
Положительные стороны урока:
_____________________________________________________________________________
Отрицательные стороны урока:
|
Дата: |
|||
|
Тема:Невесомость. Движение искусственных спутников Земли. |
|||
|
Цель урока:познакомить учащихся с подлинными пушкинскими реликвиями; сформировать речь учащихся. |
|||
|
Ожидаемый результат: познакомятся с музеями А.С. Пушкина. |
|||
|
|
Деятельность учителя |
Деятельность обучающихся |
наглядности |
|
3 мин. |
I. Организационный момент. Приветствует учеников, проверяет готовность к уроку, желает успеха. Для создания психологической атмосферы проводит игру «Рисунок на спине» |
Ученики осмысливают поставленную цель. Проводят игру «Рисунок на спине». Ученики рисуют картины на бумагах. |
Бумага А4 |
|
5 мин. |
II. Проверка домашней работы. С помощью стратегии «Толстые и тонкие вопросы» осуществляет проверку домашней работы. - |
Ученики отвечают на вопросы учителя.
-
|
Карточки |
|
20 мин. |
III. Актуализация знаний. С помощью метода «Путешествие по галерее» осуществляет усвоение нового материала. |
Ученики работают над текстом. Демонстрируют свои знания. На постерах пишут все, что узнали из этого текста. |
Постеры
Учебник
|
|
10 мин. |
IV. Закрепление урока. С помощью метода «Ромашка Блума» проводит закрепление урока. - |
Ученики демонстрируют свои знания. - |
Ромашка Блума |
|
5 мин. |
V. Итог урока. Этап рефлексии: Стратегия «Телеграмма» |
Оценивают работу своих одноклассников. |
фишки стикеры |
|
2 мин. |
VI. Домашнее задание. Объясняет особенности выполнения д/работы. |
Записывают домашнюю работу в дневниках. |
|
Итог урока:___________________________________________________________________
Положительные стороны урока:__________________________________________________
Отрицательные стороны урока:___________________________________________________
Задача №1.. С балкона бросили мяч вертикально вверх со скоростью ? = 9м/с. Найдите положение мяча относительно точки бросания мяча и его скорость спустя время t1=2с от момента бросания. Сопротивление воздуха не учитывать.
Интересным является движение тел, имеющих начальную скорость, направленную горизонтально. Рассмотрим траекторию движения тела, направление скорости и ускорения в каждой точке траектории.
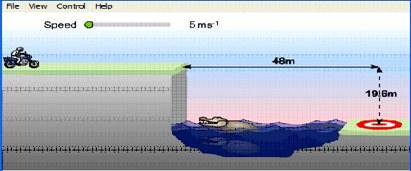
Решим задачу № 2 и проверим правильность решения с помощью действующей модели.
Задача № 2. С какой скоростью должен ехать мотоциклист, чтобы перепрыгнуть водоем?
Чаще всего в жизни встречаются движения тел, брошенных под углом к горизонту. Рассмотрим особенности такого вида движения с помощью модели. Пронаблюдайте движение снарядов и ответьте на вопросы:
1. Как зависит дальность полета от скорости движения снаряда?
2. Как зависит дальность полета снаряда от угла вылета?
3. При каком угле вылета снаряда дальность полета наибольшая?
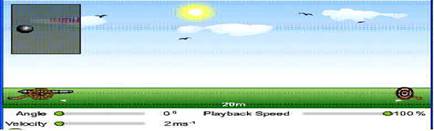
(Обратить внимание учащихся, что наибольшая дальность полета снаряда будет при угле вылета 45о).
Между любыми телами в природе существует сила взаимного притяжения, называемая силой всемирного тяготения (или силами гравитации). Закон всемирного тяготения был открыт Исааком Ньютоном в 1682 году. Когда еще ему было 23 года он высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю.
Закон всемирного тяготения: Все тела
притягиваются друг к другу с силой прямо пропорциональной произведению масс
этих тел и обратно пропорциональной квадрату расстояния между ними.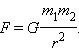
где F — сила всемирного тяготения, m1 , m2 – массы тел, R – расстояние между телами. Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной
Физический смысл гравитационной постоянной: гравитационная постоянная численно равна модулю силы тяготения, действующей между двумя точечными телами массой по 1 кг каждое, находящимися на расстоянии 1 м друг от друга.
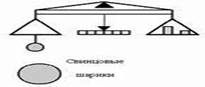 опыт Кавендиша
опыт Кавендиша
G = 6,67· 10-11 Н м2/кг2 . Впервые прямые измерения гравитационной постоянной провел Г. Кавендиш с помощью крутильных весов в 1798г.
Для тел, находящихся вблизи поверхности планет (в частности
Земли) частным случаем проявления силы тяготения является сила тяжести: ![]() где g — ускорение
свободного падения, g = 9,8 м/с2
где g — ускорение
свободного падения, g = 9,8 м/с2
Сила тяжести – это сила, с которой Земля притягивает тело, находящееся на её поверхности или вблизи этой поверхности.
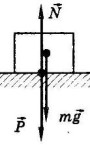
Сила тяжести (mg) направлена вертикально строго к центру Земли; в зависимости от расстояния до поверхности земного шара ускорение свободного падения различно. У поверхности Земли в средних широтах значение его составляет около 9,8 м/с2 . по мере удаления от поверхности Земли gуменьшается.
Вес тела (сила веса) – это сила, с которой
тело действует на![]()
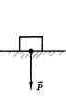 горизонтальную
опору или растягивает подвес. При этом предполагается, что тело неподвижно
относительно опоры или подвеса. Пусть тело лежит на неподвижном
относительно Земли горизонтальном столе. Обозначается буквой Р.
горизонтальную
опору или растягивает подвес. При этом предполагается, что тело неподвижно
относительно опоры или подвеса. Пусть тело лежит на неподвижном
относительно Земли горизонтальном столе. Обозначается буквой Р.
Вес тела и сила тяжести отличаются по своей природе: вес тела является проявлением действия межмолекулярных сил, а сила тяжести имеет гравитационную природу.
Если ускорение а = 0, то вес равен
силе, с которой тело притягивается к Земле, а именно ![]() . [P]
= Н.
. [P]
= Н.
Если другое состояние, то вес меняется:
· если ускорение а не равно 0 , то вес Р = mg — ma (вниз) или Р = mg + ma (вверх);
· если тело падает свободно или движется с ускорением свободного падения, т.е. а = g (рис.2), то вес тела равен 0 (Р=0). Состояние тела, в котором его вес равен нулю, называетсяневесомостью.
В невесомости находятся и космонавты. В невесомости на мгновение оказываетесь и вы, когда подпрыгиваете во время игры в баскетбол или танца.
Домашний эксперимент: Пластиковая бутылка с отверстием у дна наполняется водой. Выпускаем из рук с некоторой высоты. Пока бутылка падает, вода из отверстия не вытекает.
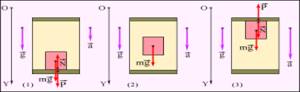 Вес тела движущегося с ускорением
(в лифте)
Вес тела движущегося с ускорением
(в лифте)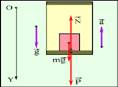 Тело в лифте испытывает
перегрузки
Тело в лифте испытывает
перегрузки
Тема 1.4 Законы
сохранения в механике. Закон сохранения импульса. Реактивное движение. Механическая энергия
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
Рассмотрим какие-либо два взаимодействующих тела, входящих в состав
замкнутой системы. Силы взаимодействия между этими телами обозначим через ![]() и
и ![]() По
третьему закону Ньютона
По
третьему закону Ньютона
![]()
Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны:
![]()
Применим к этим телам второй закон Ньютона:
![]()
Где ![]() и
и ![]() –
импульсы тел в начальный момент времени,
–
импульсы тел в начальный момент времени, ![]() и
и ![]() –
импульсы тел в конце взаимодействия. Из этих соотношений следует, что в
результате взаимодействия двух тел их суммарный импульс не изменился:
–
импульсы тел в конце взаимодействия. Из этих соотношений следует, что в
результате взаимодействия двух тел их суммарный импульс не изменился:
Закон сохранения импульса:
![]()
![]()
Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.
Рис. 1.17.1 иллюстрирует закон сохранения импульса на примере нецентрального соударениядвух шаров разных масс, один из которых до соударения находился в состоянии покоя.
|
|
|
Рисунок 1.17.1. Нецентральное соударение шаров разных масс: 1 – импульсы до соударения; 2 – импульсы после соударения; 3 – диаграмма импульсов |
Изображенные на рис. 1.17.1 вектора импульсов шаров до и
после соударения можно спроектировать на координатные оси OX и OY.
Закон сохранения импульса выполняется и для проекций векторов на каждую ось. В
частности, из диаграммы импульсов (рис. 1.17.1) следует, что проекции
векторов ![]() и
и ![]() импульсов
обоих шаров после соударения на ось OY должны быть одинаковы
по модулю и иметь разные знаки, чтобы их сумма равнялась нулю.
импульсов
обоих шаров после соударения на ось OY должны быть одинаковы
по модулю и иметь разные знаки, чтобы их сумма равнялась нулю.
Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.
При стрельбе из орудия возникает отдача – снаряд
движется вперед, а орудие – откатывается назад. Снаряд и орудие – два
взаимодействующих тела. Скорость, которую приобретает орудие при отдаче,
зависит только от скорости снаряда и отношения масс
(рис. 1.17.2). Если скорости орудия и снаряда обозначить через ![]() и
и ![]() а
их массы через M и m, то на основании закона
сохранения импульса можно записать в проекциях на ось OX
а
их массы через M и m, то на основании закона
сохранения импульса можно записать в проекциях на ось OX
![]()
|
|
|
Рисунок 1.17.2. Отдача при выстреле из орудия |
На принципе отдачи основано реактивное движение.
В ракете при сгорании топлива газы, нагретые до высокой
температуры, выбрасываются из сопла с большой скоростью ![]() относительно
ракеты. Обозначим массу выброшенных газов через m, а массу ракеты
после истечения газов через M. Тогда для замкнутой системы
«ракета + газы» на основании закона сохранения импульса (по аналогии
с задачей о выстреле из орудия) можно записать:
относительно
ракеты. Обозначим массу выброшенных газов через m, а массу ракеты
после истечения газов через M. Тогда для замкнутой системы
«ракета + газы» на основании закона сохранения импульса (по аналогии
с задачей о выстреле из орудия) можно записать:
![]()
где V – скорость ракеты после истечения газов. В данном случае предполагается, что начальная скорость ракеты равнялась нулю.
Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно. На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.
Для получения точной формулы процесс истечения газа из сопла
ракеты нужно рассмотреть более детально. Пусть ракета в момент времени t имеет
массу M и движется со скоростью ![]() (рис. 1.17.3 (1)).
В течение малого промежутка времени Δt из ракеты будет
выброшена некоторая порция газа с относительной скоростью
(рис. 1.17.3 (1)).
В течение малого промежутка времени Δt из ракеты будет
выброшена некоторая порция газа с относительной скоростью ![]() Ракета
в момент t + Δt будет иметь
скорость
Ракета
в момент t + Δt будет иметь
скорость 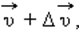 а
ее масса станет равной M + ΔM, где ΔM < 0
(рис. 1.17.3 (2)). Масса выброшенных газов будет, очевидно, равна
–ΔM > 0. Скорость газов в инерциальной системе OX будет
равна
а
ее масса станет равной M + ΔM, где ΔM < 0
(рис. 1.17.3 (2)). Масса выброшенных газов будет, очевидно, равна
–ΔM > 0. Скорость газов в инерциальной системе OX будет
равна ![]() Применим
закон сохранения импульса. В момент времени t + Δt импульс
ракеты равен
Применим
закон сохранения импульса. В момент времени t + Δt импульс
ракеты равен ![]() ,
а импульс испущенных газов равен
,
а импульс испущенных газов равен ![]() .
В момент времени t импульс всей системы был равен
.
В момент времени t импульс всей системы был равен ![]() Предполагая
систему «ракета + газы» замкнутой, можно записать:
Предполагая
систему «ракета + газы» замкнутой, можно записать:
![]()
Величиной ![]() можно
пренебречь, так как |ΔM| << M. Разделив обе
части последнего соотношения на Δt и перейдя к пределу при
Δt→0, получаем:
можно
пренебречь, так как |ΔM| << M. Разделив обе
части последнего соотношения на Δt и перейдя к пределу при
Δt→0, получаем:
![]()
|
|
|
Рисунок 1.17.3. Ракета, движущаяся в
свободном пространстве (без гравитации). 1 – в момент времени t.
Масса ракеты М, ее скорость 2 – Ракета в момент
времени t + Δt. Масса ракеты M + ΔM,
где ΔM < 0, ее скорость |
Величина ![]() есть
расход топлива в единицу времени. Величина
есть
расход топлива в единицу времени. Величина ![]() называется реактивной
силой тяги
называется реактивной
силой тяги ![]() Реактивная
сила тяги действует на ракету со стороны истекающих газов, она направлена в
сторону, противоположную относительной скорости. Соотношение
Реактивная
сила тяги действует на ракету со стороны истекающих газов, она направлена в
сторону, противоположную относительной скорости. Соотношение
![]() выражает
второй закон Ньютона для тела переменной массы. Если газы выбрасываются из
сопла ракеты строго назад (рис. 1.17.3), то в скалярной форме это
соотношение принимает вид:
выражает
второй закон Ньютона для тела переменной массы. Если газы выбрасываются из
сопла ракеты строго назад (рис. 1.17.3), то в скалярной форме это
соотношение принимает вид:
![]()
где u – модуль относительной скорости. С помощью математической операции интегрирования из этого соотношения можно получить формулу Циолковского для конечной скорости υ ракеты:
![]()
где ![]() –
отношение начальной и конечной масс ракеты.
–
отношение начальной и конечной масс ракеты.
Из нее следует, что конечная скорость ракеты может превышать
относительную скорость истечения газов. Следовательно, ракета может быть
разогнана до больших скоростей, необходимых для космических полетов. Но это
может быть достигнуто только путем расхода значительной массы топлива,
составляющей большую долю первоначальной массы ракеты. Например, для достижения
первой космической скорости υ = υ1 = 7,9·103 м/с
при u = 3·103 м/с (скорости истечения газов
при сгорании топлива бывают порядка 2–4 км/с) стартовая масса одноступенчатой
ракеты должна примерно в 14 раз превышать конечную массу. Для
достижения конечной скорости υ = 4u отношение ![]() должно
быть равно 50.
должно
быть равно 50.
Значительное снижение стартовой массы ракеты может быть достигнуто при использовании многоступенчатых ракет, когда ступени ракеты отделяются по мере выгорания топлива. Из процесса последующего разгона ракеты исключаются массы контейнеров, в которых находилось топливо, отработавшие двигатели, системы управления и т. д. Именно по пути создания экономичных многоступенчатых ракет развивается современное ракетостроение.
Механическая работа и
мощность
Кинетическая и
потенциальная энергии
Закон сохранения
механической энергии
Упругие и неупругие
соударения
Элементы гидро- и
аэродинамики
Вращение твердого тела
Законы Кеплера
|
Дата: |
|||||||||||||||||||||||||
|
Тема: Импульс тела. Закон сохранения импульса. |
|||||||||||||||||||||||||
|
Цель урока: обобщение знаний учащихся по теме «Законы сохранения импульса и энергии»; смысл и ценность законов сохранения; Ожидаемый результат: Ученики знают «Законы сохранения импульса и энергии», решают задачи с применением законов, рассматривают проявления законов сохранения энергии и импульса в окружающей среде. . |
|||||||||||||||||||||||||
|
|
Деятельность учителя |
Деятельность обучающихся |
наглядности |
||||||||||||||||||||||
|
3 мин. |
I. Организационный момент. Приветствие. - Повернитесь друг к другу, улыбнитесь. Работать на уроке будет веселее, когда у всех замечательное настроение. |
Ученики осмысливают поставленную цель. Поворачиваются друг к другу и улыбаются. |
|
||||||||||||||||||||||
|
5 мин. |
II. Проверка пройденного материала. По методу «Ромашка Блума» осуществляет проверку Что называется импульсом тела? Обозначение, единицы измерения? - Формулу для расчета импульса тела. - Вы пробегаете 60 м со скоростью 2 м/с. Чему равен ваш импульс тела? - Что называется импульсом силы? Обозначение, единицы измерения? - Что называется энергией? Виды механической энергии, единицы измерения? - Можно изменить энергию? |
Ученики отвечают на уровневые вопросы. |
Ромашка Блума |
||||||||||||||||||||||
|
20 мин. |
III. Актуализация знаний Мозговой штурм. 1.
При
быстром движении магнита над шариком шарик едва сдвигается с места, при
Хотя приведенная формулировка определения импульса силы
характеризует его как физическую величину, формула имеет функцию закона, так
как изменение значения величины в правой части приводит к изменению значения
величины в левой части. [I]=[F]⋅[t]=ньютон⋅секунда=Н⋅с. Направление вектора импульса совпадает с направлением вектора
силы. Структурная схема «Импульс. Закон сохранения импульса»
Следовательно, для характеристики движения тела важно знать его массу и скорость. Поэтому была введена еще одна специальная величина – импульс тела p (количество движения). Импульс тела – векторная физическая величина, равная произведению массы тела на скорость его движения.
Хотя приведенная формулировка определения импульса тела характеризует его как физическую величину, формула также имеет функцию закона, так как изменение значения величины в правой части приводит к изменению значения величины в левой части. За единицу импульса принят такой импульс, при котором тело массой 1 килограмм движется со скоростью 1 метр в секунду. [p]=[m]⋅[υ]=килограмм⋅метр в секунду=(кг⋅м)/с Направление импульса тела совпадает с направлением скорости тела. Понятие импульса было введено в физику французским ученым Рене Декартом, который назвал эту величину «количеством движения». Какова же связь между импульсом силы и импульсом тела? Из второго закона Ньютона следует, что импульс силы равен изменению импульса тела.
Вывод соотношения рассмотрим с помощью логической схемы. (На экран с компьютера проецируется логическая схема «Вывод соотношения между импульсом силы и импульсом тела»).
Пусть m1 - масса первого тела, m2 - масса второго тела; υ01, υ02 - начальные скорости тел, υ1, υ2 - конечные скорости тел. Тогда в замкнутой системе тел векторная сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел между собой.
Вывод закона сохранения импульса также рассмотрим с помощью логической схемы «Вывод закона сохранения импульса». (На экран с компьютера проецируется названная схема) Логическая схема «Вывод закона сохранения импульса»
Замкнутой называется система тел, взаимодействующих только между собой и не взаимодействующих с телами, не входящими в эту систему.
Закон сохранения импульса проявляется в реактивном движении. Реактивное движение – движение тела за счет отделения от него части тела, в результате чего само тело приобретает противоположно направленный импульс. Принцип реактивного движения широко применяется в авиации и космонавтике. Идея использования ракет для космических полетов была выдвинута в начале 20 века русским ученым Константином Эдуардовичем Циолковским, который разработал теорию движения ракет, вывел формулу для расчета их скорости. Задание для группы 1 группа- Практическое применение человеком закона сохранения импульса? 2группа- Вред от практического применения человеком закона сохранения импульса? 3 группа-Ваши предложения по улучшению данной ситуации? (подготовка групп в течении 7 минут) Выступление каждой группы 3-4 мин Проблемный вопрос: Законы Ньютона и законы сохранения импульса и энергии- связаны между собой или нет? (2мин на размышление). Ответы учеников. Работа по карточкам (5 мин)Взаимопроверка (2мин) Выводы: 1) Закон сохранения механической энергии позволяет найти новые, простые пути решения многих задач, но он не указывает о направлении движения отдельных тел, для этого дополнительно нужен закон сохранения импульса; 2) Закон сохранения импульса позволит провести анализ движения тел, даже когда силы взаимодействия между телами неизвестны. |
||||||||||||||||||||||||
|
10 мин. |
IV. Закрепление урока. С помощью приема «З-Х-У» проводит закрепление урока. 1. Верно или неверно? 1) Законы сохранения действуют и тогда, когда законы Ньютона теряют смысл. 2) Законы сохранения применимы ко всем явлениям природы. 3) В законах сохранения импульса и энергии отражено одно из свойств окружающего нас мира – сохранение движения материи. 4) Законы сохранения особого значения не имеют. 5) Применение законов сохранения не всегда обязательно. |
Ученики заполняют таблицу «З-Х-У» |
Таблица «З-Х-У» |
||||||||||||||||||||||
|
5 мин. |
V. Итог урока. Этап рефлексии: Стратегия «Телеграмма» Кратко написать самое важное, что уяснил с урока с пожеланиями соседу по парте и отправить. |
Оценивают работу своих одноклассников, пишут телеграммы. |
фишки
стикеры |
||||||||||||||||||||||
|
2 мин. |
VI. Домашнее задание. Объясняет особенности выполнения домашней работы. |
Записывают домашнюю работу в дневниках. |
|
||||||||||||||||||||||
Итог урока:
Положительные стороны урока: __________________________________________________________________________
Отрицательные стороны урока:___________________________________________________
|
Дата: |
||||||||||||||||||||||||||||
|
Тема: Реактивное движение. Ракеты. |
||||||||||||||||||||||||||||
|
Цель урока:ввести понятие реактивное движение, показать его практическое применение. развивать умение производить наблюдения, делать выводы, обобщать, умение сравнивать, умение выделять главное в тексте. |
||||||||||||||||||||||||||||
|
Ожидаемый результат:увидят практическое применение закона сохранения импульса, научатся применять закон сохранения импульса при решении задач |
||||||||||||||||||||||||||||
|
|
Деятельность учителя |
Деятельность обучающихся |
наглядности |
|||||||||||||||||||||||||
|
3 мин. |
I. Организационный момент. Приветствует учеников, проверяет готовность к уроку, желает успеха. |
Ученики осмысливают поставленную цель. |
|
|||||||||||||||||||||||||
|
5 мин. |
II. Мотивация к изучению нового. С помощью наводящих вопросов, учитель подводит учащихся к теме нового урока.
1. Что такое механическое движение? 2. В каких условиях может возникнуть механическое движение?
4. Запишите формулу импульса тела? 5. Какова единица измерения импульса тела в СИ? 6. При каких условиях можно применять закон сохранения импульса? 7. Что такое замкнутая система? 8. Сформулируйте закон сохранения импульса? |
Ученики отвечают на вопросы учителя. |
|
|||||||||||||||||||||||||
|
20 мин. |
III. Актуализация знаний. Под реактивным движением понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела. При этом возникает так называемая реактивная сила, сообщающая телу ускорение. Пример. Почему приходит в движение надутый воздухом воздушный шарик, если развязать нить, стягивающую его отверстие? Объяснить это явление можно с помощью закона сохранения импульса. Пока отверстие шарика завязано, шарик с находящимся внутри него сжатым воздухом покоится, и его импульс равен нулю. При открытом отверстии из него с довольно большой скоростью вырывается струя сжатого воздуха. Движущийся воздух обладает некоторым импульсом, направленным в сторону его движения. Согласно действующему в природе закону сохранения импульса суммарный импульс системы, состоящей из двух тел — шарика и воздуха в нем, — должен остаться таким же, каким был до начала истечения воздуха, т. e. равным нулю. Поэтому шарик начинает двигаться в противоположную струе сторону с такой скоростью, что его импульс равен по модулю импульсу воздушной струи. Векторы импульсов шарика и воздуха направлены в противоположные стороны. В результате суммарный импульс взаимодействующих тел остается равным нулю. Движение шарика является примером реактивного движения. Реактивное движение происходит за счет того, что от тела отделяется и движется какая-то его часть, в результате чего само тело приобретает противоположно направленный импульс. На том же принципе реактивного движения основано вращение устройства, называемого сегнеровым колесом. Вода, вытекающая из сосуда конической формы через сообщающуюся с ним изогнутую трубку, вращает сосуд в направлении, противоположном скорости воды в струях. Мы видим, что реактивное действие оказывает не только струя газа, но и струя жидкости.
Ракеты. Принцип реактивного движения широко применяется в авиации и космонавтике. В космическом пространстве нет среды, с которой тело могло бы взаимодействовать и тем самым изменять направление и модуль своей скорости. Поэтому для космических полетов могут быть использованы только реактивные летательные аппараты, то есть ракеты. Поскольку до старта импульс ракеты был равен нулю, то по закону сохранения суммарный импульс движущейся оболочки и выбрасываемого из нее газа тоже должен быть равен нулю. Отсюда следует, что импульс оболочки и направленный противоположно ему импульс струи газа должны быть равны друг другу по модулю. Значит, чем с большей скоростью вырывается газ из сопла, тем больше будет скорость оболочки ракеты. Идея использования ракет для космических полетов была выдвинута в начале XX в. русским ученым, изобретателем и учителем Константином Эдуардовичем Циолковским. Циолковский разработал теорию движения ракет, вывел формулу для расчета их скорости, был первым, кто предложил использовать многоступенчатые ракеты.
Составить синквейн Образцы и примеры синквейна учащихся
Реактивное движение - движение, при котором тело изменяет свою скорость, отбрасывая свою часть
|
|||||||||||||||||||||||||||
|
10 мин. |
Закрепление урока. По методу «Поп-корн» проводит закрепление урока. Задание для групп Задача 1. Ракета движется по инерции в космическом пространстве. На ее сопло надели изогнутую трубу выходным отверстием в сторону движения и включили двигатели. Изменилась ли скорость ракеты? Ответ. Таким способом можно остановить ракету и даже заставить ее лететь в обратном направлении. Задача 2. Будет ли вращаться сегнерово колесо в сильно разреженном воздухе под колоколом воздушного насоса? Ответ. Отсутствие воздуха приведет к увеличению скорости вращения колеса. Задача 3. Можно ли двигать парусную лодку, направляя на паруса поток воздуха из мощного вентилятора, находящегося на лодке? Что случится если дуть мимо паруса? Ответ. Когда струя воздуха попадает на парус, лодка остается на месте. Если дуть мимо паруса, лодка будет двигаться. Задача 4. Какую скорость получит модель ракеты, если масса ее оболочки равна 300 г, масса пороха в ней 100 г, а газы вырываются из сопла со скоростью 100 м/с? (Считайте истечение газа из сопла мгновенным.) Ответ. ≈ 33 м/с. |
Ученики демонстрируют свои знания.
|
|
|||||||||||||||||||||||||
|
5 мин. |
V. Итог урока. Этап рефлексии: Стратегия «Телеграмма» |
Оценивают работу своих одноклассников. |
фишки стикеры |
|||||||||||||||||||||||||
|
2 мин. |
VI. Домашнее задание. Объясняет особенности выполнения д/работы. |
Записывают домашнюю работу в дневниках. |
|
|||||||||||||||||||||||||
Итог урока:
Положительные стороны урока:_____________________________________________________________________________
Отрицательные стороны урока:
______________________________________________________________________
|
Механическая энергия и ее виды |
|
Данный вид энергии используется человеком с давних времен, самые простые примеры: лук и стрелы, нож, топор, ветряная мельница, самые разные механизмы (часы, автомобиль) и т.д. Она подразделяется на два типа: кинетическую (движущиеся тела) и потенциальную (покоящиеся тела). Чтобы легче было запомнить, кинетическую называют «Работница», а потенциальную «Лентяйка». Такие олицетворения отлично помогают детям на уроках физики. Энергией движущихся объектов предметы обладают во время полета, падения, ходьбы, езды – в общем, во время движения. Она перестает действовать, когда объект останавливается. Простой пример: бросаем камень, во время полета он обладает кинетической энергией, а когда упадет, кинетическая перейдет в потенциальную. Чем больше сила, тем большей кинетической энергией обладает тело. Она, в свою очередь, делится на два вида: поступательного и вращательного движения. Потенциальной энергией обладают объекты, находящиеся в состоянии покоя и не совершающие механической работы. Слово «потенциальный» происходит от латинского «потенцио», что значит «возможный». Т.е. тело возможно будет двигаться. Чем больше масса объекта и высота, на которую он поднят, тем большей потенциальной энергией он обладает. Механическую энергию, которую еще называют полной, можно найти, сложив потенциальную с кинетической ее «подругой». Потенциальную находят по короткой формуле «mgh», где h – высота, на которую поднят объект, g – постоянный коэффициент жесткости (по-другому, ускорение свободного падения), который равен 9,81 м/с, но обычно для облегчения расчетов это число округляют до 10, а m – масса объекта. Кинетическая энергия равна механической работе, которую совершает тело. Механическую работу находят по формуле A=Fs, где F – сила (находится по формуле «mg», m – масса, g- коэффициент жесткости), а s – расстояние, которое преодолело тело. Покажем, как найти потенциальную, кинетическую и механическую энергии на простом примере. Масса бетонного блока 100 кг. Блок поднят на крюке крана на 40 метров. Коэффициент жесткости равен 10 (округляем для более легких расчетов). Находим кинетическую энергию. Производим такие расчеты: 100 кг x10м/с=1000 Ньютонов - сила блока. 1000Н x 40 = 40000 Джоулей. Теперь вычисляем потенциальную. 100 кг x 10 м/с x 40 = 40000 Джоулей. Сложим 40000+40000 – получим 80000 Дж – полная энергия бетонного блока. |
Тема урока: «Закон сохранения механической энергии»
Цель:
Раскрытие учащимися, в ходе урока, смысла закона сохранения энергии, получение сведений о границах его применимости, приобретение умения описывать преобразования энергии при движении тел и решении задач
Задачи:
Создать условия для формирования умений, обеспечивающих самостоятельное успешное применение закона сохранения механической энергии к решению задач на преобразование энергии придвижении тел
Ожидаймый результате: умений самостоятельно выделять главное, обобщать и систематизировать имеющиеся знания. Развивать умение грамотно выражать свои мысли, строить логически выдержанный рассказ.
Тип урока: урок изучения нового материала.
Формы работы учащихся: работа в парах, фронтальный опрос, объяснение, беседа,
I. Организационный этап
Взаимные приветствия учителя и учащихся; Фиксация отсутствующих,
Организация внимания и внутренней готовности.
В природе много тайн. А физика – это наука о природе, разгадавшая больше загадок мироздания, чем любая другая. И я предлагаю Вам приоткрыть одну из таких тайн. Жажда открытий была главной движущей силой, «действующей» на ученых в их очень трудном, но и самом интересном деле – поиске истины. Есть удивительные законы и один из них мы сегодня рассмотрим.. Многие ученые посвятили жизнь изучению этого закона, а мы с Вами еще посмотрим, как он влияет на нашу жизнь. Попробуем понять, почему он необходим нам в повседневной жизнедеятельности.
Эпиграфом к нашему уроку будут слова немецкого поэта Иоганна Гете: «Опыт – вот учитель жизни вечной».
Для того, чтобы сформулировать тему и цель нашего урока, мы вспомним то, что проходили на прошлом уроке.
|
1.Организация работы (в группах- парах) с дидактическими карточками), направленной на выяснение степени усвоения заданного на дом материала, определение типичных недостатков в знаниях и их причины, ликвидацию обнаруженных недочетов.
- Я раздам карточки 2-x вариантов (дописать название, единицы физических величин, формулы) Ваша задача заполнить пустую строку таблицы для определенной физической величины: работы, потенциальной или кинетической энергии, . 1 группа
2 группа
Постарайтесь выполнить это задание за 5 минут .Взаимопроверка.(1)
|
(1 .Заполняют карточки. Работают (в группах) с предложенными учителем карточками, показывая глубину и осознанность знания данной темы.
III. Этап подготовки учащихся к активному и сознательному усвоению нового материала.
ОПЫТ ПРЕДПОЛОГАЕТ САМОСТОЯТЕЛЬНОСТЬ ПОИСКА ЗНАНИЙ
Я предлагаю вам самим сделать открытие.(опыты делают по группам, а затем делают выводы)
Демонстрационные опыты на кафедре. (учитель рассказывает как проделывать опыт, затем ученики делают выводы)
1 опыт. Опытная установка изображена на рис. 1. В ходе опыта изменяем высоту скатывания шарика, замечаем расстояние, на которое сдвигается брусок, лежащий на горизонтальной плоскости.

Рис. 1.
2. опыт. Опытная установка изображена на рис. 2. Нитяной маятник в начале висит неподвижно. Отмечаем это положение как нулевой уровень потенциальной энергии. Отклоняем маятник на некоторый угол и замечаем, что маятник проходит нулевой уровень и отклоняется в противоположное направление. Что произошло? Почему колебания прекращаются?
 |
Рис. 2.
(ПОКА УЧАЩИЕСЯ ДЕЛАЮТ ОПЫТЫ , УЧИТЕЛЬ ПОДВОДИТ РЕЗУЛЬТАТ ПРОВЕРКИ КАРТОЧЕК)
( Объясняют опыты учащиеся)
Из 1 опыта
Вывод: Чем с большей высоты скатывается шарик, тем большую скорость он приобретает и тем большую работу он может совершить, передвигая брусок.
Из 2 опыта
Вывод: Чем на больший угол отклоняем маятник из нулевого положения, тем большую скорость будет иметь маятник, проходя его. Значит, накопленная потенциальная энергия при отклонении маятника превращается в кинетическую, при прохождении нулевого положения, а затем снова превращается в потенциальную при отклонении в противоположном направлении. Колебания прекращаются потому, что механическая энергия теряется в результате действия не потенциальных сил (силы сопротивления воздуха).
Актуализация знаний
|
Из всех поставленных экспериментов какой вывод можно сделать? Учащиеся (предполагаемый ответ): Энергия не исчезает и не появляется вновь. Она только переходит от одного тела к другому или из одного вида в другой. Откроем тетради и запишем число и тему урока «Закон сохранения механической энергии» . Цель урока: Раскрыть в ходе урока, смысла закона сохранения энергии, получение сведений о границах его применимости, приобретение умения описывать преобразования энергии при движении тел и решении задач
Выразим это математически. Вызвать ученика к доске, остальные учащиеся слушают и делают дополнения к ответам ученика у доски.
Спасибо, ты можешь садиться на место. Ты получил(а) очень важное математическое соотношение, которое носит название математическая запись закона сохранения энергии. Движение мячика могло бы продолжаться сколь угодно долго, если бы не было потерь энергии на сопротивление, т.е. если бы тела взаимодействовали бы только друг с другом и не взаимодействовали бы только силами тяготения или упругости. В данном случае речь идёт о замкнутой системе тел. Если
ввести, что механической энергия можно записать в виде:
Формулировка закона: Полная механическая энергия замкнутой, или изолированной, системы при всех изменениях в системе сохраняется. Делая запись в тетради, ещё раз проследите вывод закона сохранения полной механической энергии. Закон сохранения полной механической энергии является частным случаем всеобщего закона сохранения энергии. Какой вывод вы сделали из прочитанного текста? вывод: если на взаимодействующие тела не действуют внешние силы, то сумма Ер и Ек при любых взаимодействиях тел системы остается постоянной. Записывают формулировку общего закона сохранения энергии
4.К потенциальным силам относятся силы, работа которых не зависит от формы траектории-Fт, Fупр; непотенциальные силы –Fтр, Fтяги 5. Механическая энергия не возникает и не пропадает. Она превращается из одного вида в другой. Полная энергия остается неизменной. |
Обеспечения планируемого уровня знаний
|
Законы не открываются сами по себе, их открывают люди. Вот о таких людях мы и поговорим. Немного истории. Закон сохранения энергии был открыт экспериментальным путем независимо друг от друга тремя учеными: Робертом Майером (немецкий физик и врач), Джеймсом Прескоттом Джоулем (английский физик) и Германом Гельмгольцем (немецкий ученый). Почти за сто лет к открытию этого закона очень близко подошел выдающийся русский ученый Михаил Васильевич Ломоносов. (Доклад ученика) Однажды Роберт Майер услышал от моряка, что во время сильной бури вода нагревается. Эти слова его заинтересовали. А в 1840 году судно, на котором работал Майер судовым врачом, стояло у берегов тропического острова Ява. Одному из матросов от жары стало плохо. Желая помочь, Майер вскрывает ему вену, чтобы уменьшить избыточное кровяное давление (тогда такой прием был распространен). И, к своему ужасу, обнаруживает, что вместо темной крови потекла алая. Испуг врача объяснялся тем, что алая кровь течет в артериях. Своим цветом она обязана высокому содержанию кислорода: это «свежая» кровь, которая только что омыла легкие. А по венам кровь течет уже после того, как она разнесла кислород по телу. В венозной крови кислорода мало, поэтому она темно-красная. Для кровопускания можно вскрывать только вену – кровотечение же из артерии смертельно опасно. К счастью, Майер не ошибся: он вскрыл больному вену. Но ученый задается вопросом: почему же в вене течет алая кровь? Удивление Майера усилилось, когда местные врачи сказали ему, что здесь это – обычное явление: в тропиках венозная кровь у людей такая же алая, как и артериальная. Учитель: А как бы Вы ответили на вопрос с точки зрения физики? Почему у людей, живущих в тропиках, в вене течет алая кровь? Учащиеся (предполагаемый ответ): Температура воздуха почти равна температуре человеческого тела. Организму не нужно расходовать энергию на поддержание температуры тела, поэтому кислород остается в крови – ведь энергию дает именно сгорание кислорода. А это значит, что энергия сохраняется: она только превращается из одного вида в другой, но никогда не исчезает и не появляется из ничего. ДОБАВИТЬ СООБЩЕНИЕ ОГЕЛЬМГОЛЬЦЕ и в вкратце что закон сохранения применяется на ГЭС,ПЭС,ТЭС. 1. историческая справка. 2.ГЭС, ПЭС. 3.ТЭС. 4.Вечный двигатель Об учёном, который впервые сформулировал и обосновал закон сохранения энергии, мы узнаем из доклада «Научная деятельность Германа Гельмгольца». Портрет ученого на доске. Гельмгольц Герман Людвиг Фердинанд Фон (31.08.1821 - 08.09.1894гг.) - один из величайших учёных XIX века. В 1847 году он опубликовал классическую работу “О сохранении энергии”, где изложил философские и физические основания закона сохранения и превращения энергии и дал его математическую формулировку. Работа вызвала большой шум в научных кругах. Аналогичные идеи были выдвинуты рядом других ученых, однако Гельмгольцу принадлежит наиболее четкая формулировка важнейшего закона. Джоуль открыл Закон сохранения энергии для тепловых процессов. За 100 лет до Майера и Гельмгольца М.В.Ломоносов открыл Закон сохранения энергии. В наше время главные виды энергии, за счет которых совершается работа,— это энергия, освобождающаяся при сгорании топлива (угля, нефти, газа), энергия падающей воды и так называемая ядерная энергия. Но ни один из этих видов энергии не подается непосредственно к машинам. На пути к машинам, в которых совершается работа, энергия претерпевает превращения из одной формы в другую (доклады учащихся о ТЭС, ГЭС, ПЭС) 2. Попробуйте, используя свои знания при решении задачи Пример задачи. Найти полную механическую энергию тела массой 100г, которое на высоте 4м имело скорость 36 км/ч.
|
Закрепления нового материала (По методу Аквариум)
(учащиеся выполняют тест, затем проверяют друг у друга и сверяют с экранов ответы)
Тест. Закон сохранения энергии в механике
1. Закон сохранения энергии математически записывается следующим образом:
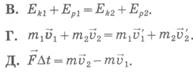
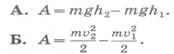
2. Систему называют замкнутой, если...
A. На нее действуют внешние силы.
Б. Сумма внешних сил равна нулю.
B. На нее действуют консервативные силы.
3. Парашютист спускается с постоянной скоростью. Kaкие преобразования энергии при этом происходят?
А. Потенциальная энергия парашютиста преобразуется полностью в его кинетическую энергию
Б. Кинетическая энергия парашютиста полностью преобразуется в его потенциальную энергию
В. Кинетическая энергия парашютиста полностью преобразуется во внутреннюю энергию парашютиста и воздуха
Г. Энергия взаимодействия парашютиста с Землей преобразуется во внутреннюю энергию взаимодействующих тел из-за сил сопротивления воздуха
4. Для системы тел, в которой действует сила тяжести, например для системы «Земля- падающее тело» или «Земля- тело, брошенное вверх» полная механическая энергия системы равна…
А. mgh + mv2/2 Б. kx2/2 + mv2/2 В. mgh2 –mgh1
5. Если между телами системы действует сила упругости, то полная механическая энергия запишется так:
А. mgh + mv2/2 Б. kx2/2 + mv2/2 В. mgh2 –mgh1
САМОПРВЕРКА- ВЗАИМОПРОВЕРКА
Ответ:1.в,2 в,3.а,4.а,5.б
Итог урока
Рефлексивно – оценочный этап
Учитель: Наш урок подходит к концу. Мы с Вами в очень активной форме изучили закон сохранения энергии, вспомнили основные формулы. Вы учились применять свои знания в новых ситуациях. И у Вас это получилось.
1)Какую задачу мы ставили перед собой на уроке?
Ответ:1)Ввели понятие замкнутой изолированной системы, полной механической энергии
Получили закон сохранение механической энергии на опыте и экспериментально
Научится решать задачи с применением закона сохранения механической энергии
- 2)Мы выполнили ее? ответ: 2)Да
- 3)Как именно мы ее выполнили? ответ: 3)Сообщения об открытии закона сохранения механической энергии, о выполнении этого закона в окружающем мире…, решили задачу,
Объявить оценки.
Тема 1.5 Статика. Момент силы. Условия равновесия твердого тела
Статика изучает равновесие тел под действием приложенных к ним сил. Равновесие — это состояние тела, при котором каждая его точка остаётся всё время неподвижной в некоторой инерциальной системе отсчёта. Условием равновесия материальной точки является равенство нулю равнодействующей (т. е. векторной суммы) всех сил, приложенных к точке. В этом случае наша точка будет двигаться равномерно и прямолинейно в произвольной инерциальной системе отсчёта. Значит, система отсчёта, связанная с точкой, также будет инерциальной, и в ней точка будет покоиться. В случае твёрдого тела ситуация сложнее. Прежде всего, важно учитывать точку приложения каждой силы. • Сила тяжести приложена в центре тяжести тела. Для тела простой формы центр тяжести совпадает с центром симметрии. • Силы упругости и трения приложены в точке или в плоскости контакта тела с соприкасающимся телом. Прямая линия, проходящая через точку приложения вдоль вектора силы, называется линией действия силы. Оказывается, точку приложения силы можно переносить вдоль линии её действия — от этого механическое состояние тела не изменится (в частности, равновесие не нарушится). Для равновесия твёрдого тела недостаточно потребовать равенства нулю векторной суммы всех приложенных к телу сил. В качестве примера рассмотрим пару сил — так называются две равные по модулю противоположно направленные силы, линии действия которых не совпадают. Пусть пара сил F~ 1 и F~ 2 приложена к твёрдому стержню (рис. 1). F~ 1 F~ 2 Рис. 1. Пара сил Векторная сумма этих сил равна нулю. Но стержень покоиться не будет: он начнёт вращаться. В данном случае не выполнено второе условие равновесия твёрдого тела. Чтобы его сформулировать, нужно ввести понятие момента силы. Как должна быть направлена линия действия силы, чтобы тело стало вращаться вокруг неподвижной оси? Для начала заметим следующее. • Если линия действия силы параллельна данной оси, то вращения не будет. • Если линия действия силы пересекает данную ось, то вращения не будет. 1 В каждом из этих случаев действие силы вызывает лишь деформацию твёрдого тела. Чтобы началось вращение, линия действия силы и ось вращения должны быть скрещивающимися прямыми. Без ограничения общности можно считать эти прямые перпендикулярными друг другу. Мы всегда можем этого добиться, разложив силу на две составляющие — параллельную и перпендикулярную оси вращения — и отбросив параллельную составляющую как не вызывающую вращения. Поэтому везде далее мы считаем, что все силы, действующие на тело, перпендикулярны оси вращения. Момент силы. Плечо силы — это расстояние от оси вращения до линия действия силы (т. е. длина общего перпендикуляра к двум этим прямым). Момент силы относительно оси вращения — это произведение силы на плечо: M = Fl. Чтобы учесть также направление вращения, вызываемого действием силы, моменту силы приписывают знак. Именно, момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке. Условия равновесия. Если тело имеет неподвижную ось вращения и если алгебраическая сумма моментов всех сил относительно этой оси обращается в нуль, то тело будет находиться в равновесии. Это так называемое правило моментов. Оказывается, что в этом случае обращается в нуль алгебраическая сумма моментов всех сил относительно любой другой оси, параллельной оси вращения. В общем случае, когда твёрдое тело может совершать как поступательное, так и вращатель- ное движение, мы имеем два условия равновесия. 1. Равна нулю векторная сумма всех сил, приложенных к телу. 2. Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной. Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону. Сейчас мы разберём одну достаточно содержательную задачу по статике и посмотрим, как работают наши условия равновесия.
5) Статика - раздел механики, в котором рассматривается равновесие тел.
Момент силы относительно оси вращения - это физическая величина, которая равна произведению силы на ее плечо.
Момент силы вычисляют при помощи
формулы: ![]()
![]()
где F - сила, l — плечо силы.
Плечо силы – это самое короткое расстояние от линии действия силы до оси вращения тела. На рисунке ниже изображено твердое тело, которое может вращаться вокруг оси. Ось вращения этого тела является перпендикулярной к плоскости рисунка и проходит через точку, которая обозначена как буква О. Плечом силы Ft здесь оказывается расстояние l, от оси вращения до линии действия силы. Определяют его таким образом. Первым шагом проводят линию действия силы, далее из т. О, через которую проходит ось вращения тела, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра оказывается плечом данной силы.

Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу необходимо приложить, чтобы получить желаемый результат, то есть один и тот же момент силы (см. рис. выше). Именно поэтому открыть дверь, толкая ее возле петель, намного сложнее, чем берясь за ручку, а гайку отвернуть намного легче длинным, чем коротким гаечным ключом.
За единицу момента силы в СИ принимается момент силы в 1 Н, плечо которой равно 1м — ньютон-метр (Н · м).
Правило моментов
Твердое тело, которое может
вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М1
вращающей его по часовой стрелке, равняется моменту силы М2,
которая вращает его против часовой стрелки: ![]()
Момент силы принято считать положительным, если тело вращается по часовой стрелке, и отрицательным, если — против.
Правило моментов есть следствие одной из теорем механики, которая была сформулирована французским ученым П. Вариньоном в 1687 г.
Пара сил
Если на тело действуют 2 равные и противоположно направленные силы, которые не лежат на одной прямой, то такое тело не находится в равновесии, так как результирующий момент этих сил относительно любой оси не равняется нулю, так как обе силы имеют моменты, направленные в одну сторону. Две такие силы, одновременно действующие на тело, называют парой сил. Если тело закреплено на оси, то под действием пары сил оно будет вращаться. Если пара сил приложена «свободному телу, то оно будет вращаться вокруг оси. проходящей через центр тяжести тела, рисунке б.
Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние l между силами, которое называется плечом пары, независимо от того, на какие отрезки l, и разделяет положение оси плечо пары:
![]()
Момент нескольких сил, равнодействующая которых равна нулю, будет одинаковым относительно всех осей, параллельных друг другу, поэтому действие всех этих сил на тело можно заме нить действием одной пары сил с тем же моментом
|
Равновесие тел - состояние механической системы, в которой тела остаются неподвижными по отношению к выбранной системе отсчета. |
|
|
Равновесие тел
при отсутствии вращения (линии действия сил пересекаются в одной
точке): Векторная сумма всех сил, действующих на тело, равна нулю(алгебраическая
сумма проекций всех сил на любую ось равна нулю). |
|
|
Момент силы - равен произведению силы
на плечо: Плечо силы - расстояние от оси вращения до линии действия силы. (обозначают буквами ℓ или d). Момент силы, вращающий тело против часовой стрелки, считают положительным, по часовой стрелке - отрицательным. |
|
|
Центр масс - точка, через которую должна проходить линия действия силы, чтобы под действием этой силы тело двигалось поступательно. Центр тяжести - точка приложения силы тяжести, действующей на тело. В однородном поле тяготения центр тяжести и центр масс совпадают. |
|
|
Рычаг (Архимед). Разновидности рычага: блок, ворот. Условие равновесия рычага: отношение сил обратно пропорционально отношению плеч этих сил. "Золотое правило механики": выигрывая в силепроигрываешь в расстоянии. |
|
|
Равновесие тел при отсутствии вращения (линии действия сил не пересекаются в одной точке): 1. Векторная сумма всех сил, действующих на тело, равна нулю; 2. Алгебраическая сумма моментов всех сил, действующих на тело, относительно любой точки равна нулю. |
|
|
Т.е. |
|
|
ПАРА
СИЛ: Момент
пары: Пару нельзя уравновесить одной силой (равной величины)! Примеры: завинчивание гайки гаечным ключом, вращение рамки с током в магнитном поле и т.д. |
|
|
Виды равновесия: Устойчивое: При малом отклонении тела от положения равновесия возникает сила, стремящаяся возвратить тело в исходное состояние. |
|
|
Безразличное: При малом отклонении тело остается в равновесии. |
|
|
Неустойчивое: При малом отклонении тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение. |
|
|
В положении устойчивого равновесия тело обладает минимальной потенциальной энергией. При выведении тела из этого положения его потенциальная энергия увеличивается. Если работу над телом совершает только сила тяжести, то в положении устойчивого равновесия центр тяжести тела находится на наименьшей высоте. Все тела стремятся к минимуму потенциальной энергии. (Потенциальная яма). |
|
|
Равновесие тел на опоре: линия действия силы тяжести проходит через площадь опоры (Пизанская башня). Чем ниже центр тяжести, тем более устойчиво равновесие. |
|
Дата: |
|||
|
Тема: Лабораторная работа № 1 «Определение ускорения тела при равноускоренном движении»
|
|||
|
Цель урока:вычислить ускорение, с которым скатывается шарик по наклонному желобу. Для этого измеряют длину перемещения (s) шарика за известное время (t). |
|||
|
|
Деятельность учителя |
Деятельность обучающихся |
наглядности |
|
3 мин. |
I. Организационный момент. Приветствует учеников, проверяет готовность к уроку, желает успеха. |
Ученики осмысливают поставленную цель. |
|
|
5 мин. |
II. Проверка домашней работы. С помощью метода
«Ромашка Блума» осуществляет проверку домашней работы. |
Ученики отвечают на разноуровневые вопросы. |
Ромашка Блума |
|
20 мин. |
III. Актуализация знаний
Средства измерения: измерительная лента, метроном. Материалы: желоб, шарик, штатив с муфтами и лапкой, металлический цилиндр. Порядок выполнения работы 1. Укрепите желоб с помощью штатива в наклонном положении под небольшим углом к горизонту (рис. 35). В нижний конец желоба положите металлический цилиндр. 2. Пустив шарик (одновременно с ударом метронома) с верхнего конца желоба, подсчитайте число ударов метронома до столкновения шарика с цилиндром. Опыт удобно проводить при 120 ударах метронома в минуту. 3. Меняя угол наклона желоба к горизонту и производя небольшие передвижения металлического цилиндра, добейтесь того, чтобы между моментами пуска шарика и его столкновения с цилиндром было четыре удара метронома (три промежутка между ударами). 4. Вычислите время движения шарика. 5. С помощью измерительной ленты определите длину перемещения (s) шарика. Не меняя наклона желоба (условия опыта должны оставаться неизменными), повторите опыт пять раз, добиваясь при этом совпадения четвертого удара метронома с ударом шарика о металлический цилиндр (цилиндр для этого можно немного передвигать). 6. Найдите значение модуля перемещения, а затем рассчитайте среднее значение модуля ускорения g=2S/t2 7. Результаты измерений и вычислений занесите в таблицу
|
Ученики работают над текстом. Демонстрируют свои знания. Выполняют упражнения.
|
учебник
карточки
Таблицы по теме «СПП»
|
|
10 мин. |
IV. Закрепление урока. Работа в парах по методике «Аквариум » |
Ученики обсуждают между собой, отвечают на вопросы своих одноклассников. |
|
|
5 мин. |
V. Итог урока. Этап рефлексии: Стратегия «Телеграмма» Кратко написать самое важное, что уяснил с урока с пожеланиями соседу по парте и отправить. |
Оценивают работу своих одноклассников, пишут телеграммы. |
фишки
стикеры |
|
2 мин. |
VI. Домашнее задание. Объясняет особенности выполнения домашней работы. |
Записывают домашнюю работу в дневниках. |
|
|
№ опыта |
S ,м |
Sср,м
|
Число ударов метронома |
t,с |
g, ’ м/с2 |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 5 |
|
|
|
|
|
Практическая работа №1 « Построение ССС»
Цель работы: научиться строить силовой многоугольник; проверять систему на равновесие.
Задание: построить систему сходящихся сил, пользуясь правилом параллельного переноса и правило треугольника.
Практическая работа №2 по теме "Определение центра тяжести плоских фигур"
Цель работы: научиться определять координаты центра тяжести плоских фигур неправильной геометрической формы методом разделения.
Задание: определить положение центра тяжести фигуры. Номер рисунка, числовые данные различных вариантов указаны в таблицах 1 и 2.
Методические указания
Метод разделения. Если тело удается разделить на такие элементы, центры тяжести которых известны, то положение центра тяжести тела может быть найдено.
Приведем формулы для определения координат центра тяжести однородного плоского тела:
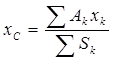
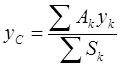
где хс, yс - координаты центра тяжести однородного плоского тела,
xk, yk - координаты центров тяжести элементов этого тела,
Аk - площади этих элементов.
При решении задач на определение центра тяжести однородных тел сложной формы
следует придерживаться следующего порядка:
1. Выбрать метод, который
наиболее применим к данной задаче (метод разбиения или метод дополнения).
2. Разбить сложное тело на
простые элементы, для которых центры тяжести известны.
3. Выбрать оси координат. При
этом необходимо помнить, что: если тело имеет плоскость симметрии, то его центр
тяжести лежит в этой плоскости; если тело имеет ось симметрии, то его центр тяжести
лежит на этой оси; если тело имеет центр симметрии, то его центр тяжести
совпадает с центром симметрии.
4. Определить координаты
центров тяжести отдельных простых тел относительно выбранных осей.
5. Используя формулы,
соответствующие выбранному методу, определить искомые координаты центра тяжести
заданного тела.
Таблица 1
|
Варианты |
1 |
2 |
|
Схема |
а, м |
|
|
1, 11, 21, 31 |
1 |
1,5 |
|
2, 12, 22, 32 |
2 |
2,4 |
|
3, 13, 23, 33 |
3 |
1,8 |
|
4,14, 24, 34 |
4 |
4,0 |
|
5, 15, 25, 35 |
5 |
3,0 |
|
6, 16, 26, 36 |
6 |
1,2 |
|
7, 17, 27, 37 |
7 |
3,0 |
|
8, 18, 28, 38 |
8 |
2,0 |
|
9, 19, 29, 39 |
9 |
1,2 |
|
10, 20, 30, 40 |
10 |
1,6 |
Таблица 2
|
Схема 1 |
Схема 6 |
|
Схема 2 |
Схема 7 |
|
Схема 3 |
Схема 8 |
|
Схема 4 |
Схема 9 |
|
Схема 5 |
Схема 10 |
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.