ПОВТОРЕНИЕ. РЕШЕНИЕ ЗАДАЧ. ГЕОМЕТРИЯ

Уроки 1–2.         Повторение. Решение задач

Цели: вспомнить с учащимися сведения, необходимые при изучении геометрии в 9 классе; повторить некоторые свойства треугольников и четырехугольников; закрепить знания учащихся в ходе решения задач.

Ход уроков

I. Повторение ранее изученного материала.

1. Сформулировать определения медианы, биссектрисы и высоты треугольника.

2. Равнобедренный треугольник и его свойства. Признаки равенства треугольников.

3. Определение средней линии треугольника и ее свойство.

4. Теорема Пифагора и обратная ей теорема.

5. Формула для вычисления площади треугольника.

6. Понятие параллелограмма, свойства и признаки параллелограмма, ромба, прямоугольника.

7. Определение трапеции, виды трапеций.

8. Площадь параллелограмма, площадь трапеции.

II. Решение задач.

Повторение можно организовать в ходе решения следующих задач:

1. В треугольниках ABC и A₁B₁C₁ дано AB = A₁B₁; AC = A₁C₁, точки D и D₁ лежат соответственно на сторонах BC и B₁C₁; AD = = A₁D₁. Докажите, что данные треугольники равны, если AD и A₁D₁: а) высоты; б) медианы.

Примечание. при решении задачи 1 (б) полезно обратить внимание учащихся на прием «удвоения медианы» – откладывание на продолжении медианы AD за точку D отрезка, равного медиане.

2. Докажите, что центр окружности, вписанной в равнобедренный треугольник, лежит на высоте, проведенной к основанию.

3. Докажите, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к его основанию, или на ее продолжении.

4. Докажите, что треугольник является равнобедренным, если две его медианы равны.

5. Докажите, что если в треугольнике две высоты равны, то центр вписанной в него окружности лежит на одной из медиан этого треугольника, а центр описанной окружности – на той же медиане или ее продолжении.

6. Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.

7. Докажите, что отрезки, соединяющие середины противоположных сторон равнобедренной трапеции, взаимно перпендикулярны.

8. Найдите длины отрезков, соединяющих середины сторон трапеции с равными диагоналями, если ее основания раны 7 см и 9 см, а высота равна 8 см.

9. Вычислите площадь треугольника АВС, если AB = 8,5 м, АС = 5 м, высота АN = 4 м и точка N лежит на отрезке BC.

10. Вершины четырехугольника ABCD являются серединами сторон четырехугольника, диагонали которого равны по 6 дм и пересекаются под углом 60°. Вычислите площадь четырехугольника ABCD.

III. Итоги уроков.

Домашнее задание: повторить материал пунктов 15; 17; 18; 19; 20; 30; 42; 43; 44; 45; 46; 49; 50; 51; 52; 53; 54; 55. Решить задачи №№ 167; 163; 502; 513; 515; 517; 524.

 

ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО  ВЕКТОРОВ. (8 часов)

Урок 1.  Тема:Понятие вектора. Равенство векторов

Цели: ввести понятие вектора, его длины, коллинеарных и равных векторов; научить учащихся изображать и обозначать векторы, откладывать от любой точки плоскости вектор, равный данному.

Ход урока

I. Изучение нового материала (лекция). Материал пунктов 76–78 .

1. Понятие векторных величин (или коротко векторов).

2. Примеры векторных величин, известных учащимся из курса физики: сила, перемещение материальной точки, скорость и другие (рис. 240 учебника).

3. Определение вектора (рис. 241, 242).

4. Обозначение вектора – двумя заглавными латинскими буквами со стрелкой над ними, например, , или часто обозначают одной строчной латинской буквой со стрелкой над ней: (рис. 243, а, б).

5. Понятие нулевого вектора: любая точка плоскости также является вектором; в этом случае вектор называется нулевым; обозначают:

 (рис. 243, а).

6. Определение длины или модуля ненулевого вектора . Обозначение: . Длина нулевого вектора = 0.

7. Найти длины векторов, изображенных на рисунках 243, а и 243, б.

8. Выполнить практические задания № 738, 739.

9. Рассмотреть пример движения тела, при котором все его точки движутся с одной и той же скоростью и в одном и том же направлении (из пп. 77 учебника), рис. 244.

10. Ввести понятие коллинеарных векторов (рис. 245).

11. Определение понятий сонаправленных векторов и противоположно направленных векторов, их обозначение (рис. 246).

12. Нулевой вектор сонаправлен с любым вектором.

13. Определение равных векторов: если  и , то .

14. Объяснение  смысла  выражения:  «Вектор  отложен  от  точки А» (рис. 247).

15. Доказательство утверждения, что от любой точки можно отложить вектор, равный данному, и притом только один (рис. 248).

16. Выполнение практического задания № 743.

17. Устно по готовому чертежу на доске решить задачу № 749.

II. Закрепление изученного материала (решение задач).№ 740 (а) на доске и в тетрадях.

№ 744--Уст., № 742, № 745 (выборочно). Устно по заготов. чертежу решить задачу № 746.

6. Доказать прямое утверждение в задаче № 750:

III. Итоги урока.

Домашнее задание: изучить материал пунктов 76–78; ответить на вопросы 1–6, с. 213 учебника; решить задачи №№ 740 (б), 747, 748, 749, 750 (обратное утверждение), 751.

Основные требования к учащимся:  №№ 741–743; 745–752.

Урок 2.  Тема:Сумма двух векторов. Законы сложения векторов.
правило параллелограмма

Цели: ввести понятие суммы двух векторов; рассмотреть законы сложения векторов; научить строить сумму двух данных векторов, используя правило треугольника и параллелограмма.

 

Ход урока

I. Анализ результатов самостоятельной работы.

II. Изучение нового материала (лекция).

Использовать таблицы «Сложение векторов», «Законы сложения», плакаты, графопроектор и др.

1. Рассмотреть пример п. 79 о перемещении материальной точки из точки А в точку В, а затем из точки В в точку С (рис. 249).

Записать: .

2. Понятие суммы двух векторов (рис. 250); правило треугольника .

3. Устно провести доказательство по рис. 251.

4. Записатьв тетрадях:

1) для любого вектора  справедливо равенство ;

2) если А, В и С – произвольные точки, то  (правило треугольника).

5. Выполнить практическое задание № 753.

6.  Рассмотреть законы сложения векторов.

7. Правило параллелограмма (рис. 252) и частное использование этого правила в физике, например при сложении двух сил.

III. Выполнение практических заданий и упражнений.

1. Начертите попарно неколлинеарные векторы . Постройте векторы .

Вопрос учащимся.

– Какие из построенных векторов равны друг другу?

2. Решите № 759 (а) без помощи чертежа. Докажите, что .

3. Упростите выражения:

1) ;    2) .

4. Найдите вектор  из условий:

1) ;    2) .

5. Докажите, что четырехугольник ABCD – параллелограмм, если , где Р и х – произвольные точки плоскости.

.IV. Итоги урока.

Домашнее задание: изучить материал пунктов 79 и 80; ответить на вопросы 7–10, с. 214; решить задачи №№ 754, 759 (б) (без чертежа), 763 (б, в).

 

Урок 3.  Тема: Сумма нескольких векторов

Цели: ввести понятие суммы трех и более векторов; научить строить сумму двух и нескольких векторов, используя правило многоугольника; учить решать задачи.

 

Ход урока

I. Устная работа.

1. Ответить на вопросы 7–10, с. 214 учебника.

2. Устно решить задачи:  1) Найдите вектор  из условия:

а) ;   б) .

2) Упростите выражение:  а) ;   б) .

II. Работа по учебнику. 1. Используя рис. 253, разобрать сложение нескольких векторов.

2. Сумма нескольких векторов не зависит от того, в каком порядке они складываются.

3. По рис. 254 учебника рассмотреть построение суммы шести векторов.

4. В чем заключается правило многоугольника сложения нескольких векторов?

5. Записать в тетради правило многоугольника: если A₁, A₂, .., A_n – произвольные точки плоскости, то . 6. Рассмотреть рис. 255, а, б.

При сложении нескольких векторов сумма данных векторов может быть равна нулевому вектору, если начало первого вектора совпадает с концом последнего вектора.

III. Закрепление изученного материала.

1. Выполнить на доске и тетрадях практическое задание № 755.

2. Решить задачу № 761 (без чертежа).

3. Решить задачу № 762 (а, б).

	Решение а)  = a. Ответ: а.
		б) Найдите .    Ответ: a.

IV. Самостоятельная работа (обучающего характера).

Вариант I

1. Начертите четыре попарно неколлинеарных вектора . Постройте вектор .

2. Упростите выражение: .

Вариант II

1. Начертите пять попарно неколлинеарных векторов . Постройте вектор .

2. Упростите выражение: .

Урок 4.   Тема:Вычитание векторов

Цели: ввести понятие разности двух векторов; научить строить разность двух данных векторов двумя способами; учить решению задач.

Ход урока

I. Анализ результатов самостоятельной работы.

1. Проанализировать характерные ошибки, допущенные в конт-рольной работе.

2. Решить на доске задачи, вызвавшие затруднения у учащихся.

II. Объяснение нового материала.

1. Напомнить учащимся  определение  разности двух чисел: а – b =
= c, то a = c+ b; например, 20 – 14 = 6, то 20 = 6 + 14.

2. Предложить учащимся самим «придумать» определение разности двух векторов.

3. Определение разности двух векторов (формулирует учитель): .

4. Рассмотреть задачу о построении разности двух векторов (рис. 256).

5. Введение понятия вектора, противоположного данному (рис. 257).

Обозначение: вектор, противоположный вектору , обозначается так: –. Очевидно, .

6. Доказательство теоремы о разности векторов: для любых векторов справедливо равенство .

7. Решение задачи о построении разности векторов  другим способом (рис. 258).

III. Решение задач.№ 756. ,№ 762 (г) по готовому чертежу. № 766 устно по рис. 259.

№ 764 (а) на доске и в тетрадях., № 765.,№ 772 на доске и в тетрадях.

IV. Проверочная самостоятельная работа.

Вариант I

Дан прямоугольный треугольник ABC с гипотенузой BC. Постройте вектор  и найдите , если AB = 8 см.

Вариант II

Дан прямоугольный треугольник ABC с гипотенузой АВ. Постройте вектор  и найдите , если BС = 9 см.

Вариант III
(для более подготовленных учащихся)

Дана трапеция ABCD с основаниями АD и BC. Постройте вектор  и найдите , если АD = 12 см, BC = 5 см.

V. Итоги урока.

Домашнее задание: повторить материал пунктов 76–82; вопросы 12, 13, с. 214; решить задачи №№ 757; 762 (д); 764 (б), 767.

Основные требования к учащимся: решать задачи типа №№ 759–771.

Урок 5.  Тема: Произведение вектора на число

Цели: ввести понятие умножения вектора на число; рассмотреть основные свойства умножения вектора на число.

Ход урока

I. Изучение нового материала (лекция).

1. Целесообразно в начале лекции привести пример, подводящий к определению произведения вектора на число, в частности такой:

Автомобиль движется прямолинейно со скоростью . Его обгоняет второй автомобиль, двигающийся со скоростью, вдвое большей. Навстречу им движется третий автомобиль, у которого величина скорости такая же, как у второго автомобиля. Как выразить скорости второго и третьего автомобилей через скорость  первого автомобиля и как изобразить с помощью векторов эти скорости?

Ответ дает рисунок. Естественно считать, что скорость второго автомобиля равна 2 (произведению скорости  первого автомобиля на число 2), а скорость третьего автомобиля равна –2 (произведению скорости  на число –2).

2. Определение произведения вектора на число, его обозначение:  (рис. 260).

3. Записать в тетрадях:

1) произведение любого вектора на число нуль есть нулевой вектор;

2) для  любого  числа  k  и  любого  вектора  векторы  и  коллинеарны.

4. Основные свойства умножения вектора на число:

Для любых чисел k, l  и любых векторов  справедливы равенства:

1°.  (сочетательный закон) (рис. 261);

2°.  (первый распределительный закон) (рис. 262);

3°.  (второй распределительный закон) (рис. 263).

Примечание. Рассмотренные нами свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях.

Например:

II. Закрепление изученного материала.

1. Выполнить практические задания № 776 (б; г; д), 777. 2. Решить задачи № 779, 781 (а; в).

Решение:  Дано:

а)

в)

3. Решить задачу № 780 (б).

III. Итоги урока.

Домашнее задание: изучить материал пункта 83; ответить на вопросы 14–17, с. 214; решить задачи №№ 775, 776 (а, в, е), 781 (б), 780 (а).

Урок 6. Тема: Решение задач. Произведение вектора на число

Цели: закрепить изученный материал в ходе решения задач; развивать логическое мышление учащихся.

Ход урока

I. Устная работа. По заранее заготовленным чертежам на доске устно решить задачи:

1. На рисунке 1 ABCD – параллелограмм, O – точка пересечения диагоналей.  Выразите  через  векторы  и  векторы: а)  б)  где  М – точка  на стороне BC, такая, что МВ : MC = 3 : 2; в)  где K – точка на стороне AD, такая, что АK : KD = 1 : 3; г)  где N – точка на диагонали AC, такая, что ON = NC.

2. На рисунке 2 ABCD – трапеция, О – точка пересечения диагоналей, ВС || AD, AD = 2BC. Выразите через векторы  и  векторы: а)  б)

        

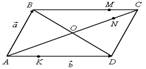
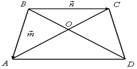
Рис. 1                                                                 Рис. 2    

II. Решение задач.1. решить задачу № 782 на доске и в тетрадях.

Решение: Из треугольника ECD (рис. 3) найдем по правилу вычитания векторов:

 тогда

Из треугольника ABG по правилу сложения векторов имеем

 отсюда

2. решить задачу № 802 на доске и в тетрадях.

III. Проверочная самостоятельная работа. Вариант I1. Начертите два неколлинеарных вектора  и так,  что  = 3 см,  = 2 см. Постройте

2. Четырехугольник KMNP – параллелограмм. Выразите через векторы  и  векторы  и , где А – точка на стороне PN, такая, что PA : AN = 2 : 1, B – середина отрезка MN.

Вариант II

1. Начертите два неколлинеарных вектора  и  так, что  = 2 см,  = 3 см. Постройте вектор

2. В параллелограмме ABCD точка M – середина стороны CD; N – точка на стороне AD, такая, что AN : ND = 1 : 2. Выразите векторы  и  через векторы  и .

IV. Итоги урока.

Домашнее задание: повторить материал пунктов 76–83; ответить на вопросы 1–17, с. 213–214 учебника; решить задачи №№ 783 и 804.

Урок 7.  Тема:Применение векторов к решению задач

Цели: на конкретных примерах показать применение векторов при решении геометрических задач; развивать логическое мышление учащихся, учить решать задачи.

Ход урока

I. Анализ результатов самостоятельной работы.

1. Указать ошибки учащихся при выполнении работ.

2. Решить задачи, вызвавшие затруднения у учащихся.

II. Повторение изученного материала.

1. Ответить на вопросы на с. 213–214.

2. Вспомнить основные правила действий с векторами.

3. Решить задачи на доске и в тетрадях:

    1) Упростите выражение

    2) Найдите вектор  из условия

4. Записать в тетрадях таблицу перевода с «геометрического» языка на «векторный»:

III. Работа по учебнику. 1. Векторы могут использоваться для решения геометрических задач. Рассмотрим вспомогательную задачу.

2. Разобрать решение задачи 1 на с. 208 учебника по рис. 264.

IV. Решение задач.

1. Решить задачу 2. Точки M и N – середины сторон AB и CD  четырехугольника ABCD. Докажите, что  

2. Решить задачу 3. Точка С лежит на отрезке AB, причем АС : СВ =
= 2 : 3. Докажите, что для любой точки О справедливо равенство

Примечание. Задача 3 является частным случаем более общей задачи 806.

3. Решить задачу № 784.,№ 786 на доске и в тетрадях.

V. Итоги урока.

Домашнее задание: повторить материал пунктов 76–84; разобрать решения задачи 2 из п. 84 и задачи № 788 и записать в тетрадь; решить задачу № 785.

 

 

Урок 8. Тема:Средняя линия трапеции

Цели: ввести понятия средней линии трапеции; доказать теорему о средней линии трапеции с помощью векторов; упражнять учащихся в решении задач.

Ход урока

I. Проверка усвоения учащимися материала. 1. Устно ответить на вопросы:

1) Какие векторы называются коллинеарными? Изобразите на рисунке сонаправленные векторы  и  и противоположно направленные векторы  и .

2) Какой вектор называется произведением данного вектора на данное число?

3) Могут ли векторы  и  быть неколлинеарными?

4) Сформулируйте основные свойства умножения вектора на число.

2. Решить задачу на доске и в тетрадях по готовому чертежу:

Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM : MD = BN : NC = = 3 : 4. Докажите, что середины отрезков AB, MN и CD лежат на одной прямой.

II. Объяснение нового материала.1. Определение трапеции. Виды трапеций.

2. Определение средней линии трапеции.

3. Доказательство теоремы о средней линии трапеции (проводит сам учитель).

III. Закрепление изученного материала (решение задач). № 793., № 795.№ 799 на доске и в тетрадях.

IV. Проверочная самостоятельная работа.

Вариант I

Точка K делит отрезок MN в отношении MK : KN = 3 : 2. Выразите вектор  через векторы  и , где A – произвольная точка.

Вариант II

Точка A делит  отрезок  EF в отношении EA : AF = 2 : 5. Выразите вектор  через векторы  и , где K – произвольная точка.

V. Итоги урока.

Домашнее задание: изучить материал пункта 85; ответить на вопросы 18–20, с. 214 учебника; решить задачи №№ 787, 794, 796.

Основные требования к учащимся:

В результате изучения параграфа учащиеся должны знать, какой вектор называется произведением вектора на число; уметь формулировать свойства умножения вектора на число; знать, какой отрезок называется средней линией трапеции; уметь формулировать и доказывать теорему о средней линии трапеции; уметь решать задачи типа №№ 782–787; 793–799.

 

 

МЕТОД КООРДИНАТ (10 часов)

Урок 1.  Тема: Разложение вектора по двум данным неколлинеарным векторам

Цели: доказать лемму о коллинеарных векторах и теорему о разложении вектора по двум неколлинеарным векторам и закрепить их знание в ходе решения задач.

Ход урока

I. Анализ результатов самостоятельной работы.

II. Устная работа.

1. Устно решить задачи  по  заранее  заготовленному  чертежу на доске:

Дан параллелограмм ABCD с диагоналями AC и BD, пересекающимися в точке О, а также отрезки MP и NQ, соединяющие соответственно середины сторон AB и CD, BC и AD. Требуется выразить:

1) вектор  через вектор ; 

 2) вектор  через вектор ;

3) вектор  через вектор ;  

4) вектор  через вектор .

2. Вопрос  учащимся:

можно ли для любой пары коллинеарных векторов подобрать такое число, что один из векторов будет равен произведению второго вектора на это число?

III. Изучение нового материала.

1. Формулировка леммы о коллинеарных векторах. Для понимания учащимися формулировки леммы полезно обсудить, во-первых, почему важно условие  и,  во-вторых,  будет  ли верно утверждение, если рассматривать произвольные (в том числе и неколлинеарные) ненулевые векторы.

2. Доказательство леммы.

3. Решить задачу по рисунку параллелограмма ABCD на доске (тем самым подвести учащихся к мысли о возможности выражения вектора через два данных неколлинеарных вектора):

Точки M и Q – середины сторон AB и AD параллелограмма ABCD. Выразите:

1) вектор  через векторы  и ;

2) вектор  через векторы  и ;

3) вектор  через векторы  и ;

4) вектор  через векторы  и .

4. Рассмотреть теорему о разложении вектора по двум данным неколлинеарным векторам, в ходе ее доказательства полезно обратить внимание на роль леммы в доказательстве.

IV. Закрепление изученного материала (решение задач).

1. Решить задачи № 911 (а, б); № 912 (б, в).

2. Решить задачи № 915 (по готовому чертежу) и № 916 (а, б).

V. Итоги урока.

Задание на дом: изучить материал пункта 86; решить задачи №№ 911 (в, г), 912 (ж, е, з), 916 (в, г).

 

Урок 2. Тема: Координаты вектора

Цели: ввести понятие координат вектора и рассмотреть правила действий над векторами с заданными координатами.

Ход урока

I. Проверка домашнего задания.

1. Устно решить задачи:

1) назвать числа х и у, удовлетворяющие равенству: ; ;    2) задача № 913.

2. На доске двое учащихся решают задачи №№ 911 (в) и 912 (и, к).

II. Изучение нового материала.

1. Напомнить задание прямоугольной системы координат и начертить ее.

2. Ввести координатные векторы  и  (рис. 275).

3. Нулевой вектор можно представить в виде ; его координаты равны нулю: (0; 0).

4. Координаты равных векторов соответственно равны.

5. Рассмотреть правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число (доказательства указанных правил учащиеся могут рассмотреть самостоятельно).

6. Записать в тетрадях правила:

 и  – данные векторы

1) ;

2) ;

3) .

III. Закрепление изученного материала (решение задач).№ 917.

 Устно по рис. 276 , № 918.,  № 919 (сам).№ 920 (а, в) ,Устно  № 922–925, используя правила, записанные в тетрадях.,№ 927 без доказательства:

1) Если два вектора коллинеарны, то координаты одного вектора пропорциональны координатам другого: если  коллинеарен вектору , то x₁ : x₂ = y₁ : y₂.

2) Если координаты одного вектора пропорциональны координатам другого вектора, то эти векторы коллинеарны.

7. Решить задачу № 928.

IV. Самостоятельная работа контролирующего характера.

Вариант I.№ 912  (а, г);  № 920  (г);  № 988  (а, б);  № 921  (а, в);№ 914 (а).

Вариант II.№№ 912 (в, д); 920 (д); 988 (в, г); 921 (б, г); 914 (б).

V. Итоги урока.

Домашнее здание: подготовиться к устному опросу по карточкам, повторить материал пунктов 76–87; ответить на вопросы 1–20, с. 213–214 и на вопросы 1–8, с. 249 учебника; решить задачи №№ 798, 795; 990 (а) (для векторов  и ).

Урок 3. Тема: Связь между координатами вектора и координатами его начала и конца.Простейшие задачи в координатах

Цели: рассмотреть связь между координатами вектора и координатами его начала и конца; разобрать задачи о нахождении координат середины отрезка, о вычислении длины вектора по его координатам и нахождении расстояния между двумя точками.

Ход урока

I. Анализ результатов контрольной работы.

1. Указать ошибки, сделанные учащимися при выполнении работы.

2. Решить на доске задачи, вызвавшие затруднения у учащихся.

II. Изучение нового материала (лекция).

1. Рассмотреть по  учебнику  рис. 277  и  рис. 278  и  ввести  понятие радиус-вектора .

а) координаты точки М равны соответствующим координатам ее радиус-вектора;

б) каждая координата вектора равна разности соответствующих координат его конца и начала:

џ Устно решить задачу № 934.

2. Введение системы координат дает возможность изучать геометрические  фигуры  и  их  свойства  с  помощью  уравнений  и  неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат.

3. Рассмотрим три вспомогательные задачи.

1) Координаты середины отрезка.

Используя формулу  из  п. 84 (1)  и координаты векторов  записать равенство в координатах:  отсюда x = ; y = .

Вывод: каждая координата середины отрезка равна  полусумме соответствующих координат его концов.

џ Устно решить задачу № 936.

2) Вычисление длины вектора по его координатам.

Используя рис. 280 учебника, вывести формулу , если   џ № 938.Устно

3) Расстояние между двумя точками.

Пусть точка M₁ (x₁; y₁) и точка M₂ (x₂; y₂); тогда вектор  (x₂ – x₁;
y₂ – y₁); следовательно, длина этого вектора может быть найдена по формуле  но = d, таким образом, расстояние d между точками M₁ (x₁; y₁) и M₂ (x₂; y₂) выражается формулой

d =

џ Решить задачу № 940 (а, б) на доске и в тетрадях.

III. Закрепление изученного материала (решение задач).

1. Решить задачу № 939. 2. Решить задачу № 941 на доске и в тетрадях.

IV. Итоги урока.

Задание на дом:  изучить  материал  пунктов  88,  89;  решить  задачи №№ 935, 952.

Урок 4.  Тема:Простейшие задачи в координатах.  Решение задач

Цели: закрепить знания учащихся в ходе решения задач; учить решать задачи в координатах.

Ход урока

I. Повторение изученного материала.

1. Двое учащихся по карточкам работают у доски:

Карточка 1. 1) Вывести формулы координат середины отрезка.             2) Решить задачу № 942.

Карточка 2. 1) Вывести формулу расстояния между двумя точками.      2) Решить задачу № 937.

2. С остальными учащимися проводится устная работа по решению задач:

1) Найдите координаты вектора , равного разности векторов  и , если (–5; 6), (0; –4).

2) Найдите координаты вектора , равного сумме векторов  и , если (3; 7), (4; –5).

3) Найдите координаты середины отрезка DK, если D (–6; 4), K (2; –8).

4) Найдите длину отрезка CP, если С (3; –2), P (–5; 4).

5) Найдите длину вектора , равного , если (5; 0) и (0; –12).

6) Найдите координаты вектора 3, если (4; –2); вектора –2, если (–2; 5).

II. Решение задач.  № 947 (а).  № 946 (б).

Решение

M₁ (–1; x) и M₂ (2x; 3); M₁M₂ = d = 7. Найти x.  d = ; (2x + 1)² + (3 – x)² = 7²;

4x² + 4x + 1 + 9 – 6x + x² = 49;  5x² – 2x – 39 = 0;     D = b² – 4ac = 4 + 780 = 784;

     Ответ: –2,6; 3.

3. Решить задачу № 948 (б) на доске и в тетрадях.

Решение

Пусть точка М (0; y) лежит на оси ординат; по условию МС = MD;

(4 – 0)² + (–3 – y)² = (8 – 0)² + (1 – y)²;  16 + 9 + 6y + y² = 64 + 1 – 2y + y²;  8y = 40;  y = 5.

Значит, точка М (0; 5).     Ответ: (0; 5).

4. Решить задачу № 950 (б) на доске и в тетрадях.

5. Решить задачу № 951 (а).

Решение

AB == 4;     CD == 4;

BC == 2;     AD ==2.

Так как AB = CD = 4 и BC = AD = 2, то по II признаку параллелограмма ABCD – параллелограмм. Найдем диагонали АС и BD параллелограмма ABCD: AC =

BD =

Если диагонали равны AC = BD, то ABCD – прямоугольник.

S = AD ∙  AB = 2 ∙  4 = 8.

Ответ: 8.

III. Итоги урока.

Домашнее здание: повторить материал пунктов 88 и 89; решить задачи №№ 947 (б), 949 (а), 951 (б), 953.

 

 

Урок 5. Тема: Уравнение линии на плоскости.  Уравнение окружности

Цели: познакомить учащихся с понятием уравнения линии на плоскости; вывести уравнение окружности и научить записывать уравнение окружности.

Ход урока

I. Математический диктант (10–15 мин).

Вариант I.  1. Найдите координаты середины отрезка AB, если A (–2; 3), B (6; –3).

2. Найдите длину отрезка EH, если E (–3; 8), H (2; –4). 

3. Какая фигура состоит из множества всех точек плоскости, каждая из которых равноудалена от двух данных точек?

4. Принадлежит ли точка A (–6; 2) графику функции y = – 0,5x?

5. Функция задана уравнением y = 2x – 3. Какая линия служит графиком этой функции?

6. На окружности радиуса 7 см даны точки А и В, расстояние между которыми равно 13 см. лежит ли центр окружности на прямой АВ?

7. Вершины треугольника ABC имеют следующие координаты: А (8; –3); В (5; 1); С (12; 0). Докажите, что B = C.

Вариант II.  1. Найдите координаты середины отрезка CD, если C (3; –4), D (–3; 6).

2. Найдите длину отрезка KB, если K (–6; –3), B (2; 3). 

3. Прямая l является серединным перпендикуляром к основанию AB треугольника ABC и проходит через вершину C. Определите вид треугольника ABC.

4. Принадлежит ли точка В (2; –8) графику функции y = – 4x?

5. Функция задана уравнением y = 5 – x. Какая линия служит графиком этой функции?

6. Какой фигурой является множество точек, равноудаленных от данной точки?

7. Вершины  четырехугольника  ABCD  имеют  следующие  координаты: А (–3; –1); В (1; 2); С (5; –1), D (1; –4). Докажите, что этот четырехугольник – ромб.

II. Объяснение нового материала.

1. Введение уравнения окружности радиуса r с центром С в заданной прямоугольной системе координат (рис. 286):

(x – x₀)² + (y – y₀)² = r²,

где C (x₀; y₀). Уравнение окружности радиуса r с центром в начале координат О (0; 0) имеет вид: x² + y² = r².

2. Не любое уравнение второй степени с двумя переменными задает окружность. Например, уравнение 4х² + у² = 4 в прямоугольной системе координат не окружность, а эллипс (с этой фигурой учащиеся знакомились в курсе черчения), уравнение х² + у² = 0 задает единственную точку – начало координат, а уравнению х² + у² = –4 не удовлетворяют координаты ни одной точки, поэтому это уравнение не задает никакой фигуры.

III. Закрепление изученного материала :. решить задачу № 959 (а, б, д).№ 960.У, № 961.

№ 964.

Решение:а) x = 3, тогда (3 – 3)² + (y – 5)² = 25;  y² – 10y + 25 = 25;

y² – 10y = 0;  y ∙  (y – 10) = 0;  y = 0 или y = 10. Точки А (3; 0) и В (3; 10).

б) y = 5, тогда (x – 3)² + (5 – 5)² = 25;  x² – 6x + 9 = 25;

x² – 6x – 16 = 0;   x₁ = 8;   x₂ = –2; точки С (–2; 5) и D (8; 5).

Решить задачу № 966 (в, г).      Разобрать решение задачи по учебнику на с. 243.

IV. Итоги урока.

Домашнее задание: изучить материал пунктов 90, 91; вопросы 15–17; решить задачи №№ 962, 963, 965, 966 (а, б), 1000.

Урок 6. Тема: Уравнение окружности. Решение задач

Цели: закрепить знания учащихся в ходе решения задач; развивать логическое мышление учащихся.

Ход урока

I. Проверка домашнего задания.

1. Результаты математического диктанта. Указать ошибки, сделанные учащимися.

2. На доске один ученик выводит уравнение окружности.

3. С остальными учащимися проверяется решение домашних задач.

II. Выполнение упражнений. 1. Решить задачу:

Напишите уравнение окружности с центром в точке А (0; 4), проходящей через точку D (–6; –4).

Решение

Центр окружности имеет координаты А (0; 4). Найдем радиус окружности r = AD по формуле: d =.  r = AD == 10;  r = 10.

Значит, искомое уравнение окружности имеет вид:

(x – 0)² + (y – 4)² = 10²;  x² + (y – 4)² = 100.          Ответ: x² + (y – 4)² = 100.

2. Решить задачу № 969 (а) на доске и в тетрадях.

3. Решить задачу № 970.

Решение:  Центр окружности лежит на оси абсцисс, то координаты центра D (x; 0);  радиус равен r = 5. Окружность проходит через точку А (1; 3), тогда AD = r, поэтому (x – 1)² + (3 – 0)² = r² = 5², (x – 1)² + 9 = 25;     x² – 2x – 15 = 0;   x₁ = –3;   x₂ = 5.

Следовательно, координаты центров окружностей D₁ (–3; 0) и D₂ (5; 0). Существует две таких окружности:  (x + 3)² + y² = 25 и (x – 5)² + y² = 25.

4. Решить задачу № 971 на доске и в тетрадях.

Решение

Центр  окружности  лежит  на оси ординат, значит, координаты центра С (0; y). По условию, окружность проходит через точки А (–3; 0) и В (0; 9), значит, расстояния АС = ВС = r радиусу:

(0 + 3)² + (y – 0)² = (0 – 0)² + (y – 9)²;

9 + y² = y² – 18y + 81;  18y = 72;  y = 4.

Следовательно, центр окружности имеет координаты С (0; 4).

Найдем радиус окружности:  r² = AC² = (0 + 3)² + (4 – 0)² = 9 + 16 = 25;  r = 5. Напишем уравнение окружности:      (x – 0)² + (y – 4)² = 5²; то есть x² + (y – 4)² = 25.

5. Решить задачу № 1002(а) на доске и в тетрадях (решение задачи объясняет учитель).

III. Итоги урока.

Домашнее задание:  повторить  материал  пунктов 86–91; решить задачи №№ 969 (б), 981 (есть решение в учебнике), 1002 (б).

 

 

 

 

Урок 7.  . Тема: Уравнение прямой

Цели: вывести уравнение прямой и показать, как можно использовать это уравнение при решении геометрических задач; развивать логическое мышление учащихся.

Ход урока

I. Самостоятельная работа (контролирующая, 10–15 мин).

Вариант I.  Решить задачи № 959 (г), 968, 960 (б).

Вариант II.   Решить задачи № 959(в), 967, 960 (в).

II. Изучение нового материала.

1. Уравнением  любой  прямой в прямоугольной системе координат является уравнение первой степени с двумя переменными (уравнение прямых, параллельных осям координат, также можно считать уравнением с двумя  переменными,  например,  уравнение  x = x₀  можно  записать  в виде  x + 0y = x₀) и, наоборот, любое уравнение первой степени с двумя переменными задает прямую.

2. Вывести уравнение данной прямой l в заданной прямоугольной системе координат (рис. 287): ax + by + c = 0.

3. Вывести уравнение прямой l, проходящей через точку M₀ (x₀; y₀) и параллельной оси ОX (рис. 288) y = y₀.

4. Ось OX имеет уравнение y = 0, а ось OY – уравнение x = 0.

III. Закрепление изученного материала (решение задач).

1. Учитель объясняет решение задачи:

напишите  уравнение  прямой,  проходящей  через  две  данные  точки Р (2; 1) и Q (–3; –1).

Решение

Уравнение прямой PQ имеет вид ax + by + c = 0. Так как точки P и Q лежат на прямой PQ, то их координаты удовлетворяют этому уравнению:

2cx – 5cy + c = 0 |: c  0,  тогда прямая PQ задана уравнением 2x – 5y +
+ 1 = 0.

Ответ: 2x – 5y + 1 = 0.

2. № 972 (а), с. 245.  3. Решить задачу № 973 на доске и в тетрадях. 4. Решить задачу № 975.

6. Решить задачу № 977.  7. Самостоятельное решение учащимися задачи № 978.

8. Решить устно задачи:   1) Окружность задана уравнением (x – 1)² + y² = 9. Назвать уравнение прямой, проходящей через ее центр и параллельной оси ординат.

Решение

Центр О (1; 0) и параллельная оси OY прямая x = 1.

2) Окружность задана уравнением (x + 1)² + (y – 2)² = 16. Назвать уравнение прямой, проходящей через ее центр и параллельной оси абсцисс.

Решение:  Центр А (–1; 2); прямая y = 2 параллельна оси OX.

IV. Итоги урока.

Домашнее задание: повторить материал пунктов 86–91; изучить материал пункта 92; вопросы 1–21, с. 249; решить задачи №№ 972 (б), 979; записать в тетрадях и разобрать решение задачи № 984 (с. 248 учебника); подготовиться к устному опросу по карточкам.

 

 

Уроки 8–9.  Тема: решение задач

Цели: закрепление знаний и умений учащихся по материалу главы; повторение и обобщение изученного материала; развитие логического мышления учащихся при решении задач.

Ход уроков

I. математический диктант (15 мин).

Вариант I.1.Лежит ли точка А(2; –1)на  окружности, заданной  уравнением  (х – 2)² + (у – 3)² = 25?

2. Напишите уравнение окружности, если ее центр – точка (4; 5), а радиус равен 3.

3. Напишите уравнение прямой, проходящей через точку М (3; –2) и параллельной оси ординат.

4. Напишите уравнение окружности с центром в начале координат, если она проходит через точку С (–2; 3).

5. Напишите уравнение прямой, проходящей через две точки М (–2; –1) и N (3; 1).

6. Найдите длину вектора (–12; 5).

7. Найдите координаты середины отрезка PQ, если P (5; –3); Q (3; –7).

8. Найдите координаты вектора , если А (2; –5), В (–3; 4).

Вариант II. 1. Лежит  ли  точка  А (2; –1)  на  прямой,  заданной  уравнением   2х – 3у – 7 = 0?

2. Напишите уравнение окружности, если ее центр – точка (4; 5), а радиус равен 2.

3. Напишите уравнение прямой, проходящей через точку N (–2; 3) и параллельной оси абсцисс.

4. Напишите уравнение прямой, проходящей через начало координат и точку D (3; –2).

5. Напишите уравнение окружности с центром в точке Р (–2; –1), если она проходит через точку

Q (1; 3).

6. Найдите расстояние между точками А (–1; 3) и В (2; –1).

7. Найдите координаты вектора , равного сумме векторов  и , если (–12; 5), (7; –3).

8. Найдите координаты вектора , если С (–1; 6), D (3; –2).

II. решение задач.  1. Устно решить задачу № 933.

2. решить устно задачу № 943 по готовому чертежу на доске.

Решение

Из прямоугольного треугольника АОС по теореме Пифагора находим AC =; из прямоугольного треугольника ВОС находим по теореме Пифагора BC =.

3. Разобрать по учебнику и записать решение задачи № 953 в тетради (подчеркнуть, что теорема: «Сумма квадратов всех сторон параллелограмма, ромба, прямоугольника, квадрата равна сумме квадратов его диагоналей» – используется часто при решении задач по стереометрии в 10 и 11 классах) (рис. 283 учебника).

4. решить задачи №№ 991, 996, 997, 999 на доске и в тетрадях.

III. Опрос учащихся по теоретическому материалу.

Примерные варианты карточек для устного опроса учащихся.

Вариант I

1. Сформулируйте теорему о разложении вектора по двум данным неколлинеарным векторам.

2. Выведите формулы координат середины отрезка по координатам его концов.

3. Напишите уравнение окружности с центром в точке В (4; 0), если она проходит через точку А (7; 4).

вариант II

1. Сформулируйте  правило  нахождения  координат  разности  двух векторов.

2. Выведите  формулу  для  вычисления  длины  вектора  по  его  координатам.

3. Напишите уравнение прямой, проходящей через две точки А (–3; –3) и В (3; 5).

Вариант III

1. Сформулируйте правило нахождения координат произведения вектора на число по заданным координатам вектора.

2. Выведите уравнение окружности данного радиуса с центром в данной точке, заданной координатами.

3. Найдите координаты середины отрезка АВ, если даны координаты его концов А (–3; 4) и В (3; –6).

Вариант IV

1. Сформулируйте утверждение о разложении произвольного вектора по координатным векторам.

2. Выведите  уравнение  прямой  l  в  прямоугольной  системе  координат,  если l является  серединным  перпендикуляром  к  отрезку с концами А (х₁; у₁) и В (х₂; у₂).

3. Найдите расстояние между точками М (2; –1) и N (5; –3).

IV. решение задач.

1. Решить задачу № 1004.                      Решение

Достаточно доказать, что данные прямые не имеют ни одной общей точки.  Для  этого  запишем  уравнения  данных прямых так: y = 2x +  и y = 2x – 3. Ясно, что эта система несовместна, то есть нет чисел х, у, удовлетворяющих этим двум уравнениям. Геометрически это означает, что данные прямые не имеют ни одной общей точки и, значит, они параллельны.

2. Решить задачу № 1007.                            Решение

Пусть ОАВС – данная трапеция с основаниями ОА = а и ВС = b (пусть а > b) и высотой h. Введем прямоугольную систему координат ОХY так, чтобы точка А лежала на положительной полуоси ОХ, а прямая ВС пересекала  положительную  полуось  ОY.  В этой системе координат вершины трапеции будут иметь координаты О (0; 0), А (а; 0), С (с; h) и В (с + b; h), где с – некоторое число. Находим координаты середин М и N диагоналей трапеции и вычисляем расстояние между ними: MN = . Таким образом, MN = (OA – BC).

3. Решить задачу № 1010 (а).                    Решение

Введем  систему  координат  так, чтобы точки А и В имели координаты А (0; 0), В (а; 0), где а = АВ. Пусть М (х; у) – произвольная точка. Условие 2АМ² – ВМ² = 2АВ², записанное в координатах, дает уравнение искомого множества. Оно приводится к виду:

(х + а)² + у² = (2а)².

Этим  уравнением  задается  окружность радиуса 2а с центром в точке (–а; 0), то есть в точке, симметричной точке В относительно точки А.

V. Итоги уроков.

Домашнее задание:  повторить  материал  пунктов  86–92; пунктов  66–67 (материал 8 класса); решить задачи №№ 1010 (б), 990, 958, 944, 945, 998.

 

 

Урок 10.                          Контрольная работа № 1

Цели: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала.

Ход урока

I. Организация учащихся на выполнение работы.

II. Выполнение работы по вариантам.

Вариант I

1. Точки E и F лежат соответственно на сторонах AD и BC параллелограмма ABCD; AE = ED, BF : FC = 4 : 3. Выразите вектор  через векторы  и .

2. Найдите  координаты  вектора ,  если  ,  (3; –2),
( –6; 2).

3. Боковые стороны прямоугольной трапеции равны 15 см и 17 см, средняя линия равна 6 см. Найдите основания трапеции.

Вариант II

1. Точки K и M лежат соответственно на сторонах AB и CD параллелограмма ABCD; AK = KB, CM : MD = 2 : 5. Выразите вектор  через векторы  и .

2. Найдите  координаты  вектора ,  если  ,  (–3; 6),
(2; –2).

3. Один из углов прямоугольной трапеции равен 120°, бóльшая боковая сторона  равна  20 см,  средняя  линия  равна  7 см.  Найдите  основания трапеции.

III. Итоги урока.

Домашнее задание: повторить материал пунктов 76–87; ответить на вопросы 1–8, с. 249.

 

 

 

 

 

 

 

 

 

 

 

 

СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА (12 часов)

Урок 1. Тема :синус, косинус, тангенс. основное тригонометрическое тождество

Цели: повторить определение синуса, косинуса и тангенса острого угла прямоугольного треугольника; ввести понятия синуса, косинуса и тангенса для углов от 0° до 180° и закрепить их знание в ходе решения задач.

Ход урока

I. Повторение ранее изученного материала.

1. Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника?

2. Какое  равенство  называют  основным  тригонометрическим  тождеством?

3. Чему равны значения синуса, косинуса и тангенса для углов 30°, 45° и 60°?

II. Изучение нового материала.

1. Ввести понятие единичной полуокружности (рис. 290).

2. Ввести понятие синуса и косинуса для углов 0° ≤ α ≤ 180°:

sin α = y;  соs α  = х.

Таким образом, для любого угла б из промежутка 0° ≤  α ≤ 180° синусом угла б называется ордината у точки М, а косинусом угла б – абсцисса х точки М, лежащей на единичной полуокружности.

0 ≤ sin α  ≤ 1;             –1 ≤ cos α ≤ 1.

3. Нахождение значений синуса и косинуса для углов 0°, 90° и 180°.

4. Определение тангенса угла α (α  90°):  tg α =  при α  90°; tg 0° = 0; tg 180° = 0.

5. Вывести основное тригонометрическое тождество sin²+cos² = 1, используя рисунок 290.

III. Закрепление изученного материала .1. Решить задачи № 1012 (для точек А, В, М₁, М₂).

2. Решить задачи № 1013 (б) на доске и в тетрадях.

3. Решить задачи № 1014 (а) и № 1015 (г).

решение

г) sin α  =  и 90° <  α < 180°.  Угол α   расположен  во  II четверти, значит, cos α < 0. Найдем cos α, используя основное тригонометрическое тождество:

cos²  = 1 – sin²

cos α = ;

найдем tg α.

tg α = .

Ответ: .

IV. Итоги урока.

Домашнее задание: изучить материал пунктов 93 и 94; ответить на вопросы 1–4, с. 271; решить задачи № 1012 (для точек М₂ и М₃), №№ 1013 (б, в), 1014 (б, в), 1015 (б).

 

 

Урок 2.  Тема:формулы приведения. формулы для вычисления координат точки

Цели:

Образовательные: вывести формулы для вычисления координат точки; развивать логическое мышление учащихся при решении задач.

Развивающие: развивать логическое мышление обучающихся; развивать математическую речь обучающихся;  развивать наблюдательность, память обучающихся.

Воспитательные:  прививать аккуратность, точность; формировать положительное отношение к предмету, интерес к знаниям.

Ход урока

I. Математический диктант (10–12 мин).

Вариант I. 1. Стороны прямоугольного треугольника равны 3 см, 4 см и 5 см. Найти синус, косинус и тангенс меньшего острого угла этого треугольника.

2. Катет прямоугольного треугольника равен 6 дм, а противолежащий угол равен 30°. Найдите гипотенузу этого треугольника.

3. Вычисляя синус острого угла, ученик получил число 1,05. Верны ли его вычисления?

4. Найти косинус острого угла, если его синус равен .

5. Найти тангенс острого угла, если его синус равен .

6. Синус острого угла прямоугольного треугольника равен . чему равен косинус второго острого угла этого треугольника?

Вариант II. 1. Стороны прямоугольного треугольника равны 10 дм, 8 дм и 6 дм. Найти  синус,  косинус  и  тангенс  большего  острого  угла  этого  треугольника.

2. Катет прямоугольного треугольника равен 8 см, а противолежащий угол равен 45°. Найти гипотенузу этого треугольника.

3. Вычисляя косинус острого угла прямоугольного треугольника, ученик получил число 1,05. Верны ли его вычисления?

4. Найти синус острого угла, если его косинус равен .

5. Найти тангенс острого угла, если его косинус равен .

6. Косинус острого угла прямоугольного треугольника равен . чему равен синус второго острого угла этого треугольника?

II. Изучение нового материала. 1. Обсудить с учащимися задачу № 1011. 2. Решить задачу:

Используя единичную полуокружность, постройте угол: а) косинус которого равен ; ; 0; –1; б) синус которого равен ; ; 1.

Для решения этой задачи полезно заготовить на доске несколько полуокружностей.

3. Предложить учащимся доказать, что синусы смежных углов равны, а косинусы смежных углов выражаются взаимно противоположными числами.

4. Записать формулы приведения:

sin (180° – α ) = sin α ; cos (180° – α ) = – cos α  при 0° ≤ α ≤ 180°;

sin (90° – α) = cos α ; cos (90° – α ) = sin α  при 0° ≤ α  ≤ 90°.

5. Объяснить учащимся содержание пункта 95 «Формулы для вычисления координат точки».

III. Закрепление изученного материала (решение задач).

1. Решить задачу № 1016 на доске и в тетрадях.

Решение

sin 120° = sin (180° – 60°) = sin 60° = ; cos 120° = cos (180° – 60°) = –cos 60° = ;

tg 120° = ;  sin 135° = sin (180° – 45°) = sin 45° = ;

cos 135° = cos (180° – 45°) = –cos 45° = ;  tg 135° =  = –1.

2. Решить задачу № 1018 (в).

Решение

ОА = 5, α = 150°; точка А (х; у) имеет координаты

x = OA cos α = 5 ∙  cos 150° = 5 ∙  cos (180° – 30°) = –5 ∙  cos 30° =;

y = OA sin  = 5 ∙  sin 150° = 5 ∙  sin (180° – 30°) = 5 ∙  sin 30° =  = 2,5.

A .

Ответ: x = ; y = 2,5.

3. Решить задачу № 1019 (в).

Решение

A (; 1); x = , y = 1.

Решим сначала задачу в общем виде. Если известны координаты х и у точки А и х  0, то из равенств у = ОА ∙  sin , х = ОА ∙  cos , разделив первое из них почленно на второе, получаем , то есть = tg , а из этого равенства можно с помощью таблиц или микрокалькулятора найти значение .

x = ОА cos α , y = OA sin α

 = ОА cos α, 1 = ОА cos α ,

тогда  tg α  = ;  tg 30° = ,  а  так  как – < 0, то угол  расположен во II четверти, значит, α – тупой угол.

Находим его: α = 180° – 30° = 150°.

Ответ: 150°.IV. Итоги урока.

Задание на дом: изучить материал пунктов 93–95; повторить материал пунктов 52, 66 и 67; решить задачи №№ 1017 (в), 1018 (б), 1019 (г).

 

Урок 3. Решение задач.

Цели: закрепить знания уч-ся в ходе решения задач;развивать умение и навыки при решении задач.

                                        Ход урока

I.Фронтальная повторение теоретического материала

Использовать настенную таблицу «Тригонометрические функции».
1. Объясните,  что  такое  синус  и  косинус  угла α из промежутка 0°≤ α ≤ 180°.

2. Что называется тангенсом угла α? для какого значения α тангенс не определен и почему?

3. Записать основное тригонометрическое тождество.

4. Написать формулы приведения.

5. Написать формулы, выражающие координаты точки  А с неотрицательной ординатой через длину отрезка ОА и угол между лучом ОА и положительной полуосью ОХ.

II. Решение задач.

1. Решить задачу 1. Найти tg , если:

    а) cos α = ;

    б) sin α = 1.

2. Решить задачу 2.  Постройте β,  если:

    а) cos β = ;

    б) sin β = .

3. Решить задачу № 1018 (г).

решение

ОА = 1; α = 180°; х = ОА cos α; х = 1 · cos 180° = –1; х = –1

y = ОА sin α = 1 · sin 180° = 1 · 0 = 0; у = 0.

Ответ: х = –1; у = 0.

III. Самостоятельная работа контролирующего характера.

Вариант I

Решить задачи №№ 1015 (а), 1017 (б), 1018 (а), 1019 (а).

Вариант II

Решить задачи №№ 1015 (в), 1017 (а), 1018 (д), 1019 (б).

IV. Итоги урока.

Домашнее задание: повторить материал пунктов 93–95; повторить материал п. 52 «Площадь треугольника»; решить задачи №№ 468, 471, 469.

 

 

Урок 4. Тема:Теорема о площади треугольника. Теорема синусов

Цели: доказать теорему о площади треугольника и теорему синусов; показать применение этих теорем при решении задач.

Ход урока

I. Проверка опорных знаний учащихся.

Провести математический диктант (10 мин).

Вариант . I1. Найдите площадь треугольника, если его основание равно 7 см, а высота равна 4 см.

2. Найдите синус угла, если его косинус равен .

3. Найдите синус угла, если синус смежного с ним угла равен 0,3.

4. Начертите треугольник АВС с тупым углом С. Проведите высоту треугольника из вершины В.

5. Луч ОС образует с положительной полуосью абсцисс угол 60°. Найдите координаты точки С, если ОС = 6 дм.

6. Определите, каким – остроугольным, прямоугольным или тупоугольным – является треугольник, два угла которого равны 43° и 48°.

Вариант II.   1. Найдите площадь треугольника, если его основание равно 10 дм, а высота равна 5 дм.

2. Найдите косинус угла, если его синус равен .

3. Найдите синус угла, если синус смежного с ним угла равен 0,7.

4. Начертите треугольник СDЕ с тупым углом Е. Проведите высоту треугольника из вершины С.

5. Луч ОВ образует с положительной полуосью абсцисс угол 30°. Найдите координаты точки В, если ОВ = 8 дм.

6. Определите, каким – остроугольным, прямоугольным или тупоугольным – является треугольник, два угла которого равны 35° и 56°.

II. Объяснение нового материала.

1. Доказательство теоремы о площади треугольника  1) чему равна площадь любого треугольника?   2) какие формулы применяются для вычисления координат точки?

2. Устно : найти площадь треугольника АВС, если АВ = 12 см, АС = 8 см, А = 30°.

3. Доказать теорему синусов, используя теорему о площади треугольника.

III. Закрепление изученного материала  1. Решить задачу № 1020 (б) на доске и в тетрадях.

Решение: S = АВ · ВС sin B = ∙  18∙  3 sin 45° = 9∙  3 ∙   = 27 (cм²). Ответ: 27 cм².

2. Решить задачу № 1022.

Решение: S = 60 см²; S = АВ · AС sin A; 60 = AB · 15 sin 30°; 60 = АВ · ; АВ = 60 : = 16

Ответ: 16 см.

3. Решить задачу № 1026.

IV. Итоги урока.

Домашнее задание: изучить материал пунктов 96 и 97; повторить материал п. 89; решить задачи №№ 1020 (а, в), 1023.

 

Урок 5. Тема: Теорема косинусов

Цели: доказать теорему косинусов и научить учащихся применять ее при решении задач.

Ход урока

I. Проверка домашнего задания.

1. Сформулировать и доказать теорему  о  площади  треугольника (вычисление площади треугольника по двум сторонам и углу между ними).

2. Сформулировать и доказать теорему синусов.

3. Проверить решение задачи № 1023.

II. Изучение нового материала.

1. Записать формулу  расстояния  между  двумя  точками:  точки
М₁ (х₁; у₁), М₂ (х₂; у₂),

d = М₁М₂ = .

2. Доказать теорему косинусов, используя рисунок 293 учебника.

3. Теорему косинусов называют иногда обобщенной теоремой Пифагора.

cosА = cos 90° = 0 и по формуле а² = b² + с² – 2bс ∙  cos А получаем а² = b² + с², то есть квадрат гипотенузы равен сумме квадратов катетов.

4. Обсудить с учащимися, какие три элемента треугольника нужно знать, чтобы вычислить четвертый элемент (сторону или угол), используя: 1) теорему синусов; 2) теорему косинусов.

III. Решение задач. 1.Найдите  сторону  АВ  треугольника АВС, если ВС = 3 см, АС = 5 см, С = 60°.

Решение

АВ² = ВС² + АС² – 2 ∙  ВС ∙  АС ∙  cos С = 3² + 5² – 2 ∙  3 ∙  5 cos 60° = 9 +
+ 25 – 15 = 19; АВ = см.    Ответ: см.

2. Решить задачу 3.  Найдите  угол  А  треугольника  АВС,  если АВ =
= АС = 1 м, ВС = м.

3. Решить задачу № 1031.

Решение

а) а = 5; b = 4; с = 4. Найдем cos А = . Так как  > 0, но меньше 1, то самый большой угол А в треугольнике будет острым. Следовательно, треугольник является остроугольным.   Ответ: остроугольный.

б) а = 17; b = 8; с = 15.

cos А = = 0;

сos А = 0, значит, А = 90°.  Ответ: прямоугольный.

 в) а = 9; b = 5; с = 6.

cos А = .

Так как –1 <  < 0, то А – тупой.  Ответ: тупоугольный треугольник.

IV. итоги урока.

Задание на дом:  выучить  материал  пунктов  96–98;  решить  задачи №№ 1027, 1032.

 

Урок 6.Тема: Решение треугольников

Цели: познакомить учащихся с методами решения треугольников; закрепить знание учащимися теорем синусов и косинусов, научить применять эти теоремы в ходе решения задач.

Ход урока

I. Проверка изученного материала.

Учащиеся на отдельных листочках доказывают изученные теоремы и сдают учителю.

Вариант I.    Сформулируйте и докажите теорему косинусов.

Вариант II.     Сформулируйте и докажите теорему о площади треугольника.

Вариант III.    Сформулируйте и докажите теорему синусов.

II. Изучение нового материала.

1.Решением треугольника называется нахождение всех его шести элементов (то есть трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.

3. Рассмотрим три задачи на решение треугольника:

1) решение треугольника по двум сторонам и углу между ними;

2) решение треугольника по стороне и прилежащим к ней углам;

3) решение треугольника по трем сторонам.

При этом будем пользоваться следующими обозначениями для сторон треугольника АВС: АВ = с; ВС = а; СА = b.

3. В тетрадях учащиеся оформляют таблицу-памятку:

III. Решение задач.

1. По рисунку 294 учащиеся самостоятельно разбирают решение примера на странице 259 учебника.

2. Решить задачу № 1025 (б, в, г, ж, и) на доске и в тетрадях, используя таблицы Брадиса и микрокалькуляторы.

3. Решить задачу № 1021 на доске и в тетрадях.

4. Совместно с учащимися разобрать и зафиксировать в тетрадях решение задачи № 1033 по рисунку 297.

5. Решить задачи № 1060 (в), 1061 (в) и 1062.

IV. Итог урока.

Задание на дом: изучить материалы пунктов 96–99; решить задачи №№ 1025 (а, д, е, з), 1060 (г), 1028.

 

Урок 7. Тема:Измерительные работы

Цель: познакомить учащихся с измерительными работами на местности, основанными на использовании теорем синусов и косинусов.

Ход урока

I. Проверка опорных знаний учащихся.

Учащиеся отвечают на вопросы 2–10 на странице 271 учебника.

II. работа по учебнику.

1. Тригонометрические формулы используются при проведении различных измерительных работ на местности.

В 8 классе учащиеся определяли высоту предмета и расстояние до недоступной точки на основе теоремы подобия треугольников. В 9 классе эти же задачи решают с применением тригонометрических функций.

2. Учащиеся самостоятельно читают материал пункта 100 учебника.

3. Обсуждение прочитанного материала, используются рисунки 295 и 296 учебника.

III. Решение задач.

1. Решить задачу № 1036 по рисунку 298.

2. Решить задачу № 1037 (использовать рисунок 296 учебника).

3. Решить задачу № 1038 по рисунку 299.

IV. Итоги урока.

Домашнее задание: повторить материал пунктов 93–100; решить задачи № 1034, 1064.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок 8.    Решение задач

Цели: систематизировать, повторить и обобщить изученный материал; научить применять полученные знания к решению задач.

Ход урока

I. Повторение и обобщение изученного материала.

1. Сформулировать теорему о площади треугольника.

2. Сформулировать теорему синусов.

3. Сформулировать теорему косинусов.

4. Объяснить применение теоремы косинусов при решении треугольников.

5. В какой задаче на решение треугольников можно применять только теорему синусов?

6. Рассказать решение задачи по нахождению высоты предмета и расстояния  до  недоступной  точки  с  помощью  тригонометрических функций.

7. Формулы приведения (записать на доске).

II. Решение задач.

1. Решить задачу № 1059 на доске и в тетрадях.

Пусть АВСD – выпуклый четырехугольник, О – точка пересечения его диагоналей, AOB = .

Тогда S_АВСD = S_АОВ + S_ВОС + S_СОD + S_АОD.

Найдем площадь каждого из четырех треугольников, пользуясь теоремой о площади треугольника.    Учитывая, что sin(180°–)= sinи АС = АО + ОС, ВD = ВО + ОD, получаем:

S_АВСD = AC ∙  BD ∙  sin .

2. Решить задачу № 1063.

Решение

S_АВС = S_АВD + S_АСD или воспользуемся формулой площади треугольника:

bc ∙  sin  = xc ∙  sin+ xb ∙  sin, где x = AD.

Отсюда, учитывая, что sin  = 2sin∙  cos, находим х:

х = .

III. Самостоятельная работа контролирующего характера.

Вариант I

Решить задачи №№ 1060 (а); 1058 (б); 1061 (а).

Вариант II

Решить задачи №№ 1060 (б); 1058 (а); 1061 (б).

IV. Итоги урока.

Домашнее задание: повторить тему «Векторы», материал пунктов 76–85 и 86–89; решить задачи №№ 1024, 1035.

Урок 9. Тема: Угол между векторами. Скалярное произведение векторов

Цели: познакомить учащихся с понятием угла между векторами; ввести скалярное произведение векторов; рассказать о применении скалярного произведения векторов в физике, механике; развивать логическое мышление учащихся.

Ход урока

I. Математический диктант (15 мин).

Вариант I

1. Диагонали параллелограмма АВСD пересекаются в точке О. какие векторы коллинеарны вектору ?

2. Диагонали параллелограмма АВСD пересекаются в точке О. Какие векторы сонаправлены с вектором ?

3. Диагонали параллелограмма АВСD пересекаются в точке О. Какие векторы равны вектору ?

4. При каком условии ?

5. Известно, что  = 3,  = 4. Найдите , если АОВD – прямоугольник.

6. В треугольнике СDЕ  DЕ = 5, СЕ = 4, угол С = 45°. Найдите сторону DЕ.

7. В треугольнике КLM КL = LМ = 5, КМ = 6. Найдите косинус угла L.

Вариант II

1. Диагонали ромба КLМР пересекаются в точке Т. Какие векторы коллинеарны вектору ?

2. Диагонали ромба КLМР пересекаются в точке Т. какие векторы сонаправлены с вектором ?

3. Диагонали ромба КLМР пересекаются в точке Т. Какие векторы равны вектору ?

4. При каком условии ?

5. Известно, что точки С и D лежат соответственно на осях ОХ и ОY прямоугольной системы координат. Найдите , если  = 5,  = 12.

6. В треугольнике АВС  АВ = ВС = 8, АС = 4. Найдите косинус угла А.

7. В треугольнике ВСD  ВС = 6, угол В = 75°, угол С = 45°. Найдите сторону ВD.

II. Объяснение нового материала. 1. Ввести понятие угла между векторами  и  (рис. 300 ).

2. В тетрадях учащиеся оформляют таблицу:

скалярное произведение векторов

III. Закрепление изученного материала.

1.      Решить задачи №№ 1039 (а, б, ж, з) и 1040 (а, д, е) № 1041 (в).

2.      Примечание. Сos 135° = cos (180° – 45°) = – cos 45° = .

IV. Итоги урока.

Домашнее задание: изучение материалов пунктов 101 и 102; повторить материал п. 87; решить задачи №№ 1039 (в, г), 1040 (г), 1042 (а, б).

 

Урок 10.Тема: Скалярное произведение в координатах.
                             Свойства скалярного произведения векторов

Цели: ввести понятие скалярного произведения в координатах; изучить свойства скалярного произведения векторов и закрепить их знание при решении задач.

Ход урока

I. Проверочная работа (10 мин).в двух вар.презентация

II. Изучение нового материала.

1. Скалярное произведение двух векторов можно вычислить, зная координаты этих векторов.

2. Изучение теоремы о скалярном произведении векторов в координатах и свойств скалярного произведения полезно построить так, чтобы учащиеся сами проводили алгебраические преобразования.

Полученные результаты можно записать в тетради и вынести в настенную таблицу:

Скалярное произведение в координатах

Свойства скалярного произведения векторов:

1) ≥ 0 ( > 0 при  0); 2) ; 3) ; 4) .

III. Закрепление изученного материала.

1. Решить задачу № 1043 (объясняет учитель):

2. Решить задачи № 1044 (а, б).3. Устно № 1045.

4. Решить задачи № 1046, 1047 (б, в) на доске и в тетрадях.5. Решить задачу № 1051.

6. Решить задачу № 1049 на доске и в тетрадях (для угла А объясняет учитель):

7. Решить задачу № 1052.

8. Решить задачу № 1066.

Ответ: 5.

IV. Итоги урока.

Домашнее задание: изучить материал пунктов 101–104; ответить на вопросы 17–20 на странице 271 учебника; решить №№ 1044 (в), 1047 (а), 1054 (разобрать решение задачи и записать в тетрадь).

 

урок 11.                Решение задач

Цели: закрепление и проверка знаний и умений учащихся, сформированных при изучении главы XI, формирование навыков решения задач, развитие навыков логического мышления.

Ход урока

I. Математический диктант (10 мин).

II. Решение задач.1. № 1025 (б, е, з) на доске и в тетрадях, используя микрокалькулятор.

2. Решить задачу № 1056 на доске и в тетрадях.

3. Решить задачу № 1042 на доске и в тетрадях.

б)

cos 120° = cos (180° – 60°) = –cos 60° = –.

в) ∙  cos 90° = 0, так как cos 90° = 0;

г) ∙  cos 0° = a ∙  a ∙  1 = a².

ответ: а) a²;   б) –a²;   в) 0;   г) а².

4. Решить задачу № 1050. Самостоятельно учащиеся находят .

III. Устный опрос учащихся по карточкам.

Вариант I

1. Что называется тангенсом угла ? Для какого значения  тангенс не существует и почему?

2. Сформулируйте и докажите теорему синусов.

3. Даны векторы (х; –4) и (2; 3). Найдите значение х, если .

Вариант II

1. Напишите формулы приведения.

2. Сформулируйте и докажите теорему косинусов.

3. Найдите скалярное произведение векторов (–5; 7) и (2; 1).

Вариант III

1. Что такое скалярное произведение векторов?

2. Сформулируйте и докажите теорему о вычислении площади треугольника по двум сторонам и углу между ними.

3. Найдите косинус угла А треугольника АВС, если АВ = 8 см, АС = 6 см, ВС = 12 см.

Домашнее задание: подготовиться к контрольной работе, повторить материал пунктов 93–104; решить задачи №№ 1065, 1068, 1060 (а, б), 1061 (а, б).

 

Урок 12.                                          Контрольная работа № 2

Цель: проверить знания, умения и навыки учащихся по теме «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов».

Ход урока

I. Организация учащихся на выполнение работы.

II. Выполнение работы по вариантам.

Вариант I

1. Найдите угол между лучом ОА и положительной полуосью ОХ, если А (–1; 3).

2. Решите треугольник АВС, если угол В = 30°, угол С = 105°, ВС =
= 3см.

3. Найдите косинус угла М треугольника KLМ,  если  К (1; 7), L (–2; 4), М (2; 0). Найдите косинусы углов K и L.

Вариант II

1. Найдите угол между лучом ОВ и положительной полуосью ОХ, если В (3; 3).

2. Решите треугольник ВСD,  если  угол  В = 45°;  угол D = 60°,  ВС =
=см.

3. Найдите  косинусы  углов  А, В и С треугольника АВС, если А (3; 9), В (0; 6), С (4; 2).

Вариант III

1. Найдите угол между лучом ОС и положительной полуосью ОХ, если С (; 1).

2. Решите треугольник СDЕ, если угол С = 60°, СD = 8 дм, СЕ = 5 дм.

3. Найдите косинус угла между векторами  и , если = 60°.

Вариант IV

1. Найдите угол между лучом ОD и положительной полуосью ОХ, если D (–2; 2).

2. Решите треугольник DЕF, если DЕ = 5 м, DF = 8 м и ЕF = 4 м.

3. Найдите косинус угла между векторами  и , если = 60°.

Домашнее задание: повторить материал пунктов 39–41 и пунктов 21, 74–75 «Вписанная и описанная окружности».

 

ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА. (11 часов)

Урок 1. Тема: Правильный многоугольник. Окружность,
                                описанная около правильного многоугольника

Цели: повторить ранее изученный материал о сумме углов выпуклого многоугольника, о свойстве биссектрисы угла, теорему об окружности, описанной около треугольника, признак равнобедренного треугольника; сформировать у учащихся понятия «правильный многоугольник», «многоугольник, вписанный в окружность»; выработать умение формулировать и доказывать теорему об окружности, описанной около правильного многоугольника.

Ход урока

I. Анализ контрольной работы.

II. Актуализация опорных знаний учащихся.

1. Повторить формулу суммы углов выпуклого многоугольника и записать ее.

2. Сформулировать свойство биссектрисы угла и признак равнобедренного треугольника.

3. Повторить теорему  об  окружности,  описанной  около  треугольника.

4. Устно решить задачи:

1) Сколько сторон имеет п-угольник, если сумма его внутренних углов равна: а) 1260°; б) 1980°?

2) Назовите выпуклый четырехугольник, у которого все внешние углы прямые.

3) Сколько сторон имеет выпуклый многоугольник, если сумма его внутренних углов равна сумме внешних?

4) Сколько сторон имеет выпуклый многоугольник, если все его внешние углы тупые?

5. Решить задачи на доске и в тетрадях: 1) Все углы выпуклого пятиугольника равны друг другу. Найдите величину каждого угла.

2) Докажите, что треугольник, две высоты которого равны, является равнобедренным.

3)Четырехугольник АВСD вписан в окружность. Докажите, чтоА ++ С = В + D.

III. Изучение нового материала.

1. Ввести понятие правильного многоугольника.

2. Задать учащимся вопросы:1) Какие правильные многоугольники уже рассматривались в курсе геометрии?   2) Приведите примеры такого выпуклого многоугольника, у которого:

а) все стороны равны, но он не является правильным (ромб с острым углом);

б) все углы равны, но он не является правильным (прямоугольник с неравными сторонами).

3. Предложить учащимся вывести формулу для вычисления угла правильного многоугольника.

4. Решить задачи № 1081 (в) и 1083 (в) на доске и в тетрадях.  Формулировка и док -во теоремы об окружности, описанной около правильного многоугольника (рис. 307).

IV. Закрепление изученного материала. 1. Решить задачи №№ 1086 и 1084 (б, д).

решение

№ 1086. Примечание. Воспользоваться тем, что биссектриса любого угла правильного многоугольника проходит через центр вписанной окружности.

№ 1084.  Ответ: б) 12, д) 20.            2. Обсудить решения задач № 1080 и 1082 (устно).

V. Итоги урока.

Домашнее задание: изучить материалы пунктов 105–106; ответить на вопросы 1–3, с. 290; решить задачи №№ 1081 (а, д), 1083 (г), 1084 (а, в), 1129.

 

Урок 2. Тема: Окружность, вписанная в правильный многоугольник

Цели: повторить теорему об окружности, вписанной в треугольник; повторить свойства касательной к окружности; сформулировать и доказать теорему об окружности, вписанной в правильный многоугольник; вырабатывать навыки решения задач.

Ход урока

I. Повторение изученного материала.

1. Сформулировать теорему об окружности, вписанной в треугольник.

2. Сформулировать свойство касательной к окружности.

3. Решить задачи №№ 1078 (устно) и 1079 (устно).

4. Решить задачи на доске и в тетрадях:

1) Окружность  радиуса  5 см  касается  сторон  угла  А в точках В и С. найдите длины отрезков АВ и АС, если центр окружности удален от вершины угла на 13 см.

2) Две окружности пересекаются в точках А и В. Докажите, что прямая, проходящая через их центры, перпендикулярна к отрезку АВ.

3) Докажите, что радиус окружности, вписанной в равносторонний треугольник, вдвое меньше радиуса описанной около него окружности.

II. Работа с учебником.

1. Определение окружности, вписанной в многоугольник.

2. Разобрать по рисунку 308 учебника доказательство теоремы об окружности, вписанной в правильный многоугольник.  3. Записать в тетради следствие 1 и следствие 2.

4. Записать в тетради правила нахождения для заданного правильного многоугольника центров описанной и вписанной окружностей, а также их радиусов:

1) Центром окружности, описанной около правильного многоугольника, является точка пересечения серединных перпендикуляров к сторонам многоугольника (достаточно найти точку пересечения серединных перпендикуляров к двум соседним сторонам), а радиусом является отрезок биссектрисы угла многоугольника, соединяющий его вершину с центром.

2) Для нахождения центра и радиуса окружности, вписанной в многоугольник, достаточно построить биссектрисы двух соседних углов, найти точку О их пересечения и опустить из нее перпендикуляр на соответствующую сторону многоугольника (точка О будет центром вписанной окружности, а перпендикуляр – ее радиусом).

III. Закрепление изученного материала.  Решить задачи на доске и в тетрадях:

1. Докажите, что все диагонали правильного многоугольника равны.

2. На каждой из сторон квадрата отмечены две точки, делящие каждую сторону в отношении 1 : : 1. Докажите, что эти точки служат вершинами правильного восьмиугольника.

3. Постройте с помощью транспортира и циркуля правильный пятиугольник.

IV. Самостоятельная работа.  Вариант I. 1. Задачи №№ 1081 (б), 1083 (б), 1084 (г).

2. Докажите, что три вершины правильного шестиугольника, взятые через одну, служат вершинами правильного треугольника.

Вариант II. 1. Задачи №№ 1081 (г), 1083 (а), 1084 (е).

2. Докажите, что четыре вершины правильного восьмиугольника, взятые через одну, служат вершинами квадрата.

V. Итоги урока.

Домашнее задание: повторить материал пунктов 105–107; ответить на вопросы 1–4, с. 290; решить задачи №№ 1085, 1131, 1130.

Урок 3. Тема: Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности

Цели: выработать у учащихся умение выводить формулы, связывающие радиус описанной окружности и радиус вписанной окружности со стороной а правильного п-угольника, на их основе научить учащихся получать формулы для вычисления а_п через R и r и конкретизировать их для случая п = 3, п = 4, п = 6, выработать навыки применения полученных знаний при решении задач.

Ход урока

I. Анализ самостоятельной работы.

II. Изучение нового материала.

1. Вывод формул (1–6) из пункта 108 учебника учащиеся проводят самостоятельно под руководством учителя по заранее заготовленному на доске рисунку 308.

2. После вывода формул для правильного п-угольника рассмотреть их частные случаи для п = 3, п = 4, п = 6.

3. Выведенные формулы оформить в виде таблицы, которую учащиеся записывают в тетради:

III. Закрепление изученного материала (решение задач).

1. Решение учащимися задач на непосредственное применение выведенных формул:

1) В окружность радиуса R = 12 вписан правильный п-угольник. Определите его сторону и периметр, если: а) п = 3; б) п = 4; в) п = 6.

2) Около окружности радиуса r = 6 описан правильный п-угольник. Определите его сторону и периметр, если: а) п = 3; б) п = 4; в) п = 6.

3) Для правильного п-угольника со стороной а = 6 см найдите радиус описанной около него окружности, если: а) п = 3; б) п = 4; в) п = 6.

2. Решить задачу № 1089.

Решение:  Р_ = 18 см; а = 18 : 3 = 6 (см); а₃ = R; R == 2(см);

а₄ = R= 2∙  = 2(см).     Ответ:  2см.

3. Решить задачу № 1090.

Решение: а₃ = 3 см; R =(см); d = 2R = 2(см).  ответ: 2см.

4. Решить задачу № 1092.

Решение

Р = 48 см; а₆ = 48 : 6 = 8 (см); а₆ == 8 (см);

r == 4(см); а₄ = 2r = 8(см) ; р = 4 ∙  а₄ = 8∙  4 = 32(см).

Ответ: 32см.

5. Решить задачу:

Правильный треугольник АВС вписан в окружность с центром О и радиусом 8 см. На стороне этого треугольника построен квадрат. Определите радиус окружности, описанной около квадрата.

IV. Итоги урока.

Задание на дом: изучить материал пункта 108; решить задачи №№ 1087, 1088, 1094 (а, б).

Урок 4. Тема:Построение правильных многоугольников

Цель: выработать у учащихся умение строить некоторые правильные многоугольники.

Ход урока

I. Проверка домашнего задания.

1. Проверить решение учащимися задач № 1087 и № 1088 по тетрадям.

2. Решить на доске часть заданий, вызвавших затруднения у учащихся.

II. Построение правильных многоугольников.

1. Рассмотреть решение задачи 1 пункта 109.

2. Построение правильного треугольника, вписанного в окружность.

3. Рассмотреть решение задачи 2 пункта 109.

4. Построение правильного двенадцатиугольника, вписанного в окружность (рис. 310).

5. Построение правильных четырехугольника, восьмиугольника, шестнадцатиугольника, вписанных в окружность.

6. Построение правильных шестиугольника, треугольника, описанных около окружности.

7. Построение правильных четырехугольника, восьмиугольника, описанных около окружности.

III. Итоги урока.

Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Оказывается, что не все правильные многоугольники допускают такое построение. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки.

Однако с помощью этих инструментов можно построить правильный семнадцатиугольник.

Домашнее задание:  выполнить  аналогичное  задание  на  чертежных листах (построение правильных многоугольников, вписанных в окружность, и построение правильных многоугольников, описанных около окружности).

Учитель может указать количество сторон правильного многоугольника. Лучшие работы пойдут в методическую копилку.

Решить задачи №№ 1095, 1096, 1097.

 

 

 

 

 

Урок 5. Тема: Длина окружности

Цели: вывести формулу, выражающую длину окружности через ее радиус; вывести формулу для вычисления длины l дуги окружности с градусной мерой ; закрепить знание формул при решении задач.

Ход урока

I. Математический диктант (15 мин).

Вариант I.  1. Найдите угол правильного десятиугольника.

2. Найдите сторону правильного треугольника, если радиус описанной около него окружности равен 2м. 3. Найдите радиус окружности, вписанной в правильный треугольник, если радиус описанной около него окружности равен 2 м.

4. Найдите площадь правильного треугольника, если расстояние от его центра до вершины равно 2 м.

5. Закончите предложение: «Угол с вершиной в центре окружности называется …»

6. Угол с вершиной в центре правильного многоугольника и сторонами, проходящими через две его соседние вершины, равен 36°. Сколько сторон имеет этот многоугольник?

7. Чему равен cos 0°?  8. С  помощью  циркуля  и  линейки  постройте  правильный  шестиугольник.

Вариант II. 1. Сколько сторон имеет правильный многоугольник, если его сторона стягивает дугу описанной окружности, равную 18°?

2. Найдите площадь квадрата, если радиус описанной около него окружности равен 2 дм.

3. Закончите предложение: «Кругом называется часть плоскости …»

4. Найдите сторону квадрата, если расстояние от его центра до вершины равно 2 дм.

5. Найдите радиус окружности, вписанной в квадрат, если радиус описанной около него окружности равен 2 дм.  6. Чему равен cos 0°?. 7. Найдите угол правильного девятиугольника.

8. С помощью циркуля и линейки постройте правильный треугольник.

II. Изучение нового материала (лекция).

1. Дать представление о длине окружности с помощью нитки, обмотанной около дна стакана.

2. Работа по рисункам 312 и 313 учебника.

3. Вывод формулы, выражающей длину окружности через ее радиус.

4. Записать в тетради вывод: отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Число π (пи).

5. Формула для вычисления длины окружности: C = 2πR; d = 2R, тогда C = πd, где d – диаметр окружности.

Найдем радиус и диаметр окружности: R = ; d = , где π ≈ 3,14.

6. Вывод формулы для вычисления длины l дуги окружности с градусной мерой :

длина дуги в 1° равна ;  длина дуги в ° равна l = ∙  .

III. Закрепление изученного материала .1. Решить задачу № 1101 2. Устно № 1102 и № 1103.

3. Решить задачу № 1109 (а, б).  4. Решить задачу № 1111 (использовать рис. 316).

IV. Итоги урока.

Домашнее задание:  изучить  материал  пункта 110; решить задачи №№ 1109 (в, г), 1106, 1104 (а), 1105 (а).

 

Урок 6. Тема: Площадь круга

Цели: вывести формулу площади круга и научить учащихся применять ее при решении задач.

Ход урока

I. Изучение нового материала (лекция). Провести в форме лекции доказательство площади круга.

1. Дать определение понятия «круг». 2. Вывести формулу площади круга (рис. 314).

3. Записать в тетрадях: для вычисления площади S круга радиуса R применяется формула .

4. В течение веков усилия многих математиков были направлены на решение задачи, получившей название задача о квадратуре круга: построить при помощи циркуля и линейки квадрат, площадь которого равна площади данного круга. Только в конце XIX века было доказано, что такое построение невозможно.

II. Закрепление изученного материала (решение задач).

1. Решить задачу. На здании МГУ установлены часы с круговым циферблатом, имеющим диаметр примерно 8,8 м. Найдите площадь циферблата этих часов и сравните с площадью вашей классной комнаты.   Ответ: 60,8 м².

2. Решить задачу № 1118 (самостоятельно). 3. Решить задачу № 1119 на доске и в тетрадях.

Решение

С = 41 м; C = 2πR; D = 2R (диаметр D);

2R = D =; D =≈ 13,06 (м) ≈ 13,1 м.

S_круга = πR²; так как R =, то S_круга = π ∙   = π ∙  ;     

S = 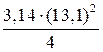 ≈ 133,84 (м²).    Ответ: ≈ 13,06 м; 133,84 м².

4. Решить задачу  № 1125 на доске и в тетрадях.

5. Решить задачу № 1116 (а) на доске и в тетрадях.

Решение

Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус описанной окружности равен половине гипотенузы.

По теореме Пифагора находим: с² = а² + b²; тогда

R = .

Значит, S_круга = πR² =.

Ответ: .

III. Итоги урока.

Домашнее задание: повторить материал пунктов 105–110; изучить материал пункта 111; решить задачи №№ 1114, 1115, 1117 (а).

 

 

Урок 7. Тема: Площадь кругового сектора

Цели: ввести понятие кругового сектора, вывести формулу для вычисления площади кругового сектора; научить применять знания при решении задач.

Ход урока

I. Проверка изученного материала.

1. Формула длины окружности. Выражение радиуса окружности через длину окружности.

2. Формулы площади круга, радиуса круга через площадь круга, формула площади круга, выраженная через диаметр круга.

3. Формула длины дуги окружности.   4. Устно решить задачу № 1115.

II. Объяснение нового материала.

1.Ввести понятие кругового сектора и понятие дуги сектора (рис. 315).

2. Вывести формулу для вычисления площади S кругового сектора радиуса R, ограниченного дугой с градусной мерой .

Так как площадь всего круга равна πR², то площадь кругового сектора, ограниченного дугой в 1°, равна .Поэтому площадь S выражается формулой     S =∙  

3. Ввести понятие кругового сегмента и познакомить учащихся с нахождением площади кругового сегмента, используя таблицу «Круговой сегмент».

III. закрепление изученного материала (решение задач).

1. Решить задачу.  АВСD – квадрат со стороной 1 дм. Найдите площадь «чечевицы», заштрихованной на рисунке.

2. Решить задачу № 1126 (самостоятельно).

Решение

R = 10 см; S_круга = πR² = 100π (см²).

l =  = 60°; S_{сектора} = (см²).

S = S_круга – S_{сектора} = 100π –≈ 262 (cм²).   Ответ: ≈ 262 см².

3. Решить задачу № 1127.

4. Вывести формулу площади кольца, ограниченного двумя окружностями с общим центром и радиусами R₁ и R₂, где R₁ < R₂.

Решение

;   S_кольца = S₂ – S₁ = .

5. Решить задачу № 1120.   6. Решить задачу № 1122 на доске и в тетрадях.

Решение

R₁ = 3 м, R₂ = 3 + 1 = 4 (м);   S_{дорожки} = π  = π (4² – 3²) = π (4 – 3) (4 + 3) = 7π (м²).

На 1 м² дорожки требуется 0,8 дм³ песка; тогда 0,8 ∙  7π = 5,6π (дм³) ≈
≈ 17,6 дм³.  Ответ: ≈ 17,6 дм³.

IV. Итоги урока.

Домашнее задание:  выучить  материал  пунктов 110–112; повторить материал пунктов 105–109; ответить на вопросы 1–12 на с. 290; решить задачи № 1121, 1128, 1124.

Урок 8. Тема:Решение задач

Цели: закрепить знания учащихся по изученной теме «Длина окружности и площадь круга»; научить учащихся применять изученные формулы при решении задач; развивать логическое мышление учащихся.

Ход урока

I. Актуализация опорных знаний учащихся.

1. Повторить определения окружности, круга, кругового сектора и кругового сегмента.

2. Записать на доске и в тетрадях формулы для вычисления длины окружности, длины дуги окружности; для вычисления площади круга, площади кольца, площади кругового сектора.

II. Решение задач. 1. Решить задачу № 1112. 2. Решить задачу № 1113 (самостоятельно).

3. Решить задачу № 1123 на доске и в тетрадях.

Решение

АВСD – квадрат; DО = ОВ = r; Sкруга = πr2; Sквадрата = а2, ВD = 2r; из ДВСD по теореме Пифагора найдем сторону квадрата АВСD: а2 + а2 = (2r)2;  2а2 = 4r2;  а2 = 2r2; тогда Sквадрата = 2r2.

Найдем площадь оставшейся части круга: S = S_круга – S_{квадрата} = πr² – 2r² = r² (π – 2).Ответ: r² (π – 2).

4. Решить задачу № 1116 (б).

Решение  АСD – прямоугольный;  А = , СD = а. АD = 2R (диаметр), АСD = 90° (вписанный угол, опирающийся на диаметр, прямой). Найдем АD.

Sin  =;  AD =, тогда радиус R описанной около прямоугольного треугольника окружности равен R =AD =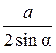. Площадь круга равна S = πR² =. Ответ: .

5. Решить задачи: 1) Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 12 дм². Найдите радиусы окружностей, если один их них в два раза больше другого.

Ответ:  дм;  дм.

2) Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 8 см². Найдите площади этих кругов, ограниченных этими окружностями, если радиус одной из них в три раза больше, чем радиус другой.  Ответ: 1 см² и 9 см².

6. Решить задачу № 1108 (самостоятельно).

III. Самост работа (10–15 мин).Вариант IРешить  №№ 1102 (в), 1115 (б), 1109 (в), 1104 (б).

Вариант II.Решить  №№ 1102 (г), 1115 (а), 1109 (г), 1116 (а).

IV. Итоги урока.

Домашнее задание: повторить материал пунктов 105–112; решить задачи №№ 1107, 1132, 1137.

Уроки 9–10.     Решение задач по материалу главы XII

Цели: закрепить знания и умения учащихся по изученному материалу главы; подготовить учащихся  к контрольной работе.

Ход уроков

I. Математический диктант (15 мин).

Вариант I

1. Площадь круга равна S. Найдите длину ограничивающей его окружности.

2. Найдите длину дуги окружности радиуса 9 м, если градусная мера дуги равна 120°.

3. Длина дуги окружности равна 3π, а ее радиус равен 8. Найдите градусную меру этой дуги.

4. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.

5. Найдите площадь кругового сектора радиуса 4 см, если его центральный угол равен 45°.

6. Площадь кругового сектора равна 18π м², а его центральный угол равен 40°. Найдите радиус сектора.

Вариант II

1. Длина  окружности  равна  С.  Найдите площадь ограниченного ею круга.

2. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 25 и 24 см.

3. Найдите площадь кругового сектора радиуса 3 см, если его центральный угол равен 20°.

4. Площадь кругового сектора равна 10π м², а его радиус равен 6 м. Найдите центральный угол сектора.

5. Найдите длину дуги окружности радиуса 6 дм, если ее градусная мера равна 120°.

6. Найдите радиус окружности, если длина дуги окружности равна 6π, а ее градусная мера равна 60°.

II. Решение задач.

1. Решить задачу 1. Докажите, что площадь S треугольника АВС вычисляется по формуле:

,

где Р – периметр треугольника, r – радиус вписанной окружности.

Доказательство

Пусть О – центр окружности, которая вписана в треугольник АВС и, следовательно, касается сторон треугольника в точках М, N и K.

Очевидно, что S = SАОС + SВОС + SАОВ. * Так как ОМ, ОN и ОK – высоты треугольников АОС, ВОС и АОВ, то SАОС = АС · ОK,  SВОС = ВС · ОМ и SАОВ =АВОN. Подставив эти значения в формулу *, получим: S =(AB+ВС+CA) · r =P · r.

2. Решить задачу 2. даны стороны треугольника АВС – а, b, с и площадь S. Выразить радиусы окружностей, описанной около треугольника и вписанной в него, через а, b, с и S.

Решение

1) Используем результат задачи 1:

S =Pr, где Р – периметр треугольника, r – радиус вписанной окружности. Р = а + b + с; 2S = r (а + b + c), отсюда:

2) Радиус R описанной окружности вычисляется по формуле:

R =, где  – угол, противолежащий стороне а.

Из формулы: S =bc · sin  получим sin  =, тогда 2sin  =. Следовательно, R =.  

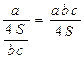3. Решить задачу № 1099 на доске и в тетрадях.

Решение

Диагонали А₃А₇ и А₄А₈ четырехугольника А₃А₄А₇А₈ являются диаметрами окружности, в которую вписан данный восьмиугольник, поэтому они равны и точкой пересечения О делятся пополам. Следовательно, четырехугольник А₃А₄А₇А₈ – прямоугольник. Так как угол А₃ОА₄ = 45°, то согласно задаче 1059 площадь прямоугольника равна R².

4. Решить задачу № 1105 (в) (объясняет учитель).

Решение

Пусть  АВС – данный  треугольник,  угол  С = 90°, угол В = , АВ = с, ВС = а,  СА = b;  Р = а + b + с, r – радиус  вписанной  окружности.  Тогда а = с · cos , b = c · sin .

Воспользуемся двумя формулами для вычисления площади S треугольника АВС (метод площадей):

  . Отсюда, получаем,

r =, поэтому C = 2πr =.

Умножив числитель и знаменатель дроби на cos  + sin  – 1, после несложных преобразований получаем: c = πc (sin  + cos  – 1).

5. Решить задачу № 1117 (в).

S_круга = .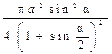

6. Решить задачи № 1110, 1138, 1116 (в).

Примечание. решения некоторых из них полезно предварительно обсудить, а затем записать в тетрадях, остальные задачи учащиеся могут решить самостоятельно с последующей проверкой ответов или решений.

III. Проверочная самостоятельная работа. Вариант I №№ 1125, 1129 (в), 1132 (а), 1134 (а).

Вариант II.  №№ 1128, 1129 (г), 1132 (б), 1134 (б).

IV. Итоги уроков.

Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 105–112 и ответив на вопросы 1–12, с. 290 учебника; решить задачи №№ 1104 (г, д), 1105 (б), 1116 (в).

Урок 11.                         Контрольная работа № 3

Цели: проверить умение учащихся решать задачи по изученной теме; выявить пробелы в знаниях учащихся для последующего их устранения.

Ход урока

I. Организация учащихся для выполнения контрольной работы.

II. Выполнение работы по вариантам.

Вариант I

1. Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.

2. Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 дм².

3. Найдите длину дуги окружности радиуса 3 см, если ее градусная мера равна 150°.

Вариант II

1. Периметр правильного шестиугольника, вписанного в окружность, равен 48 м. Найдите сторону квадрата, вписанного в ту же окружность.

2. Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72 см².

3. Найдите площадь кругового сектора, если градусная мера его дуги равна 120°, а радиус круга равен 12 см.

вариант III

1. Периметр квадрата, вписанного в окружность, равен 48 см. найдите сторону правильного пятиугольника, вписанного в ту же окружность.

2. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.

3. Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 4 м, а градусная мера дуги равна 60°.

Вариант IV

1. Периметр правильного пятиугольника, вписанного в окружность, равен 6 дм. Найдите сторону правильного треугольника, вписанного в ту же окружность.

2. Площадь кольца, ограниченного двумя окружностями с общим центром, равна 45π м², а радиус меньшей окружности равен 3 м. Найдите радиус большей окружности.

3. Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 2 см, а диаметр окружности равен 4 см.

Домашнее задание:  повторить  пункт  47  «Осевая  и  центральная  симметрии».

 

 

 

 

 

 

 

 

ДВИЖЕНИЯ. (8 часов)

Уроки 1–3. Отображение плоскости на себя.   Понятие движения

Цели: ввести понятие отображения плоскости на себя и понятие движения; напомнить построение фигур относительно центра и относительно оси; рассмотреть свойства осевой и центральной симметрии и закрепить их знание при решении задач.

Ход уроков

I. Анализ контрольной работы. 1. Указать ошибки, сделанные учащимися при решении задач.

2. Решить на доске задачи, вызвавшие затруднения у учащихся.

II. Повторение ранее изученного материала.

1. Повторение понятий точек, симметричных относительно данной прямой (оси симметрии), и точек, симметричных относительно данной точки (центра симметрии).

2. В ходе повторения нужно подвести учащихся к понятию сохранения расстояния между точками. Этой цели служат следующие задачи:

1) Для каждого из случаев, представленных на рисунке 1, а, б, в, постройте точки А₁ и В₁, симметричные точкам А и В относительно прямой l.

                        

                   а                            б                                             в

Рис. 1

2) Существует ли на плоскости такая точка, для которой нет симметричной точки относительно данной прямой?

3) Докажите,  что  в  каждом  из  рассмотренных  в  задаче  1  случаев
А₁В₁ = АВ.

4) Постройте  точки  А₁ и В₁,  симметричные А и В относительно точки О, если:

а) точка О лежит на отрезке АВ;     б) точка О не лежит на прямой АВ.

5) Существует ли такая точка плоскости, для которой нет точки, симметричной относительно данной точки?

6) Докажите,  что  в  каждом  из  рассмотренных  в  задаче  4  случаев
А₁В₁ = АВ.

III. Изучение нового материала.

1. Ввести понятие отображения плоскости на себя и проиллюстрировать его примерами осевой и центральной симметрий.

Важно подчеркнуть, что при отображении плоскости на себя выполняются два условия:

1) каждой точке плоскости ставится в соответствие какая-то одна точка плоскости и 2) каждая точка плоскости оказывается поставленной в соответствие какой-то точке плоскости.

2. Решить задачи № 1148 (а) и №1149 (а). 3. Ввести понятие движения, опираясь на задачи 3 и 6, рассмотренные в начале урока.   4. Решить задачу № 1153

5. Доказать,  что  осевая  и  центральная  симметрии  являются  движениями.

IV. Закрепление изученного материала. Решение задачи № 1150 №№ 1151, 1152 (а, б), 1158.

№ 1156 и решить задачи №№ 1154, 1157, 1155.

V. Итоги уроков.

Домашнее задание: изучить материал пунктов 113–114; ответить на вопросы 1–13, с. 303 учебника; решить задачи №№ 1149 (б), 1148 (б), 1159, 1160, 1161, 1174.     №№ 1152, 1159, 1161.

Урок 4. Тема:Параллельный перенос

Цели: ввести понятие параллельного переноса, доказать, что параллельный перенос является движением; научить решать задачи с использованием параллельного переноса.

Ход урока

I. Проверка изученного материала.

1. По таблицам «Центральная симметрия» и «Осевая симметрия» повторить построение геометрических фигур и свойства движения.

2. Ответить на вопросы 1–13 на с. 303.

II. Изучение нового материала.

Теоретический материал пункта 116 можно изложить в виде лекции, используя таблицу «Параллельный перенос».

1. Определение параллельного переноса.

2. Доказательство утверждения, что параллельный перенос является движением (рис. 329).

3. При параллельном переносе прямая отображается на параллельную ей прямую или сама на себя. Отсюда следует простой способ построения образов прямых и отрезков при параллельном переносе.

4. Построение образов прямых и отрезков при параллельном переносе учителем на доске, а учащимися в тетрадях.

III. Закрепление изученного материала.

1. Решить задачи № 1162 и №1163 (б) на доске и в тетрадях.

2. Решить задачу № 1164.

IV. Итоги урока.

Домашнее задание:  изучить материал пункта 116; решить задачи №№ 1163 (а), 1165. Принести циркули и транспортиры.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Уроки 5–6.   Поворот

Цели: ввести понятие поворота; доказать, что поворот является движением; научить учащихся построению геометрических фигур при повороте фигуры на данный угол.

Ход уроков

I. Проверочная работа (15 мин).

Задачи:

1) Даны  треугольник  МNK  и  точка  О.  Постройте фигуру F, на которую отображается треугольник MNK при центральной симметрии с центром О.

2) Даны прямая l и четырехугольник РМЕС. Постройте фигуру F, на которую отображается данный четырехугольник при осевой симметрии с осью l.

3) Даны  окружность  с  центром  О  и  прямая  l. Постройте фигуру F, на которую отображается данная окружность при осевой симметрии с осью l.

II. Объяснение нового материала (лекция).

Теоретический материал пункта «Поворот» можно изложить в форме лекции.

1. Определение поворота  плоскости  вокруг  точки  О  на  угол  (рис. 330).

2. Поворот вокруг точки О по часовой стрелке или против часовой стрелки (использовать таблицу «Поворот»).

3. Доказательство утверждения,  что  поворот  является  движением, то есть отображением плоскости на себя, сохраняющим расстояния (рис. 331).

III. Закрепление изученного материала.

1. Решить задачу № 1166 на доске и в тетрадях..2. Решить задачи № 1167 и №1169 (

3. Полезно предложить учащимся самостоятельно изучить решение задачи № 1171 (а),

4.Задачи:1) Через центр квадрата проведены две взаимно перпендикулярные прямые. Докажите, что их точки пересечения со сторонами квадрата являются вершинами другого квадрата.

2) Докажите, что при повороте правильного треугольника АВС вокруг вершины А на 60° либо вершина В переходит в вершину С, либо вершина С переходит в вершину В.

5. Решить задачу № 1170 (б).

IV. С/Р . Вариант I. 1. В трапеции АВСD боковые стороны АВ и СD равны.

1) Постройте отрезок СА₁, на который отображается сторона АВ при параллельном переносе на .

2) Найдите площадь треугольника А₁СD, если АD = 10 см, ВС = 4 см, АВ = 6 см.

2. Докажите, что правильный шестиугольник при повороте на 60° вокруг своего центра отображается на себя.

Вариант II.  1. Точка М – середина стороны АС треугольника АВС.

1) Постройте отрезок МВ₁, на который отображается сторона АВ при параллельном переносе на.

2) Найдите периметр треугольника МDС, где D – точка пересечения отрезков ВС и МВ₁, если периметр треугольника АВС равен 12 м.

2. Докажите, что правильный пятиугольник при повороте на 72° вокруг своего центра отображается на себя.

V. Итоги уроков.

Домашнее задание: изучить материал пунктов 116–117; ответить на вопросы 14–17, с. 304 учебника; решить задачи № 1168, 1170 (а), 1171 (б), 1183; подготовиться к устному опросу по карточкам, повторив материал пунктов 113–114.

 

Урок 7. Тема: Решение задач

Цели: закрепить знания учащихся по теме «Движения», развивать умение решать задачи с применением движений.

Ход  урока

I. Устный опрос учащихся по карточкам.

Карточка 1 . 1. Объясните, что такое отображение плоскости на себя.

2. Докажите, что параллельный перенос является движением.

3. Точка М – середина стороны ВС правильного треугольника АВС, точки N и K симметричны точке М относительно прямых АВ и АС. Докажите, что NK  АМ.

Карточка 2. 1. Что такое движение плоскости?

2. Докажите, что осевая симметрия является отображением плоскости на себя.

3. На окружности с центром О и радиусом r отмечена точка А. Постройте окружность, на которую отображается данная окружность при повороте вокруг точки А на 60° по часовой стрелке. найдите длину отрезка, соединяющего точки пересечения данной и построенной окружностей.

Карточка 3. 1. На какую фигуру отображается при движении отрезок?

2. Докажите, что центральная симметрия является движением.

3. Дан равнобедренный треугольник АВС с основанием ВС. Постройте точки D и Е, на которые отображаются точки А и С при параллельном переносе на вектор , и докажите, что АЕ = DВ.

Карточка 4. 1. На какую фигуру отображается при движении треугольник?

2. Докажите, что поворот плоскости вокруг точки является движением.

3. Точка пересечения диагоналей четырехугольника АВСD является его центром симметрии. Докажите, что АВСD – параллелограмм.

II. Решение задач. 1. №№ 1172, 1173, 1177, 1180.2. Полезно обсудить  № 1176, №1178.

3. Задачи №№ 1174, 1175, 1181 и 1182 можно предложить учащимся решить самостоятельно, а затем обсудить полученные решения.

Решения 1) Задача № 1173.

Пусть g – данное движение, а е – тождественное отображение плоскости на себя, то есть отображение, при котором каждая точка плоскости и, в частности, каждая вершина треугольника АВС отображается на себя. Ясно, что е – движение, поэтому согласно задаче № 1155 движения g и е совпадают, и, значит, движение g является тождественным отображением плоскости на себя.

.

Домашнее задание: подготовиться к контрольной работе: повторить материал пунктов 113–117 и ответить на вопросы 1–17, с. 303–304 учебника; решить задачи №№ 1219, 1220, 1221, 1222.

 

 

 

 

 

 

 

 

Урок 8. ТЕМА:Контрольная работа № 4

Цели: проверить знания, умения и навыки учащихся в решении задач по теме «Движения».

Ход урока

I. Организация учащихся на выполнение работы.

II. Выполнение работы по вариантам.

Вариант I

1. Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую сторону АВ.

2. Две  окружности  с  центрами  О₁ и О₂, радиусы которых равны, пересекаются в точках М и N. Через точку М проведена прямая, параллельная О₁О₂ и пересекающая окружность с центром О₂ в точке D. используя параллельный перенос, докажите, что четырехугольник О₁МDО₂ является параллелограммом.

Вариант II

1. Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой стороны СD.

2. Дан  шестиугольник  А₁А₂А₃А₄А₅А₆.  Его  стороны  А₁А₂  и  А₄А₅, А₂А₃ и А₅А₆, А₃А₄ и А₆А₁ попарно равны и параллельны. Используя центральную симметрию, докажите, что диагонали А₁А₄, А₂А₅, А₃А₆ данного шестиугольника пересекаются в одной точке.

Вариант III

1. Дана трапеция АВСD с основаниями АD и ВС. Постройте фигуру, на которую отображается эта трапеция при повороте вокруг точки А на угол, равный углу DАВ, по часовой стрелке.

2. На одной стороне угла ХОY отложены отрезки ОА и ОВ, а на другой стороне – отрезки ОМ и ОN так, что ОМ = ОА, ОN = ОВ. Используя осевую симметрию, докажите, что точка пересечения отрезков МВ и АN лежит на биссектрисе угла ХОY.

Вариант IV

1. Дана трапеция АВСD с основаниями АD и ВС. Постройте фигуру, на которую отображается эта трапеция при параллельном переносе на вектор .

2. На биссектрисе внешнего угла при вершине С треугольника АВС взята точка М. Используя осевую симметрию, докажите, что

АС + СВ < АМ + МВ.

Домашнее задание: повторить пункты 27–28 «Об аксиомах геометрии» и «Аксиома параллельных прямых».

 

 

 

 

 

 

 

 

 

 

НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ (7 часов)

Урок 1. Тема: Предмет стереометрии. Многогранник

Цели: познакомить учащихся с новым разделом геометрии – стереометрией, с геометрическими телами и их поверхностями; рассмотреть различные многогранники и научить учащихся изображать их.

Ход урока

I. Изучение нового материала. Материал пунктов 118 и 119

 1.Раздел геометрии, в котором изучаются свойства фигур в пространстве, называется стереометрией. Это слово происходит от греческих слов «стерео» – объемный, пространственный и «метрео» – измерять.

3. В стереометрии наряду с простейшими фигурами – точками, прямыми и плоскостями – рассматриваются геометрические тела и их поверхности. Представление о геометрических телах дают окружающие нас предметы. Такие поверхности называются многогранниками.

4. Рассмотрим простейший многогранник – куб (рис. 335, а) и модель куба.

Сколько граней, ребер и вершин имеет куб?

5. Познакомить учащихся с другими геометрическими телами:

1) шаром (рис. 335, б), такую же форму имеет футбольный мяч;

2) цилиндром (рис. 335, в), эту форму имеет консервная банка.

6. Ввести понятие границы геометрического тела; понятие секущей плоскости тела; понятие сечения тела (рис. 336). 7. Изображение геометрических тел на чертеже (рис. 337, а, б, в).

На доске и в тетрадях учащиеся выполняют рисунки параллелепипеда, пирамиды, конуса, цилиндра.

8. Многогранник – это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Это тело также называют многогранником (рассмотреть по учебнику рис. 339).

Тетраэдр составлен из четырех треугольников; по-гречески «тетра» – четыре.

Октаэдр составлен из восьми треугольников; по-гречески «окто» – восемь.

9. Многогранники  бывают  выпуклыми  и  невыпуклыми  (рис. 339 и рис. 340).

II. Закрепление изученного материала.  решение задач.

1. Решить устно задачу № 1184 (б) и (в), используя модели тетраэдра и октаэдра.

Ответ: б) тетраэдр имеет 4 грани, 6 ребер и 4 вершины; в) октаэдр имеет 8 граней, 12 ребер и 6 вершин.

2. Решить задачу № 1188 на доске и в тетрадях.

Перед построением сечения в тетрадях записывают следующие правила:

1) Через любые две точки проходит прямая, и притом только одна.

2) если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

3) отрезки, по которым секущая плоскость пересекает две противоположные грани параллелепипеда, параллельны.

III. Итоги урока.

– Объясните, что такое многогранник; что такое грани, ребра, вершины и диагонали многогранника. Приведите примеры многогранников.

Домашнее задание:  изучить материал пунктов 118 и 119; решить задачу № 1188 (разобрать построение сечения параллелепипеда плоскостью по учебнику на с. 322, используя рис. 356, а и б; выполнить построение сечения в тетрадях).

Урок 2. Тема: Призма. Параллелепипед

Цели: ввести понятие призмы и ее элементов; дать определение прямой и наклонной призмы, определение высоты призмы; ввести понятие параллелепипеда, понятие прямого и прямоугольного параллелепипеда; научить строить призмы и параллелепипеды.

Ход урока

I. Устная работа.

Проверить усвоение предшествующего материала в процессе решения устных задач по готовым чертежам на доске и с использованием моделей геометрических тел.

Ответить на вопросы: 1. Какой раздел геометрии называется стереометрией?

2. Что рассматривается в стереометрии?

3. Какие поверхности называются многогранниками? Приведите примеры простейших многогранников.

4. Какая плоскость называется секущей плоскостью геометрического тела?

5. Что называется сечением тела?

6. Объясните, что такое многогранник; что такое грани, ребра, вершины и диагонали многогранника. Приведите примеры многогранников.

Учитель показывает модели различных геометрических тел и многогранников, а учащиеся должны назвать их.

II. Объяснение нового материала.

1. Используя рисунок учебника (рис. 341, с. 311), учитель объясняет построение многогранника, называемого призмой.

1) две плоскости называются параллельными, если они не имеют общих точек;

2) две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Четырехугольная призма, основаниями которой являются параллелограммы, называется параллелепипедом (рис. 345). Все шесть граней параллелепипеда – параллелограммы.

III. Закрепление изученного материала.

1. Решить задачу № 1185.

2. Решить задачу № 1186.

               

3. Устно решить задачу  № 1187,  используя  модель  параллелепипеда.

Ответ: а) нет;  б) нет;  в) нет;  г) да;  д) нет.

IV. Итоги урока.

1. Объясните, как построить многогранник, называемый n-угольной призмой; что такое основания, боковые грани, боковые ребра и высота призмы.

2. Какая призма называется: а) прямой; б) правильной?

3. Объясните, что такое параллелепипед; какие многоугольники являются гранями: а) параллелепипеда; б) прямого параллелепипеда; в) прямоугольного параллелепипеда.

Домашнее задание: изучить материал пунктов 120 и 121; выполнить рисунки (рис. 346, а, б, в) и записать в тетрадях доказательство свойства диагоналей параллелепипеда.

 

 

Урок 3. Тема:  Объем тела. Свойства прямоугольного
параллелепипеда

Цели: повторить понятие площади плоских фигур, ввести понятие объема тела, единиц измерения объемов тел; изучить основные свойства объемов и прямоугольного параллелепипеда; познакомить учащихся с принципом Кавальери; развивать логическое мышление учащихся.

Ход урока

I. Проверка домашнего задания.

1. Проверить по тетрадям решение учащимися задач № 1190 (б) и № 1234 (б).

2. По готовому на доске чертежу параллелепипеда построить сечение параллелепипеда плоскостью, проходящей через:

а) точки D, С и В₁;

б) точки В, K и L, где K – середина ребра АА₁, а L – середина СС₁.

(Это задача № 1235 на с. 337 учебника.)

                                                   

II. Изучение нового материала.  1. Повторить понятие площади плоской фигуры.

2. Понятие объема тела вводится по аналогии с понятием площади плоской фигуры. За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называется кубическим сантиметром и обозначается так: 1 см³. Аналогично определяются кубический метр (м³), кубический миллиметр (мм³) и т. д.

3. Прочитать по учебнику текст (с. 314 и 315) и записать в тетрадях основные свойства объемов:

1) Равные тела имеют равные объемы.

2) Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел (рис. 347):

V = V₁ + V₂.

Доказательство записывать на доске и в тетрадях:

АС₁² = АС² + СС₁² АС² = АВ² + АD²;  СС₁ = ВВ₁ = АА₁,     следовательно, АС₁² = АВ² + АD² + АА₁².

.Поэтому формулу V = a ∙  b ∙  c можно записать в виде ,

то есть объем прямоугольного параллелепипеда равен произведению площади основания на высоту.

III. Выполнение упражнений и решение задач. № 1193 (б; в).№ 1193 (в) № 1193 (б) № 1194.

№ 1195.№ 1198 , № 1197.

IV. Итоги урока. 1. Объясните, как измеряются объемы тел.

2. Сформулируйте основные свойства объемов.

3. Что такое измерения прямоугольного параллелепипеда?

4. Сформулируйте свойство диагонали прямоугольного параллелепипеда.

5. Чему равен объем прямоугольного параллелепипеда?

Домашнее задание:  изучить  материал  пунктов  122–123;  сделать чертеж (рис. 357) и записать в тетрадях решение задач №№ 1193 (а), 1196, 1198.

 

Урок 4. Тема: Пирамида

Цели: познакомить учащихся с понятием пирамиды (ее основания, боковые грани, вершины пирамиды, боковые ребера пирамиды); дать определение правильной пирамиды, апофемы пирамиды; вывести формулу объема пирамиды; развивать логическое мышление учащихся.

Ход урока

I. Актуализация опорных знаний учащихся.1. Что называется призмой? Прямой призмой? Правильной?

2. Объясните, что такое параллелепипед? Дайте определение прямого параллелепипеда, прямоугольного параллелепипеда.

3.Сформулируйтесвойство четырех диагоналей параллелепипеда.

4. Сформулируйте основные свойства объемов.

5. Что такое измерения прямоугольного параллелепипеда?

6. Сформулируйте свойство диагонали прямоугольного параллелепипеда.

7. Чему равен объем куба? Объем прямоугольного параллелепипеда?

8. Какой формулой выражается объем призмы?

9. Проверить решение домашней задачи № 1196.

Решение

a = 8 см, b = 12 см, с = 18 см.

V = a ∙  b ∙  c = 8 ∙  12 ∙  18 (см³).

По условию объем куба равен объему прямоугольного параллелепипеда. Значит, V_куба = a³ = 8 ∙  12 ∙  18 (см³). Отсюда ребро куба равно

a == 2 ∙  2 ∙  3 = 12 (см); a = 12 см. Ответ: 12 см.

II. Работа учащихся по учебнику.

1. Учащиеся самостоятельно изучают материал пункта 124 «Пирамида» 2. Затем учитель на моделях различных пирамид объясняет учащимся, что такое пирамида, основание пирамиды, боковые грани пирамиды, вершина пирамиды, боковые ребра пирамиды.

3. Треугольную пирамиду часто называют тетраэдром.

4. На доске и в тетрадях строятся изображения пирамиды; проводится высота пирамиды и апофема

5. В тетрадях учащиеся записывают определения:

а) Отрезок, соединяющий вершину пирамиды с плоскостью ее основания  и  перпендикулярный  к  этой  плоскости,  называется  высотой  пирамиды.

б) Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.

в) Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.

6. Объем пирамиды равен одной трети произведения площади основания на высоту .

III. Выполнение упражнений. Решение задач. № 1201,  № 1202 (а) № 1203 № 1204. № 1206.

№ 1241. № 1242.

IV. Итоги урока. Выставление оценок.

Домашнее задание: изучить материал пункта 124; повторить пункты 118–123; ответить на вопросы 1–14 на с. 335–336 учебника; решить задачи № 1202 (б), № 1211 (а), № 1207.

Урок 5. Тема: Цилиндр

Цели: ввести понятие цилиндра (ось цилиндра, его высота, основания цилиндра); ввести понятие цилиндрической поверхности, образующих цилиндра; доказать теорему об объеме цилиндра и теорему о площади боковой поверхности цилиндра; научить применять эти теоремы при решении задач.

Ход урока

I. Объяснение нового материала.

1. Возьмем прямоугольник АВСD и будем вращать его вокруг одной из сторон, например, вокруг стороны АВ (рис. 360). В результате получится тело, которое называется цилиндром.

Учитель показывает модель цилиндра.

 (рис. 360 на с. 327). основаниями ,радиусом цилиндра. При вращении стороны СD образуется поверхность, состоящая из отрезков, параллельных оси цилиндра. Ее называют цилиндрической поверхностью или боковой поверхностью цилиндра, а отрезки, из которых она составлена, – образующими цилиндра. Таким образом, цилиндр – это тело, ограниченное двумя равными кругами и цилиндрической поверхностью.

3.Рассмотреть решение задачи № 1213 (рис. 366, с. 331 учебника). Пользуясь принципом Кавальери, можно доказать, что объем цилиндра равен произведению площади основания на высоту

 ,где r – радиус основания цилиндра, h – высота .

II. Закрепление изученного материала.. Решить задачу № 1214 (б; в) ,№ 1216. ,№ 1217

 № 1245.

. Решить задачу № 1246. (Учитель объясняет решение.)

Решение

По условию задачи h > r на 12 см, тогда h = r + 12 см.

= 288π см². Найти r и h.

= 2S_осн + S_бок = 2 ∙  πr² + 2πrh = 2πr² + 2πr ∙  (r + 12) = 2πr² + 2πr² + 24πr = 4πr² + 24πr.

По условию S_полн = 288π (см²), тогда 4πr² + 24πr = 288π; разделим обе части равенства на 4π, получим   r² = 6r – 72 = 0.  r₁ = 6; r₂ = – 12 – не удовлетворяет условию задачи.

Значит, радиус цилиндр аравен 6см, а высота цилиндра 6+12= 18 (см). Ответ: 6 см; 18 см.

. Решить задачу № 1247.Ответ: .

III. Итоги урока.

Ответить на вопросы:

1. Какое тело называется цилиндром? Что такое ось, высота, основания, радиус, боковая поверхность, образующие цилиндра?

2. Какой формулой выражается объем цилиндра?

3. Какой  формулой  выражается  площадь  боковой  поверхности  цилиндра?

Домашнее задание:  изучить  материал  пункта 125, решить задачи № 1214 (а) и № 1244.

Урок 6. Тема: Конус

Цели: познакомить учащихся с понятием конуса, его элементами; вывести формулу, выражающую объем конуса и формулу площади боковой поверхности конуса; учить решать задачи; способствовать развитию логического мышления учащихся.

Ход урока

I. Проверка домашнего задания.

1. Двое учащихся решают на доске задачи № 1214 (а) и № 1244, заданные на дом.

2. С остальными учащимися проводится работа по ответам на вопросы 15–18 (с. 336 учебника).

Решение задачи № 1214 (а). Дано: r = 2см; h = 3 см. Найти: V.

V = Sh = πr²h = π ∙  (2)² ∙  3 = 24π (см³). Ответ: см³.

№ 1244. Дано: d = 4 мм = 0,4 см; m = 6,8 кг; с = 2,6 г/см³. Найти: h (длину провода).

с =;   V =;   V =≈ 2615 (см³);   r = 0,2 см.  V_цил = S_осн ∙  h = πr²h,

отсюда  h =≈ 20820 (см) ≈ 208 м. Ответ: ≈ 208 м.

II. Изучение нового материала.

Учитель демонстрирует модели конуса, лейку в виде конуса; можно свернуть из бумаги кулек в виде конуса.   (рис. 362, с. 328 учебника).

Учитель показывает на доске изображение конуса, учащиеся рисуют конус в тетради.

Объем конуса равен одной трети произведения площади основания на высоту.

,  , .

III. Выполнение упражнений.№ 1220 (б, в). № 1221 ,№ 1222.№ 1248. Учитель объясняет решение задачи.№ 1249.

 Решить задачу № 1250.                    Решение

По условию α = 120°. Радиус развертки боковой поверхности конуса равен образующей конуса, то есть l = r₁ = 9 см, где r₁ – радиус сектора.

1) S_бок =∙  α =∙  120° = 27π (см²).

2) С другой стороны,  S_бок = πrl,  значит,  27π = π ∙  r ∙  9, отсюда r = 3 см (это радиус конуса).

3) S_осн = πr² = π ∙  3² = 9π (см²).

4)h²=l²–r² ,то h==== 6(см).

Ответ: 9π см²; 6см.

IV. Итоги урока.

Домашнее задание: изучить материал пункта 126; ответить на вопросы 19–22 (с. 336 учебника); решить задачу № 1220 (а); записать в тетрадь решение задачи № 1219 (с. 332 –333 учебника).

 

Урок 7. Тема: Сфера и шар

Цели: ввести понятие сферы, центра сферы, радиуса сферы, диаметра; дать определение шара; научить учащихся изображать шар; рассмотреть доказательство теоремы об объеме шара и площади сферы; развивать умение решать задачи.

Ход урока

I. Проверочная работа (10 мин).  Вариант 1

1. Объясните, какое тело называется цилиндром; что такое ось, высота, основание, радиус, боковая поверхность, образующие цилиндра. Выполните построение цилиндра.

2. Какой формулой выражается объем цилиндра? Запишите формулу.

3. Объясните, как получается и что представляет собой развертка боковой поверхности цилиндра.

4. Запишите формулу площади боковой поверхности цилиндра.

Вариант 2. 1. Объясните, какое тело называется конусом; что такое ось, высота, основание, боковая поверхность, образующие конуса. Выполните построение конуса.

2. Какой формулой выражается объем конуса? Запишите формулу.

3. Объясните, как получается и что представляет собой развертка боковой поверхности конуса.

4. Запишите формулу площади боковой поверхности конуса.

II. Работа с учебником. Изучают материал пункта 127 «Сфера и шар» (с. 330–331).

а) Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Данная точка называется центром сферы, а данное расстояние – радиусом сферы.

б) Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы.

в) Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.

г) Объем шара радиуса R равен πR³.д) Площадь сферы радиуса R равна 4πR².

                      

III. Закрепление изученного материала. Решить № 1226 (б; в).  № 1227,№ 1229.

Учащиеся решают самостоятельно. затем проверяется решение задачи.

Решение

По  условию  R = 10 см.  По  формуле S = 4πR² найдем площадь сферы (покрышки футбольного мяча).

S = 4π ∙  10² = 400π (см²) ≈ 400 ∙  3,14 ≈ 1256 (см²).8 % = 0,08 от 1256 равно 1256 ∙  0,08 = 100,48 (см²).

На покрышку футбольного мяча необходимо кожи:  1256 + 100,48 = 1356,48 ≈ 1357.Ответ: ≈ 1357 см².

№ 1228 ,№ 1231 на доске и в тетрадях.

Решение

Отношение объемов двух шаров равно кубу коэффициента подобия, так как любые шары – это подобные тела.

= k³.     = 8 = 2³,  k = 2.   = k².   так как k = 2,  то = 2² = 4,   то есть S₁ : S₂ = 4 : 1.

Ответ: 4 : 1.

IV. Итоги урока.

Домашнее задание: изучить материал пункта 127, ответить на вопросы 23–26, записать в тетради решение задач  №№ 1224, 1225 (с. 333–335 учебника).

 

Об аксиомах и планиметрии (2 часа)

При  завершении  курса  планиметрии  в  конце  9  класса  два  урока отводятся на ознакомление учащихся с аксиоматическим методом, в частности с системой аксиом, которые положены в основу изученного курса геометрии.

На первом уроке желательно провести с учащимися беседу об аксиоматическом методе в геометрии. В связи с этим необходимо напомнить им некоторые факты о возникновении и развитии геометрии. Для этой беседы рекомендуется использовать приложения 1 и 3 учебника: «Об аксиомах планиметрии» и «Некоторые сведения о развитии геометрии», а также дополнительную литературу.

В  зависимости  от  уровня  подготовки  класса  на  втором  уроке  можно разобрать один или два примера теорем, которые в курсе были доказаны на основе наглядных представлений, и доказать их с использованием принятых в учебнике аксиом. Один из таких примеров (теорема, выражающая первый признак равенства треугольников) разобран в приложении 1 учебника.

 

Решение задач

при повторении курса геометрии необходимо сконцентрировать внимание учащихся на узловых вопросах программы.

Основные факты планиметрии и применяемые в ней методы можно сгруппировать по следующим темам:

1. «Треугольник» (2 часа).

2. «Окружность» (2 часа).

3. «Четырехугольники, многоугольники» (2 часа).

4. «Векторы, метод координат, движения» (2 часа).

Рассмотрение этих вопросов может включать обобщение и систематизацию сведений об основных свойствах геометрических фигур, доказательство отдельных теорем, решение комплексных задач.

При повторении полезно обращать внимание учащихся на различные методы геометрических доказательств. В зависимости от подготовки класса повторение можно проводить по всем или отдельным вопросам рассматриваемой темы.

Для организации итогового повторения можно воспользоваться подбором задач по указанным выше темам

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Треугольник

Основные вопросы программы: равенство и подобие треугольников, сумма углов треугольника, равнобедренный треугольник, прямоугольный треугольник, площадь треугольника.

Задачи

1. В  треугольниках  АВС  и  DЕK  АВ = DЕ,  АС = DK,  ВР = ЕМ, где Р и М – середины сторон АС и DK.

1) Докажите, что треугольник АВС равен треугольнику DЕK.

2) Найдите S_АВС, если ЕМ = 3 см, DK = 4см, ЕМK = 135°.

2. В треугольниках АВС и А₁В₁С₁  АС = А₁С₁, ВС = В₁С₁, ВD = В₁D₁, где ВD и В₁D₁ – высоты треугольников, причем точки D и D₁ лежат на отрезках АС и А₁С₁.

1) Докажите, что треугольник АВС равен треугольнику А₁В₁С₁.

2) Найдите радиус окружности, описанной около треугольника В₁D₁С₁, если известно, что ВD = 6 см, DС = 8 см.

3) Найдите угол А₁С₁В₁, если ВD = 6 см, DС = 8 см.

3. На рисунке  дан прямоугольный треугольник АВС с гипотенузой АВ, DЕ  АВ.

1) Докажите, что треугольник АВС и треугольник DАЕ подобны. 2) Найдите катеты треугольника АВС, если АВ = 13 см, АЕ = 5,2 см, DЕ = 2 см. 3) Докажите, что около четырехугольника ВDЕС можно описать окружность.

4. В прямоугольном треугольнике АВС проведена высота СD к гипотенузе АВ, СD = а, АD = b.

найдите: 1) ВС; 2) радиус окружности, вписанной в треугольник АВС; 3) отношение площадей треугольников АDС и АСВ.

5. В треугольнике АВС  АВ = 14 см, АС = 15 см, ВС = 13 см.

найдите: 1) длину меньшей высоты треугольника; 2) площадь треугольника АDС, если АD – биссектриса треугольника АВС; 3) медиану АЕ треугольника АВС.

6. С помощью циркуля и линейки постройте треугольник АВС по сторонам АВ и АС и высоте, проведенной к АС.

7. Площадь треугольника АВС равна Q. Найдите площадь треугольника АОВ₁, где О – точка пересечения медиан треугольника АВС, а В₁ – середина стороны АС.

8. С помощью циркуля и линейки постройте равнобедренный треугольник АВС по основанию АС и углу В и биссектрису ВD внешнего угла этого треугольника при вершине В.

 

 

 

 

окружность

Основные вопросы программы: окружность и круг, касательная к окружности и ее свойства; окружность, описанная около треугольника; окружность, вписанная в треугольник.

Задачи

1. Хорда АВ окружности радиуса 4 см видна из центра под углом 90°.

Найдите: 1) хорду АВ и расстояние от центра окружности до этой хорды; 2) углы треугольника АВС, где С – точка, расположенная на большой дуге АВ окружности так, что АС : СВ = 5 : 4; 3) хорду ВС.

2. Две взаимно перпендикулярные хорды АВ и СD окружности пересекаются в точке K, причем АK = 6 см, ВK = 32 см, KD = 24 см.

Найдите: 1) хорды  ВD  и  СD;  2) расстояние от точки А до прямой ВD; 3) радиус данной окружности.

3. Треугольник АВС с углом В, равным 135°, вписан в окружность с центром О и радиусом R = 10см.

Найдите: 1) сторону АВ; 2) сторону АВ и S_АВС, если известно, что угол АСВ равен 30°.

4. Точки  М,  D и K лежат на окружности,  угол DМK равен 45°, хорда DK = 12 см.

Найдите: 1) радиус данной окружности; 2) угол МКD, если известно, что DМ = 6см.

5. Радиус окружности, вписанной в равнобедренный треугольник АВС с основанием АС, равен 3 см, KВ = 4 см, где K – точка касания окружности с боковой стороной.

Найдите: 1) сторону АС; 2) угол ВАС; 3) радиус окружности, описанной около треугольника АВС.

6. В равнобедренный треугольник АВС с основанием АС вписана окружность, касающаяся сторон АВ и ВС в точках М и Н.

1) Докажите, что треугольник МВН  треугольнику АВС.

2) Найдите угол ВАС и радиус окружности, если АВ = 2 м, МН = 1 м.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Четырехугольники. Многоугольники

Основные вопросы программы: параллелограмм и его свойства; признаки параллелограмма; прямоугольник, ромб, квадрат и их свойства; трапеция, многоугольник, правильные многоугольники.

Задачи

1.На рисунке1 АЕFС–прямоугольник; АС=10см, АЕ=3см, ВМ = АМ.

1) Докажите, что МN – средняя линия треугольника АВС.

2) Найдите S_АМNС.  3) Найдите S_АВС.

          

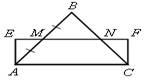
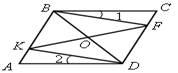
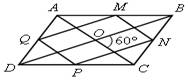
Рис. 1                                    Рис. 2                                        Рис. 3     

2. В параллелограмме АВСD биссектриса угла А пересекает сторону ВС в точке Е; АВ = а; АD = b. Найдите: 1) отрезки ВЕ и ЕС; 2) отрезки ВK и KD и S_АВЕ, если K – точка пересечения АЕ и ВD, а угол А равен 60°.

3. На рисунке 2 АВСD – параллелограмм, угол 1 равен углу 2.

1) Докажите, что четырехугольник ВFDK – параллелограмм, и найдите его площадь и периметр, если KF = 10 см, ВD = 6 см, KОD = 150°. 2) Каким условиям должны удовлетворять отрезки KF и ВD, чтобы параллелограмм ВFDK был прямоугольником (ромбом, квадратом)?

4. Меньшая диагональ параллелограмма перпендикулярна к его стороне, а высота, проведенная из вершины тупого угла, делит большую сторону на отрезки, равные 9 см и 16 см.

найдите:  1)  стороны  и высоту параллелограмма, проведенную из вершины тупого угла; 2) диагонали параллелограмма; 3) площадь параллелограмма.

5. В параллелограмме АВСD проведена биссектриса АK угла А, точка K делит сторону ВС на отрезки ВK = 4 см и KС = 2см. Расстояние между параллельными прямыми АD и ВС равно 2см.

Найдите: 1) углы параллелограмма; 2) площадь треугольника АВС; 3) радиус окружности, описанной около треугольника DКС.

6. На рисунке 3 точки М, N, Р и Q – середины сторон четырехугольника АВСD, АС = 10 см, ВD = 18 см.

1) Докажите,  что  MNPQ  –  параллелограмм, и найдите его периметр. 2) Найдите площади четырехугольников АВСD и MNPQ, если угол ВОС равен 60°.

7. В равнобедренную трапецию, основания которой равны 2 см и 8 см, вписана окружность.

Найдите: 1) боковую сторону трапеции; 2) радиус вписанной окружности; 3) площадь трапеции.

8. В равнобедренной трапеции с основаниями АD и ВС угол D равен 60°, ВС = 12 см, а угол ВСА равен 30°.

1) Докажите, что треугольник АВС равнобедренный. 2) Найдите радиус окружности, описанной около треугольника АСD. 3) Найдите площадь трапеции АВСD.

9. В ромб, сторона которого равна диагонали и равна а, вписана окружность, а в эту окружность вписан правильный треугольник.

Найдите: 1) радиус окружности; 2) сторону треугольника; 3) площади ромба, круга и правильного треугольника.

10. Каждый угол правильного п-угольника А₁А₂… А_п равен 150°.

1) Найдите число сторон этого многоугольника. 2) Найдите А₂А₃А₁₀. 3) Докажите, что треугольник А₁А₃В подобен треугольнику А₆А₁₀В, где В – точка пересечения диагоналей А₁А₆ и А₃А₁₀ этого многоугольника.

11. Внешний угол правильного п-угольника А₁А₂… А_п в три раза меньше угла этого многоугольника.

1) Найдите  число  сторон этого многоугольника. 2) Найдите А₃А₁А₆. 3) Докажите, что четырехугольник А₁А₃А₄А₈ – равнобедренная трапеция.

Векторы. метод координат. движения

Основные вопросы программы: вектор, длина вектора, сложение векторов и его свойства, умножение вектора на число и его свойства, коллинеарные векторы, прямоугольные координаты точек на плоскости, формула расстояния между двумя точками плоскости с заданными координатами, координаты середины отрезка, уравнения окружности и прямой, применение векторов и метода координат к доказательству теорем и решению задач. Движения.

Задачи

1. Четырехугольник АВСD задан координатами своих вершин: А (–3; –2), В (–1; 2), С (2; 2), D (4; –2).

1) Найдите координаты середин сторон этого четырехугольника.

2) Докажите, что середины сторон четырехугольника АВСD являются вершинами ромба, и найдите площадь этого ромба.

2. Дан четырехугольник АВСD.

1) Определите вид четырехугольника АВСD, если , и выразите вектор  через векторы  и .

2) Выразите векторы  через векторы  и , если М, N, Р и Q – середины сторон АВ, ВС, СD и АD.

3) Определите вид четырехугольника МNPQ.

3. Дан правильный шестиугольник АВСDЕF со стороной а. Найдите скалярное  произведение  векторов:  1) ; 2) ; 3) ; 4) .

4. Найдите косинусы углов треугольника АВС, если А (1; 3), В (8; 2), С (5; –1).

5. В  параллелограмме  АВСD  диагональ  ВD  равна  стороне  ВС,  точка М – середина стороны ВС, отрезок DМ перпендикулярен к диагонали АС. Найдите углы параллелограмма.

6. Две окружности радиуса r с центрами О₁ и О₂ касаются друг друга в точке М. На первой окружности отмечена точка А, а на второй – точка В так, что хорды АМ и ВМ взаимно перпендикулярны. Докажите, что: 1) при параллельном переносе на вектор  отрезок АС отображается на отрезок ВМ; 2) АВ = 2r.

7. На  сторонах  правильного треугольника построены квадраты. Докажите, что центры этих квадратов являются вершинами правильного треугольника.

Скачано с www.znanio.ru