Практическая работа №6. Тема: «Составление простых высказываний с помощью логических операции»

Практическая работа №6. Тема: «Составление простых высказываний с помощью логических операции»

Объектами логики являются высказывания. Простое суждение выражается

повествовательным предложением. Суждение может быть ЛОЖНЫМ или ИСТЕННЫМ. Высказывания будем обозначать буквами английского алфавита: A, B, C, D, и тд.

Пример высказывания: Высказывание A: В году двенадцать месяцев – ИСТИНА. Высказывание B: В январе тридцать дней –ЛОЖЬ.

Ложь и истину можно выразить знаками двоичной арифметики: ложь- обозначим 0, истину – обозначим 1. ð Высказывание А=1 (тк. оно истено). Высказывание B=0 (тк. оно ложно)

Существуют сложные высказывания, которые состоят из нескольких простых высказываний, связанных между собой операциями математической логики.

Пример сложного высказывания: Если тебе исполнилось 18 лет, то тебя пропустят в клуб. Если А, то В.

Унарные                                                                       Бинарные

Отрицание                                                             Конъюнкция, Дизъюнкция,

Импликация, Эквивалентность.

Рассматривать эти операции мы будем с помощью таблиц истинности. Таблицы истинности – это форма записи сложных логических выражений.

Решение логических выражений с 2-мя переменными.

1.      Конъюнкция (умножение) – обозначается Ù (АÙВ)или & (А&В) - читается «и».

2.      Дизъюнкция (сложение) – обозначается Ú (АÚВ) или + (А+В) - читается «или».

3.      Инверсия (отрицание)- обозначается А – читается «не А»

4.     

5.      Эквивалентность (равносильность ) – обозначается 🡘 (А🡘В)или ~(А~В) – читается А

эквивалентно В

Пример1. АÚХ                   Пример 2. АÙВ           Пример 3. АàВ

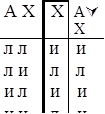
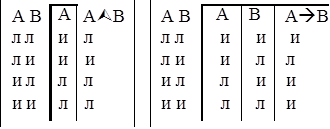
1.   УÙА    2. УÚВ    3. ВÚУ    4. ХÙА     5. АàХ    6. ХÙХ    7. ХÚХ    8. ХàУ   9. АàВ🡘АÚВ

10. (АÚВ)🡘(АàВ)