Практическая работа №6
Тема: «Нахождение площадей многогранников»
Цель: уметь применять формулы для нахождения площадей (боковой и полной поверхностей) многогранников: призмы, пирамиды, усеченной пирамиды при обосновании этапов решения задач; уметь выполнять чертежи любых многогранников по условию задачи, понимать чертежи, находить на чертежах основные элементы многогранников.
Оборудование: ручка, простой карандаш, линейка, методические рекомендации по выполнению работы.
Методические рекомендации по выполнению практической работы:
Задание №1. Основанием прямой призмы является равнобедренная трапеция с основаниями 21см и 9 см и высотой 8 см (рис. 1). Найдите площадь боковой поверхности, если боковое ребро равно 10 см.
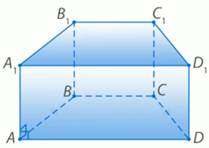
Рис. 1
Дано: AD ∥ BC, AB = CD,
AD = 21см, BC = 9см, BH = 8 см,
АА1 ⊥ АВС, АА1 = 10 см. (рис. 2)
Найти: Sбок
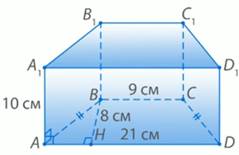
Рис. 2
Решение:
Рассмотрим
трапецию ABCD (рис. 3). ВН и CG – высоты трапеции. AD=21см,
BC=9см. Так как трапеция ABСD равнобокая, то HG=BC=9см,
(см).
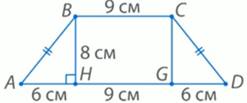
Рис. 3
Рассмотрим треугольник ∆АВН и найдем сторону АВ по теореме Пифагора:
Найдем периметр основания.
Применяем формулу для площади боковой поверхности:
Ответ: 500 см2
Задание №2. Найти площадь поверхности правильной четырёхугольной пирамиды, у которой сторона основания равна 6см, а боковое ребро равно 5см.
Решение:
Пусть ABCDE — наша пирамида (рис. 6).
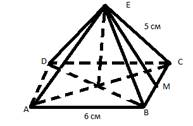
Рис. 6.
Площадь основания
пирамиды равна: Sосн = 62 = 36 см2. Остаётся
найти площадь боковой поверхности. Проведём высоту EM боковой грани пирамиды.
Треугольник BEC — равнобедренный; значит, EM является также его медианой, и
потому MC = 3см. Отсюда 
. Следовательно, площадь
S1 боковой грани равна: 
. Площадь боковой
поверхности: Sбок = 4S1 = 4
12
= 48см2. Площадь поверхности пирамиды: S = Sосн + Sбок
= 36 + 48 = 84см2.
Ответ: 84см2.
Задания для самостоятельной работы:
|
Вариант №1
Задание №1. Из заготовки в форме прямой четырехугольной призмы высотой 10 см, в основании которой лежит квадрат со стороной 6 см выточили изделие в форме шестиугольной призмы высотой 9,5 см и длиной стороны основания 5 см. Найдите площадь полной поверхности заготовки и готового изделия.
Задание №2. Вычислить стоимость конструкции, изготовленной в форме усеченной пирамиды, в основании которой лежат правильные треугольники с длинами сторон: нижнее основание 100 см, верхнее основание 80 см и высотой 65 см, если 1 м2 стали стоит 1500 рублей.
|
Вариант №2
Задание №1. Из заготовки в форме прямой треугольной призмы высотой 12 см, в основании которой лежит прямоугольный треугольник с катетами 6 см и 8 см выточили изделие в форме треугольной пирамиды высотой 10 см, в основании которой лежит правильный треугольник со сторонами 6 см. Найдите площадь полной поверхности заготовки и готового изделия.
Задание №2. Вычислить стоимость конструкции, изготовленной в форме усеченной пирамиды, в основании которой лежат квадраты с длинами сторон: нижнее основание 120 см, верхнее основание 90 см и высотой 85 см, если 1 м2 стали стоит 1500 рублей.
|
Контрольные вопросы (ответьте письменно):
1. Запишите определение призмы.
2. Запишите определение пирамиды.
3. Запишите определение усеченной пирамиды.
4. Изобразите прямую треугольную призму и укажите на рисунке основные элементы призмы.
5. Изобразите четырехугольную пирамиду и укажите на рисунке основные элементы пирамиды.
6. Изобразите усеченную пирамиду и укажите на рисунке основные ее элементы.
7. Запишите формулы для нахождения площади боковой и полной поверхности призмы.
8. Запишите формулы для нахождения площади боковой и полной поверхности пирамиды.
9. Запишите формулы для нахождения площади боковой и полной поверхности усеченной пирамиды.
10.
Практическая работа №6 Тема: «Нахождение площадей многогранников»
Рис. 3 Рассмотрим треугольник ∆
Вариант №1 Задание №1. Из заготовки в форме прямой четырехугольной призмы высотой 10 см, в основании которой лежит квадрат со стороной 6 см выточили изделие…
© ООО «Знанио»
С вами с 2009 года.
