Практическая работа на тему:" Тела вращения и их поверхности"

Практическая работа №7

Тема: «Тела вращения и их поверхности»

Цель: уметь применять формулы для нахождения площадей (боковой и полной поверхностей) тел вращения: цилиндра, конуса, усеченного конуса и шара при обосновании этапов решения задач; уметь выполнять чертежи любых тел вращения по условию задачи, понимать чертежи, находить на чертежах основные элементы тел вращения.

Оборудование: ручка, простой карандаш, линейка, методические рекомендации по выполнению работы.

Методические рекомендации по выполнению практической работы:

Задание №1. Найти стоимость металлической трубы, длина которой 10 м, а внутренний диаметр равен 30 см, если 1 м² трубы стоит 800 рублей.

Решение:

По условию задачи дан цилиндр высотой 10 м и с радиусом основания 15 см (рис. 1).

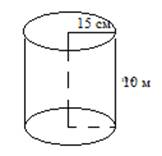
                                                                Рис. 1

Так как необходимо вычислить стоимость металлической трубы в форме цилиндра, то нужно найти площадь боковой поверхности цилиндра. Воспользуемся формулой S_бок=2ПRh, так как R=15 cм, а h=10м=1000см, то искомая площадь равна S_бок=2П·15·1000=30000П см²=3 м². Найдем теперь стоимость металлической трубы: 3·800=2400 рублей.

Ответ: 2400 рублей.

Задание №2. Найти площадь полной поверхности выточенной детали в форме конуса, если площадь его осевого сечения известна и равна 12 дм², причем высота изделия равна 10 см.

Решение:

Площадь полной поверхности конуса рассчитывается по формуле: S_полн=ПR(L+R), где L – длина образующей конуса, R – радиус основания конуса. По условию задачи известна высота конуса PO=10 см и S_сеч = 12 дм². Так как в осевом сечении конуса лежит равнобедренный треугольник, то его площадь вычисляется следующим образом:
S_сеч = 1/2·PO·AB, с другой стороны S_сеч = 12 дм², тогда получаем выражение
1/2·PO·AB= 12 дм², причем PO=10 см=1 дм, подставив в предыдущее выражение, получим уравнение: 1/2·1·AB= 12 дм², откуда AB= 24 дм. Так как R=OB=1/2AB, то R=1/2·24=12 дм.

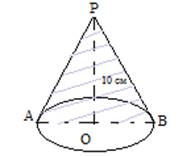
                                                                  Рис. 2

Найдем теперь длину образующей L, из прямоугольного треугольника POB по теореме Пифагора имеем: , то есть , значит  дм. Теперь можно найти площадь полной поверхности конуса S_полн=П·12·(15,6+12)=331,2П дм².

Ответ: S_полн=331,2П дм²

Задание №3. Из заготовки в форме усеченного конуса с образующей 14 см, высотой 10 см и радиусом верхнего основания 8 см выточили деталь сферической формы радиуса 5 см. Вычислите площади полной поверхности заготовки и готового изделия.

Решение:

Найдем сначала площадь полной поверхности заготовки – усеченного конуса по формуле S_полн=ПL(r+R)+. По условию задачи известны: образующая
L=BC=14 см, высота H=OT=10 см, радиус верхнего основания r=OB=5 см. Необходимо найти еще радиус нижнего основания R=TC.

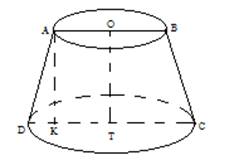
     Рис. 3

Рассмотрим прямоугольник AOTK, у которого противоположные стороны равны, то есть AO = KT = r = 5 см, AK = OT = h =10 см, тогда в прямоугольном треугольнике AKD известны гипотенуза AD=14 см и катет AK=10 см, по теореме Пифагора найдем неизвестный катет DK. Итак, , ,  см, тогда радиус нижнего основания равен R=DK+KT=9,8+5=14,8 см.

Значит, площадь полной поверхности заготовки равна S_полн = П·14·(5+14,8)+.

Найдем теперь площадь поверхности готового изделия – шара радиуса 5 см используя формулу S_шара = 4ПR², получим S_шара = 4П5² = 100П см².

Ответ: S_{полн. заготовки} = , S_{готового изделия}  = 4П·5² = 100П см²

Задания для самостоятельной работы:

Контрольные вопросы (ответьте письменно):

1.                  Запишите определение цилиндра.

2.                  Запишите определение конуса (усеченного конуса).

3.                  Запишите определение шара (сферы).

4.                  Изобразите прямой цилиндр и укажите на рисунке его основные элементы.

5.                  Изобразите конус и укажите на рисунке его основные элементы.

6.                  Изобразите усеченный конус и укажите на рисунке основные его элементы.

7.                  Изобразите шар и укажите на рисунке основные его элементы.

8.                  Запишите формулы для нахождения площади боковой и полной поверхности цилиндра.

9.                  Запишите формулы для нахождения площади боковой и полной поверхности конуса.

10.              Запишите формулы для нахождения площади боковой и полной поверхности усеченного конуса.

11.              Запишите формулу для нахождения площади поверхности шара.

12.              Запишите уравнение сферы с центром в точке (укажите любые координаты) и радиуса (укажите любое число).