Практическая работа специальности 09.02.01.

Практическое занятие № 55.

Тема: «Проектирование счетчиков»

Цель: изучить принцип работы счетчика импульсов.

Теория

Счетный триггер, или Т-триггер, который показан на Рисунок 1. (а) имеет два выхода и один вход. При положительном перепаде напряжения на счетном входе Т-триггера сигналы на его выходах меняются на противоположные. В качестве основы построения счетного триггера может быть использован динамический D-триггер. При этом его инверсный выход должен быть соединен с информационным входом (Рисунок 1 б).

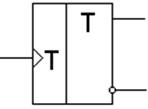
        а) условное обозначение;                              б) схема на D-триггере;

Рисунок 1 - Счетный триггер

Рассмотрим простой трехразрядный двоичный счетчик импульсов, состоящий из трех Т-триггеров, которые имеют входы R для установки нуля (Рисунок 2).

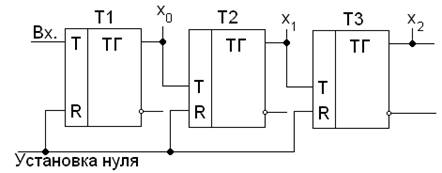
Рисунок 2 - Трехразрядный двоичный счетчик импульсов

В исходном состоянии все триггеры находятся в 0 состоянии (Рисунок 3). После подачи первого входного импульса триггер Т1 переходит в состояние 1, а после второго в состояние 1 переходит Т2, а Т1 возвращается в состояние 0 и т.д.

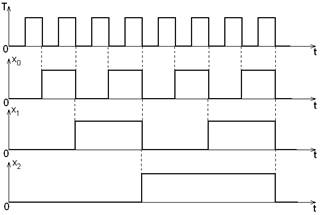
Рисунок 3 - Диаграммы сигналов в счетчике импульсов

Из таблицы 1 видно, что по состоянию триггеров можно определить сколько импульсов было подано на вход счетчика. В общем случае емкость счетчика равна 2ⁿ, где n– число триггеров в счетчике.

Таблица1. Состояние триггеров счетчика импульсов

Известно, что счётный триггер делит частоту входных импульсов на два. Сопоставив этот факт с указанной выше закономерностью, видим, что счётчик может быть построен в виде цепочки последовательно включённых счётных триггеров. Заметим, кстати, что согласно ГОСТу входы элементов изображаются слева, а выходы справа. Соблюдение этого правила ведёт к тому, что в числе, содержащемся в счётчике, младшие разряды расположены левее старших.

Двоичные счётчики с параллельным переносом и соседним кодированием

Выше рассмотрены схемы двоичных последовательных счётчиков, то есть таких счётчиков, в которых при изменении состояния определённого триггера возбуждается последующий триггер, причём триггеры меняют свои состояния не одновременно, а последовательно. Если в данной ситуации должны изменить свои состояния n триггеров, то для завершения этого процесса потребуется n интервалов времени, соответствующих времени изменения состояния каждого из триггеров. Такой последовательный характер работы является причиной двух недостатков последовательного счётчика: меньшая скорость счёта по сравнению с параллельными счётчиками и возможность появления ложных сигналов на выходе схемы. В параллельных счётчиках синхронизирующие сигналы поступают на все триггеры одновременно.

Последовательный характер переходов триггеров счётчика является источником ложных сигналов на его выходах. Например, в четырёхразрядном счётчике, ведущем счёт в обычном четырёхразрядном двоичном коде с «весами» разрядов 8-4-2-1, при переходе от состояния к состоянию на выходе появится следующая последовательность состояний:

0111₂→ 0110₂→ 0100₂→ 0000₂→ 1000₂

Это означает, что при переходе из состояния 7 в состояние 8 на входах счётчика на короткое время появятся коды, соответствующие состояниям 6; 4; 0. Смена этих промежуточных состояний может которые могут ложно изменить состояния, подключённых к ним по входам других триггеров — это нежелательное явление называют логическими «гонками» или «гонками сигналов».

Исключить гонки можно, применяя счётчики с соседним или противогоночным кодированием состояний, например, считающие в рефлексивном коде Грея вызвать ложную работу других логических схем, например, если к такому счётчику подключён дешифратор, то на его выходах 0, 4, 6 могут кратковременно возникнуть активные состояния. С целью уменьшения времени протекания переходных процессов можно реализовать счётчик в варианте с подачей входных счётных импульсов одновременно на все триггеры. В этом случае получим счётчик с параллельным переносом.

По схемам счётчиков с параллельным переносом строятся счётчики, задержка переключения одного триггера у которых соизмерима с периодом считаемых импульсов.

Пример. Если задержка переключения одного триггера 30 нс, то при построении счётчика по схеме с последовательным переносом более чем четырёхразрядного, работающего в обычном двоичном коде, при периоде счётных импульсов 120 нс и ниже начнутся сбои счёта, перенос не успевает распространиться по цепочке триггеров до прихода очередного счётного импульса.

В счётчиках с параллельным переносом на информационные входы триггеров подаются сигналы, являющиеся логической функцией состояния счётчика и определяющие конкретные триггеры, которые должны изменить своё состояние при данном входном импульсе. Принцип стробирования сводится к следующему: триггер меняет своё состояние при пропускании очередного импульса синхронизации, если все предыдущие триггеры находились в состоянии логической единицы.

Параллельные счётчики имеют более высокое быстродействие по сравнению с последовательными, поскольку логическая функция от текущего состояния счётчика и счётного импульса поступают на переключающие входы всех триггеров одновременно.

Максимальным быстродействием обладают синхронные счётчики с параллельным переносом, структуру которых найдем эвристически, рассмотрев процессы прибавления единицы к двоичным числам и вычитания её из них.

Счётчики с последовательно-параллельным переносом

В связи с ограничениями на построение счётчиков с параллельным переносом большой разрядности широкое распространение получили счётчики с групповой структурой, или счётчики с последовательно-параллельным переносом. Разряды таких счётчиков разбиваются на группы, внутри которых организуется принцип параллельного переноса. Сами же группы соединяются последовательно с использованием конъюнкторов, формирующих перенос в следующую группу при единичном состоянии всех триггеров предыдущих. При единичном состоянии всех триггеров группы приход очередного входного сигнала создаст перенос из этой группы. Эта ситуация подготавливает межгрупповой конъюнктор к прямому пропусканию входного сигнала на следующую группу.

В развитых сериях ИС обычно имеется по 5…10 вариантов двоичных счётчиков, выполненных в виде четырёхразрядных групп (секций). Каскадирование секций может выполняться путём их последовательного включения по цепям переноса, организации параллельно-последовательных переносов или для более сложных счётчиков с двумя дополнительными управляющими входами разрешения счета и разрешения переноса путём организации параллельных переносов и в группах, и между ними.

Особенностью двоичных счётчиков синхронного типа является наличие ситуаций с одновременным переключением всех его разрядов (например, для суммирующего счётчика при переходе от кодовой комбинации 11…1 к комбинации 00…0 при переполнении счётчика и выработке сигнала переноса).

При необходимости применения счётчика большей разрядности рекомендуется переходить к коду Грея, для которого переходы от одной кодовой комбинации к другой сопровождаются переключением всего одного разряда. Правда, для получения результата счета в двоичном коде придётся использовать дополнительно преобразователь кода, но это является платой за избавление от токовых импульсов большой интенсивности в цепях питания.

Ход работы.

Спроектировать следующие схемы счётчиков:                                                       

1.     Счетчик асинхронный последовательный прямого счета

2.     Счетчик асинхронный последовательный обратного счета

3.     Реверсивный последовательный асинхронный счетчик

4.     Счетчик синхронный со сквозным переносом

5.     Синхронный счетчик с параллельным переносом

6.     Счетчики с управляемым сбросом

Выбор проектируемого счётчика осуществляется по вариантам: если номер в журнале нечётный, выполняется 1, 3 и 5 задание. Если чётный – 2, 4 и 6.

Эскизы выполнить в тетради, схемы на формате А4.

Контрольные вопросы

1. Определить понятие счетчика.

2. Как работает суммирующий, вычитающий и реверсивный счетчики?

3. Объясните виды организации переносов и их влияние на быстродействие схемы.