Практическая работа №9

 

ФИНАНСОВЫЕ ФУНКЦИИ MS EXCEL В ЭКОНОМИЧЕСКИХ РАСЧЕТАХ

 

Цель: научиться использовать финансовые функции для экономических расчётов.

 

Задания:

1.

Функции даты и времени для финансовых расчетов

Время – один из важнейших факторов в финансовых операциях и сделках. Для проведения финансовых расчетов необходимо находить срок между начальной и конечной датами операции, обычно заданный в днях или годах.

Если рассчитывается точное число дней, то надо просто вычесть из конечной даты (даты завершения операции) начальную дату. 

Однако в финансовой практике есть правило, согласно которому в месяце считается 30 дней, а в году 360. В этом случае используется функция ДНЕЙ360. Ее назначение – расчет количества дней между двумя датами на основе 360-дневного года (12 30-дневных месяцев), аргументы: нач_дата – начальная дата сделки; кон_дата – конечная дата сделки; метод – логическое значение, если отсутствует, есть «ЛОЖЬ».

Аргументы «нач_дата» и «кон_дата» могут быть введены как текстовые строки в двойных кавычках или в числовом формате, могут также использоваться ссылки на ячейки, в которых заданы даты в формате дата. Если аргумент «метод» принимает значение «ЛОЖЬ» или опущен, то используется американский метод определения приближенного числа дней между двумя датами, а если «ИСТИНА» – то европейский (эти два метода различаются, только если конечная дата – 31-е число месяца).

Для определения срока между датами в годах надо использовать функцию ДОЛЯГОДА с аргументами (нач_дата, кон_дата, базис). 

Первые два аргумента имеют то же значение, что и у функции ДНЕЙ360. Аргумент «базис» может принимать пять различных значений в зависимости от правила, установленного для расчета срока в годах:

0       или опущен – правило 30/360 (приближенный срок между датами в днях

(американский метод расчета), приближенное число дней в году);

1       – АСТ/АСТ (точный срок между датами в днях, точное число дней в году);

2       – АСТ/360 (точный срок между датами в днях, приближенное число дней в году);

3       – АСТ/365 (точный срок между датами в днях, но в любом году 365 дней);

4       – 30/360 европейский (приближенный срок между датами в днях (европейский метод

расчета), приближенное число дней в году).

 

 

Пример.

Дата получения кредита – 15 января 2008 г., дата погашения – 15 марта того же года. Найти срок кредита в днях и годах.

Решение выполнить на Листе 1. 

Откройте Лист 1 и переименуйте его в Задание 1.

Точное число дней = «15/03/2008» – «15/01/2008» = 59.

Приближенное число дней = ДНЕЙ360(«15/01/2008», «15/03/2008») = 60. Срок кредита в годах по правилу

 

АСТ/АСТ = ДОЛЯГОДА(«15/01/2008», «15/03/2008») = 0,161644.

 

Расчет ипотечной ссуды осуществляются с использованием финансовой функции ПЛТ

Функция ПЛТ вычисляет величину постоянной периодической выплаты ренты (например, регулярных платежей по займу) при постоянной процентной ставке.

Синтаксис: ПЛТ(Ставка;Кпер;Пс;Бс;Тип).

Аргументы:

§  Ставка – процентная ставка по ссуде,

§  Кпер – общее число выплат по ссуде,

§  Пс – приведенная к текущему моменту стоимость, или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой,

§  Бс – требуемое значение будущей стоимости, или остатка средств после последней выплаты.

Если аргумент Бс опущен, то он полагается равным 0 (нулю), т.е. для займа, например, значение Бс равно 0, Тип – число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.

Отметим, что очень важно быть последовательным в выборе единиц измерения для задания аргументов Ставка и Кпер.

Например, если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12

% годовых, то для задания аргумента Ставка используйте 12 %/12, а для задания аргумента Кпер – 4*12. Если вы делаете ежегодные платежи по тому же займу, то для задания аргумента Ставка используйте 12 %, а для задания аргумента Кпер – 4.

Для нахождения общей суммы, выплачиваемой на протяжении интервала выплат, умножьте возвращаемое функцией ПЛТ значение на величину Кпер. Интервал выплат – это последовательность постоянных денежных платежей, осуществляемых за непрерывный период.

Например, заем под автомобиль или заклад являются интервалами выплат. В функциях, связанных с интервалами выплат, выплачиваемые вами деньги, такие как депозит на накопление, представляются отрицательным числом, а деньги, которые вы получаете, такие как чеки на дивиденды, представляются положительным числом.

Например, депозит в банк на сумму 1000 руб. представляется аргументом – 1000, если вы

вкладчик, и аргументом -1000, если вы – пpeдставитель банка.

 

Пример 1. Вычислить 30-летнюю ипотечную ссуду покупки квартиры за 201900 руб. с годовой ставкой 8% и начальным взносом 20%. Сделать расчет для ежемесячных и ежегодных выплат (табл. 1).

Решение:

1.                  Откройте Лист 2 и переименуйте его в Задание 2.

2.                  Введите в ячейки A1:B6 данные, представленные на рис. 1.

 

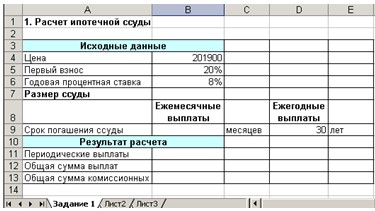
Рис. 1. Форма для расчета ипотечной ссуды

 

3.                  Для выполнения расчетов в ячейки должны быть введены формулы, показанные на рис.

2.

 

 

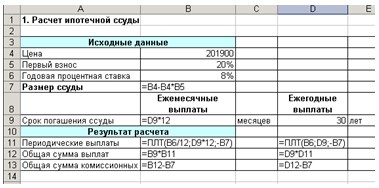
Рис. 2. Формулы для расчета ипотечной ссуды

 

4.                  Результаты расчеты должны быть следующими (рис. 3):

 

 

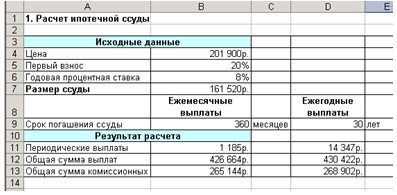
Рис. 3. Расчет ипотечной ссуды

3. Функции для расчета годовой процентной ставки

 

Функция ЧПС возвращает чистый текущий объем вклада, вычисляемый на основе ряда последовательных поступлений наличных денег и нормы амортизации.

Чистый текущий объем вклада – это сегодняшний объем будущих платежей (отрицательные значения) и поступлений (положительные значения).

Например, вам предлагают следующую сделку. У вас берут в долг некоторую сумму денег и предлагают через k1 лет вернуть сумму, равную Рk1, через k2 лет – Рk2 и т. д. и, наконец, через kn лет – Рkn. Кроме данной сделки, у вас есть альтернативный способ использования ваших денег, например, положить их в банк под i процентов годовых. Тогда чистым текущим объемом вклада является та сумма денег, которой вам нужно располагать начальный год, чтобы, положив их в банк под i % годовых, получили предлагаемую прибыль.

Синтаксис: ЧПС(Ставка;Значение1;Значение2;…..) Аргументы:

§  ставка – ставка дисконтирования за один период;

§  значение 1, значение 2, – от 1 до 29 аргументов, представляющих расходы и доходы:

• значение 1, значение 2, … должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.

ЧПС использует порядок аргументов значение 1, значение 2, … для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.

Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса 1-го значения и заканчивается с последним денежным взносом в списке.

Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов.

Функция ЧПС связана с функцией ВСД (внутренняя скорость оборота). ВСД – это скорость оборота, для которой ЧПС равняется нулю:

ЧПС(ВСД(…);…)=0.

Функция ВСД возвращает внутреннюю скорость оборота для ряда последовательных операций с наличными деньгами, представленными числовыми значениями. Объемы операций не обязаны быть регулярными, как в случае ренты.

Внутренняя скорость оборота – это процентная ставка дохода, полученного от инвестиций, состоящих из выплат (отрицательные значения) и поступлений (положительные значения), которые происходят в регулярные периоды времени.

Синтаксис: ВСД (Значения;Предположение).

Аргументы:

§     значения – массив или ссылка на ячейки, содержащие числовые величины, для которых вычисляется внутренняя ставка доходности. Значения должны включать, по крайней мере, одно положительное значение и одно отрицательное значение, для того чтобы можно было вычислить внутреннюю скорость оборота.

Функция ВСД использует порядок значений для интерпретации порядка денежных выплат или поступлений, поэтому нужно следить, чтобы значения выплат и поступлений вводились в правильном порядке.

§     предположение – величина, о которой предполагается, что она близка к результату ВСД.

Для вычисления ВСД Excel использует метод итераций. Начиная со значения прогноз, функция ВСД выполняет циклические вычисления, пока не получит результат с точностью 0,00001. Если функция ВСД не может получить результат после 20 попыток, то возвращается значение ошибки #ЧИСЛО!

В большинстве случаев нет необходимости задавать прогноз для вычислений с помощью функции ВСД. Если прогноз опущен, то он полагается равным 0,1 (10 %).

Если ВСД выдает значение ошибки #ЧИСЛО! Или результат далек от ожидаемого, можно

попытаться выполнить вычисления еще раз, но уже с другим значением аргумента прогноз.

 

Пример 3. Вас просят в долг 10000 руб. и обещают вернуть через год 2000 руб., через два года – 4000 руб., через три года – 7000 руб. При какой годовой процентной ставке эта сделка выгодна?

Решение.

1. Откройте Лист 3 и переименуйте его в Задание 3. 2. Введите в ячейки A1:B7 данные, представленные на рис. 4.

 

 

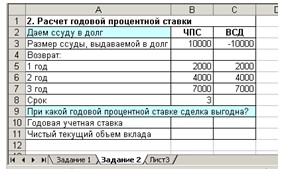
Рис. 4. Форма для расчета годовой процентной ставки

 

3.                   Для выполнения расчетов в ячейки должны быть введены формулы, показанные на рис.

5.

 

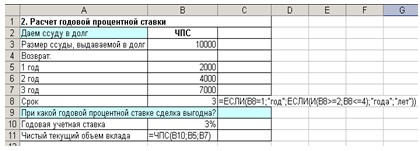
Рис. 5. Формулы для расчета годовой процентной ставки

 

4.                   Первоначально в ячейку В10 введите произвольный процент, например 3 %.

В ячейку В11 введите формулу =ЧПС(В10;В5:В7) (см. рис. 5).

5.                   В ячейку С8 введите формулу:

=ЕСЛИ(В8=1;»год»;ЕСЛИ(И(В8>=2;B8<=4) ;»года»;»лет»)) В результате должно получиться (см. рис. 6):

 

 

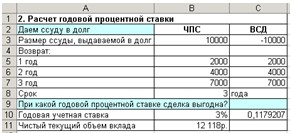
Рис. 6. Расчет чистого текущего объема вклада

 

6.                   Затем выбираем команду Сервис / Подбор параметра и заполняем открывшееся

диалоговое окно Подбор параметра, как показано на рис. 7.

 

 

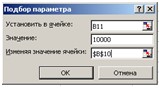
Рис. 7. Диалоговое окно Подбор параметра при расчете годовой процентной ставки

7.                   В поле Установить в ячейке: укажите ссылку на ячейку В11, в которой вычисляется чистый текущий объем вклада по формуле:

=ЧПС(B10;B5:B7).

В поле Значение установить 10000 – размер ссуды.

В поле Изменения значения ячейки укажите ссылку на ячейку В10, в которой вычисляется годовая процентная ставка.

После нажатия кнопки ОК средство подбора параметров определит, при какой годовой процентной ставке чистый текущий объем вклада равен 10000 руб. Результат вычисления выводится в ячейку В10.

8.                   В нашем случае годовая учетная ставка равна 11,79 %.

Вывод: если банки предлагают большую годовую процентную ставку, то предлагаемая сделка не выгодна. 9. Результаты расчеты должны быть следующими:

 

 

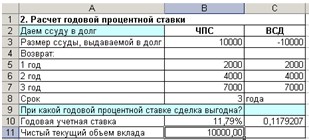
Рис. 8. Расчет годовой процентной ставки

 

 

4.   Функции для расчета эффективности капиталовложений

 

Расчет эффективности капиталовложений осуществляется с помощью функции ПС.

Функция ПС возвращает текущий объем вклада на основе постоянных периодических платежей.

Функция ПС аналогична функции ЧПС. Основное различие между ними заключается в том, что функция ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. Кроме того, в отличие от функции ЧПС, денежные взносы в функции ПС должны быть постоянными на весь период инвестиции.

Синтаксис: ПС(Ставка;Кпер;Плт;Бс;Тип) Аргументы:

§     Ставка – процентная ставка за период,

§     Кпер – общее число периодов платежей по аннуитету,

§     Плт – выплата, производимая в каждый период и не меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи и платежи по процентам, но не включают других сборов или налогов,

§     Бс – требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0),

§     Тип – число 0 или 1, обозначающее, когда должна производиться выплата.

 

Пример 4. У вас просят в долг 10000 руб. и обещают возвращать по 2000 руб. в течение 7 лет. Будет ли выгодна эта сделка при годовой ставке 7 %?

Решение:

1.  Откройте Лист 4 и переименуйте его в Задание 4.

2.  Введите в ячейки A1:B6 данные, представленные на рис. 9.

 

 

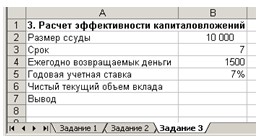
Рис. 9. Форма расчета эффективности капиталовложений

 

3.  В ячейку В6 введите формулу: =ПС(В5;В3;-В4)

4.  В ячейку С3 введите формулу:

=ЕСЛИ(В3=1; "год";ЕСЛИ(И(В3>=2;В3<=4); "года";"лет")) 5. В ячейку В7:

=ЕСЛИ (В2<В6; "Выгодно дать деньги в долг"; ЕСЛИ(В6=В2; "Варианты равносильны";

"Выгоднее деньги положить под проценты"))

 

 

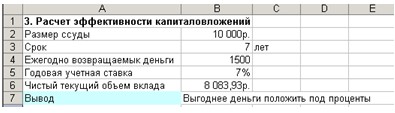
Рис. 10. Расчет эффективности капиталовложений

 

 

5.   Функции для расчета основных платежей и платы по процентам

 

Основные платежи и платы по процентам вычисляются с помощью формул или финансовых функций ОСПЛТ и ПРПЛТ.

Функция ПРПЛТ возвращает платежи по процентам за данный период на основе периодических постоянных выплат и постоянной процентной ставки.

Синтаксис: ПРПЛТ (Ставка; Период; Кпер; Пс; Бс; Тип).

Функция ОСПЛТ возвращает величину выплаты за данный период на основе периодических постоянных платежей и постоянной процентной ставки.

Синтаксис: ОСПЛТ(Ставка; Период; Кпер; Пс; Бс; Тип).

Аргументы функций ПРПЛТ: и ОСПЛТ:

§     Ставка – процентная ставка за период,

§     Период – задает период, значение должно быть в интервале от 1 до «Кпер»,

§     Кпер – общее число периодов выплат годовой ренты,

§     Пс – приведенная стоимость, то есть общая сумма, которая равноценна ряду будущих платежей,

§     Бс – требуемое значение будущей стоимости, или остатка средств после последней выплаты.

Если аргумент Бс опущен, то он полагается равным 0 (нулю), то есть для займа, например, значение Бс равно 0.

§     Тип – число 0 или 1, обозначающее, когда должна производиться выплата.

Функции ПРПЛТ и ОСПЛТ тесно связаны между собой, а именно ПЛПj= i Bj-1, ОСНПj = А -

ПЛПj, Bj = Вj-1 - ОСНПj при j ∈[0, n], где j – номер периода, п – КПЕР,

ПЛПj, ОСНПj и Bj – это ПРПЛТ, ОСПЛТ и остаток долга, соответственно, за j-й период,

ПЛПо = 0, ОСНПо = 0, Bо – Пс,

А – величина выплаты за один период годовой ренты на основе постоянных выплат и постоянной процентной ставки, вычисляемая с помощью функции ПЛТ.

 

Пример 5. Вычислить основные платежи, платы по процентам, общей ежегодной платы и остатка долга на примере ссуды 100000 руб. на срок 5 лет при годовой ставке 2 %.

Решение:

1.                  Откройте Лист 5 и переименуйте его в Задание 5.

2.                  Введите данные, представленные на рис. 13.

3.                  Ежегодная плата вычисляется в ячейке В4 по формуле: =ПЛТ(процент; срок; -размер_ссуды), где ячейки В2, В3 и В5 имеют имена: процент, срок и размер_ссуды, соответственно. 

4.                  За первый год плата по процентам в ячейке В8 вычисляется по формуле:

=D7*процент.

 

 

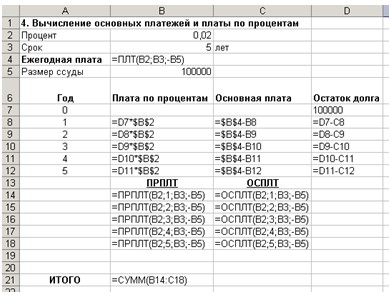
Рис. 13. Функции для вычисления основных платежей и платы по процентам.

 

5.                  Основная плата в ячейке С8 вычисляется по формуле: =ежегодная_плата-В8, где ежегодная_плата – имя ячейки В4.

Остаток долга в ячейке D8 вычисляется по формуле: =D7-C8.

6.                  В оставшиеся годы эти платы определяются с помощью протаскивания маркера заполнения выделенного диапазона B8:D8 вниз по столбцам.

7.                  Данные результаты расчетов должны быть следующими (рис. 14.):

 

 

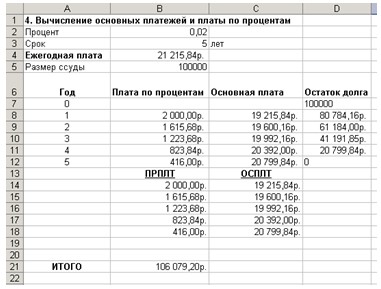
Рис. 14. Вычисление основных платежей и платы по процентам

 

 

 

 

6. Функции для расчета будущего значения вклада, процентной ставки и количества периодов выплаты долга

 

Функция БС вычисляет будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки.

Функция БС подходит для расчета итогов накоплений при ежемесячных банковских взносах. Синтаксис: БС (Ставка; Кпер; Плт; Пс; Тип).

Аргументы:

§     Ставка – процентная ставка за период,

§     Кпер – общее число периодов выплат,

§     Плт – величина постоянных периодических платежей,

§     Пс – текущее значение, то есть общая сумма, которую составят будущие платежи, § Тип – число 0 или 1, обозначающее, когда должна производиться выплата.

Если тип равен 0 или опущен, то оплата производится в конце периода, если 1 – в начале

периода. Если тип = 0 и БС = 0, то функция БС вычисляется по формуле 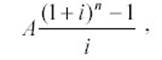(6):

 

                                                                       (6)

 

где А – Плт; i – Ставка; n – Кпер.

Функция КПЕР вычисляет общее количество периодов выплаты для данного вклада на основе периодических постоянных выплат и постоянной процентной ставки.

Синтаксис: КПЕР(Ставка; Плт; Пс; БС; Тип).

Аргументы:

§     Ставка – процентная ставка за период,

§     Плт – величина постоянных периодических платежей,

§     Пс – текущее значение, т.е. общая сумма, которую составят будущие платежи,

§     БС – будущая стоимость или баланс наличности, который нужно достичь после последней выплаты.

Если аргумент БС опущен, он полагается равным 0 (например, будущая стоимость займа равна 0), тип – число 0 или 1, обозначающее, когда должна производиться выплата. Если тип равен 0 или опущен, то оплата производится в конце периода, если 1 – то в начале периода. Если тип = 0 и БС = 0 функция КПЕР вычисляется по формуле 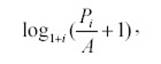(7):

 

                        (7)

где Р – ПС; i – Ставка; А – Плт.

 

Пример 6. Вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Предположим, вы собираетесь вложить 1000 руб. при годовой ставке 6 %. Вы собираетесь вкладывать по 100 руб. в начале каждого месяца в течение года. Сколько денег будет на счете в конце 12 месяцев?

Решение:

1.                   Откройте Лист 6 и переименуйте его в Задание 6.

2.                   Ведите данные в ячейки А1:С6 (см. рис. 15).

 

 

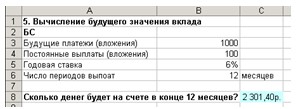
Рис. 15. Расчет будущего значения вклада

 

3.                   В ячейку С8 введите формулу:

=БС(6 %/12; 12; -100; -1000; 1) получаем ответ: 2 301,40 руб (см. рис. 16).

 

 

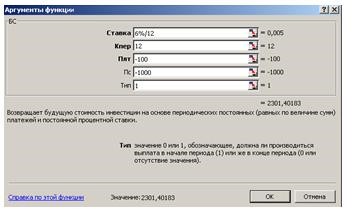
Рис. 16. Диалоговое окно Аргументы функции БС

 

Пример 7. Вы берете в долг 1000 руб. при годовой ставке 1% и собираетесь выплачивать по 100 руб. в год, Какое будет число выплат долга?

Решение:

1.                   Откройте Лист 7 и переименуйте его в Задание 7.

2.                   Ведите данные в ячейки А1:В6 (см. рис. 17).

 

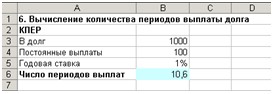
Рис. 17. Расчет количества периодов выплат

 

3.                   В ячейку В6 введите формулу: =КПЕР(B5; -B4; B3) В результате получаем ответ: ≈11. (см. рис. 18).

 

 

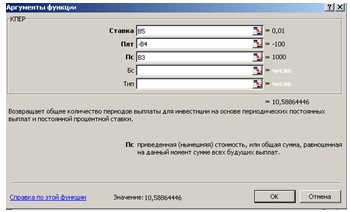
Рис. 18. Диалоговое окно Аргументы функции КПЕР

 

Вычисление процентной ставки

Функция СТАВКА вычисляет процентную ставку, необходимую для получения определенной суммы в течение заданного срока путем постоянных взносов, за один период.

Следует отметить, что функция СТАВКА вычисляет процентную ставку методом итераций, поэтому решение может быть и не найдено. Если после 20 итераций погрешность определения ставки превышает 0,0000001, то функция СТАВКА возвращает значение ошибки #ЧИСЛО!

Синтаксис: СТАВКА(КПЕР; Плт; Пс; БС; Тип; Предположение).

Аргументы:

§     КПЕР – общее число периодов платежей по аннуитету;

§     Плт – регулярный платеж (один раз в период), величина которого остается постоянной в течение всего срока аннуитета. Обычно Плт состоит из платежа основной суммы и платежа процентов, но не включает других сборов или налогов. Если аргумент опущен, должно быть указано значение аргумента БС;

§     Пс – приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей;

§     БС – требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент БС опущен, то он полагается равным 0 (например, БС для займа равно 0); тип – число 0 или 1, обозначающее, когда должна производиться выплата; предположение – предполагаемая величина ставки.

Если БС = 0 и тип = 0, функция СТАВКА является корнем уравнения 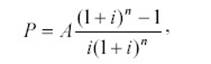(8):

 

                                                                       (8)

 

Пример 8. Определить процентную ставку для четырехлетнего займа размером в 8000 руб. с ежемесячной выплатой 200 руб.

Решение:

1.                   Откройте Лист 8 и переименуйте его в Задание 8.

2.                   Ведите данные в ячейки А1:В7 (см. рис. 19).

 

 

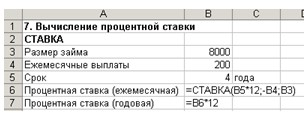
Рис. 19. Расчет процентной ставки

3.                   В ячейку В6 введите формулу: =СТАВКА(B5*12;-B4;B3).

4.                   В ячейку В7 введите формулу: = В6*12.

В результате получаем: месячная (так как период равен месяцу) процентная ставка равна 0,77 %. Процентная ставка годовая равна 9 % см. рис 20).

 

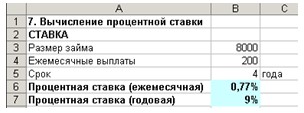
Рис.20. Результаты вычисления процентной ставки

 

Контрольные вопросы:

1.    Как рассчитать дату и временя с использованием финансовых функций?

2.    Каким образом можно рассчитать ипотечную ссуду, годовую процентную ставку в Excel?

3.    Назовите функции расчета постоянных рент.