Практикум по ЕН.01 Математика

государственное автономное профессиональное

образовательное учреждение

Челябинской области

«Политехнический колледж»

 

 

 

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

ПО ВЫПОЛНЕНИЮ практических РАБОТ

 

по учебной дисциплине

ЕН.01 Математика

 

для студентов специальности (профессии)

15.02.03 Техническая эксплуатация гидравлических машин, гидроприводов и

 гидропневмоавтоматики

 

базовой подготовки

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Магнитогорск, 2017

ОДОБРЕНО

Предметной (цикловой) комиссией ____________________

                     (название)

Руководитель _________________ / ___________________

                     (подпись)                      (И.О. Фамилия)

Протокол № _____ от _____ _______________20____

 

 

 

Составитель:

преподаватель ГАПОУ ЧО ПК          __________ / Ларкина Е.В.

               (подпись)               (И.О. Фамилия)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Методические указания по выполнению практических работ разработаны в соответствии с рабочей программой учебной дисциплины ЕН.01 Математика

Содержание практических  работ ориентировано на формирование профессиональных и общих компетенций по основной профессиональной образовательной программе по специальности 15.02.03 Техническая эксплуатация гидравлических машин, гидроприводов и гидропневмоавтоматики.

 

 

 

 

СОДЕРЖАНИЕ

 

1 Введение. 4

2 Методические указания. 6

Практическая работа № 1. 6

Практическая работа № 2. 8

Практическая работа № 3. 10

Практическая работа № 4. 11

Практическая работа № 5. 13

Практическая работа № 6. 14

Практическая работа № 7. 15

Практическая работа № 8. 16

Практическая работа № 9. 17

Практическая работа № 10. 18

Практическая работа № 11. 19

Практическая работа № 12. 20

Практическая работа № 13. 22

3 Информационное обеспечение. 23

 

 

 

 

 

 

 

 

 

 

 

 

1 ВВЕДЕНИЕ

Важную часть теоретической и профессиональной практической подготовки студентов составляют практические  работы.

Ведущей дидактической целью практических занятий является формирование практических умений - профессиональных (умений выполнять определенные действия, операции, необходимые в последующем в профессиональной деятельности) и/или учебных (умений решать задачи по математике), необходимых в последующей учебной деятельности по профессиональным модулям.

Состав и содержание практических  работ направлены на реализацию действующего федерального государственного образовательного стандарта среднего профессионального образования по специальности 15.02.03 Техническая эксплуатация гидравлических машин, гидроприводов и гидропневмоавтоматики.

В соответствии с рабочей программой учебной дисциплины ЕН.01 Математика предусмотрено проведение практических работ.

Содержание практических  работ ориентировано на овладение профессиональными компетенциями по дисциплины основной профессиональной образовательной программы по специальности:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

и на формирование общих компетенций:

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

В результате выполнения практических работ, обучающийся должен:

уметь

¾    анализировать сложные функции и строить их графики;

¾    выполнять действия над комплексными числами;

¾    вычислять значения геометрических величин;

¾    производить операции над матрицами и определителями;

¾    решать задачи на вычисление вероятности с использованием элементов комбинаторики;

¾    решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений;

¾    решать системы линейных уравнений различными методами;

Выполнение студентами практических  работ по учебной дисциплине ЕН.01 Математика направлено:

-     обобщение, систематизацию, углубление, закрепление, развитие и детализацию полученных теоретических знаний по конкретным темам дисциплины;

-     формирование умений применять полученные знания на практике, реализацию единства интеллектуальной и практической деятельности;

-     формирование и развитие умений: наблюдать, сравнивать, сопоставлять, анализировать, делать выводы и обобщения, самостоятельно вести исследования, оформлять результаты в виде таблиц, схем, графиков;

-     развитие интеллектуальных умений у будущих специалистов: аналитических, проектировочных, конструктивных и др.;

-     выработку при решении поставленных задач профессионально значимых качеств, таких как самостоятельность, ответственность, точность, творческая инициатива.

Продолжительность выполнения практической работы составляет не менее двух академических часов и проводится после соответствующего занятия, которое обеспечивает наличие знаний, необходимых для ее выполнения.

2 МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Тема 2.1 Матрицы и определители

Практическая работа № 1

Выполнение операций над матрицами и определителями

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения выполнять операции над матрицами, находить определители квадратных матриц 2-го и 3-го порядка.

Выполнив работу, Вы будете:

уметь:

- составлять и решать систему уравнений 2-го порядка различными способами (алгебраическое сложение, подстановка, графический);

- составлять основную и расширенную матрицы по заданной системе уравнений;

- выполнять операции над матрицами;

- находить определители квадратных матриц 2-го и 3-го порядка.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задания:

1. Решить задачу разными способами:

Группа туристов отправилась в поход на 6 байдарках. Часть байдарок были двухместные, а часть трехместные. Сколько двухместных и и трехместных байдарок участвовало в походе, если группа состояла из 14 человек?

2. Решить системы различными способами:

а) 

б) 

3. Для систем уравнений составить основную и расширенную матрицы, найти определитель основной матрицы:

а) 

б)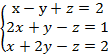 

в) 

г)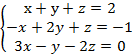 

д) 

е)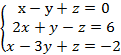 

Порядок выполнения работы:

1 Задания 1 и 3 (а, б) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 2 и 3 (в - е) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.                      В чем суть метода алгебраического сложения?

2.                      Как записать в принятых обозначениях для системы уравнений основную и расширенную матрицу?

3.                      Как найти определители квадратных матриц 2-го и 3-го порядка

 

Тема 2.2 Системы линейных уравнений

Практическая работа № 2

Решение задач профессиональной направленности с помощью систем линейных уравнений различными методами

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения решать системы уравнений 2-го и 3-го порядка.

Выполнив работу, Вы будете:

уметь:

- составлять и решать систему уравнений 2-го и 3-го порядка различными способами (метод Гаусса, формулы Крамера);

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задания:

1. Решить системы уравнений методом Гаусса и по формулам Крамера:

а)    

б)   

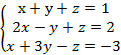
в)   

г)    

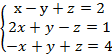
д)   

е)    

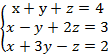
2. Составить систему уравнений по задаче:

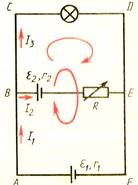В цепи, собранной для зарядки аккумулятора источник тока имеет ЭДС  и внутреннее сопротивление . ЭДС заряженного аккумулятора  и его внутреннее сопротивление . В цепь включен переменный резистор с сопротивлением  и осветительная лампа сопротивлением . Рассчитайте силы тока во всех участках цепи.

 

 

 

 

 

Порядок выполнения работы:

1 Задания 1 (а, б) и 2 выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 1 (в - е) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.    В чем суть метода решения систем уравнений по формулам Крамера?

2.    В чем суть метода Гаусса?

3.    Какой из методов решения систем уравнений (метод Гаусса, формулы Крамера) является универсальным, почему?

 

Тема 3.2 Арифметические действия с комплексными числами

Практическая работа № 3

Выполнение расчетов с комплексными числами

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения выполнять расчеты с комплексными числами.

Выполнив работу, Вы будете:

уметь:

- переводить числа из одной формы записи в другую;

- выполнять расчеты с комплексными числами.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задания:

1. Решить уравнение:

а) 

б) 

в) 

2. Для чисел (z) составить противоположное () и сопряженное (). Построить числа (z, , ) в плоскости ХОУ:

а) 

б) 

в) 

3. Числа построить в плоскости ХОУ и записать в показательной форме записи:

а)  

б)  

в)  

4. Найти значения выражений:  ,  если

а)   

б)   

в)   

Порядок выполнения работы:

1 Задания 1 (а), 2 (а), 3 (а), 4 (а) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 1 (б, в), 2 (б, в), 3 (б, в), 4 (б, в) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.        Какие числа входят во множество комплексных чисел (С)?

2.        Как записать комплексное число в алгебраической, показательной формах записи?

3.        В каких формах записи комплексного числа удобнее выполнять арифметические действия, почему?

 

 

Тема 4.1 Теория пределов и непрерывность функций одной переменной

Практическая работа № 4

Вычисление предела функции

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения для нахождения пределов.

Выполнив работу, Вы будете:

уметь:

- находить предел числовой последовательности;

- находить предел функции в точке;

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задания:

1.      Найти предел:

а)     

б)     

в)     

г)     

д)     

е)     

ж)   

з)     

и)    

к)     

л)     

м)    

н)  

о)     

п)    

р)     

с)     

т)     

у)  

ф)   

х)     

ц)    

ч)     

ш) 

щ)  

ы)   

э)     

ю)   

2. Найти предел функции  в точке

а)   

б)   

в)   

г)   

д)   

е)   

ж)  

з)   

и)   

к)   

л)  

м)   

н)   

о)   

п)   

Порядок выполнения работы:

1 Задания 1 (а – г, н - т), 2 (а - д) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 1 (д – м, у - ю), 2 (е - п) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.      Как найти предел числовой последовательности?

2.      Как найти предел функции?

3.      Любые ли числовые последовательности и функции имеют конечные пределы?

Тема 4.1 Теория пределов и непрерывность функций одной переменной

Практическая работа № 5

Исследование функции на непрерывность и асимптоты

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения для нахождения пределов.

Выполнив работу, Вы будете:

уметь:

- применять предел функции для исследования функции на непрерывность и асимптоты.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задания:

1. Является ли функция  непрерывной в точке ?

а) 

б) 

в) 

2. Найти асимптоты для графика функции и построить

а)   

б)  

в)  

3. Найти асимптоты для графика функции

а)   

б) 

в)  

г)  

д) 

е)  

Порядок выполнения работы:

1 Задания 1 (а), 2 (а), 3 (в, е) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 1 (б, в), 2 (б, в), 3 (а, б, г, д, е) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.  Какие условия должны выполняться, чтобы функция  была непрерывной в точке ?

2.    Как найти вертикальную асимптоту для графика функции?

3.    Как найти наклонную асимптоту для графика функции?

4.    Может ли график функции пересекать асимптоту?

 

Тема 4.2 Дифференциальное исчисление

Практическая работа № 6

Применение производной для исследования функции и построения графика

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения для нахождения пределов.

Выполнив работу, Вы будете:

уметь:

- применять производную и предел функции для исследования функции и построения ее графика.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задание:

1.      Исследовать функцию и построить график

а)  

б)  

в)  

г)  

д)  

е)  

ж) 

Порядок выполнения работы:

1 Задания 1 (а, б, д) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 1 (в, г, е, ж) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.  Какие условия должны проверяться для определения промежутков монотонности и экстремумов функции?

2.  Какие условия должны проверяться для определения направления кривизны линии графика функции?

Тема 4.2 Дифференциальное исчисление

Практическая работа № 7

Применение производной для решения задач профессиональной направленности

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения для нахождения пределов.

Выполнив работу, Вы будете:

уметь:

- применять производную для решения задач профессиональной направленности.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задания:

1.      Найти частные производные  для функции:

а) 

б)  

в) 

г)   

д) 

е) 

2.      Найти максимальную скорость движения, если

а)   

б)   

в)   

Порядок выполнения работы:

1 Задания 1 (а, б), 2 (а) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 1 (в - е), 2 (б, в) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.      Что показывает частная производная ?

2.      Для каких функций находят частные производные?

3.      Как найти частную производную функции?

4.      Какие условия должны проверяться для определения экстремума функции?

 

Тема 4.3 Интегральное исчисление

Практическая работа № 8

Нахождение неопределенных интегралов

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения для нахождения пределов.

Выполнив работу, Вы будете:

уметь:

- находить неопределенный интеграл при помощи методов интегрирования: непосредственное интегрирование, подстановка, по частям.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задание:

1.   Найти неопределенный интеграл ()

и выполнить проверку ()

а)  

б)  

в)  

г)  

д)  

е)  

ж) 

з)  

и)  

Порядок выполнения работы:

1 Задания 1 (а, г, ж) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 1 (б, в, д, е, з, и) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.      Какая функция называется первообразной для f(x)?

2.      В чем заключается суть метода интегрирования с помощью подстановки? В каких случаях данный метод применяется?

3.      В чем заключается суть метода интегрирования по частям? В каких случаях данный метод применяется?

 

Тема 4.3 Интегральное исчисление

Практическая работа № 9

Вычисление с помощью определенного интеграла геометрических и физических величин

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения для нахождения пределов.

Выполнив работу, Вы будете:

уметь:

- применять определенный интеграл для нахождения геометрических и физических величин.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задания:

1.      Найти площадь фигуры, ограниченной линиями

а)     

б)  

в)  

2.   Найти длину линии

а)  

б)  

в)  

3.   Найти объем и площадь боковой поверхности тела, образованного вращением

а)  

б)  

в)  

4.   По цепи идет переменный ток . Найти величину заряда q, пройденного по цепи за первые 6 с.

5.      Сила в 1 кг растягивает пружину на 3 см. Какую работу она при этом производит?

6.      Камень брошен с земли вертикально вверх. Найти наибольшую высоту подъема камня, если его скорость

7.      Найти путь, который пройдет тело за t c от начала движения, если скорость движения определяется формулой

а)  

б)  

Порядок выполнения работы:

1 Задания 1 (а), 2 (а), 3 (а), 4-6 выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 1 (б, в), 2 (б, в), 3 (б, в), 7 выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.      Какие геометрические величины можно найти с помощью определенного интеграла? Что для этого необходимо выполнить?

2.      Какие физические величины можно найти с помощью определенного интеграла?

Тема  4.4 Дифференциальные уравнения

Практическая работа № 10

Решение дифференциальных уравнений

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения для нахождения пределов.

Выполнив работу, Вы будете:

уметь:

- решать дифференциальные уравнения 1 порядка с разделяющимися переменными и линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задание:

1.      Решить уравнения:

а)  

б)  

в)  

г)  

д)  

е)  

ж) 

з)  

и)  

Порядок выполнения работы:

1 Задания 1 (а, г, ж) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 1 (б, в, д, е, з, и) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.    Как решить дифференциальное 1 порядка с разделяющимися переменными?

2.    Как решить линейное однородное дифференциальное уравнение 2 порядка с постоянными коэффициентами?

 

 

Тема  4.4 Дифференциальные уравнения

Практическая работа № 11

Решение задач профессиональной направленности

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения для нахождения пределов.

Выполнив работу, Вы будете:

уметь:

- применять дифференциальные уравнения 1 порядка с разделяющимися переменными для решения практических задач.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задание:

1.      Решить задачу: Скорость охлаждения тела в воздухе  прямо пропорциональна разности между температурой тела и температурой воздуха. Температура воздуха равна . Известно, что в течение 20 минут  тело охлаждается от  до . Определить закон изменения температуры тела (f) от времени (t). Через сколько минут тело остынет до ?

2.      Найти пройденный путь за время , если тело движется со скоростью . Определите вид движения, описанного формулой.

а)  

б)  

в)  

г)  

д)  

е)  

Порядок выполнения работы:

1 Задания 1, 2 (а, г) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 2 (б, в, д, е) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.      Какими величинами должен характеризоваться изучаемый процесс, чтобы по условию задачи нужно было составить дифференциальное уравнение?

2.      Какие виды дифференциальных уравнений используются для решения практических задач?

 

Тема  6.1 Событие. Вероятность события

Практическая работа № 12

Решение задач на определение вероятности случайного события

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения для нахождения пределов.

Выполнив работу, Вы будете:

уметь:

- находить вероятность случайного события.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задания:

1.      В коробке n шаров, m из которых белые. Наудачу взяли один за другим 2 шара. Найти вероятность того, что оба шара окажутся белыми, если

а)    n=6, m=3

б)   n=7, m=3

в)   n=6, m=4

2.      Два стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком , вторым - . Найти вероятность того, что оба стрелка попадут в цель, оба промахнуться, только один стрелок попадет в цель, хотя бы один стрелок попадет в цель, если

а) 

б) 

в) 

3.      На сборку попадают детали, изготовленные на 3 станках. Известно, что один станок дает 0,3 % брака, 2 – 0,2 %, 3 – 0,4 %. Найти вероятность попадания на сборку бракованной детали, если с 1 станка поступило 1000 деталей, 2 – 2000, 3 – 2500.

4.      На заводе изготавливают болты, 1 станок производит 25 %, 2 – 35 %, 3 – 40 % всех изделий. В продукции, изготовленной на станках, брак составляет  соответственно. Какова вероятность того, что случайно выбранный болт дефектный, если

а)   

б)   

5.      В партии из 10 деталей имеется n стандартных. Из этой партии наудачу взяли 2 детали. Какова вероятность, что только одна из выбранных деталей стандартная, если

а)      n=6

б)      n=7

в)      n=4

Порядок выполнения работы:

1 Задания 1 (а), 2 (а), 3, 5 (а) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 2 (б, в), 2 (б, в), 4, 5 (б, в) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.      В каких случаях используется классическое определение вероятности?

2.      В каких случаях используется формула полной вероятности?

3.      В каких случаях используется формула Бернулли?

 

Тема 6.2 Случайная величина

Практическая работа № 13

Вычисление характеристик случайной величины

Формируемые компетенции:

ПК 2.1. Участвовать в проектировании гидравлических и пневматических приводов по заданным условиям и разрабатывать принципиальные схемы.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Цель работы: применить знания и закрепить умения для нахождения пределов.

Выполнив работу, Вы будете:

уметь:

- использовать случайную величину для решения практических задач.

Материальное обеспечение:

конспект; тетрадь для выполнения письменных заданий.

Задания:

1.      В соревнованиях по стрельбе в финале соревновались 3 стрелка. Какие места были заняты спортсменами, если спортсменами были набраны очки

а)                 

Иванов	6	7	7	7	8	8	9	9	10	10
Петров	6	7	8	8	8	8	8	9	9	10
Сидоров	10	9	4	7	8	8	9	9	9	10

б)                 

Иванов	7	10	8	9	6	9	9	8	9	9
Петров	7	8	8	8	8	8	9	9	9	10
Сидоров	8	7	7	8	9	10	8	9	8	9

в)                 

Иванов	6	7	8	8	9	9	9	9	10	10
Петров	7	8	8	8	8	9	9	9	10	10
Сидоров	10	5	7	8	8	10	9	9	10	10

2.      В партии из 10 деталей имеется n стандартных. Из этой партии наудачу взято 2 детали. Составьте закон распределения случайной величины Х – число стандартных деталей в выборке. Найдите числовые характеристики случайной величины Х.

а)    n=6

б)   n=4

в)   n=7

Порядок выполнения работы:

1 Задания 1 (а), 2 (а) выполняются совместно группой обучающихся под контролем преподавателя.

2 Задания 2 (б, в), 2 (б, в) выполняются самостоятельно обучающимися и сдаются на проверку.

Форма представления результата: письменная работа.

Контрольные вопросы:

1.      При решении каких задач используется дискретная случайная величина?

2.      Как составить закон распределения дискретной случайной величины?

3.      Что характеризует в ряде распределения такая числовая характеристика как математическое ожидание?

4.      Что характеризует в ряде распределения такая числовая характеристика как среднее квадратическое отклонение?

 
3 ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ

 

Основные источники:

1.             Григорьев, В. П. Элементы высшей математики [Текст] : учебник для студ. учреждений сред. проф. образования / В.П. Григорьев, Ю.А. Дубинский, Т.Н. Сабурова. - М : Академия, 2017. - 400 с.

2.             Григорьев, В.П. Элементы высшей математики : учебник для студ. учреждений сред. проф. образования [текст] / В.П. Григорьев, Ю.А. Дубинский, Т.Н. Сабурова. – М. : Академия, 2016. – 400 с.

3.             Григорьев, С.Г. Математика: учебник для студ. образоват. учреждений сред. проф. образования [текст] / С.Г. Григорьев, С.В. Задулина; под ред. В.А. Гусева – М. : Академия, 2011. – 384 с.

 

Дополнительные источники:

1.             Григорьев, В.П. Элементы высшей математики : учебник для студ. учреждений сред. проф. Образования [текст] / В.П. Григорьев, Ю.А. Дубинский. – М. : Академия, 2011. – 320 с.

2.             Пехлецкий, И.Д. Математика: учебник для студ. сред. проф. Учреждений [текст] / И.Д. Пехлецкий – М. : Академия, 2011. – 304 с.

3.             Спирина, М.С. Дискретная математика : учебник для студ. образоват. учреждений сред. проф. Образования [текст] / М.С. Спирина, П.А. Спирин. – М. : Академия, 2012 –368 с.

4.             Стойлова, Л.П. Математика: учебник для студ. высш. пед. учеб. заведений [текст] / Л.П. Стойлова – М. : Академия, 2011. – 432 с.

5.             Шипачев, B.C. Основы высшей математики [текст] / B.C. Шипачев. – М.: Высшая школа, 2011. – 480 с.

 

Скачано с www.znanio.ru