ФЕДЕРАЛЬНАЯ СЛУЖБА ИСПОЛНЕНИЯ НАКАЗАНИЙ РАЛЬНОЕ  КАЗЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ  ВЫСШЕГО ОБРАЗОВАНИЯ  ПЕРМСКИЙ ИНСТИТУТ  (ФКОУ ВО ПЕРМСКИЙ ИНСТИТУТ ФСИН РОССИИ)
	ОСНОВЫ СТАТИСТИКИ

 

 

 

 

 

 

 

 

 

 

 

 

 

Щеткин Б.Н. Рабочая тетрадь «Основы статистики». – Пермь: Изд-во ПИ ФСИН России, 2022. – 54с.  

  

Настоящее издание является частью учебно-методического комплекса по дисциплине «Основы статистики». Практические занятия по «Основам статистики» имеют цель закрепить и систематизировать теоретические знания студентов по данной дисциплине, а также выработать определенные умения и навыки проведения статистического анализа экономической информации для решения социальных и экономических проблем, применять полученные знания на практике.

Содержит задания, относящиеся к основным понятиям статистика в профессиональной деятельности, которые предусмотрены для изучения образовательным стандартом.  Преимущественно это задания на усвоение теоретического материала и формирование определенного практического опыта в области статистики в ГМУ.  

 

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ 

 

к циклу практических занятий по дисциплине «Статистика»

(рабочая тетрадь по практическим занятиям)

 

Практические занятия по дисциплине «Статистика» имеют цель закрепить и систематизировать теоретические знания студентов по данной дисциплине, а также выработать определенные умения и навыки проведения статистического анализа экономической информации для решения социальных и экономических проблем, применять полученные знания на практике.

Практические занятия – одна из ведущих форм обучения в высших учебных заведениях. На практических занятиях формируются умения и навыки проведения статистических расчетов и аналитического мышления, закрепляются знания методики определения статистических показателей.

Практические занятия позволяют заинтересовать студентов в изучении данной дисциплины, а также показать её практическое применение в будущей профессиональной деятельности.

При проведении практических занятий для удобства и с целью повышения оперативности работы студентов, лучше использовать Рабочую тетрадь, содержащую перечень тем практических занятий, задания для каждого занятия и методические указания по их выполнению. 

Цель настоящей методической разработки – оказать методическую помощь студенту по освоению дисциплины «Статистика», а также выработке практических умений и навыков, закреплении на практике теоретических знаний по данной дисциплине.

 

 

ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАНЯТИЙ И РАСПРЕДЕЛЕНИЕ БЮДЖЕТА ВРЕМЕНИ 

НАИМЕНОВАНИЕ ПРАКТИЧЕСКОГО ЗАНЯТИЯ

Практическая работа №1. Проведение сводки статистических данных. Группировка и перегруппировка данных

Практическая работа №2. Построение, анализ и графическое изображение рядов распределения

Практическая работа №3. Построение и анализ таблиц и графиков в статистике

Практическая работа №4. Определение среднего уровня изучаемого явления и анализ полученных результатов

Практическая работа №5. Оценка степени вариации изучаемого признака. Графическое изображение полученных результатов.

Практическая работа №6.  Анализ структуры вариационных рядов распределения

Практическая работа №7. Анализ динамики изучаемых явлений

Практическая работа №8. Выявление и анализ основной тенденции в рядах динамики

Практическая работа №9. Изучение структурных сдвигов и факторный анализ на основе индексного метода

ПРАКТИЧЕСКАЯ РАБОТА №1

    

Тема: «Метод группировок в статистике»

 

Наименование работы: Проведение сводки статистических данных. Группировка и перегруппировка данных.

 

Цель занятия: освоить методику группировки данных в соответствии с поставленными целями и задачами, и перегруппировку данных

 

Содержание практического занятия: Изучение методов составления простых и комбинационных группировок статистических данных и составление вспомогательных, результативных и аналитических таблиц, ознакомление с приемами вторичной группировки.

 

Формируемые умения: после выполнения задания студент  должен знать: 

-     значение метода группировок в статистике;

-     виды статистических группировок; должен уметь:

-     осуществить группировку данных в соответствии с поставленными целями и задачами;

-     определить вид представленной группировки;

-     произвести перегруппировку статистических данных для обеспечения их сопоставимости.

 

Вид занятия: практическое занятие

Тип занятия: формирование умений и навыков Методы обучения: практическая работа

 

Литература: 1. Теория статистики. Учебник/ под ред. проф. Р.А. Шмойловой. – М.: «Финансы и статистика», 2000.

                       2.  Практикум по теории статистики. Учебное пособие/ под ред.проф. Р.А.Шмойловой. - М.: «Финансы и статистика», 2000.

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗАДАНИЕ: 1. Используя данные статистического наблюдения (Таблица 1) произведите группировку предприятий по численности производственного персонала. Рассчитать по каждой группе стоимость товарной продукции. Сделайте выводы о взаимосвязи межу этими двумя показателями. Результаты группировки запишите в табличной форме.    

                                                                                          Таблица 1.

Исходные данные

№ п/п	Стоимость промышленно- производствен- ных фондов млн.руб.	Стоимость нормированных оборотных средств млн.руб.	Товарная продукция в оптовых ценах предприятий, млн.руб.	Численность промышленно- производственного персонала, чел.	Фонд заработной платы тыс.руб.
1	2	3	4	5	6
1	985	79	557	4904	60975
2	506	73	676	4682	92384
3	4644	295	5892	31868	665573
4	3209	272	2402	17643	360136
5	1982	167	6393	31826	162900
6	668	106	1087	13578	177714
7	173	15	225	1245	6575
8	532	68	992	13404	130626
9	1442	72	1955	11682	71419
10	3618	218	3532	18501	470646
11	3230	234	4097	2234	130626
12	549	34	390	4102	94458
13	1002	103	1657	7235	152459
15	612	15	367	5285	105797
16	1338	188	1824	16734	143665
17	1262	182	2270	14807	301271
18	2185	144	2187	15388	316198
19	2611	210	3053	19474	4488026
20	1681	124	1064	17016	146118
21	901	70	885	5897	142797
22	927	74	1160	9873	228131
23	962	76	1018	7371	158798
24	1865	156	1768	14321	163446
25	2092	178	1067	15589	95837
26	1184	107	1509	9401	218120
27	2953	301	2836	20733	526176
28	1684	130	1024	9314	6630
29	385	35	7619	4127	96230
30	619	22	2059	15065	443553
31	1124	77	682	5055	108981
32	1003	70	1916	8620	195693
33	980	71	1071	7789	161644
34	1259	114	1853	9883	217322
35	1116	92	634	14250	13857
36	1095	96	1719	7284	148487

 

Порядок выполнения и методические указания 

 

Для построения группировки предприятий необходимо:

1.              Определить группировочный признак (основание группировки) – запишите его

Основанием группировки является –

 

2.              Определить количество групп, используя формулу Стерджеса: n = 1 + 3,322 lq N где        n – число групп              Количество групп составит: n = N – число единиц совокупности

3.              Определить интервалы групп. Величина интервала (шаг) определяется по формуле:

h _ хmax  хmin _ ^R n n

где, х_max , х_min - максимальное и минимальное значение признака в совокупности.

R =

R = х_max  х_min - размах вариации.

ⁿ -  число групп

 

h хmax хmin  n

Величина интервала (шаг) составит: 4. После определения величины интервала образуйте сами группы и впишите их в таблицу 2.

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                             Таблица 2

Группа	Величина интервала
1
2
3

 

5.                Отберите показатели, которые характеризуют группы и определите их величины по каждой группе, для этого воспользуйтесь вспомогательной таблицей №3.

Таблица 3.

Вспомогательная таблица для построения группировки предприятий.

 

Группы предприятий по численности производственного персонала, чел	Порядковый номер предприятия (гр.1 табл.1)	Товарная продукция в оптовых ценах, млн.руб. (гр.4 табл.1)	Стоимость товарной продукции в среднем на одно предприятие по группе, млн.руб.
1	2	3	4
1 группа…. интервал……………………….
Итого по группе
2 группа…. интервал……………………….
Итого по группе и т.д.
3 группа… интервал……………………….
Итого по группе
Всего по группам

 

Для расчета стоимости товарной продукции в среднем на одно предприятие по группе необходимо сумму стоимости товарной продукции по всем предприятиям группы (итог графы 3 по каждой группе табл.3) разделить на число предприятий в группе (гр. 2 табл.3).

 

6.                Результаты группировки предприятий представить в виде таблицы №4, сделайте вывод указав вид статистической группировки и взаимосвязь между численностью производственного персонала и стоимостью товарной продукции предприятия.

Таблица 4.

Группировка предприятий по численности производственного персонала.

 

№ группы	Группа предприятий по численности производственного персонала, чел. (интервал)	Число предприятий	Стоимость товарной продукции в среднем на одно предприятие по группе, млн.руб.
1
2
3
4
	Всего:

 

Вывод:

 

 

ЗАДАНИЕ 2: Перегруппируйте следующие данные о численности работающих на 55

предприятиях, образовав следующие группы: до 400-1000, 1000-3000, 3000-6000, свыше 6000

Таблица 5 Исходная группировка предприятий по численности работающих

Число работающих, человек		Число предприятий
До 100 100-500 500-1000 1000-2000 2000-5000 5000-10000 10000-20000 Свыше 20000		2 8 7 12 15 6 4 1
	Всего:	55

 

Результаты перегруппировки внести в таблицу 6.

Таблица 6. Вновь образованная группировка предприятий по численности работающих.

Число работающих, человек		Число предприятий
до 400
400 – 1000
1000 – 3000
3000 – 6000
свыше 6000
	Всего:	55

 

ЗАДАНИЯ 1.1 и 1.2 выполнить в MS Excel

 

ЗАДАНИЕ 1.1: по данным МВД России возраст преступников, совершивших грабежи в области, составил:  

Таблица 7

20	22	19	21	16	18	22	17	17	18
19	21	21	18	24	21	21	23	20	24
17	22	21	22	20	18	22	18	22	23
22	21	18	17	17	22	18	17	21	23
20	17	23	16	24	23	20	21	21	22

 

1.      Определите возможные шкалы измерения признака.

2.      Постройте ряды распределения в соответствии со шкалами измерения.

3.      Укажите вид и элементы ряда распределения.

4.      Проведите сводку данных в таблицу.

5.      Определите вид таблицы (по подлежащему и сказуемому).

6.      Сформулируйте выводы по каждому варианту.

 

ЗАДАНИЕ 1.2: при проведении плановых мероприятий по выявлению нарушений скоростного режима на автомобильных дорогах Пермского края зарегистрирована следующая скорость движения автотранспорта (в км/ч):

Таблица 8

50	115	40	125	62	84	60	110
82	60	70	67	100	65	133	102
100	65	57	105	130	87	97	99
75	110	55	45	80	120	100	108
140	92	80	78	73	105	69	60

 

Для анализа полученной информации требуется:

1. Построить интервальный ряд распределения, образовав 5 групп с равными интервалами. 2. Полученный ряд распределения изобразить на графике в виде гистограммы.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.  Что понимается под статистической группировкой?

2.  Каков порядок построения статистической группировки?

3.  Как определить величину равного интервала?

 

 

ПРАКТИЧЕСКАЯ РАБОТА №2

 

Тема: «Ряды распределения в статистике»

 

Наименование работы: Построение, анализ и графическое построение рядов распределения.

 

Цель занятия: освоить методику построения, анализа и графического изображения рядов распределения.

 

Формируемые умения: после выполнения задания студент    должен знать:

-     принципы построения и виды рядов распределения в статистике;  способы графического изображения рядов распределения.  

  должен уметь:

-     построить ряд распределения, представить его графическое изображение и произвести анализ полученных результатов.

 

 

Вид занятия: практическое занятие

Тип занятия: формирование умений и навыков Методы обучения: практическая работа

 

Литература: 1. Теория статистики. Учебник/ под ред. проф. Р.А. Шмойловой. – М.: «Финансы и статистика», 2000.

                       2.  Практикум по теории статистики. Учебное пособие/ под ред.проф. Р.А.Шмойловой. - М.: «Финансы и статистика», 2000.

ЗАДАНИЕ 1. По приводным данным постройте ряд распределения предприятий отрасли по проектной мощности.

Таблица 1.

Исходные данные.

№ предприятия	Проектная мощность, тыс.шт.	№ предприятия	Проектная мощность, тыс. шт.	№ предприятия	Проектная мощность, тыс. шт.
1 2 3 4 5 6 7 8 9	25,0 14,0 65,0 70,, 30,0 18,0 14,0 55,0 40,0	10 11 12 13 14 15 16 17 18	35,0 46,0 120,0 125,0 125,0 200,0 14,0 88,0 118,0	19 20 21 22 23 24 25	68,0 20,0 75,0 40,0 45,0 35,0 87,0

 

Порядок выполнения и методические указания

 

Для построения ряда распределения необходимо:

1.  Произвести группировку варьирующего признака: используя формулу Стерджеса:    n = 1 + 3,322 lq N

                                               Определить число групп   n =                                           

h =

Определить величину интервала по формуле:                         h X ^{max }X ^min n

 

2.  Определить границы интервалов:        

Группа	Величина интервала
1
2
3

 

3.  Построить ряд распределения, воспользовавшись таблицей 2.

Таблица 2

Ряд распределения предприятий отрасли по проектной мощности.

 

Проектная мощность, тыс. шт.	Число предприятий	% к итогу
Всего:	25	100

 

ЗАДАНИЕ 2. Используя показатели ряда распределения в задании 1, постройте гистограмму.

 

 

 

ЗАДАНИЕ 3. По нижеприведенным данным о распределении численности рабочих одной из отраслей промышленности, по тарифным разрядам за год постройте полигон распределения.

 

 

Тарифный разряд	1	2	3	4	5	6
Численность рабочих, % к итогу	4,3	12,1	20,6	32,4	24,0	6,6

 

Полигон распределения

 

 

ЗАДАНИЕ 4. На основании ряда распределения семей по размеру жилой площади (табл.3), приходящейся на одного человека построить кумуляту и огиву.

Таблица 3.

Распределение семей по размеру жилой площади, приходящейся на одного человека (цифры условные).

 

№ п/п	Группы семей по размеру жилой площади, приходящейся на 1 человека		Число семей с данными размерами жилой площади	Накопленное число семей
1	3-5		10
2	5-7		20
3	7-9		40
4	9-11		30
5	11-13		15
		ВСЕГО	115

 

Методические указания:

Необходимо помнить, что кумулята и огива как графическое изображение ряда распределения, строятся по накопленным частотам, поэтому перед построением данных графиков необходимо вначале рассчитать накопленные частоты и записать их в таблицу 3, а затем уже строить графики, обозначив оси

 

Кумулята

 

 

Огива

 

 

 

ЗАДАНИЯ 2.1. и 2.2 выполнить в MS Excel

 

ЗАДАНИЕ 2.1: ниже приведены данные опроса несовершеннолетних насильственных преступников относительно черт личности друга как идеального образа и черт личности, якобы действительно присущих их товарищам. 

 

Таблица 4

Положительные качества личности	Идеальный образ (в %)	Фактически отмеченные у у товарищей (в %)
Смелость	60,6	84,2
Верность	30,3	52,6
Сила	21,2	57,9
Честность	21,2	50,0
Преданность	15,2	-
Взаимопомощь, отзывчивость	12,2	-
Находчивость	12,1	36,8
Доброта	9,1	-

 

1.      Постройте статистический график распределения полученных ответов. 

2.      Проанализируйте результат, сделайте статистические выводы относительно перспектив предупреждения преступности.

 

Задача 2.2: имеются данные о возрасте 100 осужденных к лишению свободы:

18, 20, 32, 23, 20, 24, 22, 18, 29, 23, 19, 21, 18, 23, 18, 24, 27, 31, 19, 25, 27, 21, 28, 25, 17, 17, 27, 21, 19, 20, 19, 25, 18, 27, 22, 23, 19, 31, 32, 27, 19, 22, 30, 17, 22, 19, 18, 24, 20, 22, 17, 29, 21, 27, 17, 31, 25, 20, 24, 19, 26, 28, 21, 18, 26, 21, 20, 23, 26, 23, 19, 25, 21, 20, 18, 25, 33, 18, 33, 19, 33, 28, 31, 22, 30, 19, 26, 18, 29, 20, 29, 19, 23, 32, 17, 20, 33, 21, 33, 19.

 

На основе этих данных: а) построить вариационный ряд (интервальный, образовав 4 группы с равными интервалами); б) определить размах ряда, моду и медиану; в) построить гистограмму.

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ:

Что понимается под рядом распределения?

 

Что понимается под дискретным вариационным рядом?

 

Что показывают чистоты в вариационном ряду?

 

ПРАКТИЧЕСКАЯ РАБОТА №3

 

Тема: «Способы наглядного представления статистических данных»

 

Наименование работы: Построение и анализ таблиц и графиков в статистике

 

Цель занятия: освоить методику построения статистических таблиц и графиков. 

 

Формируемые умения: после выполнения задания студент должен знать: 

-     элементы, виды и правила построения таблиц и графиков в статистике; должен уметь:

-     разработать макет статистической таблицы в соответствии с поставленными задачами;

-     графически изобразить статистические данные;  анализировать данные, представленные в виде таблиц и графиков.

 

Вид занятия: практическое занятие

Тип занятия: формирование умений и навыков Методы обучения: практическая работа

 

Литература: 1. Теория статистики. Учебник/ под ред. проф. Р.А. Шмойловой. – М.: «Финансы и статистика», 2000.

                       2.  Практикум по теории статистики. Учебное пособие/ под ред.проф. Р.А.Шмойловой. - М.: «Финансы и статистика», 2000.

 

 

 

 

 

 

 

 

 

ЗАДАНИЕ 1. Объедините приведенные таблицы о миграции населения Российской Федерации за 2001-2002 гг (тыс. чел.) в одну и дайте ей общий заголовок.

 

Убыло из города	Всего	В том числе		Убыло из сельской местности	Всего	В том числе
		Мужчин	Женщин			В город	В сельскую местность
В город В сельскую местность	5230 1759	2627 860	2603 889	Мужчины Женщины	3362 3473	2167 2197	1195 1276
ИТОГО:				ИТОГО:

 

Таблица 1

 

(Заголовок таблицы)

 

Методические указания к заданию 1:

Для объединения таблиц в одну статистическую таблицу используйте форму комбинационной статистической таблицы, подлежащее которой содержит группировку единиц совокупности одновременно по двум и более признакам: каждая из групп, построенная по одному признаку, разбивается, в свою очередь, на подгруппы по другому признаку и т. д.

 

ЗАДАНИЕ 2. Оформите в табличном виде следующие данные. Военные расходы ФРГ возросли с 6,1 (1990г) до 31,0 млрд. дол. В 2000г., а Франции соответственно с 5,9 до 27,0 млрд. дол. За тот же период доля ФРГ в общих расходах НАТО увеличилась с 6 до 10%, а доля Франции с 5 до 9%.

 

Таблица 2

 

(Заголовок таблицы)

 

 

 

 

 

Методические указания к заданию 2.

При построении статистической таблицы лучше использовать макет таблицы со сложной разработкой сказуемого.

 

ЗАДАНИЕ 3. Имеются следующие данные, характеризующие динамику развития внешней торговли России (таблица 1).

Таблица 1.

                                       Объем внешней торговли России (млрд. дол. в текущих ценах).                  

Годы	1996	1997	1998	1999	2000	2001	2002
Оборот	183,3	121,3	97,2	101,4	116,7	135,7	148,1
Экспорт	85,5	66,8	54,2	59,2	66,2	77,8	88,3
Импорт	94,8	54,2	43,0	42,2	50,0	57,9	59,8

 

Изобразите приведенные в таблице данные при помощи линейной диаграммы (все кривые нанесите на одну диаграмму) и сделайте вывод.

 

 

(название графика)

 

 

ЗАДАНИЕ 4. Географическая структура экспорта России характеризуется следующими данными (таблица 3).

Таблица 3. Географическая структура экспорта России, (% к итогу).

 

Страны	2002	2004
1.      Европа 2.      Азия 3.      Америка 4.      Африка 5.      Страны СНГ	58,2 16,2 2,7 1,1 21,8	53,9 16,6 7,1 0,9 21,5
ИТОГО:	100	100

 

Постройте секторную диаграмму, отражающую географическую структуру экспорта России.

 

Методические указания для выполнения задания 4.

1.  Строим 2 круга одинакового радиуса, для каждого года свой круг.

2.  Определяем размер центральных углов по данным о доле группы стран в экспорте России для построения секторов, для этого удельный вес страны в общем экспорте России (%) умножаем на 3,6⁰.

     Например: Размер центрального угла для стран Европы:                         в 2002г будет равен 58,2 х 3,6⁰=209,52⁰   210⁰;

                       в 2004г                      53,9 х 3,6⁰=194⁰

Таким образом определяются размеры центральных углов для всех остальных стран.

 

3.  После того как определены размеры центральных углов, отмечаем сектора на круге с помощью транспортира.

4.  С помощью штриховки секторов, указать какой из них характеризует ту или иную группу стран.

 

Географическая структура экспорта России

                                               2002 г.                                                                         2004 г.

 

 

 

ЗАДАНИЕ 5. Постройте радиальную диаграмму по данным о производстве шоколада и шоколадных  изделий одной из кондитерских фабрик по месяцам года:

месяц	1	2	3	4	5	6	7	8	9	10	11	12
тонн	972	886	974	1013	848	929	466	730	947	964	881	920

 

Методические указания для выполнения задания 5.

1. Необходимо начертить круг с радиусом равным среднемесячному показателю, для этого необходимо: а) определить среднемесячный показатель по формуле:

х

 х_i х n

где, xi   - показатель за каждый месяц.          n – число месяцев в году (n = 12).

 

б) установим масштабную шкалу приняв 1см = 200 тонн.

в) начертим круг с радиусом ? см, согласно установленного масштаба.

 

2.                Весь круг разделить на 12 радиусов (соответственно по числу месяцев в году) каждый из них обозначает месяц.

3.                Нумерацию месяцев производить аналогично циферблату часов: январь – в том месте где на часах 1, февраль – 2 и т.д.

4.                На каждом радиусе делаются отметки в определенном месте согласно масштабу исходя из данных за соответствующий месяц. Если данные превышают среднемесячный уровень, отметка делается за пределами окружности на продолжении радиуса. 

5.                Соединить отметки различных месяцев отрезками. Таким образом будет построена радиальная диаграмма.

Сделайте вывод о сезонности производства на кондитерской фабрике.

 

Радиальная диаграмма производства шоколада и шоколадных изделий на

кондитерской фабрике по месяцам года

 

 

Вывод:

 

 

ЗАДАНИЯ 3.1 выполнить в MS Excel

 

ЗАДАНИЕ 3.1: В третьем квартале 2019 г. в г. Перми возросло число преступлений, совершаемых на улице и в других общественных местах. Обеспокоенное ростом уличной преступности руководство ГУВД г. Перми в целях более рационального использования сотрудников патрульнопостовой службы поручило Вам провести анализ временного фактора совершения данных преступлений. Было установлено следующее время совершения, выявленных преступлений (в часах):

Время (в часах)                                                                                           Таблица 4

01      23        19        21        23        15        23        22        09        22        20        11        21        22        00           18        22        17        23        19 13   03        23        19        21        13        14        00        19        20           22        19        11        00        23        23        21        22        21        23

19      12        02        23        18        21        00        23        20        18        14        22        00        11        21           13        03        15        01        15 21   19        17        01        23        00        21        20        19        23           19        00        22        20        11        21        23        20        23        13 23   21        19        18        08           23        20        21        23        22        00        23        01        22        15        12        21        16        18           20

 

Для анализа информации и принятия управленческого решения необходимо:

1.                  Определите возможные шкалы измерения признака.

2.                  Постройте ряды распределения в соответствии со шкалами измерения.

3.                  Укажите вид и элементы ряда распределения.

4.                  Проведите сводку данных в таблицы.

5.                  Определите вид таблиц (по подлежащему и сказуемому).

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ:

Что представляет собой статистическая таблица.

 

Каковы основные элементы статистической таблицы.

 

Что является подлежащим и сказуемым статистической таблицы.

 

Каковы основные элементы графика?

 

Каковы виды статистических графиков по форме графического образа.

 

Как классифицируются статистические графики по способу построения.

 

 

 

 

ПРАКТИЧЕСКАЯ РАБОТА №4

 

Тема: «Абсолютные, относительные и средние величины в статистике»

 

Наименование работы: Определение среднего уровня изучаемого явления и анализ полученных результатов.

 

Цель занятия: освоить методику расчета средней величины.

 

Содержание практического занятия: Вычисление отдельных видов относительных величин. Графическое изображение структуры совокупности.

 

Формируемые умения: после выполнения задания студент  должен знать:

-     значение и виды абсолютных показателей;

-     виды и методы исчисления относительных показателей;

-     взаимосвязи между абсолютными и относительными показателями.

-     виды степенных средних величин в статистике;  свойства средней арифметической;  методы расчета средних показателей.

должен уметь:  определить средний уровень изучаемого явления.

 

Вид занятия: практическое занятие

Тип занятия: формирование умений и навыков Методы обучения: практическая работа

 

Литература: 1. Теория статистики. Учебник/ под ред. проф. Р.А. Шмойловой. – М.: «Финансы и статистика», 2000.

                       2.  Практикум по теории статистики. Учебное пособие/ под ред.проф. Р.А.Шмойловой. - М.: «Финансы и статистика», 2000.

 

 

 

 

ЗАДАНИЕ 1. Себестоимость товарной продукции за 2002 год составила 550 тыс.руб. План предусматривал снижение себестоимости товарной продукции в 2003 году на 6%, фактически за 2003 год себестоимость была снижена на 8%. Определите плановую и фактическую величину себестоимости товарной продукции за 2003 год, а так же степень выполнения плана.

 

Порядок выполнения:

1.    Определить плановую величину себестоимости продукции в 2003 году по формуле:

Zпл.2003 =

Zпл. = Zфакт.2002 × Тр пл. / 100

где,  Z_пл. – величина себестоимости продукции планируемая в 2003 г, руб.

         Z_{факт.2002} – фактическая себестоимость достигнутая в предыдущем году (2002г), руб

           Т_{р пл.} – планируемый темп роста (снижения), %

 

2.    Определить фактическую себестоимость продукции в 2003 году, по формуле:

Zфакт.2003 =

Zфакт.2003 = Zфакт.2002 × Тр. факт / 100

где,    Z_{факт.2003} – фактическая себестоимость продукции в 2003 году, руб.

              Т_{р. факт} – фактический темп роста (снижения) себестоимости в 2003г.,%

 

3.    Определить степень выполнения плана, по формуле:

ОПРП

Фактически достигнутый показатель в 2003г

ОПРП   

Планируемый показатель на 2003г

 

ЗАДАНИЕ 2. Определите средний товарный остаток за 1 квартал если известны товарные остатки на 1 -е число каждого месяца (тыс.руб.).

Дата	1,01	1,02	1,03	1,04
Товарный остаток	18	14	16	20

 

Методические указания к выполнению задания 2:

Для определения среднего товарного остатка за 1 квартал необходимо воспользо-ваться формулой расчета средней хронологической моментного ряда:

y =

                                                                      у1 уп        n1

уi

                                                           у                i2       

n1

 где,  y - средний уровень ряда динамики;           у₁ – первый уровень ряда динамики;            у_п – последний уровень ряда динамики; у_i – i-ый уровень ряда динамики, начиная со второго

 

ЗАДАНИЕ 3. Рабочие одного цеха предприятия распределяются по стажу работы в этом цеху следующим об                                     разом:

Стаж работы, лет    xi	1	2	4	5	8	10	15
Число рабочих         fi	2	5	3	10	15	20	10

 

Определите средний стаж работы (используя среднюю арифметическую взвешенную).

 

Методические указания к выполнению задания 3:

Формула расчета средней арифметической взвешенной:

х =

х хi fi  f_i

где,    х - средняя величина признака

                 x_i – i-ый вариант осредняемого признака                  f_i – частота (вес) i-го варианта

 

ЗАДАНИЕ 4. Имеются следующие данные о распределении рабочих предприятий по размеру месячной за работной платы:

Группа рабочих по величине месячной заработной платы, тыс.руб.	Число рабочих в % к итогу
1500-2000 2000-2500 2500-3000 3000-3500 3500-4000 4000-4500 4500-5000	5 8 25 30 15 12 5

 

Определите: среднемесячную заработную плату, приходящуюся на одного рабочего.

 

Методические указания к выполнению задания 4:

1.                При расчете средней величины по данным интервального вариационного ряда вначале необходимо найти середину интервалов – х^/ , так серединой первого интервала (1500-2000)

                           20001500                     2250^^{25002000} и т.д.;  результаты расчетов середины

будет 1750                      , второго –

 2                            2           интервалов внесите в графу 2 табл. 1.

Таблица 1                                              Распределение рабочих предприятия по размеру месячной заработной платы

Группа рабочих по величине месячной заработной платы, тыс.руб.	Середина интервала, (хi/)	Число рабочих в % к итогу (fi )
1500-2000 2000-2500 2500-3000 3000-3500 3500-4000 4000-4500 4500-5000		5 8 25 30 15 12 5

 

2.                Определите средний размер заработной платы работников по формуле средней арифметической взвешенной, при расчете в качестве x_i , взять середину интервала:

х =

х х/i fi

 fi

 

ЗАДАНИЕ 5. Используя данные таблицы определить средний курс продажи акций.

Таблица 2.

Продажа акций АО «Донна-Хлеб»на торгах фондовой секции ТМБ «Гермес».

 

Сделка	Количество проданных акций, штук	Курс продажи, руб.
1 2 3	500 300 1100	1080 1050 1145

 

Для расчета использовать формулу средней арифметической взвешенной.

х =

 х/i f

                                                х             i

 fi

 

ЗАДАНИЕ 6. Используя формулу средней гармонической взвешанной определить среднюю урожайность подсолнечника по Центрально-Черноземному району.  

Таблица 3.

                                                                                                                                                                                   Валовой сбор и урожайность подсолнечника.

О б л а с т ь	Валовой сбор, тыс.т.	Урожайность, ц/га
Белгородская Воронежская Курская Липецкая тамбовская	97,0 204,0 0,5 16,0 69,0	16,1 9,5 4,8 10,9 7,0

 

Формула расчета гармонической взвешенной имеет вид:

х =

 w

х wii  xi

где,  w_i = x_i  f_i – произведение осредняемого признака на частоту (в данном случае валовой сбор подсолнечника, который определяется путем умножения урожайности на посевную площадь подсолнечнка).

 

ЗАДАНИЕ 7. Валовой сбор и посевная площадь картофеля в фермерских хозяйствах в 2000г. составили:

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                             Таблица 4

п/п фермерского хозяйства	Посевная площадь, га	Валовой сбор, т.	Урожайность, ц/га
1. Хозяйство	140	2055
2. Хозяйство	102	1484
3. Хозяйство	64	981
ИТОГО:

 

Определить:

1. Урожайность картофеля по каждому фермерскому хозяйству. 2. Среднюю урожайность картофеля в фермерских хозяйствах.

 

Методические указания к выполнению задания 7:

1. Урожайность культуры определяется путем деления валового сбора на посевную площадь. Рассчитайте урожайность картофеля по каждому хозяйству, результаты расчетов внесите в таблицу. Расчет урожайности картофеля:

х =

1. Хозяйство –

2.  Хозяйство - 3.  Хозяйство -	х =
	х =
Определите среднюю урожайность картофеля в фермерских хозяйствах, используя для расчета либо формулу средней арифметической взвешенной, либо средней гармонической взвешенной.

 

ЗАДАНИЯ 4.1, 4.2 и 4.3 выполнить в MS Excel

 

ЗАДАНИЕ 4.1: согласно данным ГИАЦ МВД России за 2009-2011 гг. наблюдается следующее распределение лиц, совершивших преступления.

Таблица 5 Характеристика лиц, совершивших преступления

Показатель	Выявлено лиц, совершивших преступления
	2009	2010	2011
Всего	1219789	1111145	1041340
в том числе:
несовершеннолетних	8545	72692	65963
женщин	194202	172375	159329
лиц, не имеющих постоянного источника дохода	785577	730314	690920
из них
безработных	55101	54304	47160
ранее совершавших преступления	390549	397403	401894
из них
ранее судимых за преступления	291285	294167	299005
совершивших преступления, признанные опасным или особо опасным рецидивом	13977	15124	15772
в состоянии опьянения:
алкогольного	186077	201440	221536
наркотического	10337	11513	15237

 

Требуется:

1.      Рассчитать относительные величины структуры.

2.      Рассчитать относительные величины сравнения.

3.      Провести сводку, имеющихся данных и полученных величин в таблицу.

4.      Интерпретировать криминологическую ситуацию.

 

ЗАДАНИЕ 4.2: Практика назначения наказания за убийство с учетом состояния виновного в момент совершения преступления выглядела следующим образом:

Таблица 6

Меры наказания	Виновные в состоянии: опьянения             трезвом		Всего
Лет лишения свободы
3	3	10	13
До 5	2	19	21
До 7	5	9	14
До 10	29	15	44
До 12	20	10	30
До 15	117	19	49
Высшая    мера	30	19	49

 

 

Вычислите удельный вес каждой группы в общем количестве осужденных, а также по срокам и видам наказания. Проанализируйте полученные данные и сделайте статистические выводы.

 

ЗАДАНИЕ 4.3: Администрация СИЗО зафиксировала телефонные разговоры подследственных, содержащихся в общей камере, продолжительность которых составила:

Распределение выявленных телефонных разговоров по продолжительности (в сек.)

Таблица 7

Продолжительность разговора (сек.)	5	30	55	90	120
Количество звонков	7	22	35	40	18

 

Требуется вычислить:

1.      Общее количество звонков; 

2.      Число звонков длительностью до 1 минуты; 

3.      Процент (долю) звонков длительностью свыше 1 минуты.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ:

Что понимается под статистическими показателями?

 

Что понимается под абсолютным показателем?

 

Что понимается под относительным показателем?

 

Что понимается под средним показателем?

 

 

 

 

ПРАКТИЧЕСКАЯ РАБОТА № 5

 

Тема: «Показатели вариации в статистике. Структурные характеристики вариационного ряда распределения».

 

Наименование работы: Оценка степени вариации изучаемого признака распределения.

 

Цель занятия: освоить методику расчета абсолютных и относительных показателей вариации признака.

 

Содержание практического занятия: Расчет различных видов средних величин и показателей вариации, анализ дисперсии.

 

Формируемые умения: после выполнения задания студент должен знать: 

-     понятие вариации и ее значение;

-     абсолютные и относительные показатели вариации; должен уметь:

-     оценить степень вариации изучаемого признака путем расчета абсолютных и относительных показателей вариации.

 

Тип занятия: формирование умений и навыков Методы обучения: практическая работа

 

Литература: 1. Теория статистики. Учебник/ под ред. проф. Р.А. Шмойловой. – М.: «Финансы и статистика», 2000.

                       2.  Практикум по теории статистики. Учебное пособие/ под ред.проф. Р.А.Шмойловой. - М.: «Финансы и статистика», 2000.

 

 

 

 

ЗАДАНИЕ 1. Имеются следующие данные о валовом сборе зерновых культур в фермерских хозяйствах.

Таблица 1

Хозяйство	Валовой сбор зерновых, ц
1 2 3 4 5 6	600 520 400 600 500 380
ИТОГО:	3000

 

На основании приведенных данных определить:

1.                Размах вариации.

2.                Среднее линейное отклонение.

3.                Дисперсию.

4.                Среднее квадратическое отклонение.

5.                Коэффициент осцилляции.

6.                Коэффициент вариации. Сделайте вывод.

 

Методические указания к выполнению задания 1:

1.  Размах вариации определяется по формуле:

R =

R = Xmax – X min  

где ,  X_max  - максимальное значение варьирующего признака

          X _min  - минимальное значение варьирующего признака

 

2.  Для определения следующих показателей необходимо построить вспомогательную таблицу для расчета дополнительных данных

Хозяйство	Валовой сбор зерновых культур, ц	 xi -x	 |xi -x |	(xi -x )2
1	2	3	4	5
1 2 3 4 5 6	600 520 400 600 500 380
Итого:	3000

 

 

Для заполнения этой таблицы необходимо определить среднее значение варьирующего признака (средний валовой сбор зерновых).

х =

Средняя величина в данном случае определяется по формуле средней арифметической простой: x nx_i

где,  x_i – величина варьирующего признака в каждом фермерском хозяйстве            n – число фермерских хозяйств.

 

3.  Определяем среднее линейное отклонение (d ) по формуле:

Расчет среднего линейного отклонения:   d =

d_  | x_i x |

_

n

где, |x_i – х | - итог графы 4 вспомогательной таблицы.

 

4.  Определяем дисперсию по формуле простой дисперсии:

Расчет дисперсии:                                         2 

2 (x_inx)²

где, (x_i - ^x )² – итог графы 5 вспомогательной таблицы

 

5.  Определяем среднее квадратическое отклонение, для этого необходимо извлечь из дисперсии квадратный корень:

Расчет среднего квадратического отклонения:                       =

 

6.  Коэффициент осцилляции  (V_R), определяется по формуле:

Расчет коэффициента осцилляции:                         VR =

R

                                                 V_R  100%

x

 

7.  Линейный коэффициент вариации (Vd), определяется по формуле:

Расчет линейного коэффициента вариации:                        Vd =

d

V_d 100%

x

 

8.  Коэффициент вариации (V_σ) определяется по формуле:

Расчет коэффициента вариации:                         V =

V_ ^100%

x

 

Если коэффициент вариации (V_σ) не превышает 33%, то совокупность считается однородной. Сделайте вывод о степени вариации признака.

 

Вывод:

 

 

ЗАДАНИЕ 2. Имеются следующие данные о распределении рабочих предприятия по размеру месячной заработной платы:

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                             Таблица 2

Месячная заработная плата, рублей	Число рабочих, % к итогу
1000-1200 1200-1400 1400-1600 1600-1800 1800-2000 2000-2200 2200-2400	5 8 25 30 15 12 5
ИТОГО:	100

Определите:

1.    среднее линейное отклонение

2.    дисперсию

3.    среднее квадратическое отклонение

4.    коэффициент вариации

На основании полученных данных сделайте вывод.

 

Методические указания к выполнению задания 2:

Для определения показателей вариации необходимо построить вспомогательную таблицу для расчета вспомогательных данных:

 

Вспомогательная таблица для расчета показателей вариации.

 

Месячная заработная плата, руб.	Число рабочих в % к итогу fi	Середина интервала x	x fi	x x	x  x   fi	x x2	x  x2  fi
А	1	2	3 = гр2 х гр1	4 = гр2 - x	5 = гр4 х гр1	6 = (гр2 - x )2	7 = гр6 х гр1
1000-1200	5
1200-1400	8
1400-1600	25
1600-1800	30
1800-2000	15
2000-2200	12
2200-2400	5
ИТОГО:	100	×		×		×

 

Для заполнения таблицы необходимо:

Во-первых, определить середину интервалов x варьирующего признака, так серединой

первого интервала (1000-1200) будет1100 ^_^12002^1000_, второго - 1200^_^{1400 1200}₂ ^_ и т.д.;  заполняем их в графу 2

 

Во-вторых, определить произведение значений середин интервалов ( x) на соответствующие им веса (fi), гр 3, подсчитать итог этой графы

 

В-третьих, определить среднее значение варьирующего признака (средний размер заработной платы), по формуле средней взвешанной:

                                              xfi fi,                                  где,_  fi      x fi- итог гр.1 - итог гр.3 ;

 

В- четвертых, определить абсолютное отклонение середины интервалов ( x) от средней величины ( x ), гр.4

 

В-пятых, определить произведение абсолютных отклонений │ x x │ на их веса fi и подсчитать сумму этих произведений, результаты записать в гр. 5

 

В-шестых, определить квадрат отклонения середины интервалов ( x) от средней величины ( x )

– x x² , результаты запишите в гр. 6.

 

        В-седьмых, квадрат отклонения середины интервалов от средней величины

x x² умножим на их веса fi и подсчитайте сумму этих произведений, результаты записать в гр. 7.

 

На основании данных вспомогательной таблицы рассчитайте:

1. Среднее линейное отклонение взвешанное по формуле:

Расчет среднего линейного отклонения:                       =

d   x x  fi,  fi

где,  x x  fi - итог графы 5

        fi - итог графы 1.

 

2.  Дисперсия определяется по формуле взвешанной дисперсии:

Расчет дисперсии:                                          2 

_2 _ x x²  fi

 fi

где , x x²  fi - итог графы 7.           fi - итог графы 1.

          

Расчет среднего квадратического отклонения:                        =

3.  Среднее квадратическое отклонение по формуле: x  x²  fi

_{ }

                                                            fi         

 

4.  Коэффициент вариации определяется по формуле:

Расчет коэффициента вариации:                          V =

V 100% x      

 

Вывод:

 

 

ЗАДАНИЯ 5.1, 5.2 и 5.3 выполнить в MS Excel

 

ЗАДАНИЕ 5.1: допустим, имеются следующие данные о размере ущерба, причиненного совершенными преступлениями:

Таблица 3

Размер ущерба	Количество уголовных дел
от 720 до 2,5 тыс. руб.	600
от 2,5 до 25 тыс. руб.	400
от 25 до 100 тыс. руб.	300
от 100 до 250 тыс. руб.	250
от 250 до 1 млн. руб.	15

 

1.                     Вычислите средний размер ущерба по приведенному количеству уголовных дел. 

2.                     Укажите, какая разновидность средних величин здесь может быть применена? 

3.                     Чем отличается она от того вида средней величины, который применялся в предыдущем примере?

 

ЗАДАНИЕ 5.2: Сведения о мерах наказания, примененных судами РФ за 1998-2001 годы.

Таблица 4

№№	Лишение свободы		Количество осужденных
		1998	1999	2000	2001
1	до 1-го года	741	820	688	714
2	св. 1 до 2 лет	1560	1525	1135	1440
3	св. 2 до 3 лет	1816	1856	1526	1623
4	св. 3 до 5 лет	2395	2168	2742	2689
5	св. 5 до 8 лет	1262	1189	1255	1353
6	св. 8 до 10 лет	370	326	354	431
7	св. 10 до 15 лет	237	256	277	307
8	св. 15 до 20 лет	45	83	82	78
9	св. 20 до 25 лет	-	12	26	16
10	св. 25 до 30 лет	-	-	1	-
11	Пожизненное лишение свободы	2	2	5	5

 

Определите: 

1.      средний срок лишения свободы по годам. 

2.      среднее линейное отклонение

3.      дисперсию

4.      среднее квадратическое отклонение

5.      коэффициент вариации 

 

ЗАДАНИЕ 5.3: В ОВД Свердловского р-на г. Перми в течение первой недели октября 2019 г. было совершено 120 квартирных краж. Количество совершенных краж распределяются по дням недели следующим образом: Понедельник – 16, Вторник – 12, Среда – 24, Четверг – 20, Пятница – 34, Суббота – 6, Воскресение – 8.

 

Определите: 

1.      среднее число краж на один день недели, моду и медиану.

2.      Проведите сводку данных в таблицу.

3.      Интерпретируйте полученные величины.

 

 

ПРАКТИЧЕСКАЯ РАБОТА № 6

 

Тема: «Показатели вариации в статистике. Структурные характеристики вариационного ряда распределения»

 

Наименование работы: Анализ структуры вариационных рядов.

 

Цель занятия: освоить методику нахождения структурных характеристик вариационного ряда распределения (мода, медиана).

 

Содержание практического занятия: Расчет показателей вариации, анализ дисперсии.

 

Формируемые умения: после выполнения задания студент должен знать:

-    структурные средние величины в статистике;

-    аналитический и графический способы определения структурных средних величин; должен уметь:  анализировать структуру вариационных рядов распределения.

 

Вид занятия: практическое занятие

Тип занятия: формирование умений и навыков Методы обучения: практическая работа

 

Литература: 1. Теория статистики. Учебник/ под ред. проф. Р.А. Шмойловой. – М.: «Финансы и статистика», 2000.

                       2.  Практикум по теории статистики. Учебное пособие/ под ред.проф. Р.А.Шмойловой. - М.: «Финансы и статистика», 2000.

 

Методические указания к выполнению практической работы.

 

Мода и медиана являются структурными характеристиками ряда распределения, они дают некоторое представление о структуре совокупности. 

Мода (Мо) – представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой, т.е. мода – это значение признака, встречающееся чаще чем другие.

 

Медиана (Ме) — это значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности, т.е. значение признака, находящееся в середине ряда и делящее его на две равные части.

 

Мода (Мо) в дискретном вариационном ряду определяется визуально, т.е. просматривая частоты (численности), которые имеют варианты (значения) признака. Отыскивается признак, имеющий частоту (в абсолютном или относительном выражении) большую чем любое другое значение, он и является модой. Если в ряду не одна, а несколько мод, например две то ряд называется двумодальным.

 

Медиана (Ме) в дискетном вариационном ряду определяется следующим образом, в начале определяют порядковый номер медианной единицы ряда, по формуле:

n 1

                                                                                                 _ме   

2

где n – объем совокупности

 

Затем определяют к какой группе относится признак имеющий медианный порядковый номер, это можно сделать, рассчитав накопленные частоты. Группа в которой находится медианный порядковый номер и будет являться медианной (Ме).

 

1. В интервальном вариационном ряду мода и медиана определяются следующим образом: 

Мода интервального ряда определяется по формуле:

                                                        Mo  x0  i f_Мо      f Мо  fМоf 1              

                                                                                             fМо1  Мо  fМо1 

где

  х₀ – нижняя граница модального интервала   i   - величина модального интервала   f_Мо - частота модального интервала

  f_{Мо –} 1   - частота интервала, предшествующего модальному   f_{Мо +} 1  - частота интервала, следующего за модульным.

 

Для определения моды необходимо определить модальный интервал, это интервал, имеющий наибольшую частоту в ряду распределения, его величину (i) для этого из верхней границы модального интервала отнять нижнюю границу и рассчитать моду по формуле.

 

Медиана (Ме) интервального ряда определяется по формуле:

1

 f  S

                                                                              е  х₀  i 2             ме1

f_ме

где

   х₀ - нижняя граница медианного интервала

  f - сумма частот

   i   - величина медианного интервала

  S_ме1- накопленная частота интервала, предшествующего медианному    f_ме - частота медианного интервала.

 

Для определения медианы (Ме) необходимо прежде всего определить интервал, в котором заключена медиана – медианный интервал. Им считается тот, до которого сумма накопленных частот меньше половины всей численности ряда, а с прибавлением его частоты – больше половины.

 

ЗАДАНИЕ 1. По ниже приведенной группировке семей по числу детей в семье, определите, моду и медиану, сделайте вывод:

Таблица 1

                                                                                                                                                                                          Группировка семей по числу детей в семье.

Число детей в семье, человек	Число семей. тыс.	Накопленная частота
0 1 2 3 4 5	15 25 20 15 10 5
ИТОГО:	90

 

Методические указания к выполнению:

При определении моды и медианы вначале определите вид ряда распределения (дискретный или вариационный). Для нахождения медианы вначале необходимо найти накопленные частоты.

Определение моды    Мо =

Mo  x0  i fМо  fМоf Мо1 fМоfМо1  fМо1  

 

Определение медианы    Ме =

1

 f  Sме1

                                               е  х0  i 2                   

f_ме

 

n1  ме     2

Определить номер медианного признака по формуле:  

 

ЗАДАНИЕ 2. По результатам весенней экзаменационной сессии одного курса студентов получена следующее распределение оценок по баллам:

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                             Таблица 2

Балл оценки знаний студентов	2	3	4	5	всего
Число оценок, полученных студентами	6	75	120	99	300

Определите:

а) моду (модальный балл успеваемости);

б) медиану (медианное значение балла). Сформируйте выводы по полученным данным.

 

а) Мода составит: Мо =

б) Медиана составит: Ме = Номер медианы: N_ме  =

 

ЗАДАНИЕ 3. По следующим данным распределение 100 ткачей по дневной выработке тканей определите моду (модальное значение дневной выработки ткани у данной совокупности ткачей) и медиану (медианное значение дневной выработки ткани).

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                             Таблица 3

Дневная выработка ткани, м	40-44	44-48	48-52	52-56	56-60	Итого
Число тканей	12	28	36	16	8	100

 

Методические указания к выполнению:

Приведенный ряд распределения является вариационным поэтому при определении моды и медианы необходимо вначале найти модальный и медианный интервалы.

 

Решение:

1.  Модальный интервал:

 

2.  Мода составляет (вначале укажите формулу расчета):

 

  Мо =

 

3.  Медианный интервал:

 

4.  Медиана составит (вначале укажите формулу расчета):

                                                                                                                               Ме =

 

Вывод:

 

 

ЗАДАНИЯ 6.1 выполнить в MS Excel

 

ЗАДАЧА 6.1: имеются данные о возрасте 100 осужденных к лишению свободы:

18, 20, 32, 23, 20, 24, 22, 18, 29, 23, 19, 21, 18, 23, 18, 24, 27, 31, 19, 25, 27, 21, 28, 25, 17, 17, 27,

21, 19, 20, 19, 25, 18, 27, 22, 23, 19, 31, 32, 27, 19, 22, 30, 17, 22, 19, 18, 24, 20, 22, 17, 29, 21, 27, 17, 31, 25, 20, 24, 19, 26, 28, 21, 18, 26, 21, 20, 23, 26, 23, 19, 25, 21, 20, 18, 25, 33, 18, 33, 19, 33, 28, 31, 22, 30, 19, 26, 18, 29, 20, 29, 19, 23, 32, 17, 20, 33, 21, 33, 19.

 

На основе этих данных: а) построить вариационный ряд (интервальный, образовав 4 группы с равными интервалами); б) определить размах ряда, моду и медиану; в) построить гистограмму.

 

ПРАКТИЧЕСКАЯ РАБОТА № 7

 

Тема: «Виды и методы анализа рядов динамики»

 

Наименование работы: Анализ динамики изучаемых явлений.

 

Цель занятия: освоить методику расчета показателей динамики.

 

Содержание практического занятия: Классификация рядов динамики, вычисление показателей динамического ряда, сглаживание рядов динамики методом, скользящей средней и аналитическое выравнивание, графическое изображение динамики явления.  Выявление сезонных колебаний.  Приведение ряда динамики к одному основанию.

 

Формируемые умения: после выполнения задания студент  должен знать:

-            понятие и составные элементы динамического ряда;

-            классификацию рядов динамики;

-            методы анализа рядов динамики; должен уметь:

-            анализировать динамику изучаемых явлений.

 

Тип занятия: формирование умений и навыков Методы обучения: практическая работа

 

Литература: 1. Теория статистики. Учебник/ под ред. проф. Р.А. Шмойловой. – М.: «Финансы и статистика», 2000.

                       2.  Практикум по теории статистики. Учебное пособие/ под ред.проф. Р.А.Шмойловой. - М.: «Финансы и статистика», 2000.

 

 

          

 

ЗАДАНИЕ 1. Имеются следующие данные о динамике производства продукции на предприятии за 1999 – 2004 г.г. в сопоставимых ценах:

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                             Таблица 1

Год	1999	2000	2001	2002	2003	2004
млн.руб.	677	732	757	779	819	844

Определите:

а) средний уровень ряда динамики.

б) цепные и базисные темпы роста и прироста,

в) для каждого года абсолютное значение одного процента прироста.

 

Результаты расчетов изложите в табличной форме. 

Сделайте вывод о динамике производства продукции на предприятии.

 

Методические указания к выполнению задания 1.

1.                 Необходимо определить средний уровень ряда динамики (среднегодовой объем производства продукции предприятием). Для расчета среднего уровня ряда динамики необходимо воспользоваться            формулой       расчета           средней          арифметической       простой,         т.к.      данный интервальный ряд динамики является с равноотстоящими уровнями:

Расчет           среднего динамики:   у =

уровня

ряда

n

y_i y i1 

n

где,  y_i – уровень ряда динамики          n – число уровней ряда.

 

2.                 Рассчитать цепные и базисные темпы роста и прироста, абсолютное значение одного процента прироста для каждого года.

Для удобства расчет цепных и базисных темпов роста и прироста, абсолютного значения одного процента прироста воспользуйтесь таблицей 1.

Таблица  

                                                                                                                                                          Динамика производства продукции на предприятии.

Год	Произведено продукции  млн. руб. (уi)	Абсолютный прирост, млн. руб.		Темп роста, %		Темп прироста %		Абсолютное значение 1% прироста млн. руб.
		c предыдущим годом	c 1999	к предыдущему году	к 1999	к предыдущему году	к 1999
1999	677
2000	732
2001	757
2002	779
2003	819
2004	844
Итого:

 

Расчет данных таблицы следует проводить следующим образом:

1.  абсолютный прирост (∆у) по формуле:

а) при сравнении с предыдущим годом: ∆ y =  y_i – y_i -1 ,

где,    y_i –  уровень i-го года,           y_{i -1}  - уровень предыдущего года

 

б) при сравнении с базисным годом (1999) по формуле: ∆ y =  y_i – y₀,    где ,  у0 – уровень базисного (1999)года.

 

2.  темп роста (Т_р) по формуле:

уⁱ 100^%

а) при сравнении с предыдущим годом:  ^Т _р    yi1

 

yⁱ 100%

б) при сравнении с базисным (1999) годом: ^Т _р        

                                                                                                            y_o

 

3.  темп прироста (Т_пр) по формуле:

у

а) при сравнении с предыдущим годом: ^Т _пр    100% уi1

 

у

б) при сравнении с базисным (1999) годом: Т_пр          100^%

                                                                                                                у_o

 

4. Абсолютное значение одного процента прироста (%) по формуле:

%  у  0,01 yi 1,

Т_пр

где,  % - абсолютное значение одного процента прироста

 

Вывод:

 

 

ЗАДАНИЕ 2. Остатки вкладов населения в сберегательных кассах города в 2005 году характеризуется следующими данными на начало месяца:

Месяц	1.01	1.02	1.03	1.04	1.05	1.06	1.07
млн.руб.	3105	3200	3154	3208	3170	3213	3250

Таблица 2

 

Определите:

а) среднемесячные остатки вкладов населения за 1 и 2 кварталы;

б) абсолютный прирост изменения среднего остатка вклада во 2 квартале по сравнению с 1 кварталом.

 

Методические указания к выполнению задания 2.

Для определения среднемесячного остатка денежного вклада населения воспользоваться формулой для определения средней хронологической: 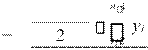у^[1]  уn

                                                                                      у                         

n 1

где,   у₁ – уровень динамики на 1-е число месяца начала квартала

уn – уровень ряда динамики на 1-е число месяца следующего за последнем месяцем квартала  у_i – уровень ряда динамики в анализируемом квартале  n- число уровней ряда динамики, в данном случае,  n = 4

 

  Для определения абсолютного прироста (Δу) воспользуйтесь формулой:

  y у₂ у₁,

где у₁ и у₂- средний уровень 1 и 2 кварталов.

 

Расчет:

     а) Среднемесячные остатки: за 1 квартал ^-

за 2 квартал ^-                                                                                                                   

          

б) абсолютный прирост изменения среднего остатка вклада во 2 квартале по сравнению с 1 кварталом ^-

 

 

ЗАДАНИЕ 3. По данным задания 1 определите: а) среднегодовой абсолютный прирост

б) среднегодовой темп роста

в) среднегодовой темп прироста.

 

Методические указания к выполнению задания 3.

                                                                                        уn  у1                                                                              =

                                                                        у             

n 1

 

2.  Среднегодовой темп роста определяется по формуле:

 

                           Т_р  ^тТ₁ Т₂ Т Т₃ ...Т_т             или Т_р  n1            ,                   =

1

где,  Т₁, Т₂, Т₃, Т_m - темп роста по сравнению с предыдущим годом          m – число коэффициентов темпа

         у₁ , у_n – уровень первого и последнего года в ряду динамики          n - число уровней

          

3.  Среднегодовой темп прироста (Т_пр) определяется по формуле:

                                                                            100.                                                  =

Т_пр Т_р 

 

ЗАДАНИЯ 7.1, 7.2 и 7.3 выполнить в MS Excel

 

ЗАДАНИЕ 7.1: Данные о вознаграждении нештатных работников двух отделов полиции разных федеральных округов. 

Таблица 3

Уровень заработной платы, руб.	Доля нештатных работников, %	Уровень заработной платы, руб.	Доля нештатных работников, %
менее 2000	50	менее 1000	10
2000-4000	20	1000-3000	20
4000-6000	15	3000-6000	40
6000-10000	10	6000-8000	20
10000 и более	5	8000-10000	10
Итого	100	Итого	100

 

Требуется: перегруппировать данные, чтобы сделать их сопоставимыми

 

ЗАДАНИЕ 7.2: согласно данным учета имеются следующие показатели динамики преступности ЮЗАО г. Москвы за период с 2008 по 2012 гг. Однако территория ЮЗАО г.

Москвы в 2010 г. претерпела реорганизацию: произошло укрупнение района.

Динамика преступности в районе

1.      Провести преобразование динамического ряда путем его смыкания.

2.      Определить сомкнутые ряды абсолютных и относительных величин.

3.      Результаты записать отдельными столбцами.

 

ЗАДАНИЕ 7.3: имеются сведения о динамике преступности лиц, ранее совершивших преступления в России в 1991-1999 г.

1.      Вычислить показатели динамики, указанные в таблице.  

2.      Провести сводку показателей в таблицу.

3.      Интерпретировать    полученные   результаты,    обрисовав      сложившуюся криминологическую ситуацию

Динамика преступности лиц, ранее совершавших преступления, в России в 1991—1999 гг.

Таблица 5

Годы	Зарегистрированные преступления лиц, ранее совершавших преступления
	Абс. число	Абс. прирост	Темп роста	Темп прироста к 1991 г.	Цепной темп прироста	Абс. значение 1 % прироста
1991	274 339
1992	320 330
1993	346 889
1994	400 815
1995	459 602
1996	493 983
1997	565 373
1998	604 557
1999	692 134

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ:

Что понимается под рядом динамики?

 

Назовите основные компоненты ряда динамики?

 

 

 

 

 

ПРАКТИЧЕСКАЯ РАБОТА № 8

 

Тема: «Методы анализа основной тенденции (тренда) в рядах динамики»

 

Наименование работы: Выявление и анализ основной тенденции в рядах динамики.

 

Цель занятия: освоить методы выявления и анализа основной тенденции в рядах динамики

 

Содержание практического занятия: Сглаживание рядов динамики методом, скользящей средней и аналитическое выравнивание. Изучение взаимосвязи факторных и результативных показателей, составление линейных уравнений, определение направления и тесноты связи, определенных параметров.

 

Формируемые умения: после выполнения задания студент  должен знать:

-            компоненты ряда динамики;

-            метод укрупнения интервалов;

-            метод скользящей средней;

-            методы аналитического выравнивания динамических рядов; должен уметь:

-            выявить и проанализировать основную тенденцию в рядах динамики. Вид занятия: практическое занятие

Тип занятия: формирование умений и навыков

Методы обучения практическая работа

 

Литература: 1. Теория статистики. Учебник/ под ред. проф. Р.А. Шмойловой. – М.: «Финансы и статистика», 2000.

                       2.  Практикум по теории статистики. Учебное пособие/ под ред.проф. Р.А.Шмойловой. - М.: «Финансы и статистика», 2000.

 

ЗАДАНИЕ 1. Имеются следующие данные о розничном товарообороте области по месяцам года:                                             

Месяц	1	2	3	4	5	6	7	8	9	10	11	12
млн.руб.	74	79	87	82	79	82	88	87	87	81	83	90

Произведите:

а) сглаживание ряда динамики розничного товарооборота методом пятичленной скользящей средней;

б) выравнивание ряда по прямой;

в) изобразите графически фактические и сглаженные уровни ряда динамики; Сделайте выводы о характере общей тенденции изучаемого явления.

 

Методические указания к выполнению задания.

1.      Для того чтобы произвести сглаживание ряда динамики методом пятичленной скользящей средней необходимо: взять данные за первые пять месяцев, определить пятидневные суммы, а затем определить среднюю по формуле:

_{у1 } у1  у2  у3  у4  у5

5

у2 у3 у4 у5 у6 у₂        

5 и т.д.

Полученные пятичленные скользящие средние необходимо записать в середину интервала.

Для удобства расчетов использовать таблицу 1.

Таблица 1.                                              Выравнивание ряда динамики методом пятичленной скользящей средней.

	Товарооборот млн.руб.(yi)	Пятичленные скользящие суммы	Пятичленные скользящие средние		Товарооборот, млн. руб. (уi)	Пятичленные скользящей суммы	Пятичленные скользящие средние
1 2 3 4 5 6	74 79 87 82 79 82	- - - -	- -  у1 = у2 = у3 = у4 =	7 8 9 10 11 12	88 87 87 81 83 90		у5 = у6= у7 = у8 = - -

 

2.      Для выравнивания ряда по прямой используют уравнение: y t = а_о + а1  t

Для нахождения параметров а_о и а1 , необходимо решить систему нормальных уравнений: 

 a0n  a1t  y a t  a1t2  ty

                                                                                       0                                         

где, у – исходные уровни ряда динамики

        n – число уровней ряда динамики

        t – показатель времени, который обозначается порядковыми номерами начиная с наименьшего.

 

Удобнее показателям времени t придавать такие значения, чтобы их сумма была равна нулю:

Σt=0

Решив систему уравнений, получим выражение для параметров:

t²   у      t        tу       ntу  t у           

                 a0  n t2                                                                            t t                   1  nt2  t t

при t =0 параметры а₀ и а₁ примут значения: а_о= _у : n                 а₁ = t_у : t²

Расчет выравненных уровней ряда динамики удобней производить в таблице 2. (гр.6)

Таблица 2 Расчет выравненных уровней ряда динамики.

 

Месяц	Товарооборот, млн. руб. у	Показатель времени t	t2	ty	yt	y- yt	y  yt 2
1	2	3	4	5=гр2хгр3	6	7=гр2-гр6	8=гр7хгр7
1	74	-6
2	79	-5
3	87	-4
4	82	-3
5	79	-2
6	82	-1
7	88	1
8	87	2
9	87	3
10	81	4
11	83	5
12	90	6
Итого:	у =	t = 0	t2 =	tу =	yt =	-	y  yt2
							=

 

Определим параметры уравнения прямой а_о и а1:

ао= у : n = 

 

а₁ = tу : t² =

 

После определения параметров уравнения прямой а_о и а1 , необходимо подставить в уравнение принятые обозначения и вычислить выравненные уровни ряда динамики:

январь у1  ао  а1 (1)=		июль
февраль у2  ао  а1 (2)=		август
март у2  ао  а1 (3) =		сентябрь
апрель		октябрь
май		ноябрь
июнь		декабрь

 

Уравнение прямой y_t =а_о  а₁t отражает основную тенденцию (тренд) ряда динамики, отклонение фактических значений от тренда (y- y_t ) объясняется влиянием случайных факторов.

Это отклонение определяется по формуле среднего квадратического отклонения:

среднего квадратического отклонения:            t 

_t 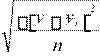

 

Относительной мерой отклонения (колеблемости) является коэффициент вариации, который определяется по формуле:

коэффициент вариации    V=

V  ^t 100 y

где y - среднее значение варьирующего признака.

 

3. Построить график ряда динамики по фактическим значениям сглаженным и рассчитанным по методу скользящей средней и по прямой.

 

Рис. 1. График динамики розничного товарооборота области по месяцам года.

 

Вывод:

 

 

ЗАДАНИЯ 8.1, 8.2 и 8.3 выполнить в MS Excel

 

Задание 8.1: имеются следующие данные, характеризующие движение уголовных дел в суде первой инстанции за десять месяцев:

Таблица 3

Месяцы	1	2	3	4	5	6	7	8	9	10
Число дел	125	110	107	135	127	128	147	135	138	150

 

Проведите сглаживание ряда динамики методом трехчленной скользящей средней величины. Сделайте статистический вывод из полученного результата.

ЗАДАНИЕ 8.2: получены следующие данные о динамике преступности в городе Н. до изменения уголовного закона и после его изменения:

Таблица 4

Годы	Число зарегистрированных преступлений
	До изменения уголовного закона	После изменения уголовного закона
1989	19100
1990	19700
1991	20000
1992	21200	22800
1993		23600
1994		24500
1995		26200
1996		28100

 

Проведите преобразование ряда динамики методом его смыкания. Установите общую тенденцию развития преступности.

 

ЗАДАНИЕ 8.3: По результатам социологического обследования, проведенного ФСИН, получены следующие данные об удовлетворенности заключенных условиями содержания в СИЗО:

Таблица 5

Удовлетворенность условиями содержания	Мужчины (чел.)	Женщины (чел.)	Итого
Удовлетворены содержанием	430	190	620
Не удовлетворены содержанием	70	310	380
Итого	500	500	1000

 

Определить существует ли связь между удовлетворенностью условиями содержания в СИЗО и полом, используя коэффициент ассоциации.

 

 

 

                                                   

 

 

 

 

 

 

 

ПРАКТИЧЕСКАЯ РАБОТА № 9

 

Тема: «Индексы в статистике»

 

Наименование работы: Изучение структурных сдвигов и факторный анализ на основе индексного метода.

 

Цель занятия: освоить методику расчета отдельных видов индексов и проведения факторного анализа с использованием индексного метода.

 

Содержание практического занятия: Решение задач на определение индексов и взаимосвязь конкретных индексов, индексный анализ.  

 

Формируемые умения: после выполнения задания студент  должен знать:

-            понятие и классификацию индексов в статистике;

-            значение индексного метода;

-            способы исчисления индексов;

-            взаимосвязи между индексами; должен уметь:

-            рассчитывать индивидуальные и общие индексы в статистике;

-            осуществить анализ структурных сдвигов на основе индексного метода;

-            произвести факторный анализ на основе индексного метода.

 

Вид занятия: практическое занятие

Тип занятия: формирование умений и навыков Методы обучения: практическая работа

 

Литература: 1. Теория статистики. Учебник/ под ред. проф. Р.А. Шмойловой. – М.: «Финансы и статистика», 2000.

                       2.  Практикум по теории статистики. Учебное пособие/ под ред.проф. Р.А.Шмойловой. - М.: «Финансы и статистика», 2000.

 

 

 

 

 

ЗАДАНИЕ 1. Известны следующие данные о продаже молочных продуктов на колхозном рынке:

Таблица 1

Продукт	Базисный период		Отчетный период
	Цена за 1кг руб.	Продано, ц.	Цена за 1кг руб.	Продано, ц.
Творог Сметана Масло животное	27,1 28,4 52,0	15,8 12,9 0,8	26,5 27,4 51,0	14,9 13,4 0,9

 

Определите: индивидуальные и сводные индексы цен, физического объема товарооборота и стоимости реализованных продуктов, а также величину экономии покупателей от снижения цен.

 

Методические указания к выполнению задания 1.

Для расчета индивидуальных индексов цен необходимо цену 1кг каждого товара в отчетном периоде отнести к цене 1кг этого же товара в базисном периоде.  Расчет произвести по формуле:

                                    iр  рр1₀ ,   где,  р0 - цена 1кг в базир1- цена 1кг в отчетном периодесном периоде.                        

Индивидуальные индексы физического объема определяются отношением объема реализации каждого товара в отчетном году к объему реализации этого же товара в базисном периоде.

Расчет произвести по формуле: q¹                       где, q₁-  объем продаж в отчетном году

                                       ⁱ_q ^ q0                                  q₀- объем продаж товара в базисном году

Индивидуальные индексы стоимости товарооборота по каждому виду товаров определяются отношением объема товарооборота в отчетном году к товарообороту отчетного года.  Расчет производится по формуле:

                                       i_pq  ^р₁^q₁                 Экономия определяется по формуле:покупателей  от снижения                                    цен

                                                     р0q0                                                 Э=Σр0q1  Σр1q1

Для оценки среднего изменения цен на продукцию используется сводный индекс цен, который  определяется по формуле:

                                                                                   I_p pq_{1 1}

p q_{0 1}

Сводный индекс физического объема товарооборота определяется по формуле:

                                                                          Iq p0q1         или     Iq I pq : I p                                 

                                                                                     p₀q₀                                                  

Сводный индекс стоимости реализованной продукции (товарооборота) определяется по формуле:

                                                   I _рq  p1q1       или    I pq  I p  I q

                                                                                    p₀q₀                                                     

 

Расчет:

 

1. Индивидуальные индексы цен: i_р  ^р1          р0 

                          Творог                                       Сметана                                    Масло животное

q 2. Индивидуальные индексы физического объема: iq  1                                                                                                                               q0                             Творог                                       Сметана		Масло животное

 

3.  Индивидуальные индексы стоимости товарооборота: i_pq  ^р1q¹

                                                                                                                                         р₀q₀

                          Творог                                       Сметана                                    Масло животное

 

4.  Сводный индекс цен:      I p  ^{p q}_{1 1} 

                                                                                                   p q0 1    

5.  Экономия покупателей от

снижения цен:                                              Э=Σр0q1  Σр1q1 =

6физического . Сводный индекс                     I_q  _p q_{0 1} 

объема товарооборота:                                                ^p q^{0 0}

7реализованной . Сводный индекс стоимости продукции         Iрq  _p q_{1 1} 

(товарооборота):                                                           p q_{0 0}

 

ЗАДАНИЕ 2. Имеются следующие данные о продаже трикотажных изделий в одном универмаге:

                                                                                                                                    Таблица 2

Вид изделия	Старая цена за 1шт. руб.	Новая цена за 1шт. руб.	Товарооборот после снижения цен тыс. руб.
А Б В	187 220 315	150 179 286	142 295 181

Определите:

а) среднее снижение цен на данную группу товаров;

б) размер экономии от снижения цен.

          

Методические указания для выполнения задания 2.

Среднее снижение цен на данную группу товаров характеризуется сводным индексом цен, который определяется по формуле:

                                             p q                        где, р1 и р0 - новая и старая цена товара                        

                                 Iр ^p1⁰q1¹            отчетный периодq1 - физический объем продаж, каждого товара в

Физический объем продаж по условиям задачи не известен, но его можно найти разделив  р¹q¹

фактический товарооборот ( р₁q₁) на новую цену за 1шт изделия q₁ ^

р₁

Затем необходимо найти размер товарооборота по старым ценам – ∑p₀q₁

Определив размер товарооборота по старым ценам можно определить сводный индекс цен, который будет характеризовать среднее снижение цен на трикотажные изделия.

 

Решение:

 

ЗАДАНИЕ 3. Имеются данные по производству стиральных машин на одном из заводов:

                                                                                                                                                                                                      Таблица 3  

Машина стиральной машины	2000		2001
	Себестоимость единицы, руб.	Количество произведенных машин тыс. руб.	Себестоимость единицы, руб.	Количество произведенных машин, тыс. руб.
А Б В	4207 3520 3830	20,3 25,1 40,8	4070 3610 3450	20,9 10,8 49,1

Вычислите:

а) индивидуальные и сводные индексы себестоимости;

б) сводный индекс физического объема продукции (взвешенный по себестоимости); 

в) сводный индекс затрат на производство продукции. Проиллюстрируйте взаимосвязь сводных индексов.   

          

Методические указания к выполнению задания 3.

1.  Расчет индивидуальных индексов себестоимости пр оизводится по формуле: z1 где,  z1- себестоимость 1 изделия в счетном пери оде i  z0 iА  z₁         z0 - себестоимость 1 изделия в базисном периоде

z₀            z1

iБ    z₀    z1

iВ    z₀    

 

2.  Сводный индекс себестоимости ( Iq ) определяется по формуле:

                                I z1q1                                                            где,  q1- количество произведенной продукц ии в

                                          z₀q₁                       отчетном периоде.

                                                          I_  z₁q₁                                      

                                                                    z₀q₁       

3.  Сводный индекс физического объема продукции (взвешенный по себестоимости) ( Iq ) определяется по формуле:

q1z₀ где, q₀ - количество продукции, произведенной в Iq _

                                         q₀z₀                      базисном периоде.

Iq q1z0 

                                                                q0z0      

 

4. Сводный индекс затрат на производство продукции ( Izq ) определяется по формуле:

Izq  z q1 1 

                                                              z q_{0 0}       

 

Между сводным индексом затрат на производство, сводным индексом себестоимости и сводным индексом физического объема продукции существует взаимосвязь

Izq  Iz *Iq 

 

 

 

ЗАДАНИЯ 9.1 и 9.2 выполнить в MS Excel

             

ЗАДАЧА 9.1: в городе Н. число зарегистрированным краж личного имущества граждан за 8 лет характеризуется следующими показателями:

Таблица 4

Определите базисным и цепным способами: 

а) абсолютный прирост (снижение) преступлений; 

б) темп роста (снижения) преступлений; 

в) темп прироста (снижения) преступлений; 

г) значение одного процента прироста (снижения) преступлений

 

ЗАДАНИЕ 9.2: согласно данным ГИАЦ МВД России и Судебного департамента при Верховном Суде Российской Федерации мы имеем следующее данные об общем состоянии преступности за 12 месяцев 2011 г. (см. таблицу 5 и вспомогательную таблицу 6).

 

Таблица 5

Виды преступлений	Зарегистрировано	Раскрыто	Выявлено лиц	Осуждено
Всего по разделам	2404807	1311846	1041340	782274
тяжкие и особо тяжкие	607507	323419	251313
убийство и покушение на убийство	14305	11525	12875	11696
умышленное причинение тяжкого вреда здоровью	38512	31710	34279	32412
изнасилование и покушение на изнасилование	4801	3929	4092	3498
хулиганство	5635	2293	2758	1504
умышленные уничтожение или повреждение имущества, совершенные из хулиганских побуждений, путем поджога	13043	2212	1424	4745
угроза           убийством      или причинением тяжкого вреда здоровью	76387	73365	64398	28977
вовлечение несовершеннолетнего в совершение преступления или антиобщественных действий	3471	3328	2271	893

Население, учтенное при всероссийской переписи населения 2010 года

Таблица 6

Показатели	Мужчины и женщины	Мужчины	Женщины
Население РФ	142946788	66105964	76840824
из него:
постоянное население РФ, находившееся на территории страны	142856536	66046579	76809957
граждане РФ, находившиеся за рубежом в связи с длительной служебной командировкой по линии органов государственной власти	90252	59385	30867
г. Москва	11503501	5304622	6198879
Московская область	7095120	3270733	3824387
Моложе трудоспособного возраста (дети и подростки в возрасте до 16 лет)
Всего по населению РФ	23125787	11842194	11283593
г. Москва	1475885	754799	721086
Московская область	1008577	518334	490243

Требуется:

1.      Рассчитать коэффициент судимости.

2.      Рассчитать индекс судимости.

3.      Рассчитать коэффициент тяжести преступлений.

4.      Рассчитать коэффициент раскрываемости по 1 и 2 строке. 5. Провести сводку, полученных величин в таблицу.

 

 

 

 

 

СПИСОК ЛИТЕРАТУРЫ

 

1)     Годин А.М. Статистика. Учебник – М.: ИТК «Дашков и К^о», 2004 г.

2)     Остроумов, С.С. Правовая статистика / С.С. Остроумов. – М.: Юридическая литература, 1986. – 415 с.

3)     Практикум   по   теории   статистики.   Учебное   пособие/   под   ред.   проф. Шмойловой Р.А. – М.: Финансы и статистика, 2002 г.

4)     Савюк Л.К. Правовая статистика. Учебник. // М.: Юристъ, 2000. 

5)     Теория статистики: Учебник/ Под ред. проф. Шмойловой Р.А. – М.: Финансы и статистика, 2002 г.

6)     Фирсова, А.В. Правовая статистика: учебное пособие / А.В. Фирсова. – М.: ИКЦ «МарТ», 2004. – 128 с.