
 |
ББК 74.102
П 68
данное пособие предназначено как для занятий на уроках математики, так и для самостоятельной работы дома. Учебный материал представлен в таблицах, что способствует его лучшему запоминанию, а также развитию зрительной памяти.
lSBN 978-5-00061-110-4 С) Оформление ООО «Искательпресс», 2016
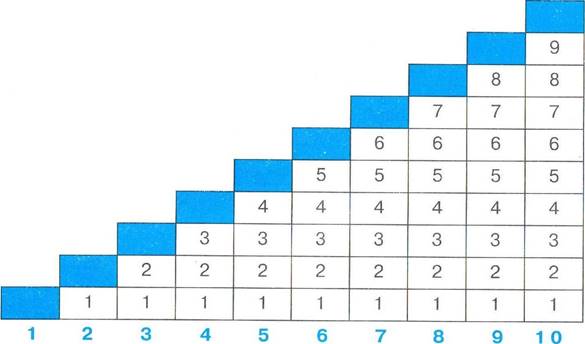
о, 1 , 2, 3, 4,
5, 6, 7,![]()
Это арабские цифры. Их всего десять.
Натуральные числа — это числа, которые применяют при счёте. Нуль не относится к натуральным числам.
|
> больше |
плюс, знак сложения |
|
М е НЬИје |
— минус, знак вычитания |
|
= равно |
• или х умножение |
: деление
Знак «РАВНО» = означает, что числа, находящиеся слева и справа от этого знака, одинаковые, то есть равны друг другу.
Знак «БОЛЬШЕ» > означает, что число, находящееся слева от этого знака, больше, чем число, находящееся справа от него.
Знак «МЕНЬШЕ» < означает, что число, находящееся слева от этого знака, меньше, чем число, находящееся справа от него.
![]()
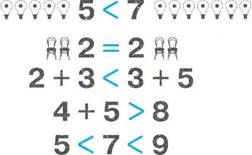
Число 7 больше 5, но меньше 9
Числа, которые делятся на 2, называются ЧЁТНЫМИ: 2, 4, 6, 8, 10 и так далее.
Числа, которые не делятся на 2, называются НЕЧЁТНЫМИ: 1 , З, 5, 7, 9, 1 1 и так далее.
При сложении чётных чисел получается чётное число, при сложении двух нечётных тоже получается чётное число:
6+4= 10
5+7= 12
При сложении нечётного числа с чётным в ответе будет нечётное число:
|
первое слагаемое |
второе слагаемое |
сумма |
От перестановки мест слагаемых сумма не меняется:
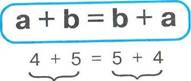
9 9
первое второе сумма
слагаемое слагаемое
Чтобы получить первое слагаемое, надо
из суммы вычесть второе слагаемое: ![]() 6 4 2
6 4 2
сумма второе первое
слагаемое слагаемое
Чтобы получить второе слагаемое, надо из суммы вычесть первое слагаемое: 6 2 4
сумма первое второе
слагаемое слагаемое
Чтобы к сумме двух чисел прибавить третье число, нужно к первому числу прибавить сумму второго и третьего чисел.
![]()
Пример:
8 8
![]()
3 + (3 + 2) = (3 + 2) + 3 = (3 + 3) + 2
![]()
8
Если одно из слагаемых равно 0, то сумма равна другому слагаемому: а+О=а, О+а=а, 3+0=3, 0+3=3
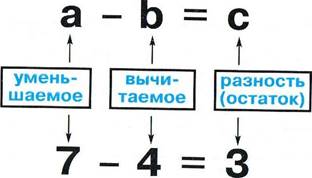
![]() Уменьшаемое— число, из которого
вычитают. Вычитаемое— число, которое вычитают.
Уменьшаемое— число, из которого
вычитают. Вычитаемое— число, которое вычитают.

(7—6) +4= 1 +4=5
Если перед скобкой стоит МИНУС,то при раскрытии скобок знаки меняются на противоположные.
![]() a-(b+c)=a-b—c а-(Ь -с) =a-b с
a-(b+c)=a-b—c а-(Ь -с) =a-b с
![]()

или

или
(а![]()
![]()
|
ппааиввпвп вааааааввш ававаавашш ааааааашше |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
6 7 8 |
|
9 10 1 1 |
|
12 13 14 |
||||
|
б |
7 8 |
|
9 10 11 |
|
12 13 14 15 |
||||
|
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
![]() Пример:
Пример:![]()
Эти цифры обозначены стрелками.![]()
Там, где
стрелки ![]() пересекаются, находим число 12.
пересекаются, находим число 12.
Одно из слагаемых надо разложить так, чтобы одна из сумм была равна 10. ![]() в= 7 + (З +5)
в= 7 + (З +5) ![]() 15
15
Таким же способом можно решать примеры на вычитание.
12-5 =
12—(2 +3) ![]()
Сто (100) — это
одна сотня, ![]() двести (200) —две сотни, триста (300) — три сотни и так далее.
двести (200) —две сотни, триста (300) — три сотни и так далее.
Тысяча — это десять сотен, то есть 10 раз по 100.
Число575содержит
5 сотен, 7 десятков, 5 единиц![]()
При сложении двузначных или трёхзначных чисел единицы складываются с единицами, десятки с десятками, а сотни с сотнями.
|
|
|
243 + 516 = 759 |
аз |
||
|
|
|
|
|
|
|
|
аз |
|
|
|
||
12+ 14=26
При вычитании
двузначных или трёхзначных чисел единицы ![]() вычитаются из единиц, десятки из десятков, сотни из
сотен.
вычитаются из единиц, десятки из десятков, сотни из
сотен.
|
|
|
||||||||||||||||||||||
26- 14= 12
Сложение
можно проверить вычитанием. Нужно из суммы вычесть одно из слагаемых, если
получится другое слагаемое — сложение выполнено верно.![]()
пример: проверка:
15 + 40 = 55 55-15=40 55-40= 15
a+b=c с—а=Ь с—Ь =а
Вычитание можно проверить сложением.
Нужно к разности прибавить
вычитаемое, если получится уменьшаемое — вычитание выполнено верно.![]()
|
пример: |
проверка: |
|
78- 27=51 |
27+51 = 78 |
|
а-Ь=с |
c+b=a |
Знаки умножения: ( е ) или (х)
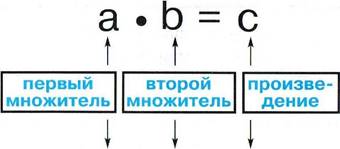
з 0 2 = 6
![]() • 7= 21
• 7= 21
5 . 5 = 25
Если один из множителей равен О, то и произведение равно О.
а • 0=0 или Оха = О
![]() 5 . или 0х5=0
5 . или 0х5=0
Если один из множителей равен то произведение равно другому множителю:
а • 1 = а или
1 • а= а![]()
4 . или 1
.![]()
От перестановки множителей значение произведения не меняется.
a • b = b • a ![]() з . 5 = 5 . з
з . 5 = 5 . з
![]() (а + Ь) • с = а c+b • c
(а + Ь) • с = а c+b • c
![]()
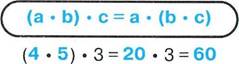
или
![]() 15 -60
15 -60
Деление
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
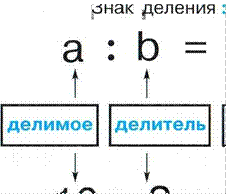 С
С
10 : 2 5
8 .![]()
15
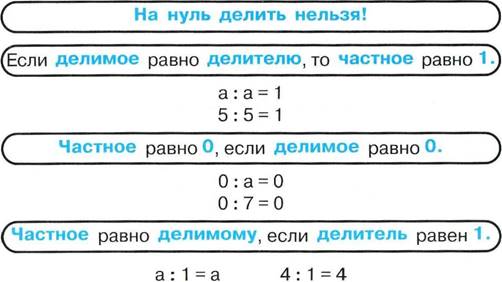
Самое большое число в частном— делимое.
![]()
![]()
Можно решить
так:![]()
![]()
Если делимое не делится на делитель, например 9 : 2, то надо подобрать
ближайшее число, меньшее 9, которое делится на 2 без остатка.![]()
![]() 1 ) :
1 ) : ![]() (остаток ) .
(остаток ) .
Остаток всегда должен быть меньше делителя.
На
делятся числа, оканчивающиеся на чётную цифру ![]() 12, 16 и так далее).
12, 16 и так далее). ![]()
На З делятся числа, сумма цифр которых делится на з.
225 : 3=75 2+2+5=9, 9 делится на З.
![]() 4 делятся числа, если двузначное число, образованное двумя последними
цифрами, делится на 4.
4 делятся числа, если двузначное число, образованное двумя последними
цифрами, делится на 4.
![]()
На 5 делятся числа, оканчивающиеся на 5 О.
40 : 5=8
155 : 5 =31
На 10 делятся числа, которые оканчиваются на О.
1000 : 100= 10
Если произведение двух чисел разделить на один из множителей, то получится другой множитель.
а . b = c с .• b = a
Проверка: 18 : З—- 6,![]()
Если делимое разделить на частное, получится делитель.
Проверка:![]()
Если делитель умножить на частное, получится делимое.
Проверка: 15 : 5 = 3,![]()
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример:
Эти цифры обозначены
стрелками.
Там, где стрелки
пересекаются,
находим число ![]()
В выражениях со скобками сначала выполняются действия в скобках, затем действия умножения и деления, а после этого остальные действия по порядку.
81 ![]()
В выражениях без скобок сначала выполняются действия умножения и деления, а после этого остальные действия по порядку.
![]()
Увеличить число на несколько единиц ![]() значит прибавить.
значит прибавить.
![]()
Увеличить число в несколько раз — значит умножить.
![]()
Уменьшить число на несколько единиц — значит вычесть.
Уменьшить число несколько раз — значит разделить.
![]()
Неизвестные числа обозначают латинскими буквами:
Х — «икс», У — «игрек» илиZ — «ЗЭТ»
Пример: Х = 21
![]() х = 21 -4, Х = 17
х = 21 -4, Х = 17
Проверка. 17=21
![]() — обыкновенная дробь,
— обыкновенная дробь,
а — числитель,
Ь — знаменатель,
Пример:![]()
Числитель — сколько равных частей взяли.
Знаменатель — на сколько равных частей разделили.
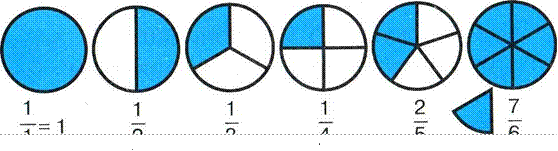
Дробь правильная, если её числитель меньше, чем знаменатель.
а< Ь, то есть З, 5 и так далее.
Дробь неправильная, если её числитель больше, чем знаменатель.
5 13
а> Ь, то есть — —и так далее.
![]()
![]()
![]() 11 1 1
11 1 1
—>—>—
ъ.) 24
со
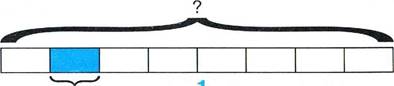
1
1
Если доля числа равна 2,
8
12

1
Если всё число равно 12 то 3 доля от него равна
12 : 3 =4
Разряды и классы
|
Класс миллионов |
Класс тысяч |
Класс единиц |
||||||
|
сотни миллионов |
десятки мил- ЛИОНОВ |
единицы миллионов |
сотни тысяч |
десятки тысяч |
единицы тысяч |
сотни |
десятки |
едини цы |
|
|
|
|
|
|
|
|
|
|
В числе 547375242
547375242 единицы
![]() 54737524 десятка
54737524 десятка![]()
5473752![]() сотни
сотни
![]() 547375 единиц тысяч
547375 единиц тысяч
54737 десятков тысяч
![]() 5473 сотни тысяч
5473 сотни тысяч
547 единиц миллионов
54 десятка миллионов
ъ.) 5 сотен миллионов

![]() — 1 1 ххх — зо
— 1 1 ххх — зо ![]() хи — 12 — 40 Xlll — 13 50
хи — 12 — 40 Xlll — 13 50
ХМ— 14 [Х — 60 ![]() 15 [ХХ — 70 хм — 16 LXXX — 80
15 [ХХ — 70 хм — 16 LXXX — 80 ![]() XVll — 17 хс — 90
XVll — 17 хс — 90
|
Vlll — 8 |
|
с— 100 |
|
|
т— 19 |
О— 500 |
|
х 10 |
|
м — 1000 |
м с м х с ” 1
![]()
|
с |
D с |
|
|
Треугольник |
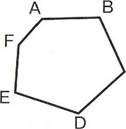
Многоугольник |
Круг |
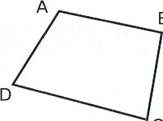 Четырёхугольник Прямоугольник Квадрат
а
Четырёхугольник Прямоугольник Квадрат
а
в 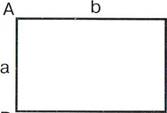 В
В 
 с
с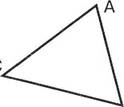 с
с 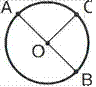
АВ
в— диаметр
ОС — радиус
Периметр — это сумма сторон любой геометрической фигуры, обозначается латинской буквой Р.
Единицы
измерения — миллиметры (мм), сантиметры (см) ![]() метры (м) и так далее.
метры (м) и так далее.
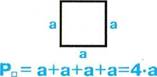
Периметр прямоугольника Периметр квадрата равен сумме всех его сторон равен его стороне, умноженной на 4
![]()
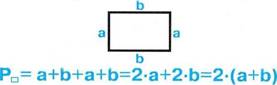 а
а
а— ширина прямоугольника, а— сторона квадрата Ь — длина прямоугольника.
Периметр многоугольника
Периметр треугольника равен сумме всех его сторон равен сумме всех его сторон
Рмн = a+b+c+d+e
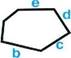
![]() Рд = а+Ь+с а с
Рд = а+Ь+с а с
Площадь — это внутренняя часть любой геометрической фигуры, ![]() обозначается латинской буквой s.
обозначается латинской буквой s.
Единицы измерения — квадратные километры (км 2 ) , квадратные метры (м 2) квадратные сантиметры (см 2) и так далее.
Площадь прямоугольника равна
произведению длин ![]() его сторон.
его сторон.
а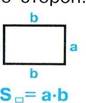
а—
ширина прямоугольника, ![]() длина прямоугольника.
длина прямоугольника.
Площадь квадрата равна квадрату длины его стороны.
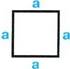
а — сторона квадрата
1 минута = 60 секунд -1 неделя суток
1 /4 часа = 15 минут 1 месяц = 30 или 31 день
1 /2 часа = 30 минут (полчаса![]() 1 /4 года = З месяца (квартал
1 /4 года = З месяца (квартал![]()
1 час = 60 минут 1
/2 года = 6 месяцев (полгода![]()
1 /2 суток = 12 часов![]() = 365 или 366суток - 12— месяцев 1
сутки часа 1 век = 100лет
= 365 или 366суток - 12— месяцев 1
сутки часа 1 век = 100лет
В феврале 28 дней.
В феврале високосного года 29 дней.
Високосный год встречается один раз в четыре года.
1 . Понедельник— день получил такое название, так как шёл после недели, а неделей называли день ОТДЫХа (от слов «не делаты»).
2. Вторник — второй день. З. Среда — середина недели. 4. Четверг — четвёртый день.
5. Пятница — пятый день.
б. Суббота — название этого дня недели произошло от слова «шаббат» — так у еврейского народа назывался день отдыха.
7. Воскресенье — день, в который, согласно Библии, воскрес Иисус Христос.
1 миллиметр![]() мм
мм
![]() 1сантиметр
1сантиметр![]() см = 10 мм
см = 10 мм
1 дециметр![]() дм = 10 см
дм = 10 см
1 метр —1 м = 10![]() дм = 100 см
дм = 100 см
![]() 1километр
1километр![]() км
км![]()
1 кв. миллиметр = 1 мм 2
1 кв, сантиметр (см 2 ) = 100 кв. мм (мм 2 )
1 кв. дециметр дм 2 ) = 100 кв, см (см 2 )
1 кв. метр (м 2 100 кв. дм (дм 2 )
1 гектар 1 га) = 10 000 кв. м (м 2 )
1 кв, километр (кг“) = 1 000 000 кв, м (м 2 )
1 миллиграмм = 1 мг = 1/1000 г
1 грамм = 1 г = 1000 мг
1 килограмм = 1 кг = 1000 г
1 центнер = 1 ц = 100 кг
1 тонна = 1 т = 1000 кг = 10 ц
Скорость — это расстояние, преодолеваемое предметом за единицу времени. Измеряется в км/ч, км/с, м/мин, м/с.
Скорость — V. Время — t. Расстояние — S.
Чтобы найти СКОРОСТЬ, нужно расстояние разделить на время:
V=S : t
Чтобы найти ВРЕМЯ, надо расстояние разделить на скорость:
Чтобы найти РАССТОЯНИЕ, надо скорость умножить на время:
цена — это стоимость одного предмета, одной единицы товара.
Ц — цена ![]()
Ст — общая стоимость Ст —![]()
К— количество ст : ц
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.