Представление информации в цифровых автоматах

Дисциплина: ИНФОРМАТИКА               

 

 

Лекция № 11

Тема: Представление информации в цифровых автоматах

 

1.     Основы представления информации в цифровых автоматах

2.     Позиционные системы счисления

3.     Методы перевода чисел

4.     Форматы представления чисел с плавающей запятой

5.     Двоичная арифметика

6.     Коды: прямой, обратный, дополнительный, модифицированный

7.     Выполнение арифметических операций с числами с фиксированной и плавающей запятой

Лекция № 11

Тема: Представление информации в цифровых автоматах

 

1.     Основы представления информации в цифровых автоматах

2.     Позиционные системы счисления

Системой счисления называется совокупность приемов и правил для записи чисел цифровыми знаками. Любая предназначенная для практического применения система счисления должна обеспечивать:

·        возможность представления любого числа в рассматриваемом диапазоне величин;

·        единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);

·        простоту оперирования числами.

Все системы представления чисел делят на позиционные и непозиционные.

Непозиционная система счисления – система, для которой значение символа не зависит от его положения в числе.

Для их образования используют в основном операции сложения и вычитания. Например, система с одним символом-палочкой встречалась у многих народов. Для изображения какого-то числа в этой системе нужно записать количество палочек, равное данному числу. Эта система неэффективна, так как запись числа получается длинной. Другим примером непозиционной системы счисления является римская система, использующая набор следующих символов: I, V, X, L, C, D, M и т. д. В этой системе существует отклонение от правила независимости значения цифры от положения в числе. В числах LX и XL символ X принимает два различных значения: +10 – в первом случае и –10 – во втором случае.

Позиционная система счисления – система, в которой значение символа определяется его положением в числе: один и тот же знак принимает различное значение. Например, в десятичном числе 222 первая цифра справа означает две единицы, соседняя с ней – два десятка, а левая – две сотни.

Любая позиционная система характеризуется основанием. Основание (базис) позиционной системы счисления – количество знаков или символов, используемых для изображения числа в данной системе.

Для позиционной системы счисления справедливо равенство

(1)

 

где A_(q) – произвольное число, записанное в системе счисления с основанием q; a_i – коэффициенты ряда (цифры системы счисления); n, m – количество целых и дробных разрядов.

 

На практике используют сокращенную запись чисел:

(2)

 

Например:

а) в двоичной системе (q=2)

11010.101₂ = 1 · 2⁴ + 1 · 2³ + 0 · 2² + 1 · 2¹ + 0 · 2⁰ + 1 · 2^-1 + 0 · 2^-2 + 1 · 2^-3;

б) в троичной системе (q=3)

22120.212₃ = 2 · 3⁴ + 2 · 3³ + 1 · 3² + 2 · 3¹ + 0 · 3⁰ + 2 · 3^-1 + 1 · 3^-2 + 2 · 3^-3;

в) в шестнадцатиричной системе (q=16)

A3F.1CD₁₆ = A · 16² + 3 · 16¹ + F · 16⁰ + 1 · 16^-1 + C · 16^-2 + D · 16^-3.

 

3.     Методы перевода чисел

Числа в разных системах счисления можно представить следующим образом:

 

 

 

 

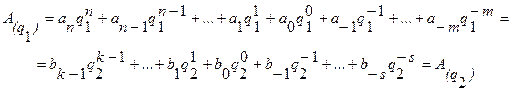
где 

Значит, в общем виде задачу перевода числа из системы счисления с основанием q₁ в систему счисления с основанием q₂ можно представить как задачу определения коэффициентов b_j нового ряда, изображающего число в системе с основанием q₂. В такой постановке задачу перевода можно решить подбором коэффициентов b_j.

Перевод чисел делением на основание новой системы

Перевод целых чисел осуществляется делением на основание q₂ новой системы счисления, правильных дробей – умножением на основание q₂. Действия деления и умножения выполняются по правилам q₁-арифметики. Перевод неправильных дробей осуществляется раздельно по указанным правилам, результат записывается в виде новой дроби в системе с основанием q₂.

Пример 1. Перевести десятичное число A = 61₁₀ в систему счисления с q = 2.

 

     61       | 2  

     60       30       | 2

b₀ = 1       30      15       | 2

            b₁ = 0     14         7      | 2

                     b₂ = 1         6        3     | 2

                                b₃ = 1        2       1 = b₅

                                          b₄ = 1

Ответ: 61₁₀ = 101111₂.

 

Табличный метод перевода

В простейшем виде табличный метод заключается в следующем: имеется таблица всех чисел одной системы с соотвествующими эквивалентами из другой системы; задача перевода сводится к нахождению соответствующей строки таблицы и выбору из нее эквивалента. Такая таблица очень громоздка и требует большой емкости памяти для хранения.

Другой вид табличного метода заключается в том, что имеются таблицы эквивалентов в каждой системе только для цифр этих систем и степеней основания (положительных и отрицательных); задача перевода сводится к тому, что в выражение ряда (1) для исходной системы счисления надо поставить эквиваленты из новой системы для всех цифр и степеней основания и произвести соответсвующие действия (умножения и сложения) по правилам q₂-арифметики. полученный результат этих действий будет изображать число в новой системе счисления.

Пример 2. Перевести десятичное число A = 113 в двоичную систему счисления, используя таблицу эквивалентов цифр и степеней основания

(q₂ = 2).

 

Таблица 1 – Таблица эквивалентов

Десятичное число	Двоичное число
100	0001
101	1010
102	110 0100

 

Решение. Подставив значения двоичных эквивалентов десятичных цифр и степеней основания в (3), получим

A = 113 = 1 · 10² + 1 · 10¹ + 3 · 10⁰ = 001 · 1100100 + 0001 · 1010 + 0011 · 0001 = 1110001₂.

Ответ: 1110001₂.

 

4.     Форматы представления чисел с плавающей запятой

Число 0,028 можно записать так: 28·10^-3, или 2,8·10^-2, или 0,03 (с округлением) и т. д. В компьютере используются две формы представления чисел.

Представление чисел с фиксированной запятой (точкой). Оно характеризуется тем, что положение разрядов числа в машинном изображении остается всегда постоянным независимо от величины самого числа.

Число А можно представить в виде

 

A=[A]_ф K_A,

 

где [A]_ф – машинное изображение числа в формате с фиксированной запятой, значение которого лежит в пределах

 

-1 < [A]_ф < 1;

 

K_A – масштабный коэффициент, выбирается так, чтобы сохранить соответствие разрадов всех чисел, которыми оперирует компьютер.

Формат (разрядная сетка) машинного изображения чисел с фиксированной запятой разбивается на знаковую часть и поле числа. В знаковую часть записывается информация о знаке числа: 0, если A≥0; 1, если A<0.

 

 

Например, числа А₁ и A₂ в прямом коде имеют машинное изображение:

 

0

0

1

0

0

1

1

1

0

0

0

1

0

1

1

1

A₁ = 0.010011100010111₂;

 

1

0

1

0

0

1

1

1

0

0

0

1

0

1

1

1

A₂ = – A₁ = 0.010011100010111_2.

Представление чисел в формате с плавающей запятой. Оно характеризуется тем, что положение разряда числа в его машинном изображении непостоянно, и число А записывается следующим образом:

 

A = m_Ap_A,

 

где m_A – мантисса числа A; при представлении числа в компьютере мантисса должна удовлетворять ограничению 2^-1 ≤ | m_A | ≤ 1 – 2^-n; n – количество разрядов для изображения мантиссы без знака; p_A – порядок числа A.

Формат машинного изображения числа с плавающей запятой содержит знаковые части и поля мантиссы и порядка.

 

5. Двоичная арифметика

В выполнении арифметических действий всегда участвуют два числа или более. В результате арифметической операции появляется новое число:

С = A Ñ B,

где Ñ – знак арифметического действия (сложение, вычитание, умножение, деление).

Операнд – число, участвующее в арифметической операции, выполняемой цифровым автоматом.

Так как цифровой автомат оперирует только машинными изображениями

[C] = [A] Ñ [B],

где [   ] – обозначение машинных изображений операндов.

Рассмотрим формальные правила двоичной арифметики операций сложения и вычитания на уровне разрядов операндов. На основе правил двоичной арифметики можно записать правила сложения и вычитания на уровне разрядов операндов.

На основе правил двоичной арифметики можно записать правила сложения двоичных цифр так, как показано в табл. 1, где a_i, b_i – разряды операндов A и B соответственно; c_i – результат сложения (сумма); П_i – перенос из данного разряда в соседний старший.

Двоичный полусумматор – устройство, выполняющее арифметические действия по правилам, указанным в табл. 2.

Таблица 2

ai	bi	ci	Пi
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Появление единицы переноса при сложении двух разрядов несколько изменяет правила сложения двоичных цифр (табл. 3).

Таблица 3

ai	bi	Пi-1	ci	Пi
0	0	0	0	0
0	1	0	1	0
1	0	0	1	0
1	1	0	0	1
0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	1	1	1

Обобщая вышеизложенное, можно сформулировать правила поразрядных действий при сложении операндов A и B:

a_i + b_i + П_i-1 = c_i + П_i,

где a_i, b_i – i-й разряд 1-го и 2-го операндов соответственно; c_i – i-й разряд суммы; П_i-1 – перенос из (i–1)-го разряда; П_i – перенос в (i+1)-й разряд (переносы принимают значения 0 или 1).

Двоичный сумматор – устройство, выполняющее арифметические действия по правилам, указанным в табл. 3.

Вычитание двоичных чисел.

На основе правил двоичной арифметики можно записать правила вычитания двоичных цифр так, как показано в табл. 4, где a_i – i-й разряд уменьшаемого; b_i – i-й разряд вычитаемого; c_i – i-й разряд разности; z_i+1 – заем в старшем разряде.

Таблица 4

ai	bi	ci	zi+1
0	0	0	0
1	0	1	0
1	1	0	0
0	1	1	–1

Заем равносилен вычитанию единицы из старшего разряда. С учетом единицы займа из старшего соседнего разряда правила вычитания двоичных цифр можно записать так, как показано в таблице 5 (чтобы отличить заем от переноса, перед единицей поставлен знак минус).

Таблица 5

ai	bi	zi	ci	zi+1
0	0	0	0	0
1	0	0	1	0
1	1	0	0	0
0	1	0	1	–1
0	0	–1	1	–1
1	0	–1	0	0
1	1	–1	1	–1
0	1	–1	0	–1

 

Если A – уменьшаемое (1-й операнд), B – вычитаемое (2-й операнд), то для поразрядных действий

a_i – b_i + z_i = c_i + z_i+1,

где a_i, b_i, c_i – соответственно i-е разряды уменьшаемого, вычитаемого и разности; z_i – заем из младшего i-го разряда; z_i+1 – заем в старшем (i+1)-м разряде.

Двоичный вычитатель – устройство, выполняющее арифметические действия по правилам, указанным в табл. 5. С точки зрения технической реализации всегда проще сложить два электрических сигнала, чем вычесть их друг из друга. Поэтому двоичные сумматоры являются основным устройством любой ЭВМ. Для того чтобы с их помощью выполнять такие арифметические действия, как вычитание, умножение, деление и др., необходимы соответствующие алгоритмы.

 

6.     Коды: прямой, обратный, дополнительный, модифицированный

Одним из способов выполнения операции вычитания является замена знака вычитаемого на противоположный и прибавление его к уменьшаемому:

A – B = A + (–B).

Этим операцию арифметического вычитания заменяют операцией алгебраического сложения. Последняя и становится основной операцией.

Для машинного представления отрицательных чисел используют коды прямой, дополнительный, обратный.

Прямой код числа A = – 0, a₁ a₂ ... a_n – машинное изображение этого числа в виде [A]_пр = 1, a₁ a₂ ... a_n.

Из определения следует, что в прямом коде все цифровые разряды остаются неизменными, а в знаковой части записывается единица. Например, если A = – 0,101110, то [A]_пр = 1,101110.

Положительное число в прямом коде не меняет своего изображения. Например, если A = 0,110101, то [A]_пр = 0,110101.

Дополнительный код числа A = – 0, a₁ a₂ ... a_n – машинное изображение этого числа [A]_д = 1, ā₁ ā₂ ... ā_n, для которого ā_i = 0, если a_i = 1, и ā_i = 1, если a_i = 0, за исключением последнего значащего разряда, для которого ā_k = 1 при a_k = 1.

Например, число A = – 0,101110 запишется в дополнительном коде так: [A]_д = 1,010010.

Дополнительный код является математическим дополнением до основания системы счисления:

| A | + [A]_д = q,

где | A | – абсолютное значение числа A.

Обратный код числа A = – 0, a₁ a₂ ... a_n – такое машинное изображение этого числа [A]_об = 1, å₁ å ₂ ... å_n, для которого å_i = 0, если a_i = 1, и å_i = 1, если a_i = 0.

Из определения следует, что обратный код двоичного числа является инверсным изображением самого числа, в котором все разряды исходного числа принимают инверсное (обратное) значение, т. е. все нули заменяются на единицы, а все единицы – на нули, например если A = – 0,101110, то [A]_об = 1,010001.

Следовательно, для обратного кода чисел, представленных в форме с запятой, фиксированной перед старшим разрядом, справедливо соотношение

| A | + [A]_об = q – q^-n,

где | A | – абсолютная величина числа A; n – количество разрядов после запятой в изображении числа.

 

7.     Выполнение арифметических операций с числами с фиксированной и плавающей запятой

Операция сложения чисел в прямом, обратном и дополнительном кодах выполняется на двоичных сумматорах соответствующего кода.

Двоичный сумматор прямого кода (ДСПК) – суматор, в котором отсутствует цепь поразрядного переноса между старшим цифровым и знаковым разрядами, поэтому на ДСПК складываются числа, имеющие одинаковые знаки; сумма чисел имеет знак любого из слагаемых.

Двоичный сумматор дополнительного кода (ДСДК) – сумматор, оперирующий изображениями чисел в дополнительном коде и имеющий цепь поразрядного переноса из старшего цифрового в знаковый разряд. Правила сложения на ДСДК основаны на следующей теореме: сумма дополнительных кодов есть дополнительный код результата.

Двоичный сумматор обратного кода (ДСОК) – сумматор, оперирующий изображениями чисел в обратном коде и характеризующийся наличием цепи циклического переноса из знакового разряда в младший разряд числа. Правила сложения на ДСОК основаны на следующей теореме: сумма обратных кодов есть обратный код результата.

При сложении чисел одинакового знака, представленных в формате с фиксированной запятой, может возникнуть переполнение разрядной сетки. Признаком переполнения разрядной сетки ДСПК является появление единицы переноса из старшего разряда цифровой части числа. Признаком переполнения разрядной сетки ДСДК и ДСОК является знак результата, противоположный знаку операндов.

Умножение чисел, представленных в формате с фиксированной запятой, осуществляется на двоичных сумматорах прямого, обратного и дополнительного кодов.

Существует несколько методов получения произведения двух чисел, все они дают результаты одинаковой точности, но требуют различных аппаратных затрат.

Наиболее распространен метод, по которому произведение получается по следующей схеме: A = 0, a₁ a₂ ... a_n – множимое, а B = 0, b₁ b₂ ... b_n = (... (((b_n x 2^-1 + b_n-1) x 2^-1 + b_n-2) x 2^-1 + ... b₂) 2^-1 + b₁) 2^-1 – множитель, произведение равно С = A x B = (...((b_n x 0.a₁ ... a_n) 2^-1 + b_n-1 x 0.a₁ a₂ ... a_n) 2^-1 + ... + b₁ x 0.a₁ a₂ ... a_n) 2^-1,

что означает, что умножение начинается с младших разрядов множителя и на каждом шаге сдвигается вправо сумма частных произведений.

При умножении чисел представленных в прямом коде, знак произведения определяется отдельно от цифровой части как SgC = SgA Å SgB, а цифровая часть формируется на двоичном сумматоре прямого кода. Произведение получается в прямом коде.

При умножении чисел, представленных в дополнительном коде, одновременно получают знаковую и цифровую части произведения. Результат представляется в дополнительном коде только при положительном множителе; при отрицательном множителе для получения результата в дополнительном коде вводится коррекция в виде прибавления [Ā]_д к произведению дополнительных кодов сомножителя.

При умножении чисел в обратном коде знаковая и цифровая части также получаются одновременно, знак формируется автоматически. Произведение обратных кодов дает обратный результат только при положительном множителе; при отрицательном множителе вводится две коррекции:

а) на первом шаге формирования произведения прибавлением поправки [A]_об;

б) на последнем шаге прибавлением к содержимому сумматора [Ā]_об.

При умножении чисел в прямом и дополнительном кодах результат имеет 2n разрядов, где n – число разрядов операндов, и может содержаться соответственно старшая часть произведения – в сумматоре и младшая часть – в освобождающихся разрядах регистра множителя.

При умножении чисел в обратном коде произведение получают сразу со знаком и длиной n разрядов, которые хранятся в сумматоре.

 

Деление двоичных чисел, представленных в формате с фиксированной запятой представляет последовательные операции алгебраического сложения делимого и делителя, а затем остатков и сдвига. Деление выполняется на двоичных сумматорах дополнительного и обратного кодов. Результат получается в прямом коде. Знаковую и цифровую часть частного получают в прямом коде. Знак частного Sg С = Sg A Å Sg B,

где Å  –  операция сложения по mod 2; Sg A – знак делимого A; Sg B – знак делителя B.

Для определения цифр частного C_i используют следующие правила.

Правило 1. Если делимое A и делитель B представлены в соответствии с таблицей 1,

Таблица 1

Sg A	+	+	–	–
Sg B	+	–	+	–
представление операндов	A+	A+B	A+B	A+

где – изменение знака операнда на противоположный, то необходимо сравнивать на каждом шаге знаки делимого A и остатков A_i и принимать C_i = 1, если знаки совпали, и C_i = 0 – при несовпадении знаков A и A_i.

Правило 2. Если делимое A и делитель B представлены в соответствии с табл. 2, то в очередной разряд частного C_i переписывается содержимое знакового разряда сумматора на каждом шаге.

Таблица 2

Sg A	+	+	–	–
Sg B	+	–	+	–
представление операндов	+ B	+	A+B	A+

Необходимым условием выполнения операции деления чисел с фиксированной запятой является | A | < | B |, B ¹ 0, в противном случае – переполнение разрядной сетки сумматора.

Для нахождения результата с точностью n разрядов надо найти (n+1)-й разряд частного, а затем округлить результат.

Признаки окончания операции деления:

1)    достижение заданной точности;

получение очередного остатка, равного нулю.