ПРЕОБРАЗОВАНИЕ ЦЕЛОГО ВЫРАЖЕНИЯ В МНОГОЧЛЕН

Преобразование  целого выражения в многочлен

Цели: ввести понятие целого выражения; формировать умение преобразовывать целые выражения.

Ход урока

I. Устная работа.

Преобразуйте в многочлен.

а) x (2x² – 4);      в) (x + 4)²;                                   б) (x + 3) (x – 3);

г) 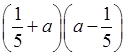;          д) (a – 1) (a² + a + 1);              ж) (x – 3) (y – 2);

е) 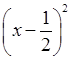;                       з) (–1 – 2n)².

II. Объяснение нового материала.

Объяснение  проводить  согласно  пункту  37  учебника  в  несколько этапов.

1. Введение понятия целого выражения.

Сначала необходимо напомнить учащимся о том, что такое математическое выражение, а затем дать определение целого выражения. Сделать вывод: математическое выражение может быть целым или нецелым.

После этого привести примеры и выполнить № 918.

2. Целое выражение и многочлен.

На основе изученного учащиеся сами смогут сделать вывод, что любой многочлен является целым выражением. После этого следует задать им вопрос: любое ли целое выражение является многочленом?

Делаются соответствующие выводы, приводятся примеры, показывающие, как целое выражение представляется в виде многочлена.

3. Преобразование целых выражений.

Сообщить учащимся, что преобразование целых выражений является одним из основных действий в математике. Чтобы выполнять такие преобразования, нужно уметь следующее:

– выполнять умножение одночлена на многочлен и многочлена на многочлен;

– приводить подобные слагаемые;

– знать формулы сокращенного умножения.

Далее привести пример 1 из учебника.

III. Формирование умений и навыков.

Для преобразования целых выражений учащиеся выполняют действия, которые уже должны быть у них отработаны в процессе изучения предыдущих тем. По сути, задания, предложенные в учебнике, служат для обобщения и систематизации знаний и умений учащихся.

1. Упростите выражение.

а) (4a – b) (a – 6b) + a (25b – 3a);

б) 2c (5c – 3) – (c – 2) (c – 4);

в) (y – 3) (5 – y) – (4 – y) (y + 6).

2. Преобразуйте в многочлен.

а)                             в)

б) 4b (3b + 6) – (3b – 5) (5 + 3b);                г)

3. Найдите значение выражения.

а)    при  х = –3,5;

б)         при  a = 1,  b = 0,7.

4. Упростите выражение.

а)

б)

Решение:

а) Можно выполнять возведение в квадрат и раскрывать скобки, но это будет нерационально. Заметим, что данное выражение является полным квадратом.

(4a³ – 1))² =
= (4a³ + 5 – 4a³ + 1)² = 6² = 36.

б)
= 4x³ – 4x² + x – 2x³ – 2 = 2x³ – 4x² + x – 2.

IV. Итоги урока.

– Какие математические выражения называются целыми?

– Приведите примеры целых выражений и выражений, которые не являются целыми.

– Являются ли многочлены целыми выражениями?

– Любое ли целое выражение можно представить в виде многочлена?

Домашнее задание: № 920, № 921, № 922.