Презентация к методическому семинару «Учебно-познавательные задачи как средство достижения метапредметных результатов на уроках математики»

Всероссийского конкурса «Учитель года России 2016» Областной этап Математ ика Конкурсное задание «Методический семинар» Учебно-познавательные задачи как средство достижения метапредметных результатов на уроках математики Волгина Наталья Александровна, учитель математики МБОУ «Называевская СОШ № 4» Называевский МР

Условия возникновения опыта Обновленная нормативная база (ФГОС, Концепция развития математического образования) Необходимость решать новые образовательные задачи: «…Обеспечение роста творческого потенциала учеников, их готовности к применению универсальных ситуациях…» (ФГОС) учебных действий в жизненных Известная методическая база (теории, технологии, диагностики) Недостаточно средств поставленных задач для решения – планируемых «Система результатов личностных, метапредметных и предметных – устанавливает и описывает классы учебно-познавательных и учебно -практических задач (УПЗ и УПрЗ), которые осваивают учащиеся в ходе обучения» (ФГОС) Проблема: новый социальный заказ школьному образованию не может быть выполнен в полной мере только средствами традиционной педагогики Необходимость переосмыслить накопленный педагогический опыт Поиск новых средств и методических решений для реализации нового социального заказа.

В глубине души учителя осознают, что на карете прошлого далеко не уедешь, тем более, когда рядом педагогическое пространство рассекают современные Теоретическая база опыта: Изучение теоретической автомобили (Е. Ямбург) другие. базы, повышение • Алёнушкина П.И., Вальтер С.Ж., и Теоретическая основа опыта учебно- Учебно-практические задачи: способы познавательные повышения образовательного потенциала учебных заданий. Омск: БОУ ДПО «ИРООО», 2013. • О.Н. Крылова, И.В. Муштавинская. квалификации и Новая дидактика Санкт-Петербург: КАРО, 2015. • О.Б. Даутова, Е.В. Иваньшина и современного урока. Идея опыта: при изучении предмета для достижения метапредметных результатов использую учебно-познавательные задачи. Цель опыта: создание условий для формирования метапредметных результатов посредством решения учебно- познавательных задач, что позволяет обеспечить базовую математическую подготовку и сформировать самостоятельного приобретения знаний и применения в их повседневной жизни. навык др. Современные технологии. КАРО, 2015. • Т.Ю. Математика. педагогические Санкт-Петербург: . Дюмина, А.А.Махонина. уровней предметных Диагностика сформированности умений и УУД. В.: Учитель, 2015. • Логинова О.Б. Экспертиза УПЗ . • А.Г. Асмолов. Формирование УУД в основной школе: от действия к мысли. М.: Просвещение, 2013. • Примерная ООП ООО.

Задачи: Детей надо учить тому, что пригодится им, когда они вырастут (Аристипп) • Изучить и проанализировать теоретические аспекты технологий деятельностного типа, методические конструкторы УПЗ, алгоритмы экспертизы УПЗ, диагностические уровней метапредметных результатов и т.д. методики оценки • Отследить уровень сформированности • Отобрать метапредметных результатов. методические УПЗ, способствующие формированию метапредметных результатов на уроках математики. приёмы, • Подобрать или разработать тексты УПЗ на основе преобразования (текстов математических задач, упражнений) и апробировать их на разных этапах урока. учебного материала • Отследить эффективность разработанных средств (оценить уровень сформированности УУД). • Сформулировать выводы исходя из анализа полученных результатов.

Лучший способ изучить что-либо - это открыть самому (Д. Пойа ) Классы учебно-познавательных и учебно-практич еских задач УПрЗ – это такая задача, которая ориентирована на применение (отработку) уже освоенных способов действий (знаний, умений) в известной школьникам ситуации, как правило, внутри конкретного учебного предмета. УПЗ – задачи на поиск и анализ информации, необходимой для решения учебно-практических задач, то задачи, обеспечивающие сам процесс научения (формирования способов понятий и предметной и метапредметной деятельности). есть

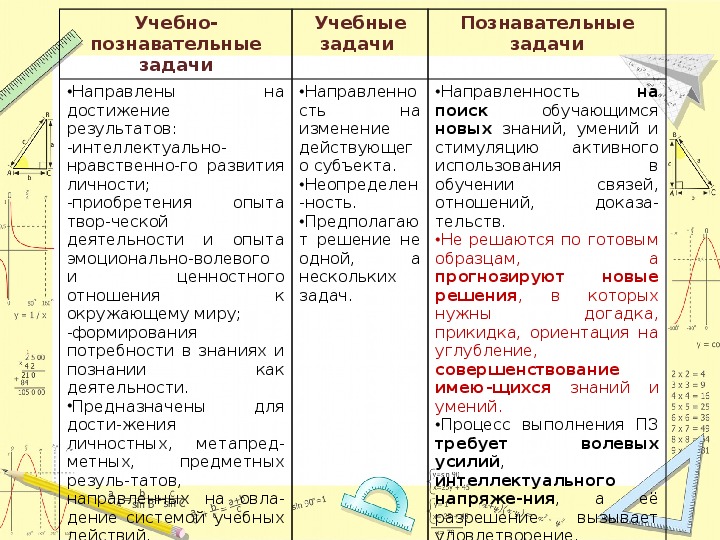
познавательные Учебно- задачи на •Направлены достижение результатов: -интеллектуально- нравственно-го развития личности; опыта -приобретения твор-ческой деятельности и опыта эмоционально-волевого и ценностного отношения к окружающему миру; -формирования потребности в знаниях и познании как деятельности. для •Предназначены дости-жения личностных, метапред- метных, предметных резуль-татов, направленных на овла- дение системой учебных действий. •Выделены 9 Учебные задачи Познавательные задачи •Направленно сть на изменение действующег о субъекта. •Неопределен -ность. •Предполагаю т решение не одной, а нескольких задач. на •Направленность поиск обучающимся новых знаний, умений и активного стимуляцию использования в связей, обучении отношений, доказа- тельств. •Не решаются по готовым образцам, а прогнозируют новые решения, которых в нужны догадка, прикидка, ориентация на углубление, совершенствование имею-щихся знаний и умений. •Процесс выполнения ПЗ требует волевых усилий, интеллектуального напряже-ния, а разрешение удовлетворение, положитель-ные её вызывает

Метапредметные результаты Технологии деятельностног о типа Технология проблемного обучения. Технология развития критического мышления. Технология «педагогических мастерских». Технология диалогового обучения. Технология организации самостоятельной деятельности. • • • • •

Цели применения учебно-познавательных задач 1. Знакомство школьников с теми или иными понятиями и правилами. 2. Систематизация знаний. 3. Развитие навыков: - исследовательской деятельности; - планирования и контрольно-оценочной деятельности; - использования ресурсов различных информационных систем; - сотрудничества; - выстраивания системы ценностей.

Примеры учебно-познавательных задач

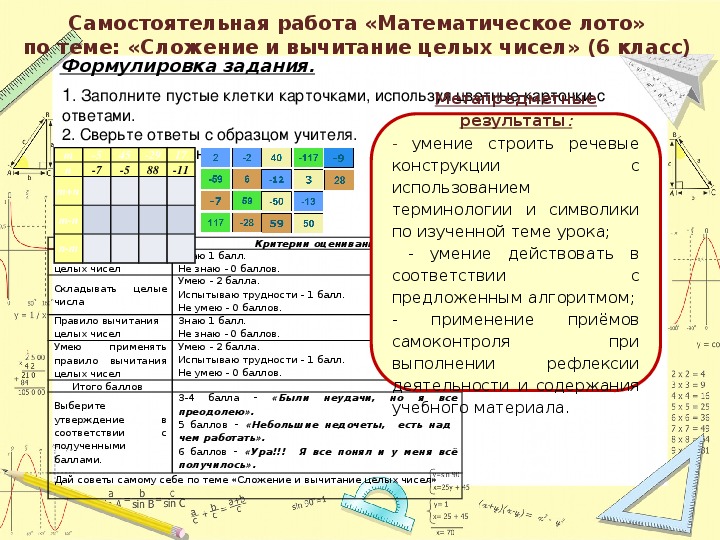
по теме: «Сложение и вычитание целых чисел» (6 класс) Самостоятельная работа «Математическое лото» Формулировка задания.  Метапредметные 1. Заполните пустые клетки карточками, используя цветные карточки с  ответами. 2. Сверьте ответы с образцом учителя. 3. Оцените свои знания и умения. m ­5 n ­7 результаты: ­29 88 17 ­11 45 ­5 m+n сложения m­n Знания и умения n­m Правило целых чисел Складывать целые числа Правило вычитания целых чисел Умею применять правило вычитания целых чисел Итого баллов Знаю 1 балл. Не знаю - 0 баллов. Умею - 2 балла. Испытываю трудности - 1 балл. Не умею - 0 баллов. Знаю 1 балл. Не знаю - 0 баллов. Умею - 2 балла. Испытываю трудности - 1 балл. Не умею - 0 баллов.   3-4 балла преодолею». 5 баллов - «Небольшие недочеты, есть над чем работать». 6 баллов - «Ура!!! Я все понял и у меня всё получилось». - «Были неудачи, но я все в с Выберите утверждение соответствии полученными баллами. Дай советы самому себе по теме «Сложение и вычитание целых чисел»   Критерии оценивания - умение строить речевые конструкции с использованием терминологии и символики по изученной теме урока; - умение действовать в соответствии с предложенным алгоритмом; - приёмов самоконтроля при рефлексии выполнении деятельности и содержания учебного материала. применение

Тема: «Сложение дробей с одинаковыми знаменателями» результаты: Метапредметные Формулировка задания (5 класс) Сформулируйте правило «Сложение дробей с одинаковыми знаменателями» и запишите его буквенным выражением. Для этого ответьте на вопрос задачи и запишите её решение. Задача. Торт разрезали на 12 равных кусочков. Саша съел три кусочка, а его друг Петя съел 2 кусочка. Какую часть торта съели мальчики вместе? Вопросы и задания: • Какую часть торта съел Саша? (запишите ответ в виде • Какую часть торта съел Петя? (запишите ответ в виде обыкновенной дроби) обыкновенной дроби) учебнике. • Сколько кусочков торта они съели вместе? • Какую часть торта они съели вместе? (запишите ответ в знаменателями. Критерии оценки виде обыкновенной дроби) • Запишите решение задачи. • Сформулируйте правило сложения дробей с одинаковыми Задание выполнено, если правильно решена задача, • Сравните сформулированное правило с правилом в верно записано решение задачи, составлено правило и буквенное выражение. • Оцените свою деятельность. Задание почти выполнено, если правильно решена задача и записан только ответ задачи, составлено правило, но не составлено буквенное выражение или правильно решена задача и записан ответ задачи, составлено частично правило, но не составлено буквенное выражение. Задание не выполнено, если даны только верные ответы на вопросы задачи, отсутствие выполненных заданий по задаче. с - работать матема- тическим текстом, - строить речевые конструкции с использованием изу-ченой терминологии; - планировать решении свою деятельность при учебных математических задач; несложные алгоритмы действо-вать соответствии ним; составлять и в с - применять приёмы самоконтроля при учебных задач. решении -

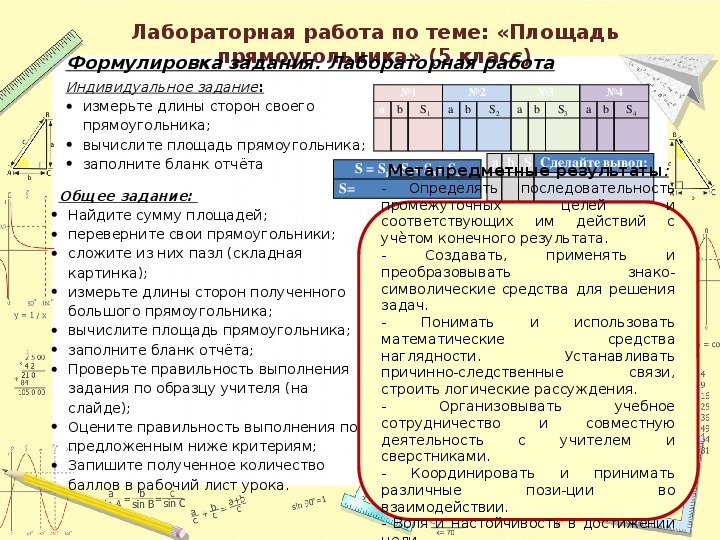
Лабораторная работа по теме: «Площадь прямоугольника» (5 класс) Формулировка задания. Лабораторная работа Индивидуальное задание: №3  измерьте длины сторон своего №1 №2 S1   a b     S2   a b     S3   №4 a b     S4   a b       S = S1+ S2+ S3+ S4 прямоугольника;  вычислите площадь прямоугольника;  заполните бланк отчёта Общее задание:  Найдите сумму площадей;  переверните свои прямоугольники;  сложите из них пазл (складная S= картинка);  измерьте длины сторон полученного большого прямоугольника;  вычислите площадь прямоугольника;  заполните бланк отчёта;  Проверьте правильность выполнения задания по образцу учителя (на слайде);  Оцените правильность выполнения по предложенным ниже критериям;  Запишите полученное количество баллов в рабочий лист урока. и целей применять a b S Сделайте вывод: Метапредметные результаты:   - Определять последовательность и промежуточных соответствующих им действий с учѐтом конечного результата. - Создавать, и преобразовывать знако- символические средства для решения задач. - Понимать математические наглядности. причинно-следственные строить логические рассуждения. - сотрудничество деятельность сверстниками. - различные взаимодействии. - Воля и настойчивость в достижении цели. использовать средства Устанавливать связи, учебное совместную и принимать во Координировать Организовывать учителем пози-ции и и с

результаты: Тема: «Умножение десятичных дробей» (6 класс) Формулировка задания. Задание. Выполни умножение десятичных дробей 3,76∙2,4. Для этого: 1. Запиши каждую дробь в виде смешанного числа. 2. Выполни умножение полученных чисел и запиши ответ в виде десятичной дроби. 3. Найди произведение натуральных чисел 376 и 24. 4. Сверь ответы с товарищем в паре. 5. Сравните записи: 3,76∙2,4=______ и 6. Сформулируйте правило умножения десятичных дробей. 7. Сравните полученное правило с правилом в учебнике на стр. 68. 8. Составьте алгоритм умножения десятичных дробей в столбик, предварительно обсудив его в паре. 9. Сверьте полученный алгоритм с эталоном. 10. Выполните умножение десятичных дробей, комментируя друг другу решение: а) 4,2∙3,6 б) 3,14∙0,25 11. Найди произведение десятичных дробей: а) 5,3∙431; б) 6,36∙2,5; в) 27,2∙0,06 12.Проверь правильность выполнения решения задания по образцу учителя. 13. Оцени правильность выполнения задания: Поставь  знак  Х  в  14. Выбери следующее задание: нужной ячейке. - если всё правильно: № 200; - есть ошибки: № 198; - всё неправильно: - возьми задание у учителя. 15. Сверь ответы с учителем. Выполни рефлексию деятельности: - «самое удачное в работе»; - «самое трудное в работе»; - «чему я научился в - процессе работы»; «пожелание себе»; - «пожелание партнеру»; Время выполнения работы: 20 минут. - формирование умения работать с математическим текстом; - умение строить рече-вые конструкции с ис- пользованием изучен-ной терминологии; - умения планировать свою деятельность при решении учебных математических задач; - составлять несложные алгоритмы действовать соответствии ними; - приёмы самоконтроля при решении учебных формирование       Всё правильно Есть ошибки Всё неправильно умение и в с применять

Задание «Астрономия на координатной плоскости»  по теме «Координатная плоскость» (6 класс)  Формулировка задания. Постройте точки созвездий на координатной плоскости и найдите эти созвездия на звездной карте.  Для этого: 1. Получите карточку с заданием: изобразить на координатной плоскости созвездие. Количество точек разделите на количество учащихся в группе. 2. Отметьте каждый по очереди точки на координат-ной плоскости. 3. После того, как все точки отмечены, получите конверт с изображением созвездия на координат-ной плоскости и его названием. 4. Проверьте правильность выполнения задания по полученному образцу. 5. Най-дите построенное созвездие на звёздной карте. 5. Прикрепите свою работу к доске. 6. Оцените работу, заполнив лист самооценки. Время работы: 10 минут.                Лист самооценки Пример образца учителя. Оцени работу своей группы, отметь галочкой вариант ответа, с которым ты согласен(а). очень 1. Все ли члены группы принимали участие в работе над задачей? (Да, все работали одинаково; нет, работал только один; кто-то работал больше, а кто-то меньше). 2. Дружно ли вы работали? Были ли ссоры? (Работали дружно, ссор не было; работали дружно, спорили, но не ссорились; было договариваться, не всегда получалось). 3. Тебе нравится результат работы твоей группы? (Да, всё получилось хорошо; нравится, но можно было бы сделать лучше; нет, не нравится. 4. Оцени свой вклад в работу группы. Отметь нужное место на линейке знаком «Х». Знак «Х» смещается влево от центра, если ты выбрал(а) «Почти всё сделали без меня», или вправо от центра, если «Я сделал очень много, без трудно и письменные) Метапредметные результаты: Пример задания для групп. Созвездие «Малой Медведицы»  (6; 6), (– 3; 5,5), (– 8; 5), (0; 7,5), (3; 7), (– 5; 7), (– 6; 3). Созвездие «Большой Медведицы»  (– 15; – 7), (– 3; – 6), (5; – 10), (– 6; - умение строить речевые конструкции – 5,5), (– 10; – 5), (6; – 6), (устные с (– 1; – 10) изученной использованием терминологии; - смысл умение поставленной задачи, осуществлять перевод с естественного языка на математический и наоборот; - умение действовать в соответствии с предложенным алгоритмом действий; - приёмы самоконтроля при решении учебных задач; - умение видеть математическую задачу в несложных практических ситуациях. применять понимать умение

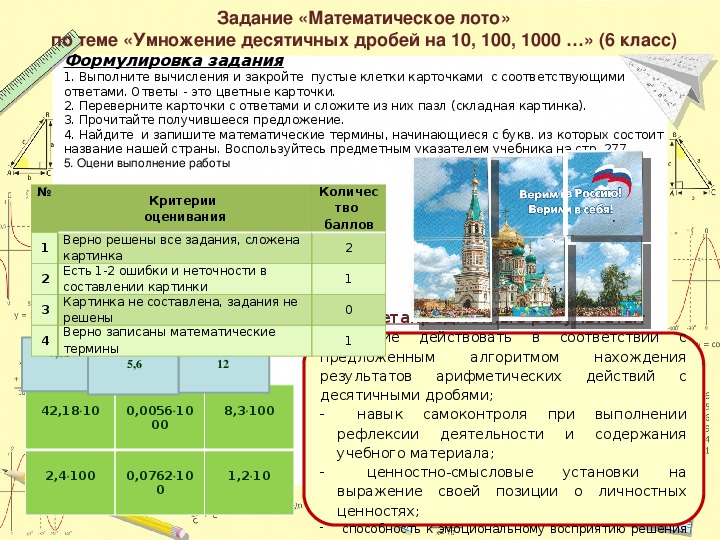
Задание «Математическое лото»  по теме «Умножение десятичных дробей на 10, 100, 1000 …» (6 класс)  Формулировка задания 1. Выполните вычисления и закройте пустые клетки карточками с соответствующими ответами. Ответы - это цветные карточки. 2. Переверните карточки с ответами и сложите из них пазл (складная картинка). 3. Прочитайте получившееся предложение. 4. Найдите и запишите математические термины, начинающиеся с букв. из которых состоит название нашей страны. Воспользуйтесь предметным указателем учебника на стр. 277. 5. Оцени выполнение работы № Критерии оценивания картинка составлении картинки 1 Верно решены все задания, сложена 2 Есть 1-2 ошибки и неточности в 3 Картинка не составлена, задания не 830 4 Верно записаны математические 7,62 термины решены 421,8 240 5,6 12 42,1810 0,005610 00 8,3100 2,4100 0,076210 0 1,210 Количес тво баллов 2 1 0 Метапредметные результаты: 1 алгоритмом - умение действовать в соответствии с нахождения предложенным результатов с десятичными дробями; - арифметических действий ценностно-смысловые самоконтроля при выполнении содержания навык рефлексии деятельности и учебного материала; на выражение своей позиции о личностных ценностях; способность к эмоциональному восприятию решения математических задач. установки - -

Результативность Метапредметные результаты Предметные учебные действия В. Афанасьевой стартовой Программа диагностики действий универсальных учащихся 5 классов под ред. Н. по основным показателям личностных, регулятивных, познавательных, Диагностический коммуникативных УУД инструментарий : 1.Методика диагностики мотивации учения и эмоционального отношения к учению (A.M. Прихожан) 2. Методика диагностики уровня сформированности общеучебных и навыков школьников (М. Ступницкая) 3. Комплексная работа умений - - - - Стартовая контрольная работа Тематические контроль ные работы Итоговая контрольная работа за I полугодие Итоговая контрольная работа за год Предметные конкурсы, турниры, олимпиады, УПЗ в рамках ТКП (работы обучающихся)

Мониторинг достижений метапредметных результатов

Мониторинг достижений Динамика достижений метапредметных результатов, 5 -А кл, 2015/2016 уч. г. ( сентябрь, декабрь) Динамика достижений метапредметных результатов, 5 -Б кл, 2015/2016 уч. г. ( сентябрь, декабрь) метапредметных результатов Колличество обучающихся, % Колличество обучающихся, % 80% 60% 70% 50% 60% 40% 50% 40% 30% 30% 20% 20% 10% 10% 0% 0% Высокий уровень Высокий уровень Средний уровень Средний уровень 100% 71% Низкий уровень Комплексная работа Низкий уровень Задания базового уровня Задания повышенного уровня 100% 100% 100% 73% 43% 43% 5-а, 09. 2015 5-а, 12.2015 5-б, 09. 2015 5-б, 12.2015

Если ученик в школе не научился сам ничего творить, то и в жизни он всегда Качество знаний будет только подражать, копировать (Л. Н. Толстой) Качество знаний Качество знаний 58% 2014/2015 40% 2015/2016, I полугодие 59% 35% 2015/2016, I полугодие 75% 36% 35% 5 класс ОУ Динамика результатов выполнения стартовых и 6 класс ОУ 5-а класс 5-б класс ОУ Учебный год Классы 2014/2015 итоговых работ Годовая I полугоди к/р Стартова я работа Стартова я работа 2015/2016 (I п/г) БУ ПУ БУ ПУ БУ ПУ БУ ПУ БУ ПУ е полугоди I е 100 42 100 40 100 45 5 Динамика и результативность участия в 6 5-А предметных олимпиадах, турнирах, конкурсах 100 62 100 22 Победители и призёры 100 20 100 45 100 60 Участники 5-Б 32 2014/2015 13 2015/2016, I полугодие 44 14

Лучшая манера учить других – это вести их тем же путем, по которому шли сами для того, чтобы образовать себя (Э. Кондильяк) - конкурс Открытые уроки (5-6 классы): Сложение и вычитание дробей с одинаковыми знаменателями Правильные и неправильные дроби - Площадь прямоугольника - Конкурсы: - Отношения и пропорции - Всероссийский «Современный учитель» - Областной конкурс учебных проектов « Проектная деятельность в информацио нной образовательной среде XXI века » (2 место) - конкурс «Методическая разработка урока (занятия) с применением ИКТ (победитель) конкурс - «Методическая разработка урока - Организация и проведение областного с соответствие (занятия) ТКП « педагогов требованиями ФГОС» ТРКМ в образовательном процессе» - Разрабатываем современный урок Всероссийский Региональные ТКП: Всероссийский для в геометрии с - Реализация междисциплинарной программы «Смысловое чтение и работа текстом» в условиях введения ФГОС (3 место) проектной и исследовательской деятельности обучающихся в условиях реализации ФГОС (лауреат) - Организация - - - на ТРКМ в (ШМО Применение обучающихся Публикации: образовательных в условиях учителей - математики (муниципальная ВКС ) - Персональный сайт Представление опыта: уроках http://volgina.teach.obr55.ru/ мастерская педагогическая «Современный урок» в рамках (для педагогов района) «Обновление деятельности учителя математики в условиях введения ФГОС ООО (РМО) Оценивание результатов начальной школе введения ФГОС начальных классов) Применение современных педагогических технологий на уроках реализации математики - « деятельностного (X Реализация стратегии смыслового чтени областной педагогический марафон) я на уроке математики средствами ТКРМ - » - Сборники методических разработок: « Компетентностно -ориентированные уроки» Компетентностно -ориентированные задания» - Статья «Применение современных педагогических технологий на уроках математики реализации компетентностного ТКП «Компетентностно-ориентированный урок» - « Исследовательская деятельность на уро ках математики Всероссийский » фестиваль методических разработок) для Статья подхода» подхода» при (VI и « Статья http://nsportal.ru/volgina­natalya­aleksandrovna

Библиографический список • Селевко Г.К. Современные образовательные технологии: Учебное пособие. – М.: Народное образование, 1998 г. • Алёнушкина П.И., Вальтер С.Ж., и другие. Учебно-практические и учебно-познавательные задачи: способы повышения образовательного потенциала учебных заданий. Омск: БОУ ДПО «ИРООО», 2013. урока. Санкт-Петербург: КАРО, 2015. технологии. . Санкт-Петербург: КАРО, 2015. сформированности предметных умений и УУД. В.: Учитель, 2015. • О.Н. Крылова, И.В. Муштавинская. Новая дидактика современного • О.Б. Даутова, Е.В. Иваньшина и др. Современные педагогические • Т.Ю. Дюмина, А.А.Махонина. Математика. Диагностика уровней • Логинова О.Б. Экспертиза УПЗ. • Л.Р. Шафигулина. Проблемное и игровое обучение. В.: Учитель, 2013. • А.Г. Асмолов. Формирование УУД в основной школе: от действия к • Возрастные возможности усвоения знаний. Под ред. Д. Б. Эльконина, В. • Концепция развития математического образования в Российской Феде мысли. М.: Просвещение, 2013. В. Давыдова. – М., 1966. рации . Педагогика, 1972. учителей. – М.: Просвещение, 1977. • Математические этюды. • Матюшкин A. M. Проблемные ситуации в мышлении и обучении. – М.: • Махмутов М. И. Организация проблемного обучения в школе. Книга для • Нестандартные задачи. • Шуба М. Ю. Учим творчески мыслить на уроках математики. – М.: • Примерная ООП ООО. • ФГОС ООО. Просвещение, 2012.