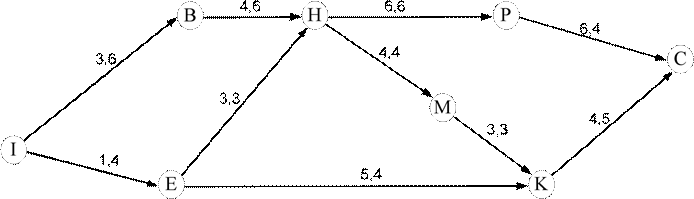
Пример построения сетевого графика. Задача оптимизации ресурсов

Пример построения сетевого графика. Задача оптимизации ресурсов

Построить сетевой график. Решить задачу оптимального распределения ресурсов по работам при постоянных интенсивностях. Наличие ресурса R=10. Работы не допускают перерыва в их выполнении.

Решение

µ_C = 0; µ_K = 4; µ_P = 6;

µ_M = +3 µ_K = + =3     4  7;

µ_H = max{6 +µ µ_P ;4 + _M }= max{6 + 6;4 + =7} max{12; 11}=12; µ_E = max{3+µ µ_H ;5 + _K }= max{3+12;5 + =4} max{15; 9}=15; µ_B = +4 µ_H = + =4 12 16; µ_I = max{3+µ µ_B;1+ _E}= max{3+16;1+15}= max{19;16}=19.

γ_IB = + = + =3 µ_B 3 16 19; γ_IE = + = + =1 µ_E 1 15 16; γ_BH = +4 µ_H = + =4 12 16; γ_EH = +3 µ_H = + =3 12 15; γ_EK = +5 µ_K = + =5 4 9; γ_HP = + = + =6 µ_P 6 6 12; γ_HM = +4 µ_M = + =4 7 11; γ_MK = +3 µ_K = + =3 4 7; γ_PC = + =6 µ_C 6; γ_KC = + =4 µ_C 4.

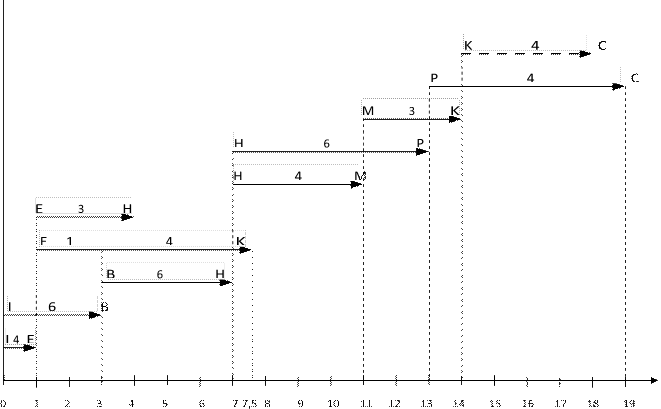
Линейная диаграмма

Рассматриваем фронт работы в момент времени 0.

ϕ(0) = {(P P₀, _i ) | i};   τ γ_0i = _0i ;  

L(0) = maxτ_0i;

∆ =τ_0i L(0) −τ_0i

Разбиваем работы на группы Q_k  с одинаковыми резервами времени и упорядочиваем эти группы по возрастанию резервов времени.

Q₀ = {( I,B)};   Q₁ = {( I,Е)}.   Наличие ресурса R=10.

R₀ = 6;  R₁ = 4;  R₀ + R₁ = R. Работы классов Q₀  и Q₁  не меняются во времени. 2 шаг.

Рассматриваем фронт работы в момент времени 1.

Разбиваем работы на группы Q_k  с одинаковыми резервами времени и упорядочиваем эти группы по возрастанию резервов времени.

Q₀ = {( I,B)};   Q₁ = {( Е,H) };   Q₂ = {( Е,K) }.   Наличие ресурса R=10. Суммы интенсивностей по группам:

R₀ = 6;  R₁ = 3;   R₂ = 4;    

R₀ = 6<R;  R₀ + R₁ = 9<R;   R₀ + R₁+ R₂ = 13>R;

l−1

R−∑ⁱ⁼⁰Ri = 10 − 9 = <1   1.  α=

                    R_l                      4       4

Работы ( I,B) и ( Е,H) не меняются во времени. Работа (Е,K) растягивается.

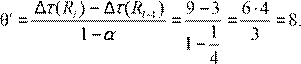
Следующего класса нет, поэтому  ^θ′′не вычисляем,

                                  ωij                    12 20 9

θ′′′ =   min     = min ;       ;  = 2

              (P P₀, _i )∈ϕ( )t β_ij                   6    1   3^       

3  шаг.

Рассматриваем фронт работы в момент времени t=3.

Q₀ = {( B,Н)};   Q₁ = {(Е,H) };   Q₂ = {( Е, K) }.   Наличие ресурса R=10. Суммы интенсивностей по группам:

R₀ = 6;  R₁ = 3;   R₂ = 4;    

R₀ = 6<R;  R₀ + R₁ = 9<R;   R₀ + R₁+ R₂ = 13>R;

Растягиваем работу ( Е,K)

l−1

R − ∑ⁱ⁼⁰Ri = 10 − 9 = 1 <1 α=

                    R_l                      4       4

4  шаг.

От t=4 до t=7 ограничение по ресурсам выполняется.

5  шаг.

Рассматриваем фронт работы в момент времени t=7.

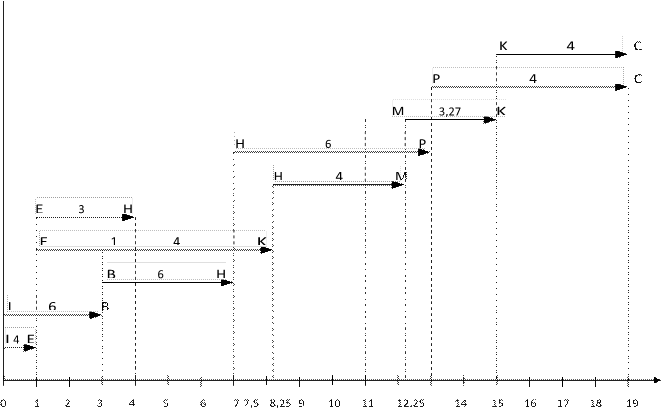
Q₀ = {( H,P)};   Q₁ = {(H,M)};   Q₂ = {( Е, K) }, Суммы интенсивностей по группам:

R₀ = 6;  R₁ = 4;  R₂ = 4.

Т.к. работу  ( Е, K) прерывать нельзя, сдвигаем на 1,25 работу  (H,M), а у работы (M,K) увеличиваем интенсивность так, чтобы уменьшить её длительность на 0,25, с 3 до 2,75. Тогда интенсивность работы (M,K) должна быть равна 9/2,75 = 36/11≈3,27.