Приёмы быстрого счёта в уме

Муниципальная научно-практическая конференция научного общества учащихся Миасского городского округа

«Интеллектуалы ХХI века»

Приёмы быстрого счёта в уме

Миасский городской округ, 2022
Содержание

Введение

В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить в уме достаточно сложные вычисления ни в коем случае не утратило своей актуальности. Гибкость ума является предметом гордости людей, а способность, например, быстро производить в уме вычисления вызывает откровенное удивление. Такие навыки помогут человеку в учёбе, в быту, в профессиональной деятельности. Кроме того, быстрый счёт – настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения. Производя математические вычисления в уме, человек пользуется, по сути, теми же правилами, что и при письменных вычислениях. И оказалось, что большие познания можно получить, обратившись к литературе. Проанализировав очень многие статьи, я открыла для себя очень интересные исторические данные о необычных способах быстрого счёта, а также много закономерностей и неожиданных результатов. И, казалось бы, «сухие» цифры всего лишь примеры, но сколько полезного и красивого в этих преобразованиях. Для меня было необычно, что приложив немного усилий, я теперь смогу и сама вести быстрый счёт и поделиться этими познаниями с одноклассниками на кружке, со взрослыми и со знакомыми. И, как правило, они, заинтересованные этим, начинают использовать такие приёмы и способы. А ведь большинство моих сверстников считают плохо. То ли думать им лень (зачем загружать себя лишней работой, если есть калькуляторы), то ли в своё время этому никто не научил. Приёмов рациональных вычислений в учебниках практически нет. Сложные формулы и алгоритмы школьной программы всё дальше и дальше уводят учеников от простых, понятных навыков устного счёта.

Я выбрала тему «Приёмы быстрого счёта» потому, что я люблю математику и хотела бы научиться считать быстро и правильно, не прибегая к использованию калькулятора.

Актуальность моей темы заключается в следующем: быстрый счёт помогает людям в повседневной жизни, а ученикам на «отлично» и «хорошо» заниматься по различным учебным предметам, в первую очередь по математике.

Цель проекта: изучить методы и приёмы устного быстрого счёта и доказать эффективность использования этих приёмов.

Объектом исследования стали различные алгоритмы счета.

Предметом исследования выступает сам процесс вычисления

В старину говорили: « Умножение – мое мученье». Значит, раньше было сложно и трудно умножать. Просты ли наши современные способы различных вычислений, а не только умножения?

Гипотеза исследования: овладение приемами устного счета позволит повысить качество и скорость шестиклассников.

Для овладения новыми приемами счета была изучена литература, проведены исследования в начале года в 6 классе, а пол года в этом же классе, чтобы проверить выдвигаемую гипотезу. Для этого были поставлены следующие задачи:

Ø  Изучить литературные источники, в которых встречаются различные приемы быстрого счета;

Ø  Сделать подборку наиболее распространенных и общедоступных приемов;

Ø  Провести констатирующий эксперимент, т. е. пробный диктант в 6 Б классе;

Ø  Познакомить учащихся класса с приемами быстрого счета, провести промежуточные диктанты, обучающие этим приемам;

Ø  По результатам изученного провести завершающий эксперимент и сравнить его данные с данными констатирующего эксперимента.

Ø  Сделать вывод о подтверждении или опровержении выдвинутой гипотезы.

 Тема быстрого счета не новая, но основательно забытая благодаря развитию современных технологий, поэтому новизна исследования заключается в создании системы применения алгоритмов, методов и приёмов, нацеленных на повышение вычислительной культуры учащихся.

Глава I

1.1.          Как люди научились считать

Мне всегда хотелось узнать, как люди научились считать, для этого я использовала интернет. Как изменился счёт, когда появилась цивилизация?

Когда первобытные люди научились считать? Скорее всего, в процессе обмена, а затем и торговли. Сначала у людей образовалось понятие "один" и "много", а лишь потом понятия "два", "три" и т.д. Для облегчения счета и для запоминания его результатов придумано множество приспособлений. Первое из них - пальцы собственных рук, которые загибают при счете. Но так можно подсчитать только небольшие числа предметов. А ведь пальцы приходится потом и разгибать, ведь не только для счета они нужны. А если нужно запомнить результаты вычислений или подсчитать число предметов большее, чем пальцев рук? Для этого древние люди делали насечки на дереве, камне или кости.

Для длительного запоминания результатов счета применяли зарубки, узелки, камешки (калькули - их латинское название, откуда происходит слово калькулятор - приспособление для счета).

Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук и ног. Наскальный рисунок, сохранившийся до наших времен от каменного века, изображает число 35 в виде серии выстроенных в ряд 35 палочек-пальцев. Первыми существенными успехами в арифметике стали концептуализация числа и изобретение четырех основных действий: сложения, вычитания, умножения и деления. Первые достижения геометрии связаны с такими простыми понятиями, как прямая и окружность. Дальнейшее развитие математики началось примерно в 3000 до н.э. благодаря вавилонянам и египтянам. [4]

Как считали наши предки, жившие в отдалённые времена, задолго до Рождества Христова, — об этом прямо и достоверно судить нельзя: письменных свидетельств не сохранилось, да их и не могло быть, потому что развитие письменного счета зависит от общего развития образования, а наши древнейшие родичи находились, очевидно, на низших ступенях образованности. Судить о первых шагах арифметики мы можем только по догадкам, сравнительно; средством же для сравнения являются т дикие и малообразованные народы, затерявшиеся в укромных уголках внутренней Африки, Америки и т. д., которые в настоящее время едва выходят из первобытного состояния.

Займемся американскими индейцами и африканскими неграми.

Индейцы Таманаки пользуются при счете пальцами рук и ног. Вместо «один» они говорят «палец» и при этом обязательно протягивают палец; вместо «два» — «два пальца», «три» — «три пальца». Пять у них зовется «рука», 6 — «палец на другой руке», 7 — «два пальца на другой руке», 10 — «две руки». Покончивши с руками, они перебираются к ногам, и так как обувь не закрывает их ног, то продолжают считать наглядно: 11 — «палец на ноге», 12 — «два пальца на ноге», 15 — «нога и две руки», 16 — «палец на другой ноге». Но вот подходит дело к 20-ти, использованы, следовательно, и руки и ноги, тогда является на помощь «человек». 20 называется «человек», так как у него 20 пальцев; как же выразить, напр., 27? Это будет «2 пальца на другой руке другого человека». Сотня заменяется у них пятью человеками, а выше сотни бедные индейцы едва ли и порываются считать, потому что у них нет для этого ни потребностей, ни развития. Кстати сказать, и эскимосы, обитатели холодных стран Северной Америки, вместо «20» говорят «человек» и вместо «100» пять человек.

Караибы на Антильских островах и по реке Ориноко дают первым четырем числам особые имена, но 5 у них заменяется словами «четыре и один», 6 — «рука и один», 7 — «рука и два», 20 — «столько, сколько руки и ноги», 30 —«столько, сколько руки и ноги, и еще 2 руки лишних».

Удивительна склонность индейцев и негров не довольствоваться одним словесным счетом, а всячески дополнять его выразительными жестами. Говоря «шесть», они протягивают 6 пальцев. Дойдя до 20, они расставляют ноги, вытягивают руки и растопыривают пальцы.

1.2 Основные понятия

Устный счёт[1]— математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор, счёты и т. п.) и приспособлений (ручка, карандаш, бумага и т. п.).[1]

Счёты (русские счёты) [2]— простое механическое устройство для произведения арифметических расчётов, усовершенствованный аналог римского абака, являются одним из первых вычислительных устройств. Счёты представляют собой раму с нанизанными на спицы костяшками, обычно по 10 штук. [2]

Концептуализация [3] — это процесс определения набора когнитивных признаков (в том числе — и категориальных) какого-либо явления реального или воображаемого мира, которые позволяют человеку хранить в сознании и пополнять новой информацией сколько-нибудь очерченное понятие и/или представление об этом явлении и отличать его от других феноменов. Этот фрагмент знания человека о мире в когнитивной лингвистике принято называть концептом, который когнитологами определяется как «дискретное образование, являющееся базовой единицей мыслительного кода человека, обладающее относительно упорядоченной внутренней структурой, представляющее собой результат познавательной (когнитивной) деятельности общества и несущее комплексную, энциклопедическую информацию об отражаемом предмете или явлении, об интерпретации данной информации общественным сознанием и отношении общественного сознания к данному явлению или предмету» [3]

Глава II

2.1 Способы быстрого умножения

2.1.1. Умножение на 11 числа, сумма цифр которого не превышает 10

Чтобы умножить на 11 число, сумма цифр которого 10 или меньше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

72х11=7(7+2)2=792;

35х11=3(3+5)5=385;

2.1.2. Умножение на 11 числа, сумма цифр которого больше 10

Чтобы умножить на 11 число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

78х11=7(7+8)8=7(15)8=858;

94х11=9(9+4)4=9(13)4=1034;

2.1.3.  Умножение на одиннадцать (по Трахтенбергу).

Разберем на примере: 633 умножить на 11.

Ответ пишется под 633 по одной цифре справа налево, как указано в правилах.

Первое правило. Напишите последнюю цифру числа 633 в качестве правой цифры результата.

633*11

3

Второе правило. Каждая последующая цифра числа 633 складывается со своим правым соседом и записывается в результат.3+3 будет 6. Перед тройкой записываем результат 6.

633*11

63

Применим правило еще раз: 6+3 будет 9. Записываем и эту цифру в результате:

633*11

963

Третье правило. Первая цифра числа 633, то есть 6, становится левой цифрой результата:

633*11

6963

Ответ: 6963.

2.1.4. Умножение на двенадцать (по Трахтенбергу).

Правило умножения на 12: нужно удваивать поочередно каждую цифру и прибавлять к ней поочередно ее «соседа».

Пример: 63247*12

Необходимо записывать цифры множимого через интервал и каждую цифру результата писать точно под цифрой числа 63247, из которой она образовалась.

063247*12 дважды 7 будет = 14, переносим 1

4

063247*12 дважды 4+7+1=16, переносим 1

64

063247*12 дважды 2+4+1 = 9

964

Следующие шаги аналогичны.

Окончательный ответ: 063247*12

758964

2.1.5. Умножение на число 111, 1111 и т. д.,

Зная правила умножения двузначного числа на число 11.

Если сумма цифр первого множителя меньше 10, надо мысленно раздвинуть цифры этого числа на 2, 3 и т.д. шага, сложить цифры и записать соответствующее количество раз их сумму между раздвинутыми цифрами. Количество шагов всегда меньше количества единиц на 1.

Пример:

24х111=2(2+4) (2+4)4=2664 (количество шагов - 2)

24х1111=2(2+4) (2+4) (2+4)4=26664 (количество шагов - 3)

При умножении числа 72 на 111111 цифры 7 и 2 надо раздвинуть на 5 шагов. Эти вычисления можно легко произвести в уме.

72 х 111111 = 7999992 (количество шагов – 5)

Если единиц во втором множителе 7, то шагов будет на один меньше, т.е. 6.

Если единиц 8, то шагов будет 7 и т.д.

61 х 11111111 = 677777771

Эти вычисления можно легко произвести в уме.

Умножение двузначного числа на 111, 1111, 1111 и т.д., сумма цифр которого равна или больше 10.

Немного сложнее выполнить устное умножение, если сумма цифр первого множителя равна 10 или более 10.

Примеры:

48 х 111 = 4 (4+8) (4+8) 8= 4 (12) (12) 8 = (4+1) (2+1) 28 = 5328.

В этом случае к первой цифре нужно прибавить 1, получим 5.

Далее 2 + 1 = 3. А последние цифры 2 и 8 оставляем без изменения.

56 х 11111 = 5 (5+6) (5+6) (5+6) (5+6) 6 = 5 (11) (11) (11) (11) 6 = 622216

67 х 1111 = 6 (6+7) …7 = 6 (13) …7 = 74437

2.1.6. Умножение двузначного числа на 101.

Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено.

 Пример:

57 * 101 = 5757 57→ 5757; 94 * 101 = 9494

быстрый счёт умножение число 59 * 101 = 5959

2.1.7. Умножение трёхзначного числа на 999.

Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только на уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9.

Например:

385 * 999 = 384615

573 * 999 = 572427 943 * 999 = 942057

2.1.8 Умножение по одиннадцать

Число нужно умножить на 10 и прибавить то число, которое мы умножаем.

Пример: 110 * 11 = 110 * (10+1) = 110 * 10 + 110 * 1= 1100 + 110= 1210

Ответ: 1210

Пример: 123 * 11 = 123 * (10+1) = 123 * 10 + 123 * 1= 1230 + 123= 1353

Ответ: 1353.

2.1.9. Умножение на двенадцать (по Берману)

При умножении на 12 можно число умножить сначала на 6, а затем на 2. Шесть в свою очередь, можно разбить на 2 множителя – это 3 и 2.

Пример: 136 * 12 = 136* 6 * 2 = 816 * 2 = 1632 или

136 * 12 = 136 * 3 * 2 * 2 = 408 * 2 * 2 = 816 * 2 = 1632

2.2. Исследование

Мной разработана презентация с информацией о приёмах быстрого устного счёта чисел. С моим наставником мы обговорили все детали презентации, с которой я пришла на урок к 6  «Б» классу в сентябре 2021 года и рассказали ребятам о приемах быстрого счета. (Приложение 1)

Затем был проведен математический диктант, на экране были представлены 20 примеров с умножением двухзначных чисел на 3 темы. (Приложение 2).  Было дано задание посчитать эти примеры на время. Мы засекали время в тот момент, когда они  начали считать эти примеры В диктанте приняло участие 16 человек 6 «Б» класса. (Приложение 3. Таблица).

Ученики 6 «Б» класса 1 раза в неделю  на уроках математики тренировались считать устно минут по 5 в начале урока.

После этого  рассказала правила, как можно умножить устно, мы попрактиковались в решении примеров таким образом, чтобы им было более понятно. (Приложение 1)

Под конец урока мной было подготовлено 20 подобных примеров, и так же как и в начале мы засекли время для сравнения результатов. Время выполнения значительно сократилось. Но были и те ученики, у кого время осталось прежним и даже увеличилось. (Приложение 3. Таблица).

Кому-то удобней считать так как он привык столбиком, но есть и ученики которым удобнее считать устно. Некоторые поняли, как считать устно сразу после объяснения, а кому-то необходимо время и тренировка, тогда и у них всё получиться.

В моём опыте принимали участие 16 учеников 6 «Б» класс, Трое из них Кира О.,

Виктория. З. и Ксения. В. показали наилучшие результаты после объяснение темы «Устный счет», примеры были решены в среднем на 3 минуты быстрее.

Основная масса ребят 62% сократили время выполнения задания в среднем на 1 минуту, что является хорошим результатом для первого раза. (Приложение 3. Диаграмма1)

Но есть ученики, у которых время выполнения задании не только не изменилось, оно увеличилось.  Двум ученикам Наташе Ш, Дарье Е. привычней считать столбиком, но я уверена, что если на уроках часто проводить устный счет, то у всех ребят время на выполнения заданий будет с каждым разом уменьшаться.

По данным таблицы (Приложение 3. Таблица 1) можно сделать вывод, что время выполнения заданий сократилось как минимум на минуту, а у некоторых и в два раза.  6-му классу очень понравились представленные правила, многие просились к доске, чтобы тоже попробовать поработать.

Заключение

Изучив в литературных источниках приемы устного счета, я отобрала самые распространенные и общедоступные. По согласованию с учителем математики, я составила математический диктант, опираясь на данные свойства. На уроке, с разрешения учителя, я провела диктант в 6 «Б» классе.

Главное условие – все вычисления ребята должны проводить в уме, а записывать только результат. Затем я показала ребятам те приемы, которые можно было применить, и через день вновь провела подобный диктант. После его проведения мы разобрали допущенные ошибки и разобрали еще несколько приемов. Ученики 6 «Б» класса 1 раза в неделю на уроках математики тренировались считать устно минут по 5 в начале урока.

Контрольный диктант мы провели в марте, за пол года тренировок время выполнения заметно улучшилось.

Вывод: Таким образом, мы видим, что наша первоначальная гипотеза о том, что знание и использование приемов быстрого счета позволит существенно увеличить скорость и качество счета, подтверждается. На самом деле это удивительно для меня, так как с некоторыми приемами я была знакома с начальной школы, но по-новому, как на своих помощников при счете, я взглянула на них только при выполнении данной работы.

Рекомендую: обязательно взять на вооружение основные приемы счета, увязав их с конкретными примерами.

Список литературы

1.             Википедия. Статья: Устный счёт. [Электронный ресурс] https://ru.wikipedia.org/wiki/Устный_счёт (посещение сайта: 11.02.22)

2.             Академик. Статья: Счёты. [Электронный ресурс] https://dic.academic.ru/dic.nsf/ruwiki/8009 (посещение сайта: 11.02.22)

3.             Википедия. Статья: Концептуализация (лингвистика). [Электронный ресурс] https://ru.wikipedia.org/wiki/Концептуализация_(лингвистика) (посещение сайта: 11.02.22)

4.             Беллюстин Всеволод Константинович, Как постепенно дошли люди до настоящей арифметики, Москва, 1909.

5.             VOLNA.ORG. Статья: Приёмы быстрого счёта. [Электронный ресурс] https://volna.org/algebra/priiemy_bystrogho_schieta.html (посещение сайта: 11.02.22)

6.      Босова Людмила Леонидовна, Босова Анна Юрьевна, учебник информатики, Москва, 2020.

Приложение 1

Рис. 1. Презентация для 6 класса

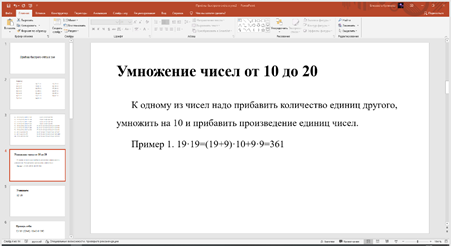
Рис. 2. Презентация для 6 класса. Умножение от 10до 20

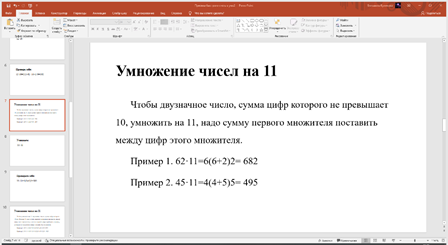
Рис. 3. Презентация для 6 класса. Умножение на число 11

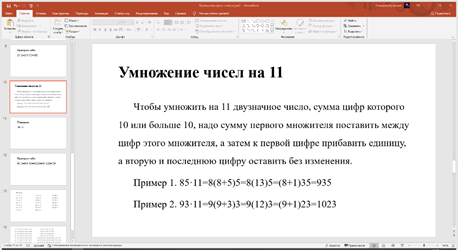
Рис. 4 Презентация для 6 класса. Умножение на число 11

Фото 1. Объяснение темы. Сентябрь 2021 г.

Фото 2. Объяснение темы. Сентябрь 2021 г.

Приложение 2

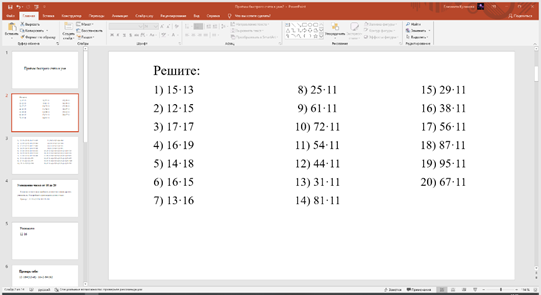
Рис 1. Примеры теста. Сентябрь 2021 г.

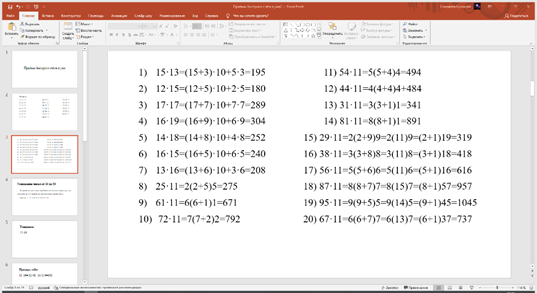
Фото 2. Ответы на примеры.

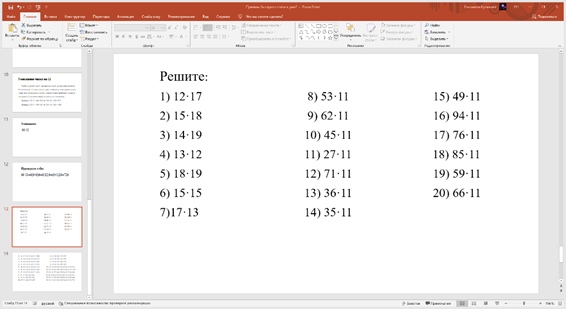
Фото 3. Примеры теста. Март  2022 г.

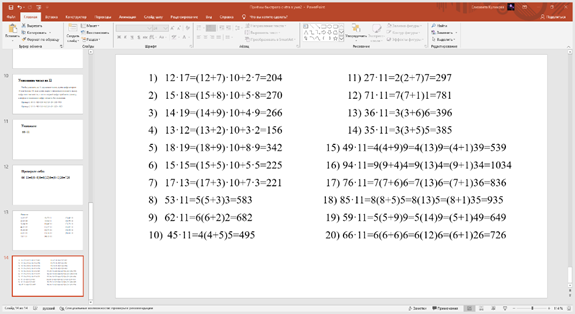
Фото 4. Ответы на примеры

Приложение 3

Таблица 1.

Диаграмма 1

Скачано с www.znanio.ru