
Проект учащихся по теме: «Многогранники».
Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Тема " Многогранники " одна из основных тем в школьном курсе геометрии. Эта тема имеет яркие приложения, в том числе в живописи, архитектуре. Кроме этого в ней, по образному выражению академика А.Д. Александрова сочетаются "Лёд" и "Пламя, т. е. живое воображение и строгая логика.
Человек проявляет интерес к правильным многоугольникам и многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие – в виде вирусов, которые можно рассмотреть с помощью электронного микроскопа.
Что такое правильный многогранник? Правильным называется такой многогранник, все грани которого равны (или конгруэнтны) между собой и при этом являются правильными многоугольниками. Сколько же существует правильных многогранников? На первый взгляд ответ на этот вопрос очень простой – столько же, сколько существует правильных многоугольников. Однако это не так. В «Началах Евклида» мы находим строгое доказательство того, что существует только пять выпуклых правильных многогранников, а их гранями могут быть только три типа правильных многоугольников: треугольники, квадраты и пентагоны (правильные пятиугольники).
Теории многогранников посвящено много книг. Одной из наиболее известных является книга английского математика М. Венниджера «Модели многогранников». В русском переводе эта книга опубликована издательством «Мир» в 1974 г.
Книга начинается с описания так называемых правильных многогранников, то есть многогранников, образованных простейшими правильными многоугольниками одного типа.
Эти многогранники принято называть Платоновыми телами (Рис. 1), названными так в честь древнегреческого философа Платона, который использовал правильные многогранники в своей космологии.

Платон (427-347 годы до н.э.)
Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и углы которых равны, причем грани - правильные многоугольники.
Платоновы тела - трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида.
Действительно, можно сконструировать только пять правильных многогранников — платоновых тел — это тетраэдр, куб, октаэдр, икосаэдр и додэкаэдр. В таблице представлены параметры, полностью характеризующие эти многогранники. Первые четыре тела были описаны Платоном (около 420-347 гг. до н.э.), хотя их знали и пифагорейцы за несколько веков до него. Предполагается, что додэкаэдр был открыт Гиппархом (? — после 127 г. до н.э.).
Все платоновы тела встречаются в природе: тетраэдр, куб и октаэдр — как элементарные формы кристаллов, а икосаэдр и додэкаэдр — квазикристаллов; форму икосаэдра и додэкаэдра имеют также некоторые вирусы. Платон, а за ним и многие другие мыслители, включая Кеплера, связывали платоновы тела с «элементами всего сущего»: тетраэдр — с огнем, куб — с землей, октаэдр — с воздухом, икосаэдр — с водой и додэкаэдр — с космосом. Важнейшим свойством каждого из платоновых тел является высокая степень симметрии.

(а)

(б) (в)
(г) (д)
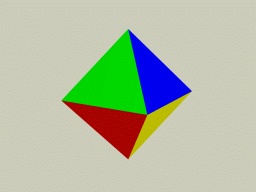
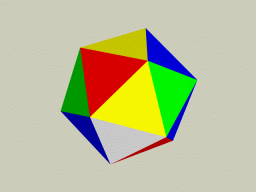
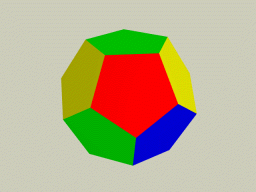
Рис 1. Платоновы тела:
(а) тетраэдр («Огонь»), (б) гексаэдр или куб («Земля»),
(в) октаэдр («Воздух»), (г) икосаэдр («Вода»), (д) додекаэдр («Вселенский разум»)
Начнем рассмотрение с правильных многогранников, гранями которых являются равносторонние треугольники. Первый из них – это тетраэдр (Рис.1-а). В тетраэдре три равносторонних треугольника встречаются в одной вершине; при этом их основания образуют новый равносторонний треугольник. Тетраэдр имеет наименьшее число граней среди Платоновых тел и является трехмерным аналогом плоского правильного треугольника, который имеет наименьшее число сторон среди правильных многоугольников.
Следующее тело, которое образуется равносторонними треугольниками, называется октаэдром (Рис.1-в). В октаэдре в одной вершине встречаются четыре треугольника; в результате получается пирамида с четырехугольным основанием. Если соединить две такие пирамиды основаниями, то получится симметричное тело с восемью треугольными гранями – октаэдр.
Теперь можно попробовать соединить в одной точке пять равносторонних треугольников. В результате получится фигура с 20 треугольными гранями – икосаэдр (Рис.1-г).
Следующая правильная форма многоугольника – квадрат. Если соединить три квадрата в одной точке и затем добавить еще три, мы получим совершенную форму с шестью гранями, называемую гексаэдром или кубом (Рис. 1-б).
Наконец, существует еще одна возможность построения правильного многогранника, основанная на использовании следующего правильного многоугольника – пентагона. Если собрать 12 пентагонов таким образом, чтобы в каждой точке встречалось три пентагона, то получим еще одно Платоново тело, называемое додекаэдром (Рис.1-д).
Следующим правильным многоугольником является шестиугольник. Однако если соединить три шестиугольника в одной точке, то мы получим поверхность, то есть из шестиугольников нельзя построить объемную фигуру. Любые другие правильные многоугольники выше шестиугольника не могут образовывать тел вообще. Из этих рассуждений вытекает, что существует только пять правильных многогранников, гранями которых могут быть только равносторонние треугольники, квадраты и пентагоны.
Существуют удивительные геометрические связи между всеми правильными многогранниками. Так, например, куб (Рис.1-б) и октаэдр (Рис.1-в) дуальны, т.е. получаются друг из друга, если центры тяжести граней одного принять за вершины другого и обратно. Аналогично дуальны икосаэдр (Рис.1-г) идодекаэдр (Рис.1-д). Тетраэдр (Рис.1-а) дуален сам себе. Додекаэдр получается из куба построением «крыш» на его гранях (способ Евклида), вершинами тетраэдра являются любые четыре вершины куба, попарно не смежные по ребру, то есть из куба могут быть получены все остальные правильные многогранники. Сам факт существования всего пяти действительно правильных многогранников удивителен — ведь правильных многоугольников на плоскости бесконечно много!
Основными числовыми характеристиками Платоновых тел является число сторон грани m, число граней, сходящихся в каждой вершине, m, число граней Г, число вершин В, число ребер Р и число плоских углов У на поверхности многогранника Эйлер открыл и доказал знаменитую формулу
В — Р + Г = 2,
связывающего числа вершин, ребер и граней любого выпуклого многогранника. Указанные выше числовые характеристики приведены в Табл. 1.
|
Многогранник |
Число сторон грани, m |
Число граней, сходящихся в вершине, n |
Число граней Г |
Число вершин В |
Число ребер Р |
Число плоских углов на поверхности У |
|
Тетраэдр |
3 |
3 |
4 |
4 |
6 |
12 |
|
Гексаэдр (куб) |
4 |
3 |
6 |
8 |
12 |
24 |
|
Октаэдр |
3 |
4 |
8 |
6 |
12 |
24 |
|
Икосаэдр |
3 |
5 |
20 |
12 |
30 |
60 |
|
Додекаэдр |
5 |
3 |
12 |
20 |
30 |
60 |
Рассмотренные выше правильные многогранники получили название Платоновых тел, так как они занимали важное место в философских школой концепции Платона об устройстве мироздания.
Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.
Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики – это правильный невыпуклый или звездчатый пятиугольник. Пентаграмма, на языке математики - это правильный невыпуклый или звездчатый пятиугольник.
Пентаграмме присваивалось способность защищать человека от злых духов. Существование только пяти правильных многогранников относили к строению материи и Вселенной.
Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды.
Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.
|
Четыре многогранника олицетворяли в ней четыре сущности или «стихии». Тетраэдр символизировал Огонь, так как его вершина устремлена вверх; Икосаэдр — Воду, так как он самый «обтекаемый» многогранник; Куб — Землю, как самый «устойчивый» многогранник; Октаэдр — Воздух, как самый «воздушный» многогранник. Пятый многогранник, Додекаэдр, воплощал в себе «все сущее», «Вселенский разум», символизировал все мироздание и считался главной геометрической фигурой мироздания.
Гармоничные отношения древние греки считали основой мироздания, поэтому четыре стихии у них были связаны такой пропорцией: земля/вода = воздух/огонь. Атомы «стихий» настраивались Платоном в совершенных консонансах, как четыре струны лиры. Напомним, что консонансом называется приятное созвучие. В связи с этими телами уместно будет сказать, что такая система элементов, включавшая четыре элемента — землю, воду, воздух и огонь, — была канонизирована Аристотелем. Эти элементы оставались четырьмя краеугольными камнями мироздания в течение многих веков. Вполне возможно отождествить их с известными нам четырьмя состояниями вещества — твердым, жидким, газообразным и плазменным.
Таким образом, представление о «сквозной» гармонии бытия древние греки связывали с ее воплощением в Платоновых телах.
Влияние знаменитого греческого мыслителя Платона сказалось и на Началах Евклида. В этой книге, которая на протяжении веков была единственным учебником геометрии, дано описание «идеальных» линий и «идеальных» фигур.
Самая «идеальная» линия – прямая, а самый «идеальный» многоугольник – правильный многоугольник, имеющий равные стороны и равные углы. Простейшим правильным многоугольником можно считать равносторонний треугольник, поскольку он имеет наименьшее число сторон, которое может ограничивать часть плоскости.
Не случайно, что один из авторов открытия фуллеренов, Нобелевский лауреат Гарольд Крото в свой Нобелевской лекции начинает свой рассказ о симметрии как «основе нашего восприятия физического мира» и ее «роли в попытках его всестороннего объяснения» именно с Платоновых тел и «элементов всего сущего»: «Понятие структурной симметрии восходит к античной древности...»
Кроме того, платоновым телам близки тела Кеплера-Пуансо, или правильные однородные невыпуклые многогранники
Известно еще множество
совершенных тел, получивших название полуправильных многогранников или Архимедовых
тел. У них также все многогранные углы равны и все грани – правильные
многоугольники, но несколько разных типов. Существует 13 полуправильных
многогранников, открытие которых приписывается Архимеду. Архимед (287 г.
до н.э. – 212 г. до н.э)
Архимед (287 г.
до н.э. – 212 г. до н.э)
Множество Архимедовых тел можно разбить на несколько групп. Первую из них составляют пять многогранников, которые получаются из Платоновых тел в результате их усечения. Усеченное тело – это тело с отрезанной верхушкой. Для Платоновых тел усечение может быть сделано таким образом, что и получающиеся новые грани и остающиеся части старых будут правильными многоугольниками.
К примеру, тетраэдр (Рис. 1-а) можно усечь так, что его четыре треугольные грани превратятся в четыре гексагональные, и к ним добавятся четыре правильные треугольные грани. Таким путем могут быть получены пять Архимедовых тел: усеченный тетраэдр, усеченный гексаэдр (куб), усеченный октаэдр, усеченный додекаэдр и усеченный икосаэдр (Рис. 2).
|
|
|
|
|
(а) |
(б) |
(в) |
|
|
|
|
(г) |
(д) |
Рис 2.
Архимедовы тела: (а) усеченный тетраэдр, (б) усеченный куб, (в) усеченный октаэдр, (г) усеченный додекаэдр, (д) усеченный икосаэдр
В своей Нобелевской лекции американский ученый Смолли, один из авторов экспериментального открытия фуллеренов, говорит об Архимеде (287-212 гг. до н.э.) как о первом исследователе усеченных многогранников, в частности, усеченного икосаэдра, правда, оговариваясь, что возможно Архимед присваивает себе эту заслугу и, возможно, икосаэдры усекали задолго до него. Достаточно упомянуть найденные в Шотландии и датированные около 2000 г. до н.э. сотни каменных предметов (по всей видимости, ритуального назначения) в форме сфер и различных многогранников (тел, ограниченных со всех сторон плоскими гранями), включая икосаэдры и додекаэдры.
Оригинальная работа Архимеда, к сожалению, не сохранилась, и ее результаты дошли до нас, что называется, «из вторых рук». Во времена Возрождения все Архимедовы тела одно за другим были «открыты» заново. В конце концов, Кеплер в 1619 г. в своей книге «Мировая гармония» («Harmonice Mundi») дал исчерпывающее описание всего набора архимедовых тел — многогранников, каждая грань которых представляет собой правильный многоугольник, а все вершины находятся в эквивалентном положении (как атомы углерода в молекуле С60).
Кеплер первым опубликовал полный список тринадцати Архимедовых тел и дал им те названия, под которыми они известны поныне.
Архимедовы тела состоят не менее, чем из двух различных типов многоугольников, в отличие от 5 Платоновых тел, все грани которых одинаковы (как в молекуле С20, например).
Конструирование Архимедового усеченного икосаэдра из
Платонового икосаэдра
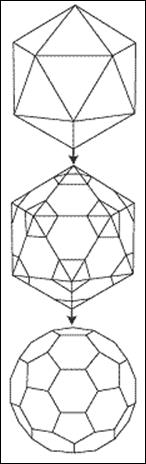 Рис 3.
Рис 3.
Итак, как же сконструировать Архимедов усеченный икосаэдр из Платонова икосаэдра? Ответ иллюстрируется с помощью рис. 3. Действительно, как видно из Табл. 1, в любой из 12 вершин икосаэдра сходятся 5 граней. Если у каждой вершины отрезать (отсечь) 12 частей икосаэдра плоскостью, то образуется 12 новых пятиугольных граней. Вместе с уже имеющимися 20 гранями, превратившимися после такого отсечения из треугольных в шестиугольные, они составят 32 грани усеченного икосаэдра. При этом ребер будет 90, а вершин 60.
Другую группу Архимедовых тел составляют два тела, именуемые квазиправильными многогранниками. Частица «квази» подчеркивает, что грани этих многогранников представляют собой правильные многоугольники всего двух типов, причем каждая грань одного типа окружена многоугольниками другого типа. Эти два тела носят название ромбокубооктаэдром и икосододекаэдром (Рис.4).
|
|
|
|
(а) |
(б) |
Рис. 4. Архимедовы тела: (а) ромбокубооктаэдр, (б) икосододекаэдр
|
|
|
|
(а) |
(б) |
Рис. 5. Архимедовы тела: (а) кубооктаэдр, (б) ромбоикосододекаэдр
Наконец, существуют две так называемые «курносые» модификации – одна для куба (курносый куб), другая – для додекаэдра (курносый додекаэдр) (Рис. 6).
|
|
|
|
(а) |
(б) |
Рис. 6. Архимедовы тела: (а) курносый куб, (б) курносый додекаэдр
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.