Проектная работа "Возникновение отрицательных чисел, их применение в математике и других науках"

МАОУ «Уральская основная школа»

Проектная работа

 

«Возникновение отрицательных чисел, их применение в математике и других науках»

 

 

 

 

 

 

 

 

 

Выполнил: Мазунина Ульяна 6 класс

Руководитель: Субботина Анна Николаевна

 

Жебреи, 2017

Содержание

 

1. Введение

1.1. Обоснование выбранной темы.

1.2. Цель и задачи проекта

2. История возникновения отрицательных чисел.

2.1. Первые представления об отрицательных числах.

2.2. Общепризнанное объяснение отрицательного числа сегодня.

3. Применение отрицательных чисел в математике и других науках.

3.1. В математике и физике (задачи на движение, координаты).

3.2. В математике и географии (температура, глубина, высота).

3.3. В истории.

3.4. В биологии.

4. Заключение.

5. Литература и интернет ресурсы.

 

 

 

 

 

 

 

 

 

 

 

 

1. Введение

«Твой ум без числа ничего не представляет». Это высказывание немецкого философа Н. Кузанского (1401 – 1464) показывает какую роль, играют любые числа в нашей жизни, поэтому тема «отрицательные числа» актуальна.

В шестом классе мне поручили сообщение «История возникновения отрицательных чисел». Изучая литературу, я понял, что отрицательные числа возникли из практических нужд людей. С их появлением произошел большой толчок развития науки. В моем представлении было самое маленькое число 0, т.е. ничего, а оказывается, что есть еще числа меньше 0. Мне захотелось понять суть отрицательных чисел, для чего они нужны людям и я решил перелистать школьные учебники, выяснить применение отрицательных чисел на различных уроках.

Мне кажется, что использование отрицательных чисел математиками, физиками и другими учеными дало им дополнительный простор для исследований и открытий, и мне захотелось разобраться, какие возможности для науки открыли отрицательные числа.

Цель работы: Изучить историю возникновения отрицательных

чисел, и исследовать применение отрицательных чисел для научных и практических потребностей людей.

Задачи:

1. Изучить литературу по данной теме.

2. Понять суть отрицательных чисел.

3.Рассмотреть историю возникновения отрицательных чисел.

3. Исследовать применение отрицательных чисел в математике и других науках (физике, географии, истории и биологии).

4.Сделать сообщение учащимся шестых классов.

 

 

 

 

 

 

 

 

 

2.История возникновения отрицательных чисел.

Мы считаем отрицательные числа чем-то естественным, но так было не всегда.

2.1. Первые представления об отрицательных числах возникли еще до нашей эры. Так, во II в. до н.э. китайский ученый Чжан Цань в книге «Арифметика в девяти главах» проводит правила действий с отрицательными числами, которые он понимает как долг, а положительные как имущество. Действия с отрицательными числами проводили, используя рассуждения о долге.

Например, если к одному долгу прибавить другой долг, то в результате получится долг, а не имущество. Знака минус тогда не знали, поэтому, чтобы отличить числа, выражавшие долг, Чжань Цань писал их другими чернилами, чем числа, выражавшие имущество (положительные).

Положительные количества в китайской математике называли “чжен”, отрицательные – “фу”. Их изображали разными цветами: “ чжен” - красным, “ фу” - черным. Такой способ изображения использовался в Китае до середины ХII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел - цифры, которые изображали отрицательные числа перечеркивали черточкой справа налево.

III в. н.э. древнегреческий математик Диофант фактически пользовался отрицательными числами, рассматривая их как «вычитаемые», а положительные как «прибавляемые».

В древности индийские ученые использовали отрицательные числа в торговых расчетах. Если вы имеете 3000 рублей и покупаете товар на 1000 рублей, то у вас остается 3000 – 1000 = 2000 рублей. Но если вы имеете 3000 рублей и покупаете товар на 5000 рублей, то у вас образуется долг 2000 рублей. Поэтому, в этом случае считали, что совершается вычитание 3000 – 5000, результатом является число 2000 со знаком «минус», означающее «две тысячи долга». Таким образом, – 2000 это отрицательное

число и в данном случае оно указывает на то, что у вас образовался долг 2000 рублей.

Индийский математик Брамагупта и астронома Брахмагупты (598 – около 660 гг.) в VII в. сформулировал правила действий над положительными и отрицательными числами.

В произведении выдающегося индийского математика говорится:

«Имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль…

Долг, который отнимают от нуля, становится имуществом, а имущество – долгом».

В Европе отрицательные числа появились благодаря

Леонардо Пизанскому (Фибоначчи), который тоже

ввёл его для решения финансовых задач с

долгами – в 1202 году он впервые использовал

отрицательные числа для подсчёта своих убытков.

Теория отрицательных чисел долго находилась в стадии становления и вплоть до XIX века математики часто отбрасывали в своих вычислениях отрицательные числа, считая их бессмысленными.

В XVII веке знаменитый французский математик Блез Паскаль утверждал, что 0-4=0 ибо нет такого числа, которое может быть меньше ничего.

Оживлённо обсуждался парадокс Арно.

Антуан Арно - французский философ и математик, друг Блеза Паскаля. Известен его учебник элементарной геометрии «Новые начала геометрии». Занимался также составлением магических квадратов.

Парадокс Арно: справедлива ли пропорция 1 : (-1) = (-1) : 1?

Здесь и левое и правое отношения равны -1, но в первом отношении предшествующий член больше предыдущего, а во втором меньше.

В Западной Европе отрицательные числа начинают использоваться примерно лишь с XIII в. При этом они обозначались словами или сокращенными словами как наименования в именованных числах. Только вначале XIX в. отрицательные числа получили всеобщее признание и современную форму обозначения.

Более современный пример можно привести, используя действия с телефонным балансом. Если на вашем счету было 200 рублей, а вы «наговорили» на 300 рублей, то на вашем счету образуется отрицательный баланс -100 рублей (минус 100 рублей). Это значит, что теперь телефонной компании вы должны 100 рублей.

Введение отрицательных чисел было связано с необходимостью развития математики как науки, дающей общие способы решения арифметических задач, независимо от конкретного содержания и исходных числовых данных. Необходимость введения в алгебру отрицательных чисел возникает уже при решении задач, сводящихся к линейным уравнениям с одним неизвестным. В индии еще в 6-11 вв. отрицательные числа систематически применялись при решении задач и истолковывались в основном так же, как это делается в настоящее время.

В европейской науке отрицательные числа окончательно вошли в употребление лишь со времени Французского математика Р.Декарта (1596 – 1650), давшего геометрическое истолкование отрицательным числам как направленных отрезков.

В 1637 году он ввел «координатную прямую».

Декарт и его последователи признавали их направление с положительными.

Но в действиях над отрицательными числами не все было ясно (например, умножение на них). Среди ученых разгорелся большой и долгий спор о сущности отрицательных чисел о том, признать отрицательные числа числами действительными или нет.

Спор этот после Декарта продолжался около 200 лет.

Полная и строгая теория отрицательных чисел была создана в XIX веке ирландским ученым и физиком Уильямом Гамильтоном и немецким математиком и филологом Германом Грассманом.

 

2.2. На сегодняшний день общепризнанное объяснение отрицательного числа следующее:

Это элемент множества отрицательных чисел, действительное число, меньшее нуля.

Все отрицательные числа, и только они, меньше, чем ноль.

Для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n, которое дополняет n до

нуля: n + (-n) = 0.

Оба числа называются противоположными друг для друга.

Вычитание целого числа a из другого целого числа b равносильно сложению b с противоположным для a: b – a = b + (-a)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.Применение отрицательных чисел в математике и других науках.

 

В математической науке отрицательные числа необходимы для решения задач и уравнений с любыми исходными числовыми данными. При вычислении высоты здания, расстояния от школы до дома, массы и температуры человеческого тела, скорости автомобиля, объема банки, силы

электрического тока, продолжительности урока или перемены — все это примеры применения отрицательных чисел, как в математике, так и в других науках.

 

 

3.1. В математике и физике (задачи на движение, координаты).

С решением задач на движение мы встречаемся как в начальной, так и в старшей школе.

Рассмотрю положительные и отрицательные числа на скоростном шоссе

при решении задач «Отрицательные числа на скоростном шоссе». Понаблюдаем за движением автомашин по шоссе, стоя на обочине лицом к дороге. Два потока машин несутся навстречу друг другу.

Вот, например, зеленый «Форд» проносится мимо нас со скоростью

100 км /ч, а грузовик движется со скоростью 70 км/ч.

Но этих чисел не достаточно, если мы хотим указать ещё и направление движения. Действительно, мы ведь должны ещё добавить, что «Форд» едет вправо, а грузовик - влево.

Таким образом, чтобы охарактеризовать движение автомобиля по шоссе,

надо не только указать, как быстро он дет (то есть указать величину его скорости), но и дополнительно пояснить, куда, в каком направлении он едет - вправо или влево.

Поэтому говорят, скорость автомобилей, движущихся вправо, считать положительной, а скорость автомобилей, движущихся влево, - отрицательной. То есть знак числа будет указывать направление скорости (направление движения) автомобилей.

Отметим, что «положительное» направление движения можно выбирать произвольно.

Например, можно было бы положительным считать скорости автомобилей, движущихся влево. Тогда скорости автомобилей, движущихся вправо, выражались бы отрицательными числами.

Широкое применение положительные и отрицательные числа получили со времени французского математика Рене Декарта при изучении тем «Координатная прямая» и «Координатная плоскость». При построении точек, графиков функций и решении геометрических задач

 

 

 

 

 

3.2.        В математике, географии и физике (температура, глубина, высота).

 

С решение задач «Положительные и отрицательные числа по температурной шкале» мы встречаемся ни только на уроках математики, но и на уроках географии, а с 7 класса и физике.

Например, применение шкалы с положительными и отрицательными числами в термометре упрощает работу с данными: не нужно пояснять «10 градусов выше нуля» или «15 градусов ниже нуля», можно использовать данные для формул и вычислений.

Знаменитое отрицательное число: −273,15°C.

Это абсолютный ноль температуры - минимальное значение температуры на земле (0 градусов по шкале Кельвина).

Холодно и тепло. Что это значит?

Посмотрим на шкалу обычного уличного термометра.

Она имеет вид, изображенный на шкале 1.

На ней нанесены только положительные числа,

и поэтому при указании численного значения

температуры приходится дополнительно пояснять

20 градусов тепла (выше нуля).

Это для физиков неудобно – ведь слова в формулу не подставишь! Поэтому в физике применяется  шкала с отрицательными числами. Если на улице тепло, то температура воздуха  выражена положительным числом, а если на улице холодно – отрицательным числом.

Температура льда выражается отрицательным числом Используя знания коордитной плоскости, определяем географические координаты.

 

 

 

 

 

 

 

 

 

 

 

 

 

Используя знания коордитной плоскости, определяем географические координаты.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Положительные и отрицательные числа на горных вершинах и в морских глубинах.

 

Посмотрим на физическую карту мира. Участки суши на ней раскрашены различными оттенками зеленого и коричневого цветов, а моря и океаны раскрашены голубым и синим. Каждому цвету соответствует своя высота (для суши) или глубина (для морей и океанов). На карте нарисована шкала глубин и высот, которая показывает, какую высоту (глубину) означает тот или иной цвет, например, такая:

Шкала глубин и высот в метрах

 

На этой шкале мы видим только положительные числа и нуль. За нуль принимается высота (и глубина тоже), на которой находится поверхность воды в Мировом океане.

Однако для физика или для математика эта шкала неудобна, так как все числа в ней положительные.

Поэтому применяется шкала с положительными числами для точек выше уровня моря и отрицательными числами для тех точек, которые ниже уровня моря. Использование этой шкалы на физике получает иной вид, обычно используют шкалу в таком виде.

 

 

Шкала 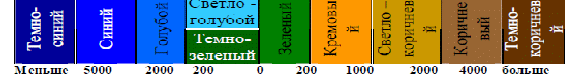высот в метрах

 

 

 

 

 

 

 

 

 

 

 

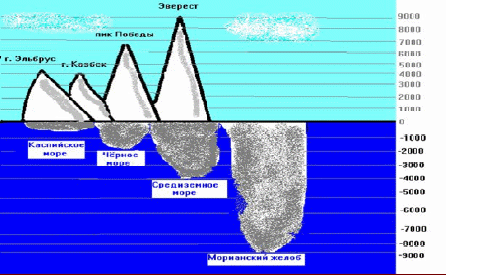
Используя такую шкалу, достаточно указать число без всяких дополнительных слов: положительные числа отвечают различным местам на суше, находящимся над поверхностью моря; отрицательные числа соответствуют точкам, находящимся под поверхностью моря.

В рассмотренной нами шкале высот за нулевую отметку принимается высота поверхности воды в Мировом океане. Эта шкала используется в геодезии и картографии. В отличие от этого, в быту мы обычно за нулевую высоту принимаем высоту поверхности земли (в том месте, в котором мы находимся).

 

 

3.3 Отрицательные числа в истории.

Как в древности считали года? В разных странах по-разному.

Например, в Древнем Египте каждый раз, когда начинал править новый царь, счёт лет начинался заново. Первый год правления царя считался первым годом, второй – вторым и так далее. Когда этот царь умирал и к власти приходил новый, вновь наступал первый год, затем второй, третий. Иным был счет лет, применявшийся жителями одного из древнейших городов мира-Рима. Год основания своего города римляне считали первым, следующий -вторым и так далее.

Счет лет, которым мы пользуемся, возник давно и связан с почитанием Иисуса Христа – основателя христианской религии.

Счёт лет от рождения Иисуса Христа постепенно был принят в разных странах. В нашей стране он введён царём Петром Первым триста лет назад. Время, исчисляемое от Рождества Христова, мы называем НАША ЭРА (а пишем сокращённо Н.Э.).

Мы говорим такие выражения:«Пифагор жил в 4 веке до нашей эры»,

«Русь находилась под игом монголо -татар в течении 13-15 веков нашей эры» «В 2014 году зимняя олимпиада пройдёт в Сочи». Продолжается наша эра две тысячи лет. Рассмотрим «линию времени» на рисунке.

«Линия времени»

Так выглядит история возникновения отрицательных чисел

на «Линии времени»

 

 

 

 

3.4.          Отрицательные числа в биологии.

 

Отрицательные числа в биологии выражают патологию глаза.

 

K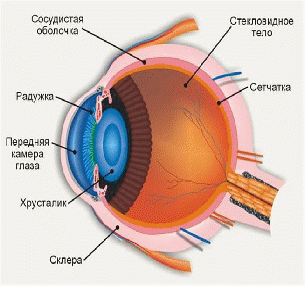ОО Отрица

 

 

 

 

ицатеисла в биологии выражают патологию глаза

 

. Близорукость (миопия) проявляется снижением остроты зрения.

 

 

 

Для того, чтобы при близорукости глаз мог ясно видеть отдаленные предметы применяют рассеивающие (отрицательные) линзы. Положительные числа означают дальнозоркость.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4. Заключение.

 

Выполняя данную работу, я значительно расширил знания по математике. Древнегреческий философ Платон прав своим утверждением «Мы…никогда не стали бы разумными, если бы исключили число из человеческой природы». Понять суть отрицательных чисел без истории их возникновения немыслимо. Подготовил сообщение и презентацию по теме «Отрицательные числа», сделал сообщение в своем классе. Работая со школьными учебниками, я выяснил, что отрицательные числа больше всего встречаются в точных науках, в математике и физике.

В физике отрицательные числа возникают в результате измерений, вычислений физических величин. Встречаются они в истории, географии и биологии. В таких науках, как география и истории, отрицательное число можно заменить словами, например, ниже уровня моря, а в истории – 157 лет до н.э.

Меня удивило, что даже философов в средние века волновала тема отрицательных чисел: они спорили, можно ли говорить о том, что меньше ничего (меньше нуля).

Мне кажется, что самым важным в применении отрицательных чисел является то, что без них многие математические задачи и уравнения не имели бы решения.

 

 

 

 

 

 

 

 

 

 

 

 

 

mi5. Литература и интернет ресурсы.

 

1.       Свободная интернет-энциклопедия http://ru.wikipedia.org/

2.       Фридман Л.М. «Изучаем математику», учебное издание, 1994

3.       Большая научная энциклопедия, 2005.

4.       Детская научная энциклопедия «Я познаю мир», Москва, «Просвещение», 1995г.

5.       Глейзер Г.И. «История математики в школе», Москва, «Просвещение»,1981г