Содержание 

1. Введение.                                                  3-4

2. Бенуа Мандельброт- отец современной фрактальной теории.    5-6

3. Что такое «фрактал»?                                        7

4. Классификация фракталов.                                    8

4.1 Алгебраические фракталы.                             9-10 4.2 Геометрические фракталы.                            11-12

4.3 Природные фракталы.                                 13-14

5. Применение фракталов.                                    15-16

6. Программы для создания изображений фракталов.            17-18         

7. Заключение.                                                19

Приложение: СD-диск: «Галерея фракталов», программы JFPCreator,    Ultra Fractal, Apophysis.

Введение

Почему геометрию часто называют холодной и сухой? Одна из причин заключается в её неспособности описать форму облака, горы, дерева или берега моря. Облака — это не сферы, горы — это не конусы,  линяя берега — это не окружности, и кора не является   гладкой, и молния не распространяется по прямой…   Природа демонстрирует нам не просто более  высокую

степень, а совсем другой уровень сложности.  Число различных масштабов длин в структурах всегда бесконечно.

Бенуа Мандельброт

   Большинство систем в природе сочетают два свойства: во-первых, они очень велики, часто многогранны, многообразны и сложны, а вовторых они формируются под действием очень небольшого количества простых закономерностей, и далее развиваются, подчиняясь этим простым закономерностям.

   Это самые разные системы, начиная от кристаллов и просто кластеров (различного рода скоплений, таких как облака, реки, горы, материки, звёзды), заканчивая экосистемами и биологическими объектами (от листа папоротника до человеческого мозга). Фракталы являются как раз такими объектами: с одной стороны — сложные (содержащие бесконечно много элементов), с другой стороны — построенные по очень простым законам. Благодаря этому свойству, фракталы обнаруживают много общего со многими природными объектами. Но фрактал выгодно отличается от природного объекта тем, что фрактал имеет строгое математическое определение и поддаётся строгому описанию и анализу.

Поэтому теория фракталов позволяет предсказать скорость роста корневых систем растений, трудозатраты на осушение болот, зависимость массы соломы от высоты побегов и многое другое.    Это новое направление в математике, совершившее в научной парадигме переворот, сравнимый по значимости с теорией относительности и квантовой механикой. Объекты фрактальной геометрии по своему внешнему виду резко отличаются от привычных нам 'правильных' геометрических фигур. Фактически, это прорыв в математическом описании систем, которые на протяжении долгого времени такому описанию не поддавались. Фрактальные множества обладают рядом необычных характеристик. Так, при 'макроскопическом' измерении их длины она зависит от длины отрезка, которым проводится измерение. При аналитическом вычислении часто оказывается, например, что длина бесконечна, а площадь равна нулю. Следовательно, такие объекты не могут считаться ни одномерными, ни двумерными. Для них разработано понятие размерности, способной принимать дробные значения.    Фрактальная геометрия не есть "чистая" геометрическая теория. Это скорее концепция, новый взгляд на хорошо известные вещи, перестройка восприятия, заставляющая исследователя по новому видеть мир.

   Современные математические модели настолько красивы и загадочны, что могут свести с ума впечатлительного студента и ученого. Разноцветные изображения фракталов поражают своей совершенной гармонией. В своей работе я хотела бы показать мир фракталов, его красоту и неизведанность. Все выше сказанное и определило цели и задачи работы.

Цель работы:

-познакомиться с понятием «фрактал» и сферами применения в жизни человека.

 Задачи работы:

-узнать что такое фрактал, классификацию фракталов;

-познакомиться с биографией создателя фракталов – Бенуа  

Мандельброта;

-изучить построение треугольника Серпинского и снежинки Коха;

-понять, как фракталы используются в разных сферах жизни человека; -изучить некоторые программы генерации фрактальных изображений; -собрать галерею фракталов.

Математика, 

если на нее правильно посмотреть,  отражает не только истину,  но и несравненную красоту.  Бертранд Рассел.

Бенуа Мандельброт - отец современной фрактальной  теории.

 Бенуа Мандельброт

   Бенуа Мaндельброт родился в Варшаве 20 ноября 1924 году в семье литовских евреев. Но уже в 1936 году семья Бенуа Мандельброта эмигрировала во Францию, в Париж. В Париже он попал под влияние своего дяди Шолема Мандельбройта, известного парижского математика, члена группы математиков, известной под общим псевдонимом «Николя Бурбаки».

   После начала войны Мандельброты бежали на свободный от оккупации юг Франции, в городок Тюль. Там Бенуа Мандельброт пошел в школу, но вскоре потерял интерес к учебе. Поэтому к шестнадцати годам он еле знал алфавит и таблицу умножения до пяти.    Но у Бенуа Мандельброта открылся необычный математический дар, который позволил ему сразу после войны стать студентом Сорбонны. Оказалось, что у Бенуа великолепное пространственное воображение. Он даже алгебраические задачи решал геометрическим способом. Оригинальность его решений позволила Бенуа Мандельброту поступить в университет.

   Окончив университет, Бенуа Мандельброт сначала стал «чистым математиком». Он получил докторскую степень.

   В 1958 он переехал в США, где приступил к работе в научноисследовательском центре IBM в Йорктауне, поскольку IBM в то время занималась как раз интересными Бенуа Мандельброту областями математики.

   Работая в IBM, Бенуа Мандельброт ушел далеко в сторону от чисто прикладных проблем компании. Он работал в области лингвистики, теории игр, экономики, аэронавтики, географии, физиологии, астрономии, физики. Ему нравилось именно переключаться с одной темы на другую, изучать различные направления.    Исследуя экономику, Бенуа Мандельброт обнаружил, что произвольные внешне колебания цены могут следовать скрытому математическому порядку во времени, который не описывается стандартными кривыми.

   Бенуа Мандельброт занялся изучением статистики цен на хлопок за большой период времени (более ста лет). Колебания цен в течение дня казались случайными, но Мандельброт смог выяснить тенденцию их изменения. Он проследил симметрию в длительных колебаниях цены и колебаниях кратковременных. Это открытие оказалось неожиданностью для экономистов.

   По сути, Бенуа Мандельброт применил для решения этой проблемы зачатки своего рекурсивного (фрактального) метода.    Само понятие «фрактал» придумал сам Бенуа Мандельброт (от латинского fractus, означающего «сломанный, разбитый»).[5]    Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора).Впервые множество Мандельброта было описано в 1905 году Пьером Фату (Pierre Fatou), французским математиком, работавшим в области аналитической динамики комплексных чисел. Фату никогда не видел изображений, которые мы сейчас знаем как изображения множества Мандельброта, потому что необходимое количество вычислений невозможно провести вручную. Профессор Бенуа Мандельброт был первым, кто использовал для этого компьютер.

   Фракталы были описаны Мандельбротом в 1975 году в его книге «Les Objets Fractals: Forme, Hasard et Dimension» («Фрактальные объекты: форма, случайность и размерность»). В этой книге Мандельброт впервые использовал термин «фрактал» для обозначения математического феномена, демонстрирующего столь непредсказуемое и удивительное поведение. Эти феномены рождались при использовании рекурсивного алгоритма для получения какой-либо кривой или множества. Множество Мандельброта — один из таких феноменов, названный по имени своего исследователя.

   14 октября 2010 года скончался Бенуа Мандельброт - человек, подаривший миру фрактальную геометрию. Он умер от рака в обычном хосписе в городе Кембридж, штат Массачусетс, в возрасте 85 лет.[9]

 Что такое фрактал.

   Фрактал (от латинского fractus, означающего «сломанный, разбитый») — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность, либо метрическую размерность, строго большую топологической.    Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:

•      Обладает нетривиальной структурой на всех шкалах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведет к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.

•      Является самоподобной или приближенно самоподобной.

•      Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.

•      Может быть построена при помощи рекурсивной процедуры.

Классификация фракталов.

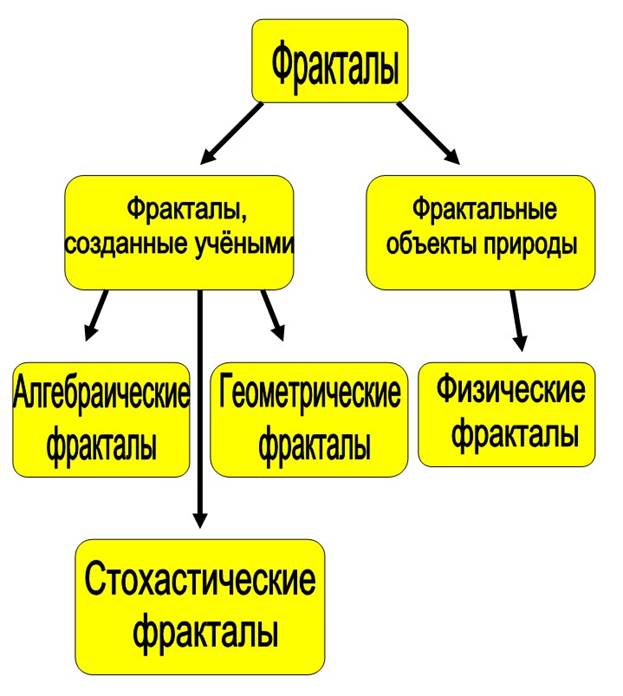
   Для чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации. 

   На рисунке приведена классификация фракталов. В этой классификационной таблице фракталы представлены двумя классами. Один класс представлен "рукотворными" фракталами, другой класс представлен природными фрактальными структурами. К классу "рукотворных" фракталов относятся геометрические, алгебраические и стохастические фракталы. Природные фрактальные структуры представлены физическими фракталами. 

     Алгебраические фракталы.

Построение треугольника Серпинского

   Равносторонний треугольник M₀ делится прямыми, параллельными его сторонам, на 4 равных равносторонних треугольника. Из треугольника удаляется центральный треугольник. Получается множество M₁, состоящее из 3 оставшихся треугольников "первого ранга". Поступая точно так же с каждым из треугольников первого ранга, получим множество M₂, состоящее из 9 равносторонних треугольников второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность.(Приложение №1)

Геометрические фракталы

Построение снежинки Коха.

   Для построения снежинки Коха выполним следующие операции (см. рис. 1). Рассмотрим в качестве нулевой итерации равносторонний треугольник. Затем каждую из сторон этого треугольника разделим на три равные части,уберем среднюю часть и в середине достроим равносторонний треугольник так, как изображено на рис. 1. На следующем шаге такой же процедуре деления на три равные части и достраивания равностороннего треугольника подвергается каждая из сторон новой фигуры, и так до бесконечности. В результате возникает симметричная, похожая на снежинку, бесконечно изломанная кривая, которая представляет собой самоподобное множество, называемое снежинкой Коха.(Приложение №2)

                          1 ЭТАППОСТРОЕНИЯСНЕЖИНКИ           2 ЭТАППОСТРОЕНИЯСНЕЖИНКИ

                      _{3 ЭТАППОСТРОЕНИЯ}СНЕЖИНКИ             4 ЭТАППОСТРОЕНИЯСНЕЖИНКИ

Природные фракталы

   Распространенность фрактальных объектов в природе чрезвычайно велика. Фрактальный характер могут иметь пористые минералы и горные породы; узоры листьев, расположение ветвей деревьев, капиллярная система растений; кровеносная, нервная, лимфатическая и др. системы в организмах животных и человека; реки, облака, линия морского побережья, горный рельеф, "морозные" узоры на стекле, снежинка - природный аналог кривой Коха, биение сердца, волнение моря, распределение пузырьков в приповерхностном слое океана, дно океанов и морей, осадки на дне океана. Фрактальная организация прослеживается в картине разветвления некоторых сердечных мышечных волокон и в так называемой системе Гиса, передающей электрические сигналы от предсердий к желудочкам. Кардиограмма - тоже фрактальная кривая. Природа недаром "любит" фрактальные формы. Это объясняется именно тем, что они получаются путем простого размножения и изменения размеров некого одного элементарного строительного блока.

Применение фракталов.

Компьютерная графика

   Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом картинки сжимаются гораздо лучше, чем это делается обычными методами (такими как jpeg или gif). Другое преимущество фрактального сжатия в том, что при увеличении картинки, не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.

   Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей и т. д.

Физика и другие естественные науки

   В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Также фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

Децентрализованные сети

   Система назначения IP-адресов в сети NETSUKUKU использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети NETSUKUKU хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.

Радиотехника

   Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Оказалось, что такая антенна работает не хуже обычной. И, хотя физические принципы работы такой антенны не изучены до сих пор, это не помешало Коэну основать собственную компанию и наладить их серийный выпуск. 

Дизайн

   Прежде всего, фракталы - область удивительного математического искусства, когда с помощью простейших формул и алгоритмов получаются картины необычайной красоты и сложности! Сейчас стало модным использовать для оригинального и неповторимого оформления дома, офиса, ресторана или клуба  фрактальные изображения.

Программы для создания изображений фракталов.

   Существует множество программ, служащих для генерации фрактальных изображений. Рассмотрим три из них.

1)

JFPCreator - программа демонстрирует очень красивый фрактал Джулия, его бесконечные трансформации при изменении коэффициентов в реальном времени, полноэкранный вид, слайд-шоу. Позволяет и во время трансформации менять параметры палитры и её тип, масштаб и область просмотра. Сохраняет созданные изображения во фрактальном формате (Очень компактно и без потери качества) и в BMP с выбранным разрешением. Форма для расчета и

сохранения в BMP формате позволяет выбрать размер сохраняемого изображения в миллиметрах,сантиметрах, дюймах и метрах, разрешение в dpi.

 2)

 Ultra Fractal - лучшее решение для создания уникальных фрактальных изображений профессионального качества. Пакет отличается дружественным интерфейсом, многие элементы которого напоминают интерфейс Photoshop (что упрощает изучение), и сопровождается невероятно подробной и прекрасно иллюстрированной документацией Созданные изображения можно визуализировать в высоком разрешении, пригодном для полиграфии, и сохранить

в собственном формате программы или в одном из популярных фрактальных форматов. Визуализированные изображения также могут быть экспортированы в один из растровых графических форматов (jpg, bmp, png и psd), а готовые фрактальные анимации - в AVI-формат.  Принцип создания фрактальных изображений достаточно традиционен, самое простое - воспользоваться одной из прилагаемых в поставке формул (сориентироваться относительно возможного вида генерируемого по выбранной формуле изображения поможет встроенный браузер), а затем подредактировать параметры формулы желаемым образом. 

   Однако не стоит думать, что таинство фрактального изображения кроется лишь в удачной формуле. Не менее важны и иные аспекты. Например, цветовая настройка, предполагающая выбор варианта окраски и точную настройку ее параметров. Настройка цвета реализована на уровне солидных графических пакетов, например градиенты можно создавать и настраивать самостоятельно, корректируя множество параметров, включая полупрозрачность, и сохранять их в библиотеке для дальнейшего использования. Применение слоев с возможностью изменения режимов их смешивания и корректировкой полупрозрачности позволяет генерировать многослойные фракталы и за счет наложения фрактальных изображений друг на друга добиваться уникальных эффектов. Использование масок непрозрачности обеспечивает маскирование определенных областей изображения. Фильтры трансформации позволяют выполнять в отношении выделенных фрагментов изображения разнообразные преобразования: масштабировать, зеркально отражать, обрезать по шаблону, искажать посредством завихрения или ряби, размножать по принципу калейдоскопа и т.д.

3)

Apophysis - интересный инструмент для генерации фракталов на основе базовых фрактальных формул. Созданные по готовым формулам фракталы можно редактировать и неузнаваемо изменять, регулируя разнообразные параметры. Так, например, в редакторе их можно трансформировать, либо изменив лежащие в основе фракталов треугольники, либо применив понравившийся метод преобразования: волнообразное искажение, перспективу, размытие по Гауссу и

др. Затем стоит поэкспериментировать с цветами, выбрав один из базовых вариантов градиентной заливки. Список встроенных заливок достаточно внушителен, и при необходимости можно автоматически подобрать наиболее подходящую заливку к имеющемуся растровому изображению, что актуально, например, при создании фрактального фона в том же стиле, что и иные изображения некоего проекта. При необходимости несложно подрегулировать гамму и яркость, изменить фон, масштабировать фрактальный объект и уточнить его расположение на фоне. Можно также подвергнуть результат разнообразным мутациям в нужном стиле. По окончании следует задать размеры конечного фрактального изображения и записать его визуализированный вариант в виде графического файла (jpg, bmp, png). 

Заключение

   Фрактальная наука ещё очень молода, и ей предстоит большое будущее. Задачи, которые открываются перед новой областью математики – фрактальной геометрией, - сложны и многообразны.

   Если раньше ученым приходилось иметь дело, в основном, с числами и формулами, то теперь их работа стала гораздо интереснее. С помощью компьютеров они могут рисовать большие красивые картинки изучаемых явлений. Некоторые из ученых так увлеклись этим, что стали художниками, и сегодня простая любопытность математиков, коей являлись фракталы еще в начале 80-х, превратилась в уважаемый вид искусства. Выставки фрактальных изображений проходят в музеях всего мира, большое количество конкурсов проводится в компьютерной сети Интернет.

   Фракталы стали незаменимыми помощниками астрофизиков, медиков, геологов. Фрактальное моделирование как инструмент для изучения неупорядоченных систем, каковыми являются нефтегазовые месторождения, стало технологической потребностью. Фрактальные модели упрощают анализ движения жидкости или газа, что важно для индустриальных технологий разработки месторождений нефти и газа. Модели, построенные на основе фрактальных изображений, позволяют с большой точностью моделировать космическое пространство и ткани внутренних органов живых организмов.

   Фракталам посвящены тысячи публикаций и огромные ресурсы в международной компьютерной сети Интернет, однако для многих специалистов далеких от информатики данный термин представляется абсолютно новым. Поэтому  фракталы, как объекты, представляющие интерес для специалистов различных отраслей знания, должны получить надлежащее место в курсах математики и информатики.

  ИСТОЧНИКИ ИНФОРМАЦИИ

1)А. А. Кириллов Повесть о двух фракталах. — Летняя школа «Современная математика». — Дубна: 2007.

2)Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.

3)Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.

4)Федер Е. Фракталы. — М: «Мир», 1991.

   Интернет-ресурсы

   5)http://ru.wikipedia.org

   6)http://www.metaphor.ru/er/misc/fractal_gallery.xml

   7)http://www.codenet.ru/progr/fract/Fractals-Around/

   8)http://www.3dfractal.ru/index.php/magazinfractalov

   9) http://lenta.ru/articles/2010/10/18/mandelbrot/