Промежуточная аттестация "Геометрия - 8"

Контрольно- измерительные материалы для проведения промежуточной аттестации по предмету геометрия за курс 8 класса

1. Цель – выявление уровня освоения предметных образовательных результатов в соответствии с требованиями ООП и стандарта.

2. Структура итоговой работы

    Структура КИМ  направлена на решение двух задач: формирования у всех обучающихся базовой математической подготовки, составляющей функциональную основу общего образования, и формирования   математической подготовки    для заданий повышенного уровня.

     В работу входит две части, соответствующие проверке на базовом и повышенном уровнях.

    Первая часть содержит 7 заданий, вторая – 3 задания.

Всего в работе 10 заданий, из которых 7 заданий базового уровня, 3 задания повышенного уровня.

3. Распределение заданий по проверяемым предметным способам действия:

4. Продолжительность диагностической работы

      На выполнение диагностической работы по математике даётся 90 минут.

5. Критерии оценивания:

      Максимальный балл за работу в целом – 13.                                                                        Задания, оцениваемые 1 баллом ( 1 часть), считаются выполненными верно, если указан номер верного ответа (в заданиях с выбором ответа), или вписан верный ответ (в заданиях с кратким ответом).

6. Текст работы. 8 класс.                                                      

               Вариант 1.

Первая часть

1. Выберите верное утверждение:

1) диагональ делит параллелограмм на два равных треугольника;

2) если диагонали параллелограмма равны, то он ромб;

3) в выпуклом четырехугольнике не может быть более двух тупых углов.

Ответ: ______________.

2. Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?

Ответ: ______________.

3.  Найдите вписанный угол АВС, если дуга АС, на которую он опирается, равна 148°.  

Ответ: ______________.

4.    Биссектриса АК угла ВАD параллелограмма АВСD делит сторону ВС  на отрезки ВК = 7 и КС = 5. Найдите периметр этого параллелограмма.

Ответ: ______________.

5.  Диагонали параллелограмма ABCD пересекаются в точке О. Сумма площадей треугольников АОВ и COD равна 5. Найдите площадь параллелограмма.  

1) 7,5;          2) 12,5;         3) 10;          4) 20;            5) 15.

Ответ:____________.

6.  В окружности   с центром О угол между диаметром MN и хордой NK равен 67°. Найдите углы KMN и MOK.

Ответ: ______________.

7.  Девочка про­шла от дома по на­прав­ле­нию на запад 880 м. Затем по­вер­ну­ла на север и про­шла 900 м. После этого она по­вер­ну­ла на во­сток и про­шла ещё 400 м. На каком рас­сто­я­нии (в метрах) от дома ока­за­лась девочка?

Ответ:____________.

Вторая часть

8.  Высоты треугольников МРК и НРК, опущенные на сторону РК, относятся, как 9 : 7. Найдите площадь треугольника НРК, если она на 14 см меньше площади треугольника МРК.

                                                  М                  Н

                                           Р                                К  

9. Катеты прямоугольного треугольника равны 12 см и 16 см. Найдите периметр треугольника, подобного данному, если его площадь равна 24 см².

10. Докажите, что четырехугольник с вершинами в точках А(0;1), В(4;3), С(5;1), D(1;-1) является прямоугольником.

Вариант 2.

Первая часть

1.  Выберите верное утверждение:

1) диагонали параллелограмма делят его на четыре равновеликих треугольника;

2) середины сторон параллелограмма являются вершинами квадрата;

3) биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

Ответ:____________.

2.   Короткое плечо шлаг­бау­ма имеет длину 1 м, а длин­ное плечо – 3 м. На какую вы­со­ту (в метрах) опу­стит­ся конец ко­рот­ко­го плеча, когда конец длин­но­го плеча под­ни­ма­ет­ся на

1,8 м?

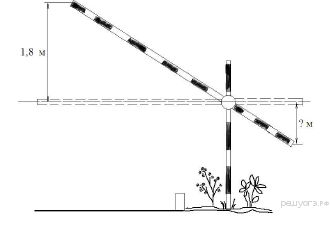
Ответ:____________.

3.  Найдите вписанный угол АВС, если дуга АС, на которую он опирается, равна 288°. 

Ответ:____________.

4.   Биссектриса СК угла ВСD параллелограмма АВСD делит сторону АВ  на отрезки АК = 4 и КВ = 6. Найдите периметр этого параллелограмма.

Ответ:____________.

5.   Диагонали параллелограмма МРКТ пересекаются в точке О. Сумма площадей треугольников РОМ и КOТ равна 8. Найдите площадь параллелограмма. 

1) 20;          2) 12,5;         3) 15,5;          4) 16;            5) 18.

  Ответ:_______

6.   В окружности   с центром О проведены хорда DC и диаметр  DM, угол CMD равен 27°. Найдите углы CDM и COD.

  Ответ:____________.

7.  Мальчик прошёл от дома по на­прав­ле­нию на во­сток 400 м. Затем по­вер­нул на север и прошёл 90 м. На каком рас­сто­я­нии (в метрах) от дома ока­зал­ся мальчик?

     Ответ:_______.

Вторая часть

8.  Высоты треугольников АВС и КВС, опущенные на сторону ВС, относятся, как 6 : 5. Найдите площадь треугольника АВС, если она на 10 см меньше площади треугольника КВС.

                                                   А                  К

                                               В                                  С

9. Площадь прямоугольного треугольника равна 54 см², а катеты треугольника, подобного данному, относятся как 3 : 4. Найдите периметр данного треугольника.

10. Докажите, что четырехугольник с вершинами в точках А(-2;0), В(2;2), С(4;-2), D(0;-4) является квадратом.

Вариант 3.

Первая часть

1. Выберите верное утверждение:

1) если диагонали параллелограмма равны, то он ромб;

2) среди четырех треугольников, на которые диагонали делят трапецию, обязательно есть два равных треугольника;

3) середины сторон квадрата являются вершинами параллелограмма.

Ответ:____________.

2.  Че­ло­век, рост ко­то­ро­го равен 1,8 м, стоит на рас­сто­я­нии 16 м от улич­но­го фо­на­ря. При этом длина тени че­ло­ве­ка равна 9 м. Опре­де­ли­те вы­со­ту фо­на­ря (в мет­рах).

Ответ:____________.

3. Найдите дугу АВ, на которую опирается вписанный угол АСВ, равный 92°.

Ответ:____________.

4. Биссектриса АК угла ВАD параллелограмма АВСD делит сторону ВС на отрезки ВК = 8 и КС = 5. Найдите периметр этого параллелограмма.

Ответ:____________.

5. Площадь параллелограмма равна 70. Найдите периметр этого параллелограмма, если его высоты равны 5 и 7.

1) невозможно определить;       2) 22;           3) 24;            4) 18;            5) 48.

Ответ:__________.

6.  В окружности   с центром О угол между хордой АВ и радиусом ВО  в раз меньше, чем угол между хордой ВС и диаметром АС. Найдите эти углы.

Ответ:____________.

7.  От стол­ба к дому на­тя­нут про­вод дли­ной 17 м, ко­то­рый за­креплён на стене дома на вы­со­те 4 м от земли (см. ри­су­нок). Вы­чис­ли­те вы­со­ту стол­ба, если рас­сто­я­ние от дома до стол­ба равно 15 м.

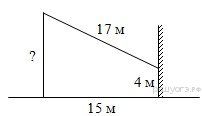
Ответ:____________.

Вторая часть

8.  Высоты треугольников МРК и НРК, опущенные на сторону РК, относятся, как 6 : 4. Найдите площадь треугольника НРК, если она на 7 см меньше площади треугольника МРК.

                                                  М                  Н

                                               Р                                  К

9. Катеты прямоугольного треугольника равны 6 см и 8 см. Найдите периметр треугольника, подобного данному, если его площадь равна 6 см².

10. Докажите, что четырехугольник с вершинами в точках А(5;1), В(-4;1), С(-4;-3), D(5;-3) является прямоугольником.

Вариант 4.

Первая часть

1. Выберите верное утверждение:

1) биссектриса треугольника делит его на два равновеликих треугольника;

2) медиана треугольника делит его на два равновеликих треугольника;

3) диагональ параллелограмма не может совпадать с его высотой.

Ответ:____________.

2. Про­ек­тор пол­но­стью осве­ща­ет экран A вы­со­той 80 см, рас­по­ло­жен­ный на рас­сто­я­нии 120 см от про­ек­то­ра. На каком наи­мень­шем рас­сто­я­нии (в сан­ти­мет­рах) от про­ек­то­ра нужно рас­по­ло­жить экран B вы­со­той 330 см, чтобы он был пол­но­стью освещён, если на­строй­ки про­ек­то­ра оста­ют­ся не­из­мен­ны­ми?

Ответ:____________.

3.  Найдите дугу АВ, на которую опирается вписанный угол АСВ, равный 102°.

Ответ:____________.

4.  Биссектриса СК угла ВСD параллелограмма АВСD делит сторону АВ  на отрезки АК = 5 и КВ = 7. Найдите периметр этого параллелограмма.

Ответ:____________.

5.  Площадь параллелограмма равна 12. Найдите периметр этого параллелограмма, если его высоты равны 2 и 3.

1) 20;             2) 22;           3) 24;            4) 18;            5) невозможно определить.

Ответ:________.

6.   В окружности   с центром О угол между радиусом ОС и хордой СВ в двое больше, чем угол между диаметром АВ и хордой АС. Найдите эти углы.

Ответ:____________.

7.  Девочка про­шла от дома по на­прав­ле­нию на запад 500 м. Затем по­вер­ну­ла на север и про­шла 300 м. После этого она по­вер­ну­ла на во­сток и про­шла еще 100 м. На каком рас­сто­я­нии (в метрах) от дома ока­за­лась девочка?

 Ответ:_______.

Вторая часть

8.  Высоты треугольников МРК и НРК, опущенные на сторону РК, относятся, как 8 : 6. Найдите площадь треугольника НРК, если она на 11 см меньше площади треугольника МРК.

                                                  М                  Н

                                               Р                                  К    

Ответ:____________.

9. Площадь прямоугольного треугольника равна 96 см², а катеты треугольника, подобного данному, относятся как 6 : 8. Найдите периметр данного треугольника.

10. Докажите, что четырехугольник с вершинами в точках А(-1;-1), В(4;-1), С(4;4), D(-1;4) является квадратом.

Ответы к заданиям