Проверочная работа по теме "Площадь фигур. Подобие фигур".

Г-8 ПР «Площадь. Подобие» В-1 ФИ _______________________

Теоретическая часть.

1. Сумма углов выпуклого п-угольника Σ= ________________________________________

2. Что Вы знаете о противоположных сторонах параллелограмма? _______________________

Что Вы знаете о соседних углах параллелограмма? ________________________________

3. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. Как называется данное утверждение? ________

______________________________________________________________________

4. Что Вы знаете о диагоналях ромба? ___________________________________________

______________________________________________________________________

Запишите формулы, по которым модно вычислить периметр и площадь ромба, если его диагонали равны d₁ и d₂, сторона равна а, а высота равна h ___________________________

______________________________________________________________________

5. Как Вы найдёте площадь треугольника, если одна из его сторон равна а, а высота, проведённая к этой стороне, равна h? ____________________________________________________

6. Как Вы найдёте площадь прямоугольного треугольника, если известны его катеты и они равны а и в? _________________________________________________________________

7. Как называются параллельные стороны трапеции? ________________________________

Чтобы найти площадь трапеции, нужно (запишите словами или формулу) _______________

______________________________________________________________________

8. Отрезки АВ и СD пропорциональны отрезкам А₁В₁ и С₁D₁, если ________________________

9. Если треугольники подобны, то отношение их сходственных сторон равно _______________

______________, а отношение их площадей равно _______________________________

10. Запишите теорему о биссектрисе угла треугольника: _______________________________

______________________________________________________________________

11. Средней линией треугольника называется ______________________________________

______________________________________________________________________

12. Медианы треугольника ___________________ в одной точке, которая делит ___________

медиану в отношении ______, считая от _______________________________________

13. Высота ___________________ треугольника, проведённая из вершины ___________ угла, есть _________________________________________ для отрезков, на которые делится __________________ этой высотой.

Практическая часть.

1. Сторона квадрата равна 5 м. Тогда его периметр равен ______ м, площадь равна _______ м², диагональ равна ________ м.

2. Смежные стороны параллелограмма равны 15 и 20 см. Высота, проведённая к большей стороне, равна 3 см. Тогда высота, проведённая к меньшей стороне, равна ____________ см, периметр параллелограмма равен __________ см, площадь параллелограмма равна ___________ см².

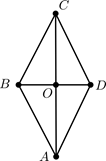
3. На рисунке АВСД – ромб, его сторона равна 10 дм, а ∠ВСО=30⁰. Найдите:

1) ∠ВОС = _____⁰

2) ∠ВСД = _____⁰

3) ∠СВД = _____⁰

4) ВО = ______ дм

5) ВД = ______ дм

6) СО = ______ дм

7) S (АВСД) = ________ дм²

4. Основания равнобокой трапеции равны 8 и 20 мм, а боковая сторона 10 мм.

Высота трапеции равна _____ мм, площадь трапеции равна _____ мм².

5. Стороны треугольника равны 7, 24 и 25 см. Площадь этого треугольника равна

_____ см². Является ли этот треугольник равнобедренным? ______. Является ли он прямоугольным? _______, так как ___________________________________________

6. 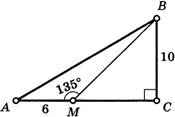По рисунку найдите:

1) ∠МВС = ____⁰

2) МС = _____ лин. ед.

3) S (∆МВС) = _____ кв. ед.

4) S (∆АВС) = _____ кв. ед.

5) S (∆АВМ) = _____ кв. ед.

7. В прямоугольном треугольнике АВС из вершины прямого угла С проведена медиана, равная 18,5 м. Катет СВ равен 12 м. Тогда гипотенуза АВ равна ______ м, катет АС равен _____ м, площадь ∆АВС равна ______ м².

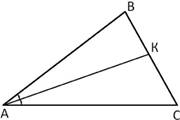
8. На рисунке АВ = 12 см, АС = 15 см, ВК = 4 см. Тогда КС = ____ см, а периметр ∆АВС равен ____ см.

9. Сходственные стороны подобных треугольников равны 25 и 5 дм. Найдите меньшую сторону большего треугольника, если сходственная ей сторона меньшего треугольника равна 2 дм.

Ответ: ____ дм.

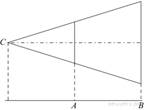
10. Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными? Ответ: ____ см

11. Биссектрисы углов А и В при боковой стороне АВ трапеции АВСD пересекаются в точке F. Найдите АВ, если АF=24, ВF=18. Ответ: _____

12. Точка Н является основанием высоты, проведённой из вершины прямого угла В ∆АВС к гипотенузе АС. Найдите АВ, если АН=10, АС=40. Ответ: ______

13. Основания ВС и АD трапеции АВСD равны соответственно 3 и 12, ВD=6. Докажите, что треугольники СВD и ВDА подобны.

Доказательство:

Г-8 ПР «Площадь. Подобие» В-2 ФИ _______________________

Теоретическая часть.

1. Чему равна сумма углов выпуклого 5-угольника? _________________________________

2. Что Вы знаете о диагоналях параллелограмма? ___________________________________

Что Вы знаете о противоположных углах параллелограмма? _________________________

3. Что Вы знаете о диагоналях прямоугольника? ____________________________________

Запишите формулы для вычисления периметра и площади прямоугольника, если его стороны равны а и в _____________________________________________________________

4. Что Вы знаете о диагоналях квадрата? _________________________________________

______________________________________________________________________

Запишите формулы для вычисления периметра и площади квадрата, если его сторона равна а

______________________________________________________________________

5. Как Вы найдёте площадь треугольника, если известны все его стороны и они равны а, в и с?

______________________________________________________________________

Как называется эта формула? ________________________________________________

6. Как Вы найдёте гипотенузу с прямоугольного треугольника, если известны его катеты а и в?

_______________. Какую теорему применяете для этого? __________________________

7. Трапеция, у которой боковые стороны равны, называется ___________________________

Трапеция, у которой есть прямой угол, называется ________________________________

Может ли у трапеции быть два прямых угла? __________. А два тупых угла? ____________

8. Треугольники называются подобными, если их соответственные углы _________________, а _____________________ стороны __________________________________________

Отношение сходственных сторон называется _____________________________________

9. Если треугольники подобны, то отношение их периметров равно ______________________

________________; отношение высот, проведённых к сходственным сторонам этих треугольников, равно ______________________________________________________

10. Запишите признаки подобия треугольников кратко: 1-й) по __________________________

2-й) по _______________________________________ 3-й) по ___________________

11. Запишите теорему о средней линии треугольника _________________________________

______________________________________________________________________

12. Высота прямоугольного треугольника, проведённая из вершины ___________ угла, разделяет треугольник на два __________ прямоугольных треугольника, каждый из которых ________ данному треугольнику.

13. Катет _________________ треугольника есть _______________________________ для гипотенузы и отрезка _________________, заключённого между катетом и ____________, проведённой из вершины ____________ угла.

Практическая часть.

1. Смежные стороны прямоугольника равны 6 и 8 м. Тогда его площадь равна ____ м², периметр равен _____ м, а диагональ равна _____ м.

2. В параллелограмме АВСД проведены высота ВН и диагональ ВД, которая образует прямой угол со стороной АВ. АВ=5 дм, ВД=12 дм. Площадь параллелограмма равна ________ дм², площадь ∆АВД равна ____ дм², ВС = ___ дм, ВН = ___ дм, периметр параллелограмма равен ____ дм.

3. Чему равна площадь ромба, если его периметр равен 40 см, а один из углов 150⁰? _______ дм²

4. По данному рисунку найдите (ВН – высота к стороне АD):

1) ∠АВС = ____⁰

2) ∠АВН = ____⁰

3) АН = ____ лин. ед.

4) ВН = ____ лин. ед.

5) S (АВСD) = ______ кв. ед.

5. Дан прямоугольный равнобедренный треугольник с гипотенузой см. Тогда его катет равен ____ см, а площадь этого треугольника равна _____ см².

6. Стороны треугольника равны 5 см, 5 см и 8 см. Площадь этого треугольника равна ______ см². Является ли этот треугольник равнобедренным? _________. Является ли он прямоугольным? _______, так как ________________________________________________________

7. В прямоугольном треугольнике АВС из вершины прямого угла С проведена медиана, равная 8,5 м. Катет СВ равен 8 м. Тогда гипотенуза АВ равна ______ м, катет АС равен _____ м, площадь ∆АВС равна ______ м².

8. На рисунке АВ = 12 см, АС = 18 см, ВК = 6 см. Тогда КС = ____ см, а периметр ∆АВС равен ____ см.

9. Площади двух подобных треугольников равны 50 и 800 дм². Найдите сторону большего треугольника, если сходственная ей сторона меньшего треугольника равна 5 дм. Ответ: ____ дм.

10. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м? Ответ: ____ м

11. Основания трапеции равны 16 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Ответ: _____

Примечание. Средняя линия трапеции – это отрезок, соединяющий средины её боковых сторон.

12. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны

АВ и ВС в точках М и N соответственно. Найдите ВN, если МN=13, АС=65, NС=28. Ответ: _____

13. Внутри параллелограмма АВСD выбрали произвольную точку Е. Докажите, что сумма площадей треугольников ВЕС и АЕD равна половине площади параллелограмма.

Доказательство:

Г-8 ПР «Площадь. Подобие» В-1 ФИ _______________________

Теоретическая часть.

14. Сумма углов выпуклого п-угольника Σ= (n – 2)180⁰

15. Что Вы знаете о противоположных сторонах параллелограмма? параллельны и равны

Что Вы знаете о соседних углах параллелограмма? их сумма равна 180⁰

16. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. Как называется данное утверждение? Т.Фалеса

17. Что Вы знаете о диагоналях ромба? пересекаются под прямым углом, точкой пересечения делятся пополам, являются биссектрисами углов ромба

Запишите формулы, по которым модно вычислить периметр и площадь ромба, если его диагонали равны d₁ и d₂, сторона равна а, а высота равна h Р=4а, S= ½d₁d₂ S= аh

18. Как Вы найдёте площадь треугольника, если одна из его сторон равна а, а высота, проведённая к этой стороне, равна h? S= ½аh

19. Как Вы найдёте площадь прямоугольного треугольника, если известны его катеты и они равны а и в? S= ½ав

20. Как называются параллельные стороны трапеции? основания

Чтобы найти площадь трапеции, нужно (запишите словами или формулу) полусумму оснований умножить на высоту трапеции, или:

21. Отрезки АВ и СD пропорциональны отрезкам А₁В₁ и С₁D₁, если АВ/А₁В₁=СD/С₁D₁

22. Если треугольники подобны, то отношение их сходственных сторон равно коэффициенту подобия, а отношение их площадей равно квадрату коэффициента подобия

23. Запишите теорему о биссектрисе угла треугольника: биссектриса угла треугольника делит его сторону на отрезки, пропорциональные прилежащим сторонам

24. Средней линией треугольника называется отрезок, соединяющий середины его сторон

25. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины треугольника

26. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.

Практическая часть.

14. Сторона квадрата равна 5 м. Тогда его периметр равен 20 м, площадь равна 25 м², диагональ равна м.

15. Смежные стороны параллелограмма равны 15 и 20 см. Высота, проведённая к большей стороне, равна 3 см. Тогда высота, проведённая к меньшей стороне, равна 4 см, периметр параллелограмма равен 70 см, площадь параллелограмма равна 60 см².

16. На рисунке АВСД – ромб, его сторона равна 10 дм, а ∠ВСО=30⁰. Найдите:

8) ∠ВОС = 90⁰

9) ∠ВСД = 60⁰

10) ∠СВД = 60⁰

11) ВО = 5 дм

12) ВД = 10 дм

13) СО = дм

14) S (АВСД) = дм²

17. Основания равнобокой трапеции равны 8 и 20 мм, а боковая сторона 10 мм.

Высота трапеции равна 8 мм, площадь трапеции равна 112 мм².

18. 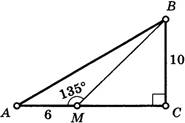Стороны треугольника равны 7, 24 и 25 см. Площадь этого треугольника равна 84 см². Является ли этот треугольник равнобедренным? нет.

Является ли он прямоугольным? да, так как 25²=24²+7²

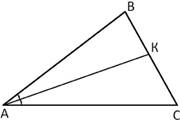
19. По рисунку найдите:

6) ∠МВС = 45⁰

7) МС = 10 лин. ед.

8) S (∆МВС) = 50 кв. ед.

9) S (∆АВС) = 80 кв. ед.

10) S (∆АВМ) = 30 кв. ед.

20. В прямоугольном треугольнике АВС из вершины прямого угла С проведена медиана, равная 18,5 м. Катет СВ равен 12 м. Тогда гипотенуза АВ равна 37 м, катет АС равен 35 м, площадь ∆АВС равна 210 м².

21. На рисунке АВ = 12 см, АС = 15 см, ВК = 4 см. Тогда КС = 5 см, а периметр ∆АВС равен 36 см.

22. Сходственные стороны подобных треугольников равны 25 и 5 дм. Найдите меньшую сторону большего треугольника, если сходственная ей сторона меньшего треугольника равна 2 дм.

Ответ: 10 дм.

23. Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными? Ответ: 495 см

24. Биссектрисы углов А и В при боковой стороне АВ трапеции АВСD пересекаются в точке F. Найдите АВ, если АF=24, ВF=18. Ответ: 30

25. Точка Н является основанием высоты, проведённой из вершины прямого угла В ∆АВС к гипотенузе АС. Найдите АВ, если АН=10, АС=40. Ответ: 20

Г-8 ПР «Площадь. Подобие» В-2 ФИ _______________________

Теоретическая часть.

14. Чему равна сумма углов выпуклого 5-угольника? 540⁰

15. Что Вы знаете о диагоналях параллелограмма? точкой пересечения делятся пополам

Что Вы знаете о противоположных углах параллелограмма? они равны

16. Что Вы знаете о диагоналях прямоугольника? они равны и точкой пересечения делятся пополам

Запишите формулы для вычисления периметра и площади прямоугольника, если его стороны равны а и в Р=2а+2в, S=ав

17. Что Вы знаете о диагоналях квадрата? они равны, взаимно перпендикулярны, точкой пересечения делятся пополам и являются биссектрисами углов квадрата

Запишите формулы для вычисления периметра и площади квадрата, если его сторона равна а

Р=4а, S=а²

18. Как Вы найдёте площадь треугольника, если известны все его стороны и они равны а, в и с?

, где р=(а+в+с)/2. Как называется эта формула? формула Герона

19. Как Вы найдёте гипотенузу с прямоугольного треугольника, если известны его катеты а и в?

с²=а²+в². Какую теорему применяете для этого? Т.Пифагора

20. Трапеция, у которой боковые стороны равны, называется равнобокой, равнобедренной

Трапеция, у которой есть прямой угол, называется прямоугольной

Может ли у трапеции быть два прямых угла? да. А два тупых угла? да

21. Треугольники называются подобными, если их соответственные углы равны, а сходственные стороны пропорциональны

Отношение сходственных сторон называется коэффициентом подобия

22. Если треугольники подобны, то отношение их периметров равно коэффициенту подобия; отношение высот, проведённых к сходственным сторонам этих треугольников, равно коэффициенту подобия

23. Запишите признаки подобия треугольников кратко: 1-й) по двум углам

2-й) по двум сторонам и углу между ними 3-й) по трём сторонам

24. Запишите теорему о средней линии треугольника средняя линия треугольника параллельна одной из его сторон и равна её половине

25. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

26. Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла.

Практическая часть.

14. Смежные стороны прямоугольника равны 6 и 8 м. Тогда его площадь равна 48 м², периметр равен 28 м, а диагональ равна 10 м.

15. В параллелограмме АВСД проведены высота ВН и диагональ ВД, которая образует прямой угол со стороной АВ. АВ=5 дм, ВД=12 дм. Площадь параллелограмма равна 60 дм², площадь ∆АВД равна 30 дм², ВС = 13 дм, ВН = дм, периметр параллелограмма равен 36 дм.

16. Чему равна площадь ромба, если его периметр равен 40 см, а один из углов 150⁰? 50 см²

17. 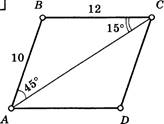По данному рисунку найдите (ВН – высота к стороне АД):

6) ∠АВС = 120⁰

7) ∠АВН = 30⁰

8) АН = 5 лин. ед.

9) ВН = лин. ед.

10) S (АВСД) = кв. ед.

18. Дан прямоугольный равнобедренный треугольник с гипотенузой см. Тогда его катет равен 6 см, а площадь этого треугольника равна 18 см².

19. Стороны треугольника равны 5, 5 и 8 см. Площадь этого треугольника равна 12 см². Является ли этот треугольник равнобедренным? да. Является ли он прямоугольным? нет, так как 8²≠5²+5²

20. В прямоугольном треугольнике АВС из вершины прямого угла С проведена медиана, равная 8,5 м. Катет СВ равен 8 м. Тогда гипотенуза АВ равна 17 м, катет АС равен 15 м, площадь ∆АВС равна 60 м².

21. На рисунке АВ = 12 см, АС = 18 см, ВК = 6 см. Тогда КС = 9 см, а периметр ∆АВС равен 45 см.

22. Площади двух подобных треугольников равны 50 и 800 дм². Найдите сторону большего треугольника, если сходственная ей сторона меньшего треугольника равна 5 дм. Ответ: 20 дм.

23. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м? Ответ: 3,5 м

24. Основания трапеции равны 16 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Ответ: 8,5

25. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны

АВ и ВС в точках М и N соответственно. Найдите ВN, если МN=13, АС=65, NС=28. Ответ: 7

Проверочная работа по теме "Площадь фигур. Подобие фигур".

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

03.12.2019