Рабочая программа

по курсу внеурочной деятельности

«Математика вокруг нас»

 

Предметная область -  общеинтеллектуальное

Класс – 8

Уровень изучения предмета – базовый

Срок реализации программы – 2020-2021 учебный год

 

 

         Составитель:

Леухина Виктория Игоревна

 

 

2020 год             

 

 

 

 

 

 

 

 

 

 

                                                                                   

Пояснительная записка

 План внеурочной деятельности МБОУ СШ № 29 обеспечивает введение в действие и реализацию требований ФГОС и определяет объем нагрузки обучающихся в рамках внеурочной деятельности, состав, структуру направлений и форм внеурочной деятельности.

    План внеурочной деятельности МБОУ СШ № 29 составлен в соответствии со следующими документами:

·     Федеральный закон от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации» (с изменениями, вступившими в силу 01.08.2020 года);

·     Постановление Главного Государственного санитарного врача Российской Федерации «Об утверждении СанПин 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» от 29.12.2010 № 189 (с изменениями 24.11.2015);

·     Приказ Министерства образования и науки Российской Федерации от 30.08.2013 № 1015 «Об утверждении Порядка организации и осуществления образовательной деятельности по основным общеобразовательным программам – образовательным программам начального общего, основного общего и среднего общего образования»;

·     Приказ Министерства образования и науки Российской Федерации от 17.12.2010 № 1897 «Об утверждении федерального государственного образовательного стандарта основного общего образования» (с изменениями и дополнениями от 29.12.2014, 31.12.2015);

·     Приказ Министерства образования и науки Российской Федерации от 28.12.2018 № 345 «О федеральном перечне учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования» (с изменениями от 08.05.2019, 22.11.2019, 18.05.2020);

·     Письмо Министерства образования и науки Российской Федерации от 28.10.2015 №08-1786 «О рабочих программах учебных предметов»;

·     Уставом муниципального бюджетного общеобразовательного учреждения «Средняя школа № 29» города Ульяновска;

·     Основной образовательной программой начального общего, основного общего, среднего общего образования МБОУ СШ № 29;

·     Положение о порядке разработки и требованиях к структуре, содержанию и оформлению рабочей программы учебного предмета (курса), утверждено приказом № 213 от 28.08.2020.

При разработке внеурочной деятельности были использованы методические рекомендации:

-     Письмо Министерства образования и науки РФ от 19 апреля 2011 г. 03-255 «0 введении федерального государственного образовательного рекомендации есть стандарта общего образования»;

-     Письмо департамента общего образования Минобрнауки России от 12 организации мая 2011 г. № 03-296 «Об организации внеурочной деятельности при внеурочном введении федерального государственного образовательного стандарта деятельности общего образования».

Организацию внеурочной деятельности МБОУ СШ №29 регламентируют следующие документы:

-     Устав муниципального бюджетного образовательного учреждения города Ульяновска «Средняя школа № 29»;

-     Локальные акты МБОУ СШ №29;

-     Правила внутреннего распорядка МБОУ СШ №29;

-     Договор образовательного учреждения с родителями (законными реализацию представителями) обучающихся;

-     Положение о формах самоуправления в МБОУ СШ №29;

-     Договор о сотрудничестве общеобразовательного учреждения и учреждений дополнительного образования детей;

-     Должностные инструкции работников МБОУ СШ №29;

-     Приказы об утверждении рабочих программ учебных курсов, дисциплин (модулей).

Рабочая программа ориентирована на реализацию учебно-методического комплекса:

1.                 Сборник программ внеурочной деятельности «Математическая гармония: метод. рекомендации для учителей математики / под общ. Ред О.В. Сафоновой. – Ульяновск: Центр ОСИ, 2015. - 72 с.-(Серия «Реализация ФГОС ООО»)

2.                 Организация внеурочной деятельности в школе в условиях ФГОС второго поколения (методические рекомендации). /Автор Е.Л.Петренко /Ульяновск: УИПК ПРО, 2013.

 

Количество часов в год – 35

Количество часов в неделю – 1.

 

Цель программы «Математика вокруг нас» - формирование всесторонне образованной личности, умеющей ставить цели, организовывать свою деятельность, оценивать результаты своего труда, применять математические знания в жизни.

Задачи:

·     расширять кругозор учащихся в различных областях элементарной математики;

·     расширять математические знания в области многозначных чисел;

·     содействовать умелому использованию символики;

·     учить правильно применять математическую терминологию;

·     развивать умения отвлекаться от всех качественных сторон и явлений,

·     сосредоточивая внимание на количественных сторонах;

·     уметь делать доступные выводы и обобщения, обосновывать собственные мысли.

 

 

Планируемые результаты освоения учебного курса

У обучающихся могут быть сформированы личностные результаты:

· ответственное отношение к учению, готовность и способность обучающихся к самообразованию на основе мотивации к обучению и познанию, осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений, с учётом устойчивых познавательных интересов;

· способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

· умение контролировать процесс и результат математической деятельности;

· коммуникативная компетентность в общении и сотрудничестве со сверстниками в образовательной, учебно-исследовательской, творческой и других видах деятельности;

· иметь опыт публичного выступления перед учащимися своего класса и на научно-практической ученической конференции;

· оценивать информацию (критическая оценка, оценка достоверности);

· критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

· креативность мышления, инициативы, находчивости, активности при решении задач.

Метапредметные:

регулятивные обучающиеся получат возможность научиться:

·     составлять план и последовательность действий;

·     определять последовательность промежуточных целей и соответствующих им действий с учётом конечного результата;

·     предвидеть возможность получения конкретного результата при решении задач;

·     осуществлять констатирующий и прогнозирующий контроль по результату и способу действия;

·     видеть математическую задачу в других дисциплинах, окружающей жизни;

·     концентрировать волю для преодоления интеллектуальных затруднений и физических препятствий;

·     самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем, а также самостоятельно интерпретировать результаты решения задачи с учётом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;

·     самостоятельно приобретать и применять знания в различных ситуациях для решения различной сложности практических заданий, в том числе с использованием при необходимости и компьютера;

·     выполнять творческий проект по плану;

·     интерпретировать информацию (структурировать, переводить сплошной текст в таблицу, презентовать полученную информацию, в том числе с помощью ИКТ);

·     логически мыслить, рассуждать, анализировать усло­вия заданий, а также свои действия;

·     адекватно оценивать правильность и ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения.

Познавательные

·          обучающиеся получат возможность научиться:

·          устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;

·          формировать учебную и общекультурную компетентность в области использования информационно-коммуникационных технологий;

·          выдвигать гипотезу при решении учебных задач и понимать необходимость их проверки;

·          планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

·          выбирать наиболее эффективные и рациональные способы решения задач;

·          интерпретировать информацию (структурировать, переводить сплошной текст в таблицу, презентовать полученную информацию, в том числе с помощью ИКТ);

Коммуникативные

обучающиеся получат возможность научиться:

·     организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников;

·     взаимодействовать и находить общие способы работы; работать в группе; находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;

·     прогнозировать возникновение конфликтов при наличии различных точек зрения;

·     разрешать конфликты на основе учёта интересов и позиций всех участников;

·     координировать и принимать различные позиции во взаимодействии;

·     аргументировать свою позицию и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности;

·     аргументировать свою позицию и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности;

·     работать в группе; оценивать свою работу.

·     слушать других, уважать друзей, считаться с мнением одноклассников.

Предметные

учащиеся получат возможность научиться:

·     решать задачи на делимость чисел и отгадывание чисел

·     разделять фигуры на части по заданному условию и из частей конструировать различные фигуры;

·     решать задачи на нахождение площади и объёма фигур, отгадывать геометрические головоломки;

·     решать сложные задачи на движение;

·     решать логические задачи;

·     применять алгоритм решения задач на переливание с использованием сосудов, на перекладывание предметов, на взвешивание предметов;

·     решать сложные задачи на проценты;

·     решать математические задачи и задачи из смежных предметов, выполнять практические расчёты;

·     решать занимательные задачи;

·     анализировать и осмысливать текст задачи, переформулировать условие, моделировать условие с помощью реальных предметов, схем, рисунков, графов; строить логическую цепочку рассуждений; критически оценивать полученный ответ, осуществлять самоконтроль, проверяя ответ на соответствие условию.

·     пользоваться предметным указателем энциклопедий, справочников и другой литературой для нахождения информации;

·     находить в пространстве разнообразные геометрические фигуры, понимать размерность пространства;

·     строить плоские и пространственные фигуры; делать оригами, изображать бордюры, орнаменты.

·     правильно употреблять термины «множество», «подмножество»;

·     составлять различные подмножества данного множества»;

·     определять число подмножеств, удовлетворяющих данному условию;

·     решать задачи, используя круги Эйлера

·     правильно употреблять термины, связанные с различными видами чисел и способами их записи;

·     самостоятельно приобретать и применять знания в различных ситуациях для решения различной сложности практических задач, в том числе с использованием при необходимости справочных материалов, калькулятора и компьютера;

·     пользоваться предметным указателем энциклопедий и справочников для нахождения информации;

·     уметь решать задачи с помощью перебора возможных вариантов;

·     выполнять арифметические преобразования выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;

·     применять изученные понятия, результаты и методы при решении задач из различных реальных ситуаций, не сводящихся к непосредственному применению известных алгоритмов;

·     первоначальные представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации.

·     понимать и применять смысл различных игр, фокусов с числами;

·     знать старинные меры измерения длин, площадей;

 

Содержание курса внеурочной деятельности

 

I. История возникновения чисел (7 часов)

История возникновения чисел и способы их записи. Римские цифры. Другие системы счисления: шестидесятеричная и двоичная. Действия в двоичной системе счисления.

II. Математика вокруг нас (8 часов)

 Решение геометрических задач на разрезание и перекраивание. Математические софизмы. Секреты некоторых математических фокусов. Решение задач с помощью максимального предположения. Решение задач методом с «конца». Решение задач методом ложного положения.

Решение практических задач, знакомство с нетрадиционными методами решения задач. Изготовление разверток куба, прямоугольного параллелепипеда. Знакомство с элементами комбинаторики. Составление и решение практических комбинаторных задач.

III. Дробные числа (4 часа)

 Обыкновенные дроби. Десятичные дроби. Решение задач на среднее арифметическое, среднюю цену, среднюю скорость.

IV. Геометрия в нашей жизни (5 часов).

Угол. Треугольник. Куб и прямоугольный параллелепипед, изготовление развёртки и каркасов. Практические задания «Вычисление количества плитки необходимой для покрытия указанной площадки». Практическая работа: «Рассчитать площадь клумбы и ее периметр по формулам».

V. Математика на каждый день (6 часов)

Сравнение понятий. Установление сходства и различий. Решение сюжетных задач. Решение логических задач с помощью таблиц. Элементы теории графов. Применение графов к решению логических задач. Решение задач на проценты. Практическая работа: «Расчет затрат электроэнергии семьи за один месяц». Правила произведения и суммы. Перестановки. Размещения. Сочетания.

VI. Математические чудеса и тайны (5 часов)

 Математические игры. Геометрические головоломки. Математические софизмы. Числовые ребусы. Математические фокусы.

 

Формы обучения: коллективные и индивидуально-групповые занятия, теоретические и практические занятия, творческие работы.

Основные методы: объяснение, беседа, иллюстрирование, решение задач, дидактические игры, убеждение.

Основные виды деятельности учащихся:

- решение различных задач

- оформление математических газет

- участие в математической олимпиаде,

- знакомство с научно-популярной литературой, связанной с математикой

- проектная деятельность

- самостоятельная работа

- работа в парах, в группах

- творческие работы

 

 

 

 

 

 

 

Список использованных источников

1.        Балк М.Б., Балк Г.Д. Математика после уроков. Пособие для учителей. М.

2.        Просвещение, 1971

3.        Генкин С.А., Итенберг И. В., Фомин Д.В. Ленинградские математические кружки

4.        Пособие для внеклассной работы. Киров: АСА, 1994 год Депман И.Л. Рассказы о математике. ГИДЛМП Ленинград 1994 год.

5.        Нагибин Ф.Ф., Канан Е.С. Математическая шкатулка. М. Просвещение 1999 год.

6.        Перельман Я.И. Занимательная арифметика. Триада-Литера Москва 2000 год.

7.        Пичурин Л.Ф. За страницами учебника алгебры, М., Просвещение, 1990 год.

8.        Приложение к учебно-методической газете «Первое сентября», Математика, издательский дом Первое сентября, 2007 год.

9.        Совайленко В.К., Лебедева О.В. Математика. Сборник развивающих задач для учащихся 5-6 классов. Ростов – на – Дону.Легион, 2005 год.

10.   Соколова И.В. Математический кружок в VI классе. Краснодар 2005 год.

11.   Фарков А.В. Математические кружки в школе 5-8 класс. Москва. Айрис-пресс 2007 год.

12.   Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия: Учебное пособие для учащихся V –VI классов. М.МИРОС, 1995 год.

13.   Шарыгин И.Ф., Шевкин А.В. Математика: Задачи на смекалку: Учебное пособие для 5 – 6 классов общеобразовательных учреждений. М.Просвещение, 1995 год.

14.   Шарыгин И.Ф., Шевкин А.В. Задачи на смекалку. М. Просвещение 2006 год.

 

 

 

 

 

 

Календарно - тематическое планирование

 

№ урока	Темы урока	Программное содержание	Дата проведения
I. История возникновения чисел
1	История возникновения чисел и способы их записи. Римские цифры.	Участвовать в игре «Как возникли числа», подбор из разных источников материал  измерять шагами длину предмета, и переводит их в другие единицы измерения подбирать из разных источников интересный материал и выступать перед одноклассниками/   Развитие аналитических способностей. Совершенствование мыслительных операций. Совершенствование воображения
2	Необычное об обычных натуральных числах. Практическая работа:  « Измерение расстояния линейкой»
3	Необычное об обычных натуральных числах. Практическая работа:  « Измерение расстояния шагами»
4	Другие системы счисления: шестидесятиричная и двоичная
5	Другие системы счисления: шестидесятиричная и двоичная
6	Действия в двоичной системе счисления
7	Действия в двоичной системе счисления
II. Математика вокруг нас
8	Решение геометрических задач на разрезание и перекраивание.	Решать математические ребусы, софизмы, показывать математические фокусы.       Выявление уровня развития внимания, восприятия, воображения, памяти и мышления. Знакомство вопросами истории математики.
9	Решение геометрических задач на разрезание и перекраивание
10	Математические софизмы
11	Секреты некоторых математических фокусов
12	Секреты некоторых математических фокусов
13	Решение задач с помощью максимального предположения
14	Решение задач методом с «конца»
15	Решение задач методом ложного положения
III. Дробные числа
16	Обыкновенные дроби	Решать числовые и алгебраические выражения; использовать различные приёмы при решении выражений.   Развитие аналитических способностей. Совершенствование мыслительных операций. Совершенствование воображения
17	Десятичные дроби
18	Решение задач на среднее арифметическое, среднюю цену, среднюю скорость
19	Решение задач на среднее арифметическое, среднюю цену, среднюю скорость
IV. Геометрия в нашей жизни
20	Угол	Решать геометрические задачи на разрезание, задачи со спичками, геометрические головоломки. Развитие аналитических способностей. Совершенствование мыслительных операций. Совершенствование воображения
21	Треугольник
22	Куб и прямоугольный параллелепипед, изготовление развёртки и каркасов
23	Практические задания «Вычисление  количества плитки  необходимой  для покрытия указанной площадки»
24	Практическая работа: «Рассчитать площадь клумбы и ее  периметр по формулам»
V. Математика на каждый день
25	Сравнение понятий. Установление сходства и различий	Сравнивать, устанавливать сходства и различия в окружающих предметах. Строить таблицы по предложенному тексту. Находить применение графов в жизненных ситуациях. Выполнять расчеты затрат своей семьи на электроэнергию. Составлять задания из практической жизни.
26	Решение сюжетных задач
27	Решение логических задач с помощью таблиц
28	Элементы теории графов. Применение графов к решению логических задач
29	Решение задач на проценты. Практическая работа: «Расчет затрат электроэнергии семьи за один месяц»
30	Перестановки. Размещения. Сочетания.
VI. Математические чудеса и тайны
31	Магические квадраты	Решать математические ребусы, софизмы, показывать математические фокусы.   Выявление уровня развития внимания, восприятия, воображения, памяти и мышления. Знакомство вопросами истории математики.
32	Математические фокусы
33	Математические «Ребусы и головоломки»
34	Решение занимательных задач в стихах
35	Решение задач повышенной трудности

 

 

 

 

 

 

 

 

 

 

 

Приложение

Правила игры «Математик-бизнесмен».

1.   В игре участвуют две команды, каждая из которых представляет правление банка. Игроки каждой команды выбирают себе президента банка (т. е. капитана команды).

2.   Президент имеет право принимать окончательное решение по данному заданию игры.

3.   Командам предлагается по очереди выбирать себе задания различной стоимости в зависимости от сложности.

4.   Стартовый капитал каждой команды – 500 рублей.

5.   Если команда дает правильный ответ, то ее капитал увеличивается на стоимость задания. Если ответ неправильный, то:

А) капитал уменьшается на 100% стоимости задания, если другая команда дает правильный ответ;

Б) капитал уменьшается на 50% стоимости задания, если другая команда не сможет ответить правильно.

6. Команда может продать свое задание сопернику или купить его задание по взаимному согласию.

7. На обдумывание задания дается от 1 до 5 минут в зависимости от сложности.

8.  Игра считается оконченной, если одна из команд обанкротилась или закончились все задания.

9.  Победителем объявляется тот, в чьем банке будет больше «денег» по окончанию игры.

 

 

 

 

 

 

 

 

Математическое изобразительное искусство        

Исторически, математика играла важную роль в изобразительном искусстве, в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая - аналитическая, вторая - эмоциональная. Математика не играет очевидной роли в большинстве работ современного искусства, и, фактически, многие художники редко или вообще никогда не используют даже использование перспективы. Однако, есть много художников, у которых математика находится в центре внимания. Несколько значительных фигур в изобразительном искусстве проложили дорогу этим индивидуумам.

Вообще-то не существует каких-либо правил или ограничений на использование различных тем в математическом в математическом искусстве. Однако, есть несколько тем, которые достаточно часто различным художниками. Среди них есть использование многогранников, тесселяций, невозможных фигур, лент Мебиуса, искаженных или необычных систем перспективы, а также фракталов.

Тесселляции, известные также как покрытие плоскости плитками (tiling), являются коллекциями фигур, которые покрывают всю математическую плоскость, совмещаясь друг с другом без наложений и пробелов. Правильные тесселляции состоят из фигур в виде правильных многоугольников, при совмещении которых все углы имеют одинаковую форму. Существует всего три многоугольника, пригодные для использования в правильных тесселляциях. Это - правильный треугольник, квадрат и правильный шестиугольник. Полуправильными тесселляциями называют такие тесселляции, в которых использованы правильные многоугольники двух или трех типов и все вершины одинаковы. Существует всего 8 полуправильных тесселляций. Вместе три правильных тесселляции и восемь полуправильных носят название Архимедовых. Тесселляции, в которых отдельные плитки являются узнаваемыми фигурами, являются одной из основных тем творчества Эшера. В его записных книгах содержатся более 130 вариантов тесселляций.[3] Он использовал их в огромном количестве своих картин, среди которых "День и ночь" (1938), серия картин "Предел круга" I-IV, и знаменитые "Метаморфозы" I-III (1937-1968). Примеры ниже - картины современных авторов ХоллистераДевида (HollisterDavid) и Роберта Фатауэра (RobertFathauer). HollisterDavid "Семь птиц". На этой картине изображены семь птиц, две из которых изображены в негативе на фоне ландшафта города Ахо в Аризоне. Последовательно уменьшающиеся фигуры птиц совмещаются друг с другом в виде фрактальной тесселляции. Хвостовые перья каждой птицы являются разделяют конструкцию напополам, отсекая примерно треть расстояния между кончиками крыльев. Каждая меньшая птица в свою очередь делит свою область аналогичным образом. Если этот процесс продолжать до бесконечности, получится набор точек, известный как множество Кантора или Канторова пыль. RobertFathauer "Фрактальные рыбы - сгруппированные группы". Это компьютерная работа, распечатанная на фотобумаге. Сквозь иллюминатор видны волны, но при ближайшем рассмотрении видно, что волны являются на самом деле фрактальной тесселляцией, состоящей из рыб.

        

Выдающиеся люди в истории математического изобразительного искусства 

Голландский художник М.К. Эшер (1898-1972) в некотором роде является отцом математического искусства. Математические идеи играют центральную роль в большинстве его картин за исключением лишь ранних работ. Большинство идей, часто используемых современными математическими художниками, были использованы Эшером, и его работы часто являются источником вдожновения для современных авторов. Надеемся, что читатель знаком с работами Эшера, которые детально рассмотрены в литературе [1]-[3]. В данном разделе перечислены другие выдающиеся личности, которые не так часто ассоциируются с математическим искусством.

Одной из частых тем математического искусства является использование многогранников, которые были изучены достаточно давно. Платон (427-348 до н.е.) описал пять правильных многогранников, которые также иногда называются телами Платона. Однако открыты они были раньше Платона, и детали открытия правильных многогранников остаются загадкой. Платон соотносил эти тела с четырьмя элементами: огонь - тетраэдр, воздух - октаэдр, вода - икосаэдр, земля - куб. Далее, он писал, что существует пятая комбинация, которой Бог ограничил Мир, это додекаэдр. Архимед (290/280-212/211 до н.э) описал 13 полуправильных многогранников. Так же как правильные многогранники называют Платоновыми, полуправильные многогранники называют архимедовыми. Записи Архимеда об этих многогранниках были утеряны вместе с фигурами многогранников. Они были открыты вновь лишь в эпоху Ренессанса, и описание всех 13 многогранников было впервые опубликовано в книге Иоганна Кеплера "HarmonicesMundi" в 1619 году, почти через две тысячи лет после смерти Архимеда.

 Леонардо да Винчи (LeonardodaVinci ) (1452-1519) известен своими достижениями в качестве изобретателя и художника. В его записных книгах содержатся первые из известных примеров анаморфного искусства, использующего искаженные сетки перспективы. Его наклонные анаморфные изображения представляют объекты, которые должны рассматриваться по углом, чтобы они выглядели неискаженными.

 Иоганн Кеплер (JohannesKepler) (1580-1630) более известен своими работами в астрономии, но также имел большой интерес к геометрическим тесселяциям и многогранникам. В своей книге "HarmonicesMundi" (1619) он опубликовал примеры заполнения плоскости плитками в виде правильных и звездчатых многоугольников в дополнение к многогранникам, о которых было сказано выше.

КоломанМозер (KolomanMoser) (1868-1918) - художник-график, преподававший в Вене и работавший в стиле модернизма. Он исполнил пару тесселляций в виде рыб в период 1899-1900 гг., выглядящие вполне в стиле Эшера. Однако, несомненно, Эшер не мог знать о работах Мозера вплоть до 1964 года.

Некоторые известнейшие художники XX века активно использовали математику в искусстве. Пит Мондриан (PietMondriaan) (1872-1944) - голландский художник, известный своими геометрическими абстракциями; несколько его работ изображают цветные блоки, разделенные черными линиями.

Сальвадо Дали (SalvadorDali) (1904-1989) - яркий и парадоксальный испанский художник использовал математические идеи в некоторых своих картинах. На картине "Распятие" ("Crucifixion") (1954) изображен гиперкуб, а на картине "LaVisagedelaGuerre" (1940) изображена фрактальная последовательность уменьшающихся гротескных лиц. Он также создал несколько эротических анаморфиных изображений.

 Макс Биль (MaxBill) (1908-1994) - художник-график и скульптор, обучавшийся в Баухаузе (Bauhaus), создавал скульптуры, основанные на ленте Мебиуса, многие из которых высталены в общественных местах.

Виктор Васарели (1908-1997) - художник, родившийся в Венгрии, известен как пионер и практик направления оптического искусства Оп-арт (OpArt). Он использовал окрашенные простые геометрические формы, часто объединенные в массивы, для создания эффекта движения, выпуклости или вогнутости на плоском рисунке.

Бенуа Мандельброт (BenoitMandelbrot) (1924-...) - математик, в значительной степени ответственный за формализацию и популяризация концепции фракталов. Он открыл множество Мандельброта, наиболее известный фрактальный объект. Он также изобрел термин "фрактал" ("fractal"), полученный из латинского слова "fractus", означающий "разбитый на куски", "сломанный". О его понимании эстетического содержания фракталов говорит следующая цитата: "Может ли чистая геометрия 'человеку с улицы' показаться прекрасной? Точнее, может ли фигура, описываемая простым уравнением или правилом построения, быть воспринята человеком, не связанным с геометрией, как фигура имеющая эстетическое значение, а именно, быть декоративной, а возможно и видом искусства? Если эта геометрическая фигура - фрактал, то ответ - да."

        

 

 

Общие темы в математическом искусстве             

Многогранники           

Правильные геометрические тела - многогранники - имели особое очарование для Эшера. Во его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона. Это - тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями. На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

Многогранник называется правильным, если он лежит по одну сторону от плоскости любой его грани, т. е. является выпуклым, и все его грани есть равные правильные многоугольники. Простой подсчет суммы углов при вершине правильного многогранника показывает, что существует только пять правильных многогранников^*. Доказательство этого факта имеется в XIII книге "Начал" Евклида, но сам факт был, безусловно, известен Платону, а правильные многогранники знали пифагорейцы задолго до Платона. Форму правильных тел, по-видимому, подсказала древним грекам сама природа: кристаллы поваренной соли имеют форму куба, кристаллы квасцов - октаэдра, а кристаллы пирита - додекаэдра. Последний, как показали раскопки в итальянских Альпах, был любимой игрушкой этрусских детей задолго до нашей эры.

^* (В самом деле, сумма плоских углов s при вершине выпуклого многогранника должна быть строго меньше 360°, а число граней при вершине m≥3. Тогда гранями правильного многогранника могут быть только три плоские фигуры: правильные треугольник, четырехугольник (квадрат) и пятиугольник, ибо уже для шестиугольников s = 120°*3 = 360°. Название правильному многограннику дается по общему числу граней М. Таким образом, из равносторонних треугольников можно составить три правильных многогранника при m = 3, 4, 5 (при m = 6 s = 60°*6 = 360°):

1. Тетраэдр (четырехгранник): m = 3, М = 4.

2. Октаэдр (восьмигранник): m = 4, М = 8.

3. Икосаэдр (двадцатигранник): m = 5, М = 20, а из квадратов и правильных пятиугольников - только по одному при m = 3 (при m = 4 s = 90°*4 = 360° - для квадратов и s = 108°*4 = 432° - для пятиугольников).

4. Гексаэдр (шестигранник), или куб: m = 3, М = 6.

5. Додекаэдр (двенадцатигранник): m = 3, М = 12.

В любом выпуклом многограннике числа вершин L, граней М и ребер N связаны формулой Эйлера L + M - N = 2.)

Правильные многогранники всегда восхищали пытливые умы симметрией, простотой и мудростью своих форм. Леонардо да Винчи любил изготовлять из дерева каркасы правильных тел и преподносить их в виде подарка различным знаменитостям.

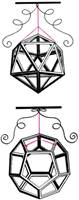
Рисунки тел Платона, выполненные Леонардо да Винчи к книге Луки Пачоли 'О божественной пропорции'. Венеция. 1509

Ко времени Платона в античной философии уже созрела концепция четырех элементов (стихий) - первооснов материального мира: огня, воздуха, воды ц земли. Огонь и землю Платон считает основными компонентами для образования космоса: "...всему, что имело произойти, надлежало, конечно, быть телесным, видимым и осязаемым. Но быть видимым ничто не может без посредства огня, точно так же и осязаемым ничто не может быть без чего-нибудь твердого, твердым же ничто не может быть без земли (Тимей)". Между основными стихиями помещаются две средние - вода и воздух, и все они связываются музыкальными отношениями. Атомам земли Платон придает форму куба, так, как и земля, и куб отличаются неподвижностью и устойчивостью. Атомам воды - форму икосаэдра, так как вода отличается текучестью, а из всех правильных тел икосаэдр - наиболее "катящийся". Атомам воздуха - форму октаэдра, ибо воздух движется взад и вперед и октаэдр как бы направлен одновременно в разные стороны. Атомам огня - форму тетраэдра как наиболее острого, мечущегося в разные стороны. Не у дел остался пятый правильный многогранник - додекаэдр. Для него Платон вводит пятый элемент - "пятую сущность"^* - мировой эфир, атомам которого придается форма додекаэдра как наиболее близкого к шару - самому совершенному по форме телу. С тех пор правильные многогранники называются также платоновыми телами.

 

 

Математика и литература          

Математики-поэты (Ломоносов М.В., Ковалевская С.В., Лобачевский Н.И., Омар Хайям)      

Математика и поэзия. Что роднит их, казалось, на первой взгляд они такие разные… Ученым не чужда поэзия. Как показывает история науки, еще со времен пифагорейцев выдающиеся математики увлекались поэзией и даже сами пробовали писать.

Ж. Дьедонне говорил: “Стимулы математиков всех времен: любознательность и стремление к красоте”. Большое математическое дарование нередко сочетается с проявлением творческого интереса к поэзии.

Ученые и поэзия.

Женщина-математик Софья Васильевна Ковалевская говорит о математике так: “Это наука, требующая наиболее фантазии, нельзя быть математиком, не будучи в то же время поэтом в душе”.

Она – великий математик, она – признанный писатель и поэт. Вот одно из ее стихотворений.

“ЕСЛИ ТЫ В ЖИЗНИ…”

Если ты в жизни, хотя на мгновенье

Истину в сердце своем ощутил,

Если луч правды сквозь мрак и сомненье

Ярким сияньем твой путь озарил:

Чтобы в решеньи своем неизменном

Рок ни назначил тебе впереди –

Память об этом мгновеньи священном

Вечно храни, как святыню, в груди.

Тучи сберутся громадой нестройной,

Небо покроется черною мглой,

С ясной решимостью, с верой спокойной

Бурю ты встреть и померься с грозой.

Великий русский ученый М. В. Ломоносов говорил о математике так: “Математику уже затем учить надо, что она ум в порядок приводит”. И вот отрывок из его стихотворения:

О вы, которых ожидает

Отечество от недр своих

И видеть таковых желает,

Каких зовет от стран чужих,

О, ваши дни благословенны!

Дерзайте ныне ободрены

Раченьем вашим показать,

Что может собственных Платонов

И быстрых разумом Невтонов

Российская земля рожать.

Писал стихи и великий русский геометр Лобачевский. Ректор Казанского университета и известный математик вдруг в 1834 году “рискнул” опубликовать свое стихотворение “Разлив Волги при Казани”. Вот отрывок его:

“Ты поражаешь ли поля опустошеньем?

Ты похищаешь ли надежды поселян?

Нет! На водах твоих всегда благословенье

Почиет благодарных стран,

Тобой, питаемых, тобой обогащенных!

Ты и земли безвредная краса,

И светлые в струях твоих невозмущенных,

Как в чистой совести, сияют небеса.

Вот образ мирного могущества России!

Ее разлив не страшен никому.

Великодушие обуздывает силы,

Всегда, везде покорные ему.

Эта публикация, по-видимому, связана с приездом Пушкина в Казань в сентябре 1833 года, где он собирал материалы о восстании Пугачева. Жена Лобачевского – сестра Великопольского, давнишнего приятеля Пушкина, на вечерах которого бывали Пушкин и Лобачевский. Встретились два гения. Может быть, после встречи с Лобачевским Пушкин сказал: “Вдохновение нужно в поэзии, как в геометрии”.

 

Пушкин и математика.

Широко распространено мнение, что А.С. Пушкин был не совсем в ладах с математикой. На самом деле, из воспоминаний старшей сестры Ольги, мы узнаем, что в детстве бывало он плакал над задачами по математике. На страницах гениальных творений Пушкина нашли отражение математические понятия, термины и идеи. Связи поэта с современной ему математикой весьма многообразны. По результатам вступительных экзаменов в лицей об Александре Пушкине записано: что «в познании языков: российского – очень хорошо, французского – хорошо, немецкого – не учился, в арифметике – знает до тройного правила, в познании общих свойств тел – хорошо. В воспоминаниях об учебе в лицее «первый друг» и «друг бесценный» Иван Пущин рассказывал: «Учитель физики и математики Яков Иванович Карцев вызвал Пушкина к доске решать алгебраическую задачу. Переминаясь с ноги на ногу, Пушкин молча делал на доске какие-то записи чисел. На вопрос учителя: «Ну, что же у Вас получилось? Чему равняется икс?» - ученик улыбнулся и ответил: «Нулю!». «Хорошо, - подытожил Карцев. – У вас, Пушкин, все в моем классе кончается нулем. Садитесь на место и пишите лучше стихи».

Как видно в лицейские годы математика не всегда принималась юным А. Пушкиным как «милые сердцу предметы». Зато в последствии, когда он писал о своем стремлении «в просвещении стать с веком на ровне», поэт несомненно проявлял большой интерес к математике, что нашло отражение в его гениальных творениях. В материалах записных книжек Пушкина за 1835 год содержится гипотеза о происхождении формы цифр: «Форма цифр арабских составлена из следующей фигуры: AD (1), ABDC (2), ABECD (3), ABD+AE (4). Русские цифры составлены по тому же образцу». Хотя, существует мнение об индийском происхождении «арабских» цифр.

Индийские цифры попади в Европу от арабов в 12 в. через Мавриатнию. Пушкин, сравнивая татарское иго с игом мавританским в Испании, отметил: «Татары не походили на мавров. Они, завоевав Россию, не подарили ей ни алгебры, ни Аристотеля».

Поистине, крылатыми стали слова из трагедии «Моцарт и Сальери» «проверил я алгеброй гармонию». Считается, что эта фраза проводит разделение между искусством Моцарта и ремесленничеством Сальери и сводится к противопоставлению искусства и науки.

В творчестве Пушкина в различных вариациях встречаются слова, загадочным образом связанные с наукой о случайном.

Дар напрасный, дар случайный,

Жизнь, зачем ты мне дана?

Иль зачем судьбою тайной

Ты на казнь осуждена?

В незаконченном стихотворении о научном творчестве Пушкин дает глубокие определения случаю, опыту и гению:

О, сколько нам открытий чудных

Готовят просвещенья дух

И опыт, сын ошибок трудных,

И гений, парадоксов друг,

И случай, бог изобретатель

Глубину этих определений специально отмечал еще академик С.И. Вавилов

В настоящее время на основе произведений Пушкина авторы современных задачников по теории вероятностей с удовольствием включают задачи на классическое определение вероятности. Например,: Из колоды карт (52 карты) Герман наугад извлекает три карты. Найдите вероятность того, что это будут 3, 7 и туз.

Друг поэта П.А. Вяземский писал о Пушкине, что от был «страстен и к наукам естественным и особенно математическим, которые составляли значительный каптал его познаний и были до конца любимым предметом его ученых занятий и глубоких исследований».

Математика в литературных произведениях (http://www.smekalka.pp.ru/old.html)

Задачи со словами (http://www.smekalka.pp.ru/word_other.html)

 

Задачи на проценты

1.      На заводе 35% всех рабочих – женщины, а остальные мужчины, которых на 252 человека больше, чем женщин. Определить общее число рабочих.

2.      Товар до снижения цен стоил 180 тыс. руб., а после снижения – 135 тыс. руб. На сколько процентов снижена цена товара?

3.      Разделить число 650 на две части так, чтобы 80% первой части были равны 24% второй части. В ответе записать большую часть.

4.      На сколько нужно увеличить число 252, чтобы 39% от него были бы равны 234?

5.      Для клуба решили купить четыре баяна и три аккордеона на сумму 1 470 000 руб. После снижения цен на баян на 20% за ту же покупку уплатили 1 326 000 руб. Найти цену аккордеона (в руб.).

6.      Цену изделия снизили на 10%. Затем новую цену снизили на 20%. После этих снижений цен стоимость изделия оказалась равной 72 тыс. руб. Найти первоначальную стоимость изделия.

7.      На сколько процентов увеличится объем параллелепипеда, если все его измерения увеличить на 10%?

8.      Кусок сплава меди с оловом весит 12 кг и содержит 45% меди. Сколько чистого олова надо прибавить к этому куску, чтобы полученный сплав содержал 40% меди?

9.      Сумма цифр двузначного числа равна 12. От перестановки цифр увеличивается на 75%. Найти это число.

10. Бригада должна была выполнить заказ за 12 дней. Ежедневно перевыполняя норму на 25%, бригада за 10 дней работы не только выполнила задание, но еще изготовила сверх плана 42 детали. Сколько деталей в день изготовляла бригада?

11. Предприятие, выпустив за год 10 800 деталей, перевыполнила план на 35%. Каково было плановое задание предприятия?

12. В сплаве олова и свинца содержится 25% олова. Сколько сплава (в кг) получится из 210 кг олова?

13. Масса меди составляет 77% массы бронзы. Сколько бронзы (в кг) можно изготовить, имея 192,5 кг меди?

14. Население города за год выросло с 80 000 до 86 400 человек. Найти годовой процент прироста населения.

15. Найти число С, если известно, что 25% его равно 45% от числа 320.

16. Два цеха должны были выпустить по плану 180 станков в год. Первый цех выполнил план на 102% и поэтому оба цеха выпустили 182 станка. Сколько станков выпустил первый цех?

17. За месяц завод должен изготавливать 50 машин. План января и марта он выполнил на 110%, а в феврале изготовил 52 машины. На сколько процентов завод перевыполнил план трех месяцев?

18. Задание ученика составляет 4/5 задания мастера. На сколько процентов задание мастера больше задания ученика?

19. Найти число, если известно, что 45% его равны 25% числа 576.

20. Цену товара снизили на 20%, затем новую цену снизили на 25%. На сколько процентов снизили первоначальную цену?

21. На сколько процентов уменьшится объем параллелепипеда, если длину его высоты уменьшить на 10%?

22. Найти число, зная, что 15% его составляет 20% от 19,5.

23. Найти 25% от 25.

 

 

 

Скачано с www.znanio.ru