Рабочая программа по математике для 5-9 классов

НЕКОММЕРЧЕСКОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ
ЧАСТНОЕ УЧРЕЖДЕНИЕ
«ШКОЛА «РАЗУМ-Л»
|
Рассмотрено на заседании педагогического совета Протокол № 1 от «29» августа 2019г.
|
|
Утверждено: Директор школы: _________ /Бачева Е. В. / «30» августа 2019 г
|
РАБОЧАЯ ПРОГРАММА
по предмету «Математика»
на 2019-2020 учебный год
Уровень образования: основное общее образование 5-9 классы
Количество часов: 845 (по 5 ч. неделю)
Учитель: Бачева Е. В. (1 категория)
г. Москва
2019 г.
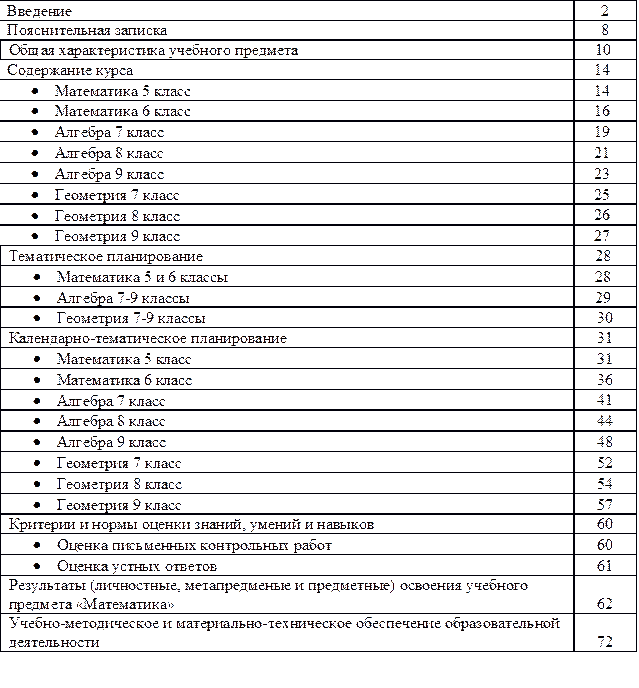 Содержание
Содержание
Введение
Один из факторов успешного процесса преобразования российского общества - высокое качество образования. Образование в обществе рассматривается с разных позиций.
Итак, образование - единый целенаправленный процесс воспитания и обучения, являющийся общественно значимым благом и осуществляемый в интересах человека, семьи, общества и государства, а также совокупность приобретаемых знаний, умений, навыков, ценностных установок, опыта деятельности и компетенции определенных объема и сложности в целях интеллектуального, духовно-нравственного, творческого, физического и (или) профессионального развития человека, удовлетворения его образовательных потребностей и интересов.
Образование - процесс и результат овладения учащимися системой знаний (математических), познавательных умений и навыков, формирования на этой основе мировоззрения, нравственных и других качеств личности, развития ее творческих сил и способностей.
Образование рассматривается в двух аспектах:
• социальном (отражающем требования общества к образованию);
• личностном (определяющем цели образования для каждой личности индивидуально).
Образованную личность характеризуют: определенность и конкретность мышления; широта и гибкость мышления; умение ориентироваться в широком круге проблем и желание решать их; разнообразие потребностей; способность прогнозировать развитие событий и моделировать свою деятельность; высокая работоспособность и т.д. Основной целью математического образования является воспитание у школьников умения рассматривать явления реального мира с математической точки зрения, видеть практическую направленность математики и её приложений.
Значение математического образования для формирования духовной сферы человека, его интеллектуальных и нравственных ценностей велико. В процессе обучения математике воспитывается настойчивость, целеустремленность, дисциплина, критичность мышления, развиваются математические способности, формируется понимание красоты математических утверждений, развивается пространственное воображение и др.
Современное преобразование системы математического образования осуществляется на основе: демократизации (обеспечение права каждому ученику на получение полноценного математического образования); гласности (наличие открытой и полной информации о состоянии преподавания и результативности обучения математике); децентрализации (право регионов и школ на выбор программ, учебных пособий, на самостоятельное решение проблем математического образования); реализма (реальная политика в области математического образования).
Цели обучения математике.
Цели образования - один из определяющих компонентов педагогической системы. Они зависят от современных условий, социального заказа общества к образованию граждан.
Основные цели обучения математике (в широком смысле):
1. Овладение всеми учащимися элементами мышления и деятельности, которые наиболее ярко проявляются в математической ветви человеческой культуры и которые необходимы каждому для полноценного развития в современном обществе.
2. Создание условий для зарождения интереса к математике и развития математических способностей одаренных школьников.
Соответственно целям обучения выделяются уровни обучения математике (рис. 1):
образование математика
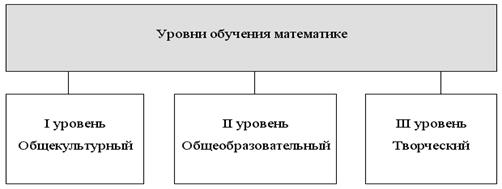
Рис. 1 Уровни обучения математике
Цели обучения математике (в узком смысле): общеобразовательные, воспитательные, развивающие.
Общеобразовательные цели: овладение учащимися системой математических знаний, умений и навыков, дающей представление о предмете математики, о математических приемах и методах познания, применяемых в математике.
Воспитательные цели: воспитание активности, самостоятельности, ответственности; воспитание нравственности, культуры общения; воспитание эстетической культуры, воспитание графической культуры школьников.
Развивающие цели: формирование мировоззрения учащихся, логической и эвристической составляющих мышления, алгоритмического мышления; развитие пространственного воображения.
Цели обучения могут формулироваться по-разному в зависимости от их ориентации. Например, можно определить цель обучения через деятельность учителя; через учебную деятельность учащихся.
Достижение целей обучения математике определяется функциями обучения математике.
Функции обучения математике.
Функции обучения математике: образовательная, воспитательная и развивающая, а также: эвристическая, прогностическая, эстетическая, практическая, контрольно-оценочная, информационная, корректирующая и интегрирующая.
Образовательная функция обучения предполагает овладение школьниками системой математических знаний, дающей представление о предмете математики, ее методах и приложениях. Образовательная функция во многом обусловливает развитие мировоззрения школьников, которое представляет собой синтез знаний, умений и убеждений.
Воспитательная функция обучения характеризуется формированием интереса к изучению математики, развитием устойчивой мотивации к учебной деятельности.
Развивающая функция обучения заключается в формировании познавательных психических процессов и свойств личности, таких как внимание, память, мышление, познавательная активность и самостоятельность, способности, а также формирование логических приемов мыслительной деятельности (анализа, синтеза, обобщения, абстрагирования и т. п.), общеучебных приемов.
Информационная функция заключается в том, что в процессе обучения ученик знакомится с историей возникновения математических идей, их развитием, биографией ученых, разными точками зрения на те или иные концепции. В процессе обучения математике ученик получает достаточно большой объем информации, знакомится с различными приложениями математики, новыми открытиями в области математики.
Эвристическая функция обучения предполагает создание учителем в процессе обучения условий, которые обеспечивают развитие способностей ребенка. К эвристической функции обучения относится применение учителем эвристических приемов и методов в обучении математике, умение применять их в различных конкретных ситуациях.
Прогностическая функция обучения математике ориентирована на формирование у школьников прогностических умений: умение обнаруживать нерешенные проблемы, выдвигать гипотезы, умение видеть альтернативное решение проблем и др.
Эстетическая функция предусматривает приобщение школьников к красоте, воспитание у них эстетических вкусов. Учебный материал должен быть изложен логически последовательно, системно и привлекательно.
Практическая функция обучения математике заключается в ориентации обучения на решение задач, на формирование умения математически исследовать явления реального мира, на практическую направленность учебного материала. Изначальным стимулом развития математического знания является потребность в решении конкретных практических задач. Движение вперед в области математики обусловлено возникновением потребностей, в большей или меньшей мере носящих практический характер. Но, раз возникшее, оно неизбежно приобретает внутренний размах и выходит за рамки непосредственной полезности, отмечает Р. Курант.
Контрольно-оценочная функция обучения математике заключается в необходимости осуществления контроля, коррекции, оценки знаний и умений школьников. В связи с этим, встает вопрос о качестве образования, компетенциях.
Качество образования - социальная категория, определяющая состояние и результативность процесса образования в обществе, его соответствие потребителям и ожиданиям общества (различных социальных групп) в развитии и формировании гражданских, бытовых и профессиональных компетенций личности.
Компетенция - это общая способность, основанная на знаниях, опыте, ценностях, склонностях, которые приобретаются в ходе обучения.
Корректирующая функция заключается в корректировании информации, получаемой учащимися. Значение и сущность информации, полученной из различных источников, может быть различной. Учитель должен предлагать учащимся откорректированную информацию. Он должен помочь ученику правильно разобраться в ней и оценить ее.
Интегрирующая функция заключается в формировании системности знаний, в понимании взаимосвязи между изучаемыми понятиями, теоремами, способами деятельности, методами.
Все функции обучения математике взаимосвязаны, они зависят друг от друга и реализуются на практике в различных сочетаниях. Обучение математике, реализуя свои функции, обеспечивает достижение основных целей обучения. Перечисленные выше цели математического образования составляют основу отбора его содержания.
Содержание математического образования.
Содержание математического школьного образования отражается в ряде нормативных документов, учебниках, учебных планах, учебных программах, методических пособиях. Учебные программы по математике включают в себя перечень тем изучаемого материала , рекомендации по количеству времени на каждую тему, перечень знаний, умений и навыков по предмету.
Расположение математического материала в учебных программах осуществляется в трех вариантах:
• линейное (материал располагается последовательно);
• концентрическое (некоторые разделы изучаются с повтором на новом уровне);
• спиральное (материал располагается последовательно по циклам).
Cодержание математического образования включает: систему знаний об окружающем нас мире; систему общих интеллектуальных и практических навыков и умений; опыт творческой деятельности, ее основные черты, которые постепенно были накоплены человечеством в процессе развития общественно-практической деятельности; опыт эмоционально-волевого отношения к миру, обществу, друг к другу.
Новые научные достижения в области математики, их внедрение в практику приводят к пересмотру школьного курса математики, обогащению его новыми приложениями. Одновременно из содержания школьного образования исключаются или сокращаются до минимума разделы, не актуальные и потерявшие свою практическую значимость. На смену им приходят вопросы, имеющие важное значение в современном образовании. Таковыми, например, являются элементы теории вероятности, математической статистики, логики и т.д.
Базисный учебный план является обязательным для всех учебных заведений, дающих среднее образование. Он является основным документом для разработки учебных программ, учебно-тематического планирования.
Составными частями содержания образования являются: знания, умения, навыки.
Знания – это понимание, сохранение в памяти и умение воспроизводить и применять на практике основные научные факты и теоретические обобщения. Любое знание выражается в понятиях, категориях, принципах, законах, закономерностях, фактах, идеях, символах, концепциях, теориях, гипотезах. Математические знания представляют собой математические понятия, законы, символику, математический язык и т.д.
Умения – это владение способами, приемами применения усваиваемых знаний на практике. Умения включают в себя знания и навыки. Формирование знаний, умений и навыков зависит от способностей человека.
Навыки – составные элементы умения, т.е. автоматизированные действия, доведенные до высокой степени совершенства.
Содержание образования строится с учетом факторов, детерминирующих на современном этапе развития общества. Таковыми сегодня являются:
• соответствие логике математики как науки;
• степень его удовлетворения принципам обучения (научности, последовательности, системности и т.д.):
• учет психологических возможностей и возрастных особенностей школьников разных ступеней обучения (младший, средний, старший школьник);
• потребности личности в образовании (дифференцированное обучение, коррекционное обучение и т.д.);
• формирование профессиональной направленности школьников.
В стандартах – результаты обучения представлены в требованиях к уровню подготовки выпускников.
Требования структурированы по 3-м компонентам:
· Знать / понимать;
· Уметь;
· Использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
Предмет математики разделен на 4 области: арифметика; алгебра; геометрия; элементы логики, комбинаторики, статистики и теории вероятности. К каждой области математики к практическим умениям сформированы определенные требования, которые включают в себя по 3 компонента. Так в области алгебры:
· Выполнения расчетов по формулам, составления формул, выражающих зависимость между реальными величинами; для нахождения нужной формулы в справочных материалах;
· Моделирование практических ситуаций и исследований построенных моделей с использованием аппарата алгебры;
· Описания зависимостей между физическими величинами, при исследовании несложных практических ситуаций;
· Интерпретации графиков реальных зависимостей между величинами.
Геометрии:
Описания реальных ситуаций на языке геометрии;
Расчетов, включающих простейшие тригонометрические формулы;
Решение геометрических задач с использованием тригонометрии;
Решение практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
Построение геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Элементы логики, комбинаторики, статистики и теории вероятности:
Выстраивания аргументации при доказательстве (в форме монолога и диалога);
Распознавания логически некорректных рассуждений;
Решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин площадей, объемов, времени, скорости;
Решения учебных и практических задач, требующих систематического перебора вариантов;
Понимания статистических утверждений.
Контрольно-измерительных материалов для того, чтобы понять овладел ли выпускник практическими знаниями, компетентен ли в математики, к сожалению (или к счастью) нет. На кафедре математики каждый учитель попытался оценить своих учащихся из собственных наблюдений. Математическую компетентность разделили на три уровня: «воспроизведение», «связи», «размышления».
«Воспроизведение»: Привычные формы представления информации, прямое применение известных фактов, стандартных приемов и методов.
«Связи»: Переход от одной формы информации к другой, создание математической модели, применение различных известных методов к решению задач, близких к известным, интерпретация полученного решения.
«Размышления»: Сложные проблемы, размышление и интуиция, творческий подход, разработка метода решения, обобщение, обоснование.
Эти три уровня сопоставимы с традиционными уровнями знаний: репродуктивным, конструктивным, творческим.
Государственный стандарт.
Стандартизация образования является одной из тенденций его развития. Основным нормативным документом наряду с Законом «Об образовании» является государственный образовательный стандарт.
Образовательный стандарт – это обязательный уровень требований к общеобразовательной подготовке выпускников и соответствующие этим требованиям содержания, методы, формы, средства обучения и контроля.
В государственном стандарте общего образования выделяются три составных компонента:
– федеральный;
– национально-региональный;
– местный, школьный.
В федеральном компоненте отражены нормативы, обеспечивающие единство педагогического пространства России и интеграцию личности в систему мировой культуры.
Национально-региональный компонент составляют нормы в области изучения родного языка, истории, географии, искусства и других учебных предметах, отражающих специфику функционирования и развития региона, населяющего его народа.
Школьный компонент отражает специфику функционирования отдельно взятого образовательного учреждения.
В рамках федерального и национально-регионального уровней стандарт образования включает:
– описание содержания образования на каждой из его ступеней, которое государство обязано предоставить обучаемому в объеме необходимой общеобразовательной подготовки;
– требования к минимально необходимой подготовке учащихся в рамках указанного объема содержания;
– максимально допустимый объем учебной нагрузки по годам обучения.
В содержательном аспекте стандарт средней общеобразовательной школы предусматривает:
– владение базовыми понятиями;
– знание теорий, концепций, законов и закономерностей основ науки, ее истории, методологии, проблем и прогнозов;
– умение применять научные знания на практике при решении познавательных (теоретических) и практических задач как в стабильной (стандартной), так и в изменяющейся (нестандартной) ситуации;
– иметь собственные суждения в области теории и практики данной образовательной области;
– знание основных проблем общества (России) и понимание своей роли в их решении;
– владение технологией непрерывного самообразования по отраслям знаний, наукам и видам деятельности.
Изложенное представляет собой общие основы стандартизации образования по ступеням, уровням образования и конкретизируется оно по образовательным областям, конкретным учебным дисциплинам, и уже на основе требований к уровню представления учебного материала и обязательной подготовке ученика разрабатывается система заданий (тестов), служащих инструментарием для контроля и оценки уровня подготовки школьников.
Государственные образовательные стандарты приобретают реальное воплощение в формировании содержания образования в следующих нормативных документах: учебном плане, учебной программе и учебной литературе (учебниках, учебных пособиях, задачниках и т. п.).
Каждый из этих нормативных документов соответствует определенному уровню проектирования содержания школьного образования. Учебный план – уровню теоретических представлений; учебная программа – уровню учебного предмета; учебная литература – уровню учебного материала.
Учебные планы.
Учебные планы – нормативные документы, направляющие деятельность школы.
В практике современной общеобразовательной школы используются несколько типов учебных планов.
Базисный план общеобразовательных учреждений – это основной государственный нормативный документ, являющийся составной частью государственного стандарта в этой области образования. Он утверждается Государственной Думой (для основной школы) либо Министерством общего и профессионального образования РФ (для полной средней школы). Являясь частью государственного стандарта, базисный учебный план представляет собой государственную норму общего среднего образования, которое устанавливает требования к структуре, содержанию и уровню образования учащихся.
Базисный учебный план охватывает следующий круг нормативов:
– продолжительность обучения (в учебных годах) общая и по каждой из его ступеней;
– недельная учебная нагрузка для базовых областей на каждой из ступеней общего среднего образования, обязательных занятий по выбору учащихся и факультативных занятий;
– максимальная обязательная недельная учебная нагрузка учащегося, включая число учебных часов, отводимых на обязательные занятия по выбору;
– итоговое количество учебных часов, финансируемое государством (максимальная обязательная учебная нагрузка школьников, факультативные занятия, индивидуальная и внеклассная работа, деление учебных групп на подгруппы).
Базисный учебный план служит основой для разработки региональных, типовых учебных планов и исходным документом для финансирования школы.
Типовой учебный план – носит рекомендательный характер и разрабатывается на основе базисного плана. Утверждается Министерством общего и профессионального образования РФ. Данный вид учебного плана не всегда подходит для новых учебных заведений (гимназий, лицеев, высших профессионально-технических училищ), которые разрабатывают свои собственные документы.
Учебный план общеобразовательной средней школы разрабатывается на основе государственного базисного и регионального учебных планов. Он отражает особенности конкретной школы. Существуют два типа учебных планов школы:
– собственно учебный план школы, который разрабатывается на основе базисного учебного плана на длительный период. Он отражает особенности конкретной школы;
– рабочий учебный план, разрабатываемый с учетом текущих условий и утверждаемый ежегодно советом школы.
Содержание образования учебного заведения любого типа отражает деление образования на фундаментальное и технологическое. Фундаментальная составляющая проявляет себя в большей степени в начальной и основной общеобразовательной школе. На старшей ступени усиливается объем технологической подготовки.
Образовательные области и на их основе комплектование учебных планов соответствующих ступеней образовательных учреждений позволяет выделить два вида обучения: теоретическое и практическое.
В структуре учебного плана выделяются инвариантная часть (ядро), обеспечивающая приобщение учащихся к общекультурным и национально значимым ценностям и формирование личностных качеств школьника и вариативная часть, обеспечивающая индивидуальный характер развития учащихся.
В учебных планах выделяют федеральный, национально-региональный и школьный компоненты.
Пояснительная записка
Рабочая программа изучения курса «Математика» разработана в соответствии с:
1. Федерального государственного образовательного стандарта основного общего образования, утвержденного приказом Министерства образования и науки Российской Федерации от 17.12.2010 г. N1897 «Об утверждении федерального государственного образовательного стандарта основного общего образования» с изменениями и дополнениями, внесенными приказом Минобрнауки РФ от 29.12.2014 г. №1644, приказом Минобрнауки РФ от 31.12.2015г. №1577.
2. Постановления Главного государственного санитарного врача РФ от 29 декабря 2010 г. N 189 "Об утверждении СанПиН 2.4.2.2821-10 "Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях" (с изменениями и дополнениями от: 29 июня 2011 г., 25 декабря 2013 г., 24 ноября 2015 г.).
3. Основной образовательной программы основного общего образования, на основе примерной Программы основного общего образования по математике и авторской программы «Математика. Сборник рабочих программ. 5-6 классы: пособие для учителей общеобразовательных организаций / (сост. Т.А. Бурмистрова). – М.: Просвещение, 2015» к учебнику для 5 класса общеобразовательной школы авторов С.М. Никольского, М.К. Потапова, Н.Н. Решетникова, А.В. Шевкина (М.: Просвещение, 2014).
1. Типовой программы «Алгебра: 7-9 классы» для общеобразовательных учреждений (базовый уровень) автор Макарычев Ю.Н. (М.: Мнемозина, 2008) для предметов алгебра и элементы логики, комбинаторики, статистики и теории вероятностей,
2. Программы общеобразовательных учреждений Бурмистровой Т.А. «Геометрия 7-9 классы» (М.Просвещение,2009) по учебнику Атанасяна Л.С.
4. Основной образовательной программы основного общего образования НОЧУ «Школа «Разум-Л» (с изменениями и дополнениями), утвержденной приказом директора школы от 26.01.2016 г.
5. Учебного плана основного общего образования для 5-9 кл. НОЧУ «Школа «Разум-Л», утвержденного на заседании педагогического совета (протокол №1 от 29.08.2019 г.).
6. Календарного учебного графика НОЧУ «Школа «Разум-Л» на 2019-2020 уч.
Данная программа реализует принцип непрерывного образования по математике, что соответствует современным потребностям личности и общества, и составлена для изучения курса математики в 5-6 классах, который является частью основной образовательной программы по математике с 5 по 9 класс. Содержание рабочей программы по математике для 7 – 9 классов (базовый уровень) отражает комплексный подход к изучению математики на ступени основного общего образования и направлено на достижение следующих целей:
1. Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
2. Интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
3. Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
4. Воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Математическое образование в 7 – 9 классах складывается из следующих содержательных компонентов: алгебра, геометрия и элементы комбинаторики, теории вероятностей, статистики и логики. По данной рабочей программе предметы алгебра и геометрия преподаются параллельно, а не блоками. Это привычно и удобно как учителю, так и ученикам. Элементы комбинаторики, теории вероятностей, статистики и логики изучаются в курсе алгебры в 9 классе.
При выборе программ для разработки Рабочей программы я ориентировалась в первую очередь на организацию преемственности математического образования между основной и старшей ступенями обучения, соблюдение единых требований к обучающимся. Так как в школе преподавание математики ведется по учебникам Л.С. Атанасяна и Ю.Н.Макарычева.
В рабочей программе соблюдается преемственность с примерными программами начального общего образования, в том числе и в использовании основных видов учебной деятельности обучающихся.
Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы. Обучение математике в основной школе направлено на достижение следующих целей:
1) в направлении личностного развития:
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
Формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
Формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
Развитие интереса к математическому творчеству и математических способностей;
2) в метапредметном направлении:
Развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
3) в предметном направлении:
Овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;
Создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
В организации учебно – воспитательного процесса важную роль играют задачи. Они являются и целью, и средством обучения. Важным условием правильной организации этого процесса является выбор рациональной системы методов и приемов обучения, специфики решаемых образовательных и воспитательных задач.
Целью изучения курса математики в 5-6 классах является систематическое развитие понятия числа, выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики, подготовка учащихся к изучению систематических курсов алгебры и геометрии. Курс строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. В ходе изучения курса обучающиеся развивают навыки вычислений с натуральными числами, овладевают навыками с обыкновенными и десятичными дробями, положительными и отрицательными числами, получают представление об использовании букв для записи выражений и свойств арифметических действий, составлении уравнений, продолжают знакомство с геометрическими понятиями, приобретают навыки построения геометрических фигур.
Целью изучения курса алгебры в 7 – 9 классах является развитие вычислительных умений до уровня, позволяющего уверенно использовать их при решении задач математики смежных предметов, усвоение аппарата уравнений и неравенств как основного средства математического моделирования задач, осуществление функциональной подготовки школьников. Курс характеризуется повышением теоретического уровня обучения, постепенным усилием роли теоретических обобщений и дедуктивных заключений. Прикладная направленность раскрывает возможность изучать и решать практические задачи.
Целью изучения курса геометрии в 7-9 классах является систематическое изучение свойств геометрических фигур на плоскости, формирование пространственных представлений, развитие логического мышления и подготовка аппарата, необходимого для изучения смежных дисциплин и курса стереометрии в старших классах.
В основе построения данного курса лежит идея гуманизации обучения, соответствующая современным представлениям о целях школьного образования и уделяющая особое внимание личности обучающегося, его интересам и способностям.
Предлагаемый курс позволяет обеспечить формирование как предметных умений, так и универсальных учебных действий школьников, а также способствует достижению определённых во ФГОС личностных результатов, которые в дальнейшем позволят обучающимся применять полученные знания и умения для решения различных жизненных задач.
Общая характеристика учебного предмета
В соответствии с видами компетенций выделены главные содержательно-целевые направления развития обучающихся средствами предмета «Математика».
Содержание математического образования в основной школе формируется на основе фундаментального ядра школьного математического образования. В программе оно представлено в виде совокупности содержательных разделов, конкретизирующих соответствующие блоки фундаментального ядра применительно к основной школе.
Содержание математического образования в основной школе включает следующие разделы: математика, алгебра, функции, вероятность и статистика, геометрия. Наряду с этим в него включены два дополнительных раздела: логика и множества, математика в историческом развитии, что связано с реализацией целей обще интеллектуального и обще-культурного развития обучающихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, пронизывающую все основные разделы содержания математического образования на данной ступени обучения.
Содержание раздела «Математика» служит базой для дальнейшего изучения обучающимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе. Завершение числовой линии (систематизация сведений о действительных числах, о комплексных числах), так же как и более сложные вопросы арифметики (алгоритм Евклида, основная теорема арифметики), отнесено к ступени общего среднего (полного) образования.
Содержание раздела «Алгебра» направлено на формирование у обучающихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики, овладения навыками дедуктивных рассуждений. Преобразование символьных форм вносит специфический вклад в развитие воображения обучающихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с иррациональными выражениями, с тригонометрическими функциями и преобразованиями, входят в содержание курса математики на старшей ступени обучения в школе.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у обучающихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Раздел «Вероятность и статистика» — обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у обучающихся функциональной грамотности — умений воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, проводить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит обучающимся рассматривать случаи, осуществлять перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и вероятности расширяются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Цель содержания раздела «Геометрия» — развить у обучающихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядности со строгостью является неотъемлемой частью геометрических знаний.
Особенностью раздела «Логика и множества» является то, что представленный в нем материал преимущественно изучается и используется распределено – в ходе рассмотрения различных вопросов курса. Соответствующий материал нацелен на математическое развитие обучающихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи.
Раздел «Математика в историческом развитии» предназначен для формирования представлений о математике как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения. На него не выделяется специальных уроков, усвоение его не контролируется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рас-смотрении проблематики основного содержания математического образования.
Ценностные ориентиры содержания учебного предмета
Математическое образование играет важную роль, как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная — с интеллектуальным развитием человека, формированием характера и общей культуры.
Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения — от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, находить в справочниках нужные формулы и применять их, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виду таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Без базовой математической подготовки невозможно стать образованным современным человеком. В школе математика служит опорным предметом для изучения смежных дисциплин. В после школьной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, где необходим высокий уровень образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и др.). Таким образом, расширяется круг школьников, для которых математика становится значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач – основной учебной деятельности на уроках математики — развиваются творческая и прикладная стороны мышления.
Обучение математике дает возможность развивать у обучающихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, сим-волические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, его отличия от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.
История развития математического знания дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
Курс математики 5-го класса – важное звено математического образования и развития школьников. На этом этапе заканчивается в основном обучение счету на множестве рациональных чисел, формируется понятие переменной и даются первые знания о приемах решения линейных уравнений, продолжается обучение решению текстовых задач, совершенствуются и обогащаются умения геометрических построений и измерений.
Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. При этом учащиеся постепенно осознают правила выполнения основных логических операций. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
Программа ориентирована, главным образом, на формирование научных (математических) понятий, а не только лишь на выработку практических навыков и умений. Это предполагает особую организацию учебного процесса в форме учебной деятельности школьников.
Содержание учебной деятельности должно развертываться в теоретической форме – от общего к частному, от абстрактного к конкретному. Освоение понятий должно происходить не в форме отработки словесных формулировок, а путем введения учащихся в новый круг задач и включением их в деятельность по поиску общего способа их решения.
Поиск способа решения новой задачи является мотивационным ядром учебной деятельности,
той ценностной установкой учеников, которая складывается в виде формального эффекта обучения как личностно-смысловое образование, основа желания и умения учиться.
Осуществление школьниками учебной деятельности способствует формированию у них таких мыслительных действий, как рефлексия, анализ и планирование, являющихся основой теоретического мышления и, одновременно развитию других познавательных процессов – восприятия, воображения, памяти.
Место учебного предмета в учебном плане
Базисный учебный план на изучение математики в основной школе отводит 5 учебных часов в неделю в течение каждого года обучения, всего 675 уроков.
Распределение учебного времени между предметами представлено в таблице.
|
Классы |
Предметы математического цикла |
Количество часов в неделю |
Количество часов в год |
|
5 |
Математика |
5 |
170 |
|
6 |
Математика |
5 |
170 |
|
7 |
Алгебра Геометрия |
3 2 |
102 68 |
|
8 |
Алгебра Геометрия |
3 2 |
102 68 |
|
9 |
Алгебра Геометрия |
3 2 |
99 66 |
|
Всего |
|
|
845 |
С учетом годового календарного учебного графика школы и расписания уроков на 2019-2020 учебный год вся программа курса Истории будет реализована в полном объеме в результате объединения тем (темы указаны в календарно-тематическом планировании).
Содержание курса
Содержание программы направлено на освоение учащимися базовых знаний и формирование базовых компетентностей, что соответствует основной образовательной программе основного общего образования. Она включает все темы, предусмотренные Федеральным государственным образовательным стандартом основного общего образования по математике и рабочей программой Т.А. Бурмистровой.
Математика
5 класс
1. Натуральные числа и нуль (46 часов)
Ряд натуральных чисел. Десятичная запись, сравнение, сложение и вычитание натуральных чисел. Законы сложения. Умножение, законы умножения. Степень с натуральным показателем. Деление нацело, деление с остатком. Числовые выражения. Решение текстовых задач арифметическими методами.
Основная цель — систематизировать и обобщить сведения о натуральных числах: об их сравнении, сложении и вычитании, умножении и делении, добиться осознанного овладения учащимися приемами вычислений с применением законов сложения и умножения, развивать навыки вычислений с натуральными числами.
При изучении данной темы вычисления выполняются сначала устно с опорой на законы сложения и умножения, на свойство вычитания, а потом столбиком. Большое внимание уделяется переместительному и сочетательному законам умножения и распределительному закону, их использованию для обоснования вычислений столбиком (на простых примерах), для рационализации вычислений. Тем самым закладывается основа осознанного овладения приемами вычислений. Вместе с тем достаточное внимание уделяется закреплению навыков вычисления столбиком, особенно в сложных случаях (нули в записи множителей или частного). Вводится понятие степени с натуральным показателем. При изучении числовых выражений закрепляются правила порядка действий.
Изучение материала предусматривает систематическую работу по развитию у учащихся умения решать текстовые задачи арифметическими способами. Решение задач требует понимания отношений «больше на ... (в ...)», «меньше на ... (в ...)» и их связи с арифметическими действиями с натуральными числами, а также понимания стандартных ситуаций, в которых используются слова «всего», «осталось» и т. п. Типовые задачи «на части», на нахождение двух чисел по их сумме и разности рассматриваются в отдельных пунктах. Работа с арифметическими способами решения задач, нацеленная на развитие мышления и речи учащихся, продолжится при изучении следующих тем. При наличии учебных часов рассматривается тема «Вычисления с помощью калькулятора».
2. Измерение величин (30часов)
Прямая, луч, отрезок. Измерение отрезков и метрические единицы длины. Представление натуральных чисел на координатном луче. Окружность и круг, сфера и шар. Углы, измерение углов. Треугольники и четырехугольники. Прямоугольный параллелепипед. Площадь прямоугольника, объем прямоугольного параллелепипеда. Единицы площади, объема, массы, времени. Решение текстовых задач арифметическими методами.
Основная цель — систематизировать знания учащихся о геометрических фигурах и единицах измерения величин, продолжить их ознакомление с геометрическими фигурами и с соответствующей терминологией.
Начальным этапом при изучении данной темы является измерение отрезков, изображение натуральных чисел на координатном луче — это освоение учащимися идеи числа как длины отрезка, точнее, как координаты точки на координатной прямой. Здесь же они вычисляют площадь прямоугольника и объем прямоугольного параллелепипеда, измерения которых — натуральные числа.
Здесь вводятся единицы измерения длины, площади и объема, устанавливаются соотношения между единицами длины, единицами площади, единицами объема, изучаются единицы массы и времени.
Введение градусной меры угла сопровождается заданиями на измерение углов и построение углов с заданной градусной мерой.
При изучении данной темы решаются задачи на движение.
При наличии учебных часов рассматривается тема «Многоугольники».
3. Делимость натуральных чисел (19 часов)
Свойства и признаки делимости. Простые и составные числа. Делители натурального числа. Наибольший общий делитель, наименьшее общее кратное.
Основная цель — познакомить учащихся со свойствами и признаками делимости, сформировать навыки их использования.
При изучении данной темы значительное внимание уделяется формированию у учащихся простейших доказательных умений. Доказательства свойств и признаков делимости проводятся на характерных числовых примерах, но методы доказательства могут быть распространены на общий случай. При этом учащиеся получают первый опыт доказательства теоретических положений со ссылкой на другие теоретические положения.
Понятия наибольшего общего делителя и наименьшего общего кратного вводятся традиционно, но следует учесть, что в дальнейшем не всегда требуется сокращать дробь на наибольший общий делитель ее числителя и знаменателя или приводить дроби обязательно к наименьшему общему знаменателю.
При наличии учебных часов рассматривается тема «Использование четности при решении задач».
4. Обыкновенные дроби (38 часов)
Понятие дроби, равенство дробей (основное свойство дроби). Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей. Законы сложения. Умножение дробей, законы умножения. Деление дробей. Смешанные дроби и действия с ними. Представление дробей на координатном луче. Решение текстовых задач арифметическими методами.
Основная цель — сформировать у учащихся умения сравнивать, складывать, вычитать, умножать и делить обыкновенные и смешанные дроби, вычислять значения выражений, содержащих обыкновенные и смешанные дроби, решать задачи на сложение и вычитание, на умножение и деление дробей, задачи на дроби, на совместную работу арифметическими методами.
Формирование понятия дроби сопровождается обучением решению простейших задач на нахождение части числа и числа по его части, а также задач, готовящих учащихся к решению задач на совместную работу. При вычислениях с дробями допускается сокращение дроби на любой общий делитель ее числителя и знаменателя (необязательно наибольший), а также приведение дробей к любому общему знаменателю (необязательно наименьшему). Но в том и в другом случаях разъясняется, когда вычисления будут наиболее рациональными.
При изучении данной темы решаются задачи на сложение и вычитание дробей, основные задачи на дроби.
Операция умножения дробей вводится по определению, из которого получается правило умножения натурального числа на обыкновенную дробь. Особое внимание уделяется доказательствам законов сложения и умножения для дробей. Они проводятся на характерных числовых примерах с опорой на соответствующие законы для натуральных чисел, но методы доказательства могут быть распространены на общий случай.
Деление дробей вводится как операция, обратная умножению. Смешанная дробь рассматривается как другая запись обыкновенной неправильной дроби. Отдельно изучаются вычисления со смешанными дробями. На характерных числовых примерах показывается, что площадь прямоугольника и объем прямоугольного параллелепипеда, измерения которых выражены рациональными числами, вычисляются по тем же правилам, что и для натуральных чисел.
Заключительный этап изучения темы — изображение дробей точками на координатной прямой.
В данной теме решаются задачи на умножение и деление дробей, а также обращается особое внимание на то, что рассмотренные ранее задачи на дроби можно решать с помощью умножения и деления на дробь. Задачи на совместную работу выделены в отдельный пункт.
5. Повторение (10 часов)
6 класс
1. Делимость чисел (20 часов)
Делители и кратные числа. Общий делитель и общее кратное. Признаки делимости на 2,3,5,9,10. Простые и составные числа. Разложение натурального числа на простые множители.
Основная цель - завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями.
В теме завершается изучение вопросов, связанных с натуральными числами. Основное внимание должно быть уделено знакомству с понятиями «делитель» и «кратное», которые применяются при сокращении дробей и приведении их к общему знаменателю. Упражнения полезно выполнять с опорой на таблицу умножения – прямым подбором.
Определенное внимание уделяется знакомству с признаками делимости, понятиям простого и составного числа. При их изучении целесообразно формировать умения проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило.
Учащиеся должны уметь раскладывать число на простые множители. Умения раскладывать число на простые множители не обязательно добиваться от всех учащихся.
2. Сложение и вычитание дробей с разными знаменателями (22 часов)
Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Понятие о наименьшем общем знаменателе нескольких дробей. Сравнение, сложение, вычитание дробей. Решение текстовых задач.
Основная цель - выработать прочные навыки преобразования дробей, сложения и вычитания дробей.
Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к общему знаменателю. Умение приводить дроби к общему знаменателю применяется при сравнении дробей.
При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа.
3. Умножение и деление обыкновенных дробей (31 часов)
Умножение и деление обыкновенных дробей. Основные задачи на дроби.
Основная цель - выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби.
В теме завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Навыки должны быть достаточно прочными, чтобы учащиеся не испытывали затруднений в вычислениях с рациональными числами, чтобы алгоритмы действий с обыкновенными дробями могли стать в дальнейшем опорой для формирования умений выполнять действия с алгебраическими дробями.
Расширение аппарата действий с дробями позволяет решать текстовые задачи, в которых требуется найти дробь от числа или число по заданному значению дроби.
4. Отношения и пропорции (18 часов)
Пропорция. Основное свойство пропорции. Решение задач с помощью пропорции. Понятие о прямой и обратной пропорциональности величин. Задачи на пропорции. Масштаб. Формулы длины окружности и площади круга. Шар.
Основная цель – Сформировать понятие пропорции, прямой и обратной пропорциональности величин.
Необходимо, чтобы учащиеся усвоили основное свойство пропорции, т.к. оно находит применение на уроках математики, физики, химии. Достаточное внимание должно быть уделено решению задач на проценты с помощью пропорции.
Понятие о прямой и обратной пропорциональности величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач.
В теме даются представления о длине окружности и площади круга. Формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром.
5. Положительные и отрицательные числа (13 часов)
Положительные и отрицательные числа. Противоположные числа. Модуль числа и его геометрический смысл. Сравнение чисел. Целые числа. Изображение чисел на координатной прямой. Координата точки.
Основная цель – расширить представления учащихся о числе путем введения отрицательных чисел.
Целесообразность введения отрицательных чисел показывается на содержательных примерах. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой. В дальнейшем она будет служить наглядной основой для правил сравнения, сложения и вычитания чисел.
Особое внимание следует уделить усвоению понятия «модуль числа», прочное знание которого необходимо для формирования умения сравнивать отрицательные числа, а в дальнейшем для овладения алгоритмами арифметических действий с положительными и отрицательными числами.
6. Сложение и вычитание положительных и отрицательных чисел (11 часов)
Сложение и вычитание положительных и отрицательных чисел.
Основная цель – выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.
Действия с отрицательными числами вводятся на основе представлений об изменении величин: сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек координатной прямой. При изучении темы отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами.
7. Умножение и деление положительных и отрицательных чисел (12 часов)
Умножение и деление положительных и отрицательных чисел. Понятие о рациональном числе. Десятичное приближение обыкновенной дроби. Применение законов арифметических действий для рационализации вычислений.
Основная цель – выработать прочные навыки арифметических действий с положительными и отрицательными числами.
Навыки умножения и деления положительных и отрицательных чисел отрабатываются сначала при выполнении отдельных действий, затем в сочетании с навыками сложения и вычитания при вычислении значений числовых выражений.
При изучении темы
учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную
необходимо (по возможности) числитель разделить на знаменатель. В каждом
конкретном случае они должны знать, в какую дробь обращается данная
обыкновенная дробь – в десятичную или периодическую. Учащиеся должны знать
представление в виде десятичной дроби таких дробей, как ![]()
8. Решение уравнений (16 часов)
Простейшие преобразования выражений: раскрытие скобок, приведение подобных слагаемых. Решение линейных уравнений. Примеры решения текстовых задач с помощью линейных уравнений.
Основная цель – подготовить учащихся к выполнению преобразований выражений, решению уравнений.
Преобразования буквенных выражений путем раскрытия скобок и приведения подобных слагаемых отрабатываются в той степени, в которой они необходимы для решения несложных уравнений.
Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одной переменной.
9. Координаты на плоскости (16 часов)
Построение перпендикуляра к прямой и параллельных прямых с помощью чертежного треугольника и линейки. Прямоугольная система координат на плоскости, абсцисса и ордината точки. Примеры графиков, диаграмм.
Основная цель – познакомить учащихся с прямоугольной системой координат на плоскости.
Учащиеся должны научиться распознавать и изображать параллельные и перпендикулярные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и чертежного треугольника, не требуя воспроизведения точных определений.
Основным результатом знакомства учащихся с координатной плоскостью должны стать знания порядка записи координат точек плоскости и их названий, умения построить координатные оси, отметить точку по заданным координатам, определить координаты точки, отмеченной на плоскости.
Формированию графических и вычислительных умений способствует построение столбчатых диаграмм. При выполнении этих упражнений найдут применение сведения о масштабе и округлении чисел.
10.Итоговое повторение курса математики 5-6 классов
Алгебра
7 класс
1.Повторение (1 час)
2.Выражения, тождества, уравнения (21 час)
Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейное уравнение с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней.
Основная цель:
- формирование представлений о целостности и непрерывности курса математики 5 и 6 класса;
- обобщение и систематизация знаний о числовых выражениях, допустимых и недопустимых значениях переменной выражения, математических утверждениях, математическом языке; выполнении действий по арифметическим законам сложения и умножения, действий с десятичными дробями, действий с обыкновенными дробями;
3.Функции (11 часов)
Координатная прямая. Алгоритм отыскания координат точки. Алгоритм построения точки M(a;b) в прямоугольной системе координат. Линейное уравнение с двумя переменными. Решение уравнения. График уравнения. Алгоритм построения графика уравнения ax+by+c=0. Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции. Линейная функция y=kx+b и ее график. Взаимное расположение графиков линейной функции.
Основная цель:
– формирование представлений о прямоугольной системе координат, об абсциссе, ординате, о числовых промежутках, числовых лучах, линейной функции и ее графике;
– формирование умений построения графика линейной функции, исследования взаимного расположения графиков линейных функций;
4. Степень с натуральным показателем (11 часов)
Степень. Основание степени. Показатель степени. Свойства степени с целым показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем.
Основная цель:
– формирование представлений о степени с натуральным показателем, о степени с нулевым показателем;
– формирование умений составления таблицы основных степеней и ее применение при решении заданий
5. Многочлены (17 часов)
Многочлен. Коэффициент одночлена. Стандартный вид многочлена. Сложение и вычитание многочленов. Умножение одночлена на многочлен. Вынесение общего множителя за скобки. Умножение многочлена на многочлен. Разложение многочлена на множители способом группировки. Доказательство тождеств.
Основная цель:
– формирование представлений о многочлене стандартного вида, об арифметических операциях над многочленами, о подобных многочленах;
– формирование умений представлять многочлен в стандартном виде, выполнять арифметические действия над многочленами
6.Формулы сокращенного умножения (19 часов)
Возведение в квадрат суммы и разности двух выражений. Разложение на множители с помощью квадрата суммы и квадрата разности. Умножение разности двух выражений на их сумму. Разложение разности квадратов на множители. Разложение на множители суммы и разности кубов. Преобразование Целого выражения в многочлен. Применение различных способов для разложения на множители. Применение преобразований целых выражений.
Основная цель:
-получение и использование формул сокращенного умножения.
7. Системы линейных уравнений (16 часов).
Линейное уравнение с двумя переменными. График линейного уравнения с двумя переменными. Системы линейных уравнений с двумя переменными. Способ подстановки. Способ сложения. Решение задач с помощью систем уравнений.
Основная цель:
-ознакомить с понятием об уравнении с двумя переменными и их решением, графиком линейного уравнения с двумя переменными;
-получение представлений о графиках нелинейных уравнений с двумя переменными;
-ознакомление с понятием систем линейных уравнений с двумя переменными, решением и графическим способом решения таких систем.
9. Обобщающее повторение (6 часов)
Основная цель:
– обобщение и систематизация знаний тем курса алгебры за 7 класс с решением заданий повышенной сложности;
– формирование понимания возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни
8 класс
1. Рациональные дроби (22 часа).
Понятие рациональных выражений. Основное свойство дроби. Сокращение дробей.
Сложение и вычитание дробей.
Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
Основная цель:
– формирование представлений об алгебраической дроби, о рациональном выражении;
– формирование умений умножения и деления, сложения и вычитания алгебраических дробей, сокращения дробей, приведения алгебраических дробей к общему знаменателю, построение графика функции у=к/х.
2. Квадратные корни (16 часов)
Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел. Функция, ее свойства и график. Область значений функции. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе дроби.
Основная цель:
– формирование представлений о квадратном корне из неотрицательного числа, о функции ;
– формирование представлений о рациональных, иррациональных и действительных числах
3. Квадратные уравнения (18 часов).
Квадратное уравнение и его корни. Решение квадратных уравнений по формуле. Решение задач с помощью квадратных уравнений. Графическое решение квадратных уравнений. Теорема Виета. Решение дробно-рациональных уравнений.
Основная цель:
– формирование представлений о квадратном уравнении и его корнях;
-формирование умений решать квадратные и дробно-рациональных уравнений, а также решать задачи с помощью уравнений.
4. Неравенства (14 часов).
Свойства числовых неравенств. Неравенство с переменной. Решение неравенств с переменной. Линейное неравенство. Равносильные неравенства. Равносильное преобразование неравенства. Квадратное неравенство. Алгоритм решения квадратного неравенства.
Основная цель:
– формирование представлений о числовых неравенствах, неравенстве с одной переменной, модуле действительного числа;
– формирование умений исследования функции на монотонность, применения приближенных вычислений
5.Степень с целым показателем (8 часов).
Определение степени с целым отрицательным показателем. Свойства степени с целым показателем. Стандартный вид числа. Запись приближенных значений и действия над ними.
Основная цель:
-формирование представления о степени с целым отрицательным показателем;
-формирование умений приводить к стандартному виду числа, записывать приближенные значения.
6. Теория вероятностей (11 часов).
Случайные опыты. Элементарные события. Равновозможные элементарные события. Вероятности событий. Опыты с равновозможными элементарными событиями. Противоположное событие. Диаграммы Эйлера. Объединение и пересечение событий. Несовместные события. Правило сложения вероятностей. Формула сложения вероятностей. Независимые события. Умножение вероятностей.
Основная цель – сформировать начальные представления о сборе и группировке статистических данных, их наглядной интерпретации.
Учащиеся получают начальные представления об организации статистических исследований. Они знакомятся с понятиями генеральной и выборочной совокупности. Приводятся примеры представления статистических данных в виде таблиц частот и относительных частот. Учащимся предлагаются задания на нахождение по таблице частот таких статистических характеристик, как среднее арифметическое, мода, размах. Рассматривается вопрос о наглядной интерпретации статистической информации. Известные учащимся способы наглядного представления статистических данных с помощью столбчатых и круговых диаграмм расширяются за счет введения таких понятий, как полигон и гистограмма.
7. Обобщающее повторение (13 часов).
Основная цель:
– обобщение и систематизация знаний тем курса алгебры за 8 класс с решением заданий повышенной сложности;
– формирование понимания возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни.
9 класс
1. Квадратичная функция (21 час).
Функция. Область определения и область значения функции. Свойства и графики основных функций. Корни квадратного трехчлена. Разложение квадратного трехчлена на множители. Функция у=ах, её график и свойства. Графики функций у=ах+п и у=а(х+п). Построение графика квадратичной функции. Степенная функция. Корень п-степени.
Основная цель:
-формирование умений находить область определения и область значений;
-формирование умений находить корни квадратного трехчлена, раскладывать его на множители;
-формирование умений построения графиков функций у=ах, у=ах+п, у=а(х+п), а также квадратичной и степенной функции.
3.Уравнения и неравенства с одной переменной (15 часов).
Целое уравнение и его корни. Решение уравнений методом введения новой переменной. Дробно-рациональные уравнения. Решение неравенств второй степени с одной переменной.
Основная цель:
-формирование умений решать уравнения и неравенства с одной переменной, решать дробно-рациональные уравнения.
3. Уравнения и неравенства с двумя переменными (12 часов).
Линейные и квадратные неравенства (повторение). Рациональное неравенство. Метод интервалов.
Множества и операции над ними. Система неравенств. Решение системы неравенств. Основная цель:
– формирование представлений о частном и общем решении рациональных неравенств и их систем, о неравенствах с модулями, о равносильности неравенств
Рациональное уравнение с двумя переменными. Решение уравнения p(x;y)=0. Равносильные уравнения с двумя переменными. Формула расстояния между двумя точками координатной плоскости. График уравнения (x-a)2+(y-b)2=r2 . Система уравнений с двумя переменными. Решение системы уравнений. Неравенства и системы неравенств с двумя переменными. Методы решения систем уравнений (метод постановки, алгебраического сложения, введения новых переменных). Равносильность систем уравнений. Системы уравнений как математические модели реальных ситуаций.
Основная цель:
– формирование представлений о системе двух рациональных уравнений с двумя переменными, о рациональном уравнении с двумя переменными
5. Прогрессии (16 часов).
Числовая последовательность. Способы задания числовых последовательностей (аналитический, словесный, рекуррентный). Свойства числовых последовательностей. Арифметическая прогрессия. Формула n – го члена. Формула суммы членов конечной арифметической прогрессии. Характеристическое свойство. Геометрическая прогрессия. Формула n – го члена. Формула суммы членов конечной геометрической прогрессии. Характеристическое свойство. Прогрессии и банковские расчеты.
Основная цель:
– формирование представлений о понятии числовой последовательности, арифметической и геометрической прогрессиях как частных случаях числовых последовательностей; о трех способах задания последовательности: аналитическом, словесном и рекуррентном;
– сформировать и обосновать ряд свойств арифметической и геометрической прогрессий, свести их в одну таблицу
6. Элементы комбинаторики, статистики и теории вероятностей (14 часов).
Комбинаторные задачи. Правило умножения. Факториал. Перестановки. Группировка информации. Общий ряд данных. Кратность варианты измерения. Табличное представление информации. Частота варианты. Графическое представление информации. Полигон распределение данных. Гистограмма. Числовые характеристики данных измерения (размах, мода, среднее значение). Вероятность. Событие (случайное, достоверное, невозможное). Классическая вероятностная схема. Противоположные события. Несовместные события. Вероятность суммы двух событий. Вероятность противоположного события. Статистическая устойчивость. Статистическая вероятность.
Основная цель:
– формирование представлений о новом математическом направлении – комбинаторике, статистике и теории вероятностей; о понятиях множества и операции над ними, о комбинаторных задачах и простейших вероятностных задачах;
– формирование умения вывода основных формул теории вероятности и статистики.
7. Обобщающее повторение (26 часов).
Основная цель:
Обобщить и систематизировать курс алгебры по основным темам за 9 класс, Формирование понимания возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни.
Геометрия
7 класс
1.Начальные геометрические сведения (11 часов)
Начальные понятия планиметрии. Геометрические фигуры. Понятие о равенстве фигур. Отрезок. Равенство отрезков. Длина отрезка и ее свойства. Угол. Равенство углов. Величина угла и ее свойства. Вертикальные и смежные углы и их свойства. Перпендикулярные прямые.
Основная цель:
– систематизировать знания учащихся об основных свойствах простейших геометрических фигур, ввести понятие равенства фигур.
2.Треугольники (15 часов).
Треугольник. Признаки равенства треугольников. Медианы, биссектрисы, высоты треугольника. Равнобедренный треугольники его свойства. Основные задачи на построение с помощью циркуля и линейки.
Основная цель:
– сформировать умение доказывать равенство данных треугольников, опираясь на изученные признаки; отработать навыки решения простейших задач на построение с помощью циркуля и линейки.
3.Параллельные прямые (12 часов).
Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых.
Основная цель:
– дать систематические сведения о параллельности прямых, ввести аксиому параллельных прямых.
4.Соотношения между сторонами и углами треугольника (22 часа).
Сумма углов треугольника. Соотношения между сторонами и углами треугольника. Неравенство треугольника. Некоторые свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Задачи на построение.
Основная цель:
– расширить знания учащихся о треугольниках.
5. Повторение. Решение задач (8 часов).
8 класс
1.Четырехугольники (15 часов).
Понятие многоугольника, выпуклого многоугольника. Параллелограмм и его признаки и свойства. Трапеция. Прямоугольник, квадрат, ромб, и их свойства. Осевая и центральная симметрии.
Основная цель:
– дать обучающимся систематические сведения о четырехугольниках и их свойствах; сформировать представления о фигурах, симметричных относительно точки или прямой.
2.Площади фигур (14 часов).
Понятие о площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
Основная цель:
– сформировать у обучающихся понятие площади многоугольника, развить умение вычислять площади фигур, применяя изученные свойства и формулы, применять теорему Пифагора.
3.Подобные треугольники (19 часов)
Подобные треугольники. Признаки подобия треугольников. Применение подобия треугольников. Применение подобия к доказательствам теорем и решению задач. Соотношения между сторонами и углами прямоугольного треугольника.
Основная цель:
– сформировать понятие подобных треугольников, выработать умение применять признаки подобия треугольников, сформировать аппарат решения прямоугольных треугольников.
4.Окружность (15 часов).
Касательная к окружности и ее свойства. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружность.
Основная цель:
– дать учащимся систематизированные сведения об окружностях и ее свойствах, вписанной и описанной окружностях.
5.Повторение. Решение задач (8 часов).
9 класс
1.Векторы. Метод координат (24 часа)
Понятие вектора. Абсолютная величина и направление вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Коллинеарные векторы. Проекция на ось. Разложение вектора по координатным осям. Координаты вектора.
Основная цель:
– сформировать понятие вектора как направленного отрезка ,показать учащимся применение вектора к решению простейших задач.
2.Соотношения между сторонами и углами треугольника. Скалярное произведение векторов (15 часов).
Синус, косинус и тангенс острого угла прямоугольного треугольника. Теорема косинусов и теорема синусов Решение треугольников. Соотношения между сторонами и углами треугольника.
Основная цель – познакомить учащихся с основными алгоритмами решения произвольных треугольников.
3.Длина окружности и площадь круга (12 часов).
Правильные многоугольники. Длина окружности и площадь круга.
Основная цель:
– расширить и систематизировать знания обучающихся об окружностях и многоугольниках.
4.Движение (8 часов).
Понятие движения. Параллельный перенос и поворот.
Основная цель – познакомить с понятием движения на плоскости: симметрии, параллельным переносом, поворотом.
5.Повторение курса геометрии 7-9 класса (7 часов).
Тематическое планирование
Математика
5 класс
|
№ |
Название темы |
Количество часов |
|
1 |
Натуральные числа и нуль |
46 |
|
2 |
Измерение величин |
30 |
|
3 |
Делимость натуральных чисел |
19 |
|
4 |
Обыкновенные дроби |
64 |
|
5 |
Повторение |
11 |
|
|
Итого |
170 |
6 класс
|
№ |
Название темы |
Количество часов |
|
1 |
Повторение курса математики 6 класса. |
3 |
|
2 |
Отношения, пропорции, проценты. |
19 |
|
3 |
Целые числа. |
33 |
|
4 |
Рациональные числа. |
39 |
|
5 |
Десятичные дроби. |
34 |
|
6 |
Обыкновенные и десятичные дроби. |
20 |
|
7 |
Повторение. |
22 |
|
|
Итого |
170 |
Алгебра
7 класс
|
№ |
Название темы |
Количество часов |
|
1 |
Выражения, тождества, уравнения |
22 |
|
2 |
Функции |
11 |
|
3 |
Степень с натуральным показателем |
11 |
|
4 |
Многочлены |
17 |
|
5 |
Формулы сокращённого умножения |
19 |
|
6 |
Системы линейных уравнений |
16 |
|
7 |
Повторение за курс 7 класса |
6 |
|
|
Итого |
102 |
8 класс
|
№ |
Наименование темы |
Количество часов |
|
1 |
Рациональные дроби |
22 |
|
2 |
Квадратные корни |
16 |
|
3 |
Квадратные уравнения |
18 |
|
4 |
Неравенства |
14 |
|
5 |
Степень с целым показателем |
8 |
|
6 |
Статистические исследования |
11 |
|
7 |
Повторение |
13 |
|
|
Итого |
102 |
9 класс
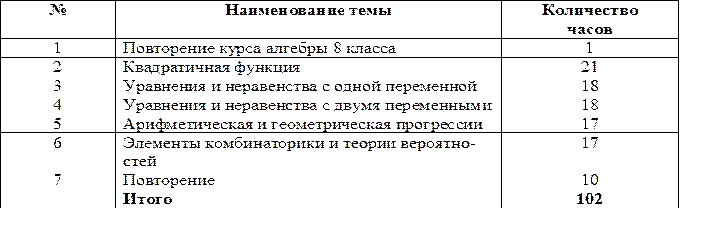
Геометрия
7 класс
|
№ |
Наименование темы |
Количество часов |
|
1 |
Начальные геометрические сведения |
12 |
|
2 |
Треугольники |
17 |
|
3 |
Параллельные прямые |
11 |
|
4 |
Соотношения между сторонами и углами треугольника |
19 |
|
5 |
Повторение Итоговая контрольная работа |
7 |
|
6 |
Резерв |
2 |
|
|
Итого |
68 |
8 класс
|
№ |
Наименование темы |
Количество часов |
|
1 |
Вводное повторение |
2 |
|
2 |
Четырехугольники |
14 |
|
3 |
Площадь |
14 |
|
4 |
Подобные треугольники |
19 |
|
5 |
Окружность |
17 |
|
6 |
Повторение |
2 |
|
|
Итого |
68 |
9 класс
|
№ |
Наименование темы |
Количество часов |
|
1 |
Вводное повторение |
2 |
|
2 |
Векторы. Метод координат |
18 |
|
3 |
Метод координат |
9 |
|
4 |
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов |
12 |
|
5 |
Длина окружности и площадь круга |
11 |
|
6 |
Движение |
8 |
|
7 |
Начальные сведения из стереометрии |
7 |
|
8 |
Об аксиомах планиметрии |
2 |
|
9 |
Повторение |
8 |
|
|
Итого |
68 |
Календарно-тематическое планирование
5 класс
|
№ урока |
№ урока в теме |
Тема урока |
Дата проведения |
Примечание |
|
|
По плану |
По факту |
||||
|
Глава №1 Натуральные числа и нуль |
|||||
|
1 |
1 |
Ряд натуральных чисел. |
|
|
|
|
2 |
2 |
Десятичная система записи натуральных чисел. Чтение и запись натуральных чисел. |
|
|
|
|
3 |
3 |
Поразрядная запись натуральных чисел. |
|
|
|
|
4 |
4 |
Правило сравнения натуральных чисел. |
|
|
|
|
5 |
5 |
Сравнение натуральных чисел. |
|
|
|
|
6 |
6 |
Правило сложения натуральных чисел. |
|
|
|
|
7 |
7 |
Сложение. Переместительный закон сложения. |
|
|
|
|
8 |
8 |
Сложение. Сочетательный закон сложения. |
|
|
|
|
9 |
9 |
Вычитание. Свойства вычитания. |
|
|
|
|
10 |
10 |
Вычитание. Проверочная работа. |
|
|
|
|
11 |
11 |
Решение уравнений. |
|
|
|
|
12 |
12 |
Решение текстовых задач с помощью сложения и вычитания. |
|
|
|
|
13 |
13 |
Решение сложных текстовых задач с помощью сложения и вычитания. |
|
|
|
|
14 |
14 |
Умножение. Переместительный закон умножения. |
|
|
|
|
15 |
15 |
Сочетательный закон умножения. |
|
|
|
|
16 |
16 |
Сочетательный закон умножения. Проверочная работа. |
|
|
|
|
17 |
17 |
Распределительный закон умножения. |
|
|
|
|
18 |
18 |
Вынесение общего множителя за скобки. |
|
|
|
|
19 |
19 |
Сложение чисел столбиком. |
|
|
|
|
20 |
20 |
Вычитание чисел столбиком. |
|
|
|
|
21 |
21 |
Решение примеров. Подготовка к контрольной работе. |
|
|
|
|
22 |
22 |
Контрольная работа №1 «Запись, сравнение, сложение и вычитание натуральных чисел» |
|
|
|
|
23 |
23 |
Анализ контрольной работы. Правило умножения чисел столбиком. |
|
|
|
|
24 |
24 |
Умножение чисел столбиком. |
|
|
|
|
25 |
25 |
Умножение многозначных чисел столбиком. |
|
|
|
|
26 |
26 |
Определение степени с натуральным показателем. |
|
|
|
|
27 |
27 |
Возведение в степень натуральных чисел. |
|
|
|
|
28 |
28 |
Деление нацело. |
|
|
|
|
29 |
29 |
Правило деления в столбик. |
|
|
|
|
30 |
30 |
Деление в столбик. |
|
|
|
|
31 |
31 |
Решение текстовых задач с помощью умножения и деления. |
|
|
|
|
32 |
32 |
Решение сложных текстовых задач с помощью умножения и деления. |
|
|
|
|
33 |
33 |
Способы решения задач «на части». |
|
|
|
|
34 |
34 |
Задачи на части. |
|
|
|
|
35 |
35 |
Решение сложных задач на части. |
|
|
|
|
36 |
36 |
Правило деления с остатком. |
|
|
|
|
37 |
37 |
Деление с остатком. |
|
|
|
|
38 |
38 |
Деление с остатком. Проверочная работа |
|
|
|
|
39 |
39 |
Числовые выражения. |
|
|
|
|
40 |
40 |
Числовые выражения. Подготовка к контрольной работе. |
|
|
|
|
41 |
41 |
Контрольная работа №2. «Умножение и деление натуральных чисел» |
|
|
|
|
42 |
42 |
Работа над ошибками. Примеры задач на нахождение двух чисел по их сумме и разности. |
|
|
|
|
43 |
43 |
Нахождение двух чисел по их сумме и разности. |
|
|
|
|
44 |
44 |
Решение сложных задач на нахождение двух чисел по их сумме и разности. |
|
|
|
|
45 |
45 |
Вычисления с помощью калькулятора. Занимательные задачи. |
|
|
|
|
46 |
46 |
Решение занимательных задач. |
|
|
|
|
Глава 2. Измерение величин. |
|||||
|
47 |
1 |
Прямая. Луч. Отрезок. |
|
|
|
|
48 |
2 |
Задачи на построение. |
|
|
|
|
49 |
3 |
Измерение отрезков. |
|
|
|
|
50 |
4 |
Задачи на построение отрезков. |
|
|
|
|
51 |
5 |
Метрические единицы длины. |
|
|
|
|
52 |
6 |
Упражнения на перевод величин в другие единицы измерения. |
|
|
|
|
53 |
7 |
Представление натуральных чисел на координатном луче. |
|
|
|
|
54 |
8 |
Представление натуральных чисел на координатном луче. Подготовка к контрольной работе |
|
|
|
|
55 |
9 |
Контрольная работа №3 «Прямая. Луч. Отрезок» |
|
|
|
|
56 |
10 |
Работа над ошибками. Окружность и круг. Сфера и шар. |
|
|
|
|
57 |
11 |
Углы. Измерение углов. |
|
|
|
|
58 |
12 |
Углы. Построение углов. |
|
|
|
|
59 |
13 |
Треугольники. Построение треугольника по трём сторонам. |
|
|
|
|
60 |
14 |
Треугольники. Периметр треугольника. |
|
|
|
|
61 |
15 |
Четырёхугольники. |
|
|
|
|
62 |
16 |
Четырёхугольники. Периметр четырёхугольника. |
|
|
|
|
63 |
17 |
Прямоугольник. Периметр прямоугольника. |
|
|
|
|
64 |
18 |
Площадь прямоугольника. Единицы площади. |
|
|
|
|
65 |
19 |
Прямоугольный параллелепипед. |
|
|
|
|
66 |
20 |
Развертка прямоугольного параллелепипеда |
|
|
|
|
67 |
21 |
Объём прямоугольного параллелепипеда. Единицы объёма. |
|
|
|
|
68 |
22 |
Решение задач на нахождение объёма прямоугольного параллелепипеда. |
|
|
|
|
69 |
23 |
Единицы массы. |
|
|
|
|
70 |
24 |
Единицы времени. |
|
|
|
|
71 |
25 |
Задачи на движение. Путь, скорость, время. |
|
|
|
|
72 |
26 |
Задачи на движение по реке. |
|
|
|
|
73 |
27 |
Задачи на движение. Подготовка к контрольной работе. |
|
|
|
|
74 |
28 |
Контрольная работа №4 «Треугольник, четырёхугольник, прямоугольный параллелепипед. Задачи на движение» |
|
|
|
|
75 |
29 |
Работа над ошибками. Многоугольники. |
|
|
|
|
76 |
30 |
Исторические сведения. Занимательные задачи. |
|
|
|
|
Глава 3. Делимость натуральных чисел. |
|||||
|
77 |
1 |
Первое и второе свойства делимости. |
|
|
|
|
78 |
2 |
Третье и четвертое свойства делимости. |
|
|
|
|
79 |
3 |
Признаки делимости на 2,5,10. |
|
|
|
|
80 |
4 |
Признаки делимости на 3, 9. |
|
|
|
|
81 |
5 |
Признаки делимости. Проверочная работа. |
|
|
|
|
82 |
6 |
Простые и составные числа. |
|
|
|
|
83 |
7 |
Простые и составные числа. Проверочная работа. |
|
|
|
|
84 |
8 |
Делители натурального числа. |
|
|
|
|
85 |
9 |
Разложение числа на простые множители. |
|
|
|
|
86 |
10 |
Разложение числа на простые множители. Проверочная работа. |
|
|
|
|
87 |
11 |
Наибольший общий делитель. Правило нахождения наибольшего общего делителя. |
|
|
|
|
88 |
12 |
Взаимно-простые числа. Наибольший общий делитель |
|
|
|
|
89 |
13 |
Решение текстовых задач. |
|
|
|
|
90 |
14 |
Наименьшее общее кратное. Правило нахождения наименьшего общего кратного. |
|
|
|
|
91 |
15 |
Нахождения наименьшего общего кратного. Проверочная работа. |
|
|
|
|
92 |
16 |
Решение текстовых задач. Подготовка к контрольной работе |
|
|
|
|
93 |
17 |
Контрольная работа №5 «Делимость натуральных чисел» |
|
|
|
|
94 |
18 |
Работа над ошибками. Использование чётности и нечётности при решении задач. |
|
|
|
|
95 |
19 |
Решение занимательных задач. |
|
|
|
|
Глава 4. Обыкновенные дроби. |
|||||
|
96 |
1 |
Понятие дроби. Доли. |
|
|
|
|
97 |
2 |
Равенство дробей. Основное свойство дроби. |
|
|
|
|
98 |
3 |
Сокращение дробей. |
|
|
|
|
99 |
4 |
Сокращение дробей. Проверочная работа. |
|
|
|
|
100 |
5 |
Задачи на дроби. Нахождение части от числа. |
|
|
|
|
101 |
6 |
Нахождение числа по его части, выраженной дробью. |
|
|
|
|
102 |
7 |
Решение задач на дроби. |
|
|
|
|
103 |
8 |
Решение сложных задач на нахождение части числа и числа по его части. |
|
|
|
|
104 |
9 |
Общий знаменатель. |
|
|
|
|
105 |
10 |
Приведение дробей к общему знаменателю. Дополнительные множители. |
|
|
|
|
106 |
11 |
Приведение дробей к наименьшему общему знаменателю. Дополнительные множители. |
|
|
|
|
107 |
12 |
Приведение дробей к общему знаменателю. Проверочная работа. |
|
|
|
|
108 |
13 |
Сравнение дробей с одинаковыми знаменателями. |
|
|
|
|
109 |
14 |
Правильные и неправильные дроби. Сравнение дробей. |
|
|
|
|
110 |
15 |
Сравнение дробей с разными знаменателями. |
|
|
|
|
111 |
16 |
Сложение дробей с одинаковыми знаменателями. |
|
|
|
|
112 |
17 |
Сложение дробей с разными знаменателями. |
|
|
|
|
113 |
18 |
Сложение дробей с разными знаменателями. Проверочная работа. |
|
|
|
|
114 |
19 |
Переместительный закон сложения дробей. |
|
|
|
|
115 |
20 |
Сочетательный закон сложения дробей. |
|
|
|
|
116 |
21 |
Применение законов сложения при выполнении упражнений. |
|
|
|
|
117 |
22 |
Применение законов сложения для решения задач. |
|
|
|
|
118 |
23 |
Вычитание дробей с одинаковыми знаменателями. |
|
|
|
|
119 |
24 |
Вычитание дробей с разными знаменателями. |
|
|
|
|
120 |
25 |
Решение уравнений и текстовых задач. Подготовка к контрольной работе. |
|
|
|
|
121 |
26 |
Контрольная работа №6 «Сравнение, сложение и вычитание дробей» |
|
|
|
|
122 |
1 |
Работа над ошибками. Умножение дробей. |
|
|
|
|
123 |
2 |
Умножение натурального числа на дробь. |
|
|
|
|
124 |
3 |
Обратная дробь. Взаимно-обратные дроби. Решение примеров. |
|
|
|
|
125 |
4 |
Решение задач на умножение дробей |
|
|
|
|
126 |
5 |
Переместительный и сочетательный законы умножения дробей. |
|
|
|
|
127 |
6 |
Распределительный закон умножения дробей. |
|
|
|
|
128 |
7 |
Деление дробей |
|
|
|
|
129 |
8 |
Деление дроби на натуральное число. |
|
|
|
|
130 |
9 |
Решение примеров. Порядок действий в числовых выражениях содержащих дроби. |
|
|
|
|
131 |
10 |
Решение задач и уравнений на деление дробей. |
|
|
|
|
132 |
11 |
Нахождение части целого. |
|
|
|
|
133 |
12 |
Нахождение целого по его части. Подготовка к контрольной работе. |
|
|
|
|
134 |
13 |
Контрольная работа №7 «Умножение и деление дробей» |
|
|
|
|
135 |
14 |
Работа над ошибками. Задачи на совместную работу. |
|
|
|
|
136 |
15 |
Методы решения задач на совместную работу. |
|
|
|
|
137 |
16 |
Решение различных типов задач на совместную работу. |
|
|
|
|
138 |
17 |
Понятие смешанной дроби. Сравнение смешанных дробей. |
|
|
|
|
139 |
18 |
Преобразование смешанной дроби в неправильную дробь. |
|
|
|
|
140 |
19 |
Преобразование неправильной дроби в смешанную дробь. |
|
|
|
|
141 |
20 |
Сложение смешанных дробей. |
|
|
|
|
142 |
21 |
Различные приемы сложения смешанных дробей. |
|
|
|
|
143 |
22 |
Решение примеров. |
|
|
|
|
144 |
23 |
Вычитание смешанных дробей. |
|
|
|
|
145 |
24 |
Вычитание дроби из целого числа. |
|
|
|
|
146 |
25 |
Различные приемы вычитания смешанных дробей. |
|
|
|
|
147 |
26 |
Умножение смешанных дробей. |
|
|
|
|
148 |
27 |
Возведение смешанных дробей в степень. Умножение смешанной дроби на натуральное число. |
|
|
|
|
149 |
28 |
Деление смешанных дробей. |
|
|
|
|
150 |
29 |
Деление смешанной дроби на число. |
|
|
|
|
151 |
30 |
Умножение и деление смешанных дробей. Подготовка к контрольной работе. |
|
|
|
|
152 |
31 |
Контрольная работа №8 «Все действия со смешанными дробями» |
|
|
|
|
153 |
32 |
Работа над ошибками. Координатный луч. |
|
|
|
|
154 |
33 |
Представление дробей на координатном луче. |
|
|
|
|
155 |
34 |
Среднее арифметическое. Подготовка к контрольной работе |
|
|
|
|
156 |
35 |
Контрольная работа №9. (Итоговая) |
|
|
|
|
157 |
36 |
Работа над ошибками. Площадь прямоугольника. |
|
|
|
|
158 |
37 |
Объём прямоугольного параллелепипеда. |
|
|
|
|
159 |
38 |
Сложные задачи на движение по реке. |
|
|
|
|
Глава 5. Повторение. |
|||||
|
160 |
1 |
Решение занимательных задач |
|
|
|
|
161 |
2 |
Запись, сравнение, сложение и вычитание натуральных чисел. |
|
|
|
|
162 |
3 |
Умножение и деление натуральных чисел. |
|
|
|
|
163 |
4 |
Прямая. Луч. Отрезок. |
|
|
|
|
164 |
5 |
Треугольник, четырёхугольник, прямоугольный параллелепипед. |
|
|
|
|
165 |
6 |
Делимость натуральных чисел. |
|
|
|
|
166 |
7 |
Сравнение, сложение и вычитание дробей. |
|
|
|
|
167 |
8 |
Умножение и деление дробей |
|
|
|
|
168 |
9 |
Все действия со смешанными дробями |
|
|
|
|
170 |
10 |
Подведение итогов года. |
|
|
|
6 класс
|
№ урока |
№ урока в теме |
Тема урока |
Дата проведения |
Примечание |
|
|
По плану |
По факту |
||||
|
Глава 1. Повторение курса математики 6 класса. |
|||||
|
1 |
1 |
Дроби. Арифметические действия с дробями. |
|
|
|
|
2 |
2 |
Решение задач. |
|
|
|
|
3 |
3 |
Входная диагностическая работа. |
|
|
|
|
Глава 2. Отношения, пропорции, проценты. |
|||||
|
4 |
1 |
Отношение чисел и величин. |
|
|
|
|
5 |
2 |
Масштаб. |
|
|
|
|
6 |
3 |
Деление числа в заданном отношении. |
|
|
|
|
7 |
4 |
Пропорции. |
|
|
|
|
8 |
5 |
Решение задач. Проверочная работа. |
|
|
|
|
9 |
6 |
Прямая и обратная пропорциональность. |
|
|
|
|
10 |
7 |
Решение задач. |
|
|
|
|
11 |
8 |
Решение задач. |
|
|
|
|
12 |
9 |
Контрольная работа № 1. |
|
|
|
|
13 |
10 |
Анализ контрольной работы. |
|
|
|
|
14 |
11 |
Понятие о проценте. |
|
|
|
|
15 |
12 |
Понятие о проценте. |
|
|
|
|
16 |
13 |
Задачи на проценты. Нахождение процентов от числа. |
|
|
|
|
17 |
14 |
Задачи на проценты. Нахождение числа по его процентам. |
|
|
|
|
18 |
15 |
Задачи на проценты. Нахождение числа по его процентам. |
|
|
|
|
19 |
16 |
Решение задач. Проверочная работа. |
|
|
|
|
20 |
17 |
Круговые диаграммы. |
|
|
|
|
21 |
18 |
Круговые диаграммы. |
|
|
|
|
22 |
19 |
Контрольная работа №2. |
|
|
|
|
Глава 3. Целые числа |
|||||
|
23 |
1 |
Отрицательные целые числа. |
|
|
|
|
24 |
2 |
Противоположные числа. Модуль числа. |
|
|
|
|
25 |
3 |
Противоположные числа. Модуль числа. |
|
|
|
|
26 |
4 |
Решение упражнений. |
|
|
|
|
27 |
5 |
Сравнение целых чисел. |
|
|
|
|
28 |
6 |
Сложение целых чисел одного знака. |
|
|
|
|
29 |
7 |
Сложение целых чисел одного знака. |
|
|
|
|
30 |
8 |
Сложение целых чисел с разными знаками. |
|
|
|
|
31 |
9 |
Сложение целых чисел с разными знаками. |
|
|
|
|
32 |
10 |
Законы сложения целых чисел. |
|
|
|
|
33 |
11 |
Законы сложения целых чисел. |
|
|
|
|
34 |
12 |
Решение упражнений. Проверочная работа. |
|
|
|
|
35 |
13 |
Решение упражнений. Проверочная работа. |
|
|
|
|
36 |
14 |
Разность целых чисел. |
|
|
|
|
37 |
15 |
Разность целых чисел. |
|
|
|
|
38 |
16 |
Решение упражнений. |
|
|
|
|
39 |
17 |
Произведение целых чисел. |
|
|
|
|
40 |
18 |
Произведение целых чисел. |
|
|
|
|
41 |
19 |
Частное целых чисел. |
|
|
|
|
42 |
20 |
Частное целых чисел. |
|
|
|
|
43 |
21 |
Распределительный закон. |
|
|
|
|
44 |
22 |
Распределительный закон. |
|
|
|
|
45 |
23 |
Раскрытие скобок и заключение в скобки. |
|
|
|
|
46 |
24 |
Раскрытие скобок и заключение в скобки. |
|
|
|
|
47 |
25 |
Решение упражнений. Проверочная работа. |
|
|
|
|
48 |
26 |
Решение упражнений. Проверочная работа. |
|
|
|
|
49 |
27 |
Действия с суммами нескольких слагаемых. |
|
|
|
|
50 |
28 |
Действия с суммами нескольких слагаемых. |
|
|
|
|
51 |
29 |
Представление целых чисел на координатной оси. |
|
|
|
|
52 |
30 |
Решение упражнений. Подготовка к контрольной работе. |
|
|
|
|
53 |
31 |
Контрольная работа № 3. |
|
|
|
|
54 |
32 |
Анализ контрольной работы. |
|
|
|
|
55 |
33 |
Фигуры на плоскости, симметричные относительно точки. |
|
|
|
|
Глава 4. Рациональные числа. |
|||||
|
56 |
1 |
Отрицательные дроби. |
|
|
|
|
57 |
2 |
Отрицательные дроби. |
|
|
|
|
58 |
3 |
Рациональные числа. |
|
|
|
|
59 |
4 |
Рациональные числа. |
|
|
|
|
60 |
5 |
Сравнение рациональных чисел. Проверочная работа. |
|
|
|
|
61 |
6 |
Сравнение рациональных чисел. Проверочная работа. |
|
|
|
|
62 |
7 |
Сложение и вычитание дробей. |
|
|
|
|
63 |
8 |
Сложение и вычитание дробей. |
|
|
|
|
64 |
9 |
Решение упражнений. |
|
|
|
|
65 |
10 |
Решение упражнений. |
|
|
|
|
66 |
11 |
Умножение дробей. |
|
|
|
|
67 |
12 |
Умножение дробей. |
|
|
|
|
68 |
13 |
Деление дробей. |
|
|
|
|
69 |
14 |
Деление дробей. |
|
|
|
|
70 |
15 |
Законы сложения и умножения |
|
|
|
|
71 |
16 |
Законы сложения и умножения |
|
|
|
|
72 |
17 |
Контрольная работа №4. |
|
|
|
|
73 |
18 |
Анализ контрольной работы. |
|
|
|
|
74 |
19 |
Сложение и вычитание смешанных дробей произвольного знака. |
|
|
|
|
75 |
20 |
Сложение и вычитание смешанных дробей произвольного знака. |
|
|
|
|
76 |
21 |
Умножение и деление смешанных дробей произвольного знака. |
|
|
|
|
77 |
22 |
Умножение и деление смешанных дробей произвольного знака. |
|
|
|
|
78 |
23 |
Решение упражнений. |
|
|
|
|
79 |
24 |
Решение упражнений. |
|
|
|
|
80 |
25 |
Изображение рациональных чисел на координатной оси. |
|
|
|
|
81 |
26 |
Изображение рациональных чисел на координатной оси. |
|
|
|
|
82 |
27 |
Решение упражнений. Проверочная работа. |
|
|
|
|
83 |
28 |
Решение упражнений. Проверочная работа. |
|
|
|
|
84 |
29 |
Уравнения. Основные понятия. |
|
|
|
|
85 |
30 |
Уравнения. Основные понятия. |
|
|
|
|
86 |
31 |
Решение упражнений. |
|
|
|
|
87 |
32 |
Решение задач с помощью уравнений. Основные типы. |
|
|
|
|
88 |
33 |
Решение задач с помощью уравнений. Основные типы. |
|
|
|
|
89 |
34 |
Решение задач. |
|
|
|
|
90 |
35 |
Решение задач. |
|
|
|
|
91 |
36 |
Решение задач. Проверочная работа. |
|
|
|
|
92 |
37 |
Решение задач. Проверочная работа. |
|
|
|
|
93 |
38 |
Контрольная работа №5. |
|
|
|
|
94 |
39 |
Анализ контрольной работы. |
|
|
|
|
Глава 5. Десятичные дроби. |
|||||
|
95 |
1 |
Понятие положительной десятичной дроби. |
|
|
|
|
96 |
2 |
Понятие положительной десятичной дроби. |
|
|
|
|
97 |
3 |
Сравнение положительных десятичных дробей. |
|
|
|
|
98 |
4 |
Сравнение положительных десятичных дробей. |
|
|
|
|
99 |
5 |
Сложение и вычитание положительных десятичных дробей. |
|
|
|
|
100 |
6 |
Сложение и вычитание положительных десятичных дробей. |
|
|
|
|
101 |
7 |
Решение упражнений. |
|
|
|
|
102 |
8 |
Решение упражнений. |
|
|
|
|
103 |
9 |
Перенос запятой в положительной десятичной дроби. |
|
|
|
|
104 |
10 |
Перенос запятой в положительной десятичной дроби. |
|
|
|
|
105 |
11 |
Умножение положительных десятичных дробей. |
|
|
|
|
106 |
12 |
Умножение положительных десятичных дробей. |
|
|
|
|
107 |
13 |
Решение упражнений. |
|
|
|
|
108 |
14 |
Деление положительных десятичных дробей. |
|
|
|
|
109 |
15 |
Деление положительных десятичных дробей. |
|
|
|
|
110 |
16 |
Решение упражнений. |
|
|
|
|
111 |
17 |
Решение упражнений. Проверочная работа. |
|
|
|
|
112 |
18 |
Анализ проверочной работы. Подготовка к контрольной работе. |
|
|
|
|
113 |
19 |
Контрольная работа № 6. |
|
|
|
|
114 |
20 |
Анализ контрольной работы. |
|
|
|
|
115 |
21 |
Десятичные дроби и проценты. |
|
|
|
|
116 |
22 |
Десятичные дроби и проценты. |
|
|
|
|
117 |
23 |
Решение упражнений. |
|
|
|
|
118 |
24 |
Решение упражнений. |
|
|
|
|
119 |
25 |
Сложные задачи на проценты. |
|
|
|
|
120 |
26 |
Сложные задачи на проценты. |
|
|
|
|
121 |
27 |
Десятичные дроби произвольного знака. |
|
|
|
|
122 |
28 |
Десятичные дроби произвольного знака. |
|
|
|
|
123 |
29 |
Приближение десятичных дробей. |
|
|
|
|
124 |
30 |
Приближение десятичных дробей. |
|
|
|
|
125 |
31 |
Приближение суммы, разности, произведения и частного двух чисел. |
|
|
|
|
126 |
32 |
Приближение суммы, разности, произведения и частного двух чисел. |
|
|
|
|
127 |
33 |
Контрольная работа № 7. |
|
|
|
|
128 |
34 |
Анализ контрольной работы. |
|
|
|
|
Глава 6. Обыкновенные и десятичные дроби. |
|||||
|
129 |
1 |
Разложение положительной обыкновенной дроби в конечную десятичную дробь. |
|
|
|
|
130 |
2 |
Разложение положительной обыкновенной дроби в конечную десятичную дробь. |
|
|
|
|
131 |
3 |
Периодические десятичные дроби. |
|
|
|
|
132 |
4 |
Периодические десятичные дроби. |
|
|
|
|
133 |
5 |
Непериодические бесконечные десятичные дроби. |
|
|
|
|
134 |
6 |
Непериодические бесконечные десятичные дроби. |
|
|
|
|
135 |
7 |
Длина отрезка. |
|
|
|
|
136 |
8 |
Длина отрезка. |
|
|
|
|
137 |
9 |
Длина окружности. Площадь круга. |
|
|
|
|
138 |
10 |
Длина окружности. Площадь круга. |
|
|
|
|
139 |
11 |
Координатная ось. |
|
|
|
|
140 |
12 |
Координатная ось. |
|
|
|
|
141 |
13 |
Декартова система координат на плоскости. |
|
|
|
|
142 |
14 |
Решение упражнений. |
|
|
|
|
143 |
15 |
Решение упражнений. |
|
|
|
|
144 |
16 |
Столбчатые диаграммы и графики. |
|
|
|
|
145 |
17 |
Столбчатые диаграммы и графики. |
|
|
|
|
146 |
18 |
Решение упражнений. Подготовка к контрольной работе. |
|
|
|
|
147 |
19 |
Контрольная работа № 8. |
|
|
|
|
148 |
20 |
Анализ контрольной работы. |
|
|
|
|
Глава 7. Повторение. |
|||||
|
149 |
1 |
Действия с дробями. |
|
|
|
|
150 |
2 |
Действия с десятичными дробями. |
|
|
|
|
151 |
3 |
Уравнения и задачи на составление уравнений. |
|
|
|
|
152 |
4 |
Проценты и пропорции. |
|
|
|
|
153 |
5 |
Итоговая контрольная работа. |
|
|
|
|
154 |
6 |
Анализ контрольной работы. |
|
|
|
|
155 |
7 |
Решение различных текстовых задач с помощью уравнений. |
|
|
|
|
156 |
8 |
Решение различных текстовых задач с помощью уравнений. |
|
|
|
|
157 |
9 |
Решение различных текстовых задач с помощью уравнений. |
|
|
|
|
158 |
10 |
Задачи на составление и разрезание фигур. |
|
|
|
|
159 |
11 |
Задачи на составление и разрезание фигур. |
|
|
|
|
160 |
12 |
Решение комбинаторных задач. |
|
|
|
|
161 |
13 |
Решение комбинаторных задач. |
|
|
|
|
162 |
14 |
Решение занимательных задач |
|
|
|
|
163 |
15 |
Решение занимательных задач. |
|
|
|
|
164 |
16 |
Решение занимательных задач. |
|
|
|
|
165 |
17 |
Решение упражнений по курсу 6 класса. |
|
|
|
|
166 |
18 |
Решение упражнений по курсу 6 класса. |
|
|
|
|
167 |
19 |
Решение упражнений по курсу 6 класса. |
|
|
|
|
168 |
20 |
Итоговый урок. |
|
|
|
|
169 |
21 |
Урок-игра. |
|
|
|
|
170 |
22 |
Подведение итогов года. |
|
|
|
Алгебра
7 класс
|
№ урока |
№ урока в теме |
Тема урока |
Дата проведения |
Примечание |
|
|
По плану |
По факту |
||||
|
Выражения, тождества, уравнения |
|||||
|
1 |
1 |
Повторение «Вычисление значений выражений» |
|
|
|
|
2 |
2 |
Числовые выражения |
|
|
|
|
3 |
3 |
Числовые выражения |
|
|
|
|
4 |
4 |
Выражения с переменными |
|
|
|
|
5 |
5 |
Выражения с переменными |
|
|
|
|
6 |
6 |
Сравнение значений выражений |
|
|
|
|
7 |
7 |
Сравнение значений выражений |
|
|
|
|
8 |
8 |
Тождества. Тождественные преобразования выражений |
|
|
|
|
9 |
9 |
Тождества. Тождественные преобразования выражений |
|
|
|
|
10 |
10 |
Контрольная работа №1 по теме «Числовые выражения. Выражения с переменными» |
|
|
|
|
11 |
11 |
Уравнение и его корни |
|
|
|
|
12 |
12 |
Линейное уравнение с одной переменной |
|
|
|
|
13 |
13 |
Линейное уравнение с одной переменной |
|
|
|
|
14 |
14 |
Линейное уравнение с одной переменной |
|
|
|
|
15 |
15 |
Решение задач с помощью уравнений |
|
|
|
|
16 |
16 |
Решение задач с помощью уравнений |
|
|
|
|
17 |
17 |
Решение задач с помощью уравнений |
|
|
|
|
18 |
18 |
Среднее арифметическое, размах, мода |
|
|
|
|
19 |
19 |
Среднее арифметическое размах, мода |
|
|
|
|
20 |
20 |
Медиана как статистическая характеристика |
|
|
|
|
21 |
21 |
Решение задач по теме «Статистические характеристики» |
|
|
|
|
22 |
22 |
Контрольная работа №2 «Статистические характеристики» |
|
|
|
|
Функции |
|||||
|
23 |
1 |
Что такое функция |
|
|
|
|
24 |
2 |
Вычисление значений функции по формуле |
|
|
|
|
25 |
3 |
Графики функций |
|
|
|
|
26 |
4 |
Графики функций |
|
|
|
|
27 |
5 |
График функции |
|
|
|
|
28 |
6 |
Прямая пропорциональность и её график |
|
|
|
|
29 |
7 |
Прямая пропорциональность и её график |
|
|
|
|
30 |
8 |
Линейная функция и её график |
|
|
|
|
31 |
9 |
Линейная функция и её график |
|
|
|
|
32 |
10 |
Линейная функция и её график |
|
|
|
|
33 |
11 |
Контрольная работа №3 по теме «Функции» |
|
|
|
|
Степень с натуральным показателем |
|||||
|
34 |
1 |
Определение степени с натуральным показателем |
|
|
|
|
35 |
2 |
Умножение и деление степеней |
|
|
|
|
36 |
3 |
Умножение и деление степеней |
|
|
|
|
37 |
4 |
Возведение в степень произведения и степени |
|
|
|
|
38 |
5 |
Возведение в степень произведения и степени |
|
|
|
|
39 |
6 |
Одночлен и его стандартный вид |
|
|
|
|
40 |
7 |
Умножение одночленов. Возведение одночлена в степень |
|
|
|
|
41 |
8 |
Умножение одночленов. Возведение одночлена в степень |
|
|
|
|
42 |
9 |
Функции y=x2 и y=x3 и их графики |
|
|
|
|
43 |
10 |
Функции y=x2 и y=x3 и их графики |
|
|
|
|
44 |
11 |
Контрольная работа №4 по теме «Степень с натуральным показателем» |
|
|
|
|
Многочлены |
|||||
|
45 |
1 |
Многочлен и его стандартный вид |
|
|
|
|
46 |
2 |
Сложение и вычитание многочленов |
|
|
|
|
47 |
3 |
Сложение и вычитание многочленов |
|
|
|
|
48 |
4 |
Умножение одночлена на многочлен |
|
|
|
|
49 |
5 |
Умножение одночлена на многочлен |
|
|
|
|
50 |
6 |
Умножение одночлена на многочлен |
|
|
|
|
51 |
7 |
Вынесение общего множителя за скобки |
|
|
|
|
52 |
8 |
Вынесение общего множителя за скобки |
|
|
|
|
53 |
9 |
Вынесение общего множителя за скобки |
|
|
|
|
54 |
10 |
Контрольная работа №5 по теме «Многочлены. Произведение одночлена на многочлен» |
|
|
|
|
55 |
11 |
Умножение многочлена на многочлен |
|
|
|
|
56 |
12 |
Умножение многочлена на многочлен |
|
|
|
|
57 |
13 |
Умножение многочлена на многочлен |
|
|
|
|
58 |
14 |
Разложение многочлена на множители способом группировки |
|
|
|
|
59 |
15 |
Разложение многочлена на множители способом группировки |
|
|
|
|
60 |
16 |
Разложение многочлена на множители способом группировки |
|
|
|
|
61 |
17 |
Контрольная работа №6 по теме «Произведение многочленов» |
|
|
|
|
Формулы сокращённого умножения |
|||||
|
62 |
1 |
Возведение в квадрат суммы и разности двух выражений |
|
|
|
|
63 |
2 |
Возведение в квадрат суммы и разности двух выражений |
|
|
|
|
64 |
3 |
Разложение на множители с помощью формул квадрата суммы и квадрата разности |
|
|
|
|
65 |
4 |
Разложение на множители с помощью формул квадрата суммы и квадрата разности |
|
|
|
|
66 |
5 |
Разложение на множители с помощью формул квадрата суммы и квадрата разности |
|
|
|
|
67 |
6 |
Умножение разности двух выражений на их сумму |
|
|
|
|
68 |
7 |
Умножение разности двух выражений на их сумму |
|
|
|
|
69 |
8 |
Разложение разности квадратов на множители |
|
|
|
|
70 |
9 |
Разложение разности квадратов на множители |
|
|
|
|
71 |
10 |
Разложение на множители суммы и разности кубов |
|
|
|
|
72 |
11 |
Разложение на множители суммы и разности кубов |
|
|
|
|
73 |
12 |
Контрольная работа №7 по теме «Формулы сокращенного умножения» |
|
|
|
|
74 |
13 |
Преобразование целого выражения в многочлен |
|
|
|
|
75 |
14 |
Применение различных способов для разложения многочлена на множители |
|
|
|
|
76 |
15 |
Применение различных способов для разложения многочлена на множители |
|
|
|
|
77 |
16 |
Применение преобразований целых выражений |
|
|
|
|
78 |
17 |
Применение преобразований целых выражений |
|
|
|
|
79 |
18 |
Применение преобразований целых выражений |
|
|
|
|
80 |
19 |
Контрольная работа №8 по теме «Преобразование целых выражений» |
|
|
|
|
Системы линейных уравнений |
|||||
|
81 |
1 |
Линейные уравнения с двумя переменными |
|
|
|
|
82 |
2 |
График линейного уравнения с двумя переменными |
|
|
|
|
83 |
3 |
График линейного уравнения с двумя переменными |
|
|
|
|
84 |
4 |
Системы линейных уравнений с двумя переменными |
|
|
|
|
85 |
5 |
Системы линейных уравнений с двумя переменными |
|
|
|
|
86 |
6 |
Способ подстановки |
|
|
|
|
87 |
7 |
Способ подстановки |
|
|
|
|
88 |
8 |
Способ подстановки |
|
|
|
|
89 |
9 |
Способ сложения |
|
|
|
|
90 |
10 |
Способ сложения |
|
|
|
|
91 |
11 |
Способ сложения |
|
|
|
|
92 |
12 |
Решение задач с помощью систем уравнений |
|
|
|
|
93 |
13 |
Решение задач с помощью систем уравнений |
|
|
|
|
94 |
14 |
Решение задач с помощью систем уравнений |
|
|
|
|
95 |
15 |
Решение систем уравнений различными способами |
|
|
|
|
96 |
16 |
Контрольная работа №9 по теме «Решение систем линейных уравнений» |
|
|
|
|
Повторение за курс 7 класса |
|||||
|
97 |
1 |
Решение линейных уравнений |
|
|
|
|
98 |
2 |
Формулы сокращенного умножения |
|
|
|
|
99 |
3 |
Решение систем линейных уравнений |
|
|
|
|
100 |
4 |
Итоговый зачёт за курс 7 класса |
|
|
|
|
101 |
5 |
Итоговая контрольная работа |
|
|
|
|
102 |
6 |
Работа над ошибками |
|
|
|
8 класс
|
№ урока |
№ урока в теме |
Тема урока |
Дата проведения |
Примечание |
|
|
По плану |
По факту |
||||
|
Рациональные дроби. Сумма и разность дробей. |
|||||
|
Рациональные дроби и их свойства. |
|||||
|
1 |
1 |
Рациональные выражения. |
|
|
|
|
2 |
2 |
Рациональные выражения. |
|
|
|
|
3 |
3 |
Основное свойство дроби. Сокращение дробей. |
|
|
|
|
4 |
4 |
Основное свойство дроби. Приведение дробей к новому знаменателю. |
|
|
|
|
5 |
5 |
Основное свойство дроби. Приведение дробей к новому знаменателю. |
|
|
|
|
Сумма и разность дробей. |
|||||
|
6 |
1 |
Сложение и вычитание дробей с одинаковыми знаменателями. |
|
|
|
|
7 |
2 |
Сложение и вычитание дробей с одинаковыми знаменателями. |
|
|
|
|
8 |
3 |
Сложение и вычитание дробей с разными знаменателями. |
|
|
|
|
9 |
4 |
Сложение и вычитание дробей с разными знаменателями. |
|
|
|
|
10 |
5 |
Сложение и вычитание дробей с разными знаменателями. |
|
|
|
|
11 |
6 |
Контрольная работа № 1 "Сложение и вычитание рациональных дробей". |
|
|
|
|
Произведение и частное дробей. Преобразование рациональных выражений. |
|||||
|
Произведение и частное дробей. |
|||||
|
12 |
1 |
Умножение дробей. |
|
|
|
|
13 |
2 |
Умножение дробей. Возведение дроби в степень. |
|
|
|
|
14 |
3 |
Деление дробей. |
|
|
|
|
15 |
4 |
Деление дробей. |
|
|
|
|
Преобразование рациональных выражений. |
|||||
|
16 |
1 |
Преобразование рациональных выражений. |
|
|
|
|
17 |
2 |
Преобразование рациональных выражений. |
|
|
|
|
18 |
3 |
Преобразование рациональных выражений. |
|
|
|
|
Функция обратная пропорциональность. |
|||||
|
19 |
1 |
Функция y=k/x и её график. |
|
|
|
|
20 |
2 |
Функция y=k/x и её график. |
|
|
|
|
21 |
3 |
Решение задач "Преобразование рациональных выражений. Построение графика функции y=k/x". |
|
|
|
|
22 |
4 |
Контрольная работа № 2 "Произведение и частное дробей. Функция y=k/x". |
|
|
|
|
Арифметический квадратный корень |
|||||
|
Действительные числа. |
|||||
|
23 |
1 |
Рациональные числа. |
|
|
|
|
24 |
2 |
Рациональные и иррациональные числа. |
|
|
|
|
Арифметический квадратный корень. |
|||||
|
25 |
1 |
Квадратные корни. Арифметический квадратный корень. |
|
|
|
|
26 |
2 |
Квадратные корни. Арифметический квадратный корень. |
|
|
|
|
27 |
3 |
Уравнение х2=а. |
|
|
|
|
28 |
4 |
Нахождение приближенных значений квадратного корня. |
|
|
|
|
29 |
5 |
Функция у=√х и её график. |
|
|
|
|
Свойства арифметического квадратного корня. |
|||||
|
30 |
1 |
Квадратный корень из произведения, дроби, степени. |
|
|
|
|
31 |
2 |
Квадратный корень из произведения, дроби, степени. |
|
|
|
|
32 |
3 |
Квадратный корень из произведения, дроби, степени. |
|
|
|
|
33 |
4 |
Контрольная работа № 3 "Арифметический квадратный корень". |
|
|
|
|
Применение свойств арифметического квадратного корня. |
|||||
|
34 |
1 |
Вынесение множителя из-под знака корня. Внесение множителя под знак корня. |
|
|
|
|
35 |
2 |
Вынесение множителя из-под знака корня. Внесение множителя под знак корня. |
|
|
|
|
36 |
3 |
Преобразование выражений, содержащих квадратные корни. |
|
|
|
|
37 |
4 |
Преобразование выражений, содержащих квадратные корни. |
|
|
|
|
38 |
5 |
Контрольная работа № 4 "Свойства арифметического квадратного корня". |
|
|
|
|
Квадратные уравнения. |
|||||
|
Квадратное уравнение и его корни. |
|||||
|
39 |
1 |
Неполные квадратные уравнения. |
|
|
|
|
40 |
2 |
Неполные квадратные уравнения. |
|
|
|
|
41 |
3 |
Формула корней квадратного уравнения. |
|
|
|
|
42 |
4 |
Формула корней квадратного уравнения. |
|
|
|
|
43 |
5 |
Формула корней квадратного уравнения. |
|
|
|
|
44 |
6 |
Теорема Виета. |
|
|
|
|
45 |
7 |
Теорема Виета. |
|
|
|
|
Решение задач с помощью квадратных уравнений. |
|||||
|
46 |
1 |
Решение задач с помощью квадратных уравнений. |
|
|
|
|
47 |
2 |
Решение задач с помощью квадратных уравнений. |
|
|
|
|
48 |
3 |
Решение задач с помощью квадратных уравнений. |
|
|
|
|
49 |
4 |
Контрольная работа № 5 "Квадратные уравнения". |
|
|
|
|
Дробные рациональные уравнения. |
|||||
|
Дробные рациональные уравнения. |
|||||
|
50 |
1 |
Решение дробных рациональных уравнений. |
|
|
|
|
51 |
2 |
Решение дробных рациональных уравнений. |
|
|
|
|
52 |
3 |
Решение дробных рациональных уравнений. |
|
|
|
|
Решение задач с помощью дробно-рациональных уравнений. |
|||||
|
53 |
1 |
Решение задач с помощью рациональных уравнений. |
|
|
|
|
54 |
2 |
Решение задач с помощью рациональных уравнений. |
|
|
|
|
55 |
3 |
Решение задач с помощью рациональных уравнений. |
|
|
|
|
56 |
4 |
Контрольная работа № 6 "Дробные рациональные уравнения". |
|
|
|
|
Неравенства. |
|||||
|
Числовые неравенства и их свойства. |
|||||
|
57 |
1 |
Числовые неравенства. |
|
|
|
|
58 |
2 |
Свойства числовых неравенств. |
|
|
|
|
59 |
3 |
Свойства числовых неравенств. |
|
|
|
|
60 |
4 |
Сложение и умножение числовых неравенств. |
|
|
|
|
61 |
5 |
Сложение и умножение числовых неравенств. |
|
|
|
|
Числовые промежутки. |
|||||
|
62 |
1 |
Пересечение и объединение множеств. |
|
|
|
|
63 |
2 |
Числовые промежутки. |
|
|
|
|
Неравенства с одной переменной и их системы. |
|||||
|
64 |
1 |
Решение неравенств с одной переменной. |
|
|
|
|
65 |
2 |
Решение неравенств с одной переменной. |
|
|
|
|
66 |
3 |
Решение неравенств с одной переменной. |
|
|
|
|
67 |
4 |
Решение систем неравенств с одной переменной. |
|
|
|
|
68 |
5 |
Решение систем неравенств с одной переменной. |
|
|
|
|
69 |
6 |
Решение систем неравенств с одной переменной. |
|
|
|
|
70 |
7 |
Контрольная работа № 7 "Неравенства с одной переменной и их системы". |
|
|
|
|
Степень с целым показателем . |
|||||
|
Степень с целым показателем и её свойства. |
|||||
|
71 |
1 |
Определение степени с целым отрицательным показателем. |
|
|
|
|
72 |
2 |
Определение степени с целым отрицательным показателем. |
|
|
|
|
73 |
3 |
Свойства степени с целым показателем. |
|
|
|
|
74 |
4 |
Свойства степени с целым показателем. |
|
|
|
|
75 |
5 |
Свойства степени с целым показателем. |
|
|
|
|
Стандартный вид числа. |
|||||
|
76 |
1 |
Стандартный вид числа. |
|
|
|
|
77 |
2 |
Стандартный вид числа. |
|
|
|
|
78 |
3 |
Контрольная работа № 8 "Степень с целым показателем". |
|
|
|
|
Теория вероятностей. |
|||||
|
Элементы теории вероятностей. |
|||||
|
79 |
1 |
Случайные опыты. |
|
|
|
|
80 |
2 |
Элементарные события. Равновозможные элементарные события. |
|
|
|
|
81 |
3 |
Вероятности событий. |
|
|
|
|
82 |
4 |
Вероятности событий. |
|
|
|
|
83 |
5 |
Опыты с равновозможными элементарными событиями. |
|
|
|
|
Вероятности случайных событий. |
|||||
|
84 |
1 |
Противоположное событие. Диаграммы Эйлера. |
|
|
|
|
85 |
2 |
Объединение и пересечение событий. |
|
|
|
|
86 |
3 |
Несовместные события. Правило сложения вероятностей. |
|
|
|
|
87 |
4 |
Формула сложения вероятностей. |
|
|
|
|
88 |
5 |
Независимые события. Умножение вероятностей. |
|
|
|
|
89 |
6 |
Контрольная работа № 9 "Элементы теории вероятностей. Вероятности случайных событий". |
|
|
|
|
Повторение |
|||||
|
90 |
1 |
Квадратные корни |
|
|
|
|
91 |
2 |
Квадратные корни |
|
|
|
|
92 |
3 |
Неравенства |
|
|
|
|
93 |
4 |
Неравенства |
|
|
|
|
94 |
5 |
Свойства степени с целым показателем. |
|
|
|
|
95 |
6 |
Свойства степени с целым показателем. |
|
|
|
|
96 |
7 |
Контрольная работа № 10 (итоговая) |
|
|
|
|
97 |
8 |
Итоговое повторение |
|
|
|
|
98 |
9 |
Решение заданий ОГЭ |
|
|
|
|
99 |
10 |
Решение заданий ОГЭ |
|
|
|
|
100 |
11 |
Решение заданий ОГЭ |
|
|
|
|
101 |
12 |
Решение заданий ОГЭ |
|
|
|
|
102 |
13 |
Решение заданий ОГЭ |
|
|
|
9 класс
|
№ урока |
№ урока в теме |
Тема урока |
Дата проведения |
Примечание |
|
|
По плану |
По факту |
||||
|
Функции. |
|||||
|
Функции и их свойства. |
|||||
|
1 |
1 |
Функция. Область определения и область значений функции. |
|
|
|
|
2 |
2 |
Функция. Область определения и область значений функции. |
|
|
|
|
3 |
3 |
Свойства функций. |
|
|
|
|
4 |
4 |
Свойства функций. |
|
|
|
|
5 |
5 |
Нахождение свойств функции без построения графика. |
|
|
|
|
Квадратный трехчлен. |
|||||
|
6 |
1 |
Квадратный трехчлен и его корни. |
|
|
|
|
7 |
2 |
Квадратный трехчлен и его корни. |
|
|
|
|
8 |
3 |
Разложение квадратного трехчлена на множители. |
|
|
|
|
9 |
4 |
Разложение квадратного трехчлена на множители. |
|
|
|
|
Квадратичная функция и её график. |
|||||
|
10 |
1 |
Функция y=ax2, её график и свойства. |
|
|
|
|
11 |
2 |
Функция y=ax2 , её график и свойства. |
|
|
|
|
12 |
3 |
Графики функций y=ax2+n и y=a(x-m)2. |
|
|
|
|
13 |
4 |
Графики функций y=ax2+n и y=a(x-m)2. |
|
|
|
|
14 |
5 |
Построение графика квадратичной функции. |
|
|
|
|
15 |
6 |
Построение графика квадратичной функции. |
|
|
|
|
16 |
7 |
Построение графика квадратичной функции. |
|
|
|
|
17 |
8 |
Практическое применение квадратичной функции. |
|
|
|
|
Степенная функция. |
|||||
|
18 |
1 |
Функция y=xn. |
|
|
|
|
19 |
2 |
Функция y=xn. |
|
|
|
|
20 |
3 |
Контрольная работа № 1 " Функции и их свойства. Квадратичная функция". |
|
|
|
|
21 |
4 |
Обобщающий урок " Функции". |
|
|
|
|
Уравнения и неравенства с одной переменной. |
|||||
|
Уравнения с одной переменной. |
|||||
|
22 |
1 |
Целое уравнение и его корни. |
|
|
|
|
23 |
2 |
Целое уравнение и его корни. |
|
|
|
|
24 |
3 |
Целое уравнение и его корни. |
|
|
|
|
25 |
4 |
Дробные рациональные уравнения. |
|
|
|
|
26 |
5 |
Подготовка к ОГЭ: Решение дробно рациональных уравнений. |
|
|
|
|
27 |
6 |
Дробные рациональные уравнения. |
|
|
|
|
28 |
7 |
Решение задач с помощью дробных рациональных уравнений. |
|
|
|
|
Неравенства с одной переменной. |
|||||
|
29 |
1 |
Решение неравенств второй степени с одной переменной. |
|
|
|
|
30 |
2 |
Решение неравенств второй степени с одной переменной. |
|
|
|
|
31 |
3 |
Решение неравенств второй степени с одной переменной. |
|
|
|
|
32 |
4 |
Решение неравенств методом интервалов. |
|
|
|
|
33 |
5 |
Решение неравенств методом интервалов. |
|
|
|
|
34 |
6 |
Решение неравенств методом интервалов. |
|
|
|
|
35 |
7 |
Контрольная работа № 2 "Уравнения и неравенства с одной переменной". |
|
|
|
|
36 |
8 |
Обобщающий урок "Уравнения и неравенства с одной переменной". |
|
|
|
|
Уравнения с двумя переменными и их системы. |
|||||
|
Уравнение с двумя переменными и его график. |
|||||
|
37 |
1 |
Уравнение с двумя переменными и его график. |
|
|
|
|
38 |
2 |
Уравнение с двумя переменными и его график. |
|
|
|
|
39 |
3 |
Графический способ решения систем уравнений. |
|
|
|
|
40 |
4 |
Графический способ решения систем уравнений. |
|
|
|
|
Системы уравнений второй степени. |
|||||
|
40 |
1 |
Решение систем уравнений второй степени. |
|
|
|
|
41 |
2 |
Решение систем уравнений второй степени. |
|
|
|
|
42 |
3 |
Решение систем уравнений второй степени. |
|
|
|
|
43 |
4 |
Решение задач с помощью систем уравнений второй степени. |
|
|
|
|
44 |
5 |
Решение задач с помощью систем уравнений второй степени. |
|
|
|
|
45 |
6 |
Решение задач с помощью систем уравнений второй степени. |
|
|
|
|
46 |
7 |
Контрольная работа № 3 "Уравнения с двумя переменными и их системы". |
|
|
|
|
47 |
8 |
Обобщающий урок "Уравнения с двумя переменными и их системы". |
|
|
|
|
Последовательности и прогрессии. |
|||||
|
Арифметическая прогрессия. |
|||||
|
48 |
1 |
Числовые последовательности. |
|
|
|
|
49 |
2 |
Числовые последовательности. |
|
|
|
|
50 |
3 |
Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии. |
|
|
|
|
51 |
4 |
Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии. |
|
|
|
|
52 |
5 |
Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии. |
|
|
|
|
53 |
6 |
Сумма первых n членов арифметической прогрессии. |
|
|
|
|
54 |
7 |
Сумма первых n членов арифметической прогрессии. |
|
|
|
|
55 |
8 |
Сумма первых n членов арифметической прогрессии. |
|
|
|
|
56 |
9 |
Контрольная работа № 4 "Арифметическая прогрессия". |
|
|
|
|
Геометрическая прогрессия. |
|||||
|
57 |
1 |
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии. |
|
|
|
|
58 |
2 |
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии. |
|
|
|
|
59 |
3 |
Формула суммы n первых членов геометрической прогрессии. |
|
|
|
|
60 |
4 |
Формула суммы n первых членов геометрической прогрессии. |
|
|
|
|
61 |
5 |
Формула суммы n первых членов геометрической прогрессии. |
|
|
|
|
62 |
6 |
Контрольная работа № 5 "Геометрическая прогрессия". |
|
|
|
|
63 |
7 |
Обобщающий урок "Последовательности и прогрессии" |
|
|
|
|
Статистика и теория вероятностей. |
|||||
|
Элементы комбинаторики. |
|||||
|
64 |
1 |
Правило умножения. |
|
|
|
|
65 |
2 |
Подготовка к ОГЭ: Вероятность. |
|
|
|
|
66 |
3 |
Перестановки. Факториал числа. |
|
|
|
|
67 |
4 |
Правило умножения и перестановки в задачах на вычисление вероятностей. |
|
|
|
|
68 |
5 |
Сочетания. |
|
|
|
|
69 |
6 |
Треугольник Паскаля. |
|
|
|
|
70 |
7 |
Испытания Бернулли. |
|
|
|
|
71 |
8 |
Вероятности событий в испытаниях Бернулли. |
|
|
|
|
Случайные величины. |
|||||
|
72 |
1 |
Примеры случайных величин. |
|
|
|
|
73 |
2 |
Распределение вероятностей случайной величины. |
|
|
|
|
74 |
3 |
Математическое ожидание случайной величины. |
|
|
|
|
75 |
4 |
Понятие о законе больших чисел. |
|
|
|
|
76 |
5 |
Контрольная работа № 6 "Элементы комбинаторики. Случайные величины". |
|
|
|
|
77 |
6 |
Обобщающий урок "Элементы комбинаторики. Случайные величины". |
|
|
|
|
Повторение курса алгебры 7-9 класса. |
|||||
|
Числа. |
|||||
|
78 |
1 |
Числовые выражения |
|
|
|
|
79 |
2 |
Изображение чисел на числовой прямой. Сравнение чисел. |
|
|
|
|
Преобразование числовых и буквенных выражений. |
|||||
|
80 |
1 |
Формулы сокращённого умножения и их применение. |
|
|
|
|
81 |
2 |
Действия с алгебраическими дробями. |
|
|
|
|
82 |
3 |
Преобразование выражений, содержащих квадратные корни. |
|
|
|
|
Уравнения, неравенства и их системы. |
|||||
|
83 |
1 |
Целое уравнение. |
|
|
|
|
84 |
2 |
Решение дробно-рациональных уравнений. |
|
|
|
|
85 |
4 |
Решение систем уравнений с двумя переменными. |
|
|
|
|
86 |
5 |
Решение неравенств с одной переменной и их систем. |
|
|
|
|
Функции и их свойства. |
|||||
|
87 |
1 |
Построение графиков функций: линейной, квадратичной, обратной пропорциональности, y=√x. |
|
|
|
|
88 |
2 |
Исследование функции по её графику. |
|
|
|
|
89 |
3 |
Арифметическая и геометрическая прогрессии. |
|
|
|
|
Текстовые задачи. |
|||||
|
90 |
1 |
Решение задач на движение. |
|
|
|
|
91 |
2 |
Решение задач на движение. |
|
|
|
|
92 |
3 |
Решение задач на работу. |
|
|
|
|
93 |
4 |
Решение задач на части, доли. |
|
|
|
|
94 |
5 |
Решение задач на проценты. |
|
|
|
|
95 |
6 |
Решение задач на проценты. |
|
|
|
|
Теория вероятностей и статистика. |
|||||
|
96 |
1 |
Диаграммы. Описательная статистика. |
|
|
|
|
97 |
2 |
Случайные события и вероятность. |
|
|
|
|
98 |
3 |
Математическое описание случайных явлений. |
|
|
|
|
99 |
4 |
Вероятности случайных событий. |
|
|
|
|
100 |
5 |
Итоговая контрольная работа. |
|
|
|
|
101 |
6 |
Обобщающий урок. |
|
|
|
|
102 |
7 |
Решение вариантов ОГЭ |
|
|
|
Геометрия
7 класс
|
№ урока |
№ урока в теме |
Тема урока |
Дата проведения |
Примечание |
|
|
По плану |
По факту |
||||
|
Начальные геометрические сведения. |
|||||
|
1 |
1 |
Прямая и отрезок. |
|
|
|
|
2 |
2 |
Луч и угол. |
|
|
|
|
3 |
3 |
Сравнение отрезков и углов. |
|
|
|
|
4 |
4 |
Измерение отрезков. |
|
|
|
|
5 |
5 |
Решение задач по теме: «Измерение отрезков». |
|
|
|
|
6 |
6 |
Измерение углов |
|
|
|
|
7 |
7 |
Смежные и вертикальные углы. |
|
|
|
|
8 |
8 |
Перпендикулярные прямые |
|
|
|
|
9 |
9 |
Решение задач по теме: «Смежные и вертикальные углы». |
|
|
|
|
10 |
10 |
Решение задач по теме: «Смежные и вертикальные углы». |
|
|
|
|
11 |
11 |
Контрольная работа №1 по теме: «Начальные геометрические сведения». |
|
|
|
|
Треугольники. |
|||||
|
12 |
1 |
Треугольник. |
|
|
|
|
13 |
2 |
Первый признак равенства треугольников |
|
|
|
|
14 |
3 |
Решение задач по теме: «Первый признак равенства треугольников». |
|
|
|
|
15 |
4 |
Медианы, биссектрисы и высоты треугольника. |
|
|
|
|
16 |
5 |
Равнобедренный треугольник и его свойства |
|
|
|
|
17 |
6 |
Решение задач по теме: «Равнобедренный треугольник» |
|
|
|
|
18 |
7 |
Второй признак равенства треугольников |
|
|
|
|
19 |
8 |
Третий признак равенства треугольников |
|
|
|
|
20 |
9 |
Решение задач на применение признаков равенства треугольников. |
|
|
|
|
21 |
10 |
Решение задач на применение признаков равенства треугольников. |
|
|
|
|
22 |
11 |
Окружность. |
|
|
|
|
23 |
12 |
Основные задачи на построения с помощью циркуля и линейки |
|
|
|
|
24 |
13 |
Основные задачи на построения с помощью циркуля и линейки |
|
|
|
|
25 |
14 |
Решение задач на применение признаков равенства треугольников. |
|
|
|
|
26 |
15 |
Решение задач на применение признаков равенства треугольников. Контрольная работа №2 по теме: «Треугольники» |
|
|
|
|
Параллельные прямые |
|||||
|
27 |
1 |
Признаки параллельности прямых |
|
|
|
|
28 |
2 |
Признаки параллельности прямых |
|
|
|
|
29 |
3 |
Признаки параллельности прямых |
|
|
|
|
30 |
4 |
Аксиома параллельных прямых |
|
|
|
|
31 |
5 |
Свойства параллельных прямых |
|
|
|
|
32 |
6 |
Свойства параллельных прямых |
|
|
|
|
33 |
7 |
Решение задач по теме: «Параллельные прямые» |
|
|
|
|
34 |
8 |
Решение задач по теме: «Параллельные прямые» |
|
|
|
|
35 |
9 |
Решение задач по теме: «Параллельные прямые» |
|
|
|
|
36 |
10 |
Решение задач по теме: «Параллельные прямые» |
|
|
|
|
37 |
11 |
Решение задач по теме: «Параллельные прямые» |
|
|
|
|
38 |
12 |
Контрольная работа №3 по теме: «Параллельные прямые». |
|
|
|
|
Соотношения между сторонами и углами треугольника |
|||||
|
39 |
1 |
Сумма углов треугольника |
|
|
|
|
40 |
2 |
Сумма углов треугольника |
|
|
|
|
41 |
3 |
Решение задач по теме: «Сумма углов треугольника» |
|
|
|
|
42 |
4 |
Соотношения между сторонами и углами треугольника |
|
|
|
|
43 |
5 |
Соотношения между сторонами и углами треугольника |
|
|
|
|
44 |
6 |
Неравенство треугольника |
|
|
|
|
45 |
7 |
Решение задач по теме: «Неравенство треугольника» |
|
|
|
|
46 |
8 |
Решение задач по теме: «Неравенство треугольника» |
|
|
|
|
47 |
9 |
Контрольная работа №4 по теме: «Соотношения между сторонами и углами треугольника» |
|
|
|
|
48 |
10 |
Некоторые свойства прямоугольных треугольников |
|
|
|
|
49 |
11 |
Некоторые свойства прямоугольных треугольников |
|
|
|
|
50 |
12 |
Признаки равенства прямоугольных треугольников |
|
|
|
|
51 |
13 |
Признаки равенства прямоугольных треугольников |
|
|
|
|
52 |
14 |
Расстояние от точки до прямой расстояние между параллельными прямыми |
|
|
|
|
53 |
15 |
Решение задач по теме: «Прямоугольные треугольники» |
|
|
|
|
54 |
16 |
Решение задач по теме: «Прямоугольные треугольники» |
|
|
|
|
55 |
17 |
Задачи на построение |
|
|
|
|
56 |
18 |
Задачи на построение |
|
|
|
|
57 |
19 |
Решение задач по теме: «Прямоугольные треугольники» |
|
|
|
|
58 |
20 |
Решение задач по теме: «Расстояние от точки до прямой, Расстояние между параллельными прямыми» |
|
|
|
|
59 |
21 |
Решение задач по теме: «Расстояние от точки до прямой, Расстояние между параллельными прямыми» |
|
|
|
|
60 |
22 |
Контрольная работа №5 по теме: «Соотношения между сторонами и углами» треугольника |
|
|
|
|
Повторение Решение задач |
|||||
|
61 |
1 |
Повторение темы: «Начальные геометрические сведения» |
|
|
|
|
62 |
2 |
Повторение темы: «Признаки равенства треугольников. Равнобедренный треугольник». |
|
|
|
|
63 |
3 |
Повторение темы: «Параллельные прямые |
|
|
|
|
64 |
4 |
Повторение темы: «Параллельные прямые». |
|
|
|
|
65 |
5 |
Решение задач. |
|
|
|
|
66 |
6 |
Итоговый контрольный тест. |
|
|
|
|
67 |
7 |
Анализ контрольной работы |
|
|
|
|
68 |
8 |
Итоговый урок. Решение задач. |
|
|
|
8 класс
|
№ урока |
№ урока в теме |
Тема урока |
Дата проведения |
Примечание |
|
|
По плану |
По факту |
||||
|
Многоугольник. |
|||||
|
1 |
1 |
Ломаная. Понятие многоугольника и его элементов. Выпуклый многоугольник. |
|
|
|
|
2 |
2 |
Сумма углов выпуклого многоугольника. Четырехугольник. |
|
|
|
|
Параллелограмм |
|||||
|
3 |
1 |
Параллелограмм. |
|
|
|
|
4 |
2 |
Параллелограмм. Свойства параллелограмма. |
|
|
|
|
5 |
3 |
Признаки параллелограмма. |
|
|
|
|
6 |
4 |
Свойства и признаки параллелограмма. |
|
|
|
|
7 |
5 |
Свойства и признаки параллелограмма. |
|
|
|
|
Трапеция. |
|||||
|
8 |
1 |
Трапеция. Виды трапеций. |
|
|
|
|
9 |
2 |
Трапеция. Виды трапеций. Теорема Фалеса. |
|
|
|
|
Прямоугольник, ромб квадрат. |
|||||
|
10 |
1 |
Прямоугольник. Свойства и признаки прямоугольника. |
|
|
|
|
11 |
2 |
Ромб. Свойства ромба. |
|
|
|
|
12 |
3 |
Ромб. Свойства ромба. |
|
|
|
|
13 |
4 |
Квадрат. |
|
|
|
|
14 |
5 |
Решение задач "Прямоугольник, ромб, квадрат". |
|
|
|
|
15 |
6 |
Контрольная работа № 1 "Четырехугольники". |
|
|
|
|
Площади. |
|||||
|
Понятие площади многоугольника. |
|||||
|
16 |
1 |
Понятие площади многоугольника. Основные свойства площадей. |
|
|
|
|
17 |
2 |
Площадь квадрата и прямоугольника. |
|
|
|
|
Площадь параллелограмма, треугольника и трапеции. |
|||||
|
18 |
1 |
Площадь параллелограмма. |
|
|
|
|
19 |
2 |
Площадь параллелограмма. |
|
|
|
|
20 |
3 |
Площадь треугольника. |
|
|
|
|
21 |
4 |
Площадь треугольника. |
|
|
|
|
22 |
5 |
Площадь трапеции. |
|
|
|
|
23 |
6 |
Площадь трапеции. |
|
|
|
|
Теорема Пифагора. |
|||||
|
24 |
1 |
Теорема Пифагора. |
|
|
|
|
25 |
2 |
Теорема Пифагора. |
|
|
|
|
26 |
3 |
Теорема, обратная теореме Пифагора. |
|
|
|
|
27 |
4 |
Формула Герона. |
|
|
|
|
28 |
5 |
Решение задач "Площади. Теорема Пифагора". |
|
|
|
|
29 |
6 |
Контрольная работа № 2 " Площади. Теорема Пифагора". |
|
|
|
|
Подобные треугольники. |
|||||
|
Подобные треугольники. |
|||||
|
30 |
1 |
Пропорциональные отрезки. Свойство биссектрисы треугольника. |
|
|
|
|
31 |
2 |
Определение подобных треугольников. |
|
|
|
|
32 |
3 |
Отношение площадей подобных треугольников. |
|
|
|
|
33 |
4 |
Отношение площадей подобных треугольников. |
|
|
|
|
Признаки подобия треугольников. |
|||||
|
34 |
1 |
Первый признак подобия треугольников. |
|
|
|
|
35 |
2 |
Второй признак подобия треугольников. |
|
|
|
|
36 |
3 |
Третий признак подобия треугольников. |
|
|
|
|
37 |
4 |
Решение задач "Признаки подобия треугольников". |
|
|
|
|
38 |
5 |
Контрольная работа № 3 "Подобные треугольники". |
|
|
|
|
Применение подобия к доказательству теорем и решению задач. |
|||||
|
Средняя линия треугольника. |
|||||
|
39 |
1 |
Средняя линия треугольника. Свойства средней линии. |
|
|
|
|
40 |
2 |
Свойство медиан треугольника. |
|
|
|
|
41 |
3 |
Решение задач "Средняя линия треугольника". |
|
|
|
|
Практические приложения подобия треугольников. |
|||||
|
42 |
1 |
Определение высоты предмета. |
|
|
|
|
Решение прямоугольных треугольников. |
|||||
|
43 |
1 |
Пропорциональные отрезки в прямоугольном треугольнике. |
|
|
|
|
44 |
2 |
Пропорциональные отрезки в прямоугольном треугольнике. |
|
|
|
|
45 |
3 |
Синус, косину и тангенс острого угла прямоугольного треугольника. |
|
|
|
|
46 |
4 |
Значения синуса, косинуса и тангенса для углов 30, 45, 60 градусов. |
|
|
|
|
47 |
5 |
Решение задач "Соотношения между сторонами и углами прямоугольного треугольника". |
|
|
|
|
48 |
6 |
Контрольная работа № 4 "Соотношения между сторонами и углами прямоугольного треугольника". |
|
|
|
|
Окружность. |
|||||
|
Касательная к окружности. |
|||||
|
49 |
1 |
Взаимное расположение прямой и окружности. |
|
|
|
|
50 |
2 |
Касательная к окружности. Свойство и признак касательной. |
|
|
|
|
51 |
3 |
Касательная к окружности. Свойство и признак касательной. |
|
|
|
|
Центральные и вписанные углы. |
|||||
|
52 |
1 |
Градусная мера дуги окружности. |
|
|
|
|
53 |
2 |
Теорема о вписанном угле. |
|
|
|
|
54 |
3 |
Решение задач "Центральный и вписанный углы". |
|
|
|
|
55 |
4 |
Решение задач "Центральный и вписанный углы". |
|
|
|
|
Вписанная и описанная окружности. |
|||||
|
56 |
1 |
Вписанная окружность. |
|
|
|
|
57 |
2 |
Вписанная окружность. |
|
|
|
|
58 |
3 |
Описанная окружность. |
|
|
|
|
59 |
4 |
Описанная окружность. |
|
|
|
|
60 |
5 |
Контрольная работа № 5 "Окружность". |
|
|
|
|
Повторение. |
|||||
|
Повторение курса 8 класса. |
|||||
|
61 |
1 |
Многоугольники. |
|
|
|
|
62 |
2 |
Площади. |
|
|
|
|
63 |
3 |
Вписанный угол. Касательная к окружности. |
|
|
|
|
64 |
4 |
Вписанная и описанная окружность. |
|
|
|
|
65 |
5 |
Решение задач ОГЭ |
|
|
|
|
66 |
6 |
Решение задач ОГЭ |
|
|
|
|
67 |
7 |
Решение задач ОГЭ |
|
|
|
|
68 |
8 |
Решение задач ОГЭ |
|
|
|
9 класс
|
№ урока |
№ урока в теме |
Тема урока |
Дата проведения |
Примечание |
|
|
По плану |
По факту |
||||
|
Векторы. |
|||||
|
Понятие вектора. |
|||||
|
1 |
1 |
Понятие вектора. |
|
|
|
|
2 |
2 |
Равенство векторов. Откладывание вектора равного данному. |
|
|
|
|
Сложение и вычитание векторов. |
|||||
|
3 |
1 |
Сумма двух векторов. Законы сложения векторов. |
|
|
|
|
4 |
2 |
Сумма нескольких векторов. |
|
|
|
|
5 |
3 |
Вычитание векторов. |
|
|
|
|
6 |
4 |
Сложение и вычитание векторов. |
|
|
|
|
Умножение вектора на число. |
|||||
|
7 |
1 |
Умножение вектора на число. |
|
|
|
|
8 |
2 |
Применение векторов для решения задач. |
|
|
|
|
9 |
3 |
Средняя линия трапеции. |
|
|
|
|
10 |
4 |
Контрольная работа № 1 "Векторы". |
|
|
|
|
11 |
5 |
Обобщающий урок "Векторы". |
|
|
|
|
Метод координат. |
|||||
|
Координаты вектора. |
|||||
|
12 |
1 |
Разложение вектора по двум неколлинеарным векторам. |
|
|
|
|
13 |
2 |
Координаты вектора. |
|
|
|
|
14 |
3 |
Связь между координатами вектора и координатами его начала и конца. |
|
|
|
|
15 |
4 |
Связь между координатами вектора и координатами его начала и конца. |
|
|
|
|
Простейшие задачи в координатах. |
|||||
|
16 |
1 |
Координаты середины отрезка. |
|
|
|
|
17 |
2 |
Вычисление длины вектора по его координатам. Расстояние между точками. |
|
|
|
|
18 |
3 |
Решение задач "Простейшие задачи в координатах". |
|
|
|
|
Уравнение окружности и прямой. |
|||||
|
19 |
1 |
Уравнение окружности. |
|
|
|
|
20 |
2 |
Уравнение прямой. |
|
|
|
|
21 |
3 |
Взаимное расположение двух окружностей. |
|
|
|
|
22 |
4 |
Решение задач "Уравнение окружности и прямой". |
|
|
|
|
23 |
5 |
Контрольная работа №2 " Метод координат". |
|
|
|
|
24 |
6 |
Обобщающий урок " Метод координат". |
|
|
|
|
Решение треугольников. |
|||||
|
Тригонометрические функции для угла от 0 до 180 градусов. |
|||||
|
25 |
1 |
Синус, косинус, тангенс, котангенс. |
|
|
|
|
26 |
2 |
Основное тригонометрическое тождество. Формулы приведения. |
|
|
|
|
27 |
3 |
Формулы для вычисления координат точки. |
|
|
|
|
Соотношение между сторонами и углами треугольника. |
|||||
|
28 |
1 |
Теорема о площади треугольника. |
|
|
|
|
29 |
2 |
Теорема синусов. |
|
|
|
|
30 |
3 |
Теорема косинусов. |
|
|
|
|
31 |
4 |
Решение треугольников. |
|
|
|
|
32 |
5 |
Решение треугольников. |
|
|
|
|
Скалярное произведение векторов. |
|||||
|
33 |
1 |
Угол между векторами. |
|
|
|
|
34 |
2 |
Скалярное произведение векторов. |
|
|
|
|
35 |
3 |
Скалярное произведение векторов в координатах. |
|
|
|
|
36 |
4 |
Свойства скалярного произведения векторов. |
|
|
|
|
37 |
5 |
Решение задач "Соотношения между сторонами и углами треугольника. Скалярное произведение векторов". |
|
|
|
|
38 |
6 |
Контрольная работа № 3 "Соотношения между сторонами и углами треугольника. Скалярное произведение векторов". |
|
|
|
|
39 |
7 |
Обобщающий урок "Решение треугольника. Скалярное произведение векторов". |
|
|
|
|
Длина окружности и площадь круга. |
|||||
|
Правильные многоугольники. |
|||||
|
40 |
1 |
Правильный многоугольник. Окружность вписанная и описанная около правильного многоугольника. |
|
|
|
|
41 |
2 |
Правильный многоугольник. Окружность вписанная и описанная около правильного многоугольника. |
|
|
|
|
42 |
3 |
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. |
|
|
|
|
43 |
4 |
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. |
|
|
|
|
44 |
5 |
Решение задач "Правильные многоугольники". |
|
|
|
|
Длина окружности. Площадь круга. |
|||||
|
45 |
1 |
Длина окружности. |
|
|
|
|
46 |
2 |
Площадь круга. |
|
|
|
|
47 |
3 |
Площадь кругового сектора, сегмента. |
|
|
|
|
48 |
4 |
Решение задач "Длина окружности". |
|
|
|
|
49 |
5 |
Решение задач "Площадь круга, сектора, сегмента". |
|
|
|
|
50 |
6 |
Контрольная работа № 4 "Длина окружности и площадь круга". |
|
|
|
|
51 |
7 |
Обобщающий урок "Длина окружности. Площадь круга". |
|
|
|
|
Геометрические преобразования. |
|||||
|
Движения. |
|||||
|
52 |
1 |
Понятие движения. Наложения и движения. |
|
|
|
|
53 |
2 |
Осевая симметрия. |
|
|
|
|
54 |
3 |
Центральная симметрия. |
|
|
|
|
55 |
4 |
Параллельный перенос. |
|
|
|
|
56 |
5 |
Поворот. |
|
|
|
|
57 |
6 |
Решение задач "Движения". |
|
|
|
|
58 |
7 |
Контрольная работа "Движение". |
|
|
|
|
59 |
8 |
Обобщающий урок "Движение". |
|
|
|
|
Повторение курса геометрии 7-9 класса. |
|||||
|
Повторение. |
|||||
|
60 |
1 |
Решение задач "Признаки равенства треугольников". |
|
|
|
|
61 |
2 |
Решение задач "Признаки равенства треугольников". |
|
|
|
|
62 |
3 |
Решение задач "Параллельные прямые". |
|
|
|
|
63 |
4 |
Решение задач "Параллельные прямые". |
|
|
|
|
64 |
5 |
Решение задач "Правильные многоугольники". |
|
|
|
|
65 |
6 |
Решение задач "Правильные многоугольники". |
|
|
|
|
66 |
7 |
Обобщающее повторение |
|
|
|
Критерии и нормы оценки знаний, умений и навыков
Единые нормы являются основой при оценке как контрольных, так и всех других письменных работ по математике. Они обеспечивают единство требований к обучающимся со стороны всех учителей образовательного учреждения, сравнимость результатов обучения в разных классах. Применяя эти нормы, учитель должен индивидуально подходить к оценке каждой письменной работы учащегося, обращать внимание на качество выполнения работы в целом, а затем уже на количество ошибок и на их характер.
Содержание и объем материала, включаемого в контрольные письменные работы, а также в задания для повседневных письменных упражнений, определяются требованиями, установленными программой. Наряду с контрольными работами по отдельным разделам темы следует проводить итоговые контрольные работы по всей изученной теме.
По характеру заданий письменные работы могут состоять:
а) только из примеров; б) только из задач; в) из задач и примеров.
Контрольные работы, которые имеют целью проверку знаний, умений и навыков учащихся по целому разделу программы, а также по материалу, изученному за четверть (триместр) или за год, как правило, должны состоять из задач и примеров.
Оценка письменной работы определяется с учетом прежде всего ее общего математического уровня, оригинальности, последовательности, логичности ее выполнения, а также числа ошибок и недочетов и качества оформления работы. Ошибка, повторяющаяся в одной работе несколько раз, рассматривается как одна ошибка. За орфографические ошибки, допущенные учениками, оценка не снижается; об орфографических ошибках доводится до сведения преподавателя русского языка. Однако ошибки в написании математических терминов, уже встречавшихся школьникам класса,
должны учитываться как недочеты в работе.
При оценке письменных работ по математике различают грубые ошибки, ошибки и недочеты. Полезно договориться о единой для всего образовательного учреждения системе пометок на полях письменной работы, например так: v — недочет, | — ошибка
(негрубая ошибка), -![]()
![]() - грубая
ошибка.
- грубая
ошибка.
1. Оценка письменных контрольных работ обучающихся по математике.
Отметка «5», если:
· работа выполнена полностью;
· в логических рассуждениях и обосновании решения нет пробелов и ошибок;
· в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
· работа выполнена полностью, но обоснования шагов решения
· недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
· допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
· допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
· допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
· работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
· полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
· изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
· правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
· показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
· продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
· отвечал самостоятельно, без наводящих вопросов учителя;
· возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4»,
· если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
· в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
· допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
· допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
· неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
· имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
· ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
· при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
· не раскрыто основное содержание учебного материала;
· обнаружено незнание учеником большей или наиболее важной части учебного материала;
· допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
· ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
-незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
-незнание наименований единиц измерения;
-неумение выделить в ответе главное;
-неумение применять знания, алгоритмы для решения задач;
-неумение делать выводы и обобщения;
-неумение читать и строить графики;
-неумение пользоваться первоисточниками, учебником и справочниками;
-потеря корня или сохранение постороннего корня;
-отбрасывание без объяснений одного из них;
-равнозначные им ошибки;
-вычислительные ошибки, если они не являются опиской;
-логические ошибки.
Кнегрубым ошибкам следует отнести:
- неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
- неточность графика;
- нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
- нерациональные методы работы со справочной и другой литературой;
- неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
- нерациональные приемы вычислений и преобразований;
- небрежное выполнение записей, чертежей, схем, графиков.
Результаты (личностные, метапредменые и предметные) освоения учебного предмета «Математика»
Планируемые результаты освоения учебного предмета «Математика» 5–9 классы
Личностными результатами изучения предмета «Математика» (в виде следующих учебных курсов: 5–6 класс – «Математика», 7–9 класс – «Алгебра» и «Геометрия» являются следующие качества:
· независимость и критичность мышления;
· воля и настойчивость в достижении цели.
Средством достижения этих результатов является:
· система заданий учебников;
· представленная в учебниках в явном виде организация материала по принципу минимакса;
· использование совокупности технологий, ориентированных на развитие самостоятельности и критичности мышления: технология системно-деятельностного подхода в обучении, технология оценивания.
Метапредметными результатами изучения курса «Математика» является формирование универсальных учебных действий (УУД).
Регулятивные УУД:
5–6-й классы
– самостоятельно обнаруживать и формулировать учебную проблему, определять цель учебной деятельности, выбирать тему проекта;
– выдвигать версии решения проблемы, осознавать (и интерпретировать в случае необходимости) конечный результат, выбирать средства достижения цели из предложенных, а также искать их самостоятельно;
– составлять (индивидуально или в группе) план решения проблемы (выполнения проекта);
– работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки самостоятельно (в том числе и корректировать план);
– в диалоге с учителем совершенствовать самостоятельно выработанные критерии оценки.
7–9-й классы
– самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности;
– выдвигать версии решения проблемы, осознавать конечный результат, выбирать средства достижения цели из предложенных или их искать самостоятельно;
– составлять (индивидуально или в группе) план решения проблемы (выполнения проекта);
– подбирать к каждой проблеме (задаче) адекватную ей теоретическую модель;
– работая по предложенному или самостоятельно составленному плану, использовать наряду с основными и дополнительные средства (справочная литература, сложные приборы, компьютер);
– планировать свою индивидуальную образовательную траекторию;
– работать по самостоятельно составленному плану, сверяясь с ним и с целью деятельности, исправляя ошибки, используя самостоятельно подобранные средства (в том числе и Интернет);
– свободно пользоваться выработанными критериями оценки и самооценки, исходя из цели и имеющихся критериев, различая результат и способы действий;
– в ходе представления проекта давать оценку его результатам;
– самостоятельно осознавать причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха;
– уметь оценить степень успешности своей индивидуальной образовательной деятельности;
– давать оценку своим личностным качествам и чертам характера («каков я»), определять направления своего развития («каким я хочу стать», «что мне для этого надо сделать»).
Средством формирования регулятивных УУД служат технология системно-деятельностного подхода на этапе изучения нового материала и технология оценивания образовательных достижений (учебных успехов).
Познавательные УУД:
5–9-й классы
– анализировать, сравнивать, классифицировать и обобщать факты и явления;
– осуществлять сравнение, сериацию и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций; строить классификацию путём дихотомического деления (на основе отрицания);
– строить логически обоснованное рассуждение, включающее установление причинно-следственных связей;
– создавать математические модели;
– составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.);
– вычитывать все уровни текстовой информации.
– уметь определять возможные источники необходимых сведений, производить поиск информации, анализировать и оценивать её достоверность.
– понимая позицию другого человека, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории. Для этого самостоятельно использовать различные виды чтения (изучающее, просмотровое, ознакомительное, поисковое), приёмы слушания.
– самому создавать источники информации разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности;
– уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей. Уметь выбирать адекватные задаче инструментальные программно-аппаратные средства и сервисы.
Средством формирования познавательных УУД служат учебный материал и прежде всего продуктивные задания учебника.
– Использование математических знаний для решения различных математических задач и оценки полученных результатов.
– Совокупность умений по использованию доказательной математической речи.
– Совокупность умений по работе с информацией, в том числе и с различными математическими текстами.
– Умения использовать математические средства для изучения и описания реальных процессов и явлений.
– Независимость и критичность мышления.
– Воля и настойчивость в достижении цели.
Коммуникативные УУД:
5–9-й классы
– самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.);
– отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами;
– в дискуссии уметь выдвинуть контраргументы;
– учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;
– понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;
– уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.
Средством формирования коммуникативных УУД служат технология проблемного обучения, организация работы в малых группах, также использование на уроках технологии личностно- ориентированного и системно-деятельностного обучения.
Предметными результатами изучения предмета «Математика» являются следующие умения.
5-й класс
Использовать при решении математических задач, их обосновании и проверке найденного решения знание:
- названий и последовательности чисел в натуральном ряду в пределах 1 000 000 (с какого числа начинается этот ряд, как образуется каждое следующее число в этом ряду);
- как образуется каждая следующая счётная единица;
- названия и последовательность разрядов в записи числа;
- названия и последовательность первых трёх классов;
- сколько разрядов содержится в каждом классе;
- соотношение между разрядами;
- сколько единиц каждого класса содержится в записи числа;
- как устроена позиционная десятичная система счисления;
- единицы измерения величин (длина, масса, время, площадь), соотношения между ними;
- десятичных дробях и правилах действий с ними;
- сравнивать десятичные дроби;
- выполнять операции над десятичными дробями;
- преобразовывать десятичную дробь в обыкновенную и наоборот;
- округлять целые числа и десятичные дроби;
- находить приближённые значения величин с недостатком и избытком;
- выполнять приближённые вычисления и оценку числового выражения;
- функциональной связи между группами величин (цена, количество, стоимость; скорость, время, расстояние;
- производительность труда, время работы, работа).
- выполнять устные вычисления (в пределах 1 000 000) в случаях, сводимых к вычислениям в пределах 100, и письменные вычисления в остальных случаях;
- выполнять проверку правильности вычислений;
- выполнять умножение и деление с 1000;
- вычислять значения числовых выражений, содержащих 3–4 действия со скобками и без них;
- решать простые и составные текстовые задачи;
- выписывать множество всевозможных результатов (исходов) простейших случайных экспериментов;
- находить вероятности простейших случайных событий;
- решать удобным для себя способом (в том числе и с помощью таблиц и графов) комбинаторные задачи: на перестановку из трёх элементов, правило произведения, установление числа пар на множестве из 3–5 элементов;
- решать удобным для себя способом (в том числе и с помощью таблиц и графов) логические задачи, содержащие не более трёх высказываний;
- читать информацию, записанную с помощью линейных, столбчатых и круговых диаграмм;
- строить простейшие линейные, столбчатые и круговые диаграммы;
- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;
- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.
деятельности), для изучения и описания которого используются математические средства.
6-й класс.
- овладеть базовыми понятиями по основным разделам содержания;
- представлениями об основных изучаемых понятиях как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
- уметь работать с математическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики;
- развить представления о числе,
- овладеть навыками устных, письменных, инструментальных вычислений;
- уметь измерять длины отрезков, величины углов;
- использовать формулы для нахождения периметра, площади и объема фигур.
7-й класс.
Алгебра
Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:
- натуральных, целых, рациональных, иррациональных, действительных числах;
- степени с натуральными показателями и их свойствах;
- одночленах и правилах действий с ними;
- многочленах и правилах действий с ними;
- формулах сокращённого умножения;
- тождествах; методах доказательства тождеств;
- линейных уравнениях с одной неизвестной и методах их решения;
- системах двух линейных уравнений с двумя неизвестными и методах их решения.
- Выполнять действия с одночленами и многочленами;
- узнавать в выражениях формулы сокращённого умножения и применять их;
- раскладывать многочлены на множители;
- выполнять тождественные преобразования целых алгебраических выражений;
- доказывать простейшие тождества;
- находить число сочетаний и число размещений;
- решать линейные уравнения с одной неизвестной;
- решать системы двух линейных уравнений с двумя неизвестными методом подстановки и методом алгебраического сложения;
- решать текстовые задачи с помощью линейных уравнений и систем;
- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;
- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.
Геометрия
Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:
- основных геометрических понятиях: точка, прямая, плоскость, луч, отрезок, ломаная, многоугольник;
- определении угла, биссектрисы угла, смежных и вертикальных углов;
- свойствах смежных и вертикальных углов;
- определении равенства геометрических фигур; признаках равенства треугольников;
- геометрических местах точек; биссектрисе угла и серединном перпендикуляре к отрезку как геометрических местах точек;
- определении параллельных прямых; признаках и свойствах параллельных прямых;
- аксиоме параллельности и её краткой истории;
- формуле суммы углов треугольника;
- определении и свойствах средней линии треугольника;
- теореме Фалеса.
- применять свойства смежных и вертикальных углов при решении задач;
- находить в конкретных ситуациях равные треугольники и доказывать их равенство;
- устанавливать параллельность прямых и применять свойства параллельных прямых;
- применять теорему о сумме углов треугольника;
- использовать теорему о средней линии треугольника и теорему Фалеса при решении задач;
- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;
- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.
8-й класс.
Алгебра
Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:
- алгебраической дроби;
- основном свойстве дроби;
- правилах действий с алгебраическими дробями;
- степенях с целыми показателями и их свойствах;
- стандартном виде числа;
-
функциях ![]() ,
, ![]() ,
, ![]() , их свойствах
и графиках;
, их свойствах
и графиках;
- понятии квадратного корня и арифметического квадратного корня;
- свойствах арифметических квадратных корней;
-
функции ![]() , её
свойствах и графике;
, её
свойствах и графике;
- формуле для корней квадратного уравнения;
- теореме Виета для приведённого и общего квадратного уравнения;
- основных методах решения целых рациональных уравнений: методе разложения на множители и методе замены неизвестной;
- методе решения дробных рациональных уравнений;
- основных методах решения систем рациональных уравнений;
- сокращать алгебраические дроби;
- выполнять арифметические действия с алгебраическими дробями;
- использовать свойства степеней с целыми показателями при решении задач;
- записывать числа в стандартном виде;
- выполнять тождественные преобразования рациональных выражений;
-
строить графики функций ![]() ,
, ![]() ,
, ![]() и
использовать их свойства при решении задач;
и
использовать их свойства при решении задач;
- вычислять арифметические квадратные корни;
- применять свойства арифметических квадратных корней при решении задач;
-
строить график функции ![]() и
использовать его свойства при решении задач;
и
использовать его свойства при решении задач;
- решать квадратные уравнения;
- применять теорему Виета при решении задач;
- решать целые рациональные уравнения методом разложения на множители и методом замены неизвестной;
- решать дробные уравнения;
- решать системы рациональных уравнений;
- решать текстовые задачи с помощью квадратных и рациональных уравнений и их систем;
- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;
- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.
Геометрия
Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:
- определении параллелограмма, ромба, прямоугольника, квадрата; их свойствах и признаках;
- определении трапеции; элементах трапеции; теореме о средней линии трапеции;
- определении окружности, круга и их элементов;
- теореме об измерении углов, связанных с окружностью;
- определении и свойствах касательных к окружности; теореме о равенстве двух касательных, проведённых из одной точки;
- определении вписанной и описанной окружностей, их свойствах;
- определении тригонометрические функции острого угла, основных соотношений между ними;
- приёмах решения прямоугольных треугольников;
- тригонометрических функциях углов от 0 до 180°;
- теореме косинусов и теореме синусов;
- приёмах решения произвольных треугольников;
- формулах для площади треугольника, параллелограмма, трапеции;
- теореме Пифагора;
- применять признаки и свойства параллелограмма, ромба, прямоугольника, квадрата при решении задач;
- решать простейшие задачи на трапецию;
- находить градусную меру углов, связанных с окружностью; устанавливать их равенство;
- применять свойства касательных к окружности при решении задач;
- решать задачи на вписанную и описанную окружность;
- выполнять основные геометрические построения с помощью циркуля и линейки;
- находить значения тригонометрических функций острого угла через стороны прямоугольного треугольника;
- применять соотношения между тригонометрическими функциями при решении задач; в частности, по значению одной из функций находить значения всех остальных;
- решать прямоугольные треугольники;
- сводить работу с тригонометрическими функциями углов от 0 до 180° к случаю острых углов;
- применять теорему косинусов и теорему синусов при решении задач;
- решать произвольные треугольники;
- находить площади треугольников, параллелограммов, трапеций;
- применять теорему Пифагора при решении задач;
- находить простейшие геометрические вероятности;
- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;
- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.
9-й класс.
Алгебра
Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:
- свойствах числовых неравенств;
- методах решения линейных неравенств;
- свойствах квадратичной функции;
- методах решения квадратных неравенств;
- методе интервалов для решения рациональных неравенств;
- методах решения систем неравенств;
-
свойствах и графике функции![]() при
натуральном n;
при
натуральном n;
- определении и свойствах корней степени n;
- степенях с рациональными показателями и их свойствах;
- определении и основных свойствах арифметической прогрессии; формуле для нахождения суммы её нескольких первых членов;
- определении и основных свойствах геометрической прогрессии; формуле для нахождения суммы её нескольких первых членов;
- формуле для суммы бесконечной геометрической прогрессии со знаменателем, меньшим по модулю единицы;
- использовать свойства числовых неравенств для преобразования неравенств;
- доказывать простейшие неравенства;
- решать линейные неравенства;
- строить график квадратичной функции и использовать его при решении задач;
- решать квадратные неравенства;
- решать рациональные неравенства методом интервалов;
- решать системы неравенств;
-
строить график функции ![]() при
натуральном n и использовать его при решении задач;
при
натуральном n и использовать его при решении задач;
- находить корни степени n;
- использовать свойства корней степени n при тождественных преобразованиях;
- находить значения степеней с рациональными показателями;
- решать основные задачи на арифметическую и геометрическую прогрессии;
- находить сумму бесконечной геометрической прогрессии со знаменателем, меньшим по модулю единицы;
- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;
- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.
Геометрия
Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:
- признаках подобия треугольников;
- теореме о пропорциональных отрезках;
- свойстве биссектрисы треугольника;
- пропорциональных отрезках в прямоугольном треугольнике;
- пропорциональных отрезках в круге;
- теореме об отношении площадей подобных многоугольников;
- свойствах правильных многоугольников; связи между стороной правильного многоугольника и радиусами вписанного и описанного кругов;
- определении длины окружности и формуле для её вычисления;
- формуле площади правильного многоугольника;
- определении площади круга и формуле для её вычисления; формуле для вычисления площадей частей круга;
- правиле нахождения суммы и разности векторов, произведения вектора на скаляр; свойства этих операций;
- определении координат вектора и методах их нахождения;
- правиле выполнений операций над векторами в координатной форме;
- определении скалярного произведения векторов и формуле для его нахождения;
- связи между координатами векторов и координатами точек;
- векторным и координатным методах решения геометрических задач.
- формулах объёма основных пространственных геометрических фигур: параллелепипеда, куба, шара, цилиндра, конуса;
- применять признаки подобия треугольников при решении задач;
- решать простейшие задачи на пропорциональные отрезки;
- решать простейшие задачи на правильные многоугольники;
- находить длину окружности, площадь круга и его частей;
- выполнять операции над векторами в геометрической и координатной форме;
- находить скалярное произведение векторов и применять его для нахождения различных геометрических величин;
- решать геометрические задачи векторным и координатным методом;
- применять геометрические преобразования плоскости при решении геометрических задач;
- находить объёмы основных пространственных геометрических фигур: параллелепипеда, куба, шара, цилиндра, конуса;
- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;
- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.
Изучение предметной области "Математика" должно обеспечить:
- осознание значения математики в повседневной жизни человека;
- формирование представлений о социальных, культурных и исторических факторах становления математической науки;
понимание роли информационных процессов в современном мире;
формирование представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления.
В результате изучения предметной области "Математика" обучающиеся:
- развивают логическое и математическое мышление;
- получают представление о математических моделях;
- овладевают математическими рассуждениями;
- учатся применять математические знания при решении различных задач и оценивать полученные результаты;
- овладевают умениями решения учебных задач;
- развивают математическую интуицию;
- получают представление об основных информационных процессах в реальных ситуациях.
Предметные результаты изучения предметной области "Математика" должны отражать:
Математика. Алгебра. Геометрия:
1) формирование представлений о математике как о методе познания действительности, позволяющем описывать и изучать реальные процессы и явления:
- осознание роли математики в развитии России и мира;
- возможность привести примеры из отечественной и всемирной истории математических открытий и их авторов;
2) развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования, доказательства математических утверждений:
- оперирование понятиями: множество, элемент множества, подмножество, принадлежность, нахождение пересечения, объединения подмножества в простейших ситуациях;
- решение сюжетных задач разных типов на все арифметические действия;
- применение способа поиска решения задачи, в котором рассуждение строится от условия к требованию или от требования к условию;
- составление плана решения задачи, выделение этапов ее решения, интерпретация вычислительных результатов в задаче, исследование полученного решения задачи;
- нахождение процента от числа, числа по проценту от него, нахождения процентного отношения двух чисел, нахождения процентного снижения или процентного повышения величины;
- решение логических задач;
3) развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками устных, письменных, инструментальных вычислений:
- оперирование понятиями: натуральное число, целое число, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число, иррациональное число;
- использование свойства чисел и законов арифметических операций с числами при выполнении вычислений;
- использование признаков делимости на 2, 5, 3, 9, 10 при выполнении вычислений и решении задач;
- выполнение округления чисел в соответствии с правилами;
- сравнение чисел;
- оценивание значения квадратного корня из положительного целого числа;
4) овладение символьным языком алгебры, приемами выполнения тождественных преобразований выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умения моделировать реальные ситуации на языке алгебры, исследовать построенные модели с использованием аппарата алгебры, интерпретировать полученный результат:
- выполнение несложных преобразований для вычисления значений числовых выражений, содержащих степени с натуральным показателем, степени с целым отрицательным показателем;
- выполнение несложных преобразований целых, дробно рациональных выражений и выражений с квадратными корнями; раскрывать скобки, приводить подобные слагаемые, использовать формулы
сокращенного умножения;
- решение линейных и квадратных уравнений и неравенств, уравнений и неравенств, сводящихся к линейным или квадратным, систем уравнений и неравенств, изображение решений неравенств и их систем на числовой прямой;
5) овладение системой функциональных понятий, развитие умения использовать функционально-графические представления для решения различных математических задач, для описания и анализа реальных зависимостей:
- определение положения точки по ее координатам, координаты точки по ее положению на плоскости;
- нахождение по графику значений функции, области определения, множества значений, нулей функции, промежутков знакопостоянства, промежутков возрастания и убывания, наибольшего и наименьшего значения функции;
- построение графика линейной и квадратичной функций;
- оперирование на базовом уровне понятиями: последовательность, арифметическая прогрессия, геометрическая прогрессия;
- использование свойств линейной и квадратичной функций и их графиков при решении задач из других учебных предметов;
6) овладение геометрическим языком; развитие умения использовать его для описания предметов окружающего мира; развитие пространственных представлений, изобразительных умений, навыков геометрических построений:
- оперирование понятиями: фигура, точка, отрезок, прямая, луч, ломаная, угол, многоугольник, треугольник и четырехугольник, прямоугольник и квадрат, окружность и круг, прямоугольный параллелепипед, куб, шар; изображение изучаемых фигур от руки и с помощью линейки и циркуля;
- выполнение измерения длин, расстояний, величин углов с помощью инструментов для измерений длин и углов;
7) формирование систематических знаний о плоских фигурах и их свойствах, представлений о простейших пространственных телах; развитие умений моделирования реальных ситуаций на языке геометрии, исследования построенной модели с использованием геометрических понятий и теорем, аппарата алгебры, решения геометрических и практических задач:
- оперирование на базовом уровне понятиями: равенство фигур, параллельность и перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция;
- проведение доказательств в геометрии;
- оперирование на базовом уровне понятиями: вектор, сумма векторов, произведение вектора на число, координаты на плоскости;
- решение задач на нахождение геометрических величин (длина и расстояние, величина угла, площадь) по образцам или алгоритмам;
8) овладение простейшими способами представления и анализа статистических данных;
формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о простейших вероятностных моделях; развитие умений извлекать информацию, представленную в таблицах, на диаграммах, графиках, описывать и анализировать массивы числовых данных с помощью подходящих статистических характеристик, использовать понимание вероятностных свойств окружающих явлений при принятии решений:
- формирование представления о статистических характеристиках, вероятности случайного события;
- решение простейших комбинаторных задач;
- определение основных статистических характеристик числовых наборов;
- оценивание и вычисление вероятности события в простейших случаях;
наличие представления о роли практически достоверных и маловероятных событий, о роли закона больших чисел в массовых явлениях;
- умение сравнивать основные статистические характеристики, полученные в процессе решения прикладной задачи, изучения реального явления;
9) развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, компьютера, пользоваться оценкой и прикидкой при практических расчетах:
- распознавание верных и неверных высказываний;
- оценивание результатов вычислений при решении практических задач;
- выполнение сравнения чисел в реальных ситуациях;
- использование числовых выражений при решении практических задач и задач из других учебных предметов;
- решение практических задач с применением простейших свойств фигур;
- выполнение простейших построений и измерений на местности, необходимых в реальной жизни;
10) формирование информационной и алгоритмической культуры; формирование представления о компьютере как универсальном устройстве обработки информации; развитие основных навыков и умений использования компьютерных устройств;
11) формирование представления об основных изучаемых понятиях: информация, алгоритм, модель и их свойствах;
12) развитие алгоритмического мышления, необходимого для профессиональной деятельности в современном обществе; развитие умений составить и записать алгоритм для конкретного исполнителя; формирование знаний об алгоритмических конструкциях, логических значениях и операциях; знакомство с одним из языков программирования и основными алгоритмическими структурами линейной, условной и циклической;
13) формирование умений формализации и структурирования информации, умения выбирать способ представления данных в соответствии с поставленной задачей таблицы, схемы, графики, диаграммы, с использованием соответствующих программных средств обработки данных;
14) формирование навыков и умений безопасного и целесообразного поведения при работе с компьютерными программами и в Интернете, умения соблюдать нормы информационной этики и права;
15) для слепых и слабовидящих обучающихся:
- владение правилами записи математических формул и специальных знаков рельефно-точечной системы обозначений Л. Брайля;
- владение тактильно-осязательным способом обследования и восприятия рельефных изображений предметов, контурных изображений геометрических фигур и т.п.;
- умение читать рельефные графики элементарных функций на координатной плоскости, применять специальные приспособления для рельефного черчения;
- владение основным функционалом программы невизуального доступа к информации на экране ПК, умение использовать персональные тифлотехнические средства информационно-коммуникационного доступа слепыми обучающимися;
16) для обучающихся с нарушениями опорно-двигательного аппарата:
- владение специальными компьютерными средствами представления и анализа данных и умение использовать персональные средства доступа с учетом двигательных, речедвигательных и сенсорных нарушений;
- умение использовать персональные средства доступа".
Учебно-методическое и материально-техническое обеспечение образовательной деятельности
1. Математика: учеб. для 5 кл. общеобразоват. учреждений / [С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин].- М.: Просвещение, 2018.
2. Математика: Дидакт. материалы для 5 кл./ М.К.Потапов, А.В.Шевкин. – М.: Просвещение, 2017.
3. Чесноков А.С., Нешков К. И. «Дидактические материалы по математике для 5 класса», - М. Просвещение, 2019
4. Математика: учеб. для 6 кл. общеобразоват. учреждений /
[С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин].- М.: Просвещение,
2018.
5. Математика: Дидакт. материалы для 6 кл./ М.К.Потапов, А.В.Шевкин. – М.:
Просвещение, 2017.
6. Макарычев Ю.Н., Миндюк Н.Г.и др.; Под ред. Теляковского С.А. «Алгебра: 7 класс». - М.: Просвещение, 2017г.
7. Макарычев Ю.Н., Миндюк Н.Г., Крайнева Л.Б., Алгебра 7 класс Дидактический материал, М.: Просвещение, 2016
8. Макарычев Ю.Н., Миндюк Н.Г.и др.; Под ред. Теляковского С.А. «Алгебра: 8 класс». - М.: Просвещение, 2017г.
9. Макарычев Ю.Н., Миндюк Н.Г., Крайнева Л.Б., Алгебра 8 класс Дидактический материал, М.: Просвещение, 2017
10. Макарычев Ю.Н., Миндюк Н.Г.и др.; Под ред. Теляковского С.А. «Алгебра: 9 класс». - М.: Просвещение, 2017г.
11. Макарычев Ю.Н., Миндюк Н.Г., Крайнева Л.Б., Алгебра 9 класс Дидактический материал, М.: Просвещение, 2015
12. Геометрия: 7—9 кл. / J1. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. — М.: Просвещение, 2004—2017.
13. Зив Б. Г. Геометрия: дидакт. материалы: 7 кл. / Б. Г. Зив, В. М. Мейлер. — М.: Просвещение, 2004—2011.
14. Зив Б. Г. Геометрия: дидакт. материалы: 8 кл. / Б. Г. Зив, В. М. Мейлер. — М.: Просвещение, 2006—2011.
15. Зив Б. Г. Геометрия: дидакт. материалы: 9 кл. / Б. Г. Зив. — М.: Просвещение, 2004—2011.
16. Изучение геометрии в 7, 8, 9 классах: метод, рекомендации: кн. для учителя / Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков и др. — М.: Просвещение, 2003—2011.
17. Сайты:
1. http://www.edu.ru - Федеральный портал Российское образование;
2. http://www.school.edu.ru - Российский общеобразовательный портал
3. www.ug.ru - «Учительская газета»;
4. www.1september.ru - все приложения к газете «1сентября»;
5. www.informika.ru/text/magaz/herald – «Вестник образования»;
6. http://school-collection.edu.ru – единая коллекция цифровых образовательных ресурсов;
7. http://www.krug.ural.ru/keng/ - Кенгуру;
8. http://math.child.ru - Сайт и для учителей математики;
9. http://www.uroki.net/docmat.htm - для учителя математики, алгебры и геометрии;
10. http://www.uotula.ru/cgi-bin/index.cgi?id=98 - методические рекомендации учителям математики;
11. http://www.alleng.ru/edu/math1.htm - к уроку математики.
Скачано с www.znanio.ru
© ООО «Знанио»
С вами с 2009 года.
![]()

