РАБОЧАЯ ТЕТРАДЬ

ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

 

Фамилия_______________________________________________

Имя___________________________________________________

Отчество_______________________________________________

Специальность __________________________________________

Группа _________ Курс_______

Период, за который представлены документы и материалы

с_______________________ 20_____ года

по______________________20______ года.

 

Личная подпись студента ____________________

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зачем тебе изучать математику?

 

 

 

 

 

Математическое образование является средством активного интеллектуального развития человека, его мыслительных способностей.

Человек, изучающий математические термины, утверждения, доказательства, умеющий решать задачи, вырабатывать стиль мышления. Оно характеризуется краткостью, лаконичностью, логикой суждений.  Человек, знающий математику, и в своей профессиональной деятельности стремится строго следовать тому предписанию и набору правил, которые приводят к получению правильного результата. Поэтому одной из задач математики является высокоинтеллектуальное развитие человека, способного творчески решать поставленные задачи и адаптироваться к динамически развивающемуся обществу. С этой точки зрения, конкретные математические знания рассматриваются как основы для дальнейшей профессиональной деятельности, а сам процесс изучения математики – как развивающая функция, способствующая повышению интеллектуального уровня обучающегося.

 

 

 

 

 

 

 

 

Критерии оценивания

 

Тема	Отметка	Критерий
Математический анализ.	5(отлично)	правильное решение всех заданий
	4(хорошо)	допущена ошибка в пятом задании
	3(удовлетворительно)	неправильное решение двух любых заданий
	2(неудовлетворительно)	неправильное решение любых 3 заданий
Дифференциальное и интегральное исчисление.	5(отлично)	правильное решение всех заданий
	4(хорошо)	решение первых трех обязательных заданий  на применение производной и интегралов, или неправильное решение одного задания из шести
	3(удовлетворительно)	решение только трёх первых заданий или неправильное решение двух заданий
	2(неудовлетворительно)	неправильное решение любых 3 заданий
Линейная алгебра	5(отлично)	правильное решение всех заданий
	4(хорошо)	решение первых трех обязательных заданий  и двух на действия над матрицами, или неправильное решение одного задания из шести
	3(удовлетворительно)	решение только трех обязательных заданий, или неправильное решение двух заданий из шести
	2(неудовлетворительно)	неправильное решение любых 3 заданий
Теория вероятности и математическая статистика	5(отлично)	правильное решение всех заданий
	4(хорошо)	неправильное решение одного из первых двух заданий при правильном решении третьего.
	3(удовлетворительно)	решение только двух первых заданий
	2(неудовлетворительно)	неправильное решение одного из первых заданий

          Задание засчитывается, как выполненное при верном решении и правильном ходе рассуждений, но допущенной одной вычислительной ошибки.

Самоотчёт об успеваемости по математике

 

№	Наименование	Дата контроля	Дата сдачи рабочей тетради	оценка	Роспись преподавателя
Решение заданий:
1.	Линейная алгебра.
2.	Дифференциальное и интегральное исчисление.
3.	Линейная алгебра.
4.	Теория вероятности и математическая статистика.
5.	Творческая работа

 

 

 

 

Творческие работы

 

1.     Написание реферата (в соответствии с требованиями к оформлению и содержанию)

 

Темы рефератов:

1)    Применение математических методов в профессиональной деятельности.

2)    Дифференциально-интегральные исчисления в практике.

3)    Роль математики в вашей профессии.

 

 

 

 

 

 

 

Тема: «Математический анализ».

 

Знания:

-       определение последовательности;

-       определение возрастающей, убывающей последовательности;

-       определение предела функции;

-       свойства пределов функций.

 

Умения:

-       находить пределы функций.

Предел функции

1.Найдите предел функции в точке  .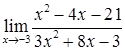

Решение:

 

 

 

 

 

2.Найдите предел функции в точке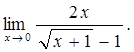 

Решение:

 

 

 

 

 

 

 

3.Найдите предел функции     

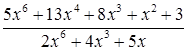
Решение:

 

 

 

 

 

 

 

 

 

4.Написать первые пять членов последовательности, и изобразить их на числовой прямой:

х_п = n²+2n-1

Решение:

 

 

 

 

 

 

5.Найдите предел функции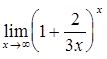     

Решение:

 

 

 

 

 

 

 

 

 

 

 

Тема:  «Дифференциальное и интегральное исчисление. Неопределенный и определенный интегралы и их свойства.

Применение определенного интеграла к решению прикладных задач».

Знания:

-         определение непрерывности и дифференцируемости функции;

-         приращение функции, приращение аргумента;

-         определение производной ее геометрический и механический смысл;

-         таблицу производных;

-         определение дифференциала.

-         определение первообразной функции; определение неопределенного интеграла;

-         свойства неопределенного интеграла;

-         таблицу неопределенных интегралов;

-         методы интегрирования;

-         формулу Ньютона-Лейбница для вычисления определенных интегралов;

-         методы вычисления определенных интегралов.

 

Умения:

-         находить производные элементарных и сложных функций;

-         вычислять дифференциалы функции;

-         применение дифференциала к приближённым вычислениям.

-         находить неопределенный интеграл различными методами;

-         применять формулу Ньютона-Лейбница для вычисления определенного интеграла.

 

 

 

 

Физический и геометрический смысл производной

1.     Составьте уравнение касательной к графику функции  в точке с абсциссой  х₀=2.

 

Решение:

 

 

 

 

 

 

 

Применение производной при исследовании функции и построении её графика

 

2.     Постройте график функции

 

Решение:

 

 

Методы интегрирования

 

3. а) Вычислить интеграл  способом непосредственного интегрирования.

 

Решение:

 

 

 

 

 

 

 

 

б) Вычислить интеграл  подстановкой.

Решение:

 

 

 

 

 

 

 

 

 

в) Вычислить интеграл  методом интегрирования по частям

Решение:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Определенный интеграл: Формула Ньютона-Лейбница.

 

 

4. Вычислить определенный интеграл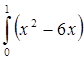  

Решение:

 

 

 

 

 

 

 

 

Применение определенного интеграла

 

 

5. Найти площадь фигуры, ограниченной  осью абсцисс и графиком функции

Решение:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Правила дифференцирования

 

6. а) Найдите производную функции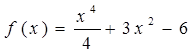

Решение:

 

 

 

 

 

 

 

б) Найдите производную сложной функции 

 

Решение:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема: «Линейная алгебра ».

Знания:

-       знание основных методов линейной алгебры;

-        перечисление последовательности действий над матрицами;

-       последовательности действий при решении систем линейных уравнений по формулам Крамера.

 

Умения:

-        выполнять действия над матрицами;

-       вычислять определители;

-       решать системы линейных уравнений по формулам Крамера.

 

 

Матрицы и определители

1.                 Вычислить определитель: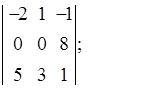

Решение:

 

 

 

 

 

 

 

 

Решение систем линейных уравнений

2. Решить систему линейных уравнений по формулам Крамера.

 

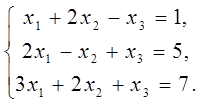
Решение:

 

 

 

 

 

 

 

 

 

Аналитическая геометрия

3.Даны векторы  и  

a)   Найти .

b)  Найти .

c)   Найти .

d)  Найти .

 

Решение:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Матрицы и определители

 

4. Найти матрицу C=A+3B, если , .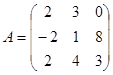

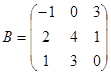Решение:

 

 

 

 

 

 

 

Аналитическая геометрия

5. Даны три точки с координатами: P(4; 0; 0), K(0; 2; 0), T(2; 0; 4). а) Докажите, что треугольник PKT – равнобедренный.

б) Вычислите площадь треугольника PKT.

 

Решение:

 

 

 

 

 

 

 

 

 

 

6.Даны векторы  и .

 Найти координаты векторов , , .

Решение:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема: «Теория вероятности и математическая статистика»

 

Знания:

-       определение статистики;

-       задачи статистики;

-       понятие статистической совокупности, единицы измерения, учетные признаки;

-       этапы статистического исследования, их характеристику.

-       определение вероятности события;

-       основные теоремы и формулы теории вероятности;

-       определение математического ожидания и дисперсии случайной величины.

 

Умения:

-       различать структурные элементы статистической совокупности (совокупность, генеральная и выборочная совокупность, единица наблюдения, факторная и результативная признаки);

-       шифровать учетные признаки;

-       составлять различные виды таблиц и строить диаграммы.

-       применять основные теоремы и формулы при нахождении вероятности события, математического ожидания и дисперсии случайной величины.

 

 

1.Ответить письменно на вопросы:

а). Объясните на примере,  как по таблице частот находят:

среднее арифметическое,  размах, моду, медиану.

б). Какие способы наглядного представления статистической

информации вам известны?

 

Ответ: ________________________________________________________

______________________________________________________________

________________________________________________________________

______________________________________________________________

________________________________________________________________

______________________________________________________________

________________________________________________________________

______________________________________________________________

________________________________________________________________

______________________________________________________________

 

 

 

2.Проведение исследования согласно этапам статистического исследования:

 

Измерив рост 50 студентов в сантиметрах, результаты записали в таблицу:

149	150	150	151	151	152	152	153	154	154
155	155	155	156	156	157	157	157	158	158
159	159	159	159	161	161	161	162	162	162
162	165	165	166	166	166	167	167	169	170
171	171	173	173	173	175	176	178	180	182

 

Сгруппировав данные по классам 145-149, 150-154,…,180-184,представить частотное распределение студентов по этим группам с помощью :

1) таблицы;   2) полигона частот;  3) столбчатой диаграммы.

 

Решение:

 

 

 

 

 

 

 

 

 

 

 

Теория вероятности. Случайные величины

 

 

3.Случайная величина Х имеет закон распределения:

 

хi	1	2	3
mi	7	1	2
pi

 

Найдите:

-       вероятности p_i;

-       математическое ожидание;

-       дисперсию;

-       среднее квадратическое отклонение;

-       постройте многоугольник распределения.

 

Решение:

-       вероятности p_i:

 

 

 

 

 

 

-       математическое ожидание:

 

 

 

 

-       дисперсию:

 

 

 

 

 

-       среднее квадратическое отклонение:

 

 

 

 

 

 

 

 

-       многоугольник распределения: