
Краевое государственное бюджетное профессиональное образовательное учреждение «Зеленогорский техникум промышленных технологий и сервиса»
ТЕХНИЧЕСКАЯ МЕХАНИКА
Рабочая тетрадь по контролю знаний
студентов 2 – го курса
Выполнил студент: _________________________________________Гр____________
Проверил: ____________________________ Оценка________________
Зеленогорск 2021
Лекция №1. Аксиомы статики. Связи и их реакции.
Цель: Изучить основные понятия и аксиомы раздела статики.
Тема 1. Основные понятия статики
Основной задачей статики является изучение общих законов равновесия материальных точек и твердых тел.
Для изучения законов равновесия статики необходимо знать следующие понятия.
Материальная точка — это условно принятое тело, размерами которого можно пренебречь по сравнению с расстоянием, на котором оно находится.
Абсолютно твердое тело — это условно принятое тело, которое не деформируется под действием внешних сил.
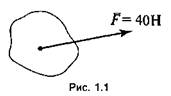
Сила — это векторная величина, характеризующая взаимодействие между телами. Действие силы характеризуется тремя факторами: точкой приложения, направлением, численным значением (рис. 1.1). За единицу силы принимается 1 Н: 1 кН = 103 Н; 1 МН = 106 Н.
 Обозначение различных типов сил:
F — внешняя сила; Fx, Fy — проекция силы на
ось х и у соответственно; R — реакция опоры или
связи; FΣ — равнодействующая
сила.
Обозначение различных типов сил:
F — внешняя сила; Fx, Fy — проекция силы на
ось х и у соответственно; R — реакция опоры или
связи; FΣ — равнодействующая
сила.
Система сил — это совокупность всех сил, действующих на тело. Две силы или две системы сил называются эквивалентными, если они оказывают на тело одинаковое действие.
Равнодействующей называется сила, которая оказывает такое же действие на тело, как и несколько сил, вместе взятых. Равнодействующая сила равна геометрической сумме всех сил, действующих на тело:
![]()
где i — 1, 2,..., п — порядковый номер силы.
Уравновешивающей называется такая сила, которая равна по величине равнодействующей силе, но направлена в противоположную сторону.
Тема 2. Основные аксиомы статики
В основу статики положено пять аксиом.
![]() 1. Принцип
инерции: материальная
точка находится вравновесии, если
равнодействующая всех сил, действующих на нее, равна нулю, т.е.
1. Принцип
инерции: материальная
точка находится вравновесии, если
равнодействующая всех сил, действующих на нее, равна нулю, т.е.
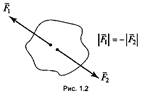
2.Принцип равенства двух сил: две силы, действующие на одно тел о, являются взаимоуравновешивающими, если они равны по величине, противоположны по направлению и лежат на одной прямой (рис. 1.2).
 3.Принцип
присоединения или исключения взаимоуравновешивающих сил: механическое
состояние тела не изменится, если к нему присоединить или исключить
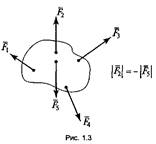
взаимоуравновешивающую систему сил (рис. 1.3).
3.Принцип
присоединения или исключения взаимоуравновешивающих сил: механическое
состояние тела не изменится, если к нему присоединить или исключить
взаимоуравновешивающую систему сил (рис. 1.3).
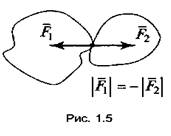
 4.Принцип
параллелограмма: равнодействующая
двух сил, приложенных к телу в одной точке и направленных друг к другу под
углом, равна геометрической сумме этих сил и изображается диагональю
параллелограмма, построенного на этих силах как на сторонах (рис. 1.4).
4.Принцип
параллелограмма: равнодействующая
двух сил, приложенных к телу в одной точке и направленных друг к другу под
углом, равна геометрической сумме этих сил и изображается диагональю
параллелограмма, построенного на этих силах как на сторонах (рис. 1.4).
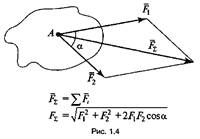
5. Принцип действия и противодействия: силы, с которыми два тела действуют друг на друга, равны по величине, противоположны по направлению и лежат на одной прямой (однако не уравновешивают друг друга, так как приложены к разным телам) (рис. 1.5).
Тема 3. Связи и их реакции
 Свободное тело — это тело,
движению которого ничто не препятствует.
Свободное тело — это тело,
движению которого ничто не препятствует.
Несвободное тело — это тело, движению которого препятствуют другие тела.
Связь — это тело, которое препятствует
движению других тел. Реакция связи — это сила, с которой связь действует
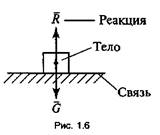
на тело, препятствуя его движению. Существуют шесть основных типов связи: 1) в
виде гладкой поверхности (поверхность стола,
ровной дороги). Реакция связи направлена перпендикулярно поверхности связи (рис
1.6);
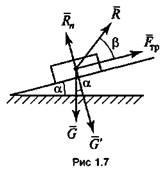 2) в
виде шероховатой поверхности. Условно изображается наклонной плоскостью
(рис 1.7). Полная
2) в
виде шероховатой поверхности. Условно изображается наклонной плоскостью
(рис 1.7). Полная
реакция связи R направлена под углом β (Rn — нормальная реакция опоры);
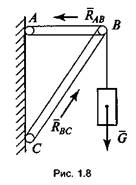
3) в виде прямого жесткого
стержня с шарнирным
закреплением концов. Реакция стержня направлена
вдоль его оси (рис 1.8);
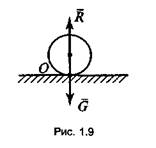
4) в виде точечной опоры. Реакция направлена перпендикулярно поверхности опоры (рис 1.9);
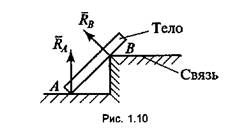
5) в виде ребра двухгранного угла. Реакция направлена перпендикулярно поверхности тела опор (рис. 1.10);
 6) в
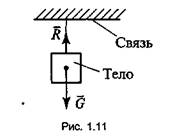
виде гибкой связи (ремень, канат, цепь). Реакция направлена вдоль связи
(рис 1.11).
6) в
виде гибкой связи (ремень, канат, цепь). Реакция направлена вдоль связи
(рис 1.11).
Лекция №2 Плоская система сходящихся сил.
Цель: Изучить плоскую систему сходящихся сил и ее равновесие.
Тема 4. Системы сил и условия их равновесия
Плоская система сходящихся сил и условие ее равновесия
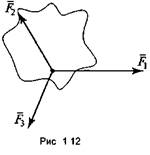
Плоской системой сходящихся сил называется система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке (рис. 1.12).
Чтобы выяснить, будет ли данное тело находиться в равновесии под действием плоской системы сходящихся сил, необходимо найти ее равнодействующую силу. Если равнодействующая равна нулю, система находится в равновесии, если не равна нулю — не находится в равновесии. Существует два способа определения равнодействующей силы плоской системы сходящихся сил: геометрический и аналитический.
 Геометрический
способ определения равнодействующей — построение силового многоугольника: в
произвольно выбранную точку переносится объект равновесия, в эту точку
помещается начало первого вектора, перенесенного параллельно самому себе; к
концу первого вектора переносится начало второго вектора, к концу второго — начало
третьего и т.д.
Геометрический
способ определения равнодействующей — построение силового многоугольника: в
произвольно выбранную точку переносится объект равновесия, в эту точку
помещается начало первого вектора, перенесенного параллельно самому себе; к
концу первого вектора переносится начало второго вектора, к концу второго — начало
третьего и т.д.
Если построенный силовой многоугольник окажется незамкнутым, значит, данная система сил не находится в равновесии. В этом случае вектор равнодействующей силы соединит начало первого вектора с концом последнего (рис. 1.13, а).
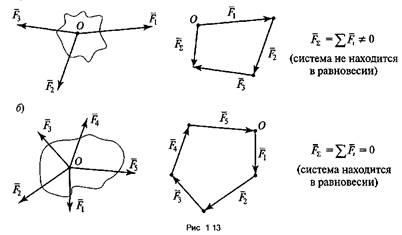 Геометрическое
условие равновесия плоской системы сходящихся сил заключается в
замкнутости силового многоугольника, т.е. при построении силового
многоугольника конец последнего вектора совпадает с началом первого (рис.
1.13,6).
Геометрическое
условие равновесия плоской системы сходящихся сил заключается в
замкнутости силового многоугольника, т.е. при построении силового
многоугольника конец последнего вектора совпадает с началом первого (рис.
1.13,6).
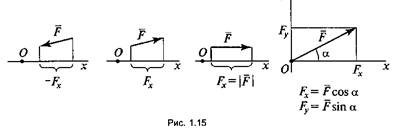 Аналитический
способ определения равнодействующей: все силы проектируются на две взаимно
перпендикулярные оси координат, а затем находится алгебраическая сумма проекций
всех сил на ось х и ось у. Если алгебраическая сумма проекций
всех сил равна нулю, данная система сил находится в равновесии. Аналитическое
условие равновесия плоской системы сходящихся сил:
Аналитический
способ определения равнодействующей: все силы проектируются на две взаимно
перпендикулярные оси координат, а затем находится алгебраическая сумма проекций
всех сил на ось х и ось у. Если алгебраическая сумма проекций
всех сил равна нулю, данная система сил находится в равновесии. Аналитическое
условие равновесия плоской системы сходящихся сил:
![]()
Осью координат называется произвольно выбранный направленный отрезок прямой (рис. 1.14).
Проекция силы на ось координат — отрезок оси, отсекаемый перпендикулярами, опущенными из начала и конца вектора (рис. 1.15).
Плоская система пар сил и условие ее равновесия
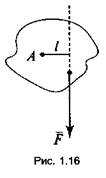 Если на тело,
закрепленное в некоторой точке А, действует сила F , то тело
повернется относительно этой точки. Вращательное движение тела характеризуется вращающим
моментом М.
Если на тело,
закрепленное в некоторой точке А, действует сила F , то тело
повернется относительно этой точки. Вращательное движение тела характеризуется вращающим
моментом М.
Моментом силы F относительно точки А называется величина, численно равная произведению силы на плечо (рис. 1.16):
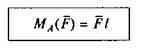 где l— плечо
(перпендикуляр, опущенный из точки на линию действия силы). За единицу
вращающего момента принимается 1 Нм: 1кНм=103Нм.
где l— плечо
(перпендикуляр, опущенный из точки на линию действия силы). За единицу
вращающего момента принимается 1 Нм: 1кНм=103Нм.
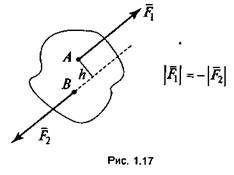
Парой сил называется система двух сил, равных по величине, противоположных по направлению и не лежащих на одной прямой (рис. 1.17).
Пара сил оказывает на тело вращающее действие, которое характеризуется вращающим моментом М.
Вращающий момент пары сил равен произведению одной из сил пары на плечо:
![]()
 где h — плечо пары сил
(перпендикуляр, восстановленныймежду
линиями действия сил). Пара сил на схемах изображается дугообразной стрелкой
(рис. 1.18). Пару сил нельзя заменить одной равнодействующей силой. Пара
сил не имеет проекций на оси
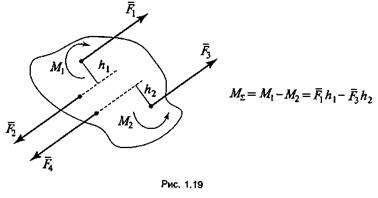
координат. Если на тело действует несколько пар сил, то их можно заменить
одной равнодействующей парой, момент которой равен алгебраической сумме
моментов слагаемых пар сил, действующих на тело (рис. 1.19):
где h — плечо пары сил
(перпендикуляр, восстановленныймежду
линиями действия сил). Пара сил на схемах изображается дугообразной стрелкой
(рис. 1.18). Пару сил нельзя заменить одной равнодействующей силой. Пара
сил не имеет проекций на оси
координат. Если на тело действует несколько пар сил, то их можно заменить
одной равнодействующей парой, момент которой равен алгебраической сумме
моментов слагаемых пар сил, действующих на тело (рис. 1.19):
![]()
Две пары сил называются эквивалентными, если они оказывают на тело одинаковое действие. У эквивалентных пар сил вращающие моменты должны быть одинаковы как по величине, так и по направлению.
Условие равновесия плоской системы пар сил: алгебраическая сумма моментов слагаемых пар сил должна быть равна нулю, т.е.
![]()
Тест – задания для самопроверки по лекциям №1-2
|
1. Какие законы равновесия изучает статика –
|
|
2.Что такое сила в статике, от чего зависит и чем характеризуется –
|
|
|
|
|
|
5. Что называется связью в статике, и какие типы приняты в расчетных схемах –
|
|
6. Определите проекцию равнодействующей силы на ось Ох если известно F1 = 10 кН; F2 =20кН; F3 =30 кН
|
|
7. Как понятие «момент силы» связано с понятием «пара сил» -
|
|
8.Запишите условие равновесия плоской системы сил
|
|
9. Проверьте условие равновесия ситемы представленной на рисунке 1.19 если F1 = 10 кН F2=10кН h1=5 м F3 = 25кН F4 =25кН h2 = 1.5м
|
|
10. Что называется геометрическим условием равновесия плоской системы сил , и чем оно отличается от аналитического условия равновесия |
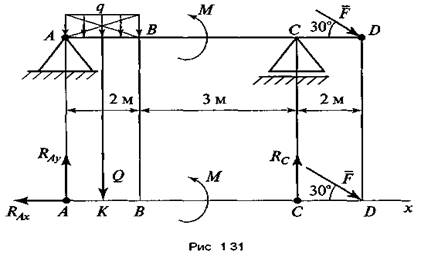
Задача №1. (подставь и посчитай)
Определение реакций системы сходящихся сил.
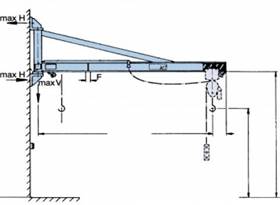 Определить реакции
стержней консольного
Определить реакции
стержней консольного
крана , удерживающих груз весом
F1 кН (рис. 1),
рассматривая их как систему
сходящихся сил. Массой стержней пренебречь.
Дано: F= кН
Найти: R1 , R2
Решение.
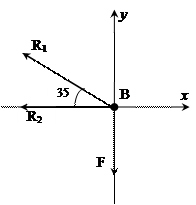
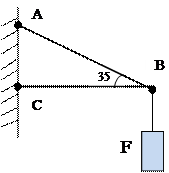
1. Рассматриваем равновесие шарнира В (рис. 1) рис .1
 |
|||||
 |
 |
||||
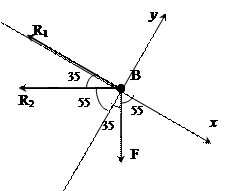
а) б) в)
Рис. 2.Основная схема расчета (а), векторная схема решения (б), проверочная векторная схема (в).
2.
Освобождаем
шарнир В от связей и изображаем действующие
на него активные силы и реакции, связей (рис. 1,6).
3.
Выбираем
систему координат, совместив ось x по направлению
с реакцией R2 (рис. 1,6) и
составляем уравнения равновесия для
системы сил, действующих на шарнир В:
![]() ; (1)
; (1)![]() ; (2)
; (2)
4. Определяем реакции стержней R1 и R2, решая уравнения (1), (2).
Из уравнения (1)
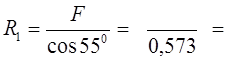 кН.
кН.
Подставляя найденное значение R1 в уравнение (1), получаем
![]() кН.
кН.
Знак минус перед значением R2 указывает на то, что первоначально выбранное направление реакции неверное — следует направить реакцию R2 в противоположную сторону.
5.
Проверяем
правильность полученных результатов, выбрав новое
расположение осей координат х и у (рис. 2,в ). Относительно этих осей
составляем уравнения равновесия:
![]() (3)
(3)
![]() (4)
(4)
из уравнения (4) находим
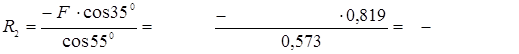 кН.
кН.
Подставляя найденное значение R2 в уравнение (3), получаем
![]() кН
кН
Вывод: Значения реакций R1 и R2, полученные при решении уравнений (1) и (2), совпадают по величине и направлению со значениями, найденными из уравнений (3) и (4), следовательно, задача решена правильно.
Варианты заданий.
|
№ варианта |
Сила F , кН |
№ варианта |
Сила F , кН |
|
1 |
10 |
20 |
200 |
|
2 |
20 |
21 |
210 |
|
3 |
30 |
22 |
220 |
|
4 |
40 |
23 |
230 |
|
5 |
50 |
24 |
240 |
|
6 |
60 |
25 |
250 |
|
7 |
70 |
26 |
260 |
|
8 |
80 |
27 |
270 |
|
9 |
90 |
28 |
280 |
|
10 |
100 |
29 |
290 |
|
11 |
110 |
30 |
300 |
|
12 |
120 |
31 |
310 |
|
13 |
130 |
32 |
320 |
|
14 |
140 |
33 |
330 |
|
15 |
150 |
34 |
340 |
|
16 |
160 |
35 |
350 |
|
17 |
170 |
36 |
360 |
|
18 |
180 |
37 |
370 |
|
19 |
190 |
38 |
380 |
Лекция №3 Произвольная плоская система сил. Балочные системы.
Цель: Изучить произвольную плоскую систему сходящихся сил и ее равновесие.
Плоская система произвольно расположенных сил и условие ее равновесия
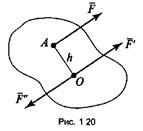 Приведение силы к
данной точке
заключается
в том, что рассматриваемую силу F переносят
параллельно самой себе в произвольно выбранную точку О. Для того чтобы
механическое состояние тела не изменилось, силу F' уравновешивают
силой F" (рис. 1.20). В
результате приведения силы F к точке О получилась
система сил, состоящая из силы F', равной и
параллельной данной силе F , и пары сил (F и F"), момент которой
равен моменту данной силы F относительно
точки О:
Приведение силы к
данной точке
заключается
в том, что рассматриваемую силу F переносят
параллельно самой себе в произвольно выбранную точку О. Для того чтобы
механическое состояние тела не изменилось, силу F' уравновешивают
силой F" (рис. 1.20). В
результате приведения силы F к точке О получилась
система сил, состоящая из силы F', равной и
параллельной данной силе F , и пары сил (F и F"), момент которой
равен моменту данной силы F относительно
точки О:
 М = M0(F).
М = M0(F).
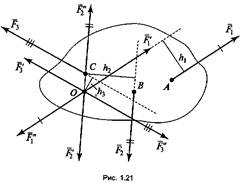
Плоской системой произвольно расположенных сил называется система сил, линии, действия которых лежат в одной плоскости, но не пересекаются в одной точке (рис. 1.21). Для того чтобы привести данную систему произвольно расположенных сил к произвольно выбранной точке О (см. рис. 1.21), необходимо:
1) перенести по очереди каждую силу в эту точку;
2) уравновесить силы (F1', F2’, F3’) силами. (F1'’, F2’’, F3’’)
В результате приведения сил (F1, F2, F3) к точке О получили новую систему сил, состоящую из плоской системы сходящихся сил (F1,F2,F3), которые равны и параллельны данным силам, т.е.
F1'= F1 , F2,= F2’, F3' = F3 . (1.1)
![]() Эту вновь полученную
систему сходящихся сил (1.1) заменяем равнодействующей силой, которая равна
геометрической сумме данных сил и называется главным вектором системы:
Эту вновь полученную
систему сходящихся сил (1.1) заменяем равнодействующей силой, которая равна
геометрической сумме данных сил и называется главным вектором системы:
В результате приведения получили еще одну систему пар сил
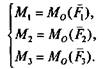
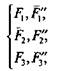
(1.2)
моменты которых равны моментам данных сил
относительно точки О, т.е.
Вновь полученную систему пар сил (1.2) заменим одной равнодействующей парой, момент которой равен алгебраической сумме моментов слагаемых пар сил и называется главным моментом системы:
![]()
Таким образом, для того чтобы тело под действием плоской системы произвольно расположенных сил находилось в равновесии, необходимо, чтобы главный вектор и главный момент системы были равны нулю:
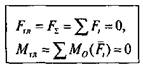 Выразив главный
вектор вновь полученной системы сходящихся сил в аналитической форме, получим
два уравнения равновесия:
Выразив главный
вектор вновь полученной системы сходящихся сил в аналитической форме, получим
два уравнения равновесия:
![]()
![]() Главный момент
системы заменим алгебраической суммой моментов данных сил относительно точки
приведения:
Главный момент
системы заменим алгебраической суммой моментов данных сил относительно точки
приведения:
Таким образом, получаем условие равновесия плоской системы произвольно расположенных сил: алгебраическая сумма проекций всех сил на оси х и у должна быть равна нулю и алгебраическая сумма моментов всех сил относительно точки приведения должна быть равна нулю, т.е.
Балочные опоры и их реакции.
Балка — это элемент конструкции, который имеет длину гораздо больше поперечных размеров и несет на себе поперечные нагрузки.
 При расчете балок
на прочность при изгибе учитываются не только внешние нагрузки, но и реакции
со стороны опор балок.
При расчете балок
на прочность при изгибе учитываются не только внешние нагрузки, но и реакции
со стороны опор балок.
Существуют три типа балочных опор:
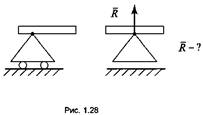
1) шарнирно-подвижная
(рис. 1.28). Дает возможность балке вращаться вокруг центра шарнира и
перемещаться в горизонтальном направлении. Для этой опоры известны точка приложения реакции
(находится в центре
шарнира) и направление реакции (направлена перпендикулярно поверхности опоры).
Неизвестна только величина реакции;
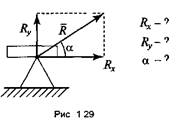
2) шарнирно-неподвижная (рис. 1.29). Позволяет балке поворачиваться вокруг оси шарнира, но не дает возможности перемещаться в горизонтальном направлении. Для этой опоры известна только точка приложения реакции (находится в центре шарнира). Неизвестны величина и направление реакции. Поэтому для данной опоры необходимо найти две составляющие реакции: Rx и Ry;
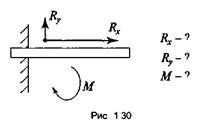
 3)
с жестким защемлением, или заделка (рис. 1.30). Не позволяет балке
ни поворачиваться, ни перемещаться. О реакции этой опоры ничего не известно.
Поэтому для этой опоры необходимо найти три составляющие реакции: Rx, Ry, M.
3)
с жестким защемлением, или заделка (рис. 1.30). Не позволяет балке
ни поворачиваться, ни перемещаться. О реакции этой опоры ничего не известно.
Поэтому для этой опоры необходимо найти три составляющие реакции: Rx, Ry, M.
Лекция №4. Пространственная система сил.
Определение координат центра тяжести.
Цель: Изучить пространственную систему сил и методы определения координат центров тяжести.
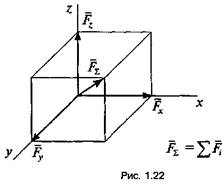 Пространственной
системой сходящихся
сил называется система сил, линии действия которых не лежат в одной
плоскости, но пересекаются в одной точке. Равнодействующая такой системы сил
изображается диагональю прямоугольного параллелепипеда, построенного на этих
силах как на сторонах (рис. 1.22).
Пространственной
системой сходящихся
сил называется система сил, линии действия которых не лежат в одной
плоскости, но пересекаются в одной точке. Равнодействующая такой системы сил
изображается диагональю прямоугольного параллелепипеда, построенного на этих
силах как на сторонах (рис. 1.22).
Условие равновесия пространственной системы сходящихся сил: алгебраическая сумма проекций всех сил на три взаимно перпендикулярные оси координат должны быть равны нулю, т.е.
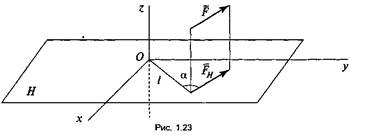
Для того чтобы найти момент силы F относительно оси z, надо спроектировать силу F на плоскость Н, перпендикулярную оси z (рис. 1.23), затем найти момент проекции FH относительно точки О, которая является точкой пересечения плоскости Не осью z. Момент проекции FH и будет являться моментом силы F относительно оси z'.
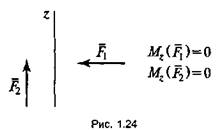
Моменты сил, перпендикулярных или параллельных оси z, будут равны нулю (рис. 1.24).
![]()
 Пространственной
системой произвольно расположенных сил называется система сил, линии, действия
которых не лежат в одной плоскости и не пересекаются в одной точке.
Равнодействующая такой системы сил также равна геометрической сумме этих сил,
но изображается диагональю сложных объемных фигур (тетраэдр, октаэдр и т.д.).
Пространственной
системой произвольно расположенных сил называется система сил, линии, действия
которых не лежат в одной плоскости и не пересекаются в одной точке.
Равнодействующая такой системы сил также равна геометрической сумме этих сил,
но изображается диагональю сложных объемных фигур (тетраэдр, октаэдр и т.д.).
 Условие
равновесия пространственной системы произвольно расположенных сил: алгебраическая
сумма проекций всех сил на три взаимно перпендикулярные оси координат должна
быть равна нулю и алгебраическая сумма моментов всех сил относительно тех же осей
координат должна быть равна нулю, т.е.
Условие
равновесия пространственной системы произвольно расположенных сил: алгебраическая
сумма проекций всех сил на три взаимно перпендикулярные оси координат должна
быть равна нулю и алгебраическая сумма моментов всех сил относительно тех же осей
координат должна быть равна нулю, т.е.
Центры тяжести
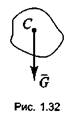
 Сила тяжести — это сила, с
которой тело притягивается к земле. Центр тяжести — это точка приложения
силы тяжести (рис. 1.32). Положение центра тяжести простых геометрических
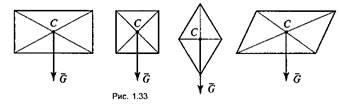
фигур: 1) в прямоугольнике, квадрате, ромбе, параллелограмме — на пе ресечении диагоналей (рис. 1.33);
Сила тяжести — это сила, с
которой тело притягивается к земле. Центр тяжести — это точка приложения
силы тяжести (рис. 1.32). Положение центра тяжести простых геометрических
фигур: 1) в прямоугольнике, квадрате, ромбе, параллелограмме — на пе ресечении диагоналей (рис. 1.33);
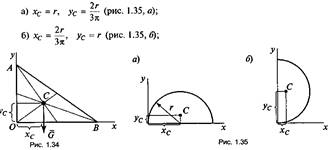
2) в треугольнике — на пересечении медиан (рис. 1.34):
![]()
3) в круговом секторе или полукруге — в точке с координатами:
4)в конусе или полной пирамиде — на 1/3 высоты от основания (рис. 1.36):
 Положение центра
тяжести плоских фигур прокатных профилей:
Положение центра
тяжести плоских фигур прокатных профилей:
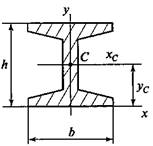
1)в балке двутавровой (рис. 1.37) — в точке c координатами
хс=0, yc=h/2,
 где h — высота двутавра.
где h — высота двутавра.
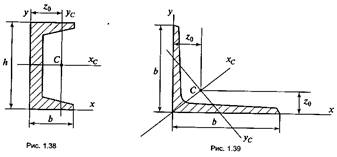
2)в швеллере (рис. 1.38) — в точке с координатами xc = z0, yc=h/2,
где h — высота швеллера;
Z0 — расстояние от центра тяжести и ус до наружной грани стенки;
3)в равнополочном уголке (рис. 1.39) — в точке с координатами XC = YC = Z0
Если плоская фигура имеет неправильную геометрическую форму, то центр тяжести такой фигуры можно определить двумя способами:
 1)методом
подвешивания фигуры на острие;
1)методом
подвешивания фигуры на острие;
2) теоретическим методом. Рис.1.37
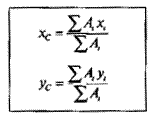 В этом случае
плоская фигура разбивается на определенное количество элементарных фигур,
имеющих правильную геометрическую форму. Затем определяется положение центра
тяжести и площади каждой элементарной фигуры. Для того чтобы найти координаты
центра тяжести заданной сложной фигуры, используются следующие формулы:
В этом случае
плоская фигура разбивается на определенное количество элементарных фигур,
имеющих правильную геометрическую форму. Затем определяется положение центра
тяжести и площади каждой элементарной фигуры. Для того чтобы найти координаты
центра тяжести заданной сложной фигуры, используются следующие формулы:
где Аi — площади элементарных фигур, на которые разбита сложная фигура;
хi ; уi — координаты центра тяжести каждой элементарной фигуры относительно случайных осей X и Y.
Тест – задания для самопроверки по лекциям № 3 - 4
|
11. Поясните цель приведение силы к точке –
|
|
12.Чем отличается произвольная система сил от плоской системы сил (пояснить формулами) –
|
|
13. Определите суммарную силу шарнирно-неподвижной опоры если известно Rx = 8 кН ; Ry = 6 кН |
|
14. В чём состоит сущность условия равновесия пространственной системы сил |
|
15. В чем отличие главного вектора системы сил от равнодействующей силы системы сил |
|
16. В чем отличие и в чем сходство между шарнирно-неподвижной опорой и шарнирно – подвижной опорой? |
|
17. Запишите основную форму уравнений равновесия балочной системы |
|
18.Как определяется момент силы расположенной в пространстве относительно оси перпендикулярной заданной плоскости |
|
19. зарисуйте рисунок характеризующий геометрическое условие равновесия пространственной системы сил |
|
20. Запишите уравнения равновесия пространственной системы сил
|
|
21. Как определить координаты центра тяжести плоской конструкции если известны площади элементарных фигур из которых состоит конструкция |
Задача №2 (подставь и посчитай)
Определение реакций опор двухопорной кран балки.
Определить реакции двухопорной кран балки, нагруженной внешними силами
Дано: q = кН/м М = кН·м F = кН
Найти : RAx, RAy, RC
Решение
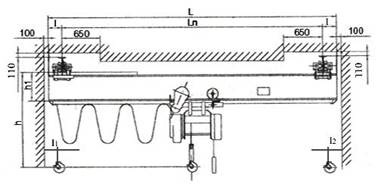
1. Строим расчетно-графическую схему,
под схемой балки проводим прямую, параллельную ее оси, и к этой прямой переносим все действующие нагрузки, а вместо опор изображаем их реакции
 На участке АВ действует
равномерно распределенная нагрузка с интенсивностью q.
На участке АВ действует
равномерно распределенная нагрузка с интенсивностью q.
При решении эту нагрузку заменим равнодействующей силой Q :
Q = q·AB = · 2 = кН
2 .Проводим оси координат ось х вдоль оси балки, ось у перпендикулярно ей.
3 .Составляем три уравнения равновесия
![]()
![]()
![]()
для двухопорной балки сначала составляют уравнение момента, причем относительно той или другой точки, где приложены неизвестные реакции.
4. Решаем уравнения равновесия относительно неизвестных реакций опор балки:
![]()
![]() (1)
(1)
Из (1) ![]() кН
кН
![]()
![]() (2)
(2)
Из (2) ![]() кН
кН
Из (3) ![]() кН
кН
5.Проверка. Составим еще одно уравнение равновесия, которое не использовалось при решении задачи:
![]()
![]() (4)
(4)
Из (4) ![]()
Ответ: RС = кН; RAy= кН; RAx= кН
Варианты заданий.
|
№ варианта |
Сила F , кН |
Момент М, кНм |
Распределен-ная нагрузка q ,кН/м |
№ варианта |
Сила F , кН |
Момент М, кНм |
Распределен-ная нагрузка q ,кН/м |
|
1 |
11 |
83 |
5 |
20 |
30 |
91 |
7 |
|
2 |
12 |
73 |
10 |
21 |
31 |
81 |
17 |
|
3 |
13 |
63 |
15 |
22 |
32 |
71 |
27 |
|
4 |
14 |
53 |
20 |
23 |
33 |
61 |
37 |
|
5 |
15 |
43 |
25 |
24 |
34 |
51 |
47 |
|
6 |
16 |
33 |
30 |
25 |
35 |
41 |
57 |
|
7 |
17 |
23 |
35 |
26 |
36 |
31 |
67 |
|
8 |
18 |
13 |
40 |
27 |
37 |
21 |
87 |
|
9 |
19 |
102 |
45 |
28 |
38 |
11 |
97 |
|
10 |
20 |
92 |
50 |
29 |
39 |
100 |
107 |
|
11 |
21 |
82 |
55 |
30 |
40 |
90 |
8 |
|
12 |
22 |
72 |
60 |
31 |
41 |
80 |
18 |
|
13 |
23 |
62 |
65 |
32 |
42 |
70 |
28 |
|
14 |
24 |
52 |
70 |
33 |
43 |
60 |
38 |
|
15 |
25 |
42 |
75 |
34 |
44 |
50 |
48 |
|
16 |
26 |
32 |
80 |
35 |
45 |
40 |
58 |
|
17 |
27 |
22 |
85 |
36 |
46 |
30 |
68 |
|
18 |
28 |
12 |
90 |
37 |
47 |
20 |
78 |
|
19 |
29 |
101 |
95 |
38 |
48 |
10 |
98 |
|
|
|
|
|
|
|
|
|
КИНЕМАТИКА
Лекция №5. Основные понятия кинематики. Кинематика точки
Цель: Изучить основные понятия и законы кинематики точки.
Основной задачей кинематики является изучение общих законов движения материальных точек и твердых тел без учета причин, их вызывающих. Кинематика отвечает на вопрос: как движется тело.
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Любое механическое движение характеризуется следующими параметрами:
1. Траектория движения — это линия, вдоль которой движется тело. В зависимости от траектории движение может быть прямолинейным и криволинейным.
2. Путь s — это расстояние, пройденное телом вдоль линии траектории (рис. 1.40).
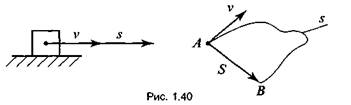 3. Перемещение S— это направленный отрезок прямой,
соединяющий начальное
и конечное положение тела (см. рис. 1.40).
3. Перемещение S— это направленный отрезок прямой,
соединяющий начальное
и конечное положение тела (см. рис. 1.40).
4. Скорость v — это величина, характеризующая быстроту изменения пройденного пути за
единицу времени: ![]()
5. Касательное ускорение аτ — это величина, которая характеризует быстроту
изменения величины скорости за единицу времени: ![]()
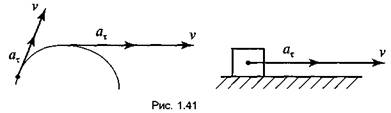 Касательное
ускорение всегда направлено по линии вектора скорости (рис. 1.41).
Касательное
ускорение всегда направлено по линии вектора скорости (рис. 1.41).
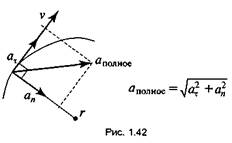
6. Нормальное ускорение ап — это величина, которая характеризует изменение направления вектора скорости:
![]() где
r — радиус кривизны
траектории. Полное ускорение
где
r — радиус кривизны
траектории. Полное ускорение ![]()
Нормальное ускорение всегда направлено по радиусу к центру кривизны траектории (рис. 1.42).Виды движения точки в зависимости от ускорения:
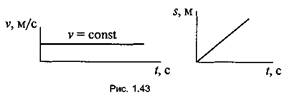
 1) равномерное — это движение точки с постоянной по
величине скоростью. Характеризуется следующими величинами:
1) равномерное — это движение точки с постоянной по
величине скоростью. Характеризуется следующими величинами:
v = s/t = const; s = vt; aτ=0; an = v2/r.
Равномерное движение можно изобразить графически (рис. 1.43);
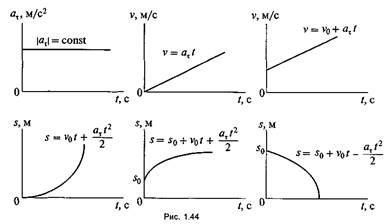
2) равнопеременное , равноускоренное, равнозамедленное — это движение точки с постоянным касательным ускорением. Характеризуется следующими величинами (рис. 1.44):
![]()
![]()
![]()
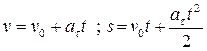 ;
; 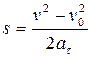
Простейшие движения твердого тела
К простейшим движениям твердого тела относится поступательное и вращательное движение
Поступательное движение твердого тела
— это такое движение, при котором прямая, проведенная в теле между
любыми двумя точками, перемещается параллельно самой себе.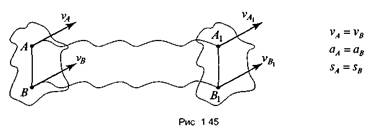 При поступательном движении все точки тела имеют одинаковые скорости, одинаковые
ускорения и проходят одинаковые отрезки пути (рис 1. 45)
При поступательном движении все точки тела имеют одинаковые скорости, одинаковые
ускорения и проходят одинаковые отрезки пути (рис 1. 45)
Работа большинства машин и механизмов основана на вращательном движении
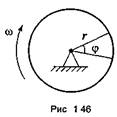 Вращательным движением твердого тела вокруг неподвижной оси называется такое движение,
при котором все точки тела движутся по окружностям, лежащим в плоскостях, перпендикулярных оси вращения, с центрами на этой
оси. Любое вращательное движение характеризуется
следующими параметрами (рис 1.46)
Вращательным движением твердого тела вокруг неподвижной оси называется такое движение,
при котором все точки тела движутся по окружностям, лежащим в плоскостях, перпендикулярных оси вращения, с центрами на этой
оси. Любое вращательное движение характеризуется
следующими параметрами (рис 1.46)
1) φ, рад — угол поворота, или угловое перемещение(1 рад = 57,3°),
2) ω = ∆φ/∆t — угловая скорость (характеризует изменение угла поворота за единицу времени)
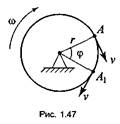 Средняя угловая скорость
Средняя угловая скорость ![]()
Угловое ускорение — это
величина, которая характеризует изменение угловой скорости за единицу времени
![]()
Виды вращательного движения твердого тела в зависимости от ускорения
1) равномерное — это движение тела с постоянной угловой скоростью
![]()
Линейные скорости и ускорения точек
равномерно вращающегося тела (рис. 1.47) определяются по формулам: ![]()
2) равнопеременное — это движение с постоянным угловым ускорением:
![]()
Линейные скорости и ускорения точек при равнопеременном вращении тела определяются по формулам:
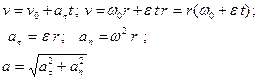
Сложное движение точки
В некоторых случаях движущиеся тела, которые принимаются за материальные точки, могут совершать сложное движение (например, движение человека в вагоне движущегося поезда).
Сложное движение точки — это движение точки относительно неподвижной системы координат. Скорость сложного движения называется абсолютной скоростью.
Сложное движение точки складывается из переносного движения, т.е. движения подвижной системы координат относительно неподвижной (например, движение поезда относительно Земли), и относительного движения, т.е. движения точки относительно подвижной системы координат.
Таким образом, скорость абсолютного движения точки равна геометрической сумме скоростей переносного и относительного движения:
![]() (теорема сложения скоростей).
(теорема сложения скоростей).
Лекция № 6. Плоскопараллельное движение твердого тела.
Цель: Изучить законы плоскопараллельного движения твердого тела.
Плоскопараллельным движением называется такое движение, при котором все точки тела перемещаются в плоскостях параллельно какой-то одной плоскости, называемой основной. Пример такого движения: движение колеса автомобиля на прямом участке пути, движение шатуна кривошипно-шатунного механизма.
Плоскопараллельное движение изучается двумя методами:
1) методом разложения плоскопараллельного движения на поступательное и вращательное;
2) методом мгновенных скоростей.
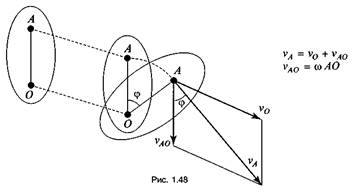 В
основе первого метода лежит теорема:
всякое плоскопараллельное движение может
быть получено с помощью одного поступательного и одного вращательного
движения (рис. 1.48).
В
основе первого метода лежит теорема:
всякое плоскопараллельное движение может
быть получено с помощью одного поступательного и одного вращательного
движения (рис. 1.48).
Плоскопараллельное движение тела может осуществляться путем одновременно происходящих вращательных и поступательных движений.
Поступательное движение тела можно считать переносным, а вращательное — относительным. Тогда вектор абсолютной скорости какой-то точки А будет равен скорости поступательного движения какой-то другой точки О плюс скорость вращательного движения точки А относительно точки О (см. рис. 1.48):
![]()
Точка, вокруг которой происходит относительное вращательное движение, называется полюсом вращения.
Таким образом, скорость любой точки тела при
плоскопараллельном движении
в данный момент времени равна сумме скорости полюса вращения и вращательной
скорости данной точки относительно полюса: ![]()
В основе второго метода лежит понятие мгновенного центра скоростей (МЦС).
Мгновенный центр скоростей — это точка плоской фигуры, скорость которой в данный момент времени равна нулю.
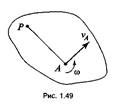 Всегда можно на фигуре найти такую точку. Например, возьмем скорость какой-то точки А, которую примем за полюс вращения. Отложим
отрезок АР, перпендикулярный vA, где АР = vA / ω, тогда скорость
точки Р равна
Всегда можно на фигуре найти такую точку. Например, возьмем скорость какой-то точки А, которую примем за полюс вращения. Отложим
отрезок АР, перпендикулярный vA, где АР = vA / ω, тогда скорость
точки Р равна ![]() , причем
, причем ![]() (рис. 1.49).
(рис. 1.49).
Таким образом, ![]()
Мгновенный центр скоростей всегда лежит на прямой, проведенной из какой-либо точки фигуры перпендикулярно направлению скорости этой точки.
Скорость любой точки фигуры прямо пропорциональна ее расстоянию до МЦС:
![]()
Способы нахождения МЦС:
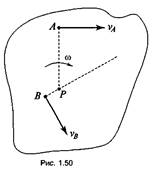
 1. Известны угловая скорость и скорость какой-то точки.
1. Известны угловая скорость и скорость какой-то точки.
В этом случае МЦС точки Р находится на перпендикуляре, восстановленном из точки А к вектору скорости на расстоянии АР = vA / ω (см. рис. 1.49):
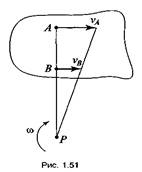
2. Известны направления скоростей двух точек vA и vB.
В этом случае МЦС лежит на пересечении перпендикуляров, восстановленных из точек А и В к направлениям их скоростей (рис. 1.50).
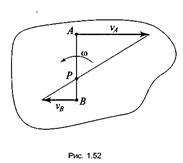
3. Известно, что векторы скорости двух точек vA и vB параллельны друг другу, направлены в одну сторону перпендикулярно отрезку АВ и не равны повеличине.
В этом случае МЦС находится в точке пересечения прямой, соединяющей начала векторов vA и vB, с прямой, соединяющей их концы (рис. 1.51).
 4. Известно, что векторы скорости двух точек vA и vB параллельны друг другу, но направлены в противоположные стороны.
4. Известно, что векторы скорости двух точек vA и vB параллельны друг другу, но направлены в противоположные стороны.
В этом случае МЦС находится на пересечении прямых, соединяющих начала и концы векторов скорости (рис. 1.52).
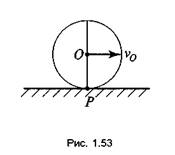
5. Известно, что плоская фигура без скольжения катится по неподвижной прямой.
В этом случае МЦС находится в точке соприкосновения фигуры с прямой (рис.1.53).
Тест – задания для самопроверки по лекции № 5 - 6
|
22. Запишите основные характеристики механического движения
|
|
23.Что называется полным ускорением точки? Определите полное ускорение если дано: v = 10 м/с ;v0 = 5 м/с ; t = 2 c ; r = 2м
|
|
24. Чем отличается равномерное движение от равноускоренного (поясните формулами ) |
|
25. Что называется угловым ускорением при
вращательном движении точки? Определите угловое ускорение
|
|
26. Из каких параметров складывается сложное движение точки |
|
27. Что называется плоскопараллельным движением |
|
|
|
29. Что называется мгновенным центром скоростей (МЦС)? Укажите основные способы его определения.
|
|
30. Определите положение МЦС если известно vА = 5 м/с ; |
Задача №3 (подставь и посчитай)
Определение силы сопротивления движению автомобиля
Автомобиль массой m движется с заданной скоростью va вверх по склону с углом наклона α = 30. Определить силы сопротивления движению, если известны следующие расчетные параметры: f =0,018 коэффициент сопротивления качению; K=0,6-кэфициент сопротивления воздуха; F =6,68 м2 –лобовая площадь автомобиля
Дано: m = кг ; va = км/ч
Найти: силы и мощности сопротивления
Решение.
1.Сила сопротивления качению. При движении автомобиля тяговое усилие Pd на ведущих колесах расходуется на преодоление сил в уравнении тягового баланса, одной из которых является сила сопротивления качению колес Pf. К сопротивлению качения относится также трение в подшипниках колес и в элементах подвески. В целом сила сопротивления качению зависит от конструкции и материала шины, скорости движения, приложенных к колесу крутящего момента, внешних сил и дорожных условий.
Линия действия силы ZK (равнодействующей нормальных реакций), равной по значению силе тяжести Ga = mg , смещается от вертикального диаметра вперед на некоторую величину ас, т.е. создается плечо сопротивления качению вследствие действия крутящего момента Md образующего тангенциальную силу Тг. В результате смещения ас возникает пара сил ZK и Ga сила ZK создает момент ZK ac, противодействующий качению колеса. Момент этой пары уравновешивает момент ZK ac. Значение силы сопротивления качению Pf , Н, находят из условия равновесия колеса:
![]()
Отношение ![]() обозначается буквой f и называется коэффициентом сопротивления качению, следовательно сила сопротивления качению колес Pf определим по формуле:
обозначается буквой f и называется коэффициентом сопротивления качению, следовательно сила сопротивления качению колес Pf определим по формуле:
![]() · 9,81· 0,018· 0,866
= Н
· 9,81· 0,018· 0,866
= Н
Мощность Nf , необходимая для преодоления сопротивления качению, кВт:
![]()
где Gh = Ga cos30 = mg· cos30 при движении автомобиля на подъеме при α = 30 (рис.1).
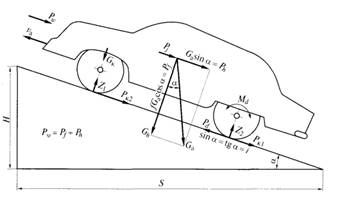
Рис. 1. Силы, действующие на автомобиль при подъеме
2.Сила сопротивления воздушной среды.
Сила сопротивления воздуха Рw составляется из силы давления встречных частиц воздуха, силы, создаваемой разрежением за автомобилем, и силы трения воздуха о поверхность автомобиля. Сила сопротивления воздуха зависит от лобовой площади автомобиля, его формы, скорости движения, плотности воздуха и может быть подсчитана по полученной опытным путем формуле, Н:
![]()
где К — коэффициент сопротивления воздуха, зависящий от обтекаемости автомобиля, т.е. его формы и качества поверхности кузова или кабины, Нс2/м4; F — лобовая площадь автомобиля, м2; va — скорость движения автомобиля, м/с.
Мощность, необходимая для преодоления силы сопротивления воздуха, кВт соответственно:
![]()
3.Силы сопротивления подъему и дороги. Ранее были рассмотрены основные силы, действующие на ведущих колесах автомобиля. Однако при ускоренном его движении и особенно при преодолении подъема (см. рис. 1) появляются дополнительные силы. В общем случае движения автомобиля на подъеме действуют три группы сил.
Первую группу составляют силы Pd, движущие автомобиль. Они образуются вследствие взаимодействия ведущих колес с дорогой и называются силами тяги.
Вторую группу составляют силы, оказывающие сопротивление движению. Это силы сопротивления качения задних Рк1 и передних Рк2 колес, действующих в плоскости дороги; сила сопротивления воздуха Pw, приложенная к центру лобовой площади автомобиля; сила сопротивления подъему Ph — направленная параллельно плоскости дороги и являющаяся составляющей силы тяжести Ga = mg , автомобиля; сила инерции Рj, приложенная в центре тяжести автомобиля и называемая силой сопротивления разгону.
Третью группу сил составляют нормальные реакции дороги на передние Z1 и задние Z2 колеса, вызванные перпендикулярной составляющей Gh силы тяжести (массы) автомобиля. Эта группа сил рассматривается отдельно.
Величины коэффициента f и уклона i в совокупности характеризуют качество дороги. Поэтому сила суммарного сопротивления дороги Рψ, слагающаяся из сил сопротивления качению и подъему, будет иметь следующий вид:
![]()
![]()
Знак «плюс» берется при движении на
подъем, знак «минус» — при движении на спуске. Выражение в скобках обозначается
буквой ψ =![]() и называется коэффициентом суммарного сопротивления дороги.
и называется коэффициентом суммарного сопротивления дороги.
Мощность при суммарном сопротивлении дороги составит:
![]()
Ответ :
Варианты заданий
|
№ варианта |
Масса автомобиля m , кг |
Скорость движения va , м/с2 |
Угол наклона пути α ,град |
№ варианта |
Масса автомобиля m , кг |
Скорость движения va , м/с2 |
Угол наклона пути α |
|
1 |
4350 |
110 |
30 |
19 |
5300 |
85 |
30 |
|
2 |
4400 |
100 |
30 |
20 |
5350 |
75 |
30 |
|
3 |
4450 |
90 |
30 |
21 |
5400 |
65 |
30 |
|
4 |
4500 |
80 |
30 |
22 |
5450 |
55 |
30 |
|
5 |
4550 |
70 |
30 |
23 |
5500 |
45 |
30 |
|
6 |
4600 |
60 |
30 |
24 |
5550 |
35 |
30 |
|
7 |
4650 |
50 |
30 |
25 |
5600 |
80 |
30 |
|
8 |
4700 |
40 |
30 |
26 |
5650 |
70 |
30 |
|
9 |
4750 |
30 |
30 |
27 |
5700 |
60 |
30 |
|
10 |
4800 |
105 |
30 |
28 |
5750 |
50 |
30 |
|
11 |
4850 |
95 |
30 |
29 |
5800 |
40 |
30 |
|
12 |
4900 |
85 |
30 |
30 |
5850 |
40 |
30 |
|
13 |
4950 |
75 |
30 |
31 |
5900 |
30 |
30 |
|
14 |
5000 |
65 |
30 |
32 |
5950 |
105 |
30 |
|
15 |
5050 |
55 |
30 |
33 |
6000 |
95 |
30 |
|
16 |
5100 |
45 |
30 |
34 |
4500 |
85 |
30 |
|
17 |
5150 |
35 |
30 |
35 |
4600 |
75 |
30 |
|
18 |
5200 |
25 |
30 |
36 |
4700 |
65 |
30 |
Лекция 7. Работа при поступательном и вращательном движении
Цель: Изучить работы в механике мощность и основные теоремы динамики .
Воспитательная цель: Показать применение математических методов при решении технических задач
 Механическая работа — это процесс перемещения тела
под действием приложенной
силы.
Механическая работа — это процесс перемещения тела
под действием приложенной
силы.
I. Работа при поступательном движении равна произведению силы на перемещение и на косинус угла между ними (рис. 1.63):
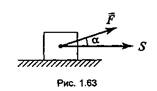
![]()
Величина работы зависит от угла между направлением силы и перемещением:
 1) если α = 0° ( рис 1.64, a), W = FS
1) если α = 0° ( рис 1.64, a), W = FS
 2) если α = 180° ( рис 1.64, б),
W = - FS
2) если α = 180° ( рис 1.64, б),
W = - FS
3) если α = 90° ( рис 1.64, в), W = 0.
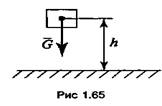
1. Работа силы тяжести равна
произведению силы тяжести на
высоту (рис. 1.65):
![]()
2.Работа силы упругости равна произведению
силы упругости на величину
деформации (рис. 1.66):![]()
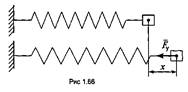 где k — коэффициент жесткости материала.
где k — коэффициент жесткости материала.
3. Работа силы трения определяется по следующим формулам:
а) если тело движется горизонтально (рис. 1.67),
![]()
Сила трения (величина, возникающая в результате взаимодействия двух трущихся поверхностей)
![]()
где R n — сила нормального давления ; f — коэффициент трения скольжения, величина которого зависит от свойств трущихся поверхностей.
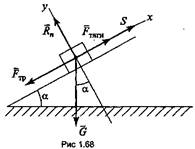 б) если тело движется по наклонной плоскости (рис.
1.68),
б) если тело движется по наклонной плоскости (рис.
1.68),
 W = -
Fтр S = -
mg cosα
f S
W = -
Fтр S = -
mg cosα
f S
![]()
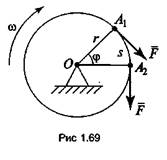
II. Работа при вращательном движении (рис. 1.69) определяется по формуле
W = F S = F r φ, или W = М φ
где s = r φ, M = M0 (F) = F r.
За единицу работы принимается 1 Дж: 1Дж =1Нм.
Механическая мощность
при поступательном и вращательном движении
Мощность — это величина, численно равная работе, совершенной за единицу времени:
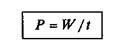 или W = Р t
или W = Р t
Мощность при поступательном движении Р = W /t = F S cosα/t = Fv cosα P = F v cosα
Если a = 0, то P=Fv.
Мощность при вращательном движении P = W/t = M φ/t = M ω, Р = М ω
КПД машин и механизмов — это величина, которая показывает, какая часть от всей
выполненной работы расходуется полезно: ![]()
где Wnonл , Wзатр — полезная и затраченная работа; Р пол , Р затр — полезная и затраченная мощность.
За единицу мощности принимается 1 Вт: 1 Вт = 1 Дж/с.
Теоремы динамики
При поступательном движении теоремы динамики имеют следующий вид.
Теорема об изменении количества движения: изменение количества движения материальной точки равно импульсу некоторой силы, приложенной к этой точке, т.е.
F t = mv - mv0
где Ft — импульс силы; mv — количество движения.
Теорема об изменении кинетической энергии: изменение кинетической энергии материальной точки равно работе некоторой силы по перемещению этой точки, т.е.
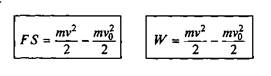 где W=FS —работа; mv2/2 — кинетическая энергия.
где W=FS —работа; mv2/2 — кинетическая энергия.
Тест – задания для самопроверки по лекции № 7
|
31. Что называется механической работой , и в каком случае она принимает отрицательное значение
|
|
32.Что общего между работой силы тяжести и работой силы упругости (пояснить формулами)
|
|
33. Чем отличается равномерное движение от равноускоренного (поясните формулами ) |
|
34. Определите работу движущегося а) горизонтально;
б) и по наклонной плоскости , твёрдого тела если известно : m = 100 кг; f = 0,45 ; S = 20 м ; α
=
|
|
35. Что такое мощность и от как она зависит от скорости движущегося тела |
|
36. Что такое КПД и как он зависит от скорости движения твердого тела |
|
37. Определите величину силы создаваемой импульс движения твердого тела если известно v=10 м/с v0 = 5 м/с ; t = 2 c; m = 100 кг
|
|
38. Определите величину кинетической энергии движущегося тела v=10 м/с; v0 = 5 м/с ; m = 100 кг
|
Лекция №8 Основные понятия сопротивления материалов деформация растяжения сжатия.
1. Основные понятия сопротивления материалов
Цель: Изучить основные понятия сопротивления материалов деформация растяжения сжатия.
Сопротивление материалов — это раздел технической механики, в котором изучаются методы расчета элементов конструкций на прочность, жесткость и устойчивость при различных видах деформаций.
Для выполнения расчетов на прочность, жесткость и устойчивость необходимо учитывать не только внешние силы, действующие на тело, но и внутренние силы упругости, которые возникают в теле под действием внешних сил. Для определения величины и направления внутренних сил упругости используют метод сечений. Физический смысл метода сечений заключается в том, что брус мысленно рассекают на две части, одна из которых отбрасывается. Оставшаяся (отсеченная) часть будет находиться в равновесии, так как внутренние силы упругости, возникающие в сечении бруса, не только уравновешивают внешние силы, действующие на эту часть, но и заменяют действие отброшенной части на оставшуюся часть.
 Внутренний силовой фактор (ВСФ) — это
равнодействующая величина внутренних сил упругости. При
простых видах деформации в поперечных сечениях бруса могут
возникать один-два ВСФ.
Внутренний силовой фактор (ВСФ) — это
равнодействующая величина внутренних сил упругости. При
простых видах деформации в поперечных сечениях бруса могут
возникать один-два ВСФ.
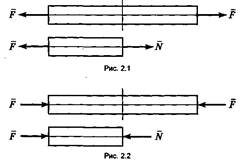
1. При растяжении один ВСФ — продольная сила N (рис. 2.1).
2. При сжатии один ВСФ — продольная сила N (рис. 2.2).
3. При сдвиге (или срезе) один ВСФ - поперечная сила Q (рис. 2.3).
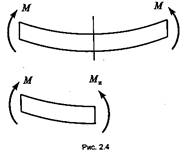
4. При чистом изгибе один ВСФ - изгибающий момент Ми (рис. 2.4).
 5.
При кручении один ВСФ — крутящий
момент Мкр (рис. 2.5).
5.
При кручении один ВСФ — крутящий
момент Мкр (рис. 2.5).
Метод сечений позволяет определить только величину и направление внутренних силовых факторов, но не дает возможности определить характер их распределения по сечению. С этой целью вводится понятие напряжения.
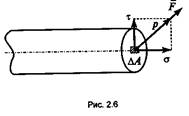 Напряжение р — это величина, численно равная внутреннему силовому фактору, действующему на единицу геометрической характеристики сечения (рис. 2.6):
Напряжение р — это величина, численно равная внутреннему силовому фактору, действующему на единицу геометрической характеристики сечения (рис. 2.6):
![]() где ∆А
— площадь бесконечно малой площадки. За
единицу напряжения принимается1Па: 1
Па = 1 Н/м2; 1МПа =1Н/мм2.
где ∆А
— площадь бесконечно малой площадки. За
единицу напряжения принимается1Па: 1
Па = 1 Н/м2; 1МПа =1Н/мм2.
При расчетах используются составляющие полного напряжения:
нормальное напряжение о, линия действия которого направлена перпендикулярно плоскости сечения.
касательное
напряжение т, линия действия которого направлена вдоль сечения. Полное напряжение ![]()
С нормальным напряжением связан отрыв частиц от тела, а с касательным — сдвиг отдельных частиц или элементов относительно друг друга. Под действием рабочей нагрузки в поперечном сечении бруса возникают рабочие напряжения (σ или τ), которые определяются по
формулам, выраженным через внутренний силовой фактор и площадь сечения.
Рабочее напряжение должно быть меньше или равно допускаемому
напряжению: ![]()
где [σ] —допускаемое нормальное напряжение; [τ] — допускаемое касательное напряжение.
Допускаемое напряжение — это напряжение, при котором данный элемент конструкции работает в нормальном (заданном) режиме.
Предельное напряжение σпред , τпред — это напряжение, при котором элемент конструкции или разрушается, или недопустимо деформируется. Недопустимая деформация — это большая остаточная (пластическая) деформация в теле.
2. Растяжение и сжатие
Растяжением или сжатием называется такой вид деформации, при
котором в поперечном сечении бруса возникает один ВСФ —
продольная сила N. Она равна алгебраической сумме проекций
на продольную ось внешних сил, действующих на отсеченную часть
бруса: ![]()
Так как величина продольных сил в разных сечениях бруса неодинакова, то строится эпюра продольных сил. Эпюра продольных сил - график, показывающий изменения величины продольных сил в сечении бруса по его длине.
Последовательность построения эпюр продольных сил:
1. Разбиваем брус на участки, ограниченные точками приложения сил (нумерацию участков ведем от незакрепленного конца).
2. Используя метод сечений, определяем величину продольных сил в сечении каждого участка.
3. Выбираем масштаб и строим эпюру продольных сил, т.е. под изображением бруса (или рядом) проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответствующие в выбранном масштабе продольным силам (положительное значение откладываем вверх (или вправо), отрицательное — вниз (или влево)).
Под действием продольных сил в поперечном сечении бруса возникает нормальное напряжение, которое определяется по
формуле: ![]()
Где А — площадь поперечного сечения участка.
 Гипотеза плоских сечений устанавливает, что при растяжении (сжатии) сечение бруса остается плоским и перпендикулярным линии действия силы. Закон Гука при растяжении - нормальное
напряжение, возникающее в поперечных
сечениях при растяжении в пределах упругости, прямо
пропорционально продольной деформации:
Гипотеза плоских сечений устанавливает, что при растяжении (сжатии) сечение бруса остается плоским и перпендикулярным линии действия силы. Закон Гука при растяжении - нормальное
напряжение, возникающее в поперечных
сечениях при растяжении в пределах упругости, прямо
пропорционально продольной деформации:
![]()
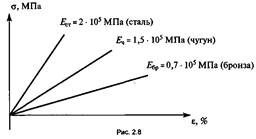
где Е — коэффициент пропорциональности, который называется модулем упругости.. Он характеризует жесткость материала, из которого изготовлен элемент конструкции. Для различных материалов его значения определены экспериментально. Закон Гука можно изобразить графически (рис. 2.8).
![]() Закон Гука для определения деформации растяжения:
Закон Гука для определения деформации растяжения:
где ![]() — абсолютное изменение продольных
размеров; l0 — первоначальные
размеры элемента; ЕА — величина, характеризующая жесткость сечения
бруса.
— абсолютное изменение продольных
размеров; l0 — первоначальные
размеры элемента; ЕА — величина, характеризующая жесткость сечения
бруса.
Условие прочности
при растяжении: рабочее напряжение должно быть меньше или равно
допускаемому напряжению, т.е. ![]()
Используя это условие, можно выполнить три вида расчетов на прочность при растяжении.
1.Проверочный — проверка
прочности: по заданной рабочей нагрузке и заданному
размеру сечения определяем рабочее напряжение и сравниваем его с
допускаемым напряжением. Если ![]() - удовлетворяет условию прочности , если
- удовлетворяет условию прочности , если![]() - не удовлетворяет условию прочности
- не удовлетворяет условию прочности
2.Проектный — подбор размера сечения по заданной рабочей нагрузке и допускаемому
напряжению: (например для вала) - 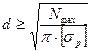
3. Проверочно-уточненный— определение допускаемого значения рабочей нагрузки по заданному размеру сечения и допускаемому напряжению. (например для
круглого бруса): ![]()
Тест – задания для самопроверки по лекции № 8
|
39. Что называется внутренним силовым фактором (ВСФ) , и какие ВСФ используются в расчетах сопротивления материалов
|
|
40.Что такое напряжение в сопротивлении материалов и какие параметры его характеризуют
|
|
41. Что такое Закон Гука, и от чего он зависит при растяжении - сжатии |
|
42. Определите величину удлинения стального бруса, если известно N = 100 кН; d = 100 мм; l0 = 3м |
|
43. Чем характеризуется условие прочности при растяжении сжатии |
|
44. Проведите проектный расчет геометрического параметра сечения вала, если Nmax = 100 кН;
|
|
45. Какие виды расчетов на прочность проводят при растяжении сжатии , в чем их основное отличие |
Задача № 4 (подставь и посчитай)
Определение деформации растяжения – сжатия ступенчатого бруса.
Построить эпюры продольных сил и нормальных напряжений для нагруженного стального винта(3) съёмника подшипников (рис. 2.9). Определить удлинение (укорочение) винта, если Ест= 2 ·105 МПа.
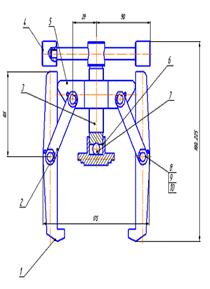
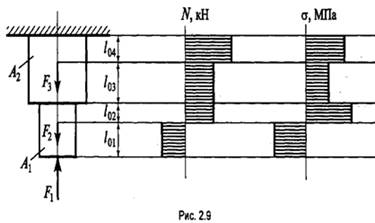
Дано: F1 = кН; F2 = кН ; F3 = кН ;
А1 = 2 см2 = 2 ·102 мм2 ; А2 = 4 см2 = 4 ·102 мм2 ; Ест = 2 ·105 МПа ; l01 = 100 мм ; l02 = 50 мм ; l03 = 200 мм ; l04 = 150 мм
Определить: ∆l
Решение.
1.Определяем продольные силы и строим их эпюру:
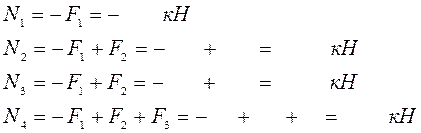
2.Определяем величину нормальных напряжений и строим их эпюру:
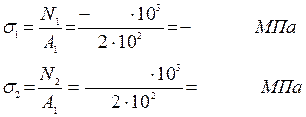
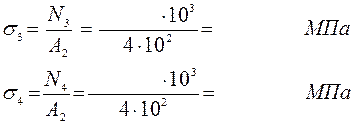
3. Используя видоизмененный закон Гука, определяем удлинение бруса:
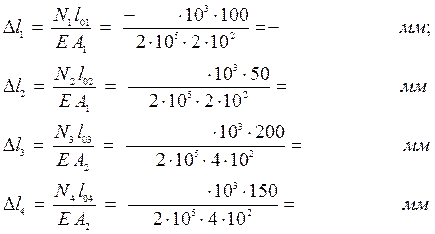
∆l = ∆l1 + ∆l2 + ∆l3 + ∆l4 = - + + + = мм.
Положительный знак ∆l говорит о том что брус растягивается
Ответ: ∆l = мм.
Варианты заданий.
|
№ варианта |
Сила F1 , кН |
Сила F2 , кН |
Сила F3 , кН |
№ варианта |
Сила F1 , кН |
Сила F2 , кН |
Сила F3 , кН |
|
1 |
2 |
20 |
5 |
20 |
4 |
6 |
8 |
|
2 |
3 |
19 |
10 |
21 |
14 |
12 |
10 |
|
3 |
4 |
18 |
15 |
22 |
6 |
8 |
10 |
|
4 |
5 |
17 |
20 |
23 |
18 |
14 |
10 |
|
5 |
6 |
16 |
25 |
24 |
20 |
22 |
5 |
|
6 |
7 |
15 |
30 |
25 |
40 |
10 |
19 |
|
7 |
8 |
14 |
35 |
26 |
42 |
11 |
6 |
|
8 |
9 |
13 |
40 |
27 |
43 |
12 |
18 |
|
9 |
10 |
12 |
45 |
28 |
44 |
13 |
7 |
|
10 |
11 |
11 |
50 |
29 |
45 |
14 |
17 |
|
11 |
12 |
10 |
6 |
30 |
48 |
15 |
8 |
|
12 |
13 |
9 |
7 |
31 |
50 |
16 |
16 |
|
13 |
14 |
8 |
15 |
32 |
52 |
17 |
9 |
|
14 |
15 |
7 |
16 |
33 |
54 |
18 |
15 |
|
15 |
16 |
6 |
21 |
34 |
56 |
19 |
10 |
|
16 |
17 |
5 |
22 |
35 |
58 |
20 |
14 |
|
17 |
18 |
4 |
8 |
36 |
60 |
21 |
11 |
|
18 |
19 |
3 |
9 |
37 |
62 |
22 |
13 |
|
19 |
20 |
2 |
10 |
38 |
64 |
23 |
12 |
Лекция № 9. Деформация среза и смятия. Кручение круглого бруса.
Цель: Изучить деформация среза, смятия и кручения.
Многие элементы конструкции, служащие для соединения деталей (болты, винты, заклепки, шпонки, швы сварных, клеевых соединений и т.д.), испытывают в процессе работы деформацию среза и смятия.
Рассмотрим практические расчеты на прочность при срезе и смятии на примере соединения заклепками.
Под действием внешней силы F, действующей на соединенные листы, заклепка испытывает деформацию среза по поперечному сечению аb (рис. 2.12). В этом сечении возникает один ВСФ — поперечная сила Q = F.
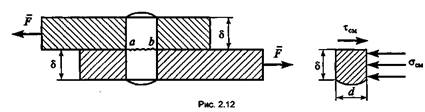
Под действием поперечной силы Q в сечении заклепки ab возникает касательное напряжение
![]() где Аср
— площадь среза.
где Аср
— площадь среза.
Боковая поверхность заклепки под действием внешних сил F испытывает деформацию смятия.
Смятие — это местная деформация сжатия на участках передачи давления одним элементом другому. На боковой поверхности заклепки возникает нормальное напряжение смятия
![]() где Асм — площадь смятия.
где Асм — площадь смятия.
Условие прочности на срез: рабочее напряжение на срез должно быть меньше или равно допускаемому напряжению на срез, т.е.
![]() ; Q = F ;
; Q = F ; ![]()
где п — количество срезов данного элемента;
т — количество элементов в данном соединении.
Три расчета на прочность при срезе.
1. Проверочный — проверка прочности при известных значениях F, d, [τср], n, т определяют
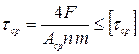
2. Проектный — подбор размера сечения , если известны F, [τср], n, т то диаметр среза
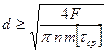
3. Проверочно-уточненный — определение величины нагрузки при известных
значениях d, [τср], n, т ![]()
Условие прочности на смятие: рабочее напряжение на смятие должно быть меньше или равно допускаемому
напряжению на смятие, т.е. 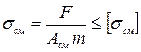 ; Асм
= dδ
; Асм
= dδ
где δ — толщина листов.
Три расчета на прочность при смятии.
1. Проверочный![]() 2.
Проектный:
2.
Проектный: ![]()
3.Проверочно – уточненный: ![]()
Кручение
При кручении в поперечном сечении бруса под действием ВСФ — крутящего момента Мкр — возникает касательное напряжение, которое распределяется по радиусу сечения по линейному закону: минимальное напряжение (равное нулю) — в центре сечения, максимальное — на поверхности бруса (рис. 2.13). Векторы напряжения направлены перпендикулярно радиусу сечения.
 Касательное напряжение
Касательное напряжение ![]()
где Мкр — крутящий момент; ρ — расстояние от произвольной точки сечения А до центра сечения;
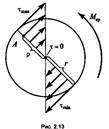 Jp — полярный момент
инерции сечения.
Jp — полярный момент
инерции сечения.
Крутящий
момент ![]()
Где Р— мощность; п — частота вращения; ω — угловая скорость. Полярный момент инерции сечения Jp определяется по формулам:
а) для круга (рис. 2.14, а) ![]()
б) для кольца (рис. 2.14, б) ![]() где c = dвн/dн.
где c = dвн/dн.
![]() Выведем формулу напряжения при учении:
Выведем формулу напряжения при учении: ![]()
где W = Jp /r —полярный момент сопротивления сечения (величина, характеризующая способность бруса сопротивляться деформации кручения). Полярный момент сопротивления сечения определяется по формулам:
а) для круга (см. рис. 2.14, а) ![]()
б) для кольца (см. рис. 2.14,6) ![]()
При кручении бруса
его ось испытывает скручивание на некоторый угол ![]() который называется углом
закручивания. Его величина определяется по формуле
который называется углом
закручивания. Его величина определяется по формуле
![]() где l — длина бруса; G — модуль сдвига.
где l — длина бруса; G — модуль сдвига.
Расчеты на жесткость ведутся по единичному углу закручивания, т.е. углу закручивания, приходящемуся на единицу длины бруса:
Условие прочности при кручении: рабочее напряжение, возникающее при деформации кручения, должно быть меньше или равно допускаемому напряжению, т.е
![]()
Три расчета на прочность при кручении.
1. Проверочный ![]() где 106
— коэффициент для мощности,
выр-ой в кВт.
где 106
— коэффициент для мощности,
выр-ой в кВт.
2. Проектный ![]() 3. Проверочно-уточненный
3. Проверочно-уточненный ![]()
Условие жесткости при кручении: рабочий единичный угол закручивания должен быть меньше или равен допускаемому углу закручивания, т.е.
Расчеты на жесткость при кручении.
1. Проверочный — проверка жесткости ![]()
2. Проектный ![]()
Тест – задания для самопроверки по лекции № 9
|
46. Чем отличается деформация среза от деформации смятия (пояснить формулами)
|
|
47. От чего зависит расчет на прочность при срезе , при проверочном , при проектном и при проверочно –уточнённом расчетах
|
|
48. Проверьте условие - выдержит ли заклёпоное
соединение нагрузку в 200 кН если δ =5 мм; d=10 мм ; m = 3;
|
|
49. Что называется деформацией кручения
|
|
50.Определите полярный момент инерции сечения и момент сопротивления сечения круглого бруса d= 54 мм |
|
51.Что такое угол закручивания и чем он отличается от угла сдвига |
|
52. Что называется условием прочности при кручении.
Оцените прочность вала d= 54 мм если он испытывает
Мкр = 1500 кН при |
Задача № 5. ( подставь и посчитай)
Определение деформации кручения круглого бруса.
Для стального вала d = 75 мм построить эпюру крутящих моментов и наибольших касательных напряжений (рис. 2.15). Определить угол закручивания наиболее нагруженного участка бруса.
Дано: М 0 = 5 кН м ; М 1 = кН м ; М 2 = кН м ; М 3 = кН м ;
G = 0,8 · 10 5 МПа ; d = 75 мм
Определить : угол закручивания φ на опасном участке
Решение:
1. Определяем значение крутящего момента по участкам бруса
М к р 1 = М 1 = кН м ;
М к р 2 = М 1 – М 0 = – = кН м;
М к р 3 = М1 – М 0 + М 2 = – + = кН м;
2. Определим касательное напряжение при кручении по
участкам бруса, и выберем наиболее нагруженный участок. Преобразуем
формулу для расчета напряжения с учетом круглого сечения 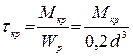
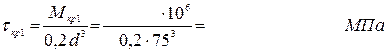
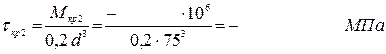
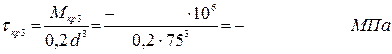
3. Определяем угол закручивания на наиболее нагруженном участке
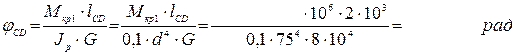
4. Строим эпюры крутящих моментов и касательных напряжений по участкам бруса.
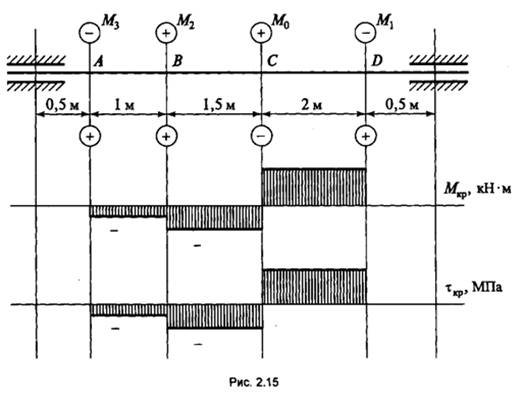
Ответ: φCD = рад
Варианты заданий
|
№ варианта |
Момент М1 , кНм |
Момент М2 , кНм |
Момент М3 , кНм |
№ варианта |
Момент М1 ,кНм |
Момент М2 , кНм |
Момент М3 , кНм |
|
1 |
0,6 |
0,25 |
0,15 |
20 |
0,25 |
0,15 |
0,6 |
|
2 |
0,65 |
0,2 |
0,1 |
21 |
0,2 |
0,1 |
0,65 |
|
3 |
0,7 |
0,3 |
0,2 |
22 |
0,3 |
0,2 |
0,7 |
|
4 |
0,8 |
0,4 |
0,3 |
23 |
0,4 |
0,3 |
0,8 |
|
5 |
0,9 |
0,45 |
0,35 |
24 |
0,45 |
0,35 |
0,9 |
|
6 |
1 |
0,5 |
0,4 |
25 |
0,5 |
0,4 |
1 |
|
7 |
0,4 |
0,5 |
1 |
26 |
0,5 |
1 |
0,4 |
|
8 |
0,3 |
0,6 |
0,7 |
27 |
0,6 |
0,7 |
0,3 |
|
9 |
0,2 |
0,7 |
0,8 |
28 |
0,7 |
0,8 |
0,2 |
|
10 |
0,1 |
0,8 |
0,7 |
29 |
0,8 |
0,7 |
0,1 |
|
11 |
0,2 |
0,9 |
0,6 |
30 |
0,9 |
0,6 |
0,2 |
|
12 |
0,55 |
1 |
1,2 |
31 |
1 |
1,2 |
0,55 |
|
13 |
0,56 |
2 |
1,5 |
32 |
2 |
1,5 |
0,56 |
|
14 |
0,6 |
0,1 |
1 |
33 |
0,1 |
1 |
0,6 |
|
15 |
0,5 |
0,2 |
0,9 |
34 |
0,2 |
0,9 |
0,5 |
|
16 |
0,4 |
0,23 |
0,15 |
35 |
0,23 |
0,15 |
0,4 |
|
17 |
0,7 |
0,38 |
0,2 |
36 |
0,38 |
0,2 |
0,7 |
|
18 |
0,3 |
0,45 |
0,36 |
37 |
0,45 |
0,36 |
0,3 |
|
19 |
0,9 |
0,95 |
1,1 |
38 |
0,95 |
1,1 |
0,9 |
Лекция №10. Деформация изгиба и расчет его параметров.
Цель: Изучить деформация изгиба и расчет его параметров.
Изгибом называется деформация от момента внешних сил, действующих в плоскости, проходящей через геометрическую ось балки.
В зависимости от места приложения действующих сил различают прямой и косой изгиб.
Изгиб называется прямым, если внешние силы, действующие на балку, лежат в главной плоскости сечения. Главной плоскостью сечения называется плоскость, проходящая через ось балки и одну из главных центральных осей сечения.
Изгиб называется косым, если внешние силы не лежат в главной плоскости сечения.
В зависимости от характера внутренних силовых факторов, возникающих в поперечных сечениях балки, изгиб может быть чистым и поперечным.
Изгиб называется чистым, если в поперечном сечении балки (бруса) возникает один ВСФ — изгибающий момент Ми .
Изгиб называется поперечным, если под действием внешних сил в сечении балки (бруса) возникают два ВСФ — изгибающий момент Ми , и поперечная сила Qy.
Изгибающий момент в
любом сечении балки равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть балки: ![]()
Поперечная сила в
любом сечении балки равна алгебраической сумме проекций внешних сил, действующих на отсеченную часть балки: ![]() .
.
Значения поперечных сил и изгибающих моментов в различных сечениях балки могут быть неодинаковы, поэтому строятся эпюры поперечных сил и изгибающих моментов.
Для определения поперечных сил и изгибающих моментов необходимо знать правила знаков.
![]() 1. Правила знаков для поперечных сил.
1. Правила знаков для поперечных сил.
![]() 1.1.Прямое
правило: поперечная
сила считается положительной в том случае,
если внешние силы поднимают левый конец балки или опускают правый (рис.
2.16).
1.1.Прямое
правило: поперечная
сила считается положительной в том случае,
если внешние силы поднимают левый конец балки или опускают правый (рис.
2.16).
1.2.Обратное правило: поперечная сила считается отрицательной в том случае, если внешние силы опускают левый конец балки или поднимают правый конец (рис. 2.17).
2. Правила знаков для изгибающих моментов.
![]()
![]() 2.1.
Прямое правило: изгибающий момент считается положительным, если внешние силы, действующие на левый конец балки, поворачивают его по часовой стрелке, а действующие на правый -против часовой стрелки(рис. 2.18).
2.1.
Прямое правило: изгибающий момент считается положительным, если внешние силы, действующие на левый конец балки, поворачивают его по часовой стрелке, а действующие на правый -против часовой стрелки(рис. 2.18).
2.2.Обратное правило: изгибающий момент считается отрицательным, если внешние силы, действующие на левый конец балки, поворачивают его против часовой стрелки, а действующие на правый — по часовой стрелке (рис. 2.19).
Последовательность построения эпюр поперечных сил и изгибающих моментов:
1. Под нагруженной балкой строим расчетно-графическую схему.
2.Используя три уравнения: ![]() ;
; ![]() ;
;
![]() , определяем реакции опор балки (обязательно выполнить проверку решения).
, определяем реакции опор балки (обязательно выполнить проверку решения).
3.Используя метод сечений, определяем значения поперечных сил в характерных точках, т.е. точках, в которых приложены внешние нагрузки (при этом удобнее использовать прямое правило знаков, т.е. разбивать балку слева направо).
4.По полученным значениям поперечных сил строим эпюру Qy: под балкой проводим прямую, параллельную ее оси, и от этой прямой в характерных точках откладываем перпендикулярные поперечным силам отрезки, соответствующие выбранному масштабу.
5. Используя метод сечений, определяем величину Мк в тех же характерных точках и по полученным значениям строим эпюру изгибающих моментов.
Условие прочности при изгибе.
Условие прочности при изгибе заключается в
следующем - рабочее напряжение должно быть меньше или равно
допускаемому напряжению, т.е. ![]()
где Wx - осевой момент сопротивления (величина, характеризующая способность элементов конструкции сопротивляться деформации изгиба). Осевой момент сопротивления сечения определяется по формулам:
![]() а) для
круга
(рис. 2.21, а)
а) для
круга
(рис. 2.21, а) ![]() б) для кольца (рис. 2.21, б)
б) для кольца (рис. 2.21, б) ![]() где
с = dвн /dн;
где
с = dвн /dн;
в) для прямоугольника (рис. 2.21, в)
![]()
![]() При прямом поперечном изгибе в поперечных сечениях бруса возникают два ВСФ — изгибающий момент Ми, который обусловливает
возникновение нормального напряжения σи, и
поперечная сила Qy, которая обусловливает возникновение в
этом же сечении касательного напряжения τи (рис. 2.22):
При прямом поперечном изгибе в поперечных сечениях бруса возникают два ВСФ — изгибающий момент Ми, который обусловливает
возникновение нормального напряжения σи, и
поперечная сила Qy, которая обусловливает возникновение в
этом же сечении касательного напряжения τи (рис. 2.22):
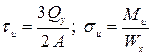
![]() Под действием внешних сил ось бруса испытывает линейное перемещение у
и угловое перемещение φ (рис. 2.23).
Линейные и угловые перемещения определяют по формулам,
которые составлены с учетом вида нагрузок, направления их к оси бруса и места приложения к брусу. Эти формулы занесены в
специальные
таблицы.
Под действием внешних сил ось бруса испытывает линейное перемещение у
и угловое перемещение φ (рис. 2.23).
Линейные и угловые перемещения определяют по формулам,
которые составлены с учетом вида нагрузок, направления их к оси бруса и места приложения к брусу. Эти формулы занесены в
специальные
таблицы.
Например, если Z = ½ l, то ![]()
где EJx — жесткость сечения бруса при изгибе. ![]()
Условие жесткости
при изгибе: рабочее линейное или угловое перемещение должно быть меньше или равно допускаемому линейному или угловому перемещению, т.е.![]() где [у] = (0,05 – 0,001) l ; [φ] = 0,001 град.
где [у] = (0,05 – 0,001) l ; [φ] = 0,001 град.
Тест – задания для самопроверки по лекции № 10
|
53. Что такое косой изгиб, и чем он отличается от прямого изгиба
|
|
54. Какие внутренние силовые факторы могут вызывать деформацию изгиба
|
|
55. Что называется эпюрой, и какие эпюры строят при изгибе |
|
56. Определить величину поперечной силы в сечениях 1 – 1 .
|
|
57. Определите осевые моменты сопротивления сечения прямоугольного бруса b= 73 мм; h=32 мм |
|
58. Определить величину изгибающего момента в точке D. m1= 15 кН м; m2 = 28 кН м; F1 =20кН; F2 = 30кH.
|
|
59. Что называется условием прочности при изгибе. Оцените прочность вала d= 54 мм если он испытывает Ми = 1500 кН при σи= 160 МПа |
|
F = 200кН
|
Задача №6 . (подставь и посчитай )
Определение деформации изгиба двухопорной балки.
Для заданной двухопорной балки (рис. 18, а) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения (h, b, d) в форме прямоугольника, приняв для прямоугольника h/b = 1,5. Считать [ σ ] = 160 МПа.
Дано:F1 = кН ; F2 = кН ; М1
= кН м, М2= кНм, ![]() =10 кН,
=10 кН, ![]() = 22 кН
= 22 кН
Найти : Qy ; Mx; Wx подобрать сечение бруса
Решение.
1. Делим балку на участки по характерным сечениям О, В, С, D (рис. 18, б).
2. Определяем в характерных сечениях значения поперечной силы Qy
и
строим эпюру слева направо (рис. 18, в):
4. Вычисляем в характерных сечениях значения изгибающего момента Mx и строим эпюру (рис. 18, г):
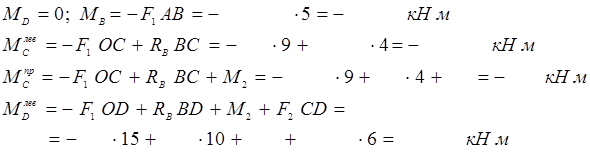
5. Вычисляем размеры сечения данной балки из условий
прочности
на изгиб по двум вариантам: а)
сечение - прямоугольник с заданным соотношением сторон (рис. 18, е) б) сечение - круг (рис. 18, д).
Вычисление размеров прямоугольного сечения:
![]()
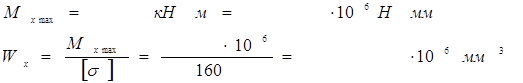
Используя формулу ![]() и учитывая, что h = 1,5b, находим
и учитывая, что h = 1,5b, находим
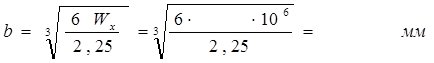
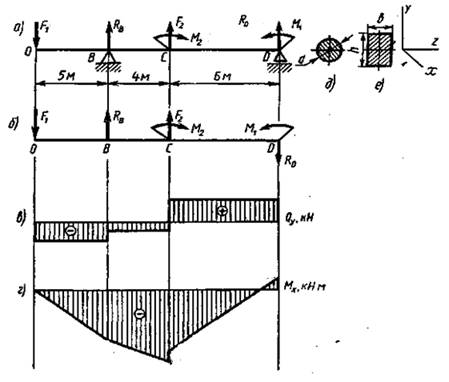
Варианты заданий
|
№ варианта |
F1 кН |
F2 кН |
М1 кНм |
М2 кНм
|
№ варианта |
F1 кН |
F2 кН |
М1 кНм |
М2 кНм
|
|
1 |
2 |
11 |
15 |
20 |
20 |
2 |
7 |
6 |
30 |
|
2 |
3 |
12 |
16 |
21 |
21 |
11 |
9 |
8 |
25 |
|
3 |
4 |
13 |
17 |
23 |
22 |
3 |
11 |
10 |
14 |
|
4 |
5 |
14 |
18 |
25 |
23 |
12 |
23 |
12 |
12 |
|
5 |
6 |
15 |
19 |
10 |
24 |
4 |
13 |
14 |
10 |
|
6 |
7 |
16 |
20 |
12 |
25 |
13 |
8 |
16 |
5 |
|
7 |
8 |
17 |
21 |
19 |
26 |
5 |
14 |
18 |
4 |
|
8 |
9 |
18 |
22 |
22 |
27 |
14 |
7 |
20 |
5 |
|
9 |
10 |
19 |
23 |
15 |
28 |
6 |
15 |
22 |
8 |
|
10 |
9 |
20 |
24 |
10 |
29 |
15 |
6 |
23 |
10 |
|
11 |
8 |
2 |
25 |
9 |
30 |
7 |
16 |
24 |
12 |
|
12 |
7 |
4 |
1 |
7 |
31 |
16 |
7 |
25 |
15 |
|
13 |
6 |
6 |
5 |
8 |
32 |
8 |
14 |
24 |
8 |
|
14 |
5 |
8 |
10 |
12 |
33 |
17 |
6 |
23 |
9 |
|
15 |
4 |
10 |
15 |
5 |
34 |
20 |
15 |
10 |
10 |
|
16 |
3 |
12 |
20 |
15 |
35 |
4 |
16 |
9 |
12 |
|
17 |
2 |
1 |
25 |
9 |
36 |
19 |
5 |
12 |
15 |
|
18 |
1 |
3 |
2 |
16 |
37 |
3 |
17 |
10 |
11 |
|
19 |
10 |
5 |
4 |
8 |
38 |
18 |
7 |
9 |
12 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.