Работа по схемам

Выполнили: Хильман В. Велижанина В. 11а

 

 

 

 

 

 

 

 

 

 

 

Задания к схеме №13

1. При построении схемы использованы различные геометрические формы

(овалы и прямоугольники), чтобы даже визуально подчеркнуть различие

изучаемого материала по его характеру: теоретический (общее) и практический (частное). Сформулируйте обобщенные, теоретические знания, необходимые для осознанного применения и усвоения приемов сложения и

вычитания чисел первого десятка: а) прибавления и вычитания по одному

или по частям; б) перестановки слагаемых; в) вычитания на основе взаимосвязи вычитания со сложением.

Прибавление (или вычитание) по частям предполагает раскладывание второго слагаемого (или вычитаемого) на удобные для выполнения вычислений составные части, и последовательное их прибавление (или вычитание).

 

От перестановки мест слагаемых сумма не меняется.

Знать законы сложения.

Сочетательный закон сложения.

Чтобы к сумме двух чисел прибавить третье, можно к первому числу прибавить сумму второго и третьего чисел.

Распределительный закон.

Чтобы число умножить на сумму двух других чисел, нужно это число умножить на каждое слагаемое и результат сложить.

Переместительный закон умножения.

От перестановки множителей произведение не меняется.

результат одного арифметического действия можно проверить другим действием (сложение вычитанием и наоборот).

Другими словами, с помощью вычитания проверяется правильность выполнения сложения, а с помощью сложения - результат выполнения вычитания.

 

И если неизвестен один из компонентов этих действий (слагаемое, уменьшаемое, вычитаемое), то его можно найти вычитанием / сложением.

2. Какая из фигур (овал или прямоугольник) избранный: а) вопросы теории, б) практические вопросы данной темы?

К вопросам теории относится фигура «овал», к практических вопросам фигура «прямоугольник».

3. Почему каждый из овалов соединен стрелкой с каким-либо прямоугольником? Можно ли эту стрелку повернуть в противоположное направление? Что будет обозначать данная стрелка?

Каждый из овалов соединён стрелкой, потому что осуществляется взаимосвязь между данными.  Стрелку можно повернуть в противоположное направление, так как из практики можно вывести теорию. Стрелка будет обозначать противоположное значение, выведение теории из практики.

4. Что обозначают стрелки, соединяющие прямоугольники? Можно ли их

направить в противоположную сторону?

Стрелки соединяющие прямоугольники, обозначают поэтапность порядка изучения сложения, постепенно переходя к изучению вычитания. Нельзя направить их в противоположную сторону, потому что детям будет сложно изучать сложение и вычитания, необходимо начинать с самого начала с единички.

5. Некоторые из вопросов арифметической теории уже в концентре "Десяток" доводятся до уровня обобщения, т.е. до формулировки и символической записи соответствующих правил, свойств, законов арифметических

действий, а некоторые используются в практике вычислений неявно, т.е.

на основе интуиции, здравого смысла и пока еще небольшого опыта детей.

Какие из вопросов арифметической теории в первом классе применяются

неявно? Как этот факт отражен в соответствующих овалах?

На основе интуиции составлен 2 овал «a+b= b+a», т.е. применяется неявно, так как дети без затруднения смогут догадаться и вывести правило «от перемены мест слагаемых сумма не меняется»

6. Каким оперативным правилом, т.е. правилом, которое дети проговаривают и непосредственно применяют в практике вычислений, пользуются

учащиеся при решении примеров вида 2+7?

Изучают прием сложения для случаев «прибавить 5, 6, 7, 8, 9». Если при вычислениях применить перестановку слагаемых, то все эти случаи сведутся к ранее изученным видам, а + 1, а + 2, а + 3, а + 4. Для этого знакомятся с переместительным свойством сложения.

7. Правило нахождения неизвестного слагаемого (третий овал) также

можно сформулировать в виде оперативного правила, используя для этого

термины "целое" и "часть". Закончите его формулировку: "Если от целого

отнять его часть, то ... "

Если от целого отнять его часть, то останется вторая часть этого целого.

8. Назовите этапы работы по теме "Сложение и вычитание".

1. Подготовительный этап: раскрытие конкретного смысла действий сложения и вычитания, запись и чтение примеров, случаи прибавить и вычесть 1, где результаты находятся на основе знания свойства натурального ряда чисел (когда к числу прибавляем 1, получаем число, следующее за ним при счете, а когда вычитаем из числа 1, то получаем предыдущее число).

2. Изучение приемов присчитывания и отсчитывания по одному и группами для случаев 2, 3, 4.

3. Изучение приема перестановки слагаемых для случаев + 5, 6, 7, 8, 9. Таблица сложения и состав чисел из слагаемых.

4. изучение приема вычитания на основе знания связи между суммой и слагаемыми для случаев – 5,6, 7, 8, 9.

 

9. Какой смысл имеет завершающее схему слово "Автоматизм"? Сформулируйте цель и задачи изучения темы "Сложение и вычитание в пределах десятка".

Когда дети научатся считать, то будут делать это без опоры на оперативные правила, посредством автоматизма.

Цели:

• Обеспечить усвоение детьми рациональных вычислительных приемов сложения и вычитания;

• Сформировать прочные вычислительные навыки;

• Научить решать простые задачи на сложение и вычитание различных видов (нахождение суммы, остатка, увеличение и уменьшение числа на несколько единиц, разностное сравнение, нахождение неизвестного слагаемого)

Задачи:

1. Знакомство с вычислительными приемами и формирование умения применять их при составлении таблиц сложения и вычитания.

2. Заучивание таблиц сложения и вычитания в тесной связи с усвоением состава числа в пределах Формирование навыков сложения.

10. Что включается в подготовительную работу к введению приемов: а)

прибавления и вычитания числа по его частям; б) перестановки слагаемых;

в) вычитания из чисел второго пятка?

А) Подготовительная работа: раскрытие конкретного смысла действий сложения и вычитания, запись и чтение примеров, случаи вида «+, - »1, где результаты находятся на основе свойства натурального ряда. прибавление и вычитание числа по его частям
1. Понимание концепции десятичной системы счисления и значений разрядов.
2. Знакомство с терминами, используемыми в математике при работе с числами по их частям, такими как целая часть, дробная часть, десятичная дробь, десятичное число.
3. Освоение приемов преобразования десятичных дробей в обыкновенные и обратно, таких как сокращение дробей, перевод в проценты и др.
4. Умение выделять целую и дробную части числа, проводить операции с ними (сложение, вычитание) и связывать результаты в одно число.
5. Практические задания на сложение и вычитание числа по его частям, использование столбикового метода для проведения операций.
6. Решение задач, в которых необходимо использовать приемы прибавления и вычитания числа по его частям, таких как расчеты стоимости товаров с учетом налога, решение задач на финансовые расчеты и т.д.
Б) перестановка слагаемых
1. Понимание основных свойств операций сложения и вычитания, таких как коммутативность и ассоциативность.
2. Знакомство с понятиями слагаемое, сумма, вычитаемое и разность.
3. Освоение приемов раскрытия скобок и преобразования выражений для удобства проведения операций.
4. Понимание принципов и правил перестановки слагаемых при сложении.
5. Практические задания на перестановку слагаемых при сложении, использование различных методов для повышения эффективности расчетов.
6. Решение задач на применение приемов перестановки слагаемых при сложении, таких как расчеты среднего значения, доли и т.д.
В) вычитание из чисел второго порядка
1. Понимание системы счисления и значений разрядов.
2. Знакомство с терминами, используемыми в математике при работе с числами второго порядка, такими как сотни, десятки, единицы, разряды.
3. Освоение арифметических операций сложения и вычитания, проведение устных и письменных вычислений.
4. Правильное понимание процесса переноса и занимание разрядов при вычитании.
5. Практическая работа над проведением операций вычитания, использование столбикового метода.
6. Решение задач, в которых необходимо применять приемы вычитания из чисел второго порядка, такие как расчеты объема и массы продуктов и т.д.

11. Объясните смысл термина «состав числа».

‍Состав числа — это сумма чисел, которая равна изначальному числу. Например, состав числа 5 — это 5 и 0, 1 и 4, 2 и 3.

Как правильно объяснить состав числа ребенку? Можно взять обыкновенные счетные палочки. Они продаются в любом магазине канцтоваров. Например, как объяснить ребенку состав числа 5? Необходимо взять пять палочек. Желательно одного цвета. От пяти палочек отложить в сторону одну и пересчитать оставшиеся. Получается четыре палочки и одна. Вот четыре и один – это и есть состав числа пять. Далее, следует к одной палочке переложить еще одну палочку. Получается три палочки и две. Таким образом, три и два – это тоже состав числа пять. Далее следует переложить еще одну палочку. Получается один и четыре. Это также состав числа пять.

12. С какой целью учитель предлагает систему заданий вида:

а) прочитать запись 5+3=8 слева направо и справа налево?

Для того, чтобы у детей формировался правильный математический «язык», умение правильно читать математические записи.

б) дополнить записи числами 5+3=; + =8; 5 + =8?

Для умения понимать состав числа 8, для запоминания чисел при сложении (чтобы позже называть уже устно).

 

 

 

 

 

 

 

 

 

 

 

 

 

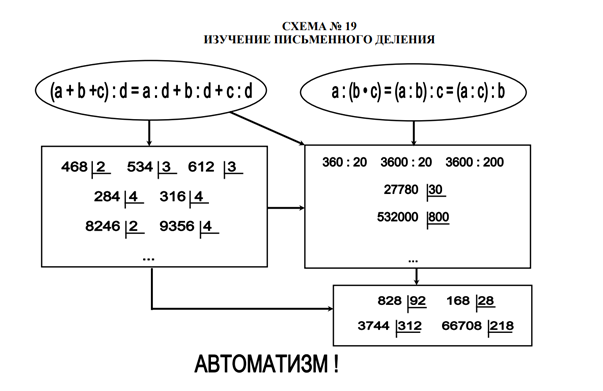
Задания к схеме №19

1. По аналогии с заданиями для других схем по изучению арифметических

действий самостоятельно сформулируйте вопросы к данной опорной схеме.

Назовите компоненты схемы?

Что обозначают стрелки, соединяющие прямоугольники?

Можно ли их направить в противоположную сторону?

Почему каждый из овалов соединен стрелкой с каким-либо прямоугольником? Можно ли эту стрелку повернуть в противоположное направление? Что будет обозначать данные стрелки?

Как вы понимаете смысл слова «автоматизм»?

2. Сравните все опорные схемы по изучению арифметических действий и

сделайте несколько выводов об общности принципов построения обучения

младших школьников устным и письменным вычислениям.

Изучение арифметических действий во всех опорных схемах построено поэтапно, с изучения самого лёгкого, переходя к сложному, начиная с правил (теории), затем прорешивая примеры (практика).

 

 

 

 

3. Какое практическое применение в теме "Письменное деление" находят

правила: деления суммы на число, деления числа на произведение.

Чтобы разделить сумму на число, можно каждое слагаемое разделить на это число, а полученные частные сложить. (6 + 4): 2 = 6: 2 + 4: 2.

4. Выделите элементы нового на уроке ознакомления с алгоритмом письменного деления на однозначное число? Как, в связи с этим можно подвести

детей к новой форме записи деления?

При делении на числа дети должны уметь образовывать деление и устанавливать число цифр частного.

5. Почему отработке навыка применения алгоритма письменного деления

на однозначное число следует уделять особенно много внимания?

Обработке навыка применения алгоритма письменного деления на однозначное число следует уделять особенного много внимания, так как деления изначально изучается на однозначное число, и в дальнейшем, чтобы дети не путали с делением на двузначное и на трёхзначное число.

6. Какие новые операции включаются в алгоритм письменного деления на

двузначное (многозначные) число? Предложите виды упражнений для отработки умения выполнять только эти новые операции.

Задание 1.  Если необходимо решать примеры с делением двузначных чисел, то лучше всего использовать метод подбора. Но как он работает? Рассмотрим, например, такое выражение: . Будем решать его, рассуждая так. Умножим делитель на 2, получим 58 и сравним его с делимым.

.

Если полученное число меньше делимого, необходимо увеличивать число, на которое умножаем делитель, до тех пор, пока не получим нужное произведение, которое совпадает с делимым.

.

Таким образом:

.

Задание 2.

Зачеркните пример с ошибкой:

38: 19 = 2

42: 14 = 2

64: 16 = 3

Ошибка в примере 42: 14 = 2 и 64: 16 = 3.

Задание 3.

Вставьте пропущенные числа:

54: 27 = ____, так как 27 ∙ ___ = 54;

Ответ: 54: 27 = 2, так как 27∙ 2 = 54.

Задание 4.

Расшифруйте, расставляя ответы в порядке возрастания, название одного из самых высоких деревьев в мире:

Я 78: 26

С 99: 33

В 78: 13

Й 64: 16

К 84: 12

О 70: 14

Е 88: 11

Ответ:

11 8 7 6 5 4 3

С Е К В О Й Я

7. Какое место в системе изучения письменного деления занимают случаи

деления с остатком?

Деление с остатком вводится после внетабличного умножения и деления и является подготовкой к письменному делению многозначных чисел. Для того чтобы учащиеся хорошо усвоили новый материал, им необходимо знать из ранее пройденного такие вопросы: 1) смысл деления; 2) табличные случаи деления без.

8. Каким способом выполняется деление значений величин, т.е. именованных чисел на отвлеченные числа? Какое место в системе обучения

письменному делению занимают такие виды заданий?

При делении именованного числа на отвлеченное частное есть число именованное, ибо в этом случае разбивают, или разделяют, делимое на несколько равных частей.

Чтобы разделить именованное число на отвлеченное, нужно начинать деление с единиц большего наименования.

Если делитель не содержится или если получается остаток, раздробляют единицы большего в единицы следующего меньшего наименования, к полученному произведению присоединяют однородные единицы делимого и разделяют на делитель.

С остатком поступают подобным же образом и продолжают деление до тех пор, пока не получат полного частного.

 

9. Объясните целесообразность такого построения изучения письменного

умножения и письменного деления, когда сразу же после рассмотрения случая умножения на однозначное число (на разрядные числа, на двузначные

и многозначные числа) вводится аналогичный случай деления.

На каждом этапе целесообразно изучать сначала умножение, затем деление. Это благоприятствует усвоению обучающимися начальной школы каждого арифметического действия в их взаимосвязи, формирует у них познавательный интерес к изучаемой теме.

10. В каких случаях деления сначала находят пробные цифры частного, а

потом окончательные? Почему их называют "пробные"? Проверку пробной цифры частного осуществляют путем умножения на делитель. Нужно ли

в этих случаях произведение вычислять или достаточно только прикинуть

его границы?

понятие «пробная цифра частного», т.е. рассматриваем случаи, когда при округлении делителя получаем такую цифру, которая не подходит, следовательно, её нужно либо увеличить, либо уменьшить. Её называют пробной цифрой. В этих случаях нужно вычислять произведение.

11. В каких учебных ситуациях, по вашему мнению, можно и даже очень полезно предложить учащимся выполнить деление многозначных чисел на

калькуляторе?

Использование калькулятора позволяет детям быстро выполнить задание, а учителю проверить и обсудить различные варианты, предложенные учащимся. Калькулятор может заменять работу с кассой цифр, обеспечив оперативность при выполнении заданий. С этой же целью калькулятор можно использовать при формировании умения переводить предметные действия на язык математических символов.

12. Известно, что чаще всего учащиеся допускают ошибки в тех случаях

письменного деления, когда в частном получаются нули (в середине или в

конце). Какие методические приемы способствуют предупреждению подобных ошибок?

Ошибки в письменном делении на двузначное и трехзначное число, обусловленные неправильной записью неполных произведений, например:

Для предупреждения таких ошибок необходимо, чтобы ученики хорошо усвоили, почему второе неполное число начинаем подписывать под десятками. С этой целью на этапе ознакомления с приемом надо добиться, чтобы ученики, выполняя деление, давали развернутое объяснение.

Скачано с www.znanio.ru