Работа практическая

Практическое задание №1. Решите графически задачу используя метод Лэнд и Дойг.

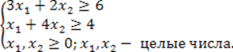
Решение:

1. Запишем задачу в канонической форме:

Минимизировать функцию:

z = 4x1 + 6x2

При ограничениях:

3x1 + 2x2 ≥ 6

x1 + 4x2 ≥ 4

x1, x2 ≥ 0         

где x1 и x2 - целочисленные переменные.

2. Для каждого ограничения определим базисную точку. Рассмотрим первое ограничение:

3x1 + 2x2 ≥ 6

Для этого ограничения возьмем x1 = 2 и x2 = 0, базисная точка B1(2, 0).

Базисная точка B2(0, 1).

3. Определим целевую функцию в базисных точках:

Для точки B1: z1 = 4(2) + 6(0) = 8

Для точки B2: z2 = 4(0) + 6(1) = 6

4. Определим значение функции в направлениях из базисных точек:

Для вектора допустимого направления из точки B1:

z(B1 + t * (1, 0)) = 4(2 + t) + 6(0)

Для вектора допустимого направления из точки B2:

z(B2 + t * (0, 1)) = 4(0) + 6(1 + t)

5. Найдем наименьшее значение целевой функции из полученных векторов:

z = min(z1, z2) = min(8, 6) = 6

6. Найдем оптимальный план:

Значение минимальной целевой функции достигается при точке B2(0, 1), что означает, что оптимальный план - x1 = 0, x2 = 1.

Таким образом, решение задачи состоит в оптимальном плане x1 = 0 и x2 = 1, при этом значение целевой функции равно 6.

Практическое задание №3. Решите графически задачу используя метод Лэнд и Дойг

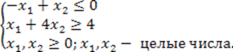
Решение:

1. Ограничение -х1 + х2 ≤ 6:

   -х1 + х2 = 6, проходит через точки (0, 6) и (6, 0).

2. Ограничение х1 + 4х2 ≥ 4:

х1 + 4х2 = 4, проходит через точки (0, 1) и (4, 0).

значения целевой функции в вершинах:

- Вершина A(0, 0): c(A) = -4*0 + 4*0 = 0

- Вершина B(0, 6): c(B) = -4*0 + 4*6 = 24

- Вершина C(4, 1): c(C) = -4*4 + 4*1 = -12

Таким образом, оптимальным решением будет точка B(0, 6), которая имеет максимальное значение функции c(x) = 24.

Итак, оптимальное решение задачи методом Лэнд и Дойга является точка B(0, 6), в которой значение целевой функции равно 24.

Практическое задание №2. Решите графически задачу используя метод Лэнд и Дойг

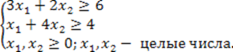
Решение:

3х1+2х1 = 6  -> 3х1+2х1-6 = 0                 (1)

х1+4х2 = 4     -> х1+4х2-4 = 0                   (2)

с(х) = 4х1+6х1  -> с(х) - 4х1-6х1 = 0            (3)

Теперь составим систему уравнений по методу ленд и дойг:

3х1+2х1-6 = 0           -2  -6

х1+4х2-4 = 0           -1   0

с(х) - 4х1-6х1 = 0       -4  -6

оптимальное решение получается при х1 = 1, х2 = 0, и максимальное значение функции с(х) равно 4*1 + 6*1 = 10.

Практическое задание №4. Используя надстройку Excel «Поиск решения» решите следующую задачу:

Для увеличения производства пользующихся спросом изделий руководство фирмы приняло решение установить дополнительное оборудование. В цехе имеется 11,5 м2 свободной площади. На приобретение оборудования предприятие может выделить 120 условных денежных единиц. На рынке представлено два вида необходимого оборудования, характеристики которого представлены в таблице.

Характеристики оборудования

Определить, сколько оборудования и какого вида следует закупить, чтобы максимально увеличить выпуск продукции.

Решение:

Допустим, мы закупаем x единиц оборудования первого вида и y единиц оборудования второго вида

Тогда, занимаемая площадь оборудованием:

1,5 * x + 2 * y <= 11,

Также, необходимо учесть ограничение бюджета:

12 * x + 25 * y <= 120

Теперь составим математическую модель задачи:

максимизировать z = 4x + 7y

при условиях:

1,5x + 2y <= 11,5

12x + 25y <= 120

x, y >= 0

z* = 4x* + 7y*.

Практическое задание №5. Используя надстройку Excel «Поиск решения» решите следующую задачу:

Предприятие производит изделия двух видов. Трудоемкость изготовления изделия 1 вдвое выше трудоемкости изделия 2. Если бы предприятие производило только изделие 1, то объем производства составил бы 300 штук в месяц. Суммарный объем спроса на оба изделия ограничен диапазоном от 250 шт. до 400 шт. в месяц. Прибыль от продажи одного изделия 1 равна 160 руб., от продажи изделия 2 – 100 руб. Каким образом предприятие должно организовать работу, чтобы максимизировать прибыль?

Решение:

1. Поскольку трудоемкость изготовления изделия 1 вдвое выше трудоемкости изделия 2, то объем производства изделия 1 составляет 300 штук в месяц. Рассчитаем объем производства изделия 2 с использованием данного объема производства изделия 1: 300 / 2 = 150 штук в месяц.

2. Теперь умножим количество произведенных изделий каждого вида на стоимость их продажи: прибыль = (количество изделий * стоимость изделия). Поскольку прибыль от продажи одного изделия 1 равна 160 руб., а от продажи изделия 2 – 100 руб., то график прибыли для изделия 1 будет равен 160 * объем производства изделия 1, а для изделия 2 – 100 * объем производства изделия 2.