Равноускоренное прямолинейное движение 10 класс

Урок 3-5. Перемещение, скорость, ускорение. Равномерное прямолинейное движение. Равноускоренное прямолинейное движение. § § 4 – 10 (конспект + ответы на вопр. письменно)

Проблемный вопрос: С чего начинается движение?

Задание «Исторические сведения»

Текст.

Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:

• о разыскании касательной к произвольной линии;
• о разыскании скорости при произвольном законе движения.

Еще раньше понятие производной встречалось в работах итальянского математика Николо Тартальи (около 1500 – 1557гг.) – здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.

В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной.

Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л.Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

http://www.krugosvet.ru/images/1012636_image008.gif

Мгновенная скорость о разыскании скорости при произвольном законе движения.

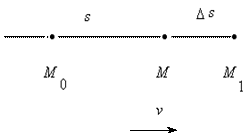
Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M₀ , зависит от времени t , т.е. s есть функция времени t: s = f(t). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M₀, а в некоторый следующий момент t + ∆t оказалась в положении M₁ – на расстоянии s + ∆s от начального положения (см. рис.1)

Таким образом, за промежуток времени ∆t расстояние s изменилось на величину ∆s. В этом случае говорят, что за промежуток времени ∆t величина s получила приращение ∆s. (изменение «на»)

Отношение  представляет собой среднюю скорость движения точки за время ∆t:ν_ср = .

Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t. Если, например, тело в начале промежутка ∆t перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t. Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени ∆t. Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при ∆t → 0, как бесконечно малая величина. Этот предел называют скоростью движения в данный момент:

ν = .

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути ∆s к приращению времени ∆t, когда приращение времени стремится к нулю. Так как ∆S = f (t + ∆t) - f(t),

то ν = .

 В жизни, мгновенной скоростью движения автомобиля, является скорость на спидометре в данный момент времени.

Вопросы:

1. Назовите имена учёных, которые участвовали в создании производной. Что их к этому подвигло?

2.Почему в физике существует необходимость говорить о мгновенной путевой скорости?

3. Автомобиль едет по закруглённому участку дороги, обладает ли он мгновенной скоростью? Почему?

4. Зная решение задачи о мгновенной скорости движения, предположите ключевые слова к понятию «производной».

1. Средней путевой скоростью называется физиче­ская величина, равная отношению величины пройденного телом пути ко времени, в течение которого этот путь был пройден.

Если обозначить путь буквой s, время – буквой t, a среднюю путевую скорость буквой υ, получим следующую формулу:

                   .                                              

2. Движение называется равномерным, если за любые равные промежутки времени тело проходит одинаковые пути.

Путевой скоростью равномерного движения называется величина, равная отношению пути s ко времени t, за которое этот путь был пройден

.

Если тело начало равномерное движение по заданной траектории из координаты х₀ в момент времени t₀ с путевой скоростью υ, то его координата х в момент времени t > t₀ будет равна

х(t) = x₀ + υ(t – t₀),

если движение происходит в положительном направлении, и

х(t) = x₀ – υ(t – t₀),

если движение происходит в отрицательном направлении.

 3. Мгновенной путевой скоростью называется  величина, равная отношению  при, где Ds – приращение пути, пройденного телом за время Dt.

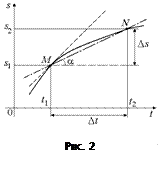Секущая  к  графику  s(t),  проходящая  через  точки М (t₁;s₁) и  N (t₂;s₂) представляет собой график равномерного движения (рис. 2), скорость которого равна средней путевой скорости на интервале времени [t₁; t₂].  Чем круче идет секущая MN, т.е. чем больший угол a она составляет с осью t, тем бóльшую среднюю скорость имеет тело на участке [t₁; t₂].

Если устремить Dt к нулю, секущая превратится в касательную к графику s(t).

Чем больше угол наклона касательной к графику s(t), тем больше мгновенная путевая скорость в данный момент.

4. Мгновенной скоростью по направлению (проекцией скорости)  υ_х  называется  величина, равная  отношению  при Dt ® 0, где Dх – изменение координаты, а Dt – промежуток времени, в течение которого это изменение произошло.

Связь между мгновенной путевой скоростью υ и мгновенной скоростью по направлению υ_х:

υ = | υ_х |.

5. Средним путевым ускорением называется величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло:

.

6. Мгновенным путевым ускорением  называется величина, равная отношению:  при Dt ®0, где Dυ – изменение мгновенной путевой скорости, а Dt – промежуток времени, в течение которого это изменение произошло.

Если тело движется так, что его мгновенное путевое ускорение положи­тельно: а > 0, то такое движение называется ускоренным.

Если тело движется так, что его мгновенное путевое ускорение отри­цательно: а < 0, то такое движение называется замедленным.

Ускоренное движение называется равноускоренным, если среднее путевое ускорение   одинаково за любой промежуток времени Dt.

Замедленное движение называется равнозамедленным, если среднее путевое ускорение   одинаково за любой промежуток времени Dt.

7. Средней проекцией ускорения на данное направление или средним ускорением по направлению за время Dt называется величина, равная отношению изменения проекции скорости  Dυ_х ко времени Dt, за которое это изменение произошло:

.

8. Мгновенной проекцией ускорения на данное направление или мгновенным ускорением по направлению называется величина, равная:

  при Dt ®0,

где Dυ_х – изменение мгновенной скорости по направлению за время Dt.

Отсюда вытекает, что справедливо  соотношение:

Урок 3-5.Справочные материалы.                                               

Проблемный вопрос: С чего начинается движение?

Кинематические уравнения равнопеременного движения.

Движение по данной траектории называется равнопеременным, если среднее ускорение по направлению  одно и то же за любой промежуток времени Dt.

Вывод: ответ на проблемный вопрос….

Элементы Начала математического анализа.

Решить задачи.

1. Координата тела х меняется с течением времени t согласно закону х = 4-2t. Все величины выражены в СИ. Определите проекцию υ_х скорости этого тела.

2. Координата тела х меняется с течением времени t согласно закону х = 4+3t-5t². Все величины выражены в СИ. Определите проекцию а_х ускорения этого тела.

Задачи легкие

А1. По графикам зависимости мгновенного путевого ускорения от времени (рис. 5.9) указать промежутки времени, в течение которых движение: 1) ускоренное; 2) замедленное. Движение происходит вдоль естес­твенной траектории в одном направлении.

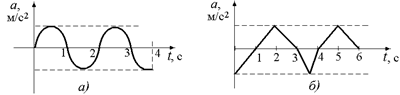
Рис. 5.9

Задачи средней трудности

В3. Тело двигалось вдоль оси х в соответствии с графиком, показанном на рис. 5.11. В какие моменты времени путевое ускорение а и ускорение по напра­влению а_х  положительны и в какие отрицательны? В какие моменты времени движение этого тела ускоренное и в какие – замедленное?

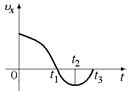 Ответы: 1. -2 м/с; 2. -10 м/с²

А2. а) a(t) > 0, при t Î (0; 1); t Î (4; 5); t Î (6; 10).

В3. (0; t₁) а_х < 0; а < 0; замедленное.

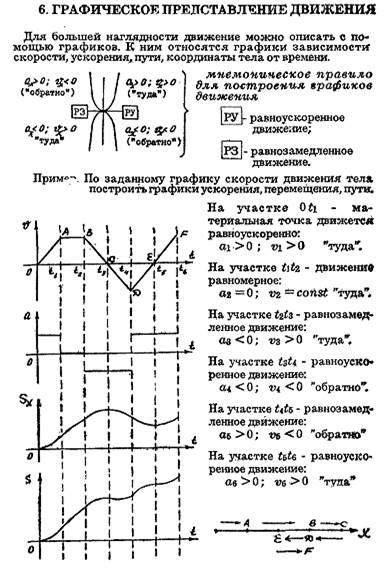
Пример 1. По графику х = х(t)  на рис. 4.7,а  построить график s = s(t).

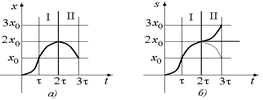      Рис. 4.7

График  х = х(t)  состоит из двух участков:  на первом участке [0; 2t]  х(t) воз­растает, а на втором участке [2t; 3t] – убывает, т.е. тело движется в отрицательном направлении оси х. Поэтому для построения графика s = s(t) первую часть графика х = х(t)  мы оставляем без изменения, а вторую часть зеркально отражаем относительно прямой, проходящей через точку поворота (2t, 2х₀) параллельно оси t (рис. 4.7,б).

Утверждение. Пусть дан график зави­симости υ_х(t), х(t₁) = x₀ (рис. 4.8). Значения площадей над графиком s⁺ и под гра­фиком s^–, выраженные с учетом масшта­бов в единицах длины, известны. Тогда путь, пройденный за промежуток времени [t₁, t₂], равен:

s = s^–+ s⁺.                        (4.2)

Координата в момент времени t₂ равна:

х(t₂) = x₀ – s^–+ s⁺.                 (4.3)

Задача 2. По графику зави­симости координаты от времени (рис. 4.9,а) построить графики зависимостей υ_х = υ_х(t)  и  υ = υ (t).

Решение. Рассмотрим промежуток времени [0; 1]. На этом промежутке  Dх = = 1 м, Dt = 1 с, отсюда = 1 м/с, υ = = |υ_х| = 1 м/с.

Рассмотрим  промежуток  времени  [1; 2]. На этом промежутке  Dх = 0, значит, υ_х = υ = 0.

Рассмотрим  промежуток  времени  [2; 3]. На этом промежутке Dх = (–2) – 1 = = –3 м, Dt = 1 с, значит,   = –3 м/с,  υ = |υ_х| = 3 м/с.

Рассмотрим  промежуток  времени  [3; 4]. На этом промежутке Dх = 0, следовательно, υ_х = υ = 0.

Графики приведены на рис. 4.9,б и 4.9,в.

СТОП! Решите самостоятельно: В3 (а,б,в).

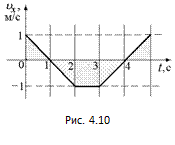Задача 3.  По графику зависимости υ_х = υ_х(t) (рис. 4.10) найти  значения  пройденного пути и координаты в моменты времени 1c,  2 с, 3 с, 4 с, 5 с, если х(0) =  2,0 м.

Ответ: s(1) = 0,5 м,  s(2) = 1 м, s(3) = 2 м,  s(4) = 2,5 м, s(5) = 3 м;

х(1) = 2,5 м,   х(2) = 2 м,  х(3) = 1 м,  х(4) = 0,5 м, х(5) = 1 м

 Домашнее задание. Оформить решение задач и решить Задачу 3. (повторить формулы площадей геометрических фигур).

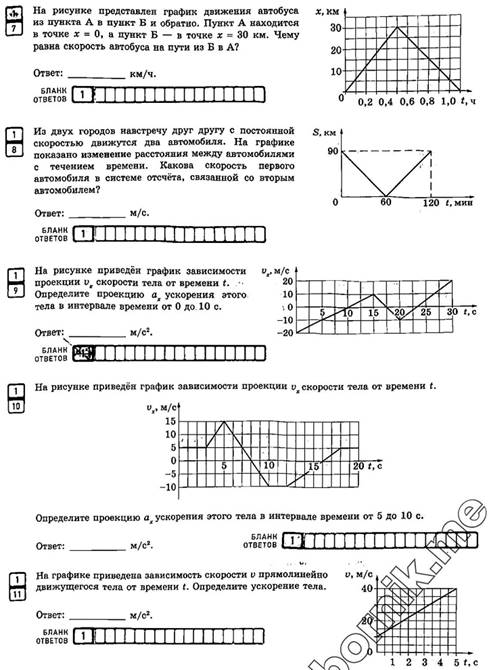
Урок 3-5. Тренировочные задания.

Типовые задания.

Ответы:

Скачано с www.znanio.ru