РАЗЛОЖЕНИЕ РАЗНОСТИ КВАДРАТОВ НА МНОЖИТЕЛИ

Разложение разности квадратов на множители

Цель: изучить формулу разности квадратов и формировать умение её применять при разложении на множители многочленов.

Ход урока

I. Устная работа.

1. Представьте в виде квадрата двучлена.

а) 81х²;                           в) 4с¹⁰;                                  д) b¹²;

б) a⁴;                        г) 0,0009п⁸;                        е) 1,44а²х⁶.

2. Выполните умножение.

а) (х – 8) (х + 8);                                  в) (2х² – 1) (1 + 2х²);

б) 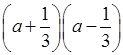;                            г) (c³ + 5) (5 – c³).

II. Проверочная работа.

Вариант 1

Упростите выражение.

а) (а + 11)² – 20а;                               в)

б)              г) (х – 1) (х + 1) – (y + 1) (y – 1).

Вариант 2

Упростите выражение.

а) 4х² – (х – 3y)²;                                 в)

б)                 г) (a + 2) (a – 2) – (b – 2) (2 + b).

III. Объяснение нового материала.

1. Актуализация знаний.

– Что значит «разложить многочлен на множители»?

– Какие вы знаете способы разложения многочлена на множители?

– Как разложить на множители трёхчлен, используя формулу квадрата суммы или разности?

На доску выносится запись: 

2. Вывод формулы разности квадратов.

На доску выносится запись: 

3. Рассмотрение примеров.

IV. Формирование умений и навыков.

1. № 883.

К доске вызываются сразу несколько учащихся, остальные выполняют задания в тетрадях.

2. № 885.

Решение:

а)

г)

е) (0,8x – 0,7y) (0,8x + 0,7y);

ж)

1. № 886.

Решение:

г)

е)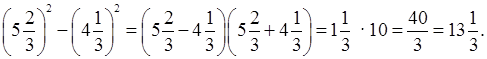

2. № 887.

Решение:

а)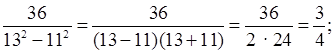

б)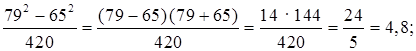

в)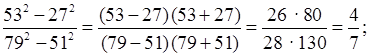

г)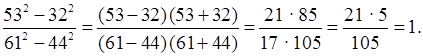

V. Итоги урока.

– Какие существуют способы разложения многочленов на множители?

– Как разложить на множители разность квадратов?

– Можно ли разложить на множители следующие многочлены:

а)  – x²;                                   в) –п² + 121;

б) а² + 9;                                    г) –x²y² – 49?

Домашнее задание: № 884, № 888.