Практическая работа № 30.

Тема: Алгоритмизация.

Наименование: Разработка алгоритмов с разветвляющейся структурой.

Цель работы: Ознакомить с различными способами записи алгоритма и видами алгоритмов. Научить составлять алгоритмы с разветвляющейся  структурой.

1. Краткие теоретические сведения.

Существует широкий круг задач, при решении которых необходимо сделать определенный выбор в зависимости от выполнения некоторых условий. Процесс решения таких задач описывается алгоритмом, тип  которого определяется как разветвляющийся.

Разветвляющимися называются такие алгоритмы, в которых выбирается один из нескольких возможных путей (вариантов) вычислительного процесса.

Структура ветвление существует в вариантах:

• если—то;
• если—то—иначе;                                                                                                   Таблица 1

если условие

   то действия

если условие

   то действия 1

   иначе действия 2

Примеры структуры ветвление                                                    Таблица 2

если x > 0

   то y := sin(x)

если a > b

   то a := 2*a; b := 1

   иначе b := 2*b

все

Задача: если с клавиатуры вводим число³0, то на экран выводится значение квадратного корня этого числа, иначе – возводится в квадрат.

Дано: х – значение аргумента

Требуется: y – значение функции (значение квадратного корня или квадрат числа).

Математическая модель этой задачи:

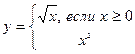
Запишем алгоритм на алгоритмическом языке

алг Вычисление (вещ x, y)

       арг x

       рез y

нач

если х ³0,

то y:=

иначе y:=x^2

все

кон

Составим графическую форму:

На схеме наглядно проявляется важное свойство разветвляющихся алгоритмов: их исполнение  всегда проходит только по одному из возможных путей, который определяется конкретными текущими условиями, причем в каждом случае от начала алгоритма до его конца.

Это свойство присуще всякому логически правильно составленному алгоритму и является признаком правильной организации ветвлений.

2. Задания.

1. Внимательно изучите теоретический материал.

2. Определите по условию форму ветвления и обозначьте ее (полная или неполная).

а) если m<n, то S=S+5;

б) при k=0 d=3,25 , иначе d= -3,25;

в) при S=5 найти R=3S², при других значениях S   R=2S³;

г) T=1 при x<0 и T=12 при других x;

д) если p>g, то p-максимальное, иначе p- минимальное;

е) если x=t, то a=x²;

ж) если a=b, то это квадрат, иначе - прямоугольник;

з)

3. По записи на алгоритмическом языке определите форму ветвления: Запишите эти алгоритмы в виде блок-схем.

а)

если t1<t2

то min:=t1

иначе min:=t2

все 

б)

если k=5

то Z:=2

все

в) 

если b=a

то с:=(2*b)^2

все

4. Запишите алгоритмы решения задач в виде блок-схем и на алгоритмическом языке.

а) Найдите значение выражения учитывая, что делить на ноль нельзя.

б) Определите минимальное среди чисел a и b.

в) Успеет ли пассажир доехать за t часов до города, расположенного за S км на автомобиле, который едет со скоростью 60 км/ч?

Вопросы:

1. Решение каких задач требует составления разветвляющихся алгоритмов?

2. Сформулируйте характерный признак правильности организации ветвлений?

3. Оформление отчета:

1. Переписать определение разветвляющегося алгоритма, типы структур ветвления, таблицы 1 и 2  из методического пособия в тетрадь.

2. Выполнить п. 2, 3 и 4 задания.

3. Дать ответы на вопросы задания и объяснить их.

4. Контрольные вопросы.

1. Какие способы записи алгоритма вы знаете?

2. Как различаются разветвляющиеся алгоритмы по структуре?

3. Какие типы алгоритмов вы знаете?