Разработка урока по математике 6 класс по теме "Осевая симметрия"

Конспект урока «Осевая симметрия»

Работу выполнила:

Мареева Элеонора Олеговна

2021 г.

Конспект урока «Симметрия»

Учитель: Мареева Элеонора Олеговна

Предмет: математика

Класс: 6

Тема урока: «Осевая симметрия»

Цели урока:

Образовательные: создание условий для формирования умений определять симметрию точек (фигур) относительно прямой, строить симметричные точки (фигуры) относительно прямой, формировать навыки самостоятельного приобретения знаний;

Развивающие: развитие логического мышления, умений анализировать, сравнивать, сопоставлять, делать выводы;

Воспитательные: воспитание трудолюбия, целеустремленности, положительного отношения к предмету.

Образовательные ресурсы: презентация, раздаточный материал (карточки, кроссворд и т.д.), толковые словари.

Структура урока

1.                 Организационный момент. Мотивация

Добрый день, ребята! Верите ли вы в чудеса?

В каком жанре литературы они чаще всего происходят? (отвечают: сказка).

А возможны ли чудеса в математике? (отвечают да или нет).

Сегодня мы вместе с вами постараемся доказать, что чудесные вещи есть и в математике. Для этого я приглашаю вас в путешествие по сказке «Королевство кривых зеркал», мы станем её главными героями. По сюжету сказки герои передвигались в одиночку или по парам. Вы перед началом урока разбились на пары.

Автором этого замечательного произведения является Виталий Губарев.

Все зеркала в королевстве кривые и изображения в них искажаются.  Высокий красивый мальчик может отражаться в зеркале маленьким, толстым и некрасивым. Кусочек хлеба может отражаться в зеркале большим праздничным тортом. В королевстве есть только лишь одно прямое зеркало, отражающее действительность. Это зеркало надёжно спрятано в тронном зале короля.

Скажите, что нам нужно, чтобы открыть дверь? (отвечают: ключ).

Но заполучить ключ от двери тронного зала  не так уж и просто. Король Йагупоп 77 держит ключ у себя, чтобы никто не смог увидеть зеркало, отражающее правду. Ключ он доверит только самым умным и сообразительным. Король объявил поиск математиков, которые будут ему помогать выполнять задания. Но король очень хитрый. Он сделал дубликат ключа и разрубил его на несколько частей. На ваших столах есть шаблон ключа (Приложение 1).. Чтобы получить часть ключа король Йагупоп прислал нам первое задание.

2. Введение в тему, актуализация знаний и фиксация затруднений. Проблемная ситуация.

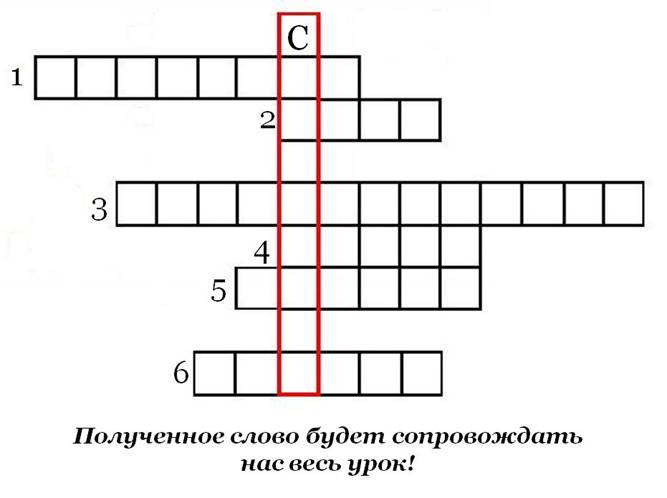
На ваших партах лежит кроссворд (Приложение 2). Отгадывая кроссворд, вы вспомните ранее изученный материал, который пригодятся нам на сегодняшнем уроке (работа в парах). Даю вам 2 минуты. Время пошло……Итак, давайте проверим, что у вас получилось. (Выдаются части ключа).

Получилось слово симметрия. Это слово будет с нами на протяжении всего урока-путешествия!

Вам знакомо понятие симметрия? Кто-то сможет сказать, что такое симметрия?

Значит, точного определения вы не знаете и сформулировать не можете. Ну, ничего! Король Йагупоп был благосклонен и прислал нам в помощь различные источники информации. На каждом столе лежит толковый словарь. Как вы заметили, они есть не у всех. Я же вам говорила, что король очень хитрый. Но мы его обхитрим, мы же с вами одна команда. Давайте объединимся в группы и посмотрим в словарях. Время на выполнение 3 минуты. Приступайте!

Итак, кто готов дать ответ, что же такое симметрия?

В древности слово симметрия употреблялось как «красота», «гармония». Хочу обратить ваше внимание на произношении слова. Вы можете услышать, что некоторые люди могут говорить симметрия, а правильное произношение симметрия. Известный немецкий математик Герман Вейль дал такое определение симметрии: «Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство». Симметрия окружает нас повсюду. Красоту и гармонию мы можем наблюдать в архитектуре, одежде, быту. Так же симметрия существует в природе.

Король Йагупоп прислал нам очередное задание. На ваших рабочих местах лежит конверт №1. В нём находятся представители природы (Приложение 3). Давайте попробуем выяснить, действительно ли они симметричны? Даю вам время 2 минуты.

Как вы это выяснили? Правильно, мы можем согнуть их пополам. Есть фигуры, которые некрасивые, негармоничные, т.е. несимметричные? Как вы поняли, что фигуры несимметричны? Всё верно, при сгибании мы наблюдаем, что их части не совпадают друг с другом. Посмотрите внимательно на слайд и фигурки, которые вы сгибали. Что у них есть общего? Правильно линия сгиба. Можем мы назвать линию сгиба прямой? Да. Значит, у нас получилась симметрия относительно прямой. Такая симметрия называется осевой. Давайте откроем тетради, запишем число, классная работа и тему урока — Осевая симметрия.

3. Открытие нового знания. Реализация построенного знания.

Как вы думаете, существует ли красота в математике?

Предлагаю провести эксперимент. На ваших рабочих местах есть конверт № 2. В нем — бумага и зубочистка. Возьмите лист бумаги и согните его пополам. Разогните лист. Проведите прямую по линии сгиба. Согните лист обратно. Проткните сложенный лист зубочисткой. Развернув лист, вы увидите две точки, расположенные по разные стороны линии сгиба. Обозначьте точку в правой стороне точкой А, а в левой стороне точкой В. Проведите через полученные точки прямую и обозначьте её буквой . Обозначьте пересечение прямых точкой О. Что вы можете сказать о расположении полученных точек? Они находятся на одинаковом расстоянии. Это можно выяснить при помощи циркуля. Получаем равные отрезки АО и ОВ. Но это ещё не всё. Как называется отрезок, который вы измеряли? Посмотрите внимательнее на чертёж. Если вы затрудняетесь ответить, король Йагупоп оставил нам в качестве подсказок кроссворд. Посмотрите кроссворд. Перпендикуляр. С помощью угольника вы можете убедиться, что прямая перпендикулярна линии сгиба, а точки находятся от неё на одинаковом расстоянии. Это важное свойство симметричных точек. С его помощью можно строить точки, симметричные относительно некоторой прямой, и без перегибания листа бумаги.

Существует алгоритм построения точек, симметричных относительно некоторой прямой.

Пусть дана прямая  и точка M, не лежащая на этой прямой. Построим точку К, симметричную точке М относительно прямой .

1.                 Проведём через точку М перпендикуляр к прямой 𝑙 и обозначим его МО.

2.                 Продолжим перпендикуляр МО.

3.                 Измерим расстояние от точки М до точки О.

4.                 Отложим расстояние равное МО на продолжении перпендикуляра.

5.                 Отметим точку и обозначим её К.

Точки М и К симметричны относительно прямой 𝑙.

Мы научились строить точки, симметричные относительно некоторой прямой, и король Йагупоп предлагает нам продолжить эксперимент, чтобы получить еще одну частичку ключа.

Возьмите лист бумаги. Проткните его 4 раза в разных местах. Разверните лист. У вас получились точки. Соедините точки последовательно сначала на одной стороне, потом на другой с помощью линейки. Что у вас получилось? Две симметричные фигуры. Это тоже осевая симметрия. Полученные фигуры равны между собой? Таким образом, мы получили ещё одно важное свойство осевой симметрии: если фигуры симметричны, то они равны. Давайте запишем.

Возьмите фигуры, которые вы сгибали ранее. Посмотрите на линию сгиба? Как она может проходить? Внутри фигуры, она делится на две равные части. А ещё линия сгиба может проходить вне фигуры, и получаются две равные фигуры.

А поменялось ли расположение фигур? Симметричная фигура повернулась в другую сторону. А где в жизни мы с вами можем наблюдать такое явление? Зеркало. Получается наша линия сгиба, некоторая прямая – это своего рода зеркало и осевую симметрию мы можем назвать  зеркальной. Король Йагупоп очень доволен проделанной нами работой, поэтому вы заслуженно получаете еще одну часть ключа.

4.Физкультминутка.

Хватит с вас экспериментов! Пора подумать о здоровье. Предлагаю немного размяться. Наше тело-это прямая, относительно которой должны выполнять симметричные движения.

Поднять правую руку.

Отставить левую ногу.

Сжать в кулак левую руку 10 раз.

Согнуть правую ногу, не отрывая стопу от пола (приседание).

5. Первичное закрепление с комментированием во внешней речи.

Мы с вами путешествуем по сюжету сказки «Королевство кривых зеркал». Каждый, кто попадает в королевство, становится своим отражением. Имя тоже становится отражённым как в зеркале. Попробуйте записать моё имя ЭЛЕОНОРА, как оно будет отражаться в зеркале. При этом соблюдайте своства симметрии. И не збывайте о том, что мы выяснили в нашем эксперименте. В нашем кабинет, по счастью, находиться зеркало, подходя парами проверьте себя с помощью него. Молодцы! Вы получаете часть ключа.

6. Самостоятельная работа с взаимопроверкой по эталону.

Осевая симметрия может встречаться не только в математике, но и в других учебных предметах. Например, в русском языке. В буквах русского алфавита, в словах-палиндромах. Это слова, одинаково читающиеся в обоих направлениях. Но стоит забывать про проделанные эксперименты.

Не будем терять ни минуты! Король Йагупоп отправил нам задание, за которое готов отдать сразу две части ключа! На ваших столах лежит конверт №3. В конвертах слова-палиндромы (Приложение 4).. Определите, какие из них симметричны. Время на выполнение задания 3 минуты. Приступайте! ……Итак, проверяем (выполняют взаимопроверку в соответствии со слайдом).  Поднимите руки те, у кого задание выполнено без ошибок! Вы получаете еще две частички ключа.

7. Итоги урока

У кого получилось собрать ключ? (Приложение 5). Молодцы, вы становитесь математиками  самого короля Йагупопа 77-го. И вы награждаетесь оценкой 5. Если у вас не хватило 1-2 деталей, то не расстраивайтесь, вы получаете за урок 4. Остался последний шаг — открыть таинственную дверь, за которой  спрятано единственное прямое зеркало (на слайде открывается дверь, за которой сидит король). Так вот почему король прятал единственное прямое зеркало! Он боялся, что люди узнают его настоящее имя (слайд Йагупоп-Попугай).

8. Домашнее задание.

Мы узнали тайну короля! Чтобы его развеселить, вашим домашним заданием будет следующее: записать свое имя, отраженное в «кривом» зеркале письменными буквами и печатными. Так же разделитесь на группы по три человека и подготовьте к следующему занятию сообщения «Симметрия в природе», «Симметрия в логотипах», «Симметрия в архитектуре», «Симметрия в узорах». Давайте откроем наши дневники и запишем. Вся информация, которая была дана на уроке, поможет вам выполнить домашнее задание. А король Попугай с помощью  прямого зеркала проверит ваши работы!

9. Рефлексия

Ребята, на ваших столах остался конверт №4!Давайте посмотрим, что же в нем! (открывают конверты)

Возьмите лист цветной бумаги, сложите пополам и вырежьте из нее симметричную фигуру – это открытка (Приложение 6).. Напишите на ней комплимент уроку. Оцените свою деятельность на уроке, прикрепив открытку на том уровне шкалы, на который вы сегодня поработали (Приложение 7).

Мне было очень приятно с вами работать! Спасибо за урок!

Приложение 1

Приложение 2

Приложение 3

Приложение 4

КАЗАК

МАДАМ

АННА

ТОПОТ

ОКО

ПОТОП

БОБ

ТОТ

Приложение 5

Разрезать по линиям. В итоге, получились части ключа.

В конце урока дожжен собраться ключ.

Приложение 6

Приложение 7