Разработка урока по математике «Производная и её практическое применение» /деловая игра/

Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 9» Артемовского городского округа                                                   

Разработка урока

по математике

«Производная и её практическое применение»

/деловая  игра/

Учитель высшей

квалификационной категории

Ходова С.В.

г. Артём

2023 г.

Цели урока:

Обучающие: обобщение и систематизация знаний  учащихся по теме «Производная» (основные формулы и правила дифференцирования, применение производной к исследованию функции, нахождению наибольшего и наименьшего значения функции, физический и геометрический смысл производной).

Развивающие: содействовать развитию мыслительных операций: анализ, синтез, обобщение, развитие умений применять знания на практике, находить оптимальные решения, развитие уверенности в своих силах, настойчивости, умения преодолевать трудности, добиваться намеченной цели, умения работать в коллективе, умения самооценки и взаимооценки.

Воспитательные: воспитание познавательного интереса к математике, собираться с мыслями и принимать решения,  содействовать формированию творческой деятельности учащихся, воспитывать чувство ответственности за качество и результат выполняемой работы, воспитание умения не растеряться в проблемных ситуациях.

Задачи урока:

• возбуждение и поддержание интереса к предмету;

·         воспитание ответственного отношения к учению;

• вовлечение учащихся в творческую, поисковую деятельность.

Тип урока: урок обобщения, систематизации знаний, умений и навыков.

Вид урока:  деловая игра

Формы обучения: фронтальная, индивидуальная, групповая.

Метод обучения – исследовательский метод.

Структура урока:

1. Организационный этап: проверка готовности к уроку.

2. Постановка цели и задач урока. Мотивация учебной деятельности обучающихся.

3. Актуализация прежних знаний.

4. Работа в группах. На уроке, учащиеся объединяются в пять групп по три человек. Каждая группа получает письмо от организации с заданием.

5. Защита учащимися у доски своих ответов и расчётов. Контроль усвоения, обсуждение допущенных ошибок и их коррекция. В процессе ответа у доски учащиеся отвечают на вопросы учеников других групп.

6. Рефлексия (подведение итогов занятия).

7. Анализ и содержание итогов работы, формирование выводов по изученному материалу.

Ход урока

1.       Организационный этап: проверка готовности к уроку.

2.       Нам всем кажется, что в повседневной жизни мы великолепно обходимся без математики. Не правда, ли? Но это совсем не так. Сегодня на уроке мы убедимся в этом.

Начинаем деловую игру по теме «Производная и её практическое применение». Сегодня Ваш класс – научно-расчётный центр. Вы сотрудники этого центра. Центр имеет 5отделов: отдел транспорта, отдел архитектуры, отдел экономики, поисковый отдел и отдел экономической теории. Вам предстоит защитить теоретические знания по теме «Производная», показать умения и навыки применять теоретические знания к решению практических задач.

В научно-расчётный центр пришли письма от различных организаций, которые хотят получить ответы и расчёты на интересующие их вопросы. Вы должны дать полные, обоснованные ответы и расчёты, которые потом будут отправлены заказчикам. Выступающим можно задавать вопросы по теме, помогать искать наилучшие варианты ответов.

3.       Прежде чем раздать Вам письма, давайте вспомним:

Чему равна производная суммы?

Чему равна производная степенной функции у = х³ ?

В чём заключается геометрический смысл производной?

В чем заключается механический смысл производной?

Производная от скорости по времени есть…?

Что можно сказать о производной в точке экстремума?

В каком случае функция возрастает на некотором промежутке?

В каком случае функция убывает на некотором промежутке?

Если в точке х₀ производная меняет знак с плюса на минус, то х₀ есть точка…?

Если в точке х₀ производная меняет знак с минуса на плюс, то х₀ есть точка…?

4.       Работа в группах.

Сейчас я раздам письма, которые Вы проработаете в своем отделе, после чего представитель от каждого отдела у доски даст расчёты и ответы на вопросы в письмах.

1.                 Отдел транспорта.

Уважаемые сотрудники научно-расчётного центра!

На трассе Артем-Владивосток произошла авария. Для выяснения степени виновности водителя нам необходимо знать:

а) в течении какого времени осуществлялось торможение до полной остановки машины?

б) сколько метров двигалась машина с начала торможения?

в) чему равно ускорение в любой момент времени?

Нами установлено, что тормозной путь определяется по формуле: S (t) =120t-10t³, где t (c), S (м)

С уважением сотрудники транспортной полиции г. Артема.

2.                 Отдел архитектуры.

Уважаемые сотрудники научно-расчётного центра!

Строительная фирма просит Вас помочь в решении следующей проблемы. Нам необходимо провести мост через реку. Мост имеет форму параболы у(х) = рх². Каким надо сделать уклон насыпи к мосту, чтобы переход с моста на шоссе был плавным? Пролет моста имеет длину L=20 м., стрела провеса f=0,5 м. Предлагаем чертёж нашей работы:

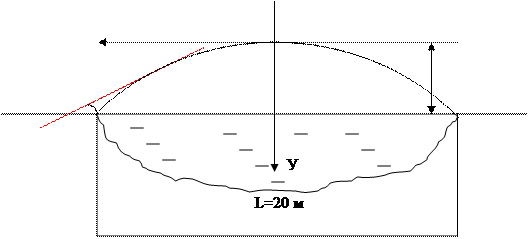                        Х                                       

                                                               О

                                                                                                f=0,5 м

                   α

Заранее Вам благодарны.

3.                 Отдел экономики.

Уважаемые сотрудники научно-расчётного центра!

В зоомагазинах используют аквариумы, имеющие форму прямоугольного параллелепипеда, для содержания в них рыб, змей, мышей, хомяков, свинок, ящериц. На завод по изготовлению стеклянной тары обращаются с просьбой изготовить большое количество аквариумов с квадратным дном объёмом 500 л. С целью экономии стекла, просим Вас рассчитать при какой стороне основания площадь поверхности аквариума (без крышки) будет наименьшей?

С уважением сотрудники  завода по изготовлению стеклянной тары.

4.                 Отдел поиска.

Уважаемые сотрудники научно-расчётного центра!

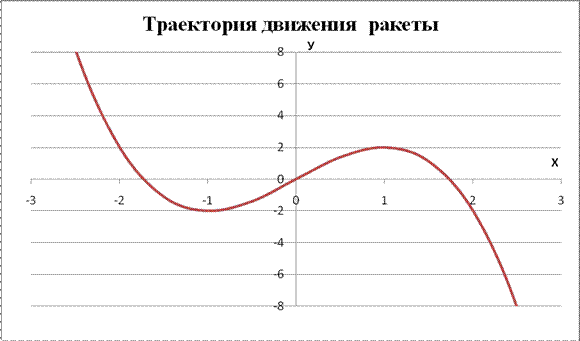
Исследователи поверхности суши и подводного пространства океана запустили ракету, которая перемещалась по закону у(х) =3х-х³. Чтобы сделать необходимые выводы, нам надо знать:

а) траекторию движения ракеты;

б) где ракета летит под водой;

в) где ракета летит над водой;

г) в какой точке ракета достигает максимальной высоты и чему она равна;

д) в какой точке ракета погружается на максимальную глубину и чему она равна;

е) в каких точках ракета входит и выходит из воды.

В нашей просьбе просим не отказать.

5.                 Отдел экономической теории.

Уважаемые сотрудники научно-расчётного центра!

Наш цементный завод по договору должен ежедневно поставлять строительной фирме не менее 20 т. цемента. Производственные мощности завода таковы, что выпуск цемента не может превышать 90 т. в день.

При каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид: К=-х³+98х²+200х. Удельные затраты составляют    .

С уважением сотрудники цементного завода.

5. Защита учащимися у доски своих ответов и расчётов.

 Отдел транспорта.

Ответ:

Воспользуемся механическим смыслом производной: производная от координаты по времени есть скорость, то есть S'(t)= V(t)=(120t-10t³)' = 120-30t².

Так как машина остановилась, то V(t)=0. Имеем:

120-30t² =0; t=±2 (с). t=-2 не удовлетворяет условию задачи, значит в течении 2 секунд осуществлялось торможение до полной остановки машины.

Найдём путь, пройденный машиной за 2 с.:

S (t) = 120t - 10t³; S (2) =120*2-10*2³ =160 (м), значит с начала торможения машина двигалась 160 м.

      Производная от скорости по времени есть ускорение, значит:

a (t)=(120-30t²)'= - 60*t

Отдел архитектуры.

Ответ:

Направление подхода к мосту должно совпадать с направлением касательной в конце моста. Нам необходимо найти угловой коэффициент касательной к графику функции  у(х) = рх² в точке (10;0,5).

Парабола проходит через эту точку, значит, её координаты удовлетворяют уравнению у(х) = рх², то есть 0,5=р10², откуда р = 0,005.

Геометрический смысл производной заключается в том, что значение производной функции y=f(x) в точке х=х₀ равно угловому коэффициенту касательной к графику функции в точке х₀, то есть  f '(x₀)=k=tg α.

Имеем: у'(х) = (рх²)'=(0,005х²)'=0,01х

у'(10)=0,01*10=0,1

k=tg α=0,1

a = arctg 0,1.

Отдел экономики.

Ответ: 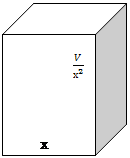                        Пусть сторона квадрата основания будет х дм.  х€(0;+∞)

                                    V=x²h, следовательно h=

                                   S_пол = S_бок+S_осн = 4xh+x² =+x²

                                              Если аквариум вмещает 500 л воды, то объём равен 500 дм³.

                              S_пол =+x² = +x²  ,    S'=2х-

На промежутке (0;+∞) критических точек нет, а стационарная только одна при х=10.

Заметим, что при х<10 S'<0, а при х>10, S' >0. Значит, х=10 – точка минимума на заданном промежутке, а поэтому в этой точке функция достигает своего наименьшего значения. Следовательно, сторона квадрата, служащего основанием аквариума, равна 10 дм.

Отдел поиска.

Ответ:

Нас просят найти траекторию движения ракеты. Для этого надо построить график функции у (х) =3х-х³.

Проведём исследование данной функции:

1.     D (у) = R, так как у - многочлен.

2.     Найдём точки пересечения графика с осями координат:

с осью ОУ:  х=0, у=0        (0;0)

с осью ОХ:  у=0, х=0 или х = ±      (0;0), (;0), (-;0)

3.     у' (х) = (3х-х³)'=3-3х

4.     у' (х) =0; х=±1

5.               -                +               -

                            -1              1                    х

6.      

Отдел экономической теории.

Ответ:

К=-х³+98х²+200х. Удельные затраты составят =-х²+98х+200

Наша задача сводится к отысканию наибольшего и наименьшего значения функции У= -х²+98х+200. На промежутке [20;90].

У'=-2х+98

-2х+98=0,  х=49 - критическая точка функции. Вычисляем значение функции на концах промежутках и в критической точке.

У (20)=1760   У (49)=2601      У (90)=920.

Таким образом, при выпуске 49 тонн цемента в день удельные издержки максимальны, это экономически не выгодно, а при выпуске 90 тонн в день минимально, следовательно можно посоветовать работать заводу на предельной мощности.  

6. Рефлексия (подведение итогов занятия). Выставление оценок.

7. Анализ и содержание итогов работы, формирование выводов по изученному материалу.

Сегодня мы выяснили, зачем нужно изучать производную, где можно использовать знания, связанные с производной в жизни. Не зря Н.И. Лобачевский сказал: «… нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…».

С помощью производной можно находить:

·       скорость, ускорение;

·       исследовать функции на монотонность и экстремумы и строить их графики;

·       находить наибольшее и наименьшее значение функции на промежутке;

·       решать задачи на нахождение наибольших и наименьших значений величин;

·       находить уравнение касательной к графику функции.