Разработка урока "Сложение и вычитание алгебраических дробей с разными знаменателями"

Предмет: Алгебра                          Дата:                                     Класс: 8

Учитель: Петрушина Е.П.

Тема: Сложение и вычитание алгебраических дробей с разными знаменателями.

Цели: 1. Сформировать знания и умения выполнять сложение и вычитание алгебраических дробей с разными знаменателями.

2. Развивать практические навыки сложения и вычитания обыкновенных дробей с разными знаменателями; умения анализировать, сопоставлять, выделять главное и переносить знания в новую ситуацию.

3. Воспитывать чувство коллективизма; формировать самооценку, коммуникатив-ные навыки. 

 

Задания для актуализации знаний.

1. ;      2.  ;    3.    ;       4.  ;                              

 

5. ;     6.  ;     7.  ;

 

8.  ;    ;      35у³.        ;     ;   

 

9.  ;

 

Эталоны:

1.Алгоритм сложения и вычитания обыкновенных дробей с разными знаме-нателями.

Чтобы сложить или вычесть обыкновенные дроби с разными знаменателя-ми, надо:

·         Привести данные дроби к наименьшему общему знаменателю.

·         Сложить или вычесть полученные дроби.

2.Алгоритм приведения алгебраических дробей к общему знаменателю.

·         Разложить все знаменатели на множители.

·          Из первого знаменателя выписать произведение всех его множителей, из остальных знаменателей приписать к этому произведению недостающие множители. Полученное произведение и будет общим (новым) знаменате-лем.

·         Найти дополнительные множители для каждой из дробей: это будут произ-ведения тех множителей, которые имеются в общем (новом) знаменателе, но которых нет в старом знаменателе.

·         Найти для каждой дроби новый числитель: это будет произведение старого числителя и дополнительного множителя.

·         Запишем каждую дробь с новым числителем и общим (новым) зна-менателем.

3. Для работы в группах.

1.   ;      2.      ;                                                             

 

3.   =0.

 

4. Для самостоятельной работы.

 

Вариант 1.

 1.    ;     

 2.    ;

 3.   

 

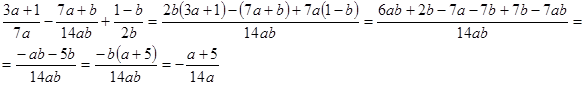
Вариант 2.

^{1.     ;} 

  ^{2.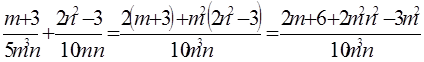 ;.             3.}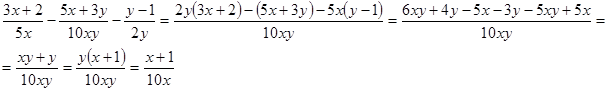                                                                   

5.Задания для включения в систему знаний и повторения:

 

1.     ;        2.    ;        3.    ;       4.      ;      

 

5.     ;        6.    ;          7.        .

6.Карточка для этапа рефлексии:

 

 1.    I----I----I----I----I----I         Владеете новым материалом в совершенстве.

 2.    I----I----I----I----I----I         Есть вопросы для уточнения.

      3.    I----I----I----I----I----I         Есть вопросы по отдельным моментам.

      4.    I----I----I----I----I----I         Не все понятно, есть еще над чем поработать.

 

7. Девиз:  Успех - это не пункт назначения, это движение.   (Т. Фастер).

 

Ход урока:

 

1. Мотивация к учебной деятельности.

Цели этапа: 

 1. Включение учащихся в учебную деятельность.(Девиз).

 2. Определение  содержательных рамок урока: продолжение работать с алгебраическими дробями.

Организация учебной деятельности на 1-ом этапе.

Учитель: Здравствуйте, ребята. Девизом нашего урока будут слова … (На экране высвечиваются слова Т. Фастера: «Успех - это не пункт назначения, это движе-ние»)

 Дома узнайте, пожалуйста, кто он такой?

-А сейчас давайте вспомним. чем мы занимались на прошлом уроке? (Складывали и вычитали алгебраические дроби с одинаковыми знаменателями).

-Сегодня мы продолжим работать с алгебраическими дробями. Все ли алгебраи-ческие дроби мы умеем складывать и вычитать? (Если сравнивать эту тему с аналогичной темой «Сложение и вычитание обыкновенных дробей», то мы не умеем еще складывать и вычитать  алгебраические дроби с разными знаменате-лями).

-Молодцы! Тогда продолжим работу? (Да).

2. Актуализация знаний и фиксация затруднений в деятельности.

Цели этапа: 

1. Актуализировать знания о выполнении действий с дробями с одинаковыми знаменателями.
2. Зафиксировать затруднение.

Организация учебной деятельности на 2-ом этапе.

На доске записано и на экране высвечиваются несколько примеров на выполнение действий с дробями:

1. ;      2.  ;    3.    ;       4.  ;        5. ;       6.    ;                     

7.   ;     8.  ;    ;      35у³.       9.  Учитель: как сложить эти дроби?

Учащиеся отвечают  и проговаривают правила к каждому примеру. На экране появляются эталоны правильных ответов.

Эталоны:

Пример 1. ;

 Чтобы сложить две дроби с одинаковыми знаменателями надо:

Сложить их числители, а знаменатель оставить тем же.

 Пример2.

Чтобы сложить две дроби с разными знаменателями надо:

-посмотреть на больший из них;

-если он делится на меньший, то берем его в качестве  ОЗ;

-найти дополнительные множители к каждой дроби;

-умножить их на числители каждой дроби;

- сложить по правилу сложения дробей с одинаковыми знаменателями.

Пример3. ;

Чтобы сложить две дроби с разными знаменателями надо:

-разложить каждый знаменатель на множители;

-выписать все множители первого знаменателя;

-и дописать к ним те множители, которых не достает в первом знаменателе;

-полученное произведение и будет искомым ОЗ;

-найти дополнительные множители к каждой дроби;

-умножить  их на числители каждой дроби;

- сложить по правилу сложения дробей с одинаковыми знаменателями.

Пример 4. ;

Чтобы сложить две дроби с разными знаменателями надо:

 т. к. здесь знаменатели взаимно простые числа, то

-ОЗ будет произведение  знаменателей данных дробей;

-дополнительными множителями будут к первой дроби знаменатель второй и нао-борот;

- умножить  их на числители каждой дроби;

- сложить по правилу сложения дробей с одинаковыми знаменателями.

 Пример 5,6.

Аналогично примеру 1.

Пример 7.  ;

Чтобы сложить две дроби с противоположными знаменателями надо:

-в знаменателе второй дроби вынести  «-» перед дробь;

- сложить по правилу сложения дробей с одинаковыми знаменателями.

Пример 8. ;    ;      35у³.        ;      

Чтобы привести две дроби к заданному знаменателю надо:

-заданный знаменатель разделить на знаменатель каждой дроби (найти дополнительные множители);

-умножить числитель и знаменатель на дополнительный множитель.

Пример 9. = ?;

Примерные слова учеников:

Я затрудняюсь выполнить этот пример т. к. здесь дроби не с одинаковыми знаме-нателями.

3. Выявление места и причин затруднений, постановка цели деятельности.

Цели этапа: 

1. Зафиксировать отличительное свойство задания, вызвавшего затруднение в учебной деятельности.
2. Сформулировать цель и тему урока.

Организация учебной деятельности на 3-ем этапе.

Учитель: Где у вас возникло затруднение? (В примере 9).

-почему не готовы дать ответ?

-я не знаю правила, по которому можно складывать алгебраические дроби с разными знаменателями;

- я не могу доказать, что выполнил сложение правильно т.к. не знаю правило сложения алгебраических дробей с разными знаменателями.

-Сформулируйте цель вашей деятельности.

Узнать правило, по которому можно складывать алгебраические дроби с разными знаменателями.

Уточняем тему урока: «Сложение и вычитание алгебраических дробей с разными знаменателями», которую ученики записывают в тетрадь, а учитель на доске.

4. Построение проекта выхода из затруднения. (?   мин.).

Цели этапа: 

1. Построение учащимися нового способа действий.
2. Фиксация алгоритма приведения алгебраических дробей к ОЗ.

Организация учебной деятельности на 4-ом этапе.

Учитель: Итак, у вас возникло затруднение при сложении алгебраических дробей с разными знаменателями.

- что вы раньше использовали, что бы сложить дроби ? (Использовали правило сложения дробей с разными знаменателями).

Фиксируем во внешней речи правило сложения обыкновенных дробей с разными знаменателями после чего (на экране появляется эталон):

а) находим НОЗ обеих дробей;

б) находим дополнительные множители и умножаем на них дроби;

в) применяем правило сложения обыкновенны дробей с одинаковыми знаменате-лями.

Шаги для реализации цели: (работа в группах). Разрезанный алгоритм сложения и вычитания алгебраических дробей с разными знаменателями.

Учитель: правильно расположите шаги алгоритма.

·         Разложить все знаменатели на множители.

·          Из первого знаменателя выписать произведение всех его множите-лей, из остальных знаменателей приписать к этому произведению недостающие множители. Полученное произведение и будет общим (новым) знамена-телем.

·         Найти дополнительные множители для каждой из дробей: это будут произведения тех множителей, которые имеются в общем (новом) знамена-теле, но которых нет в старом знаменателе.

·         Найти для каждой дроби новый числитель: это будет произведение старого числителя и дополнительного множителя.

·         Запишем каждую дробь с новым числителем и общим (новым) знамена-телем.

Группы вывешивают свои варианты алгоритма.

Проводим анализ каждого варианта, сверяя его со  слайдами эталоном – прави-лом «Как складываются и вычитаются алгебраические дроби с разными знаме-нателями».

Итак, мы с вами построили алгоритм  сложения алгебраических дробей с разны-ми знаменателями. Применим его для решения примера, с которым вы раньше не могли справится. Учитель под диктовку учащихся записывает решение примера 8 на доске.

Совместными усилиями ликвидировали затруднение.

5.Первичное закрепление во внешней речи. (?мин.)

Цели этапа:

1.Развивать навыки приведения алгебраических дробей к общему знаменателю.

2.Фиксировать во внешней речи правила сложения и вычитания алгебраических дробей .

Организация учебной деятельности на 5-ом этапе.

Фронтально: (один ученик у доски, остальные работают в тетрадях).

Ученик вслух проговаривает план решения (ученики с места или учитель могут исправлять неточности, если они были допущены).

 Пример: 

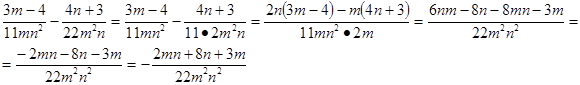
План решения может быть таким:

• т.к.. число 22 делится на 11, то наименьшим общим знаменателем будет вы-ражение 22;
• дополнительным множителем к первой дроби будет выражение 2n, а ко вто-рой m;
• перемножаем соответствующие дополнительные множители на каждый числитель;
• вычитаем данные дроби по правилу вычитания дробей с одинаковыми знаменателями.

Еще раз во внешней речи фиксируем правило сложения алгебраических дробей.

Предлагаю каждой группе сложить следующие дроби:  Примеры

 1.   ;      2.      ;           3.    .   

После окончания работы организатор или член группы показывает решение, кото-рое обсуждается всеми учениками.

А теперь немножко отдохнем (физкультминутка).

Закройте глаза, расслабьте тело,

представьте – вы птицы, вы вдруг полетели!

теперь в океане дельфином плывете,

теперь в саду яблоки спелые рвете,

налево, направо, вокруг посмотрели,  

открыли глаза и снова за дело!

6. Самостоятельная работа с самопроверкой. (? мин.) 

 Цели этапа: 

1. Провести самостоятельную работу.
2. Провести самопроверку по готовому эталону для самопроверки.
3. Зафиксировать затруднения, определить причины ошибок и исправить их.

Организация учебной деятельности на 6-ом этапе.

 Учитель: Как вы думаете, что сейчас мы должны сделать? (Проверить, как каждый из нас понял, как складывать и вычитать дроби с разными знаменателя-ми). Появляется слайд с самостоятельной работой. 

 

Вариант 1.

 1.    ;     

 2.    ;

 3.    .

 

Вариант 2.

 ^{1.     ;} 

  ^{2.   ;.}         

   ^3. .                                                               

Учитель: когда вы проделаете все по новому алгоритму необходимо вспомнить и давно изученный материал, например, приведение подобных слагаемых или сок-ращение дробей.

После выполнения самостоятельной работы проводится проверка по эталону, а так же анализ и исправление ошибок.

Вопросы учителя:

• У кого задание вызвало затруднение?
• На каком шаге?
• В чем причина возникшего затруднения?
• Кто справился со всеми заданиями?

7.Включение новых знаний в систему знаний (мин.)

Цели этапа: 

1. Повторить и закрепить изученный на уроке алгоритм сложения и вычитания алгебраических дробей с разными знаменателями.

Организация учебной деятельности на 7-ом этапе.

А теперь давайте выясним какие  действия мы можем выполнить сегодня, а какие еще не умеем?

1.     ;        2.    ;        3.    ;       4.      ;      

 

5.     ;        6.    ;          7.        .

Предполагаемые ответы: примеры 4 и 5 мы не сможем сегодня выполнить т. к. у этих дробей в знаменателях многочлены.

Учитель: эти примеры мы научимся решать на следующем уроке.

8.Рефлексия урока. (?мин.)

Цели этапа:

1. Зафиксировать новое содержание, оценить собственную деятельность.

 Организация учебной деятельности на 8-ом этапе.

• Какую цель вы перед собой ставили вначале урока? (Научиться складывать и вычитать алгебраические дроби с разными знаменателями).
• Вы достигли полученной цели? (Да. Мы узнали правило, с помощью кото-рого можно складывать и вычитать алгебраические дроби с разными знаме-нателями).
• Где вы можете применить полученные знания? (При выполнении домаш-него задания, при сдаче ГИА, а вообще, возможно, и в будущей профессии.)

А теперь возьмите ручку и напротив каждого вопроса пометьте насколько вы владеете новым материалом.

Молодцы!

Дети отмечают и показывают учителю.

Домашнее задание: § 4; № 4.7(б); № 4.13(б); №4.18(г) -всем; № 4.19(а, в)-по желанию.