Разработка урока "Умножение дробей. Возведение дроби в степень"

Учитель: Петрушина Е.П.                                                                                  Класс:8

Предмет: Алгебра                                      Дата:                                                 № урока:

Тема урока:  Умножение дробей. Возведение  дроби в степень.

Цели урока: Познакомить учащихся с  правилом умножения дробей, нахождения степени рациональных дробей. Умение выполнять указанные действия.  Развитие кругозора, мышления, любознательности, внимания, культуры математической речи, привитие интереса к изучению математики. Воспитание аккуратности, чувство коллективизма, самоконтроля.

Ход урока

I.                   Организационный момент

II.                 Мотивация

Выдающийся французский философ, ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя. А начать наш урок я хотела бы с выяснения вопроса: встречался кто-нибудь из вас в повседневной жизни со словом «степень»? Давайте приведем примеры словосочетаний из жизни, в которых оно используется, и попытаемся с их помощью разобраться, что же в жизни означает слово «степень».

Каким же близким по смыслу словом можно заменить слово “степень”?

А где мы можем уточнить его значение?

(в толковом словаре) 

       - Степень – это мера, сравнительная величина; уровень чего-нибудь.

       - Слово “степень” находит широкое применение и в математике.

III.              Актуализация опорных знаний

Сформулируйте  правило умножения дроби на дробь.

Чтобы умножить дробь на дробь, надо:

1. найти произведение числителей и произведение знаменателей этих дробей;

 2. первое произведение записать числителем, а второе – знаменателем.

При умножении и трёх и более дробей:

1.Удобнее сначала в числителе записать произведение всех числителей, в знаменателе – произведение всех знаменателей.

2.Сократить получившуюся дробь.

3.Выполнить умножение оставшихся множителей.

4.Если надо, выделить целую часть.

И соберём по капельке всё, что  учили по теме: «Степень» в младших классах.

1.     Дайте определение степени с натуральным показателем. (Степенью числа, а с натуральным показателем п, большим 1, называется произведение п множителей, каждый из которых равен а.)

2.     Как называется число, которое возводим в степень? (Число, которое возводим в степень, называют основанием)

3.     Как называется число, в которое возводим степень? (Число, в которое возводим степень, называют показателем)

4.     Какое число получаем при возведении в степень положительного числа? (При возведении в степень положительного числа получаем положительное число)

5.     Какое число получаем при возведении отрицательного числа с четным показателем? (При возведении отрицательного числа с четным показателем получаем положительное число)

6.     Какое число получаем при возведении отрицательного числа с нечетным показателем? (При возведении отрицательного числа с нечетным показателем получаем отрицательное число).

Вычисли устно.

0,3²           (- 2)3           (- 0,2)¹           – 9²             (- 10)²∙26⁰              – 4² + 4²                  2⁶

46⁰               5²                 4³               (3²)²

IV.              Сообщение темы и цели урока

V.                Работа по теме

Эти же правила выполняются и при умножении алгебраических дробей.

Повторим свойства степеней.

a^m aⁿ=а^m+n

а^m/аⁿ=а^m-n

(аⁿ)^m=а^nm

(ab)ⁿ= аⁿbⁿ

(a/b)ⁿ=aⁿ/bⁿ

Историческая пауза.

Первыми в списке арифметических действий идут сложение, вычитание, умножение и деле­ние. Представление о возведении в степень как о самостоятельной операции у математиков сложилось не сразу, хотя задачи на вычисле­ние степеней встречаются в самых древних математических текстах Древнего Египта и Междуречья.

Своеобразно описывает первые натураль­ные степени чисел Диофант Александрийский в своей знаменитой «Арифметике»:

«Все числа… состоят из неко­торого количества единиц; ясно, что они про­должаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения не­которого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато - квадраты — от умножения квадратов самих на себя, далее квадрато - кубы, получающиеся от умно­жения квадрата на куб его стороны, далее кубо - кубы — от умножения кубов самих на себя».

Решить №144, 146(1-5), 158(1, 2) № 153, 155(4, 5, 6), 177(2, 3).

Вычислите устно:            

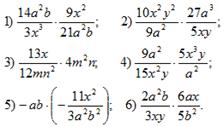
VI.              Итог урока

Решить № 147(1-3), № 156(1, 3).

VII.           Домашнее задание (Рефлексия)

·         Трудным ли для тебя был материал урока?

·         На каком из этапов урока было труднее всего, легче всего?

·         Что нового ты узнал на уроке? Чему научился?

Выучить правило  п.5, решить № 154, 156(2, 4), № 145, 147(4-6).