
Краткосрочный план урока №
|
Раздел долгосрочного плана: |
Школа: |
|
|
Дата: |
Имя учителя:. |
|
|
Класс: 8 |
Количество присутствующих: |
Количество отсутствующих: |
|
Тема урока: Теорема Фалеса.Проперциональные отрезки |
||
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) |
8.3.1.7. Знать и применять теорему Фалеса. 8.3.1.8. Знать и применять теорему о пропорциональных отрезках. 8.3.1.9. Делить отрезок на n равных частей с помощью циркуля и линейки. 8.3.1.10. Строить пропорциональные отрезки. |
|
|
Цели урока |
Все учащиеся смогут: доказывают теорему Фалеса, делят произвольный отрезок на n равных частей выбирают и формулируют познавательную цель, выражают смысл ситуации с помощью различных примеров Большинство учащихся будут уметь: самостоятельно формулируют познавательную цель и строят свои действия в соответствии с ней регулируют собственную деятельность посредством речевых действий; Некоторые учащиеся смогут: проверить умение применять теоретические знания на практике; Учащиеся работают по устному тексту на основе аудиовидеоматериала |
|
|
Критерии оценивания |
обеспечить закрепление ранее усвоенного теоретического материала; осуществить взаимоконтроль знаний учащихся; сформулировать и доказать теорему Фалеса; ввести понятие «пропорциональные отрезки». . изучить обобщенную теорему Фалеса, отработать навыки применения пропорциональности отрезков при решении задач. |
|
|
Языковые цели |
формируется навыки культурного общения в повседневной жизни. Предметная лексика Знает об основных Теорема параллельные, равные отсекают, пересекают, делят прямые отсекают равные отрезки Равенство Серия полезных фраз для диалога/письма Докажем прямым методом, что... |
|
|
Привитие ценностей |
Поддержка взаимного уважения. Необходимость совместной работы и планирования обеспечивает терпимость и дружелюбные отношения учащихся. Учащиеся открыто и свободно высказывают собственное мнение |
|
|
Межпредметные связи |
Связь с литературой: умение обосновывать (доказывать) свою точку зрения, опираясь на известные факты, жизненный опыт |
|
|
Первоначальные знания |
Аксиомы планиметрии |
|
|
Тип урока |
Комбинированный |
|
Ход урока
|
Запланиро-ванные этапы урока |
Запланированная деятельность на уроке |
Деятельность учащихся |
Оценивание |
|
1 мин |
Учитель знакомит учащихся с темой и целью урока. |
|
|
|
3 мин |
Актуальность изучаемой темы. Создание коллаборативной среды. Физминутка «гимнастика сидя» Формируют группы Проверка домашнего задания 1.1. «Верно/неверно» 1) По первому признаку треугольники равны по двум сторонам и углу между ними. (Да). 2) По второму признаку треугольники равны по двум углам и двум сторонам. (Нет) 3) Две прямые пересечены секущей. Образовалось три пары внутренних накрест лежащих углов. (Нет) 4) Две прямые пересечены секущей. Образовалось две пары внутренних односторонних углов. (Да) 5) Сумма внутренних накрест лежащих углов равна 1800(Нет) 6) Вертикальные углы не равны (Нет) 7) У параллелограмма противолежащие стороны равны (Да) 8) У параллелограмма противолежащие углы не равны (Нет) 9) Диагональ – это отрезок, соединяющий две противолежащие вершины параллелограмма (Да) 10) По третьему признаку треугольники равны по трем углам (Нет) Ученики заполняют 1-ю колонку “Знаю” при актуализации знаний. В колонку “Хочу узнать” предлагается внести свои спорные мысли и вопросы, возникшие в ходе обсуждения темы урока. Затем ученики читают новый текст, пытаясь найти ответы на поставленные ими вопросы. После чтения текста заполняют колонку “Узнал”. Ответы располагают напротив поставленных вопросов. Далее обучающимся предлагаем сравнить, что они знали раньше с информацией, полученной из текста. Организую обсуждение: «Можно ли без помощи линейки со шкалой разделить отрезок пополам? Как разделить отрезок на 4 равные части? На 8?Как разделить отрезок на 3 равные части? Создаю проблемную ситуацию. 1. Таблица «З-Х-У» (заполнить столбик «Х» - «Хочу узнать») 2. Ребус «Теорема Фалеса»
|
|
|
|
Середина урока
|
Метод «Фишбон» по теореме Фалеса. Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они равные отрезки и на другой его стороне.
1. Метод «INSERT» стр. 34 Пример 1 «Разделить отрезок на 3 равные части» Учащиеся читают текст, делая пометки на полях: “v” – известная информация; “+” – новая информация; “–” – информация, идущая вразрез с имеющимися представлениями и знаниями; “?” – непонятная информация. После работы с текстом – обсуждение с обязательным обращением к исходному тексту и составление алгоритма. Алгоритм деления данного отрезка на N равных частей без измерения длины · Постройте отрезок АВ. · Постройте луч АК, не совпадающий с АВ. · На луче АК отложите N равных отрезков. · Через точку В и последнюю точку на луче проведите прямую. · Через концы отрезков, отложенных на луче АК, проведите прямые, параллельные первой прямой. · Сравните отрезки, получившиеся на отрезке АВ. · Сделать вывод и заполнить таблицу «З-Х-У» (заполнить столбик «У» - «Узнал»). 2. Критерии успеха (вырабатываются вместе с учащимися): - верно построен луч, не совпадающий с данным отрезком - верно на луче отложены N равных отрезков - верно проведены параллельные прямые - верно найдены точки пересечения параллельных прямых и отрезка - верно сделан вывод о равенстве полученных отрезков 3. Метод «Перепутанная логическая цепочка» (групповая работа по алгоритму деления отрезка на части) Приложение №1 (Количество правильных ответов – количество баллов, максимум - 10) 4. Выставление оценок в оценочные листы по набранным баллам Приложение №2 5. Домашнее задание: 3) Составить кластер по теореме Фалеса. Задачи для урока: № 1. В треугольнике АВС на стороне АВ взята точка К так, что АК : ВК = 1 : 3, а на стороне ВС – точка L так, что CL : BL = 2 : 1. Пусть Q – точка пересечения прямых AL и СК. Найти площадь треугольника АВС, если площадь треугольника BQC равна 2. (Ответ: 3) № 2. В треугольнике АВС, площадь которого равна 5, на стороне АВ взята точка К, делящая эту сторону в отношении АК : ВК = 2 : 3, а на стороне АС – точка L, делящая её в отношении AL : АС = 5 : 8. Точка Q пересечения прямых CK и BL удалена от прямой АВ на расстояние 1. Найти длину стороны АВ. (Ответ: 5) № 3. В треугольнике
АВС на стороне АС взята точка К, а на стороне ВС точка М так, что СК : КА = 5
: 1, № 4. На медианах
АК, BL и CN треугольника АВС взяты точки Р, Q и
R так, что AP : PK = 1 : 1, BQ
: QL = 1 : 2, CR : CN = 9 : 4.
Найти площадь треугольника PQR, если площадь треугольника АВС равна 1. (Ответ: Закрепление изученного материала №1 Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A, B и C, D соответственно. Найдите OA, если OB = 15 см и OC : OD = 2 : 5.
№2 Определите, пропорциональны ли пары отрезков а, b и c, d, если: а) a = 0,8 см, b = 0,3 см, с = 2,4 см, d = 0,9 см; б) а = 50 мм, b = 6 см, с = 10 см, d = 18,5 см. |
|
|
|
Конец урока
|
Стратегия «Открытые мысли» Метод «Синквейн» Ученикам объясняется правила написания синквейна: · 1 строка – тема (одно существительное); · 2 строка – описание предмета (два прилагательных); · 3 строка – описание действия (три глагола); · 4 строка – фраза из четырех слов, выражающая отношение к предмету; · 5 строка – синоним, обобщающий или расширяющий смысл темы (одно слово). |
|
|
|
3 мин |
Рефлексия: - достигли ли цели урока? - какие затруднения возникли? - а сейчас я предлагаю оценить свои знания полученные на уроке (Цветок «Где Я?») Записывают на стикерах свои впечатления и наклеивают на соответствующий лепесток. |
|
|
|
Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
|
Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Теорема. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
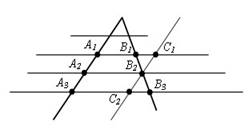 Доказательство.
Доказательство.
Пусть
точки A1, A2, A3 – точки пересечения
параллельных прямых с одной из сторон угла. А точки B1, B2,
B3 – соответствующие точки пересечения этих прямых с другой стороной
угла. Докажем, что если A1A2 = A2A3,
то B1B2=B2B3.
Проведем через точку В2 прямую С1С2,
параллельную прямой A1A2. Получаем параллелограммы A1C1BA2
и A2B2C2A3. По свойствам
параллелограмма, A1A2 = C1B2 и A2A3
= B2C2. Так как A1A2 = A2A3,
то C1B2 = B2C2.
Δ C1B2B1 = Δ C2B2B3
по второму признаку равенства треугольников (C1B2 = B2C2,
∠ C1B2B1
= ∠ C2B2B3,
как вертикальные, ∠ B1C1B2
= ∠ = B3C2B2,
как внутренние накрест лежащие при прямых B1C1 и C2B3
и секущей С1С2). Из равенства треугольников следует, что
B1B2=B2B3. Теорема доказана.
То есть что имеется в виду.
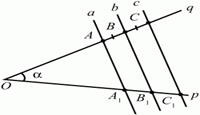
(АВ = BC, AA1||BB1||CC1) A1B1 = В1С1
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.