Разработка урока по геометрии на тему : Пирамида

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ВЛАДИВОСТОКСКИЙ МОРСКОЙ ТЕХНИКУМ»

 

 

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКАЯ  РАЗРАБОТКА

 

По дисциплине «Математика»

   Раздел: Геометрия

Тема: Пирамида

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Владивосток 2013 год

Рассмотрено на заседании цикловой методической комиссии		Утверждаю Зам. директора по УВР
Протокол №_____________		__________О. А. Гречухина
«______»____________2013 г.
Председатель ЦМК		«____»____________2013 г.
___________ И. Б. Горовая

 

 

 

 

 

 

 

 

 

 

 

 

Автор (разработала):                                                       преподаватель математики 

                                                                                  и информатики ВМТ 

                                                                                  А.С.Кантаева                                         

 

 

Рецензент:                                                                          

 

 

                                                                                            

 

 

 

 

 

Аннотация.

Методическая разработка по предмету «Математика», раздел «Геометрия» на тему «Пирамида». Данная разработка может быть использована как методический материал для проведения урока по данной теме  с учащимися первых курсов средних учебных заведений. Здесь рассмотрен урок с использованием средств мультимедиа.  Разработка соответствует ФГОС 3 поколения и минимуму содержания и уровню подготовки выпускников  всех специальностей среднего профессионального образования.

 

 

Содержание

 

		Стр.
	Введение	4
1.	Структура урока	5
	1.1. Цели урока 1.2. Тип урока 1.3. План урока 1.4. Оборудование
2.	Ход урока
	2.1. Организационный момент	6
	2.2. Актуализация знаний	6
	2.3. Изучение нового материала
	2.3.1. Пирамида	7
	2.3.2. Правильная пирамида	7
	2.3.3. Усеченная пирамида	8
	2.4. Решение задач	9
	2.5. Закрепление материала	14
	2.6. Домашнее задание	14
	Заключение	15
	Список использованной литературы	16

 

Введение.

 

Учебный процесс в новых условиях, а именно — в информационной образовательной среде, сильно отличается от прежнего. Он направлен на создание опыта работы с информацией, её целесообразного применения, обеспечивающего саморазвитие и самоактуализацию учащегося.

Поэтому на первое место ставится развитие умений самостоятельного приобретения и применения знаний в соответствии с личностными целями и потребностями, решение актуальных для учащихся проблем. Большое значение отводится формированию способов деятельности, применимых как в рамках образовательного процесса, так и при решении проблем в реальных жизненных ситуациях.

Процесс обучения планируется, организуется и направляется учителем как результат его совместной деятельности с учащимися в соответствии с содержанием образования (программой), личным опытом, познавательными интересами и потребностями детей. Предпочтение отдаётся методам обучения, которые помогают освоить универсальные способы деятельности (познавательная, ценностноориентационная, практическая, коммуникативная деятельность). Отсюда вытекает требование наполнить учебный процесс в информационной образовательной среде таким содержанием, которое наиболее эффективно может быть усвоено  с помощью средств информационно-коммуникационных технологий (ИКТ).

Следовательно, высокая познавательная активность возможно только на интересном для учащихся уроке, когда ему интересен предмет изучения и в какой форме это проходит.

 

 

 

1. Структура урока

1.1. Цели урока:

Обучающие:

·        изучить новый вид многогранников – пирамиды,

·        выйти на понятие правильной пирамиды,

·        рассмотреть задачи, связанные с пирамидой и с правильной пирамидой,

·        закрепление навыков построения сечений на примере пирамиды.

Развивающие:

·        развивать познавательный интерес через творческую активность,

·        развивать геометрическую зоркость, пространственное воображение

·        развитие технического, логического, образно-пространственного мышления учащихся.

Воспитательные:

·        воспитывать эмоционально-положительное отношение к изучению геометрии,

·        воспитывать культуру графического труда.

1.2. Тип урока: Лекция, практическая работа (комбинированный).

1.3. План урока:

1. Организационный момент.
2. Актуализация знаний.
3. Изучение нового материала.
4. Решение простейших задач.
5. Закрепление материала.
6. Домашнее задание.

1.4. Оборудование: учебник, компьютер, мультимедийный проектор, презентация.

2. Ход урока:

2.1. Организационный момент. (2-3 мин.)

Сегодня мы совершим путешествие во времени.

Слайд1 Фараон Джосер повелел создать для себя необычную гробницу, похожую на гигантскую каменную лестницу, по которой фараон после смерти должен был подняться на небо. Его замысел воплотил в жизнь великий египетский зодчий Имхотеп. Правившие после Джосера фараоны тоже строили себе ступенчатые пирамиды, пока фараону Снофру не пришла в голову мысль выстроить для своей гробницы не ступенчатую, а гладкую пирамиду.       

Слайд2  Вслед за Снофру Древним Египтом правил его сын, фараон Хуфу, или, как мы его привыкли называть, - Хеопс. За 23 года своего правления он сумел выстроить самую грандиозную и удивительную пирамиду, которую мы называем первым чудом света.

Пирамиды – самое грандиозное из всех чудес света. Построенная около 2600 г. до н.э., она имеет высоту 146 метров, состоит из 2 300 000 каменных блоков, каждый весом примерно 3 тонны.

Даже сегодня при современных машинах и механизмах выстроить такую громадную пирамиду было бы нелегко.

Но мы сегодня должны научиться строить пирамиды.

2.2. Актуализация знаний.

Термин «пирамида» заимствован из греческого «пирамис» или «пирамидос». Греки  в свою очередь позаимствовали это слово из египетского языка. В папирусе Ахмеса встречается слово «пирамис»  в смысле ребра правильной пирамиды. Другие считают, что термин берет свое начало от формы хлебцев в Древней Греции («пирос» - рожь). В связи с тем, что форма пламени напоминает образ пирамиды, некоторые ученые считали, что термин происходит от греческого слова «пир» - огонь.

Итак, тема нашего сегодняшнего  урока, как вы, наверное, уже догадались - “Пирамида”.

2.3. Изучение нового материала.

Мы с вами рассмотрим пирамиду с математической точки зрения.

 

 

 

2.3.1. Пирамида.

Что мы можем узнать о пирамиде?  Познакомиться с понятием пирамида, ее видами, элементами, составляющими частями, свойствами, решить простейшие задачи.

Итак, цель урока: изучить новый вид многогранников – пирамиды. Рассмотреть задачи, связанные с пирамидой.

-  Опишите фигуры, изображенные на Слайде3 (основание, вершина, ребра)

- Что объединяет эти тела? (в основании n-угольник, боковые грани – треугольники).

Итак,  пирамидой называется многогранник, составленный из n-угольника и n-треугольников. Многоугольник называется – основанием пирамиды, треугольники – боковыми гранями пирамиды. Точка  Р -  называется вершиной пирамиды, а отрезки, соединяющие вершину пирамиды с точками основания – боковыми ребрами пирамиды.

-  Слайд4  Дайте определение высоты пирамиды. (Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания).

Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т.е. основания и боковых граней). Площадью боковой поверхности пирамиды – сумма площадей ее боковых граней. Очевидно,

- Слайд5  Что это за многогранник?   Дайте определение тетраэдра (поверхность, состоящая из четырех правильных треугольников или многогранник, состоящий их четырех треугольников). Понимаем, что тетраэдр – является треугольной пирамидой.

2.3.2. Правильная пирамида.

- Слайд6  Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.

- Слайд7  Какие пирамиды могут быть правильными? (в основании лежит правильный треугольник – треугольная пирамида, в основании лежит квадрат - четырехугольная пирамида, в основании лежит правильный шестиугольник – шестиугольная пирамида)

- Слайд8  Свойства боковых ребер и боковых граней правильной пирамиды. (Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками)

Построим пирамиду Хеопса.

Постройка Великих пирамид Хеопса, Хефрена и Микерина требовала огромных усилий всех свободных египтян. Их труд был настоящим чудом. Строители работали с большим энтузиазмом над возведением гробницы своего великого фараона. Они верили: фараон – сын бога, и после смерти он окажется среди богов. Если они выскажут ему подлинное уважение, он позаботится о них, простых людях, об их детях, внуках и правнуках.

Давайте и мы покажем ему свое уважение. Построим пирамиду Хеопса.

Итак, что лежит в основании пирамиды Хеопса (квадрат)

- Как изображается квадрат на плоскости? (параллелограммом)

-  Слайд9  построим основание,

- отметим вершину параллелограмма,

- соединим вершину боковыми ребрами с вершинами основания.

Построим треугольную пирамиду.

-  Слайд10  Построим основание,

- отметим вершину пирамиды,

- соединим вершину боковыми ребрами с вершинами основания.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется – апофемой.

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

2.3.3. Усеченная  пирамида.

Если в любой пирамиде провести секущую плоскость, параллельную основанию и пересекающую боковые ребра пирамиды в некоторых точках, то основная  фигура разобьется на два многогранника. Многогранник,  гранями  которого являются n-угольники (нижнее и верхнее основания), расположенные в параллельных плоскостях и n-четырехугольников (боковые грани), называется усеченной пирамидой. Слайд11

Отрезки, соединяющие вершины оснований называются боковыми ребрами усеченной пирамиды. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой  усеченной пирамиды. Боковыми гранями усеченной пирамиды являются трапеции.

Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усеченной пирамиды  - правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций являются – апофемами.

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров  оснований на апофему.

2.4.  Решение задач.

Слайд12  1. В основании пирамиды Хеопса – квадрат со стороной  230м, тангенс угла наклона боковой грани к основанию равен 1,2. Найти высоту самой высокой египетской пирамиды, если основание ее лежит в центре квадрата.

 

			Решение 1. AC Ç ВD = О 2. Пирамида правильная Þ SО ^ (АВС) 3. ОЕ çç АD Þ ОЕ ^ АD Þ 4. SЕ ^ СD (по теореме о 3 перпендикулярах) Чему равен тангенс острого угла в прямоугольном треугольнике? (отношению противолежащего катета к прилежащему катету) 5. D SОЕ – п\у     tg E = SО : ОЕ = 1,2 6. ОЕ = 0,5АD =115м 7. SО = ОЕ •  tg E = 1,2 • 115 = 138 м Ответ:  138м

 

 

 

 

 

 

 

 

 

 

 

 

 

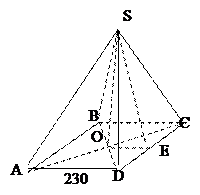
Решение 1. AC Ç ВD = О 2. D АОD – п\у, р\б  по т. Пифагора  АD2 = DО2+ОА2 2ОD2= 2302 = 52900 ОD2 = 26450 3. Пирамида правильная Þ SО ^ (АВС) 4. D SОD – п\у по т. Пифагора  DS2 = DО2+ОS2 = 26450 + 1382= = 26450 +19044 = 45494 DS » 213 м Ответ:  213м

Слайд13  2. В основании пирамиды Хеопса – квадрат со стороной  230м, высота пирамиды 138 м. Найти боковое ребро самой высокой египетской пирамиды.

 

 

 

 

 

 

 

 

 

 

 

 

 

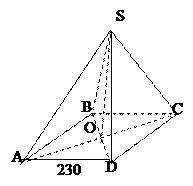
- Слайд14  Из чего состоит поверхность пирамиды? (из основания, и боковых граней)

- Чем является боковая грань? (треугольником)

Слайд15  3.Чему равна площадь поверхности правильного тетраэдра с ребром 1?

			Решение 1. Sпов=4Sтр 2. Sтр = 0,5а2sin600 3. Sпов= 4 • 0,5а2sin600 = Ответ:

 

 

 

 

 

 

 

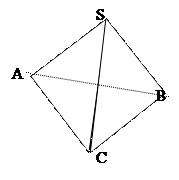Решение 1. Sб.пов=4Sтр 2. AC Ç ВD = О 3. Пирамида правильная Þ SО ^ (АВС) 4. ОЕ çç СD Þ ОЕ ^ АD Þ 5. SЕ ^ АD (по теореме о 3 перпендикулярах) 6. DЕОS- п\у по т. Пифагора ЕS2 = ЕО2+ОS2 = 1152 + 1382 =  = 13225 +19044 = 32269 ЕS » 180 7. ES - высота DАSD SАSD = 0,5 ЕS•АD » 0,5 •180 • 230 »20700 м2 8. Sб.пов=4Sтр » 4 • 20700 » 82800 м2 Ответ: 82800 м2

Слайд16 

S

4.  Найдите площадь боковой поверхности пирамиды Хеопса, сторона основания которой равна 230м и высота 138м.

138

С

В

                                                     

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

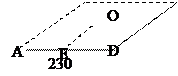
Слайд17  5. (устно) Боковое ребро правильной пирамиды вдвое больше ее высоты.  Определите угол наклона бокового ребра к плоскости основания. (30⁰)

 

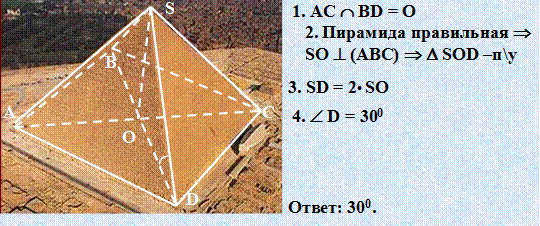
Построение сечений пирамиды. Слайд18, 19

Перед учащимися ставится задача, в ходе решения которой повторяются основные аксиомы и теоремы. Осуществляется пошаговая проверка построения сечения.

Слайд20  На каких рисунках сечение построено не верно?  (1,3,4)

 

         Построение сечений пирамиды. Задачи  Слайд21 – 25

 

 

 

 

 

 

 

 

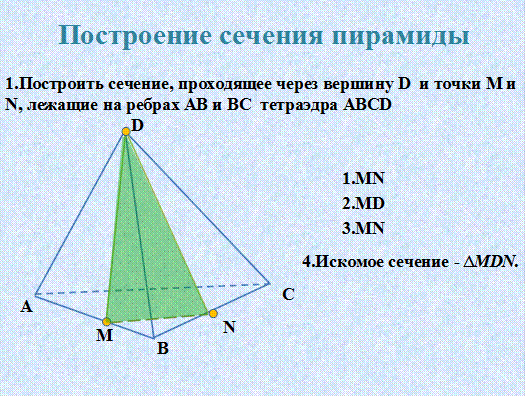
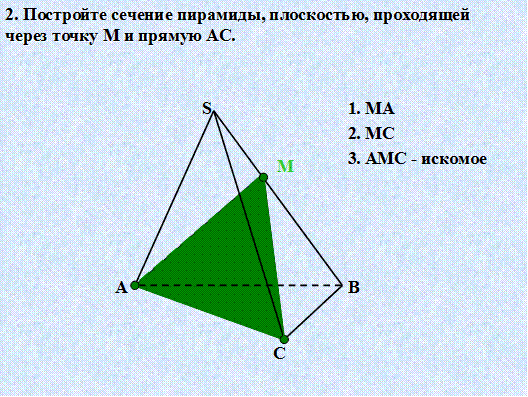
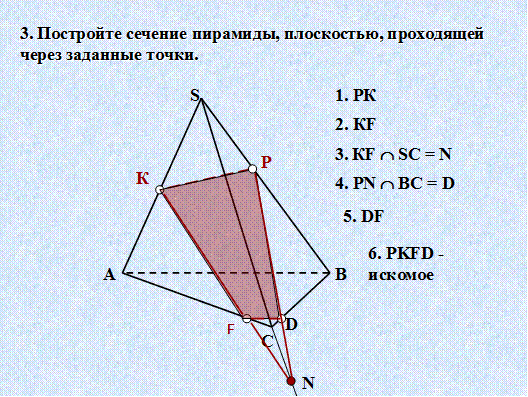
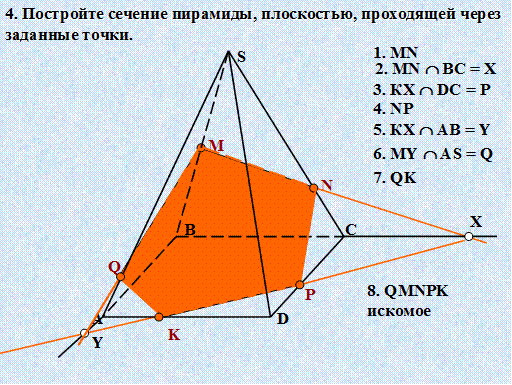
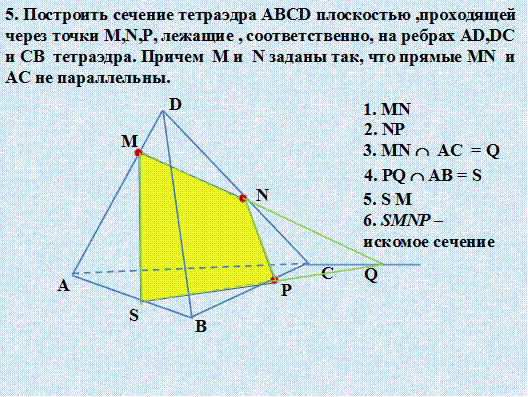
2.5. Закрепление материала.

Подведем итоги нашей совместной работы.

Что такое пирамида? Где и когда начали использовать пирамиды? Какая самая маленькая пирамида (из скольки ребер она состоит)? Что было сложного? Выставление оценок.

 

2.6. Домашнее задание.

1.      Глава 3  пункт 32-34   №239

2.      Слайд26, 27 Если в правильной треугольной пирамиде высота H равна стороне основания a, то боковые ребра составляют с плоскостью основания углы в 60⁰. Верно ли это утверждение?

3.      Сторона квадрата равна 10 см. Доказать, что нельзя, используя его в качестве основания, построить правильную четырехугольную пирамиду с боковым ребром 7 см.

4.      Доказать или опровергнуть утверждение: «если в пирамиде все ребра равны, то пирамида правильная».

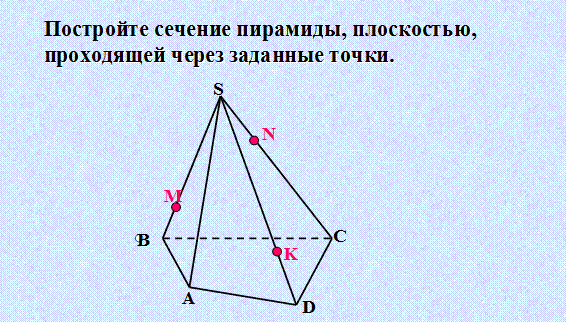
4).

 

 

Заключение.

Благодаря изучению математики человек осваивает искусство построения правильного расчлененного логического анализа ситуаций и вывода следствий из известных фактов путем логических рассуждений, искусство определять и умение работать с определениями, умение отличать известное от неизвестного, доказанное от недоказанного, искусство анализировать, классифицировать, ставить гипотезы, опровергать их или доказывать, пользоваться аналогиями.

Опыт приобретаемый в процессе решения математических задач, способствует развитию как навыков рационального мышления и способов выражения мысли (лаконизм, точность, полнота, ясность и т.п.), так и интуиции - способности предвидеть результат и предугадать путь решения. Математика - путь к первым опытам научного творчества, путь к пониманию научной картины мира.

Наконец, курс математики содержит имеющую самостоятельное значение практическую  составляющую. Для ориентации в современном мире каждому совершенно необходим некоторый набор знаний и умений математического характера (навыки вычислений, элементы практической геометрии - измерение геометриче6ских фигур, распознавание и изображение геометрических фигур, работа с функцией и графиком, составление и решение пропорций, уравнений, неравенств и их систем и т.д.).

В заключении хотелось бы отметить, что использование средств мультимедиа на уроках математика (и не только), способствует интересу учащихся к изучаемому предмету, пространственному воображению и практическому применению изучаемой темы на уроке.

 

Список использованной литературы.

1. Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Л.С.Киселева, Э.Г.Позняк Геометрия 10-11:Учебник для общеобразовательных учреждений. – М.: Просвещение, 2003.
2. Юрченко О. Методы мотивации и стимулирования деятельности учащихся.: Учебно–методическая газета Первое сентября. Приложение математика. №1, 2005.
3. http://www.uchportal.ru
4. http://subscribe.ru/archive/job.education.uchinfo/200808/17000944.html
5. http://www.google.ru
6. http://otherreferats.allbest.ru/mathematics/00084188_0.html
7. http://images.yandex.ru/yandsearch?source

 

 

Скачано с www.znanio.ru