
Публикация является частью публикации:
Министерство образования Московской области
Государственное образовательное учреждение высшего образования Московской области
«Государственный гуманитарно-технологический университет»
«Социально-технологический техникум» (СТТ ГГТУ)
Методическая разработка открытого урока по учебной дисциплине:
«Математика: алгебра, начала математического анализа, геометрия»
Тема урока: «Применение формул дифференцирования к нахождению производной»
Выполнила преподаватель
Курбатова Ю.Н.
г.о. Орехово-Зуево
2018 г.
|
Дата урока |
|
Уровень освоения |
2 |
|
Тема урока |
Применение формул дифференцирования к нахождению производной |
||
|
Цель урока |
Уметь использовать правила нахождения производной, применять их для решения конкретных задач |
||
|
Методическая цель |
Применение игровых технологий на уроках математики |
||
|
Задачи урока |
- Закрепить алгоритм нахождения производной, используя правила нахождения производной, применять их для решения конкретных задач. - Сформировать глубину и оперативность мышления, развивать творческую и мыслительную деятельность обучающихся, способность к «видению проблемы», формировать умение чётко и ясно излагать свои мысли, аргументировать доводы. - Воспитывать умение работать с имеющейся информацией, умение слушать товарищей, оказывать помощь в коллективной деятельности. |
||
|
Результаты освоения |
Личностные: - сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики; - развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования; - овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественно-научных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки. Метапредметыне: - умение самостоятельно выбирать успешные коммуникативные стратегии в различных ситуациях общения; - владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства; - владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения. Предметные: - - сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; - сформированность умения использовать математические понятия как средство для получения информации в образовательных и самообразовательных целях. |
||
|
Тип урока |
Урок обобщения и систематизации полученных ранее знаний |
||
|
Форма урока |
Урок - викторина |
||
|
Педагогическая технология (элемент технологии), если применяются на уроке |
Элементы технологий: игровые технологии (Шмаков С. А., Никитина Б. П., Эльконин Д. Б., Выготский Л.С.); ИКТ (М.В.Моисеева, Е.С.Полат, М.В.Бухаркина). |
||
|
Методы урока |
Эвристический (метод создания эмоционально-нравственных ситуаций), словесный; инструктивно-практический; частично-поисковый; практический. |
||
|
Средства обучения |
Дидактический материал: презентация, таблицы, карточки с заданиями. Оборудование: компьютер, проектор, экран. |
||
|
Структура урока (с указанием отведенного времени) |
План урока: 1. организационный момент (2 мин.): - оценка внешней и внутренней (психологической) готовности обучающихся к уроку (1 мин.); - заполнение журнала, отметка присутствующих на уроке (1 мин.); 2. актуализация знаний и умений обучающихся (5 мин.); 3. постановка цели урока перед обучающимися. (3 мин); 4. творческое применение и добывание знаний, освоение способов деятельности путем решения проблемных задач, построенных на основе ранее усвоенных знаний и умений (30 мин.); Подведение итогов викторины (2 мин.). Заключительная часть рефлексия, подведение итога урока, выставление оценок (2 мин.) домашнее задание (1 мин.)
|
||
Ход урока:
1. Организационный момент (2 мин.):
- оценка внешней и внутренней (психологической) готовностью обучающихся к уроку (1 мин.):
- заполнение журнала, отметка присутствующих на уроке (1 мин.).
2. Актуализация знаний и умений обучающихся (5 мин.)
Эмоциональное вхождение в урок.
Урок начинается с "настройки" в полушуточной манере.
Преподаватель: "Сначала мы вместе восхитимся вашими глубокими знаниями — а для этого проведем маленький устный опрос:
(на экран выводится презентация Слайд №2):
Фронтальный опрос по вопросам:
Обобщение ответов обучающихся.
1. Определение производной функции в точке.
Пусть функция f(x) определена
на промежутке (a; b), ![]() и
и ![]() -
точки этого промежутка. Производной функции f(x) в
точке
-
точки этого промежутка. Производной функции f(x) в
точке ![]() называется предел
отношения приращения функции к приращению аргумента при
называется предел
отношения приращения функции к приращению аргумента при ![]() .
Обозначается
.
Обозначается 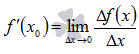 .
.
2. Штрих, предел
3. Операция нахождения производной называется дифференцированием.
4. Физический смысл производной.
Если точка движется вдоль оси х и ее координата
изменяется по закону x(t), то мгновенная скорость точки: ![]()
5.
· Равно нулю
·
![]()
·
![]()
Преподаватель: «Разомнёмся и потренируем мозги — порешаем примеры и, наконец, вытащим из тайников памяти кое-что ценное... (называется тема повторения – Правила нахождения производной)" (на экран выводится презентация Слайд № 3,4,5).
3. Постановка цели занятия перед обучающимися (3 мин)
Девиз урока – слова Гете: «Числа не управляют миром, но они показывают, как управляется мир».
Обучающиеся заранее распределены по группам. Преподаватель объясняет правила викторины. Все задания выполняются в тетрадях. Преподаватель контролирует работу групп.
Критерии оценки заданий викторины. За каждый правильно выполненное задание, группа получает три балла. Результаты заносятся в таблицу (см. Приложение 1).
Команда, набравшая не менее 15 баллов, считается победителем, и все обучающиеся получают оценку «отлично», набравшие не менее 12 баллов, получают оценку «хорошо», набравшие менее 12 баллов, получают оценку «удовлетворительно».
4. Творческое применение и добывание знаний, освоение способов деятельности путем решения проблемных задач, построенных на основе ранее освоенных знаний и умений (30 мин.)
Преподаватель:
«На уроке мы затронем и ваши знания в области географии по странам мира. Мы будем применять полученные ранее формулы дифференцирования для нахождения производных. Параллельно мы будем проверять, а может даже, дополнять наши знания о странах мира».
Викторина (на экране Слайд № 6-12)
I. Вычислите производные следующих функций и определите страну по данной информации. Выберите правильный ответ из четырех вариантов.
|
1)
|
Государство в центральной части полуострова Индокитай, столица – Вьентьян. |
|
1. 3x2- 6x – 15 |
Вьетнам |
|
2. 3x2- 12x – 15 |
Лаос |
|
3. 3x – 6x + 15 – 2 |
Непал |
|
4. 3x2+ 6x -15 |
Кувейт |
|
2)
|
Государство на северо-востоке Африки и Синайском полуострове в Азии. Государственный язык – арабский. Подавляющее большинство населения – мусульмане. |
|
1. 3x2+4x+9 |
Ливия |
|
2. 3x – 4 x -9 |
Алжир |
|
3. 3x2- 4x + 9 |
Египет |
|
4. 3x2+ 4x – 9 |
Мали |
|
3)
|
Государство на юго-западе Аравийского полуострова. Столица – Сана. Крупнейший порт страны – Аден. Государственный язык – арабский. Государственная религия – ислам. |
|
1. 2x – 9 |
Йемен |
|
2. 2 – 9 |
Камбоджа |
|
3. 2x + 9 |
Ирак |
|
4. x -9 |
Сирия |
|
4)
|
Владение Великобритании в северо-западной части Атлантического океана, занимает 150 островов. Только около 20 обитаемы, 10 из них соединены мостами и путепроводами и образуют так называемый основной остров Мэйн-Айленд. Административный центр и порт – Гамильтон. |
|
1. (3x3 + 5x2)/(x+5)2 |
Виргинские острова |
|
2. (x3 – x2)/(x+5)2 |
Каймановы острова |
|
3. (2x3 – 5x2)/(x+5)2 |
Соломоновы острова |
|
4. (2x3 +15x2)/(x+5)2 |
Бермудские острова |
|
5)
|
Государство на севере Европы, занимающее западные и северные части Скандинавского полуострова. Конституционная монархия. Высший законодательный орган – стортинг /парламент/. Государственная церковь – лютеранская. Денежная единица – крона. |
|
1. 2x cos (x2 -7) |
Норвегия |
|
2. x cos (x2 -7) |
Финляндия |
|
3. – 2x cos (x2 -7) |
Дания |
|
4. – x cos (x2 -7) |
Ирландия |
|
6)
|
Государство на юге Азии. Одна из древнейших стран мира. В течение почти 200 лет находилась под господством английских колонизаторов. |
|
1. |
Китай |
|
2.
|
Малайзия |
|
3.
|
Индия |
|
4. |
Бутан |
|
7)
|
Государство в Африке. Столица – Банги. Государственный язык – французский. Ведется промышленная добыча алмазов. Добывается золото. |
|
1. lnx – 1 |
Чад |
|
2. lnx + 1 |
Центральноафриканская Республика |
|
3. xlnx + 1 |
Уганда |
|
4. xlnx – 1 |
Эфиопия |
Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И.Ньютона и …
Фамилию второго математика вы узнаете, прочитав первые буквы правильных ответов /стран/.
Лейбниц. (на экран выводится презентация Слайд № 13,14)
Преподаватель:
Ньютон и Лейбниц — спор о приоритете открытия дифференциального и интегрального исчисления между Исааком Ньютоном (1642—1727) и Готфридом Вильгельмом Лейбницем (1646—1716). Свою версию теории Ньютон создал ещё в 1665—1666 годах, однако не публиковал её до 1704 года. Независимо от него Лейбниц разработал свой вариант дифференциального исчисления (с 1675 года), хотя первоначальный толчок, вероятно, его мысль получила из слухов о том, что такое исчисление у Ньютона уже имеется, а также благодаря научным беседам в Англии и переписке с Ньютоном. В отличие от Ньютона, Лейбниц сразу опубликовал свою версию и в дальнейшем, вместе с Якобом и Иоганном Бернулли, широко пропагандировал это открытие по всей Европе. Большинство учёных на континенте не сомневались, что анализ открыл Лейбниц. Когда Ньютон решил опубликовать свои труды на эту тему, возник вопрос о приоритете совершённого открытия. Ожесточённый спор не завершился со смертью Лейбница и продолжался усилиями сторонников основных участников, прекратившись только со смертью Ньютона.
Полярные точки зрения по поводу приоритета Ньютона или Лейбница высказывались историками математики вплоть до начала XX века. С середины прошлого века существенно возросло число известных источников, и современные исследователи пришли к выводу о том, что Ньютон и Лейбниц совершили свои открытия независимо друг от друга.
Подведение итогов викторины (3 мин.).
Заключительная часть
Рефлексия. Подведение итога урока, выставление оценок (2 мин.)
Домашнее задание: решить кроссворд. (1 мин.)
|
КРОССВОРД |
|||||||||||||||||||||||||||
|
По горизонтали: 1. Столица Норвегии. 4. Ее
производная равно нулю. 9. Ее
производная равна единице. 12.
Столица Индии. |
|
По вертикали: 2.
Кинематический смысл производной. |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы:
По горизонтали: 1. Осло. 4. Константа. 7. Производная. 9. Аргумент. 10. Предел. 11. Суперпозиция. 12. Дели. 13. Тангенс.
По вертикали: 2. Скорость. 3. Каир. 5. Австралия. 6. Расстояние. 8. Функция.
Домашнее задание: решить кроссворд. (2 мин.)
Приложение 1
|
Задания № команды |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Дополнительные баллы |
ИТОГО |
|
I |
|
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
|
|
III |
|
|
|
|
|
|
|
|
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.