Разработка урока "Теорема Пифагора (8 класс, геометрия)"

Разработка урока геометрии.

Тема: теорема Пифагора

Класс: 8

Тип урока: урок открытия нового знания

Вид урока: комбинированный урок

Цель: доказать теорему Пифагора двумя способами, применять теорему Пифагора в ходе решения задач.

Планируемые результаты:

Личностные: умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, выстраивать аргументацию;

Метапредметные:

 осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь;

развитие способности видеть математическую задачу в других дисциплинах, в окружающей жизни;

развитие способности организовывать учебное сотрудничество;

Предметные:

находить стороны треугольника, используя теорему Пифагора для решения задач практического характера и задач из смежных дисциплин

Ход урока:

Орг. момент. Приветствие, проверка готовности класса к уроку, представление гостей.

Проверка домашнего задания.

Мы с вами посвятили несколько уроков нахождению площадей фигур. Перечислите, пожалуйста, площади каких фигур мы определяли  и какими формулами пользовались?

Площади параллелограмма, квадрата, прямоугольника, треугольника, трапеции.

Дома я попросила вас еще  раз уделить внимание площади треугольника со сторонами 3, 4 и 5 см. Для этого вы сначала его должны были построить. Как вы это делали?

С помощью циркуля.

 Как затем находили его площадь?

Ученики высказывают предположение, что это треугольник прямоугольный, стороны длиной 3 и 4 – это катеты, поэтому его площадь равна 3∙4=12 см²).Учитель выказывает сомнения в том, что треугольник прямоугольный.

Что мы знаем о прямоугольном треугольнике?

Знаем его площадь – она равна половине произведения его катетов, знаем, что напротив угла 30⁰ лежит катет равный половине гипотенузы, что сумма острых углов прямоугольного треугольника равна 90⁰.

Все верно, но о соотношении сторон треугольника тут ничего не сказано. (Какими могут быть стороны прямоугольного треугольника? Если это будут стороны 3, 4 и 5 см?) Есть ли в геометрии такая теорема, как вы думайте?

Есть, теорема Пифагора.

Значит, пришло время с ней познакомиться. Запишите тему урока.

Записывают тему.

Открытие нового знания.

О чем должна быть эта теорема?

О том, как связаны между собой стороны прямоугольного треугольника?

Оставим в тетради место для формулировки теоремы и дополнительных построений. Не будем записывать конечный результат сразу, а попытаемся его получить (так мы делали и при доказательстве предыдущих теорем).

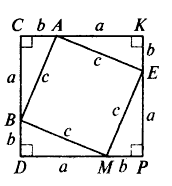
Строим прямоугольный треугольник. Выполним дополнительное построение такое же как при доказательстве теоремы о площади прямоугольника – по есть достроим треугольник до квадрата со стороной а+b, где а и b – катеты треугольника. А дальше – ваша очередь. Что мы можем для этого квадрата рассчитать?

Площадь квадрата равна сумме площадей 4-х таких треугольников и площади квадрата со стороной с (с – это гипотенуза).

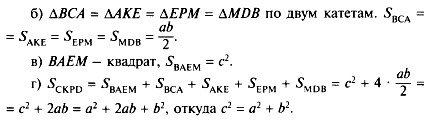Теорема формулируется так: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Легче всего доказать эту теорему для равнобедренного прямоугольного треугольника. Квадраты,  построенные на катетах, состоят из 2-х  одинаковых треугольников. А квадрат, построенный на гипотенузе, состоит из 4-х таких треугольников. Следовательно, сумма площадей маленьких квадратов равна площади большого квадрата, т.е. с²=а²+b². На этот случай есть шуточная формулировка: пифагоровы штаны во все стороны равны. Сути не отражает, но настроение поднимает.

Сейчас очень сложно сказать, в каком виде предложил доказательство теоремы Пифагор. Согласно легендам, доказательство теоремы появилось за 200 лет до Пифагора. Мы сейчас познакомились с древнекитайским доказательством.

 Пифагор – по древне-гречески означает «убеждающий речью». По мнению  современников он любую истину доказывал очень убедительно.

К настоящему времени существует более 300 доказательств. Еще с одним доказательством познакомит нас Дмитрий.

Дима представляет доказательство Дж. Гардфилда:

Домашнее задание: выучите любое из двух доказательств теоремы Пифагора.

Отработка навыков применения теоремы Пифагора в простейших ситуациях.

Переходим к практической части урока. Начнем с простого – научимся применять теорему Пифагора в простых ситуациях.

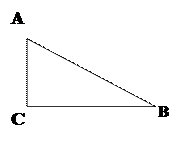1)                                        2)                                                    3)

AC=7 см; BC=24см; AB=?                MK=17см; MN=15см; NK=?              FH= 13см;  DH=5см;  FD=?

Отв: 25,  8,   12

			Задачу 1 учитель решает на доске, ученики комментируют, отвечая на наводящие вопросы учителя; задачу 2 на доске решает ученик; задачу 3 и 4 ученики решают самостоятельно, учитель оказывает помощь, ученики выявляют проблему – не извлекается квадратный корень, обсуждают все вместе, как в этом случае поступить (один из множителей вынести из под корня).

4)

                                      LM=4см  MP=2см  LP=?

                                      (отв: 2√5)

Контрольные треугольники:

1 вариант.                                                                                         2 вариант

5)                                                                                         5)

MQ=√10 см MN=√6   QN=? (отв:2)                                                   CH=4см;  PH=√7  CP =? (отв:3)

Задача 5 – контроль полученных навыков, решается самостоятельно, с взаимопроверкой этой задачи и предыдущих 4-х. За решенные верно 5 задач – 3 балла. За каждую не решенную или решенную с ошибкой вычитается 1 балл.

Теорему Пифагора мы с вами изучили, пришла пора подумать, для чего?

Она имеет практическое применение.

Межпредметная задача и задача практического применения.

От пристани одновременно отплыли два парохода: один на юг со скоростью 30 км/ч, а другой на запад со скоростью 40 км/ч. Какое расстояние будет между пароходами через 2ч?

 Работа в парах по задаче практического применения.  Обучающиеся знакомятся с задачей, затем предлагают в парах пути её решения по очереди. Каждый из обучающихся должен стать «Пифагором», т.е. «убеждающий речью». Даже если пути решения одинаковые, все равно каждый своими словами описывает решение. Если один из обучающихся не смог объяснить решение, то второй объясняет еще раз. Если оба не могут найти решение, нужно поднять руку и попросить помощи ближайших соседей через проход (у них та же задача). Через 2 минуты обсуждение прекращается, каждый самостоятельно оформляет решение задачи. Проверяется ответ. Оценивание работы: если смог объяснить и затем правильно решить задачу – 2 балла. Если объяснить не смог, но понял и правильно решил- 1 балл.

Подведение итогов. По общему количеству баллов выставляется оценка в тетрадь. Вопросы для рефлексии: получилось ли у вас быть Пифагором? Будет ли полезной для вас в дальнейшем теорема Пифагора?

Запишем домашнее задание: выучить любое доказательство теоремы Пифагора, решить задачи 483,484

Подведение итогов  урока.

Вернемся к нашему «домашнему» треугольнику со сторонами 3,4 и 5. Является ли он прямоугольным?

Да, потому что в нем выполняется равенство 3²+4²=5²

Вспомним, как звучит теорема Пифагора. Видим, что это утверждение является  обратной теореме Пифагора. А выполняется ли теорема, обратная теореме Пифагора? Рассмотрим этот вопрос на следующем уроке. До встречи.

Технологическая карта урока.

Тема: «Теорема Пифагора»

Класс: 8б

Тип урока: урок открытия нового знания

Вид урока: комбинированный урок

Цель: познакомиться с  теоремой Пифагора, несколькими её доказательствами, применять теорему Пифагора в ходе решения задач.

Планируемые результаты:

·         Личностные: умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, выстраивать аргументацию;

·         Метапредметные:

ü  осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь;

ü  развитие способности видеть математическую задачу в других дисциплинах, в окружающей жизни;

ü  развитие способности организовывать учебное сотрудничество;

·         Предметные:

находить стороны прямоугольного треугольника, используя теорему Пифагора для решения задач практического характера и задач из смежных дисциплин.

Формы работы на уроке: индивидуальная,  работа в парах.

Техническое сопровождение: ноутбук, проектор.

Содержание основных этапов урока: