
Разработки уроков по математике, 6 класс
(Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд)
Урок 1
Цели: ввести понятие делителей и кратных чисел; научить находить делители числа и кратные числа; развивать логическое мышление учащихся.
Ход урока
I. Повторение материала.
I. Вспомнить правила действий с десятичными дробями:
а) сложение и вычитание десятичных дробей;
б) умножение десятичных дробей;
в) деление десятичной дроби на натуральное число, на десятичную дробь.
2. Устно решить № 22 (а – б), 20 (а – в), 15 (а, б), 16 (б).
П. Изучение нового материала.
1. Когда одно число делится на другое без остатка, то говорят, что первое число делится на второе. Каждое натуральное число делится на 1 и само на себя. Многие натуральные числа делятся не только на 1 и сами на себя, но и на другие натуральные числа. Например, число 15 делится на 1, на 3, на 5, на 15. Эти числа называются делителями числа 15.
2. Решение задачи.
20 яблок можно разделить поровну между 4 ребятами. Каждый получит по 5 яблок. А если надо разделить (не разрезая) 20 яблок между 6 ребятами, то каждый получит по 3 яблока, а еще 2 яблока останутся. Говорят, что число 4 является делителем числа 20, а число 6 не является делителем числа 20.
3. Определение делителя натурального числа а.
4. Устно решить задачу 1.
5. Задача № 2 (а, б) из учебника на странице 4.
6. Решение задачи.
Пусть на столе лежат пачки, в каждой из которых по 8 печений.
а) Не раскрывая пачек, сколько можно взять печений?
б) Можно ли взять 18 печений, 25 печений?
в) Говорят, что числа 8, 16, 24, 48 кратны числу 8, а числа -18, 25 не кратны числу 8.
7. Определение кратного натуральному числу а. Слово «крата» – старинное русское слово, означающее «раз».
8. Любое натуральное число имеет бесконечно много кратных. Их можно получить, если данное число умножить на 1, на 2, на 3, на 4 и т. д. Например, кратными числу 7 будут числа:
7 · 1 =7; 7 · 2= 14; 7 · 3 = 21 и т. д.
9. Число 0 кратно любому натуральному числу, так как 0 делится без остатка на любое натуральное число.
10. Устно решить задачи № 3 (а – е), с. 4 учебника.
11. Учащиеся самостоятельно читают текст под рубрикой Г (раздел «Говори правильно») на странице 5 учебника.
III. Закрепление изученного материала.
1. Решить № 5 (а; б) и № 4 на доске и в тетрадях.
2. Задачу № 8 учащиеся решают, комментируя решение с места.
3. Повторить понятие координатного луча и выполнить задания № 10 (рис. 1), на с. 6 учебника, № 17 (рис. 3), на с. 7 учебника.
IV. Итог урока.
Ответить на вопросы:
а) Какое натуральное число называют делителем данного числа?
б) Какое натуральное число является делителем каждого натурального числа?
в) Какое число является наибольшим делителем данного натурального числа?
г) Какое число называют кратным данному натуральному числу?
д) Какое число является кратным любому натуральному числу?
Домашнее задание: изучить пункт 1; решить № 27 (а; б), № 30 (а; б).
Урок 2
Цели: закрепить изученный материал и упражнять учащихся в нахождении делителей и кратных чисел; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить № 15 (в) и 16 (а). При решении учащиеся формулируют правила действий с десятичными дробями.
2. Ответить на вопросы к пункту 1 (на странице 4 учебника).
П. Работа по учебнику.
Прочитать исторический материал о делимости чисел по учебнику на странице 33 (1-й абзац).
III. Выполнение упражнений.
1. Устно решить № 5 (в; г).
2. С комментированием учащиеся в тетрадях решают № 7 (а; в; г) на с. 5 учебника.
3. Самостоятельно решить № 9.
4. Устно решить № 13.
5. Самостоятельно учащиеся решают №11 из учебника на с. 6.
Решение.
Делители числа 6:
1; 2 и 3; их сумма 1 + 2 + 3 = 6;
Делители числа 28:
1;2;4; 7; 14; их сумма 1+7 + 2 + 4+14 = 28.
Делители числа 496:
1; 2; 4; 8; 16; 31; 62; 124; 248; их сумма равна
1+2 + 4 + 8+16 + 31+62+ 124 + 248 = 496.
6. Повторение изученного ранее материала:
а) решить устно № 18;
б) решить на доске № 19 (в) и записать в тетради решение:
1075 = 37 · 29 + 2; неполное частное в = 37; остаток при делении г = 2.
Формула а = вс + г.
в) самостоятельно решить № 19 (а; б);
г) заполнить таблицу в упражнении № 21 (1-й и 3-й столбцы таблицы);
д) Задачу № 25 (1) решить на доске и в тетрадях. Решение.
1) 54,4 : 1,7 = 544 : 17 = 32 (кг) крупы было во втором мешке.
2) 32 + 2,6 = 34,6 (кг) крупы было в третьем мешке.
3) 54,4 + 32 + 34,6 = 121 (кг) крупы было в трех мешках. Ответ: 121 кг.
IV. Итог урока:
I. Какое число называют делителем данного натурального числа? Привести свои примеры.
2. Какое число называют кратным натуральному числу а? Привести свои примеры.
Домашнее задание: решить № 24, 26, 28 (г).
Урок 3
Цели: закрепить изученный материал в ходе выполнения упражнений; проверить знания и умения учащихся по изученному материалу.
Ход урока
I. Устная работа.
1. Сформулировать правила действий с десятичными дробями.
2. Решить устно № 15 (г).
3. Из чисел 10, 12, 15, 18, 25 назовите те, которые являются делителями числа:
а) 30; б) 36; в) 50; г) 60; д) 75.
4. Из чисел 30, 36, 50, 60, 75 назовите те, которые являются кратными числу:
а) 10; б) 12; в) 15; г) 18; д) 25.
II. Выполнение упражнений.
1. Устно решить № 22 (в, г).
2. Решить на доске и в тетрадях № 6 (в).
3. С комментированием на месте ученики решают № 6 (а; г).
4. Самостоятельно решить № 12.
5. Решить задачу № 14 (рис. 2), коллективно обсуждая ее решение, а затем полусамостоятельно записать в тетрадях ее решение.
6*. Решить задачи:
а) На складе имеются гвозди в ящиках по 16 кг, 17 кг и 40 кг. Может ли кладовщик отпустить 100 кг гвоздей, не вскрывая ящика?
Решение.
Числа, кратные числу 16: 16; 32; 48; 64; ...
Числа, кратные числу 17: 17; 34; 51; 68; ...
Числа, кратные числу 40: 40; 80; 120; 160; ...
Кладовщик может взять 2 ящика по 16 кг и 4 ящика по 17 кг, тогда он отпустит 100 кг гвоздей:
16 · 2 +17 · 4 = 32 + 68 = 100 (кг).
Ответ: может.
б) Из 48 красных и белых гвоздик составили букеты так, что на каждые 7 красных гвоздик пришлось 5 белых. Сколько было красных и белых гвоздик в отдельности?
Решение.
Числа, кратные числу 7: 7; 14; 21; 28; 35; ...
Числа, кратные числу 5: 5; 10; 15; 20; 25; ...
28 + 20 = 48 (гвоздик). Значит, в отдельности было 28 красных и 20 белых гвоздик.
Ответ: 28 красных; 20 белых.
III. Повторение изученного ранее материала.
1. Решить № 20 (г; д; е) на доске и в тетрадях.
2. Решить задачу № 25 (2).
Решение.
1) 4,5 · 1,4 = 6,3 (т) погрузили на вторую машину.
2) 6,3 – 1,6 = 4,7 (т) погрузили на третью машину.
3) 4,5 + 6,3 + 4,7 = 15,5 (т) погрузили на все три машины вместе.
Ответ: 15,5 т.
3. Устно решить № 21 (2-й столбец таблицы).
IV. Самостоятельная работа (10 мин).
Вариант I.
1. Напишите все делители: а) числа 30; б) числа 23.
2. Напишите шесть чисел, кратных: а) числу 13; б) числу 12; в) числу а.
3. Докажите, что: а) 22016 кратно 43; б) 89 является делителем 25276; в) 15534 не кратно 49; г) 83 не является делителем 35782.
Вариант II.
1. Напишите все делители: а) числа 24; б) числа 17.
2. Напишите шесть чисел, кратных:
а) 15; б) 18; в) числу k.
3. Докажите, что: а) 22154 кратно 53; б) 97 является делителем 20758; в) 17938 не кратно 43; г) 73 не является делителем 37382.
Домашнее задание: решить № 27 (в; г), 29, 30 (в).
Урок 1
Цели: изучить признаки делимости на 10, на 5 и на 2; ввести определение четных и нечетных чисел; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Результаты самостоятельной работы.
2. Выполнение заданий, вызвавших затруднения у учащихся.
3. Устно решить № 41, 44 и 39 (1-е задание каждого столбика).
II. Объяснение нового материала.
1. Для того чтобы узнать, делится ли одно число на другое, не всегда нужно выполнять деление. Существуют признаки, позволяющие в некоторых случаях получить ответ на этот вопрос уже по самой записи числа.
2. Мы знаем, что при умножении на 10 получается число, оканчивающееся нулем. Поэтому любое число, оканчивающееся цифрой 0, делится на 10. Остальные числа, не оканчивающиеся нулем, не делятся на 10.
Например, числа 340, 1280, 30500 делятся на 10; числа 445, 5007 не делятся на 10.
3. Известно также, что при умножении на 5 получается число, оканчивающееся нулем или пятеркой. Поэтому любое число, оканчивающееся цифрой 0 или цифрой 5, делится на 5.
Число, оканчивающееся любой другой цифрой, не делится на 5.
4. Привести примеры чисел, делящихся на 5 и чисел, не делящихся на 5.
5. Ввести определение четных и нечетных чисел. Цифры 0, 2, 4, 6, 8 называют четными, а цифры 1,3, 5, 7, 9 – нечетными.
6. Признак делимости на 2. Привести примеры чисел, делящихся на 2 и не делящихся на 2.
III. Закрепление изученного материала.
1. Устно решить № 32, 33 и 40.
2. Самостоятельно решить № 47 (с последующей проверкой).
3. На доске и в тетрадях решить № 52 (а; г).
Решение.
а) (х + 2,3) · 0,2 = 0,7 г) 0,39 : х – 0,1 = 0,16
х + 2,3 = 0,7 : 0,2 = 7 : 2 0,39 : х = 0,16 + 0,1
х + 2,3 = 3,5 0,39: х = 0,26
х = 3,5 -2,3 х = 0,39 : 0,26 = 39 : 26
х = l,2. х =1,5.
Ответ: х = 1,2. Ответ: х = 1,5.
4. Записать наибольшее пятизначное число, которое делится:
а) на 2; б) на 5; в) на 10; г) на 2 и на 5.
5. Записать цифрами 1; 3; 6; 5 два четырехзначных числа, которые:
а) делятся на 2;
б) делятся на 5.
IV. Итог урока.
Ответить на вопросы к пункту 2 на странице 9 учебника.
Домашнее задание: выучить правила п. 2; решить № 52, № 57 (а; в).
Урок 2
Цели: в ходе выполнения упражнений и решения задач закрепить знание признаков делимости на 2, на 5 и на 10.
Ход урока
I. Устная работа.
1. Решить № 41 (2-е и 3-е задания каждого столбика).
2. Решить № 42 по рисунку 4 учебника.
3. Устно № 45 решить, приводя примеры и записывая их на доске.
4. Сформулировать признаки делимости чисел на 2, на 5, на 10. Привести свои примеры.
II. Выполнение упражнений.
1. Какие из чисел 6538, 6780, 7835, 9391, 10032, 10060, 24575 делятся:
а) на 2; б) на 5; в) на 10.
2. Решить № 31 (устно).
3. Решить № 33 на доске и в тетрадях.
4. решить устно № 35 и № 37.
5. Написать три двузначных числа, кратных:
а) 2; б) 5; в) 2 и 5.
6. Решить № 52 (б, в) самостоятельно.
7. Решить задачу № 54 (1) на доске и в тетрадях.
Решение.
Пусть задумано число х.
11х – 2,75 = 85,25
11х = 85,25 + 2,75
11х = 88
х = 8.
Ответ: число 8.
8. Назовите все четные числа, находящиеся между числами 30 и 45.
9. Назовите нечетные числа, находящиеся между числами 51 и 66.
III. Итог урока.
1. Как по записи натурального числа определить, делится оно без остатка на 10 или не делится на 10?
2. Как по записи натурального числа узнать, делится оно без остатка на 5 или не делится на 5?
3. Как по записи натурального числа узнать, делится оно без остатка на 2 или не делится на 2?
Домашнее задание: выучить правила пункта 2; решить № 57, № 55, № 56 (а), № 59 (б).
Урок 3
Цели: способствовать выработке умений и навыков в применении признаков делимости на 10, на 5 и на 2 при выполнении упражнений и решении задач.
Ход урока
I. Повторение изученного материала.
1. Устно решить № 41 (4-е и 5-е задания каждого столбика).
2. Устно решить № 50, 51.
3. Сформулировать признаки делимости на 10, на 5 и на 2.
4. Игра «Кто самый внимательный».
Учитель называет любые числа, делящиеся на 2, на 5 или на 10 и не делящиеся на 2, на 5, на 10. Если числа делятся на 2, на 5 или на 10, то ученик поднимает руку; если не делятся на 2, или на 5, или на 10, то не поднимают руку.
II. Тренировочные упражнения.
1. Какие из чисел 6754, 8755, 9348, 10020, 20037, 108025, 60029 и 10000 делятся: а) на 2; б) на 5; в) на 10.
2. Напишите два пятизначных числа: а) кратных 2; б) кратных 5.
3. Напишите два шестизначных числа: а) кратных 2 и 5; б) крат-ных 5 и 10.
4. Запишите все четные числа, которые удовлетворяют неравенству 257 < x < 270.
5. Запишите все нечетные числа, которые удовлетворяют неравенству 1237 < x < 1242, и все нечетные числа, которые удовлет-воряют неравенству 1237 < x < 2395.
6. Устно решить задачи № 32 и № 49.
7. Решить № 38 самостоятельно с последующей проверкой.
8. Устно решить № 34. Сформулировать признаки делимости на 100, на 1000.
9. Решить задачу № 54 (2) на доске и в тетрадях.
Решение.
I способ (арифметический).
1) 110 : 11 = 10;
2) 10 – 9,2 = 0,8.
Ответ: 0,8.
II способ (с помощью уравнения).
Пусть задумано число х.
(х + 9,2) · 11 = 110
х + 9,2 = 110 : 11
х + 9,2 = 10
х = 10 – 9,2
х = 0,8.
Ответ: 0,8.
10*. Как разделить поровну 8 л молока, если молоко находится в восьмилитровом ведре, а имеется 2 пустых бидона – трехлитровый и пятилитровый?
III. Итог урока.
Сформулировать признаки делимости на 2, на 5, на 10, на 100, на 1000.
Домашнее задание: повторить правила п. 2; решить № 55, № 56 (б), № 57 (г).
Урок 1
ПРИЗНАК
ДЕЛИМОСТИ НА 9
Цели: изучить признак делимости на 9 и закрепить его знание при решении задач; выработать навыки применения этого признака при выполнении упражнений.
Ход урока
I. Устная работа (10 мин).
1. Решить № 69 (первые и вторые задания каждого столбика).
2. Решить № 61, 66 и 70.
II. Изучение нового материала.
1. Мы изучили признаки делимости на 10, на 5 и на 2, в которых узнали, делится или не делится число на 10, 5 и 2.
Иначе «устроены» признаки делимости на 9 и на 3. На этом уроке мы изучим признак делимости на 9.
2. Узнаем, не выполняя деления, можно ли 846 яиц разложить в 9 корзин поровну. (Решение этой задачи приведено в учебнике на странице 13.)
3. Формулировка признака делимости на 9.
4. Учащиеся называют числа, которые делятся на 9, и находят сумму цифр числа.
5. Делятся ли числа 225, 321, 675, 1004, 2382, 2841, 7235, 6264 на 9?
III. Закрепление изученного материала.
1. Решить № 62 (самостоятельно).
2. Решить № 64 (б) на доске и в тетрадях.
3. Устно решить № 75.
4. Найдите неизвестную цифру числа, обозначенную *, если известно, что оно делится на 9:
318*; *56; 48 * 25; 8 * 1.
5. Повторить ранее изученный материал, решив задания:
а) № 84 (1; 3) на доске и в тетрадях.
Решение.
1) 17n – 11n – 2n = 511 3) 4x + 6x – x = 21,6
n · (17 – 11 – 2) = 511 x(4 + 6 –1) = 21,6
4n = 511 x (4 + 6 –1) = 21,6
n = 511 ; 4 9x = 21,6
n = 127,75. x = 21,6 : 9
x = 2,4.
Ответ: n = 127,75. Ответ: х = 2,4.
б) Устно решить № 74.
в) Вычислите (54,72 : 5,7 + 1,3 · 4,5) : 5 – 3,01.
Учитель записывает на доске числа:
а) 54,72; б) 15,45; в) 1; г) 0,08.
Учащиеся решают пример, получают ответ и среди этих чисел находят получившийся у них ответ. (Это задание подготавливает учащихся к тестированию.)
IV. Итог урока.
Повторить признак делимости на 9, привести примеры.
Домашнее задание: выучить признак п. 3 (1); решить № 86, № 91 (а; б), № 92.
Урок 2
ПРИЗНАК
ДЕЛИМОСТИ НА 3
Цели: изучить признак делимости на 3; закрепить знание признаков делимости на 9, на 2, на 5 и на 10; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить № 69 (3-е и 4-е задания каждого столбика).
2. Решить № 72 (а; б).
3. Решить № 76, № 77 и № 78 (повторить признаки делимости на 10 и на 5).
II. Объяснение нового материала.
1. Разделим на 3 каждое из чисел:
162, 201, 111, 205, 317, 824. Обнаружим, что первые три числа делятся на 3, а последние три числа не делятся на 3. Обратим внимание, что сумма цифр каждого из трех первых чисел делится на 3.
2. Сформулировать признак делимости на 3.
3. Выпишите числа, которые делятся на 3:
123; 110; 834; 2383; 882; 1111.
4. Верно ли утверждение:
а) Если число делится на 9, то оно делится на 3? Ответ объясните.
б) Если число делится на 3, то оно делится на 9? Привести примеры.
5. Придумайте 3 числа, которые:
а) делятся на 2 и на 3;
б) делятся на 3 и на 5;
в) делятся на 10 и на 9.
III. Закрепление изученного материала.
1. Самостоятельно решить № 65 и № 63.
2. Решить № 71 (а) на доске и в тетрадях.
3. Устно решить № 67, 68.
4. Напишите два пятизначных числа:
а) кратных 3; б) кратных 2 и 3.
5. Решить № 82 и № 83 (на доске и в тетрадях).
Решение.
№ 82. ![]()
№ 83. ![]()
IV. Итог урока.
Как по записи натурального числа узнать, делится оно на 3 или не делится на 3?
Домашнее задание: выучить правила п. 3; решить № 87, № 90, № 91 (в; г).
Урок 1
Цели: ввести понятие простых и составных чисел; познакомить с таблицей простых чисел и научить учащихся использовать таблицу при выполнении заданий.
Ход урока
I. Устная работа.
1. Решить № 103 (1-е и 2-е задания каждого столбика).
2. Решить № 111.
3. Двое учащихся работают на доске: выполняют домашние задания № 90 и № 91 (в; г).
4. Вопросы: а) Какое число называют делителем данного натурального числа?
б) Какое число является делителем любого натурального числа?
II. Объяснение нового материала.
1. Найти делители чисел 7, 9 и 18.
2. Определение простого числа; определение составного числа. Привести примеры.
3. Число 1 не считают ни простым, ни составным.
4. Первыми десятью простыми числами являются 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Число 2 – наименьшее простое число. Это – единственное четное простое число, остальные простые числа нечетные.
5. Познакомить с таблицей простых чисел на форзаце учебника.
6. Любое составное число можно разложить на два множителя, каждый из которых больше 1. Простое число так разложить на множители нельзя.
III. Закрепление изученного материала.
1. Решить № 93 на доске и в тетрадях.
2. Устно решить № 94, 95, 96.
3. Разложить всеми возможными способами число 24:
а) на два множителя;
б) на три множителя;
в) на четыре множителя.
4. Решить № 107 (а, в) с комментированием.
5. Решить задачу.
Маша задумала число и сказала, что это число меньше 30; его называют, когда считают тройками и когда считают пятерками. Назовите это число.
Ответ: 15.
6. Известно, что число делится на 2, 3 и 5. На какие еще числа делится это число?
7. Придумайте несколько чисел, которые имеют только три делителя. Какую закономерность можно заметить?
IV. Итог урока.
Какие натуральные числа называют простыми? Какие натуральные числа называют составными? Почему число 1 не является ни простым, ни составным?
Домашнее задание: изучить п. 4; выучить правила; решить № 115, № 116, № 117.
Урок 2
Цели: выработать навыки и умения разложения чисел на множители; повторить понятие процента числа и нахождения дроби от числа; развивать логическое мышление учащихся.
Ход урока
I. Повторение изученного материала.
1. Устно решить № 103 (3-е и 4-е задания каждого столбика).
2. Что называется процентом? Как выразить в процентах числа?
3. Устно решить № 105 и № 106.
4. Решить устно № 104 (для а = 33).
II. Работа по учебнику.
1. Изучить по учебнику исторический материал «Решето» Эратосфена на страницах 33–34.
2. В настоящее время составление таблиц простых чисел можно «поручить» компьютерам, с их помощью уже получены огромные простые числа, которые «вручную», наверно, никогда бы не были найдены.
Однако компьютеры, даже и очень мощные, тоже имеют ограниченные возможности. И возникает такой естественный вопрос: можно ли построить, хотя бы в далеком будущем, такой мощный компьютер, чтобы он нашел, наконец, все простые числа? Оказывается, что ответ на этот вопрос уже есть и найден… больше двух тысяч лет назад. Мы уже прочитали, что великий математик Древней Греции Евклид доказал, что полный список составить просто невозможно. Можно сказать также, что среди простых чисел нет самого большого числа. Так две с лишним тысячи лет назад Евклид лишил математиков надежды получить когда-нибудь полный список простых чисел.
III. Выполнение тренировочных упражнений.
1. Устно решить № 98 и № 97.
2. Решить № 99 на доске и в тетрадях.
3. Самостоятельно решить № 100.
4. Устно решить № 101 и № 102.
5. Повторить признаки делимости на 2 и на 9.
Решить № 110 (б; г).
6. Повторить нахождение дроби от числа. Решить задачу № 113.
7. Решить № 108 на доске и в тетрадях.
IV. Итог урока.
1. Повторить определение простого и составного чисел.
2. Найдите два составных числа х, которые удовлетворяют неравенству 22 < x < 31.
3. Найдите два простых числа, каждое из которых больше 10 и меньше 20.
Домашнее задание: повторить п. 2 и 3; решить № 118, 119, 120.
рАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ
Урок 1
Цели: познакомить учащихся с разложением на простые множители числа; повторить признаки делимости чисел и научить использовать их при разложении чисел на простые множители.
Ход урока
I. Устные упражнения.
1. Решить № 125 (1-е и 2-е задания каждого столбика).
2. Устно решить № 126 и № 132 (а–в).
3. Изучением свойств простых чисел занимался русский математик Пафнутий Львович Чебышев. Он доказал, что между любым натуральным числом, большим 1, и числом, вдвое большим, всегда имеется не менее одного простого числа. Проверить это на примере нескольких чисел.
II. Изучение нового материала.
1. Задача. Нужно выделить участок земли прямоугольной формы площадью 18 м2. Какими могут быть размеры этого участка, если они должны выражаться натуральными числами?
Решение.
1) 18 = 1 · 18; 2) 18 = 2 · 9; 3) 18 = 3 · 6.
Ответ: размеры участка могут быть: 1 м и 18 м; 2 м и 9 м; 3 м и 6 м.
Решая задачу, мы число 18 представили в виде произведения натуральных чисел. Говорят: разложили на множители. Если в разложении, например, числа 18 = 3 · 6 составной множитель 6 представить в виде произведения двух простых множителей 2 и 3, то тогда число 18 будет разложено на простые множители: 18 = 3 · 6 = = 3 · 2 · 3. Обычно записывают множители в порядке возрастания: 18 = 2 · 3 · 3.
2. Разложить (натуральное) число на простые множители – значит представить это число в виде произведения простых чисел.
3. Нередко для разложения натурального числа на простые множители сначала разлагают его в виде произведения составных множителей, а затем каждый из них разлагают на простые множители.
4. Прочитать по учебнику теоретический материал (п. 5) на с. 20–21.
5. Записать на доске и в тетрадях несколько первых простых чисел:
2; 3; 5; 7; 11; 13; 17; 19;…
Объяснение учителем разложения числа 3276 на простые множители (повторяются признаки делимости чисел на 2, на 3, на 5).

III. Закрепление изученного материала.
1. Разложить число на простые множители:
а) 16; б) 18; в) 15; г) 20; д) 72; е) 150.
2. Решить № 121 (а) на доске и в тетрадях.
3. Решить с комментированием № 122 (а).
4. Решить № 124 (а; б) с объяснением.
5. Повторение ранее изученного материала:
а) решить № 127 и 132 (г; д; е);
б) решить задачу № 133.
6*. Знаменитый ученый Христиан Гольдбах (1690–1764), работавший в Петербургской академии наук, высказал догадку (в 1742 г.), что любое натуральное число, большее 5, может быть представлено в виде суммы трех простых чисел. Проверить это на примере нескольких чисел.
IV. Итог урока.
Вопросы:
а) Существуют ли составные числа, которые нельзя разложить на простые множители?
б) Чем могут отличаться два разложения одного и того же числа на простые множители?
Домашнее задание: изучить п. 5; решить № 141 (а), № 142 (а; в), № 143, № 140 (устно).
Урок 2
Цели: выработать навык разложения чисел на простые множители; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить № 125 (3-е и 4-е задания каждого столбика).
2. Решить № 126, 128 и 129.
3. Проверить выполнение учащимися домашнего задания:
а) устно № 140 по рисунку 6 учебника;
б) устно по тетрадям проверить № 142 (а; в);
в) на доске один учащийся записывает решение задачи № 143.
Решение.
Пусть первый тракторист вспахал х га земли, тогда второй вспахал 1,2х га.
Вместе они вспахали 12,32 га земли. Составим и решим уравнение:
х + 1,2х = 12,32
2,2х = 12,32
х = 12,32 : 2,2 = 123,2 : 22
х = 5,6.
Первый тракторист вспахал 5,6 га земли, второй вспахал 12,32 – 5,6 = 6,72 (га).
Ответ: 5,6 га; 6,72 га.
II. Выполнение упражнений.
1. Решить № 121 (б; в) на доске и в тетрадях.
Показать более простой способ разложения на простые множители чисел, оканчивающихся нулями: так как 10 т = 2 · 5, то
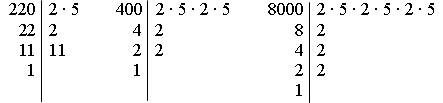
220 = 22 · 5 400 = 22 · 22 · 52 8000 = 26 · 53
2. Решить № 122 (б) самостоятельно (с последующей проверкой).
3. Устно решить № 124 (в; г).
4. Решить № 123 с комментированием.
5. Повторение материала:
а) решить № 131.
Ответ: ![]()
б) решить № 135.
6. Самостоятельно решить № 139 (1; 3).
III. Итог урока.
Вопросы:
1) Что значит разложить число на простые множители?
2) Сформулировать признаки делимости на 2, на 5, на 10, на 3, на 9.
Домашнее задание: изучить п. 5; решить № 141 (б), № 142 (б), № 144 (а).
НОД. ВЗАИМНО ПРОСТЫЕ ЧИСЛА
Урок 1
Цели: ввести понятие наибольшего общего делителя и показать нахождение наибольшего общего делителя; дать определение взаимно простых чисел.
Ход урока
I. Устная работа.
1. Решить № 154 (а; б) и № 158.
2. Решить № 159.
II. Подготовка к изучению нового материала.
1. Решить № 160 с комментированием.
2. Решить № 157 (а) на доске и в тетрадях (вызвать к доске сразу трех учащихся).
3. Решить № 146 (а).
III. Изучение нового материала.
1. Разобрать решение задачи на с. 25 учебника.
2. Определение НОД (наибольшего общего делителя).
3. Определение взаимно простых чисел.
4. Правило нахождения наибольшего общего делителя нескольких натуральных чисел.
5. Иногда наибольшим общим делителем чисел является наименьшее из данных чисел. Например, для чисел 13, 26 и 39 наибольшим общим делителем будет число 13.
Просто определить наибольший общий делитель также, например, таких чисел 300, 500 и 700:
НОД (300; 500; 700) = 100.
IV. Закрепление нового материала.
1. Назовите два числа, для которых наибольшим делителем будет число: 9; 11; 13; 20; 25; 30.
2. Решить № 146 (б; в).
3. Устно решить № 144 (б).
4. Решить № 148 (а) с комментированием.
5. Решить № 149 (а; в) на доске и в тетрадях.
6. решить задачу:
Какое наибольшее число одинаковых подарков можно сделать из 320 орехов, 240 конфет и 200 шоколадок? Сколько конфет, орехов и шоколадок будет в каждом пакете?
Решение.
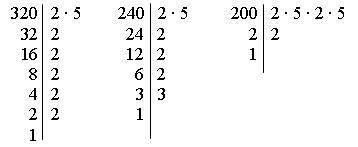
НОД (320; 240; 200) = 2 · 2 · 2 · 5 = 40.
Можно сделать 40 одинаковых подарков, в каждом пакете будет по 8 орехов; по 6 конфет, по 5 шоколадок.
7. Самостоятельно решить задачу № 138 (1).
V. Итог урока.
Вопросы:
1) Какое число называют наибольшим общим делителем двух натуральных чисел?
2) Какие два числа называют взаимно простыми?
3) Как найти наибольший общий делитель нескольких натуральных чисел?
Домашнее задание: выучить правила п. 6; решить № 169 (а), 170 (а), 173, 177.
Урок 2
Цели: отрабатывать навыки разложения чисел на простые множители и нахождения наибольшего общего делителя; закрепить знания и умения при нахождении дроби от числа.
Ход урока
I. Устная работа.
1. Решить № 154 (в; г; д).
2. Решить № 155, используя рисунок 7 учебника.
3. Какое число называют наибольшим общим делителем данных чисел?
Найдите наибольший общий делитель чисел: 1) 10 и 30; 2) 8 и 12; 3) 11 и 33; 4) 5 и 21; 5) 28 и 14; 6) 18; 27; 45; 7) 24; 36 и 48.
4. Какие два числа называют взаимно простыми? Найдите число, взаимно простое с числом: 6; 9; 15; 21; 25; 32; 40.
II. Выполнение упражнений.
1. Решить № 157 (б). Вызвать трех учеников к доске, каждый из них раскладывает одно из чисел на простые множители, остальные учащиеся в тетрадях раскладывают все данные числа на множители, а затем проверяют решение.
2. Решить задачу № 152 на доске и в тетрадях.
Решение.

3. Решить № 145 (б) с комментированием.
4. Решить № 148 (б; д) на доске и в тетрадях.
5. Решить № 147 (часть устно, некоторые письменно).
6. Повторение материала:
а) Решить задачу № 165 (1).
Решение.
1) 820 : 5 · 2 = 328 (м) отремонтировали во вторник;
2) 820 – 328 = 492 (м) осталось отремонтировать;
3) 492 : 3 · 2 = 328 (м) отремонтировали в среду;
4) 492 – 328 = 164 (м) отремонтировали в четверг.
Ответ: 164 м.
б) Решить № 166 и № 167.
III. Итог урока.
Доказать, что взаимно простые числа: 35 и 72; 27 и 28.
Домашнее задание: п. 6; решить № 169 (б); № 170 (б; в), № 175, 178 (б).
Урок 3
Цели: упражнять в нахождении наибольшего общего делителя; проверить знания учащихся и выявить пробелы; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить № 159 и № 162.
2. Решить задачу:
Какое наибольшее число одинаковых комплектов можно составить из елочных игрушек, если имеется:
8 зайцев, 24 лисицы, 16 морковок и 48 яблок? По скольку зайцев, лисиц, морковок и яблок будет в каждом комплекте?
II. Выполнение упражнений.
1. Решить № 151 на с. 26 учебника.
Ответ: ![]()
2. Решить № 148 (г; е) на доске и в тетрадях.
3. Решить задачу № 153.
Решение.

Или можно решить по-другому:
1) 424 + 477 = 901 (человек) поехали за город.
2) 901 : 53 = 17 (автобусов) было выделено.
4. Решить № 157 (2) (коллективное решение, а затем полусамостоятельно в тетрадях записывают решение задачи).
III. Самостоятельная работа (10–15 мин).
Вариант I.
1. Найдите наибольший общий делитель чисел 7425 и 12375.
2. Запишите два простых числа у, которые удовлетворяют неравенству 17 < y < 24.
3. Докажите, что 209 и 171 не взаимно простые.
4. На станции стоят три пассажирских поезда: в первом – 418 мест в купейных вагонах, во втором – 494, а в третьем – 456. Сколько купейных вагонов в каждом поезде, если в каждом вагоне одинаковое число мест и их число больше 20?
Вариант II.
1. Найдите наибольший общий делитель чисел 1456 и 1560.
2. Запишите два простых числа у, которые удовлетворяют неравенству 19 < y < 30.
3. Докажите, что числа 299 и 184 не взаимно простые.
4. На нефтебазу прибыло три состава цистерн с нефтью: в первом составе было 360 т нефти, во втором – 432 т, а в третьем – 792 т. Сколько цистерн с нефтью было в каждом составе, если в каждой цистерне одинаковое число тонн нефти и это число больше 50?
IV. Итог урока.
Домашнее задание: решить № 170 (г), 171, 172, 174, 178 (а).
НОК.
Урок 1
Цели: ввести понятие наименьшего общего кратного; изучить правило нахождения наименьшего общего кратного и научить учащихся находить его при решении задач.
Ход урока
I. Анализ самостоятельной работы.
1. Указать ошибки, допущенные учащимися при выполнении работы.
2. Решить на доске и в тетрадях задания, вызвавшие затруднения у учащихся.
II. Устная работа.
1. Решить № 186 (а; б).
2. Решить № 189 (а; б) и № 190 (г).
III. Объяснение нового материала.
1. Задача. Из порта А в порт В одновременно вышли два теплохода. Первый из них тратит на рейс туда и обратно 3 суток, а второй 4 суток. Через сколько суток оба теплохода окажутся снова вместе в порту А?
Решение.
Искомое число суток должно делиться и на 3, и на 4, то есть оно должно быть общим кратным чисел 3 и 4. Запишем кратные каждого из этих чисел в порядке возрастания:
Числа, кратные 3: 3; 6; 9; 12; 15; 18; 21; 24; 27; 30; 33; 36.
Числа, кратные 4: 4; 8; 12; 16; 20; 24; 28; 32; 36, …
Общие кратные чисел 3 и 4 (они подчеркнуты): 12; 24; 36; … Наименьшее из этих чисел – число 12. Значит, через 12 суток оба теплохода окажутся снова вместе в порту А. При этом первый теплоход совершит за это время 4 рейса туда и обратно (12 : 3 = 4), а второй – 3 рейса (12 : 4 = 3).
Наименьшее натуральное число, которое делится на каждое из данных натуральных чисел, называется наименьшим общим кратным.
2. Изучить по учебнику пункт 7 на с. 29–30.
3. Изучить правило нахождения наименьшего общего кратного для трех и более чисел.
4. Решить устно № 179 (а).
IV. Закрепление изученного материала.
1. Решить № 180 (а; б) с комментированием.
2. Решить № 181 (а; г; е) на доске и в тетрадях.
Решение.
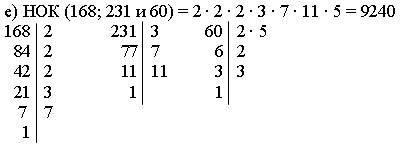
Ответ: 9240.
3. Повторение изученного ранее материала:
а) Решить № 195 и № 196 с комментированием.
б) Решить № 201, используя таблицу простых чисел на форзаце учебника.
V. Итог урока.
Вопросы:
1) Какое число называют наименьшим общим кратным натуральных чисел а и в?
2) Как найти наименьшее общее кратное нескольких чисел?
3) Какое число является наименьшим общим кратным чисел m и n, если число m кратно числу n?
Домашнее задание: изучить п. 7; решить № 202 (а), № 203 (а), № 206 (а; в).
Урок 2
Цели: способствовать выработке навыков нахождения наименьшего общего кратного; учить применять наименьшее общее кратное чисел при решении задач; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить № 186 (в; г) и № 189 (в; г).
2. Укажите среди данных произведений разложение числа 700 на простые множители:
а) 4 · 5 · 5 · 7; б) 2 · 2 · 7 · 25; в) 2 · 2 · 5 · 5 · 7; г) 2 · 14 · 25.
Ответ: в).
3. Найдите НОД чисел 350; 420 и 210.
Ответ: 70.
4. Найдите НОК чисел 40; 60 и 70.
Ответ: 840.
II. Выполнение упражнений.
1. Решить № 179 (б) и № 180 (в) на доске и в тетрадях.
2. Решить № 181 (в) (коллективное обсуждение решения, а затем самостоятельное решение учащимися).
3. Решить задачу № 184.
Решение.
45 = 3 · 3 · 5; 60 = 2 · 5 · 2 · 3
НОК (45; 60) = 2 · 5 · 2 · 3 · 3 = 180.
Ответ: 180 м.
4. Решить задачу.
Какой наименьшей длины ленту должна купить Мальвина, чтобы разрезать ее на ленты по 35 см или по 50 см, не получив обрезков?
Решение.
35 = 5 · 7; 50 = 2 · 5 · 5; НОК (35; 50) = 2 · 5 · 5 · 7 = 350.
Ответ: 350 см = 3 м 50 см.
5. Проверить равенство НОК (а; в) · НОД (а; в) = а · в, если а = 28, в = 21.
Решение.
28 = 2 · 2 · 7; 21 = 3 · 7.
НОД (28; 21) = 7; НОК (28; 21) = 2 · 2 · 7 · 3 = 84.
а · в = 28 · 21 = 588; НОК (а; в) · НОД (а; в) = 84 · 7 = 588.
Равенство верно.
III. Повторение ранее изученного материала.
1. Решить № 191.
2. Как находится среднее арифметическое чисел?
Решить № 198.
3. Решить задачу № 199.
Решение.
Пусть второе число равно х, тогда первое число 2х.
(х + 2х) : 2 = 54
3х = 54 · 2
3х = 108
х = 108 : 3
х = 36.
Второе число равно 36, первое число 72.
Ответ: 72 и 36.
4. Самостоятельно решить задание –
найти наибольший общий делитель чисел:
а) 465 и 870; б) 645 и 680.
IV. Итог урока.
1. Повторить правило нахождения НОК.
2. Найти наименьшее общее кратное чисел (устно):
а) 3 и 7; б) 8 и 6; в) 9 и 14; г) 180 и 120.
Домашнее задание: изучить п. 7; решить № 202 (б; в), № 204, № 207, № 210 (а).
Урок 3
Цель: тренировать учащихся в нахождении НОД и НОК чисел при выполнении упражнений.
Ход урока
I. Устная работа.
1. Решить № 188, 189 (д; е) и № 192.
2. Найти наибольший общий делитель и наименьшее общее кратное чисел:
а) 5 и 25; б) 25 и 75; в) 8; 12 и 24; г) 18; 27 и 54; д) 60; 40; 120; е) 2 и 3; ж) 8 и 9; з) 5; 8 и 3; и) 120; 180 и 360.
II. Тренировочные упражнения.
1. Решить № 180 (г) с комментированием.
2. Решить № 181 (д) на доске и в тетрадях.
3. Решить № 182 с обсуждением и решением в тетрадях. Записать вывод: наименьшее общее кратное двух взаимно простых чисел равно произведению этих чисел.
4*. Решить задачу: Саша ходит в бассейн один раз в 3 дня, Вася – в 4 дня, а Ваня – в 5 дней.
Они встретились в бассейне в этот понедельник. Через сколько дней и в какой день недели они встретятся снова?
Решение.
НОК (3; 4; 5) = 60. Через 60 дней, в пятницу (60 : 7 = 8 недель и 4 дня пройдет) они встретятся снова.
Ответ: через 60 дней, в пятницу.
5. Решить самостоятельно задачу:
Какой наименьшей длины должна быть доска, чтобы ее можно было разрезать поперек на части, равные 20 см или 27 см, не получив обрезков?
НОК (20; 27) = 540.
Длина доски должна быть 540 см = 5 м 40 см.
Ответ: 5 м 40 см.
6. Решить № 175 на доске и в тетрадях. Сделать вывод.
III. Самостоятельная работа (10–15 мин).
Вариант I.
1. Найдите наименьшее общее кратное чисел:
а) 18 и 27; б) 7875 и 4725.
2. На базар привезли арбузы. Если их считать десятками, то получится целое число десятков. Если их считать дюжинами (по 12), то опять получится целое число дюжин. Сколько арбузов привезли на базар, если их больше 300, но меньше 400?
3. Проверьте
равенство НОК (m; n) = ![]() если m = 35, n = 49.
если m = 35, n = 49.
Вариант II.
1. Найдите наименьшее общее кратное чисел:
а) 40 и 56; б) 7425 и 4455.
2. Солдаты выстроились в ряды, по 12 человек в каждом, а затем перестроились по 8 человек в ряду. Сколько было солдат, если их больше 180, но меньше 200?
3. Проверьте
равенство НОД (с; d) = ![]() если с = 42, d = 35.
если с = 42, d = 35.
IV. Итог урока.
Повторить выводы упражнений № 182 и 183, придумать свои примеры.
Домашнее задание: решить № 202 (г), № 205, № 208, № 210 (б).
Урок 4
Цели: повторение и закрепление изученного материала, подготовка к контрольной работе; способствовать развитию навыков решения задач и упражнений.
Ход урока
I. Анализ самостоятельной работы.
Указать сделанные учениками ошибки и решить задачи, вызвавшие затруднения у учащихся.
II. Устные упражнения.
1. Решить № 190 (б; в) и № 193.
2. Решить № 187.
III. Выполнение упражнений.
1. Решить № 181 (б) самостоятельно.
2. Найти наименьшее общее кратное чисел:
а) 48 и 72; б) 350 и 420.
3. Найти наибольший общий делитель чисел 840 и 1260.
4. Доказать, что числа 136 и 119 не взаимно простые.
5. Решить задачу № 185.
НОК (15; 20; 12) = 2 · 2 · 3 · 5 = 60
15 = 3 · 5; 20 = 2 · 5 · 2; 12 = 2 · 2 · 3.
Ответ: через 60 суток.
6. Повторение материала:
а) Решить задачу № 200 (1) с коллективным обсуждением и решением на доске и в тетрадях.
б) Самостоятельно решить № 200 (2).
Решение.
1) Пусть во второй день израсходовали х т керосина, тогда в первый день – 2,4х т.
х + 2,4х = 38 –9,1
3,4х = 28,9
х = 28,9 : 3,4 = 289 : 34
х = 8,5.
Во второй день израсходовали 8,5 т, тогда в первый день 20,4 т.
Ответ: 20,4 т.
2) Пусть после обеда выдали у т муки, тогда до обеда выдали 3,2у т.
у + 3,2у = 19 – 4,3
4,2у = 14,7
у = 14,7 : 4,2 = 147 : 42
у = 3,5.
До обеда выдали 3,5 · 3,2 = 11,2 (т).
Ответ: 11,2 т.
IV. Итог урока. Беседа о свойствах НОД и НОК.
Домашнее задание: решить № 203 (б), 206 (б; г), № 209, № 170 (б; в).
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ
ДЕЛИТЕЛИ И КРАТНЫЕ
Урок 1
Цели: ввести понятие делителей и кратных чисел; научить находить делители числа и кратные числа; развивать логическое мышление учащихся.
Ход урока
I. Анализ контрольной работы.
Обратить внимание учащихся на сделанные ошибки, решив неправильно выполненные задания.
II. Устная работа.
1. Решить № 222 (а; б).
2. Решить № 226, используя рисунок 12.
III. Объяснение нового материала.
1. Объяснение учителем материала пункта 8 с использованием рисунка 8 учебника и модели «Доли. Дроби» (с. 34–35).
2. Записать в тетрадях основное свойство дроби: «Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь».
Примеры: а) умножьте числитель и знаменатель каждой дроби на 2:
![]()
б) разделите числитель и знаменатель каждой дроби на 3:
![]()
IV. Закрепление изученного материала.
1. Решить устно № 211 по рисунку 9 учебника.
2. Решить устно № 212 (а; б) по рисунку 10.
3. Решить № 214 на доске и в тетрадях.
Учитель пользуется цветными мелками, а ученики цветными карандашами при изображении отрезков.
4. Самостоятельно учащиеся выполняют задания № 216 и № 217 (с последующей проверкой).
5. Устно решить № 221 (а), № 213 (а; б) и № 219.
V. Повторение ранее изученного материала.
1. Решить № 224 на доске и в тетрадях.
Решение.
а) 23 + 2,6 = 8 + 2,6 = 10,6;
в) (1,6 –0,7)2 = 0,92 = 0,81;
б) 0,32 + 1,1 = 0,09 + 1,1 = 1,19;
г) (0,6 · 0,5 + 0,7)3 = (0,3 + 0,7)3 = 13 =1.
2. Решить № 231 на доске и в тетрадях (вызвать к доске сразу четвертых учащихся, они решают на доске, учащиеся самостоятельно решают в тетрадях, а затем проверяют решение).
Решение.
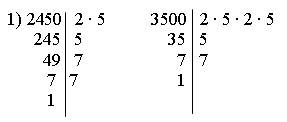
НОД (2450; 3500) = 2 · 5 · 5 · 7 = 350.
НОК (2450; 3500) = 2 · 5 · 2 · 5 · 5 · 7 · 7 = 3500 · 7 = 24500.

VI. Итог урока.
Ответить на вопросы:
1) Сформулируйте основное свойство дроби.
2) Изменится ли дробь, если ее числитель и знаменатель умножить на 15, а потом разделить на 3?
Домашнее задание: изучить п. 8; решить № 237, № 239 (а); № 241 (а).
Урок 2
Цели: способствовать выработке навыков и умений учащихся при решении задач и упражнений; научить применять основное свойство дроби при выполнении упражнений.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Двое учащихся работают на доске:
а) первый решает задачу № 233 (1);
б) второй учащийся решает № 241 (б).
2. Устно решить № 222 (в; г; д).
3. Устно решить № 223.
II. Работа по учебнику.
Прочитать по учебнику раздел «Говорите правильно» на странице 35.
III. Выполнение упражнений.
1. По рисунку 10 устно решить № 212 (в; г).
2. Устно решить № 213 (а). Повторить основное свойство дроби. Решить № 220 на доске и в тетрадях.
3. Решить № 215, начертив на доске и в тетрадях координатный луч.
4. Решить устно № 218 и 221 (в –г) с коллективным обсуждением.
5. Повторение изученного материала:
а) Решить № 230 (1) с комментированием.
б) Устно решить № 234.
в) Решить самостоятельно: № 235.
8,12 · 0,25 + 3,24 · 0,25 = 0,25 · (8,12 + 3,24) = 0,25 · 11,36 = 2,84.
г) Решить № 233 (2).
Решение.
1) 5,2 · 4,5 = 23,4 (км) прошли по дороге.
2) 32,4 – 23,4 = 9 (км) осталось пройти.
3) 9 : 2,5 = 90 : 25 = 3,6 (ч) шли по болотистой местности.
4) 4,5 + 1,6 + 3,6 = 9,7 (ч) затрачено на весь переход.
Ответ: 9,7 ч.
IV. итог урока.
1. Используя основное свойство дроби, найдите значения х:
а) ![]()
2. Беседа об истории дробей (прочитать исторический материал на с. 116).
Домашнее задание: выучить определения из п. 8; решить № 238, № 239 (б), № 240 (а; б; в), № 241 (б).
СОКРАЩЕНИЕ ДРОБЕЙ
Урок 1
Цели: повторить основное свойство дроби и научить применять его при сокращении дробей; дать определение несократимой дроби.
Ход урока
I. Устная работа.
1. Решить № 253 (а; б).
2. Решить № 256. Повторить основное свойство дроби.
3. Решить № 257 (а; б).
II. Изучение нового материала.
1. Подготовительные упражнения к изучению нового материала:
а) повторить основное свойство дроби; привести свои примеры;
б) устно решить № 261 (а; б) и № 260 (а; б).
2. Числитель и
знаменатель дроби ![]() При этом
получилась дробь, значение которой равно данной дроби, но с меньшими числителем
и знаменателем. Такое преобразование называют сокращением дроби.
При этом
получилась дробь, значение которой равно данной дроби, но с меньшими числителем
и знаменателем. Такое преобразование называют сокращением дроби.
3. Определение сокращения дроби.
4. При сокращении дроби изменится лишь ее запись, числовое значение дроби не меняется.
5. Дробь ![]() сократить нельзя,
так как числа 3 и 4 – взаимно простые числа. Такую дробь называют несократимой.
сократить нельзя,
так как числа 3 и 4 – взаимно простые числа. Такую дробь называют несократимой.
Записать в тетрадях определение:
Дробь, числитель и знаменатель которой числа взаимно простые, называется несократимой.
6.
Дробь ![]() можно
сразу сократить на наибольший общий делитель числителя и знаменателя, то есть
на 60:
можно
сразу сократить на наибольший общий делитель числителя и знаменателя, то есть
на 60:
![]() но можно вести
постепенно:
но можно вести
постепенно: ![]()
Дробь сокращают до тех пор, пока не получат в числителе и знаменателе взаимно простые числа.
7. Иногда удобно при сокращении дроби разложить числитель и знаменатель на несколько множителей, а потом уже сократить.
Например, ![]()
Сократим на 3 · 3
· 5 и получим ![]() Дробь
Дробь ![]() несократимая.
несократимая.
III. Закрепление изученного материала.
1. Решить на доске и в тетрадях № 244 (а).
2. Решить № 242 с комментированием.
3. Устно решить № 246.
4. Решить задачу № 263.
Решение.
1) 12,8 + 1,7 = 14,5 (км/ч) скорость по течению реки.
2) 12,8 –1,7 = 11,1 (км/ч) скорость катера против течения реки.
Ответ: 14,5 км/ч; 11,1 км/ч.
5. Решить самостоятельно № 266 (по вариантам).
6. Выпишите несократимые дроби:
![]()
7. Какую часть составляет:
а) 20 от 70; б) 12 от 60; в) 14 от 49?
IV. Итог урока.
1. Что называют сокращением дроби?
2. Какую дробь называют несократимой?
3. Привести свои примеры сократимых и несократимых дробей.
Домашнее задание: выучить правила п. 9; решить № 268 (а; б), № 271 (а; в), № 274 (а).
Урок 2
Цели: упражнять учащихся в сокращении дробей и нахождении наибольшего общего делителя; закрепить знание основного свойства дроби; развивать логическое мышление учащихся.
Ход урока
I. Повторение изученного материала.
1. Решить устно № 253 (в; г; д).
2. Решить устно № 255.
3. решить устно:
а) Какую часть прямого угла составляет угол, равный: 1) 15°; 2) 30°; 3) 60°?
б) Какую часть метра составляют: а) 40 см; б) 36 см; в) 75 см?
II. Тренировочные упражнения.
1. Решить № 244 (б) на доске и в тетрадях.
2. Решить № 243 с комментированием.
3. Решить № 247, коллективно обсуждая решение, а затем учащиеся самостоятельно записывают решение в тетради.
4. Решить № 249 (а; в) на доске и в тетрадях.
5. Решить задачу № 250.
Решение.
1) 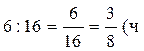 ) тратил первый
рабочий на одну деталь.
) тратил первый
рабочий на одну деталь.
2) 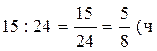 ) тратил второй
рабочий на деталь.
) тратил второй
рабочий на деталь.
3) 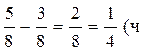 ) больше времени
тратил второй рабочий на изготовление одной детали.
) больше времени
тратил второй рабочий на изготовление одной детали.
Ответ: на ![]() ч больше.
ч больше.
6. Решить № 252 (а; б) (решение объясняет учитель).
Решение.
Распределительный закон умножения относительно сложения или вычитания:
![]() или
же
или
же
![]()
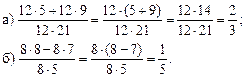
III. Повторение ранее изученного материала.
1. Решить задачу № 264 на доске и в тетрадях.
Решение.
1) 22,7 – 1,9 = 20,8 (км/ч) собственная скорость катера.
2) 20,8 – 1,9 = 18,9 (км/ч) скорость теплохода против течения.
Ответ: 20,8 км/ч; 18,9 км/ч.
2. Решить задачу № 267 (1; 2) самостоятельно.
Решение.
№ 267 (1) 1) 24 – 3 = 21 (км/ч) скорость лодки против течения реки.
2) 21 · 3 = 63 (км) весь путь.
3) 63 : 3 = 21 (ч) затрачено на обратный путь.
Ответ: 21 ч.
№ 267 (2) 1) 75 : 25 = 3 (км/ч) скорость течения реки.
2) 28 – 3 = 25 (км/ч) скорость лодки против течения реки.
3) 75 : 25 = 3 (ч) затратил путешественник на обратный путь.
Ответ: 3 ч.
IV. Итог урока.
1. Вопросы: а) Какая дробь называется несократимой?
б) На каком свойстве основано сокращение дробей?
в) Что меняется при сокращении дроби?
2. Сократите дроби
![]()
3. Сократите: а) ![]()
Домашнее задание: решить № 268 (в), № 269, № 271 (б; г), № 273.
Урок 3
Цели: закрепление и повторение изученного материала; упражнять учащихся в сокращении дробей; проверить усвоение учащимися материала в ходе выполнения самостоятельной работы.
Ход урока
I. Устная работа.
1. Решить № 254. Повторить правила умножения и деления на десятичную дробь.
2. Решить № 257 (в; г).
II. Выполнение упражнений.
1. Решить № 243 (б) с комментированием.
2. Решить № 245 на доске и в тетрадях.
3. Решить № 247 (первые четыре числа – вместе, остальные полусамостоятельно).
4. Решить № 249 (б; г) самостоятельно (с проверкой).
5. Решить № 252 (в; г) (учащиеся решают на доске и в тетрадях).
6. Решить задачу № 251 (учащиеся решают самостоятельно, потом проверяют).
Решение.
1) 20 : 8 = ![]() (м) пошло на одно
взрослое платье.
(м) пошло на одно
взрослое платье.
2) 12 : 8 = ![]() (м) пошло на одно
детское платье.
(м) пошло на одно
детское платье.
Ответ: 1,5 м; 2,5 м.
7. Решить задачу № 265 на доске и в тетрадях.
Решение.
1) 6000 : 3 · 1 = 2000 (деталей) изготовлено в первый день.
2) 5100 : 5 · 2 = 2040 (деталей) во второй день.
3) 6000 – (2000 + 2040) = 6000 – 4040 = 1960 (деталей) изготовлено в третий день.
Ответ: 1960 деталей.
III. Самостоятельная работа (10–15 мин).
Вариант I.
1. Сократите дроби
![]()
2. Сократите: ![]()
3. Найдите
наибольший общий делитель числителя и знаменателя дроби ![]() и сократите эту
дробь.
и сократите эту
дробь.
4. Запишите дроби 0,6; 0,36; 0,075; 0,008; 0,0025 в виде несократимой обыкновенной дроби.
Вариант II.
1. Сократите дроби
![]()
2. Сократите ![]()
3. Найдите
наибольший общий делитель числителя и знаменателя дроби ![]() и сократите дробь.
и сократите дробь.
4. Запишите дроби 0,8; 0,56; 0,035; 0,004; 0,0075 в виде несократимой обыкновенной дроби.
Домашнее задание: решить № 270, № 272, № 274 (б), № 259.
ПРИВЕДЕНИЕ ДРОБЕЙ К ОБЩЕМУ ЗНАМЕНАТЕЛЮ
Урок 1
Цели: познакомить учащихся с понятием приведения дроби к новому знаменателю и понятием дополнительного множителя; показать приведение дроби к наименьшему общему знаменателю; закрепить знание основного свойства дроби.
Ход урока
I. Устная работа.
1. Анализ самостоятельной работы. Указать ошибки и решить задания, вызвавшие затруднения у учащихся.
2. Решить № 284 (а; б).
3. Решить № 286.
4. Повторить основное свойство дроби и решить № 290 (а; б).
II. Объяснение нового материала.
Объяснение учителем материала пункта 10 (учебник, с. 43).
1. Приведение
дроби ![]() к новому
знаменателю 8.
к новому
знаменателю 8.
2. Определение дополнительного множителя.
3. Разобрать пример 1 на странице 43 учебника.
4. Любые две дроби
можно привести к одному и тому же знаменателю, или иначе к общему знаменателю.
Например, ![]()
5. Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
6. Разобрать пример 2 на странице 44 учебника.
7. Изучить правило приведения дроби к наименьшему общему знаменателю.
III. Закрепление изученного материала.
1. Решить № 275 (а; б; в) с комментированием.
2. Решить № 277 (а; в; д) на доске и в тетрадях.
3. Решить № 283 (а; б; в). Учитель объясняет решение зада- ния в).
в) ![]()
Остальные задания решают двое учащихся на доске с помощью учителя.
Решение.
![]()
![]()
4. Самостоятельно решить № 289 (а; б).
5. Решить № 294 (на доске и в тетрадях с помощью учителя).
Решение.
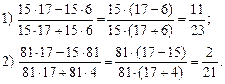
IV. Итог урока.
Вопросы:
1) К какому новому знаменателю можно привести данную дробь?
2)
Можно ли привести дробь ![]() к знаменателю 35? к
знаменателю 25?
к знаменателю 35? к
знаменателю 25?
3) Какое число называют дополнительным множителем?
4) Как найти дополнительный множитель?
5) Как привести дроби к наименьшему общему знаменателю?
6) Объясните,
почему несократимы дроби: ![]()
Домашнее задание: изучить п. 10; решить № 297 (а; б), № 300 (а; б), № 303 (а).
Урок 2
Цели: упражнять учащихся в нахождении наименьшего общего знаменателя и приведении к наименьшему общему знаменателю дроби.
Ход урока
I. Устная работа.
1. Решить № 284. Повторить правила действий с десятичными дробями.
2. Решить № 290 (в; г). Повторить основное свойство дроби.
3. Решить № 288 (1-я, 2-я дроби) с комментированием.
II. Тренировочные упражнения.
1. Решить на доске и в тетрадях № 275 (г) и № 277 (б; г; е).
2. Решить № 281 (из а), б), в) вторые и первые дроби).
Решение.

3. Решить № 283 (г; д; е). Трое учащихся решают на доске, остальные в тетрадях.
а) Используя
признаки делимости, докажите, что сократимы дроби: ![]()
Сократите данные дроби.
б) Решить задачу № 291, используя рисунок 15 учебника.
Решение.
1) 6 · 5 = 30 (см) проползёт жук за 5 с.
2) 60 + 30 = 90 (см) на это расстояние удалится жук от гусеницы через 5 с.
3) 100 – 90 = 10 (см) проползет гусеница за 5 с.
4) 10 : 5 = 2 (см/сек) скорость гусеницы.
Ответ: 2 см/с.
5. Решить № 283 (1; 2) самостоятельно.
Решение.
![]()
III. Итог урока.
1. Вопросы для повторения:
1) Как привести дроби к наименьшему общему знаменателю?
2) На каком свойстве основано правило приведения дробей к общему знаменателю?
3) Как найти общий знаменатель данных дробей?
4) Как найти дополнительный множитель для каждой дроби?
2. Сократить ![]()
3. Приведите дробь
![]() к знаменателю 20,
а дробь
к знаменателю 20,
а дробь ![]() к знаменателю 18.
к знаменателю 18.
4. Приведите к наименьшему общему знаменателю дроби:
![]()
Домашнее задание: решить № 297 (в; г), № 300 (в; г), № 302.
Урок 3
Цели: закрепить изученный материал в ходе выполнения упражнений; способствовать развитию навыков и умений сокращения дробей, приведению дробей к наименьшему общему знаменателю; развивать логическое мышление учащихся.
Ход урока
I. Повторение изученного материала.
1. Решить № 284 (в; г; д) устно. Повторить правила действий с десятичными дробями.
2. Решить № 288 (3-я и 4-я дроби).
3. Устно: сократить дроби так, чтобы они имели общий знаменатель:
![]()
II. Выполнение упражнений.
1. Решить № 278 на доске и в тетрадях.
2. Решить № 280 с комментированием.
3. Решить № 281 (из а), б), в) третьи и четвертые дроби).
Учащиеся решают на доске с объяснением, остальные – в тетрадях.
4. Решить № 283 (ж; з; и). Сначала обсуждается коллективно решение, находится для дробей наименьший общий знаменатель, а затем учащиеся самостоятельно записывают в тетрадях решение.
Решение.
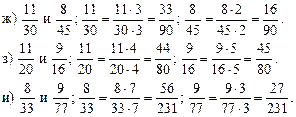
5. Приведите дроби к наименьшему общему знаменателю, предварительно сократив их:
![]()
III. Повторение ранее изученного материала.
1. Решить задачу № 292 на доске и в тетрадях.
Решение.
1) 34 + 46 = 80 (км/с) скорость сближения кораблей;
2) 15 мин = 15 · 60 = 900 (с)
80 · 900 = 72000 (км) расстояние между кораблями за 15 мин до встречи.
Ответ: 72000 км.
2. Решить № 283 (3; 4) самостоятельно.
IV. Самостоятельная работа (10–15 мин).
Вариант I.
1. Сократите ![]()
2. Приведите дробь
![]() к знаменателю 28,
а дробь
к знаменателю 28,
а дробь ![]() к знаменателю 9.
к знаменателю 9.
3. Приведите к наименьшему общему знаменателю дроби:
а) ![]()
4. Приведите дроби к наименьшему общему знаменателю, предварительно сократив их:
а) ![]()
Вариант II.
1. Сократите ![]()
2. Приведите дробь
![]() к знаменателю 36,
а дробь
к знаменателю 36,
а дробь ![]() к знаменателю 15.
к знаменателю 15.
3. Приведите к наименьшему общему знаменателю, предварительно сократив их:
а) ![]()
4. Приведите к наименьшему общему знаменателю, предварительно сократив их:
а) ![]()
Домашнее задание: решить № 299, 300 (д; ж), № 301.
СРАВНЕНИЕ, СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ
Урок 1
Цель: используя правило нахождения наименьшего общего знаменателя и приведения к общему знаменателю, показать сравнение дробей, сложение и вычитание дробей с разными знаменателями.
Ход урока
I. Повторение изученного материала.
1. Решить устно № 346 (а; б).
2. Повторить правило приведения к наименьшему общему знаменателю дроби. Решить № 351 (а).
3. Анализ самостоятельной работы. Решить задания, вызвавшие затруднения у учащихся.
II. Изучение нового материала.
1. Сравните дроби, выполните сложение и вычитание дробей с одинаковыми знаменателями:
а) ![]()
2. Определите,
какая из дробей: ![]() – наибольшая,
какая – наименьшая. Расположите дроби в порядке возрастания.
– наибольшая,
какая – наименьшая. Расположите дроби в порядке возрастания.
3. Расположите
дроби ![]() в порядке
убывания.
в порядке
убывания.
4. Работа по учебнику – изучение пункта 11:
а) Изучить правило сравнения (сложения и вычитания) дробей с разными знаменателями.
б) Разобрать
решение примера 1. Сравнить дроби ![]()
в) Разобрать решение примеров 2 и 3 (по учебнику).
![]()
![]()
III. Закрепление нового материала.
1. Решить № 304 (а; б) на доске и в тетрадях.
2. Решить № 305 с комментированием.
3. Решить задачу № 314 на доске и в тетрадях.
Решение.
1) ![]() (м) составляет шаг
папы.
(м) составляет шаг
папы.
2) ![]() (м) составляет
шаг сына.
(м) составляет
шаг сына.
![]() значит, шаг сына
короче.
значит, шаг сына
короче.
Ответ: короче шаг сына.
4. Решить задачу № 316. Коллективно учащиеся разбирают решение задачи, а затем самостоятельно записывают решение в тетрадях.
Решение.
1) ![]() (м) одна седьмая
часть трехметрового бревна.
(м) одна седьмая
часть трехметрового бревна.
2) ![]() (м) одна десятая
часть четырехметрового бревна.
(м) одна десятая
часть четырехметрового бревна.
![]()
Ответ: длиннее часть трехметрового бревна.
5. Решить № 319 (а; б; ж; з) и № 321 (а; г) на доске и в тетрадях.
6. Решить № 321 (б; в) с комментированием.
7. Решить № 312 (объясняет учитель).
8. Повторение материала:
1) Решить № 352 (а). Повторить основное свойство дроби и признаки делимости чисел на 2, на 5, на 3, на 9.
2) Решить задачу № 356 (1).
Решение.
1) 600 · 0,5 = 300 (км) пролетит первый самолет за 0,5 ч.
2) 750 – 600 = 150 (км/ч) больше скорость второго самолета, чем первого.
3) 300 + 225 = 525 (км) на столько больше километров должен пролететь второй самолет.
4) 525 : 150 = 3,5 (ч) через столько часов второй самолет после своего вылета будет впереди на 225 км.
Ответ: через 3,5 ч.
IV. Итог урока.
1. Выучить правила из пункта 11.
2. Прочитать на странице 50 учебника текст «Говорите правильно».
Домашнее задание: изучить п. 11; решить № 359 (а; б; в), № 360 (а; д), № 361, № 373 (в).
Урок 2
Цели: упражнять учащихся в сравнении дробей, сложении и вычитании дробей с разными знаменателями; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Проверить выборочно номера домашнего задания.
2. Решить № 346 (в) и № 351 (б).
II. Выполнение упражнений.
1. Решить № 304 (в; г) с комментированием.
2. Решить № 306 с комментированием.
3. Решить № 307 (а) на доске и в тетрадях.
4. Решить № 313 (самостоятельно).
5. Решить № 319 (в; г; д; k). Четверо учеников самостоятельно решают на доске, остальные в тетрадях, а потом проверяют решение.
6. Решить № 322 (а; в) на доске и в тетрадях.
Решение.
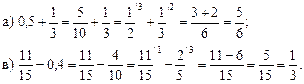
7. Решить задачу № 344 (решение объясняет учитель).
Решение.
Все поле составляет 1.
1) 1 : 6 = ![]() (часть) убирает
за 1 день первый комбайн.
(часть) убирает
за 1 день первый комбайн.
2) 1 : 4 = ![]() (часть) убирает
за 1 день второй комбайн.
(часть) убирает
за 1 день второй комбайн.
3) ![]() (часть) уберут за
1 день оба комбайна.
(часть) уберут за
1 день оба комбайна.
Ответ: ![]() части.
части.
8. Выполнить задание № 318 на координатном луче.
9. Самостоятельно решить № 356 (2).
Решение.
1) 60 · 0,5 = 30 (км) проедет автобус за 0,5 ч.
2) 75 – 60 = 15 (км/ч) больше скорость легковой машины.
3) 30 + 45 = 75 (км) больше должна проехать легковая машина.
4) 75 : 15 = 5 (ч) через столько часов после своего выезда легковая машина будет впереди автобуса на 45 км.
Ответ: 5 ч.
10. Решить № 352 с комментированием.
Повторить признаки делимости на 10, на 2, на 3.
Решение.
![]() НОК (8; 24; 9) =
72
НОК (8; 24; 9) =
72
![]()
III. Итог урока.
1. Повторить правило сравнения дробей.
2. Решить задачи:
а) Длина первой
доски ![]() м, а длина второй
доски –
м, а длина второй
доски – ![]() м. Какая из этих
досок длиннее?
м. Какая из этих
досок длиннее?
б) Оля уложила в ящик 15 кг яблок за 8 мин, Катя – 20 кг яблок за 11 мин. Кто из них работал быстрее?
Условия этих задач заранее записаны на доске; учитель привлекает к решению этих задач многих учащихся, выясняя степень усвоения ими материала, а решения задач учитель записывает на доске.
Домашнее задание: решить № 359 (г; д; е), № 360 (б; е), № 363, № 371.
Урок 3
Цели: способствовать развитию навыков сравнения дробей, сложения и вычитания дробей с разными знаменателями; закрепить знание нахождения наименьшего общего кратного чисел.
Ход урока
I. Устные упражнения.
1. Решить задание № 346 (в; г).
2. Укажите наибольшую дробь:
Найдем а) ![]() НОК (63; 315;
105) = 315.
НОК (63; 315;
105) = 315.
3. Не приводя дроби к общему знаменателю, определите, какая из них меньше:
а) ![]()
II. Работа по учебнику.
1. Для сложения и вычитания дробей верны изученные ранее свойства этих действий. Они иногда помогают упрощать вычисления.
2. Разобрать решение примеров 4 и 5 на странице 49 учебника.
3. Устные упражнения: найти значение выражения:
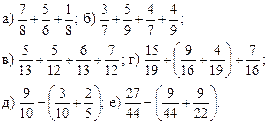
III. Выполнение упражнений.
1. Решить № 330 (а), № 331 (а), № 332 (а) на доске и в тетрадях.
Решение.
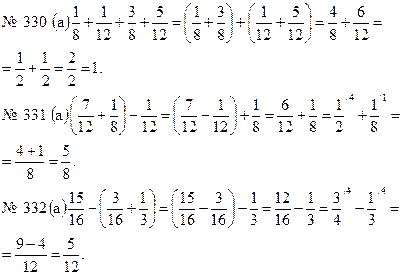
2. Решить № 307 (б) с комментированием.
3. Решить задачу № 317.
Решение.
НОК (5; 9; 15) = 45.
![]()
На решение задачи
Юра затратил ![]() урока, Нина –
урока, Нина – ![]() урока, а Миша –
урока, а Миша – ![]() урока.
урока.
4. Решить задачу № 342 самостоятельно.
5. Решить № 322 (б; г) на доске и в тетрадях.
Решение.
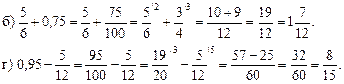
6. Решить № 319 (е; и) самостоятельно (с проверкой).
7. Решить № 321 (д; е; ж) самостоятельно.
8. Решить № 327 (а; в) на доске и в тетрадях.
Решение.
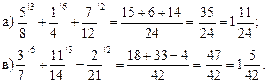
9. Повторение ранее изученного материала. Самостоятельно решить № 348, а затем проверить решение по тетрадям.
Решение.
а) 0,72 – 0,62 = 0,49 – 0,36 = 0,13;
б) 32 – 17,5 = 27 – 17,5 = 9,5;
в) 0,52 · 8 = 0,25 · 8 = 2;
г) 2,6 : 0,13 = 2,6 : 0,001 = 260.
IV. Итог урока.
1. Повторить правило сравнения дробей.
2. Сравните ![]()
Домашнее задание: решить № 359 (ж; з), № 360 (в; г; з), № 369 (б), № 364, № 373 (г).
Урок 4
Цели: упражнять учащихся в сравнении, сложении и вычитании дробей; научить решать уравнения и задачи; проверить знания и умения учащихся в ходе самостоятельной работы.
Ход урока
I. Проверка домашнего задания.
1. Двое учащихся работают на доске, решая № 364 и № 369 (б).
2. С остальными учащимися устно решить № 347 (а).
3. Сравните: ![]()
![]()
4. Назвать дроби в том порядке, как они расположены на координатном луче:
![]()
II. Изучение нового материала.
1. Разобрать решение № 309. Сформулировать правило сравнения двух дробей с одинаковыми числителями и разными знаменателями: из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше.
2. Решить № 310.
Решение.
![]()
III. Тренировочные упражнения.
1. Решить № 308 (а; б; в) с комментированием решения.
Решение.
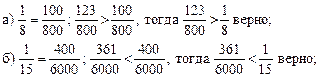
в) НОК (1575; 630) = 3150.
![]() , тогда
, тогда ![]() .
.
2. Решить задачу № 315 (учитель объясняет решение).
Решение.
Весь бассейн примем за 1.
![]() часть бассейна
наполняется узкой трубой за 1 ч.
часть бассейна
наполняется узкой трубой за 1 ч.
![]() часть бассейна
наполняется широкой трубой за 1 ч.
часть бассейна
наполняется широкой трубой за 1 ч.
![]() части бассейна
наполняется узкой трубой за 7 ч.
части бассейна
наполняется узкой трубой за 7 ч.
![]() части бассейна
наполняется широкой трубой за 3 ч.
части бассейна
наполняется широкой трубой за 3 ч.
Сравним ![]() НОК (10; 4) = 20
НОК (10; 4) = 20
![]()
Узкая труба дает меньше воды.
Ответ: узкая.
3. Решить № 319 (л; м) и № 321 (з; и) самостоятельно.
4. Решить № 325 (а; б) самостоятельно.
Двое учащихся решают на доске, остальные – самостоятельно в тетрадях, потом проверяется решение на доске и в тетрадях.
5. Решить уравнение № 328 (а; б) (учитель объясняет решение).
Решение.
а) Сначала вспомним, как найти неизвестное слагаемое:
х + 5 = 20; х = 20 – 5; х = 15.
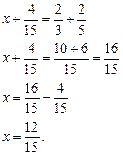
Ответ: ![]()
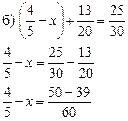
![]()
Вспомним, как найти неизвестное вычитаемое:
18 – х = 10
х = 18 – 10
х = 8.
Решаем:
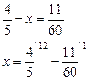
![]()
Ответ: ![]()
6. Решить задачу № 345 с комментированием решения.
Решение.
1) ![]() части бака
израсходует первый мотор за 5 ч.
части бака
израсходует первый мотор за 5 ч.
2) ![]() части бака
израсходует второй мотор за 7 ч.
части бака
израсходует второй мотор за 7 ч.
3) ![]() (части)
израсходуют оба мотора.
(части)
израсходуют оба мотора.
Ответ: ![]() части.
части.
7. Решить задачу № 336 самостоятельно.
8. Решить задачу № 337. Сначала коллективно разбирается решение задачи, а затем учащиеся самостоятельно записывают ее решение.
Решение.
1) ![]() (км) дороги
покрыли асфальтом за второй день.
(км) дороги
покрыли асфальтом за второй день.
2) ![]() (км) дороги
покрыли асфальтом за два дня.
(км) дороги
покрыли асфальтом за два дня.
Ответ: ![]() км.
км.
9. Задача на повторение материала № 357 (1).
Решение.
1) 0,7 · 3 = 2,1 (км) пробежал пес за 3 мин.
2) 2,1 – 1,8 = 0,3 (км) прошел хозяин пса за 3 мин.
3) 0,3 : 3 = 0,1 (км/мин) скорость хозяина пса.
Ответ: 0,1 км/мин.
IV. Итог урока. Повторяя правила и привлекая к работе многих учащихся, решить:
1) Выполните действие:
![]()
2) Решите
уравнение ![]()
Домашнее задание: решить № 360 (ж; и; k); № 368 (а), № 366, № 372.
Урок 5
Цели: закрепить знания и умения учащихся по изученному материалу; способствовать развитию навыков решения задач и уравнений; развивать логическое мышление учащихся; проверить степень усвоения учащимися материала в ходе выполнения самостоятельной работы.
Ход урока
I. Устная работа.
1. Решить № 347 (б).
2. Назвать дроби,
которые меньше ![]()
![]()
![]()
3. Сравните числа, не приводя дроби к общему знаменателю:
![]()
II. Выполнение упражнений.
1. Решить № 311 (а; в) на доске и в тетрадях.
2. Решить № 321 (k; л; м) самостоятельно.
3. Решить № 323 самостоятельно, предварительно повторив, как обыкновенную дробь превратить в десятичную дробь.
Решение.
![]()
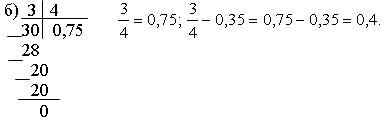
4. Решить № 329 (в; г) с комментированием.
Решение.
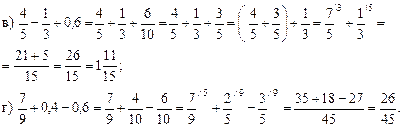
5. Решить уравнения № 328 (в; г) на доске и в тетрадях.
Решение.
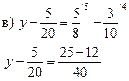
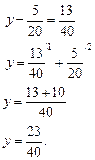
Ответ:![]()
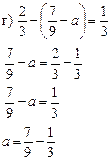
![]()
![]()
Ответ: а = ![]() .
.
6. Решить задачу № 335. Коллективно разрабатывается решение задачи, затем учащиеся самостоятельно решают задачу.
7. Решить задачу № 339 на доске и в тетрадях.
III. Самостоятельная работа (10–15 мин).
Вариант I.
1. Выполните
действие: ![]()
2. Выполните
действие: ![]()
3. Найдите значение выражения:
![]()
4. Купленную муку
высыпали в два пакета. В первый пакет высыпали ![]() кг, а во второй –
на
кг, а во второй –
на ![]() кг меньше. Какова
масса всей купленной муки?
кг меньше. Какова
масса всей купленной муки?
5. Решите уравнение:
![]()
Вариант II.
1. Выполните
действия: ![]()
2. Выполните
действия: ![]()
3. Найдите значение выражения:
![]()
4. Купили молотый
кофе и кофе в зернах. В зернах купили ![]() кг, а молотого – на
кг, а молотого – на ![]() кг меньше.
Сколько килограммов всего купили кофе?
кг меньше.
Сколько килограммов всего купили кофе?
5. Решите уравнение:
![]()
Домашнее задание: решить № 360 (м; н), № 368 (в), № 374 (б), № 367, № 373 (а).
Урок 6
Цели: повторить и систематизировать изученный материал; отработать навыки и умения сложения и вычитания обыкновенных дробей с разными знаменателями; подготовить учащихся к контрольной работе.
Ход урока
I. Анализ самостоятельной работы.
1. Указать ошибки, сделанные учащимися при выполнении работы.
2. Решить задания, вызвавшие затруднения у учащихся.
II. Тренировочные упражнения.
1. Решить № 324 на доске и в тетрадях.
2. Решить № 326. (Учащиеся решают с комментированием.)
Решение.
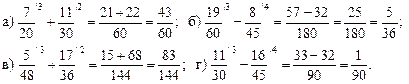
3. Решить № 330 (б), № 331 (б) и № 332 (б).
Решение.
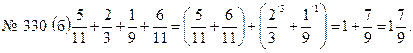
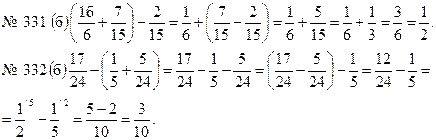
4. Решить задачу № 338. Повторить формулу нахождения периметра прямоугольника Р = (а + в) · 2.
Решение.
![]() (м) ширина
прямоугольника.
(м) ширина
прямоугольника.
![]() (м) периметр
прямоугольника.
(м) периметр
прямоугольника.
Ответ: ![]()
5. Решить задачу № 340 самостоятельно, а затем проверить решение по тетрадям.
6. Решить задачи № 341 и № 342 на доске и в тетрадях.
III. Повторение ранее изученного материала.
1. Изучить по учебнику № 350.
2. Решить № 353. Повторить определение правильной и неправильной дроби.
3. Решить задачу № 357 (2).
Решение.
1) 19 · 0,2 = 3,8 (км) пробежала собака за 0,2 ч.
2) 3,8 – 1,8 = 2 (км) пробежал нарушитель.
3) 2 : 0,2 = 20 : 2 = 10 (км/ч) скорость нарушителя.
Ответ: 10 км/ч.
4. Самостоятельно решить № 327 (г; д) и № 332.
IV. Итог урока.
1. Повторить правила приведения дробей к наименьшему общему знаменателю; правила сравнения дробей, сложения и вычитания дробей с разными знаменателями.
2. Вычислите наиболее удобным способом:
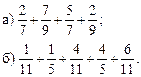
3. Не выполняя сложения, объясните, почему вычисление выполнено неверно:
![]()
Домашнее задание: решить № 360 (л; о; п), № 368 (б), № 374 (а), № 362, № 370, № 369 (а).
КОНТР РАБОТА
КОНТРОЛЬНАЯ РАБОТА № 2 (1 час)
Цели: проверить знания, умения и навыки учащихся; выявить пробелы в знаниях учащихся.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение работы по вариантам.
Вариант I.
1. Сократите
дроби: ![]()
2. Сравните дроби:
![]()
3. Выполните действия:
![]()
4. В первые сутки
поезд прошел ![]() всего пути, во
вторые сутки – на
всего пути, во
вторые сутки – на ![]() пути меньше, чем
в первые. Какую часть всего пути поезд прошел за эти двое суток?
пути меньше, чем
в первые. Какую часть всего пути поезд прошел за эти двое суток?
5. Найдите две
дроби, каждая из которых больше ![]() и меньше
и меньше ![]() .
.
Вариант II.
1. Сократите
дроби: ![]()
2. Сравните дроби:
![]()
3. Выполните действия:
![]()
4. В первый день
скосили ![]() всего луга, во
второй день скосили на
всего луга, во
второй день скосили на ![]() луга меньше, чем
в первый. Какую часть луга скосили за эти два дня?
луга меньше, чем
в первый. Какую часть луга скосили за эти два дня?
5. Найдите две
дроби, каждая из которых меньше ![]() и больше
и больше ![]() .
.
Вариант III.
1. Сократите
дроби: ![]()
2. Сравните дроби:
![]()
3. Выполните действия:
![]()
4. В первый день
истратили ![]() ящика гвоздей, а
во второй день – на
ящика гвоздей, а
во второй день – на ![]() ящика меньше, чем
в первый. Какую часть ящика гвоздей истратили за эти два дня?
ящика меньше, чем
в первый. Какую часть ящика гвоздей истратили за эти два дня?
5. Найдите две
дроби, каждая из которых больше ![]() , но меньше
, но меньше ![]()
Вариант IV.
1. Сократите
дроби: ![]()
2. Сравните дроби:
![]()
3. Выполните действия:
![]()
4. В первые сутки
подводная лодка прошла ![]() намеченного пути,
а во вторые сутки она прошла на
намеченного пути,
а во вторые сутки она прошла на ![]() пути меньше, чем в первые. Какую часть
намеченного пути прошла подводная лодка за эти два дня?
пути меньше, чем в первые. Какую часть
намеченного пути прошла подводная лодка за эти два дня?
5. Найдите две
дроби, каждая из которых меньше ![]() , но больше
, но больше ![]()
Домашнее задание: прочитать исторический материал на странице 68 учебника.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ СМЕШАННЫХ ЧИСЕЛ
Урок 1
Цели: повторить переместительное и сочетательное свойства сложения и показать их применение при сложении смешанных чисел; закрепить знания и умения учащихся при приведении дробей к наименьшему общему знаменателю.
Ход урока
I. Анализ контрольной работы.
1. Сообщение результатов контрольной работы.
2. Указать ошибки, сделанные учащимися при выполнении работы.
3. Решить задания, вызвавшие затруднения у учащихся.
II. Устные упражнения.
1. Решить № 401 (а; б).
2. Повторить свойства сложения:
а) а + в = в + а – переместительное свойство;
б) (а + в) + с = а + (в + с) – сочетательное свойство.
Привести свои примеры сложения чисел.
3. Повторить понятие смешанного числа. Привести примеры и записать в тетради.
III. Изучение нового материала.
1. Переместительное и сочетательное свойства сложения позволяют свести сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.
2. Разбор решения примера 1 учебника на странице 59:
![]()
3. Решение примера 2 (пишут короче):
![]()
4. Правило сложения смешанных чисел учащиеся формулируют самостоятельно, а затем читают формулировку правила по учебнику.
IV. Закрепление изученного материала.
1. Устно выполнить сложение:
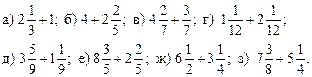
2. Решить № 376 (а; б; д; е) на доске и в тетрадях.
3. Решить № 379 (а) с комментированием решения.
Решение.
![]()
Ответ: n = ![]()
5. Решить задачу № 376 на доске и в тетрадях:
Р = АВ + ВС + АС; Р = ![]()
![]()
Ответ: ![]() м.
м.
6. Решить № 400 (а). Разобрать решение, вспомнив переместительное и сочетательное свойства сложения.
Решение.
![]()
Ответ: ![]() .
.
7. Самостоятельно решить № 407.
8. Сравните сумму с числом 10:
![]()
Дать оценку дробей слагаемых (при решении этого задания не обязательно складывать дроби, приводя их к наименьшему общему знаменателю):
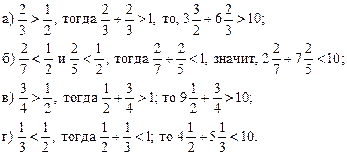
V. Итог урока.
1. Повторить правило сложения смешанных чисел.
2. Решить устно: ![]()
Домашнее задание: выучить правило п. 12 (1), решить № 414 (а; б; ж; з), № 421, № 425 (а).
Урок 2
Цели: изучить правило вычитания смешанных чисел и закрепить это правило при выполнении упражнений; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить № 401 (в; г; д). Повторить правила действий с десятичными дробями.
2. Повторение: решить № 408 (г; д; k) с комментированием.
3. Решить № 376 (в; г; ж; з).
II. Работа по учебнику.
1. При вычитании смешанных чисел пользуются свойствами вычитания суммы из числа и вычитания числа из суммы.
2. Разобрать по учебнику решение примера 3 на странице 60.
![]()
3. Разобрать по учебнику решение примера 4:
![]()
4. Сформулировать правило вычитания смешанных чисел.
5. Устно выполнить вычитание:
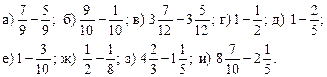
III. Закрепление изученного материала.
1. Решить № 377 (а; д; з; и) на доске и в тетрадях.
Решение.
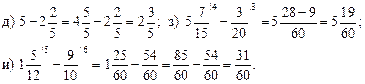
2. Решить № 377 (б; ж; k) самостоятельно.
3. Решить № 384 с комментированием.
Решение.
![]() (м) осталось
ленты.
(м) осталось
ленты.
Ответ:![]() м.
м.
4. Решить задачу № 390 на доске и в тетрадях.
Решение.
![]() (т) груза на
другой машине.
(т) груза на
другой машине.
![]() (т) груза на двух
машинах.
(т) груза на двух
машинах.
Ответ: 8 т.
5. Решить задачу № 391 самостоятельно.
Решение.
![]() (т) винограда в
другом ящике.
(т) винограда в
другом ящике.
![]() (т) винограда в
двух ящиках.
(т) винограда в
двух ящиках.
Ответ: 13,4 т.
6. Повторение ранее изученного материала: решить № 413 (1) самостоятельно.
7. сравните, какое из выражений больше (устно решить):
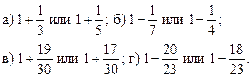
8. Придумайте правило, по которому составлена последовательность чисел, и запишите еще три члена этой последовательности. Найдите сумму этих чисел.
![]()
IV. Итог урока.
1. Повторить правило вычитания смешанных чисел.
2. Решить устно: ![]()
![]()
Домашнее задание: выучить правило п. 12 (2); решить № 414 (в; г), № 415 (а; б; е; ж), № 418, № 426 (б).
Урок 3
Цели: вырабатывать навыки и умения сложения и вычитания смешанных чисел; учить решать задачи; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить № 402.
2. Рассказать, как сложить смешанные числа и на каких свойствах сложения основано сложение смешанных чисел.
3. Рассказать, как выполнить вычитание смешанных чисел и на каких свойствах основано правило вычитания смешанных чисел.
4. Двое учащихся работают на доске, выполняя домашнее задание № 418 и № 414 (в; г).
II. Выполнение упражнений.
1. Решить № 377 (в; е; н) на доске и в тетрадях.
2. Решить № 377 (г; л) с комментированием на месте.
3. Решить № 378 (а; в; г) на доске и в тетрадях.
Решение.
![]()
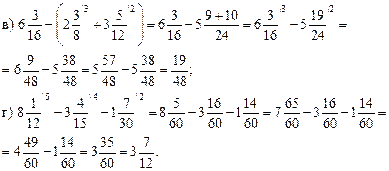
4. Решить № 378 (б) с комментированием на месте.
Решение.
![]()
5. Решить уравнения № 380 (а; г) на доске и в тетрадях.
Решение.
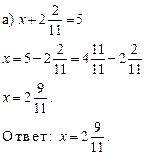
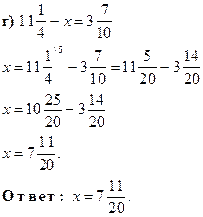
6. Решить задачу № 383. Учитель объясняет решение задачи.
Решение.
Вся канава составляет 1 часть.
![]() часть канавы
выкопает новая машина за 1 ч.
часть канавы
выкопает новая машина за 1 ч.
![]() части канавы
выкопает новая машина за 3 ч.
части канавы
выкопает новая машина за 3 ч.
![]() часть канавы
выкопает старая машина за 1 ч.
часть канавы
выкопает старая машина за 1 ч.
![]() части канавы
выкопает старая машина за 5 ч.
части канавы
выкопает старая машина за 5 ч.
![]() (части) канавы
выкопают обе машины.
(части) канавы
выкопают обе машины.
![]() (части) канавы
осталось выкопать.
(части) канавы
осталось выкопать.
Ответ: ![]() части.
части.
7. Решить задачу № 382 самостоятельно.
8. Самостоятельно решить № 392 (с последующей проверкой).
Решение.
![]() (кг) пошло на
окраску дверей.
(кг) пошло на
окраску дверей.
![]() (кг) всего
израсходовали.
(кг) всего
израсходовали.
Ответ: 20 кг.
9. Повторение материала: решить задачу № 409.
Решение.
1) 10 – 1 = 9 (частей) на столько частей больше получил средний брат, чем младший.
2) 765 : 9 = 85 (овец) получил младший сын.
3) 850 · 10 = 850 (овец) получил средний сын.
4) 85 · 25 = 2125 (овец) получил старший сын.
5) 2125 + 850 + 85 = 3060 (овец) было в отаре.
Ответ: 3060 овец.
III. Итог урока.
1. Повторить правила сложения и вычитания смешанных чисел.
2. Выполните
действие: ![]()
3. Решите уравнение:
![]()
4. Угадайте корень
уравнения ![]() ответ:
у = 9.
ответ:
у = 9.
Домашнее задание: решить № 414 (д; е), № 415 (в; г; з), № 417 (а; б), № 419, № 426 (а).
Урок 4
Цели: закрепить изученный материал; отрабатывать навыки сложения и вычитания смешанных чисел; способствовать развитию умения решать задачи.
Ход урока
I. Проверка изученного материала.
1. Двое учащихся работают на доске и выполняют задания № 419 и № 417 (в; г) из домашней работы.
2. Третий учащийся по карточке решает на доске задачу:
23 января 1960 г.
люди побывали на наибольшей глубине Мирового океана в Марианском желобе (11022
м), при этом спуск батискафа продолжался 4![]() ч, пребывание на дне длилось лишь
ч, пребывание на дне длилось лишь ![]() ч (так как под
огромным давлением через броню батискафа в 30 см пробивались струйки воды), и
ч (так как под
огромным давлением через броню батискафа в 30 см пробивались струйки воды), и ![]() ч исследователи
поднимались на поверхность. Сколько времени заняла вся эта операция?
ч исследователи
поднимались на поверхность. Сколько времени заняла вся эта операция?
3. Решить устно № 403.
4. Повторить правила сложения и вычитания смешанных чисел.
II. Тренировочные упражнения.
1. Решить № 377 (м; n) на доске и в тетрадях.
2. Решить № 377 (о; р) с комментированием на месте.
3. Решить № 378 (д; е) самостоятельно (с проверкой).
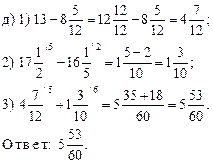
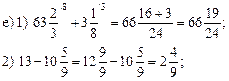
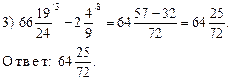
4. Решить № 380 (б) с комментированием на месте.
Решение.
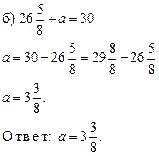
5. Решить № 400 (б; г) на доске и в тетрадях.
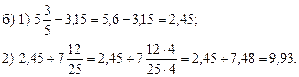
Ответ: 9,93.
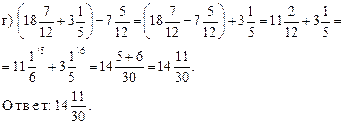
6. Решить задачу № 385 с комментированием на месте.
Решение.
![]() (ч) затрачено на
третью партию.
(ч) затрачено на
третью партию.
7. Решить задачу № 398 самостоятельно.
Решение.
![]() (км/ч) скорость
Феди.
(км/ч) скорость
Феди.
Ответ: 4,9 км/ч.
III. Самостоятельная работа (15 мин).
Вариант I.
1. Найдите значение выражения:
![]()
2. Выполните действие:
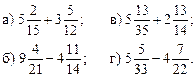
3. Решите
уравнение: а) ![]()
4. Угадайте корень
уравнения ![]()
Вариант II.
1. Найдите значение выражения:

2. Выполните действие:
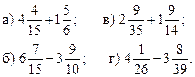
3. Решите
уравнение: ![]()
4. Угадайте корень
уравнения ![]()
Домашнее задание: повторить правила п. 12; решить № 415 (д; и), № 417 (в; г), № 420, № 426 (б).
КОНТРОЛЬНАЯ РАБОТА № 1 (1 час)
Цели: выявление знаний и умений учащихся; выяснение степени усвоения учащимися материала.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение работы по двум вариантам.
Вариант I.
1. Разложите на простые множители число 5544.
2. Найдите наибольший общий делитель и наименьшее общее кратное чисел 504 и 756.
3. Докажите, что числа:
а) 255 и 238 не взаимно простые;
б) 392 и 675 взаимно простые.
4. Выполните действия: 268,8 : 0,56 +6,44 · 12.
5. Может ли разность двух простых чисел быть простым числом?
Вариант II.
1. Разложите на простые множители число 6552.
2. Найдите наибольший общий делитель и наименьшее общее кратное чисел 1512 и 1008.
3. Докажите, что числа:
а) 266 и 285 не взаимно простые;
б) 301 и 585 взаимно простые.
4. Выполните действия: 355,1 : 0,67 + 0,83 · 15.
5. Может ли сумма двух простых чисел быть простым числом?
III. Итог урока.
Домашнее задание: принести на следующий урок карандаши (простые и цветные), линейки и циркули.
Урок 5
Цели: способствовать выработке навыков и умений решать задачи, уравнения, примеры, используя правила сложения и вычитания смешанных чисел; закрепить в ходе упражнений полученные знания.
Ход урока
I. Анализ самостоятельной работы.
1. Сообщить результаты самостоятельной работы.
2. Решить задания, вызвавшие затруднения у учащихся.
3. Устно решить № 405.
Решение.
10 ч 40 мин + 5 ч 15 мин + 1 ч 37 мин = 17 ч 32 мин.
II. Выполнение упражнений. Решение задач.
1. Решить № 408 (з; и) на доске и в тетрадях.
Решение.
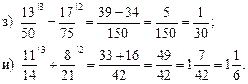
2. Решить № 379 (б; в; г). Вызвать трех учащихся к доске, они решают самостоятельно на доске, остальные учащиеся решают в тетрадях, а затем проверяется решение.
3. Решить № 380 (д) на доске и в тетрадях.
Решение.
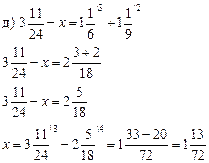
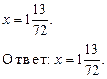
4. Решить задачу № 394. Сначала учащиеся составляют план решения задачи, коллективно обсуждая ход действий, а затем самостоятельно записывают в тетрадях решение задачи.
Решение.
![]() (т) привезли во вторник.
(т) привезли во вторник.
![]() (т) привезли в среду.
(т) привезли в среду.
![]() (т) всего
привезли на сахарный завод.
(т) всего
привезли на сахарный завод.
4) 1330 : 7 = 190 (т) сахара получится из привезенной свеклы.
Ответ: 190 т.
5. Решить задачу № 395. Решение объясняет на доске учитель.
Решение.
![]() (л) молока в
третьем бидоне.
(л) молока в
третьем бидоне.
![]() (л) молока было
во втором бидоне.
(л) молока было
во втором бидоне.
![]() (л) молока было в
первом бидоне.
(л) молока было в
первом бидоне.
Ответ: ![]()
6. Решить задачу № 380 с комментированием на месте.
Решение.
![]() (га) площадь
третьего участка.
(га) площадь
третьего участка.
![]() (га) площадь
второго участка.
(га) площадь
второго участка.
![]() (га) площадь
первого участка.
(га) площадь
первого участка.
Ответ: ![]()
7. Решить самостоятельно № 400 (в).
Решение.
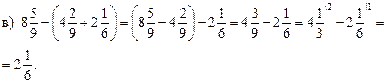
Ответ: ![]()
8. Повторить решение задач на части. Решить № 412 (1) на доске и в тетрадях.
Решение.
1) 50 – 6 = 44 (части) на столько частей больше надо взять воды, чем серы.
2) 8,8 : 44 = 0,2 (кг) приходится на 1 часть.
3) (6 + 3 + 50) · 0,2 = 59 · 0,2 = 11,8 (кг) отвара получится.
Ответ: 11,8 кг.
9. Решить задачу № 412 (2) самостоятельно.
Ответ: 8,4 кг.
III. Итог урока:
1. Повторить правила сложения и вычитания смешанных чисел.
2. Решить на доске вместе с учениками:
а) ![]()
б) Доску разрезали
на три части. Длина первой части ![]() м. Она короче второй части на
м. Она короче второй части на ![]() м и длиннее
третьей части на
м и длиннее
третьей части на ![]() м. Найти
длину всей доски.
м. Найти
длину всей доски.
Домашнее задание: решить № 416 (а), № 422 (а), № 424.
Урок 5
Цели: способствовать выработке навыков и умений решать задачи, уравнения, примеры, используя правила сложения и вычитания смешанных чисел; закрепить в ходе упражнений полученные знания.
Ход урока
I. Анализ самостоятельной работы.
1. Сообщить результаты самостоятельной работы.
2. Решить задания, вызвавшие затруднения у учащихся.
3. Устно решить № 405.
Решение.
10 ч 40 мин + 5 ч 15 мин + 1 ч 37 мин = 17 ч 32 мин.
II. Выполнение упражнений. Решение задач.
1. Решить № 408 (з; и) на доске и в тетрадях.
Решение.
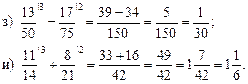
2. Решить № 379 (б; в; г). Вызвать трех учащихся к доске, они решают самостоятельно на доске, остальные учащиеся решают в тетрадях, а затем проверяется решение.
3. Решить № 380 (д) на доске и в тетрадях.
Решение.
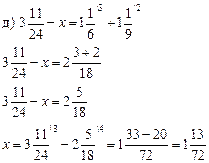
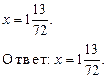
4. Решить задачу № 394. Сначала учащиеся составляют план решения задачи, коллективно обсуждая ход действий, а затем самостоятельно записывают в тетрадях решение задачи.
Решение.
![]() (т) привезли во
вторник.
(т) привезли во
вторник.
![]() (т) привезли
в среду.
(т) привезли
в среду.
![]() (т) всего
привезли на сахарный завод.
(т) всего
привезли на сахарный завод.
4) 1330 : 7 = 190 (т) сахара получится из привезенной свеклы.
Ответ: 190 т.
5. Решить задачу № 395. Решение объясняет на доске учитель.
Решение.
![]() (л) молока в
третьем бидоне.
(л) молока в
третьем бидоне.
![]() (л) молока было
во втором бидоне.
(л) молока было
во втором бидоне.
![]() (л) молока было в
первом бидоне.
(л) молока было в
первом бидоне.
Ответ: ![]()
6. Решить задачу № 380 с комментированием на месте.
Решение.
![]() (га) площадь
третьего участка.
(га) площадь
третьего участка.
![]() (га) площадь
второго участка.
(га) площадь
второго участка.
![]() (га) площадь
первого участка.
(га) площадь
первого участка.
Ответ: ![]()
7. Решить самостоятельно № 400 (в).
Решение.

Ответ: ![]()
8. Повторить решение задач на части. Решить № 412 (1) на доске и в тетрадях.
Решение.
1) 50 – 6 = 44 (части) на столько частей больше надо взять воды, чем серы.
2) 8,8 : 44 = 0,2 (кг) приходится на 1 часть.
3) (6 + 3 + 50) · 0,2 = 59 · 0,2 = 11,8 (кг) отвара получится.
Ответ: 11,8 кг.
9. Решить задачу № 412 (2) самостоятельно.
Ответ: 8,4 кг.
III. Итог урока:
1. Повторить правила сложения и вычитания смешанных чисел.
2. Решить на доске вместе с учениками:
а) ![]()
б) Доску разрезали
на три части. Длина первой части ![]() м. Она короче второй части на
м. Она короче второй части на ![]() м и длиннее
третьей части на
м и длиннее
третьей части на ![]() м. Найти
длину всей доски.
м. Найти
длину всей доски.
Домашнее задание: решить № 416 (а), № 422 (а), № 424.
КОНТРОЛЬНАЯ РАБОТА № 3
Цели: выявить степень усвоения учащимися изученного материала; развивать навыки самостоятельной работы.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение работы по вариантам.
Вариант I.
1. Найдите значение выражения:
![]()
2. На автомашину
положили сначала ![]() т груза, а потом
на
т груза, а потом
на ![]() т больше. Сколько
всего тонн груза положили на автомашину?
т больше. Сколько
всего тонн груза положили на автомашину?
3. Ученик рассчитывал за ![]() ч приготовить
уроки и за
ч приготовить
уроки и за ![]() ч закончить
модель корабля. Однако на всю работу он потратил на
ч закончить
модель корабля. Однако на всю работу он потратил на ![]() ч меньше,
чем предполагал. Сколько времени потратил ученик на всю работу?
ч меньше,
чем предполагал. Сколько времени потратил ученик на всю работу?
4. Решите
уравнение ![]()
5. Разложите число 90 на два взаимно простых множителя четырьмя различными способами (разложения, отличающиеся только порядком множителей, считать за один способ).
Вариант II.
1. Найдите значение выражения:
![]()
2. С одного
опытного участка собрали ![]() т пшеницы, а с
другого – на
т пшеницы, а с
другого – на ![]() т меньше. Сколько
тонн пшеницы собрали с этих двух участков?
т меньше. Сколько
тонн пшеницы собрали с этих двух участков?
3. Ученица
рассчитывала за ![]() ч приготовить
уроки и
ч приготовить
уроки и ![]() ч потратить на
уборку квартиры. Однако на все это у нее ушло на
ч потратить на
уборку квартиры. Однако на все это у нее ушло на ![]() ч больше.
Сколько времени потратила ученица на всю эту работу?
ч больше.
Сколько времени потратила ученица на всю эту работу?
4. Решите
уравнение ![]()
5. Разложите число 84 на два взаимно простых множителя четырьмя различными способами (разложения, отличающиеся только порядком множителей, считать за один способ).
Вариант III.
1. Найдите значение выражения:
![]()
2. Масса одной
детали ![]() кг, что меньше
массы другой детали на
кг, что меньше
массы другой детали на ![]() кг. Какова масса
двух деталей вместе?
кг. Какова масса
двух деталей вместе?
3. Садовник
рассчитывал за ![]() ч приготовить
раствор и за
ч приготовить
раствор и за ![]() ч опрыснуть
этим раствором деревья. Однако на всю работу он потратил на
ч опрыснуть
этим раствором деревья. Однако на всю работу он потратил на ![]() ч меньше,
чем рассчитывал. Сколько времени ушло у садовника на всю эту работу?
ч меньше,
чем рассчитывал. Сколько времени ушло у садовника на всю эту работу?
4. Решите
уравнение: ![]()
5. Разложите число 60 на два взаимно простых множителя четырьмя различными способами (разложения, отличающиеся только порядком множителей, считать за один способ).
Вариант IV.
1. Найдите значение выражения:
![]()
2. Масса одного
станка ![]() т, а другого – на
т, а другого – на
![]() т меньше. Найдите
общую массу обоих станков.
т меньше. Найдите
общую массу обоих станков.
3. Хозяйка
рассчитывала за ![]() ч приготовить
обед и
ч приготовить
обед и ![]() ч потратить
на стирку белья. Однако на всю работу у нее ушло на
ч потратить
на стирку белья. Однако на всю работу у нее ушло на ![]() ч больше.
Сколько времени хозяйка потратила на всю эту работу?
ч больше.
Сколько времени хозяйка потратила на всю эту работу?
4. Решите
уравнение: ![]()
5. Разложите число 126 на два взаимно простых множителя четырьмя различными способами (разложения, отличающиеся только порядком множителей, считать за один способ).
Домашнее задание: повторить «Основное свойство дроби» (п. 8) и «Сокращение дробей» (п. 9).
УМНОЖЕНИЕ ДРОБЕЙ
Урок 1
Цели: вывести правило умножения дроби на натуральное число и правило умножения дроби на дробь; повторить основное свойство дроби и закрепить его знание при сокращении дробей.
Ход урока
I. Анализ контрольной работы.
1. Сообщение результатов контрольной работы.
2. Указать ошибки, сделанные учащимися в ходе работы.
3. Решить задания, вызвавшие затруднения у учащихся.
II. Объяснение нового материала.
1. Повторить основное свойство дроби.
2. Разобрать по учебнику решение задачи 1 на странице 68. Сформулировать правило умножения дроби на натуральное число.
3. Решить устно № 427 (а; д; е; ж; з).
4. Разобрать решение задачи 2 на странице 69 учебника, используя рисунок 19 на странице 69. Сформулировать правило умножения дроби на дробь.
5. Решить устно № 433 (а; б; г; д; ж).
III. Закрепление изученного материала.
1. Решить № 427 (б; в; г) с комментированием на месте.
2. Решить задачу № 428 на доске и в тетрадях.
Решение.
Р = 4а; а
= ![]() м; р =
м; р = ![]() (м).
(м).
Ответ: 3,5 м.
3. Решить № 431 на доске и в тетрадях. (Четыре человека решают на доске, остальные – в тетрадях, а затем проверяется решение.)
4.
Решить № 433 (в; е; з; и; k; л; н) с комментированием
на месте.
5. Решить задачу № 434 самостоятельно, повторив формулу площади квадрата:
![]()
6. Решить задачу № 421 самостоятельно, вспомнив формулу объема куба:
![]()
7. Решить № 441 и № 442 на доске и в тетрадях; № 439 решить самостоятельно.
8. Решить № 435 (а; б) самостоятельно, с проверкой.
Решение.
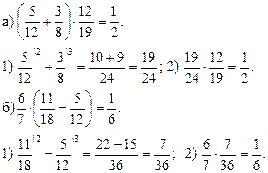
IV. Повторение изученного материала.
1) Решить № 467. Вспомнить, что называется процентом:
1% = ![]() =0,01.
=0,01.
2) Решить уравнение № 470. Двое учащихся самостоятельно решают на доске, остальные – в тетрадях, а потом проверяют решение.
Решение.
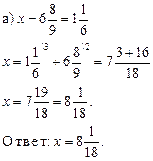
V. Итоги урока:
1) выучить правила пункта 13 (1; 2);
2) прочитать по учебнику раздел «Говори правильно» на странице 71;
3) решить № 427 (в; г).
Домашнее задание: выучить правила п. 13 (1; 2); решить № 472 (ж; з; а; б), № 474, № 478 (а; б), № 479.
Урок 2
Цели: закрепить правило умножения дробей и умножения дроби на натуральное число; изучить правило умножения смешанных чисел и научить применять его при решении задач; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить № 455 (а; б; в; г).
2. Решить № 457.
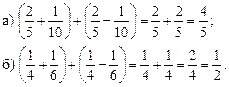
3. Повторить правила умножения дроби на натуральное число и правило умножения дробей, правило сокращения дробей.
4. Вычислить устно:
![]()
5. Повторить правило представления смешанного числа в виде неправильной дроби. Привести примеры.
II. Изучение нового материала.
1. Разобрать по учебнику решение задачи 3 на с. 69–70. Сформулировать правило умножения смешанных чисел.
2. Устно выполнить умножение:
![]()
![]()
III. Закрепление изученного материала.
1. решить № 433 (м; п; о) на доске и в тетрадях.
2. Решить задачу № 429 (второе значение решаем вместе, 1-е и 3-е решаются с комментированием на месте).
3. Решить № 446 (б; д; в) на доске и в тетрадях; № 446 (а; г; е) решаются комментированием на месте.
4. Решить задачу № 450.
Решение.
![]() (км/ч) скорость
второго велосипедиста.
(км/ч) скорость
второго велосипедиста.
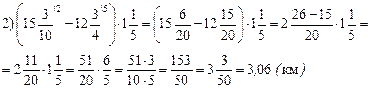
будет расстояние
между велосипедистами через![]() ч.
ч.
Ответ: 3,06 км.
5. решить задачу № 452. Сначала в ходе обсуждения разобрать решение этой задачи, а затем учащиеся решают самостоятельно.
Решение.
![]() (ч) заливали
каток вторым шлангом.
(ч) заливали
каток вторым шлангом.
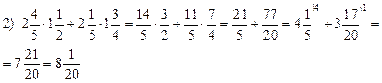
(м3) воды израсходовали на заливку катка.
Ответ: ![]() м3.
м3.
6. Повторение ранее изученного материала:
а) решить № 461 (а; г; ж) (три человека решают на доске, остальные – в тетрадях);
б) решить задачу № 469 (1).
Решение.
Объем всей работы примем за единицу.
![]() всей работы
выполнят рабочие за два дня.
всей работы
выполнят рабочие за два дня.
![]() (части) работы
выполнили в третий день.
(части) работы
выполнили в третий день.
Ответ: ![]() части.
части.
IV. Итог урока.
1. Расскажите, как умножить дробь на натуральное число. Привести свои примеры.
2. Расскажите, как выполнить умножение двух дробей и как выполнить умножение смешанных чисел. Привести свои примеры.
3. Вычислите квадрат и куб числа:
а) ![]()
Домашнее задание: выучить правила п. 13; решить № 472 (в; и; k; л), № 473 (а), № 476, № 478 (в), № 482 (а).
Урок 3
Цели: способствовать выработке навыков и умений при умножении дробей; изучить свойства умножения дробей, свойства нуля и единицы при умножении; развивать логическое мышление учащихся.
Ход урока
I. Проверка изученного материала.
1. Двое учащихся работают на доске, выполняя номера из домашнего задания:
а) № 476; б) № 478.
2. С остальными учащимися проводится устная работа:
При данных
значениях в 4; 100; 2; 6; ![]() сравните:
сравните:
1) в и в
· ![]() 2) в и в
· 1
2) в и в
· 1![]()
Увеличится или уменьшится число, если его умножить на дробь:
1) меньшую единицы; 2) большую единицы?
3. Какой смысл имеет слово «умножение» в русском языке? Сохраняется ли смысл этого слова, когда мы говорим об умножении дробных чисел?
4. Решить № 459 (по рис. 20 учебника).
II. Работа по учебнику.
1. Разобрать решение задачи 4 на странице 70.
2. Умножение дробей обладает переместительным и сочетательным свойствами:
1) а · в = в · а; 2) (а · в) · с = а · (в · с).
3. Вычислите устно, применяя законы умножения:
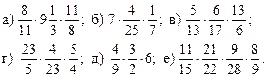
4. Для любого значения а:
а · 0 = 0 · а = 0; а · 1 = 1 · а = а.
Например, ![]()
5. Устно решить № 446 (н; о; п).
III. Выполнение упражнений.
1. Решить задачи № 436, 437, 432 самостоятельно, с последующей проверкой.
2. Решить задачу № 430 на доске и в тетрадях.
Решение.
![]() (м) сторона ВС;
(м) сторона ВС;
![]() (м) сторона АС;
(м) сторона АС;
![]() (м) периметр
треугольника АВС.
(м) периметр
треугольника АВС.
Ответ: ![]() м.
м.
3. Решить № 446 (ж; з; и; к; л; м) с комментированием на месте.
4. Решить задачу № 448, повторив сокращение дробей.
Решение.
V = a в c; V = ![]() (дм3) объем.
(дм3) объем.
Ответ: 3,5 дм3.
5. Решить задачу № 447 (а; б) самостоятельно.
6. Решить № 454 (а; б). Двое учащихся решают самостоятельно на доске, остальные учащиеся – в тетрадях, а затем решение проверяется.
IV. Самостоятельная работа (10–12 мин).
Вариант I.
1. Выполните
умножение: ![]() г)
г) ![]()
2. Найти объем
прямоугольного параллелепипеда, если его измерения равны ![]() дм,
дм, ![]() дм и
дм и ![]() дм.
дм.
3. Найти значение выражения:
![]()
Вариант II.
1. Выполните
умножение: ![]() г)
г) ![]()
2. Найти объем
прямоугольного параллелепипеда, если его измерения равны ![]() м,
м, ![]() м,
м, ![]() м.
м.
3. Найти значение выражения:
![]()
Домашнее задание: повторить правила п. 13; решить № 472 (м; н; о; п), № 473 (б), № 477, № 482 (б).
Урок 4
Цели: закрепление изученного материала; развитие навыков и умений учащихся при умножении дробей, сложении и вычитании дробей, решении задач.
Ход урока
I. Анализ самостоятельной работы.
1. Указать ошибки, сделанные учащимися при выполнении работы.
2. Решить задания, вызвавшие затруднения у учащихся.
II. Выполнение упражнений.
1. Решить № 442 и № 438 самостоятельно, с проверкой.
2. Решить задачу № 443 самостоятельно.
3. Известно, что некоторое число с больше 1. Сравните с2 и с3.
4. Известно, что некоторое число в меньше 1. Сравните в2 и в3.
5. Вычислите (на доске и в тетрадях):
![]()
6. Решить задачу № 451 на доске и в тетрадях.
Решение.
![]() (км/ч) скорость
Веры.
(км/ч) скорость
Веры.
![]() (км/ч) скорость
сближения девочек.
(км/ч) скорость
сближения девочек.
![]() (км) расстояние
между селами.
(км) расстояние
между селами.
Ответ: 10 км.
7. Решить задачу № 453 на доске и в тетрадях.
Решение.
![]() (га) площадь
второго поля.
(га) площадь
второго поля.
![]() (ц) пшеницы
собрали с первого поля.
(ц) пшеницы
собрали с первого поля.
![]() (ц) пшеницы
собрали со второго поля.
(ц) пшеницы
собрали со второго поля.
![]() (ц) пшеницы
собрали с двух полей.
(ц) пшеницы
собрали с двух полей.
Ответ: 4370 ц.
8. Самостоятельно решить задачу № 449.
9. Решить задачу.
Скорость слабого
ветра ![]() м/с, умеренного –
в 2 раза больше, скорость сильного ветра в
м/с, умеренного –
в 2 раза больше, скорость сильного ветра в ![]() раза больше скорости слабого и умеренного
ветров вместе. Определите скорость сильного ветра.
раза больше скорости слабого и умеренного
ветров вместе. Определите скорость сильного ветра.
III. Повторение материала.
Провести самостоятельную работу по вариантам, используя задания учебника.
Вариант I. Вариант II.
1) Решить № 431 (в; г). 1) Решить № 431 (д; е).
2) Решить № 440 (г). 2) Решить № 440 (в).
3) Решить № 447 (д). 3) Решить № 447 (е).
4) Решить задачу № 454 (2). 4. Решить задачу № 454 (1).
Домашнее задание: решить № 478 (г; ж; з), № 481, № 483, № 471.
ИТОГОВЫЙ УРОК
ПО МАТЕРИАЛУ I ЧЕТВЕРТИ (1 час)
Цели: подвести итоги работы I четверти, решить занимательные задачи.
Ход урока
I. Анализ и результаты самостоятельной работы.
II. Подведение итогов работы в I четверти.
III. Итоги работы математического кружка.
1. Сообщение результатов работы математического кружка.
2. Решить несколько занимательных задач:
1) Как проще всего вычислить сумму:
![]()
Указание. Каждую из дробей представить в виде разности:
![]()
2) Как быстро найти сумму чисел от 1 до 100?
Решение.
(1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + … + (50 + 51) = 101 + + 101 + 101 + … + 101 = 101 · 50 = 5050.
Ответ: 5050.
3) В записи 88888888 = 1000 поставьте между некоторыми цифрами знак сложения так, чтобы получилось верное равенство.
Решение.
888 + 88 + 8 + 8 + 8 = 1000.
4) Какую долю составляют сутки от года?
Ответ: ![]() или
или ![]() .
.
5) Замените звездочки цифрами:
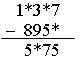
Ответ: 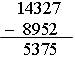
6) Решить № 460. Кто быстрее?
Домашнее задание: подобрать интересные задачи для математического кружка.
НАХОЖДЕНИЕ ДРОБИ ОТ ЧИСЛА
Урок 1
Цели: познакомить с задачами на нахождение дроби от числа и решением их с помощью умножения; сформулировать правило нахождения дроби от числа.
Ход урока
I. Устные упражнения.
1. Решить устно № 508 (а; б) и № 510 (а).
2. Подготовить учащихся к восприятию нового материала, решив задачи:
а) Маша нашла в
лесу 20 грибов, из них ![]() грибов были
белыми. Сколько белых грибов нашла Маша?
грибов были
белыми. Сколько белых грибов нашла Маша?
Решение.
– Задачи этого типа мы решали в 5 классе.
20 : 5 · 2 = 4 · 2 = 8 (белых) грибов.
б) Мама дала Коле
12 конфет; Коля съел ![]() этих конфет.
Сколько конфет осталось у Коли?
этих конфет.
Сколько конфет осталось у Коли?
1) 12 : 4 · 3 = 9 (конфет) съел Коля.
2) 12 – 9 = 3 (конфеты) осталось у Коли.
Ответ: 3 конфеты.
II. Изучение нового материала.
1. Разобрать по учебнику на странице 78 решение задачи 1 и ввести оформление задачи:
![]() (км).
(км).
2. Используя рисунок 21 на странице 79 учебника, разобрать решение задачи 2 и записать в тетрадях решение:
![]() (всего участка).
(всего участка).
3. Такие задачи называют задачами на нахождение дроби от числа и решают их с помощью умножения.
4. Формулировка и запись в тетрадях правила нахождения дроби от числа.
III. Закрепление изученного материала.
1. Решить устно № 484 по рисунку 22 учебника.
2. Решить устно № 485 по рисунку 23 учебника.
3. Решить № 486 (а; г) на доске и в тетрадях.
4. Решить № 486 (б; в) с комментированием на месте.
5. Решить задачу № 490 на доске и в тетрадях.
Решение.
![]() (м2) площадь второй
комнаты.
(м2) площадь второй
комнаты.
2) 21 + 9 = 30 (м2) площадь двух комнат.
Ответ: 30 м2.
6. Решить задачу № 500 (объясняет учитель).
Решение.
![]() (части) книги
осталось прочитать после первого дня.
(части) книги
осталось прочитать после первого дня.
![]() (часть) книги прочитала
Ира во второй день.
(часть) книги прочитала
Ира во второй день.
![]() (часть) книги
прочитана за два дня.
(часть) книги
прочитана за два дня.
Ответ: ![]() часть;
часть; ![]() часть.
часть.
7. Решить задачу № 505 самостоятельно, предварительно разобрав решение вместе с классом.
Решение.
1) 39 – 7 = 32 (дня) затрачено на ремонт комбайнов.
![]() (дней) затрачено
на ремонт прицепного инвентаря.
(дней) затрачено
на ремонт прицепного инвентаря.
3) 39 – 14 = 25 (дней) больше длился ремонт тракторов, чем ремонт прицепного инвентаря.
Ответ: на 25 дней больше.
8. Повторение изученного материала: решить с комментированием на месте № 513 (а; г; ж; з).
IV. Итоги урока: повторить правило нахождения числа по его дроби.
Домашнее задание: изучить пункт, выучить правило п. 14 (1 часть); решить № 523, № 533, № 534 (а). Индивидуальное задание № 535 (а).
Урок 2
Цели: разобрать решение еще двух задач на нахождение дроби от числа; способствовать развитию навыков решения задач и упражнений; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Двое учащихся решают на доске домашнее задание № 523 и № 533.
2. С остальными учащимися решить № 508 (в) и № 510 (б) устно.
3. Решить № 509, используя для решения черновики.
II. Работа по учебнику.
Разобрать по учебнику решение еще двух задач на нахождение дроби от числа на странице 79 (пункт 14).
1. Задача 3. Путешественник прошел за два дня 20 км. В первый день он прошел 0,6 всего пути. Сколько километров прошел путешественник в первый день?
Решение.
20 · 0,6 = 12 (км) прошел в первый день.
2. Задача 4. Огород занимает 8 га. 45% площади этого огорода занято картофелем. Сколько гектаров занято картофелем?
Решение.
45% = 0,45;
1) 8 · 0,45 = 3,6 (га) занято картофелем.
III. Закрепление изученного материала.
1. Решить задачи № 487, № 486 и № 488 на доске и в тетрадях и сравнить ответы.
Сделать вывод, что
так как ![]() и 80% = 0,8, то
ответы при решении этих задач одинаковые.
и 80% = 0,8, то
ответы при решении этих задач одинаковые.
2. Решить № 485 (д, з, л) на доске и в тетрадях.
Решение.
д) 0,4 от 30; 30 · 0,4 = 12;
з) 4,2 · 0,7 = 2,94;
л) 42% = 0,42; ![]()
3. Решить № 485 (ж; k) с комментированием на месте.
Решение.
ж) 0,8 · 0,2 = 0,16; k) 12,6 · 0,35 = 4,41.
4. Решить задачу № 476 самостоятельно, с последующей проверкой.
Решение.
1) 90 · 0,3 = 27 (марок) у брата.
2) 90 – 27 = 63 (марки) у сестры.
Ответ: 63 марки.
5. Решить задачу № 494 на доске и в тетрадях.
Решение.
1) 75% =0,75; 102,8 · 0,75 = 77,1 (км) построено
2) 102,8 – 77,1 = 25,7 (км) осталось построить.
Ответ: 25,7 км.
6. Решить задачу: Плоды ананаса содержат 84% воды. Остальное – сахар и другие питательные вещества. Сахар составляет 25% массы остатка. Сколько сахара содержится в 175 кг плодов ананаса?
Решение.
84% =0,84; 25% =
0,25 = ![]() .
.
1) 175 · 0,84 = 147 (кг) содержится воды.
2) 175 – 147 = 28 (кг) остаток.
3) 28 · ![]() = 7 (кг)
содержится сахара.
= 7 (кг)
содержится сахара.
Ответ: 7 кг.
7. Повторение материала: а) решить № 513 (б; д; и);
б) повторив нахождение объема прямоугольного параллелепипеда V = авc, решить задачу № 519.
Решение.
1) 1,1 · 1,1 = 1,21 (дм2) площадь основания.
2) 2,42 : 1,21 = 2 (дм) высота параллелепипеда.
Ответ: 2 дм.
IV. Итог урока.
1. Сформулируйте правило нахождения дроби от числа.
2. Расскажите, как найти несколько процентов от числа.
Домашнее задание: изучить п. 14; решить № 524, 526, 534 (б); индивидуальное задание: № 535 (б).
Урок 3
Цели: закрепить знание правил действий с десятичными дробями в ходе выполнения упражнений; вырабатывать навыки решения задач на нахождение дроби от числа.
Ход урока
I. Повторение изученного материала.
1. Решить устно № 507 (а; б; в) и № 511.
2. Сформулировать правила нахождения дроби от числа и решить задачи устно:
а) На ветке сидело
12 птиц, ![]() их числа улетело.
Сколько птиц улетело?
их числа улетело.
Сколько птиц улетело?
б) В тетради 24
страницы. Записи занимают ![]() числа всех страниц тетради. Сколько в
тетради чистых страниц?
числа всех страниц тетради. Сколько в
тетради чистых страниц?
в) Опыляя
растения, вертолет совершает каждый круг в среднем за ![]() ч. Сколько минут
длится каждый круг вертолета?
ч. Сколько минут
длится каждый круг вертолета?
II. Выполнение упражнений.
1. Решить № 485 (е; и; м) на доске и в тетрадях.
Решение.
е) 40 · 0,55 = 22; и) 50 · 0,3 = 15;
м) ![]()
2. Решить задачу:
У мальчика было 240 р. Он потратил ![]() этой суммы и
этой суммы и ![]() остатка. Сколько
денег он потратил?
остатка. Сколько
денег он потратил?
Решение.
1) ![]() (р.) потратил
сначала.
(р.) потратил
сначала.
2) 240 – 60 = 180 (р.) осталось.
3) ![]() (р.) еще потратил.
(р.) еще потратил.
4) 60 + 90 = 150 (р.) всего потратил.
Ответ: 150 р.
3. Решить задачу № 492 с комментированием на месте.
Решение.
1) 86,5 · 0,2 = 17,3 (кг) масса одного ягненка.
2) 86,5 + 17,3 · 6 = 190, 3 (кг) масса овцы с шестью ягнятами.
Ответ: 190,3 кг.
4. Решить задачу № 481 самостоятельно.
5. Решить задачу № 483 на доске и в тетрадях.
Решение.
120% = 1,2
1) 45 · 1,2 = 54 (детали) изготовил рабочий.
Ответ: 54 детали.
6. Решить задачу № 505.
Решение.
Месячная норма составляет 100%.
1) 30% · 0,8 = 24% было выполнено во вторую неделю.
2) 24% · ![]() было выполнено в
третью неделю.
было выполнено в
третью неделю.
3) 100% – (30% + 24% + 16%) = 100% – 70% = 30% месячный нормы осталось выполнить бригаде в четвертую неделю.
Ответ: 30%.
7. Повторение ранее изученного материала:
а) решить № 513 (в; е; k) самостоятельно;
б) решить задачу № 518 с комментированием на месте.
Решение.
1) 40 · ![]() (км/ч) скорость
скворца.
(км/ч) скорость
скворца.
2) 48 · ![]() (км/ч) скорость
голубя.
(км/ч) скорость
голубя.
Ответ: 56 км/ч.
III. Итог урока. Решить задачи:
1) Найдите: а) 15%
от 84 р.; б) ![]() от 6,3 кг.
от 6,3 кг.
2) В колхозе под
пшеницей занято ![]() всего поля, под
кукурузой – 0,3 остальной площади, а оставшаяся площадь отведена под
овощи. Сколько гектаров земли отведено под овощи, если вся площадь поля 450 га?
всего поля, под
кукурузой – 0,3 остальной площади, а оставшаяся площадь отведена под
овощи. Сколько гектаров земли отведено под овощи, если вся площадь поля 450 га?
Домашнее задание: п. 14; решить № 527, № 528, № 534 (в), № 532; на сообразительность решить № 512.
Урок 4
Цели: упражнять учащихся в нахождении дроби от числа, умножении и сокращении дробей; проверить знания и умения учащихся в ходе проведения самостоятельной работы.
Ход урока
I. Устная работа.
1. Решить № 507 (г; д). Повторить правила действий с десятичными дробями.
2. Устно решить № 515.
3. Повторить правило нахождения дроби от числа. Устно найти:
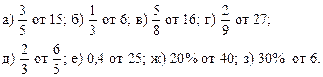
II. Тренировочные упражнения.
1. Найдите: а)
35,2% от 75 р.; б) ![]() от 25,5 кг; в)
0,72 от 14,5 га.
от 25,5 кг; в)
0,72 от 14,5 га.
2. Решить задачу № 493 на доске и в тетрадях.
Решение.
1) 72 · ![]() = 60 (рис.)
выполнены акварелью.
= 60 (рис.)
выполнены акварелью.
2) 72 – 60 = 12 (рис.) остальные.
3) 12 · 0,25 = 12
· ![]() = 3 (рис.)
выполнены карандашами.
= 3 (рис.)
выполнены карандашами.
Ответ: 3 рисунка.
3. Решить задачу № 495 с комментированием на месте.
Решение.
1) 6 · ![]() = 4 (м) ширина.
= 4 (м) ширина.
2) 4 · 0,6 = 2,4 (м) высота.
3) 6 · 4 = 24 (м2) площадь комнаты.
4) 24 · 2,4 = 57,6 (м3) объем комнаты.
Ответ: 24 м2; 57,6 м3.
4. Решить задачу № 499 на доске и в тетрадях.
Решение.
1) 60 · 0,15 = 9 (м) понизился уровень в июне.
2) 60 – 9 = 51 (м) стал уровень озера в июне.
3) 51 · 0,12 = 6,12 (м) понизился уровень в июле.
4) 51 – 6,12 = 44,88 (м) стала глубина озера к началу августа.
Ответ: 44,88 м.
5. Решить задачу: От куска материи отрезали сначала 30%, а потом еще 20% остатка. Сколько процентов куска материи осталось?
Решение.
Весь кусок материи составляет 100%.
1) 100% – 30% = 70% осталось материи.
2) 70% · 0,2 = 14% материи отрезали потом.
3) 70% – 14% = 56% материи осталось.
Ответ: 56%.
6. Решить задачу № 503.
Решение.
Весь намеченный путь примем за 1.
1) 0,75 · ![]() (часть) пути
пройдена после обеда.
(часть) пути
пройдена после обеда.
2) ![]() (часть) весь
путь.
(часть) весь
путь.
Ответ: да, прошел.
III. Самостоятельная работа (15 мин).
Вариант I.
1. Найдите: а)
2,5% от 80 р.; б) ![]() от 25,2 т; в)
0,18 от 3,5 м3.
от 25,2 т; в)
0,18 от 3,5 м3.
2. Посадки леса занимают 420 га. Ели занимают 63,5% этой площади, а сосны 29 %. На сколько гектаров площадь, занятая елями, больше площади, занятой соснами?
3. Учитель 0,4
урока объяснял новый материал, ![]() остального времени урока ушло на решение
задач, а в оставшееся время учащиеся писали самостоятельную работу. Сколько
минут учащиеся писали работу, если урок длился 45 минут?
остального времени урока ушло на решение
задач, а в оставшееся время учащиеся писали самостоятельную работу. Сколько
минут учащиеся писали работу, если урок длился 45 минут?
4. Сначала продали 40% привезенного картофеля, а потом 30% остатка. Сколько процентов привезенного картофеля осталось?
Вариант II.
1. Найдите: а)
7,5% от 40 р.; б) ![]() от 37,2 ц; в)
0,14 от 7,5 га.
от 37,2 ц; в)
0,14 от 7,5 га.
2. Сад занимает 80 га. Яблони занимают 58,5% этой площади, а вишни 39%. На сколько гектаров площадь под вишнями меньше площади под яблонями?
3. Для обработки
детали потребовалось 180 мин. Обработка детали на токарном станке заняла 0,8
этого времени, ![]() остального
времени ушло на сверление отверстий, а оставшееся время пошло на окончательную
отделку. Сколько времени пошло на окончательную отделку?
остального
времени ушло на сверление отверстий, а оставшееся время пошло на окончательную
отделку. Сколько времени пошло на окончательную отделку?
4. Сначала Витя прочитал 60% всей книги, а потом 40% остатка. Сколько процентов книги осталось прочитать Вите?
Домашнее задание: решить № 525, № 529, № 531, № 535 (б).
ПРИМЕНЕНИЕ РАСПРЕД СВОЙСТВА УМНОЖЕНИЯ
Урок 1
Цели: повторить распределительное свойство умножения относительно сложения и относительно вычитания и научить применять их при нахождении значений выражений и умножении смешанного числа на натуральное число.
Ход урока
I. Анализ самостоятельной работы.
1. Указать ошибки, сделанные учащимися в ходе выполнения работы.
2. Решить задания, вызвавшие затруднения у учащихся.
3. Устно решить № 553 (а) и № 554 (а; б).
II. Изучение нового материала.
1. Повторить распределительное свойство умножения относительно сложения и относительно вычитания:
а · (в + с) = ав + ас;
а · (в – с) = ав – ас.
2. Разобрать по учебнику из пункта 15 «Применение распределительного свойства умножения», примеры 1 и 2 на странице 87.
Пример 1. Найдем значение выражения:
![]() .
.
Пример 2. Найдем значение произведения:
![]()
3. Сформулировать и изучить правило умножения смешанного числа на натуральное число.
III. Закрепление изученного материала.
1. Решить № 536 (а; б) и № 537 (а; в) на доске и в тетрадях.
2. Решить № 537 (б; г) с комментированием на месте.
3. Решить № 538 (а; б; в) на доске и в тетрадях.
Решение.
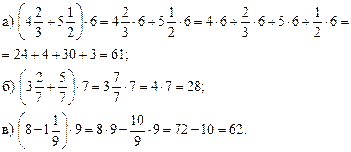
4. Решить задачу № 541 с комментированием на месте.
5. Решить задачу № 542, с. 89 в учебнике.
Решение.
1) 150 · ![]() =150 ·
=150 · ![]() (лет) живет сосна.
(лет) живет сосна.
2) 350 · 5 = 1750 (лет) живет мамонтово дерево.
Ответ: 1750 лет.
6. Повторение ранее изученного материала:
а) решить № 565 (а; в; д); три человека самостоятельно решают на доске, остальные – в тетрадях, а потом проверяется решение;
б) решить задачу № 559 самостоятельно на с. 91 в учебнике.
IV. Итог урока.
1. Повторить распределительное свойство; повторить правило пункта 15.
2. Устно. Выполнить действия наиболее удобным способом:
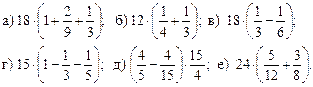
Домашнее задание: выучить правило из п. 15; решить № 567 (а; б; г), № 568 (а; б), № 573.
Урок 2
Цели: научить применять распределительное свойство умножения для представления суммы в виде произведения суммы и числа при нахождении значений выражений; закрепить знания и умения умножения дробей.
Ход урока
I. Устная работа.
1. Проверить выполнение учащимися домашнего задания.
2. Повторить распределительное свойства умножения относительно сложения и относительно вычитания. Привести свои примеры.
3. Решить устно № 553 (б) и № 555.
II. Работа по учебнику.
Изучить пункт 15 (до конца) на страницах 87–88 учебника.
1. Найдем значение выражения (пример 3):
![]() .
.
Решение.
Запишем распределительный закон умножения относительно сложения в таком виде.
а · в + а · с = а · (в + с), тогда получим
![]()
2. Решить: ![]()
![]()
3. Используя распределительное свойство умножения, можно упрощать выражения вида:
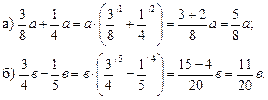
4. В простых случаях можно писать сразу:
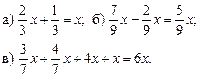
III. Закрепление изученного материала.
1. Решить № 536 (в; г) на доске и в тетрадях.
2. Решить № 537 (д; ж; е; з) с комментированием на месте.
3. Решить № 538 (д; е) на доске и в тетрадях.
Решение.

4. Решить № 539 (а; д; k) на доске и в тетрадях.
Решение.
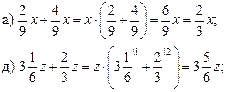
![]()
5. Решить № 539 (б; л) с комментированием на месте.
6. Решить задачу № 543 на доске и в тетрадях.
Решение.
![]() площадь
площадь
![]() (м2) меньше площадь
меньшей комнаты.
(м2) меньше площадь
меньшей комнаты.
Ответ: на 8 м2.
7. Решить самостоятельно № 529, предварительно разобрав решение задачи.
Решение.
![]()
8. Повторение ранее изученного материала:
а) решить задачу № 561 с комментированием на месте;
б) решить № 565 (б; е) самостоятельно с последующей проверкой.
IV. Итог урока.
1. Рассказать, как можно умножать смешанное число на натуральное число.
2. Написать на доске распределительное свойство умножения относительно сложения и относительно вычитания.
3. Устно: ![]()
![]()
Домашнее задание: изучить п. 15; решить № 567 (в; д; е), № 568 (в; г), № 569 (а), № 571.
Урок 3
Цели: способствовать выработке навыков и умений в применении распределительного свойства умножения относительно сложения и относительно вычитания при нахождении значений выражений, упрощении выражений и решении задач.
Ход урока
I. Устная работа.
1. Просмотреть по тетрадям выполнение учащимися домашнего задания.
2. Решить устно № 553 (в) и № 554 (в).
3. Разобрать решение задачи № 557.
II. Выполнение упражнений.
1. Решить № 538 (ж; з) на доске и в тетрадях.
Решение.
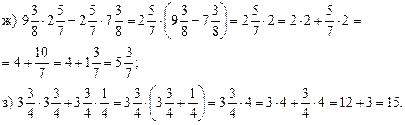
2. Решить задачу № 544.
Решение.
![]() осталось
невспаханной.
осталось
невспаханной.
Если а =
57, то![]() .
.
Если а =
234, то![]() .
.
Если а =
142![]() , то
, то![]() .
.
3. Решить задачу № 546.
Решение.
1) с · 0,36 = 0,36с (м2) площадь первой комнаты.
2) 0,36с![]() (м2) площадь второй
комнаты.
(м2) площадь второй
комнаты.
3) 0,36с + 0,3с = 0,66с (м2) площадь двух комнат вместе.
Если с = 50, то 50 · 0,66 = 33;
если с = 75, то 75 · 0,66 = 49,5.
4. Решить № 539 (в; е) (на доске решить е), устно решить в)).
5. Решить уравнение № 540 (в).
Решение.
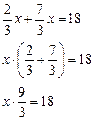
3х = 18
х = 18 : 3
х = 6.
Ответ: х = 6.
6. Решить № 549 (а; б) на доске и в тетрадях.
Решение.
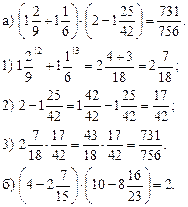

7. Повторение ранее изученного материала: учащиеся самостоятельно решают задачи № 560 и 562, а затем проверяется их решение.
III. Итог урока.
Выполнить действия наиболее удобным способом:
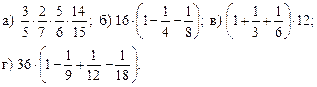
Домашнее задание: решить № 568 (д), № 569 (б; в), № 574, № 576 (а).
Урок 4
Цели: закрепить знания учащихся при умножении дробей и применении распределительного закона умножения относительно сложения и относительно вычитания; развивать логическое мышление учащихся.
Ход урока
I. Проверка домашнего задания.
1. Двое учащихся решают на доске домашнее задание № 569 (б) и 574.
2. По тетрадям с
остальными учащимися проверяем решение
№ 568 (д) и 576 (а).
3. Устно решить № 556 (а) по рисунку 27 (с. 91 учебника).
4. Устно решить № 552 (а; д).
II. Тренировочные упражнения.
1. Решить № 537 (и; k). Двое учащихся решают самостоятельно на доске, остальные – в тетрадях, а затем решение проверяется.
2. Решить № 540 (а; г). Решение объясняет учитель.
Решение.
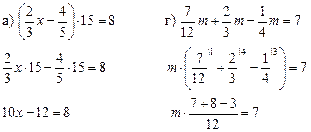

х = 20 : 10 Ответ: m = 7.
х = 2.
Ответ: х = 2.
3. Решить задачу № 547.
Решение.
1) а · ![]() (л) налили в
кастрюлю.
(л) налили в
кастрюлю.
2) ![]() (л) молока налили
в кувшин.
(л) молока налили
в кувшин.
3) а –![]() (л) молока
осталось в бидоне.
(л) молока
осталось в бидоне.
4. Решить № 549 (в; г) и № 551 (а).
Решение.
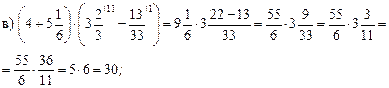
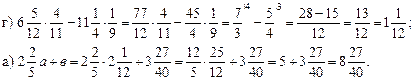
III. Самостоятельная работа.
Вариант I.
1. Найдите значение выражения:
![]()
2. Найдите значение выражения:
![]()
3. Решите
уравнение ![]()
4. Докажите, что
значение выражения ![]() не зависит от
значения t.
не зависит от
значения t.
Вариант II.
1. Найдите значение выражения:
![]()
2. Найдите значение выражения:
![]()
3. Решите
уравнение ![]()
4. Докажите, что
значение выражения ![]() не зависит от
значения x.
не зависит от
значения x.
Домашнее задание: решить № 569 (г), № 570, № 575.
Урок 5
Цели: закрепить и систематизировать изученный материал; подготовить учащихся к контрольной работе; развивать логическое мышление учащихся.
Ход урока
I. Сообщение результатов самостоятельной работы.
II. Устная работа.
1. Решить № 552 (б; в; г).
2. Повторить правило умножения смешанного числа на натуральное число. Привести примеры.
3. Повторить распределительный закон умножения относительно вычитания и относительно сложения. Привести свои примеры.
III. Выполнение упражнений.
1. Решить № 539 (г; ж; и) на доске и в тетрадях на с. 88–89 в учебнике.
2. Решить № 539 (з; м) с комментированием на месте.
Решение.
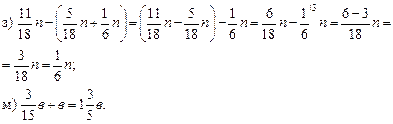
3. Решить уравнение № 540 (б).
Решение.
![]()
15 – 14у = 1; 14у = 15 – 1; 14у = 14; у = 1.
Ответ: 1.
4. Решить задачу № 548.
5. Решить № 550 на доске и в тетрадях.
Решение.
Сравните выражения:
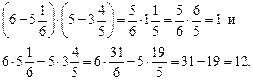
1 < 12, значит, первое выражение меньше второго.
6. Решить № 551 (б) на доске и в тетрадях.
7. Решить задачи на повторение изученного материала:
а) № 563.
Решение.
Весь уголь на складе составляет 100%.
1) 100% – 40% = 60% угля осталось после первого дня.
2) 60% · 0,75 = 45% угля вывезли во второй день.
3) 60% – 45% = 15% угля осталось на складе.
Ответ: 45%; 15%.
б) № 564.
Решение.
1) 658 ![]() (кг) персиков продали в первый день.
(кг) персиков продали в первый день.
2) 658 – 188 = 478 (кг) персиков осталось.
3) 478 · 0,3 = 141 (кг) персиков продали во второй день.
Ответ: 141 кг.
в) Задача. За
три дня вспахали 192 га земли. В первый день вспахали 62,5% этой площади, во
второй день – ![]() оставшейся
площади. Сколько гектаров земли вспахали в третий день?
оставшейся
площади. Сколько гектаров земли вспахали в третий день?
IV. Итог урока.
Домашнее задание: решить № 568 (е), № 572, № 576 (б), № 558.
КОНТРОЛЬНАЯ РАБОТА № 4
Цели: выявление степени усвоения учащимися изученного материала; проверка знаний и умений учащихся по изученному материалу.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение контрольной работы по вариантам.
Вариант 1.
1. Найдите произведение:
![]()
2. Выполните
действия: ![]()
3. Фермерское
хозяйство собрало 960 т зерна. 75% собранного зерна составляла пшеница, а ![]() остатка – рожь.
Сколько тонн ржи собрало фермерское хозяйство?
остатка – рожь.
Сколько тонн ржи собрало фермерское хозяйство?
4. В один пакет
насыпали 1![]() кг сахара, а в
другой – в 4 раза больше. На сколько больше сахара насыпали во второй пакет,
чем в первый?
кг сахара, а в
другой – в 4 раза больше. На сколько больше сахара насыпали во второй пакет,
чем в первый?
5. Не приводя к
общему знаменателю, сравните дроби ![]()
Вариант II.
1. Найдите произведение:
![]()
2. Выполните
действия: ![]()
3. Во время
субботника заводом было выпущено 150 холодильников. ![]() этих
холодильников было отправлено в больницы, а 60% остатка – в детские сады.
Сколько холодильников было отправлено в детские сады?
этих
холодильников было отправлено в больницы, а 60% остатка – в детские сады.
Сколько холодильников было отправлено в детские сады?
4. Масса гуся 4![]() кг, а масса
страуса в 7 раз больше. На сколько килограммов масса гуся меньше массы страуса?
кг, а масса
страуса в 7 раз больше. На сколько килограммов масса гуся меньше массы страуса?
5. Не приводя к
общему знаменателю, сравните дроби ![]()
Вариант III.
1. Найдите произведение:
![]()
2. Выполните
действия: ![]()
3. Завод изготовил
сверх плана 120 телевизоров. ![]() этих телевизоров отправлено строителям
гидростанции, а 80% остатка – в рисоводческий совхоз. Сколько телевизоров было
отправлено в рисоводческий совхоз?
этих телевизоров отправлено строителям
гидростанции, а 80% остатка – в рисоводческий совхоз. Сколько телевизоров было
отправлено в рисоводческий совхоз?
4. Масса козленка
6![]() кг, а масса
поросенка в 3 раз больше. На сколько килограммов масса козленка меньше массы
поросенка?
кг, а масса
поросенка в 3 раз больше. На сколько килограммов масса козленка меньше массы
поросенка?
5. Не приводя к
общему знаменателю, сравните дроби ![]()
Вариант IV.
1. Найдите произведение:
![]()
2. Выполните
действия: ![]()
3. Электричкой,
автобусом и катером туристы проехали 150 км. Расстояние, которое проехали
туристы электричкой, составляет 60% всего пути, а автобусом – ![]() оставшегося.
Сколько километров туристы проехали автобусом?
оставшегося.
Сколько километров туристы проехали автобусом?
4. Длина одного
отрезка 5![]() дм, а другого – в
3 раза больше. На сколько дециметров длина второго отрезка больше первого?
дм, а другого – в
3 раза больше. На сколько дециметров длина второго отрезка больше первого?
5. Не приводя к
общему знаменателю, сравните дроби ![]()
III. Итог урока.
ВЗАИМНООБРАТНЫЕ ЧИСЛА
Урок 1
Цели: ввести понятие взаимно обратных чисел; повторить правило умножения дробей, сокращения дробей; развивать логическое мышление учащихся.
Ход урока
I. Анализ контрольной работы.
1. Сообщить результаты контрольной работы.
2. Выполнить на доске задания, вызвавшие затруднения у учащихся.
3. Устно решить № 582 и 586 (а; б).
II. Изучение нового материала.
1. Выполнить умножение чисел:
![]()
2. Определение взаимно обратных чисел.
![]() при а ≠ 0 и в ≠ 0.
при а ≠ 0 и в ≠ 0.
3. Найти число,
обратное числу 3![]()
Запишем число 3![]() в виде
неправильной дроби:
в виде
неправильной дроби: ![]() Значит, обратным
Значит, обратным ![]() будет число
будет число ![]()
III. Закрепление изученного материала.
1. Решить № 577 (а; г; д) на доске и в тетрадях.
2. Решить № 578 (а; е) на доске и в тетрадях; № 578 (б; в; г) решить с комментированием на месте.
Решение.
![]()
3. Решить уравнения № 564 (а; б).
Решение.
4. Повторение ранее изученного материала:
а) решить № 583;
б) самостоятельно решить № 590 (1);
в) решить на доске и в тетрадях № 589.
Решение.
Вспомнить правило нахождения среднего арифметического чисел.
Пусть первое число равно х, тогда второе число (х + 0,9), а третье число 2х. Составим и решим уравнение:
(х + х + 0,9 + 2х) : 3 = 3,1
4х + 0,9 = 3,1 · 3
4х + 0,9 = 9,3
4х = 9,3 – 0,9
4х = 8,4
х = 8,4 : 4 = 2,1.
Первое число равно 2,1; второе число 2,1 + 0,9 = 3; третье число 2,1 · 2 = 4,2.
Ответ: 2,1; 3; 4,2.
IV. Итог урока.
1. Ответить на вопросы:
а) Какие числа называют взаимно обратными?
б) Как записать
число, обратное дроби ![]()
в) Как записать число, обратное натуральному числу?
г) Как записать число, обратное смешанному числу?
2. Привести свои примеры.
Домашнее задание: п. 16, решить № 591 (а); № 592 (а; в), № 595 (а).
Урок 2
Цели: закрепить понятие взаимно обратных чисел в ходе выполнения упражнений; закрепить правило умножения дробей; развивать навыки решения уравнений и задач.
Ход урока
I. Устная работа.
1. Проверить по тетрадям выполнение домашних заданий № 591 (а) и № 592 (а; в).
2. Решить устно № 584 (а; в) и № 586 (в; г; д).
II. Работа по учебнику.
1. Разобрать по учебнику пример 2 на странице 94.
Найдем значение произведения
![]()
2. Сделать вывод: если число х сначала умножить на некоторое число а, а потом умножить на число, обратное а, то получим опять х.
III. Выполнение упражнений.
1. Решить № 577 (б; в; е).
2. Решить № 578 (д; ж; з) на доске и в тетрадях.
Решение.
д) ![]()
3. Решить уравнения № 580 (д; е) (устно); № 580 (в; г) на доске и в тетрадях.
Решение.
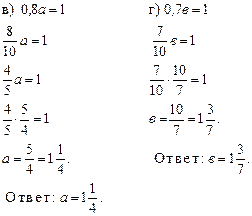
4. Решить № 579 с комментированием на месте. Повторить сочетательный и переместительный законы умножения.
Решение.
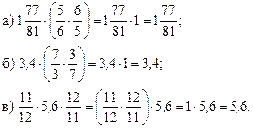
5. Повторение ранее изученного материала:
а) Решить задачу № 588.
Решение.
1) 100% – (40% + 30%) = 100% – 70% = 30% пути прошел турист в третий день;
2) 40 · 0,3 = 12 (км) прошел турист в третий день.
Ответ: 12 км.
б) Решить № 571 (в; г; д) самостоятельно с последующей проверкой по тетрадям.
в) Найти значение выражения:
1) 3![]()
Решение.
Повторить распределительное свойство умножения относительно сложения и относительно вычитания.

IV. Итог урока.
1. Какие числа называются взаимно обратными?
2. Назовите число, обратное числу:
а) ![]()
3. Будут ли взаимно обратными числа:
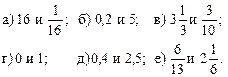
Домашнее задание: изучить п. 16; решить № 591 (б), № 593, № 592 (б; г), № 585.
ДЕЛЕНИЕ
Урок 1
Цели: ввести понятие деления дроби на дробь и закрепить при решении задач и упражнений; закрепить правило умножения дроби на дробь и сокращения дробей.
Ход урока
I. Устная работа.
1. Проверить по тетрадям домашнее задание.
2. Решить устно № 622 и № 623.
3. Вспомнить правило округления чисел и решить устно № 629 (а).
II. Изучение нового материала.
1. Разобрать решение задачи на странице 97 учебника.
2. Правило деления одной дроби на другую.
3. Разобрать решение примера 1 на странице 97. Сделать вывод: при делении смешанных чисел сначала представляют числа в виде неправильных дробей, а затем выполняют деление дробей.
4. Разобрать решение примера 2 на странице 97.
![]()
III. Закрепление изученного материала.
1. Решить № 596 (а; в; ж; л) на доске и в тетрадях, № 596 (б; г; е; н) на местах с комментированием.
Решение.
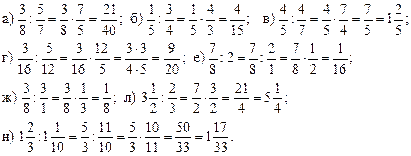
2. Решить задачу № 599 самостоятельно.
3. Решить задачу № 601 на доске и в тетрадях.
Решение.
Пусть первое
число равно х, тогда второе число равно ![]() . Сумма двух чисел
равна
. Сумма двух чисел
равна ![]() Составим и решим
уравнение:
Составим и решим
уравнение:
х + 1![]()
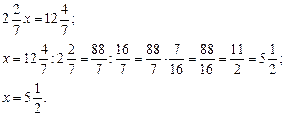
Первое число 5![]() второе число
второе число ![]()
Ответ: ![]()
4. Решить задачу № 610 с комментированием на месте.
Решение.
Пусть Митя нашел у
грибов, тогда Коля нашел ![]() у грибов.
Всего мальчики нашли 64 гриба.
у грибов.
Всего мальчики нашли 64 гриба.
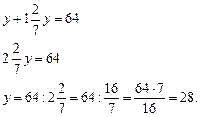
Митя нашел 28 грибов, Коля нашел 64 – 28 = 36 (гриба).
Ответ: 36 грибов; 28 грибов.
IV. Повторение ранее изученного материала.
1. Решить устно № 627 (а; б) и № 626 (а; б).
2. Решить № 628 (а; б). Повторить правила деления на десятичную дробь и правила округления чисел.
V. Итог урока.
1. Вопросы: а) Сформулировать правило деления дробей. б) Как выполняется деление смешанных чисел?
2. Выполнить деление (устно):
![]()
Домашнее задание: изучить п. 17; решить № 633 (а; б; в), № 634 (а), № 645 (а), № 646 (а; б).
Урок 2
Цели: способствовать выработке умений и навыков деления и умножения дробей; развивать навыки решения задач с помощью уравнения; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Повторить правила умножения дробей и деления одной дроби на другую; правило деления смешанных чисел.
2. Устно решить № 626 (в; г; д).
3. Устно решить № 629 (б), повторив правило округления чисел.
II. Изучение частных случаев деления дробей.
1. Деление нуля на дробное число дает нуль.
Примеры: 1) 0 : 5 = 0; 2) 0 : ![]() =0; 3) 0 :
=0; 3) 0 : ![]() Проверить с
помощью умножения.
Проверить с
помощью умножения.
Делить на нуль нельзя!
2. При делении дроби на 1 частное равно делимому.
Примеры: ![]()
3. При делении 1 на дробь в частном получаем дробь, обратную делителю.
Пример: ![]()
Замечания: 1) При делении числа на правильную дробь частное будет больше делимого.
Пример: ![]()
2) При делении числа на неправильную дробь, бóльшую единицы, частное будет меньше делимого.
Пример: ![]()
4. Устно. Не выполняя деления, укажите, каким будет частное (больше, равно или меньше делимого):
![]()
III. Выполнение упражнений.
1. Решить № 596 (д; з; м) на доске и в тетрадях, № 580 (и; k; о; с; т; у) с комментированием на месте.
2. Решить № 597 (а).
3. Решить задачу № 600.
Решение.
![]() (кг) масса 1 дм3.
(кг) масса 1 дм3.
![]() (дм3) объем 1 кг соснового
бруска.
(дм3) объем 1 кг соснового
бруска.
Ответ: ![]() кг; 2 дм3.
кг; 2 дм3.
4. Решить задачу № 612 с помощью уравнения.
Решение.
Пусть сыну х
лет, тогда отцу 3![]() х лет. По условию
задачи сын моложе отца на 28 лет. Составим и решим уравнение:
х лет. По условию
задачи сын моложе отца на 28 лет. Составим и решим уравнение:
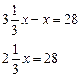
х = 28 : 2![]()
х = 12.
Сыну 12 лет, отцу 12 + 28 = 40 (лет).
Ответ: 12 лет, 40 лет.
5. Решить задачу № 614 с комментированием.
Решение.
350 грибов всего; пусть белка собрала х грибов, тогда бельчонок собрал 0,75х грибов.
х + 0,75х = 350
1,75х = 350
х = 350 : 1,75 = 35000 : 175
х = 200.
Белка собрала 200 грибов, а бельчонок 350 – 200 = 150 (грибов).
Ответ: 200 грибов; 150 грибов.
IV. Итог урока.
1. Выполните деление:
![]()
2. Не выполняя умножения, сравните:
87![]()
Домашнее задание: изучить п. 17; решить № 633 (г; ж; и), № 634 (б), № 637, № 645 (б), № 646 (в).
Урок 3
Цели: развивать навыки и умения учащихся при умножении и делении дробей; развивать логическое мышление учащихся.
Ход урока
I. Проверка изученного материала.
1. Двое учащихся работают по карточкам:
Карточка 1
1) Найти значение выражения:
![]()
2) Сформулировать правило деления дроби на другую дробь.
Карточка 2
1) Выполнить действия:
![]()
2) Как выполняется деление смешанных чисел?
2. С остальными учащимися устно решить № 627 (б) и № 621 (а; в).
3. Проверить по тетрадям выполнение домашнего задания № 634 (б), № 637 и № 646 (в).
II. Тренировочные упражнения.
1. Решить № 596 (п; р; м; ф). Четыре ученика (сразу все) решают на доске, остальные – в тетрадях, а потом проверяется решение.
2. Решить № 597 (б; в) на доске и в тетрадях.
Решение.
![]()
3. Решить № 602, составляя уравнение.
Решение.
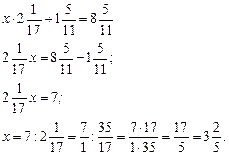
Ответ: ![]()
4. Решить № 607 (б; г; а; в) на доске и в тетрадях.
Решение.
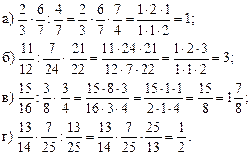
5. Решить задачу № 615 с помощью составления уравнения.
Решение.
Пусть второй
плотник сделал х рам, тогда первый плотник сделал ![]() рам.
рам.
По условию задачи известно, что первый плотник сделал на 9 оконных рам меньше, чем второй. Составим и решим уравнение.
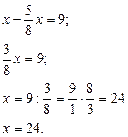
Второй плотник сделал 24 рамы, первый плотник сделал 15 рам.
Ответ: 15 рам; 24 рамы.
6. Решить № 625 устно.
7. Самостоятельно решить № 631 (1).
Проверить решение этой задачи.
Решение.
1) 250 · 0,7 = 175 (лошадей) были серыми.
2) 250 – (30 + 175) = 45 (лошадей) были рыжей масти.
Ответ: 45 лошадей.
8. Решить задачу:
В первом пакете 2
кг пшена, что в ![]() раза больше, чем
во втором, и в
раза больше, чем
во втором, и в ![]() раза меньше, чем в
третьем. Сколько килограммов пшена в трех пакетах вместе?
раза меньше, чем в
третьем. Сколько килограммов пшена в трех пакетах вместе?
Решение.
![]() (кг) пшена во
втором пакете.
(кг) пшена во
втором пакете.
![]() (кг) пшена в
третьем пакете.
(кг) пшена в
третьем пакете.
![]() (кг) пшена в трех
пакетах вместе.
(кг) пшена в трех
пакетах вместе.
Ответ: 6 кг.
III. Итог урока.
Домашнее задание: решить № 633 (д; з), № 634 (в), № 635 (а), № 639, № 644.
Урок 4
Цели: проверить знания, умения и навыки учащихся в ходе выполнения самостоятельной работы; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Сформулировать правила умножения дробей, правило деления одной дроби на другую дробь.
2. Как выполняется умножение смешанных чисел?
3. Повторить частные случаи деления дробей:
а) деление нуля на дробное число (привести свои примеры);
б) деление дроби на 1 (привести свои примеры);
в) деление 1 на дробь (привести примеры);
г) деление числа на правильную дробь и на неправильную дробь.
4. Устно решить № 624 (а; б) и № 621 (б; г).
II. Выполнение упражнений.
1. Решить № 603 самостоятельно, повторив формулы периметра Р = (а + в) · 2 и площади S = a · в прямоугольника.
2. Решить № 607 (д; ж; з) на доске и в тетрадях, № 607 (е; и) самостоятельно, с последующей проверкой.
Решение.
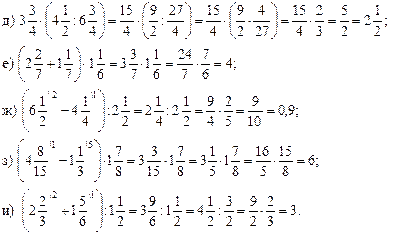
3. Решить уравнения № 609 (а; ж; з) на доске и в тетрадях; № 609 (б; в; е) с комментированием на месте.
4. Решить задачу № 613 с помощью уравнения.
Решение.
Пусть во второй
день турист прошел х км, тогда в первый день прошел![]() км.
км.
Всего за два дня турист прошел 26 км.
![]()
Во второй день турист прошел 14 км, тогда в первый день 12 км.
Ответ: 12 км; 14 км.
III. Самостоятельная работа (15 мин).
Вариант I.
1. Выполните деление:
![]()
2. Найдите значение выражения:
![]()
3. В первом ящике
8 кг винограда, что в 1![]() раза больше, чем
во втором, и в
раза больше, чем
во втором, и в ![]() раза меньше, чем
в третьем. Сколько килограммов винограда в трех ящиках?
раза меньше, чем
в третьем. Сколько килограммов винограда в трех ящиках?
4. Не выполняя умножения, сравните:
![]()
Вариант II.
1. Выполните деление:
![]()
2. Найдите значение выражения:
![]()
3. Мост состоит из
трех пролетов. Длина первого пролета 12 м, что в 1![]() раза больше длины второго пролета и в
раза больше длины второго пролета и в ![]() раза меньше
третьего. Найдите длину моста.
раза меньше
третьего. Найдите длину моста.
4. Не выполняя умножения, сравните:
![]()
Домашнее задание: решить № 633 (е; k), № 634 (г), № 635 (б), № 636 (а), № 638.
Урок 5
Цели: повторить, систематизировать и закрепить изученный материал; подготовить учащихся к контрольной работе.
Ход урока
I. Анализ и результаты самостоятельной работы.
1. Указать ошибки, сделанные учащимися при выполнении работы.
2. Решить на доске задания, вызвавшие затруднения у учащихся.
II. Выполнение упражнений.
1. Решить задачу № 598 (б) на доске и в тетрадях, № 598 (а) самостоятельно.
2. Решить задачу № 604 с комментированием на месте.
Решение.
![]() (м) ширина
другого прямоугольника.
(м) ширина
другого прямоугольника.
Ответ: ![]() м.
м.
3. Выполнить действия № 607 (к; л; м). Три человека самостоятельно решают на доске, остальные учащиеся решают в тетрадях и потом проверяется решение.
Решение.
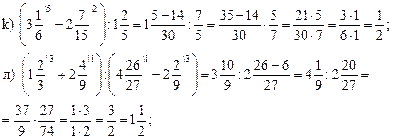
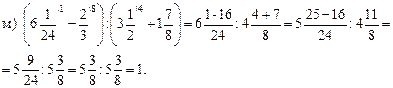
4. Решить задачу № 616 с комментированием на месте.
Решение.
Пусть скорость
второго пешехода х км/ч, тогда скорость первого пешехода ![]() км/ч. Пешеходы
встретились через
км/ч. Пешеходы
встретились через ![]() часа, а прошли
вместе 5 км. Составим и решим уравнение.
часа, а прошли
вместе 5 км. Составим и решим уравнение.
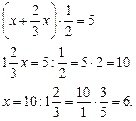
Скорость второго
пешехода 6 км/ч, а скорость первого пешехода 6 · ![]() = 4 (км/ч).
= 4 (км/ч).
Ответ: 4 км/ч, 6 км/ч.
5. Решить уравнения № 609 (г; k; д; и).
Решение.
![]()
Ответ: k = 5.
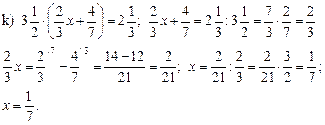
Ответ: ![]()
![]()
Ответ: ![]()
![]()
![]()
Ответ: ![]()
6. Решить задачу № 618 на доске и в тетрадях.
Решение.
Пусть геологи прошли пешком х км, тогда на автомашине они проехали 14х км. Весь их путь оказался равным 225 км.
х + 14х = 225
15х = 225
х = 225 : 15
х = 15.
15 км геологи прошли пешком, 225 – 15 = 210 (км) проехали на машине.
![]() (км/ч) скорость
пешком;
(км/ч) скорость
пешком;
![]() (км/ч) скорость
автомашины.
(км/ч) скорость
автомашины.
Ответ: 2 км/ч; 24 км/ч.
7. Решить задачу № 619, а потом проверить ее решение по тетрадям.
Решение.
Пусть в бочонке у
л кваса, тогда в бидоне ![]() л кваса. Всего 60
л кваса.
л кваса. Всего 60
л кваса.
![]()
В бочонке 48 л кваса, а в бидоне 80 – 48 = 32 (л) кваса.
1) 48 : 20 = 2,4 (л) кваса в одном кувшине;
2) 32 : 32 = 1 (л) кваса в одной банке;
3) 2,4 – 1 = 1,4 (л) больше кваса в одном кувшине.
Ответ: 2,4 л; 1 л; на 1,4 л.
III. Итог урока.
Домашнее задание: решить № 635 (в; г), № 636 (б), № 640; 641, 646 (г).
КОНТРОЛЬНАЯ РАБОТА № 5
Цели: выявление степени усвоения учащимися изученного материала; развитие логического мышления учащихся.
Ход урока
I. Организация учащихся на проведение работы.
II. Выполнение контрольной работы по вариантам.
Вариант 1.
1. Выполните действия:
![]()
2. За два дня было
вспахано 240 га. Во второй день вспахали ![]() того, что было вспахано в первый день.
Сколько гектаров земли было вспахано в каждый из этих дней?
того, что было вспахано в первый день.
Сколько гектаров земли было вспахано в каждый из этих дней?
3. За ![]() кг конфет
заплатили
кг конфет
заплатили ![]() р. Сколько стоят
р. Сколько стоят ![]() кг таких конфет?
кг таких конфет?
4. Решите уравнение
![]()
5. Представьте в
виде дроби выражение ![]()
Вариант II.
1. Выполните действия:
![]()
2. В два
железнодорожных вагона погрузили 117 т зерна, причем зерно второго вагона
составляет ![]() зерна первого
вагона. Сколько тонн зерна погрузили в каждый из этих вагонов?
зерна первого
вагона. Сколько тонн зерна погрузили в каждый из этих вагонов?
3. Масса ![]() дм3 гипса равна
дм3 гипса равна ![]() кг. Найдите массу
кг. Найдите массу ![]() дм3
дм3
гипса.
4. Решите
уравнение ![]()
5. Представьте в
виде дроби выражение ![]()
Вариант III.
1. Выполните действия:
![]()
2. За два часа
самолет пролетел 1020 км. За первый час он пролетел ![]() того пути,
который он пролетел во второй час. Сколько километров пролетел самолет в каждый
из этих двух часов?
того пути,
который он пролетел во второй час. Сколько километров пролетел самолет в каждый
из этих двух часов?
3. За ![]() кг конфет
заплатили
кг конфет
заплатили ![]() р. Сколько стоят
р. Сколько стоят ![]() кг таких конфет?
кг таких конфет?
4. Решите
уравнение ![]()
5. Представьте в
виде дроби выражение ![]()
Вариант IV.
1. Выполните действия:
![]()
2. В двух
автоцистернах 32 т бензина. Количество бензина первой цистерны составляло ![]() количества
бензина второй цистерны. Сколько тонн бензина было в каждой из этих двух
автоцистерн?
количества
бензина второй цистерны. Сколько тонн бензина было в каждой из этих двух
автоцистерн?
3. За ![]() м ткани заплатили
м ткани заплатили
![]() р. Сколько стоят
р. Сколько стоят ![]() м такой ткани?
м такой ткани?
4. Решите
уравнение ![]()
5. Представьте в
виде дроби выражение ![]()
III. Итог урока. Повторить правило деления дроби на дробь (п. 17) и правило умножения обыкновенных дробей (п. 13).
НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ
Урок 1
Цель: ввести правило нахождения числа по его дроби и показать его применение при выполнении упражнений и решении задач.
Ход урока
I. Анализ контрольной работы.
1. Сообщить учащимся результаты контрольной работы и указать ошибки.
2. Решить на доске задания, вызвавшие затруднения у учащихся.
II. Объяснение нового материала.
1. Повторить правила деления числа на дробь, деления дроби на дробь, умножения дробей.
2. Сформулировать основное свойство дроби.
3. Решить задачу 1 на странице 104 учебника.
Задача 1. Расчистили от
снега ![]() катка, что
составляет 800 м2, то есть
катка, что
составляет 800 м2, то есть ![]() Значит,
Значит, ![]() Площадь катка
равна 2000 м2.
Площадь катка
равна 2000 м2.
Ответ: 2000 м2.
4. Записать в тетрадях правило: чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.
5. Разобрать решение задачи 2 на страницах 104–105 учебника.
Пшеницей засеяно 2400 га, что составляет 0,8 всего поля. Найдите площадь всего поля.
Решение.
Так как 2400 : 0,8 = 24000 : 8 = 3000, то площадь всего поля равна 3000 га.
Ответ: 3000 га.
6. Решить задачу 3 (решение на странице 105 учебника).
III. Закрепление изученного материала.
1. Решить задачу № 647 на доске и в тетрадях.
Решение.
1) 300 : ![]() (м) длина
дистанции.
(м) длина
дистанции.
Ответ: 800 м.
2. Решить задачу № 648 с комментированием на месте.
Решение.
1) 1,5 : ![]() (м) длина всей
сваи.
(м) длина всей
сваи.
Ответ: 8 м.
3. Решить задачу № 650 (решение объясняет учитель).
Решение.
18% = 0,18
1) 68,4 : 0,18 = 6840 : 18 = 380 (км/ч) средняя скорость самолета с прежним двигателем.
Ответ: 380 км/ч.
4. Решить задачи самостоятельно:
а) Девочка
потеряла 30 бусинок, что составляло ![]() всей нити бус. Сколько бусинок было на
нитке?
всей нити бус. Сколько бусинок было на
нитке?
Ответ: 36 бусинок.
б) Турист проплыл на байдарке 504 км, что составило 36% всего пути. Найдите длину всего пути.
Решение.
36% = 0,36;
1) 504 : 0,36 = 50400 : 36 = 1400 (км).
Ответ: 1400 км.
IV. Итог урока.
1. Сформулируйте правило нахождения числа по данному значению его дроби.
2. Расскажите, как найти число по данному значению его процентов.
Домашнее задание: выучить правило п. 18; решить № 680, 683, 678 (3; 4).
Урок 2
Цели: способствовать выработке навыков и умений при решении задач на нахождение числа по его дроби; учить учащихся решению задач.
Ход урока
I. Проверка выполнения домашнего задания.
1. Двое учащихся решают на доске задачи № 680 и 683.
2. С остальными учащимися проводится устная работа:
1) сформулировать правило нахождения числа по его дроби;
2) решить задачи:
а) Какова сумма
денег, если 12 р. составляют ![]() имеющейся суммы?
имеющейся суммы?
б) Определите
длину отрезка, ![]() которого имеют
длину 15 см.
которого имеют
длину 15 см.
в) Сыну 10 лет.
Его возраст составляет ![]() возраста отца.
Сколько лет отцу?
возраста отца.
Сколько лет отцу?
3) Решить № 671 (а).
II. Выполнение упражнений.
1. Решить задачу № 649 на доске и в тетрадях.
Решение.
1) 211,2 : 0,88 = 21120 : 88 = 240 (т) зерна намолотили за день.
Ответ: 240 т.
2. Решить задачу № 651 с комментированием на месте.
Решение.
1) 231 : 0,55 = 23100 : 55 = 420 (кг) свежей рыбы.
Ответ: 420 кг.
3. Решить задачу № 656 на доске и в тетрадях.
Решение.
1) 24 : 0,8 = 240 : 8 = 30 (км) прошли туристы в первый день.
2) 30 : ![]() (км) намеченный
путь.
(км) намеченный
путь.
Ответ: 144 км.
4. Решить задачу № 661.
Решение.
1) 100% – (40% + 53%) = 100% – 93% = 7% тетрадей продано в третий день.
2) 847 : 0,07 = 84700 : 7 = 12100 (тетрадей) продал киоск за три дня)
Ответ: 12100 тетрадей.
5. Повторение ранее изученного материала.
а) Решить № 678 (1; 2). Двое учащихся решают на доске, остальные – в тетрадях, затем проверяется решение.
Решение.
![]()
![]()
б) Решить задачу № 675.
Решение.
![]() (км/ч) скорость
велосипедиста.
(км/ч) скорость
велосипедиста.
2) 12,5![]() (км) путь
велосипедиста.
(км) путь
велосипедиста.
Ответ: 31,25 км.
III. Итог урока.
1. Сформулировать правило нахождения числа по данному значению его дроби.
2. Устно решить задачу:
Дочери 12 лет. Ее
возраст составляет ![]() возраста матери.
Сколько лет матери?
возраста матери.
Сколько лет матери?
Ответ: 30 лет.
3. Рассказать, как найти число по данному значению его процентов.
4. Устно решить задачу:
Найти число, если 1% его равен 85.
Ответ: 8500.
Домашнее задание: изучить п. 18; решить № 681, 679(2), 684, 691(а).
Урок 3
Цели: закрепить правило нахождения числа по его дроби; развивать навыки решения задач; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Повторить правило деления дроби на дробь и правило умножения дробей.
2. Сформулировать основное свойство дроби.
3. Решить устно № 674 (б; в; г) и № 668 (а).
4. Повторить правило нахождения числа по его дроби и правило нахождения дроби от числа.
5. Устно решить задачи:
а) Ласточка живет
9 лет, что составляет ![]() продолжительности
жизни жаворонка. Сколько лет живет жаворонок?
продолжительности
жизни жаворонка. Сколько лет живет жаворонок?
Ответ: 30 лет.
б) Кровь
составляет ![]() массы тела
человека. Сколько крови у человека, масса которого 65 кг?
массы тела
человека. Сколько крови у человека, масса которого 65 кг?
II. Решение задач и упражнений.
1. Решить задачу № 653. Решение объясняет учитель.
Решение.
Пусть все полученные магазином лыжи составляют 1.
![]() осталось после
продажи лыж.
осталось после
продажи лыж.
![]() (лыжи) получено
магазином.
(лыжи) получено
магазином.
Ответ: 192 лыжи.
2. Решить задачу № 655 на доске и в тетрадях.
Решение.
1) 100% + 3% = 103% составила стоимость акций через год.
103% = 1,03.
2) 576,8 : 1,03 = 57680 : 103 = 560 (млн р.) стоили акции раньше.
Ответ: 560 млн р.
3. Разобрать решение задачи № 659 и записать в тетрадях.
Решение.
![]() нашли
нашли ![]() от числа 12.
от числа 12.
![]() – неизвестное
число.
– неизвестное
число.
Ответ: 28,8.
4. Решить задачу № 660. Коллективно разобрать решение задачи, а затем учащиеся самостоятельно записывают решение в тетрадях.
Решение.
1) 35% = 0,35; 49% = 0,49
128,1 · 0,35 : 0,49 = 91,5 – неизвестное число.
Ответ: 91,5.
5. Самостоятельно решить № 678 (3), потом проверить решение.
Решение.
![]()
Ответ: ![]()
III. Итог урока.
1. Решить задачу.
В первый час автобус прошел 40% всего пути, во второй час ![]() пути, а в третий
– остальные 28 км. Какое расстояние прошел автобус за эти 3 ч?
пути, а в третий
– остальные 28 км. Какое расстояние прошел автобус за эти 3 ч?
Решение.
Весь путь примем за единицу (за 1).
40% = 0,4 части пути прошел автобус в первый час.
![]() части пути за два
часа;
части пути за два
часа;
![]() части пути прошел
автобус за третий час;
части пути прошел
автобус за третий час;
![]() (км) прошел
автобус за 3 ч.
(км) прошел
автобус за 3 ч.
Ответ: 105 км.
2. Найдите значение величины, если:
![]() ее равны 36 л;
б) 0,8 равны 576 г;
ее равны 36 л;
б) 0,8 равны 576 г;
в) 2,3% ее равны 2,07 р.
Домашнее задание: решить № 682, 686, 691 (б).
Урок 4
Цели: проверить знания и умения учащихся в ходе проведения самостоятельной работы; закрепить навыки решения задач на нахождение дроби от числа и числа по его дроби.
Ход урока
I. Устные упражнения.
1. Проверить выборочно решение номеров домашнего задания.
2. Устно решить № 674 (д; е; з) и № 668 (б), № 667 (а; д).
II. Тренировочные упражнения.
1. Решить задачу.
В совхозе ![]() всей земли
занимают луга, а
всей земли
занимают луга, а ![]() –посевы. Какова
площадь всей земли в совхозе, если луга занимают на 270 га больше, чем посевы?
–посевы. Какова
площадь всей земли в совхозе, если луга занимают на 270 га больше, чем посевы?
Решение.
![]() всей земли больше
занимают луга, чем посевы.
всей земли больше
занимают луга, чем посевы.
![]() (га) площадь всей
земли в совхозе.
(га) площадь всей
земли в совхозе.
Ответ: 2430 га.
2. Найти значение величины, если:
а) 0,38 ее равны
57 т; б) ![]() ее равны 12,6 л;
ее равны 12,6 л;
в) 43% ее равны 223,6 см; г) 2,8% ее равны 1,96 р.
3. Решить задачу № 652 на доске и в тетрадях.
Решение.
![]() (кг) винограда во
втором ящике;
(кг) винограда во
втором ящике;
2) 21 + 27 = 48 (кг) винограда было в двух ящиках.
Ответ: 48 кг.
4. Решить задачу № 662 с помощью уравнения.
Решение.
Пусть на базе было х т картофеля.
В первый день отпустили 0,4х т, осталось х – 0,4х = 0,6х т картофеля, во второй день отпустили 0,6х · 0,6 = 0,36х т картофеля, после этого осталось 0,6х – 0,36х = 0,24х т картофеля для продажи в третий день.
0,24х = 72
х = 72 : 0,24 = 7200 : 24 = 300
х = 300.
На базе было 300 т картофеля.
Ответ: 300 т.
III. Самостоятельная работа (15 мин).
Вариант I
1. Найдите значение величины, если:
а) 0,85 ее равны
340 г; б) ![]() ее равны 120 см3;
ее равны 120 см3;
в) 36% ее равны 75,6 м.
2. Трактористы
вспахали поле за три дня. В первый день они вспахали ![]() поля, во второй
день 40% поля, а в третий день – остальные 48 га. Найти площадь поля.
поля, во второй
день 40% поля, а в третий день – остальные 48 га. Найти площадь поля.
3. В первый день
на мельнице смололи ![]() привезенного
зерна, во второй день
привезенного
зерна, во второй день ![]() привезенного
зерна. Сколько зерна привезли на мельницу, если во второй день смололи на 780
кг больше, чем в первый день?
привезенного
зерна. Сколько зерна привезли на мельницу, если во второй день смололи на 780
кг больше, чем в первый день?
4. 30% от 30% числа х равны 7,2. Найдите число х.
Вариант II.
1. Найдите значение величины, если:
а) 0,56 ее равны
168 ц; б) ![]() ее равны 210 дм2;
ее равны 210 дм2;
в) 27% ее равны 32,4 см.
2. Туристы шли три
дня. В первый день они прошли 40% всего пути, во второй день ![]() всего пути, а в
третий – оставшиеся 8 км. Найдите длину всего пути.
всего пути, а в
третий – оставшиеся 8 км. Найдите длину всего пути.
3. Кладовщик выдал
по первому ордеру ![]() всей имевшейся на
складе проволоки, а по второму ордеру –
всей имевшейся на
складе проволоки, а по второму ордеру – ![]() всей проволоки. Сколько килограммов
проволоки было на складе, если по первому ордеру было выдано на 25 кг больше,
чем по второму?
всей проволоки. Сколько килограммов
проволоки было на складе, если по первому ордеру было выдано на 25 кг больше,
чем по второму?
4. 60% от 60% числа у равны 7,2. Найдите число у.
Домашнее задание: правила п. 18; решить № 685, 689, 691 (в).
Урок 5
Цели: систематизировать изученный материал, закрепить знания, умения и навыки в ходе выполнения упражнений и решения задач; развивать логическое мышление учащихся.
Ход урока
I. Результаты самостоятельной работы.
1. Указать ошибки, сделанные учащимися в ходе работы.
2. Показать решение задач, вызвавших затруднения у учащихся.
II. Устная работа.
1. Решить устно № 674 (ж; з; и), № 669 (1-е и 2-е числа) и № 667 (б; г).
2. Устно решить
задачу. В классе 18 мальчиков и 16 девочек, ![]() мальчиков и
мальчиков и ![]() девочек
занимаются в литературном кружке. Сколько учащихся занимаются в литературном
кружке?
девочек
занимаются в литературном кружке. Сколько учащихся занимаются в литературном
кружке?
III. Выполнение упражнений.
1. Решить задачу № 654 на доске и в тетрадях.
Решение.
1) 100% – 85,7% = 14,3% составляет сушеный картофель.
2) 71,5 : 0,143 = 71500 : 143 = 500 (т) сырого картофеля надо взять.
Ответ: 500 т.
2. Решить задачу № 665 на доске и в тетрадях.
Решение.
Весь путь примем за 1 (за единицу).
![]() части пути
осталось пройти после первого часа движения автомобиля.
части пути
осталось пройти после первого часа движения автомобиля.
![]() части пути прошел
автомобиль во второй час.
части пути прошел
автомобиль во второй час.
![]() пути пройдено в
третий час.
пути пройдено в
третий час.
![]() части пути прошел
в третий час меньше, чем во второй час.
части пути прошел
в третий час меньше, чем во второй час.
![]() (км) прошел
автомобиль за 3 часа.
(км) прошел
автомобиль за 3 часа.
Ответ: 360 км.
3. Решить задачу № 663 с помощью уравнения.
Решение.
Пусть рабочие изготовили у деталей. Тогда первый рабочий изготовил 0,3у деталей, после этого осталось у – 0,3у = 0,7у деталей, второй рабочий изготовил 0,7у · 0,6 = 0,42у деталей, а третий рабочий изготовил 0,7у – 0,42у = 0,28у деталей.
0,28у = 84
у = 84 : 0,28 = 8400 : 28 = 300
у = 300.
Рабочие изготовили 300 деталей.
4. Решить задачу.
Комбайнеры убрали
рожь с поля за три дня. В первый день они убрали ![]() поля, во второй
день – 40% поля, а в третий – остальные 72 га. Найдите площадь поля.
поля, во второй
день – 40% поля, а в третий – остальные 72 га. Найдите площадь поля.
5. Повторение ранее изученного материала:
а) Решить задачу № 672 двумя способами.
Решение.
I способ.
1) 20 см = 0,2 м,
0,2 · 0,2 = 0,04 (м2) площадь плитки;
2) 5,6 · 4,4 = 24,64 (м2) площадь пола в комнате;
3) 24,64 : 0,04 = 2464 : 4 = 616 (плиток) понадобится.
II способ.
1) 5,6 : 0,2 = 56 : 2 = 28 (плиток) потребуется по длине пола для одного ряда;
2) 4,4 : 0,2 = 44 : 2 = 22 (плиток) потребуется по ширине пола для одного ряда;
3) 28 · 22 = 616 (плиток) понадобится для настилки пола в комнате.
Ответ: 616 плиток.
б) Решить № 677 (1; 2; 3).
IV. Итог урока.
1. Повторить правила пункта 18.
2. Решить задачи:
а) Когда прочитали
35 страниц, то осталось прочитать ![]() книги. Сколько страниц в книге?
книги. Сколько страниц в книге?
б) Было 1000 р. На
первую покупку потратили ![]() этой суммы, а на
вторую –
этой суммы, а на
вторую – ![]() остатка. Сколько
рублей осталось?
остатка. Сколько
рублей осталось?
Домашнее задание: решить № 687, № 688, № 691 (г).
ДРОБНЫЕ ВЫРАЖЕНИЯ
Урок 1
Цели: ввести понятие дробного выражения, разобрать решение дробных выражений; повторить правила действий с обыкновенными дробями.
Ход урока
I. Повторение изученного материала.
1. Повторить правила умножения, деления и возведения в степень обыкновенных дробей. На доске приводить свои примеры.
2. Решить устно № 703 (а; в) и № 708.
3. Составить задачу по уравнению № 706 (а).
II. Изучение нового материала.
1. Ввести понятие дробного выражения, разобрав пример на странице 110 учебника.
2. Определение числителя и знаменателя дробного выражения.
3. Числителем и знаменателем дробного выражения могут быть любые числа, а также числовые или буквенные выражения.
4. С дробными выражениями можно выполнять действия по тем же правилам, что и с обыкновенными дробями.
5. Разобрать на доске примеры 1–3 учебника на страницах 110–111.
Пример 1. Найдем
значение выражения ![]() .
.
Решение.
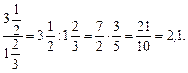
Пример 2. Найдем
произведение ![]() и
и ![]()
Решение.
![]()
Пример 3. Найдем
сумму ![]()
Решение.
![]()
III. Закрепление изученного материала.
1. Решить устно № 692.
2. Решить № 693 и № 694 на доске и в тетрадях.
3. Решить № 695 (а; г; k) на доске и в тетрадях.
Решение.

4. Решить задачу № 709 самостоятельно на с. 114 учебника.
Решение.
1) 3 : 0,15 = 300 : 15 = 20 (га) скосил комбайнер за день.
Ответ: 20 га.
5. Решить № 712 (а; б) самостоятельно с последующей проверкой; решить № 712 (в) на доске.
Решение.
![]()
![]()
в) 49: 0,35 = 4900 : 35 = 140.
IV. Итог урока.
1. Какое выражение называют дробным?
2. Как называют выражение, находящееся над чертой? под чертой?
Домашнее задание: изучить п. 19; решить № 716 (б; в; е), № 720; индивидуальное задание № 721.
Урок 2
Цели: упражнять учащихся в нахождении значений дробных выражений; закрепить знания, умения и навыки решения задач на нахождение числа по его дроби и нахождение дроби от числа.
Ход урока
I. Устная работа.
1. Проверить домашнее задание на доске № 720 и 716 (б; в; е).
2. Решить устно № 701 (а; в) и № 703 (в).
3. Составить задачу по уравнению № 706 (б).
II. Выполнение упражнений.
1. Решить № 695 (б; е) самостоятельно, № 695 (и) решить на доске.
Решение.

2. Решить № 696 (а; k) на доске и в тетрадях, № 696 (д; б; л) с комментированием на месте.
Решение.

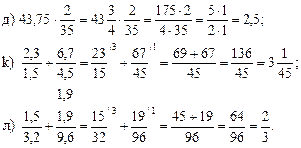
3. Решить № 697 (а; в) на доске и в тетрадях.
Решение.

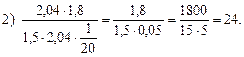
4. Повторение изученного материала:
а) Решить задачу № 710 с комментированием на месте.
Решение.
1) 100% – 25% = 75% составляют яблони;
2) 150 : 0,75 = 15000 : 75 = 200 (деревьев) в саду;
3) 200 – 150 = 50 (грушевых) деревьев.
Ответ: 50 грушевых деревьев.
б) Решить задачу № 714 на доске и в тетрадях.
Решение.
1) 2100 : 0,3 = 21000 : 3 = 7000 (м) = 7 км отремонтировали за первую неделю;
2) 7 : 0,25 = 700 : 25 = 28 (км) длина всей дороги.
Ответ: 28 км.
III. Итог урока.
1. Привести свои примеры дробного выражения. Назвать числитель и знаменатель дробного выражения.
2. По каким правилам можно выполнять действия с дробными выражениями?
3. Решить № 696 (е; з; и).
Домашнее задание: изучить п. 19; решить № 716 (г; д; а), № 717, № 711, № 713.
Урок 3
Цели: проверить знания учащихся в ходе выполнения самостоятельной работы; подготовить к контрольной работе; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Решить устно № 701 (б; г; д).
2. Устно решить № 702 по рисунку 30 учебника на с. 113
3. Повторить правила нахождения дроби от числа и нахождения числа по его дроби. Привести свои примеры на доске.
4. Повторить правила умножения и деления дробей. Привести свои примеры.
II. Тренировочные упражнения.
1. Решить № 695 (в; д; з) на доске и в тетрадях.
Решение.

![]()
2. Решить № 696 (в; ж).
Решение.
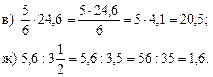
3. Решить № 697 (б) на доске и в тетрадях.
Решение.
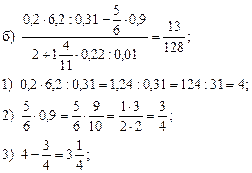
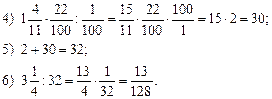
4. Решить № 699 (а) на доске и в тетрадях.
![]() если х =
18,1 – 10,7 = 7,4; у = 35 – 23,8 = 11,2.
если х =
18,1 – 10,7 = 7,4; у = 35 – 23,8 = 11,2.
![]()
Ответ: ![]() .
.
III. Самостоятельная работа (15 мин).
Вариант I.
1. Найдите значение выражения:

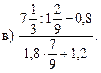
2. Представьте в
виде дроби выражение ![]()
Вариант II.
1. Найдите значение выражения:
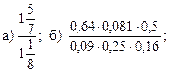
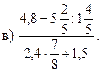
2. Представьте в виде дроби выражение ![]()
Домашнее задание: повторить правила п. 18 и 19; решить № 716 (ж), № 718, № 715 (1), № 749.
КОНТРОЛЬНАЯ РАБОТА № 6
Цели: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение контрольной работы по вариантам.
Вариант 1.
1. Найдите
значение выражения 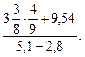
2. Скосили ![]() луга. Найдите
площадь луга, если скосили 21 га.
луга. Найдите
площадь луга, если скосили 21 га.
3. В первый час автомашина прошла 27% намеченного пути, после чего ей осталось пройти 146 км. Сколько километров составляет длина намеченного пути?
4. Решите
уравнение ![]()
5. Два одинаковых
сосуда заполнены жидкостью. Из первого сосуда взяли ![]() имевшейся там
жидкости, а из второго
имевшейся там
жидкости, а из второго ![]() имевшейся там
жидкости. В каком сосуде осталось жидкости больше?
имевшейся там
жидкости. В каком сосуде осталось жидкости больше?
Вариант II.
1. Найдите
значение выражения 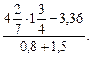
2. В первый час
автомашина прошла ![]() намеченного пути.
Каков намеченный путь, если в первый час автомашина прошла 70 км?
намеченного пути.
Каков намеченный путь, если в первый час автомашина прошла 70 км?
3. Было отремонтировано 29% всех станков цеха, после чего осталось еще 142 станка. Сколько станков в цехе?
4. Решите
уравнение ![]()
5. У двух сестер
денег было поровну. Старшая сестра израсходовала ![]() своих денег, а
младшая сестра израсходовала
своих денег, а
младшая сестра израсходовала ![]() своих денег. У кого из них денег осталось
меньше?
своих денег. У кого из них денег осталось
меньше?
Вариант III.
1. Найдите
значение выражения 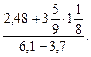
2. Было
отремонтировано ![]() всех станков цеха.
Сколько станков в цехе, если отремонтировано 28 станков?
всех станков цеха.
Сколько станков в цехе, если отремонтировано 28 станков?
3. Заасфальтировали 83% дороги, после чего осталось заасфальтировать 51 км. Найдите длину всей дороги.
4. Решите
уравнение ![]()
5. Двое рабочих
получили одинаковое задание. До обеденного перерыва первый рабочий выполнил ![]() своего задания, а
второй
своего задания, а
второй ![]() своего задания. У
кого из них осталось больше работы?
своего задания. У
кого из них осталось больше работы?
Вариант IV.
1. Найдите
значение выражения 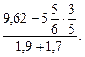
2. Отремонтировали
![]() дороги. Найдите
длину всей дороги, если отремонтировали 30 км дороги.
дороги. Найдите
длину всей дороги, если отремонтировали 30 км дороги.
3. Скосили 32% луга, после чего осталось скосить еще 136 га. Найдите площадь луга.
4. Решите
уравнение ![]()
5. Две автомашины должны пройти один и тот же путь. За
час первая автомашина прошла ![]() этого
пути, а вторая
этого
пути, а вторая ![]() этого пути. Какой
автомашине осталось идти меньше?
этого пути. Какой
автомашине осталось идти меньше?
ОТНОШЕНИЯ
Урок 1
Цели: ввести понятие отношения двух чисел; определить, что показывает отношение двух чисел; показать, где применяется понятие отношения двух чисел, двух величин; повторить и закрепить умения и навыки деления чисел, деления десятичных и обыкновенных дробей.
Ход урока
I. Анализ контрольной работы.
1. Сообщить результаты контрольной работы.
2. Работа над ошибками, сделанными учащимися в работе.
3. Решить задания, вызвавшие затруднения у учащихся.
II. Объяснение нового материала.
1. Разобрать решение задачи 1 на странице 117 учебника.
2 :![]()
2. Определение отношения двух чисел. Что показывает отношение двух чисел?
3. Если две величины измерены одной и той же единицей измерения, то отношение их значений называют также отношением этих величин (отношением длин, отношением масс, отношением площадей и т. д.).
4. Разобрать по учебнику решение задачи 2.
Решение.
![]() всей дороги
электрифицировано.
всей дороги
электрифицировано.
2) 360 : 240 = ![]() раза длиннее вся
дорога, чем ее электрифицированная часть.
раза длиннее вся
дорога, чем ее электрифицированная часть.
5. Числа ![]() и
и ![]() взаимно обратны,
поэтому и отношения 2 к 3 и 3 к 2 также называют взаимно обратными.
взаимно обратны,
поэтому и отношения 2 к 3 и 3 к 2 также называют взаимно обратными.
III. Закрепление изученного материала.
1. Решить № 722 (а; б; д; е).
2. Решить задачу № 728 на доске и в тетрадях.
Решение.
1) 20 : 45 = ![]() (части урока)
заняла самостоятельная работа.
(части урока)
заняла самостоятельная работа.
Ответ: ![]()
3. Решить задачу № 729 с комментированием на месте.
Решение.
1) 36 – 15 = 21 (девочка) в классе;
2) 15 : 36 = ![]() (части)
составляют мальчики;
(части)
составляют мальчики;
3) 21 : 36 = ![]() (части)
составляют девочки;
(части)
составляют девочки;
4) 21 : 15 = ![]() = 1,4 (раза)
больше девочек в классе, чем мальчиков.
= 1,4 (раза)
больше девочек в классе, чем мальчиков.
4. Решить № 732 (устно).
5. Решить задачу № 725 самостоятельно.
Решение.
1) 22,05 : 10,5 = 220,5 : 105 = 2,1 (дм) ширина прямоугольника;
2) 10,5 : 2,1 = 105 : 21 = 5 (раз) длина больше ширины;
3) 21 : 105 = ![]() обратное
отношение показывает, какую часть длины прямоугольника составляет его ширина.
обратное
отношение показывает, какую часть длины прямоугольника составляет его ширина.
6. Повторение ранее изученного материала. Решить № 747 (е; в) самостоятельно, а затем проверить решение.
Решение.
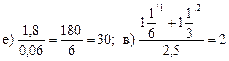
![]()
IV. Итог урока:
1) Что называют отношением двух чисел?
2) Что показывает отношение двух чисел?
Домашнее задание: изучить п. 20; решить № 751, № 759 (а; в), № 746 (устно).
Урок 2
Цели: упражнять учащихся в нахождении отношений двух величин; закрепить знания учащихся при решении задач на проценты; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить устно № 741 (а; в; д) и № 745.
2. Решить устно № 747 (а; б); повторить правила умножения и деления дробей.
Решение.
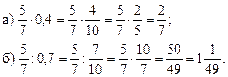
II. Работа по учебнику.
1. Если величины измерены разными единицами измерения, то для нахождения их отношения надо предварительно перейти к одной единице измерения.
2. Разобрать по учебнику решение задачи 3 на странице 118.
Решение.
9,6 ц = 960 кг.
![]()
Ответ: 3,75%.
III. Выполнение упражнений.
1. Решить № 722 (в; г; ж) на доске и в тетрадях.
2. Решить № 726 (устно).
3. Решить № 723 самостоятельно.
Решение.
1) 14,4 + 9 = 23,4 (м) длина всей проволоки.
2) 9 : 23,4 = ![]() всей проволоки
составляет первый кусок.
всей проволоки
составляет первый кусок.
3) 14,4 : 23,4 = ![]() всей проволоки
составляет второй кусок.
всей проволоки
составляет второй кусок.
4) 9 : 14,4 = ![]() части составляет
первый кусок от длины второго куска.
части составляет
первый кусок от длины второго куска.
Ответ: ![]()
4. Решить задачу № 735 на доске и в тетрадях двумя способами.
Решение.
I способ.
1) 300 : 240 = ![]() составляет выпуск
холодильников после установки нового оборудования;
составляет выпуск
холодильников после установки нового оборудования;
2) 125% – 100% = 25% на столько процентов увеличилось производство холодильников за смену.
II способ.
1) 300 – 240 = 60 (холодильников) – увеличился выпуск за смену.
2) 60 : 240 · 100% = 25% – увеличился выпуск холодильников за смену.
Ответ: на 25%.
5. Решить устно № 739.
6. Решить задачу № 748 самостоятельно, разобрав предварительно решение задачи и повторив правило нахождения дроби от числа.
Решение.
![]() (ц) израсходовано
на подкормку овощей и фруктовых деревьев.
(ц) израсходовано
на подкормку овощей и фруктовых деревьев.
![]() (ц) израсходовано
на подкормку овощей.
(ц) израсходовано
на подкормку овощей.
Ответ: 9 ц.
7. Прочитать исторический материал на странице 116 учебника.
IV. Итог урока.
1. Сформулировать правило пункта 20 на странице 117 учебника.
2. Как узнать, какую часть число а составляет от числа в?
3. Как узнать, сколько процентов одно число составляет от другого?
Домашнее задание: изучить п. 20; решить № 753, 752, 756, 759 (г).
Урок 3
Цели: закрепить изученный материал в ходе выполнения упражнений; способствовать выработке умений и навыков учащихся при решении задач; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Двое учащихся решают номера 753 и 756 домашнего задания.
2. Проверить с остальными учащимися по тетрадям выполнение домашнего задания № 752 и № 759 (г).
3. Решить устно № 742 (а) и № 758 (а).
II. Тренировочные упражнения.
1. Решить задачу № 727 на доске и в тетрадях.
Решение.
1) 1,52 + 0,76 = 2,28 (кг) масса сплава;
2) 1,52 : 0,76 = 152 : 76 = 2; значит, свинца в сплаве будет в 2 раза больше, чем олова, поэтому свинец и олово взяты в отношении 2 к 1.
3) 0,76 : 2,28 = ![]() часть составляет
олово в сплаве;
часть составляет
олово в сплаве;
4) 1,52 : 2,28 = ![]() части составляет
свинец в сплаве.
части составляет
свинец в сплаве.
Ответ: 2 : 1; ![]() часть;
часть; ![]() части.
части.
2. Решить задачу № 724. При построении углов использовать транспортиры.
Решение.
1) 56° + 40° = 96° = ÐАОС.
2) 56 : 96 = ![]() части ÐАОС составляет ÐАОВ.
части ÐАОС составляет ÐАОВ.
3) 40 : 96 = ![]() части ÐАОС составляет ÐВОС.
части ÐАОС составляет ÐВОС.
Ответ: ![]() части и
части и ![]() части.
части.
3. Решить № 730 самостоятельно.
4. Решить задачу № 734, объяснив сначала учащимся, что означает понятие «всхожесть семян».
Решение.
I способ.
1) 10 : 250 · 100% = 4% семян погибло;
2) 100% – 4% = 96% семян взошло.
II способ.
1) 250 – 10 = 240 (семян) взошло;
2) 240 : 250 · 100% = 96% составляет всхожесть семян.
Ответ: 96%.
5. Решить задачу № 733 самостоятельно с последующей проверкой.
6. Решить задачу № 737 устно.
7. Решить № 747 (г) самостоятельно.
Решение.
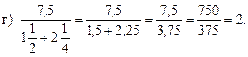
III. Итог урока.
1. Что называется отношением двух чисел?
2. Что показывает отношение двух чисел?
3. Как узнать, сколько процентов одно число составляет от другого?
4. Решить задачу:
В поселке 224 дома. Двухэтажных домов 84, а остальные дома одноэтажные. Сколько процентов всех домов составляют одноэтажные дома?
Решение.
1) 224 – 84 = 140 (домов) одноэтажные;
2) 140 : 224 · 100% = 62,5% составляют одноэтажные дома.
Ответ: 62,5%.
Домашнее задание: изучить п. 20; решить № 754, 759 (б), № 758 (б).
ПРОПОРЦИИ
Урок 1
Цели: ввести понятие пропорции, ее членов; научить чтению пропорции и составлению пропорций из отношений; закрепить правила деления десятичных дробей, обыкновенных дробей.
Ход урока
I. Устная работа.
1. Решить устно № 767 (а; б) и № 766 (а; г; д).
2. Повторить определение отношения двух чисел, двух величин. Решить № 768 (а; в), записывая решение только на доске.
3. Проверить выполнение домашнего задания выборочно.
II. Изучение нового материала.
1. Найдем числовые значения двух отношений: 6 : 3 и 10 : 5. Мы видим, что они равны: 6 : 3 = 2 и 10 : 5 = 2, следовательно, можно записать равенство 6 : 3 = 10 : 5. Такое равенство отношений называют пропорцией.
2. Определение. Пропорцией называется равенство двух отношений. Числа, составляющие пропорцию (6; 3; 10; 5), называются членами пропорции.
3. Пропорцию можно
записать с помощью букв: а : в = с : d, или ![]() .
.
4. Эти записи читают: «Отношение а к в равно отношению с к d» или «а так относится к в, как с относится к d».
5. Числа а и d называют крайними членами, а числа в и с – средними членами.
В дальнейшем считают, что все члены пропорции отличны от нуля:
а ¹ 0, в ¹ 0, с ¹ 0, d ¹ 0.
6. Чтобы проверить, верно ли составлена пропорция, вычисляют числовое значение каждого отношения, составляющего пропорцию. Если эти отношения равны, то пропорция составлена верно; если не равны, то пропорция составлена неверно.
Примеры: 1) Пропорция 40 : 8 = 65 : 13 составлена верно, так как 40 : 8 = 5 и 65 : 13 = 5.
2) Пропорция 2,7 : 9 = 2 : 5 составлена неверно, так как 2,7 : 9 = 0,3, а 2 : 5 = 0,4.
III. Закрепление изученного материала.
1. Решить устно: а) Прочитайте пропорцию:
1) 18 : 6 = 24 : 8; 2) 30 : 5 = 42 : 7; 3) 36 : 9 = 50 : 10.
б) Назовите крайние и средние члены пропорции.
в) Верно ли составлены пропорции? Проверьте.
2. Составьте, если можно, пропорции из следующих отношений:
а) 20 : 4 и 60 : 12; б) 6,3 : 0,9 и 2,8 : 0,4; в) 0,25 : 5 и 0,3 : 6.
3. Составить три пропорции (учащиеся на доске и в тетрадях приводят свои примеры пропорций).
4. Решить № 760 (а) на доске и в тетрадях.
5. Решить № 761 самостоятельно.
6. Решить уравнение № 763 (г; е).
Решение.
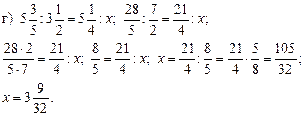
Ответ: ![]()
![]()
Ответ: ![]()
7. Повторение ранее изученного материала.
1. Решить задачу № 772.
Решение.
1) 50 – 5 = 45 попаданий;
2) 45 : 50 · 100% = 90% процент попаданий.
Ответ: 90%.
2. Решить задачу № 774.
Решение.
1) 350 : 280 · 100% = 125% на столько процентов бригада выполнила задание;
2) 125% – 100% = 25% на столько процентов бригада перевыполнила задание.
Ответ: на 25%; на 125%.
IV. Итог урока:
1. Вопросы: а) Что такое пропорция?
б) Как называются числа х и у в пропорции х : а = в : у?
в) Как называются числа m и n в пропорции а : m = n : в?
2. Привести свои примеры верных пропорций.
Домашнее задание: выучить из п. 21 (1-ю часть); решить № 776, 778, 781 (а).
Урок 2
Цели: изучить основное свойство пропорции; научить решению уравнений с использованием основного свойства пропорции; развивать логическое мышление учащихся.
Ход урока
I. Проверка изученного материала.
1. Что называется пропорцией? Как называются члены пропорции?
2. Какие из равенств являются пропорциями?
а) 2,5 : 0,5 = 45 : 9; б) 2,5 : 0,5 = 3 + 2; в) 0,5 · 12 = 24 : 4.
3. Прочитать пропорцию и проверить, верно ли она составлена: а) 9 : 3 = 24 : 8; б) 1,5 : 0,1 = 0,3 : 0,2; в) 0,38 : 0,01 = 7,6 : 0,2.
4. Составить, если можно, пропорции из следующих отношений:
а) 2,8 : 0,07 и 4 : 0,01; б) 500 : 125 и 3,2 : 0,8; в) 0,3 : 0,5 и 0,7 : 0,8.
5. Решить устно № 766 (б; в) и № 768 (б; г).
II. Объяснение нового материала.
1. Вычислим произведение крайних и произведение средних членов каждой пропорции:
а) 20 : 5 = 8 : 2; 20 · 2 = 40; 5 · 8 = 40;
б) 1,2 : 0,4 = 30 : 10; 1,2 · 10 = 12; 0,4 · 30 = 12.
2. Можно сделать вывод: произведение крайних членов верной пропорции равно произведению средних членов пропорции.
Это свойство называют основным свойством пропорции.
Для пропорции а : в = с : d оно записывается
![]()
3. Чтобы убедиться в том, что пропорция составлена верно, достаточно проверить, равны ли произведения крайних и средних членов. Если эти произведения равны, то пропорция составлена верно.
Примеры: 1) Пропорция 0,9 : 3,6 = 0,4 : 1,6 составлена верно, так как 0,9 · 1,6 = 1,44 и 0,4 · 3,6 = 1,44.
2) Пропорция 5,4 : 1,8 = 4 : 3 составлена неверно, так как 5,4 · 3 = 16,2; а 1,8 · 4 = 7,2.
III. Закрепление изученного материала.
1. Решить № 762 (а; в; д) на доске и в тетрадях.
Решение.
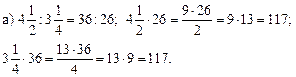
Пропорция верная.
![]()
Пропорция составлена неверно.
![]()
2. Решить № 760 (б) на доске и в тетрадях.
3. Проверить (двумя способами), верно ли равенство:
а) 28 : 7 = 20 : 4; б) 7,5 : 1,5 = 120 : 24; в) 4,2 : 0,3 = 2,8 : 0,2.
4. Даны равенства: а) 30 · 3 = 18 · 5; б) 4 · 9 = 0,2 · 180;
в) 0,48 · 0,5 = 0,6 · 0,4.
Каждое равенство представить в виде пропорции, применяя основное свойство пропорции.
Образец: а) 30 : 5 = 18 : 3 или 18 : 30 = 3 : 5.
5. Составить, если можно, пропорции из четырех данных чисел:
а) 100; 80; 4; 5; б) 5; 10; 9; 4,5; в) 45; 15; 8; 75.
6. Решить № 765 самостоятельно.
7. Повторение ранее изученного материала:
а) Решить устно № 771.
б) Решить задачу № 773.
Решение.
![]() части составляет
угол А от угла В.
части составляет
угол А от угла В.
![]() (раза) угол В
больше угла А.
(раза) угол В
больше угла А.
Ответ: ![]()
IV. Итог урока.
1. Сформулируйте основное свойство пропорции. Привести свои примеры.
2. Верны ли равенства 60 : 20 = 18 : 6 и 20 : 60 = 6 : 18?
3. Из следующих равенств составить пропорцию:
а) 40 · 30 = 20 · 60; б) 18 · 8 = 9 · 16.
Домашнее задание: выучить правила п. 21; решить № 780, 781 (б), № 804, 805.
Урок 3
Цели: закрепить знание учащимися основного свойства пропорции; научить применять основное свойство пропорции при решении уравнений; в ходе выполнения упражнений закрепить правила умножения и деления дробей.
Ход урока
I. Устная работа.
1. Что называется пропорцией? Основное свойство пропорции. Привести свои примеры.
2. Составьте, если можно, пропорции из четырех данных чисел:
а) 16; 12; 3; 4; б) 0,7; 0,3; 2; 1; в) 0,15; 0,25; 0,03; 0,05.
3. Проверьте (двумя способами), верно ли равенство:
а) 49 : 14 = 14 : 4; б) 2,5 : 0,4 = 3,5 : 0,56; в) 0,002 : 0,005 = 0,1 : 0,25.
II. Изучение нового материала в виде беседы.
1. Пропорция 20 : 16 = 5 : 4 верна, так как 20 · 4 = 16 · 5 = 80. Поменяем местами в этой пропорции средние члены. Получим новую пропорцию: 20 : 5 = 16 : 4. Она тоже верна, так как при такой перестановке произведение крайних и произведение средних членов не изменилось. Эти произведения не изменяются, если в пропорции 20 : 5 = 16 : 4 поменять местами крайние члены: 4 : 5 = 16 : 20.
2. Сделать вывод: если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.
3. В пропорции можно менять местами правую и левую части, то есть 16 : 4 = 20 : 5. Любая пропорция может быть записана восемью различными способами.
4. Записать восемью различными способами пропорцию:
10 : 5 = 6 : 3.
Решение.
1) 3 : 5 = 6 : 10; 2) 10 : 6 = 5 : 3; 3) 6 : 3 = 10 : 5; 4) 3 : 6 = 5 : 10;
5) 5 : 10 = 3 : 6; 6) 6 : 10 = 3 : 5; 7) 5 : 3 = 10 : 6; 8) 10 : 5 = 6 : 3.
5. Используя основное свойство пропорции, можно найти ее неизвестный член, если все остальные члены известны.
Пример 1. Найдите х, если х : 4 = 15 : 5. В заданном уравнении неизвестное число х является крайним членом пропорции. Используя основное свойство пропорции, можно записать:
х · 5 = 4 · 15. Отсюда находим:
![]()
Правило. Неизвестный крайний член пропорции равен произведению средних членов, деленному на известный крайний член пропорции.
Пример 2. Решим уравнение 16 : х = 12 : 6.
Неизвестное число х является средним членом пропорции. Используя основное свойство пропорции, можно записать.
х · 12 = 16 · 6. Отсюда находим
![]()
Правило. Неизвестный средний член пропорции равен произведению крайних членов, деленному на известный средний член пропорции.
6. Работа по учебнику. Разобрать решение примеров 1 и 2 на странице 124 учебника.
III. Закрепление изученного материала.
1. Решить № 764 (а; б) самостоятельно.
2. Решить № 763 (а; б; в; д) на доске и в тетрадях.
Решение.
а) у : 51,6
= 11,2 : 34,4; ![]()
![]()
Ответ: у = 16,8.
(Числа 129 и 215 сокращаем на 43).
б) в : ![]()
Ответ: в = 2,5.
д) ![]()
Ответ: х = 1,23.
3. Решить № 763 (з) (объясняет учитель).
Решение.
![]()
х – 2 = 1; х = 1 + 2 = 3.
Ответ: х = 3.
4. Решить задачу на повторение № 775 самостоятельно.
IV. Итог урока.
Ответить на вопросы к пункту 21 на странице 124 учебника. привести свои примеры.
Домашнее задание: ответить на вопросы к п. 21; решить № 777, № 779 (т), № 802.
Урок 4
Цели: проверить степень усвоения учащимися изученного материала и знания, умения, навыки в ходе выполнения самостоятельной работы; способствовать развитию логического мышления учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Проверка домашнего задания (выборочно взять тетради учеников и проверить выполнение ими домашнего задания).
2. Сформулировать основное свойство пропорции. Привести свои примеры.
3. Как найти неизвестный член пропорции? Найдите неизвестный член пропорции х:
а) х : в = с : d; б) а : х = с : d.
4. Решить устно № 797, № 798, № 799.
II. Тренировочные упражнения.
1. Решить № 803 (а; б) на доске и в тетрадях.
Решение.
а) 4,5 : (3х)
= 4 : 28; 3х · 4 = 4,5 · 28; ![]()
Ответ: х = 10,5.
б) (2х) : 9
= ![]()
![]()
Ответ: х = 2.
2. Верна ли пропорция 11,2 : 3,2 = 15,75 : 4,5?
Двое учащихся на доске решают разными способами, остальные – в тетрадях, потом проверяется решение.
3. Составьте из чисел 16; 6; 8 и 12 верную пропорцию (самостоятельно).
4. Решите уравнение (на доске и в тетрадях):
![]()
III. Самостоятельная работа (10–15 мин).
Вариант I.
1. Верна ли пропорция 8154 : 302 = 664,2 : 24,6?
2. Составьте из чисел 2,4; 4,2; 7,2 и 12,6 верную пропорцию.
3. Решите уравнение:
![]()
Вариант II.
1. Верна ли пропорция 15466 : 407 = 1185,6 : 31,2?
2. Составьте из чисел 1,5; 4,9; 2,1 и 3,5 верную пропорцию.
3. Решите уравнение:
![]()
IV. Итоги урока. Прочитать исторический материал о «Пропорции» на страницах 144–146 учебника.
Домашнее задание: решить № 803 (в; г), 807, 819 (а).
ПОВТОРЕНИЕ.
РЕШЕНИЕ ЗАДАЧ.
ОБОБЩЕНИЕ МАТЕРИАЛА ii ЧЕТВЕРТИ (1 час)
Цели: систематизировать, обобщить и повторить ранее изученный материал; закрепить знания, умения и навыки учащихся при решении задач и упражнений.
Ход урока
I. Анализ самостоятельной работы учащихся.
II. Повторение и обобщение изученного материала.
Можно решить задачи и упражнения № 731, 736, 738, 749, 750 (1), 769, 770, 800 (а; в; д), 831 (а; б), 833 и 834.
III. Итог урока.
Домашнее задание: решить № 750 (2), 800 (б; г), 831 (в; г).
ОТНОШЕНИЯ И ПРОПОРЦИИ
ПРЯМАЯ И ОБРАТНАЯ ЗАВИСИМОСТИ…..
Урок 1
Цели: ввести понятие прямой пропорциональной зависимости и научить решать задачи, используя прямо пропорциональную зависимость величин; закрепить навыки решения уравнений с помощью пропорции.
Ход урока
I. Повторение ранее изученного материала.
1. Что такое пропорция?
2. Как называются числа х и у в пропорции х : а = в : у?
3. Как называются числа m и n в пропорции а : m = n : в?
4. Сформулируйте основное свойство пропорции? Приведите свои примеры.
5. Решите уравнения:
а) 21 : х =
36 : 12; б) х : 30 = 54 : 40; в) ![]()
II. Изучение нового материала.
1. Рассмотреть решение задачи:
За каждый час велосипедист проезжает 12 км. Какой путь он проедет за 1 ч, за 2 ч, за 3 ч, за 4 ч?
Решение.
t = 1 ч, то S = 12 км;
t = 2 ч, то S = 24 км;
t = 3 ч, то S = 36 км;
t = 4 ч, то S = 48 км.
Мы видим, что при увеличении одной величины (времени) в 2, 3, 4 раза значение другой величины тоже увеличивается в 2, 3, 4 раза. Такие величины называют прямо пропорциональными величинами.
2. Разобрать решение задачи по учебнику пункта 22 на странице 128 (об изготовлении деталей станком с числовым программным управлением).
3. Определение прямо пропорциональных величин.
4. Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
5. Задачи на прямо пропорциональные величины можно решать с помощью пропорции.
Задача. За 1,6 ч мальчик прошел 6,4 км. Сколько километров пройдет мальчик за 2,8 ч при той же скорости?
Решение.
![]()
Зависимость между временем и пройденным расстоянием при постоянной скорости прямо пропорциональная, так как с увеличением времени пройденный путь увеличится во столько же раз.
Запишем пропорцию:
![]()
![]()
Ответ: 11,2 км.
6. Разобрать решение задачи 1 по учебнику на страницах 12–129.
III. Закрепление изученного материала.
1. Решить устно № 782 (а; б; г).
2. Решить письменно задачу № 783 на доске и в тетрадях.
Решение.
![]()
![]()
Ответ: 19,5 г.
3. Решить задачу № 784 самостоятельно.
Решение.
![]()
![]()
Ответ: 1,7 кг.
4. Найти неизвестный член пропорции (с комментированием на месте).
1) у : 7,2 = 75 : 30 2) 0,01 : у = 3,5 : 7.
5. Решить задачу самостоятельно:
Со 125 гусей получают 4 кг пуха. Сколько пуха можно получить с 875 гусей?
Решение.
I способ.
![]()
![]()
Ответ: 28 кг.
II способ.
1) 875 : 125 = 7 (раз) гусей больше.
2) 4 · 7 = 28 (кг) пуха можно получить.
Ответ: 28 кг.
IV. Итог урока.
1. Какие величины называют прямо пропорциональными?
2. Что можно сказать об отношениях соответствующих значений таких величин?
3. Приведите примеры прямо пропорциональных величин.
Домашнее задание: изучить п. 22 (1-я часть); решить № 811, № 813, № 819 (б).
Урок 2
Цели: ввести понятие обратно пропорциональных величин; способствовать выработке навыков решения задач, связанных с обратно пропорциональными величинами; закреплять навыки и умения решения пропорций.
Ход урока
I. Устная работа.
1. Решить устно № 795 (а; в; д).
2. Какие величины называют прямо пропорциональными? Можно ли считать прямо пропорциональными величины:
а) время движения и путь, пройденный теплоходом, идущим со скоростью 18 км/ч;
б) объем бензина и его массу;
в) количество метров материи и ее стоимость при одной и той же цене;
г) приведите пример прямо пропорциональных величин.
3. Решить задачи, составив пропорцию:
а) Четыре гнома посадили для Белоснежки 8 кустов роз. Сколько кустов роз посадят за то же время три гнома?
Ответ: 6 кустов.
б) Велосипедист за 3 ч проезжает 75 км. За сколько времени проедет велосипедист 125 км с той же скоростью?
Ответ: 5 ч.
II. Объяснение нового материала.
1. Разобрать по учебнику решение задачи на с. 128 (2-я часть):
Пусть путь из города А в город В поезд со скоростью 40 км/ч проходит за 12 ч…
2. Ввести понятие обратно пропорциональных величин. Привести свои примеры.
3. Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины.
Это свойство обратно пропорциональных величин используется при решении задач.
4. Разобрать решение задачи 2 на с. 129 учебника.
5. Решить задачу (объясняет учитель):
Два каменщика могут сложить стену за 15 дней. За сколько дней могут сложить эту стену 5 каменщиков при той же производительности труда?
Решение.
![]()
![]()
Ответ: 6 дней.
III. Закрепление материала.
1. Решить № 782 (д; е) устно.
2. Не всякие две величины являются прямо пропорциональными или обратно пропорциональными. Например, рост ребенка увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, так как при удвоении возраста рост ребенка не удваивается.
3. Решить № 782 (ж; з; в) устно.
4. Решить задачу № 786 на доске и в тетрадях.
Решение.
![]()
Зависимость между количеством машин и их грузоподъемностью обратно пропорциональная.
![]() .
.
Ответ: 40 машин.
5. Решить задачу № 785 с комментированием.
Решение.
![]()
![]() .
.
Ответ: 150 мин.
6. Решить задачи самостоятельно (с помощью пропорции).
а) Мотоциклист проехал 3 ч со скоростью 60 км/ч. За сколько часов он проедет то же расстояние со скоростью 45 км/ч?
Ответ: 4 ч.
б) Три ученика пропололи грядку за 4 часа. За сколько часов выполнят работу два ученика?
Ответ: 6 ч.
7. Упростите
выражение ![]() и найдите его
значение при а = 1,6.
и найдите его
значение при а = 1,6.
IV. Итог урока.
1. Вопросы к пункту 22 на с. 130 учебника.
2. Можно ли считать обратно пропорциональными величинами:
а) время и количество голов скота, которое можно прокормить запасенным количеством корма;
б) цену товара и количество товара, которое можно купить на определенную сумму денег?
Домашнее задание: выучить правила п. 22; решить № 812, 836, 808 (а), 806.
Урок 3
Цели: обобщить и закрепить знания учащихся о прямой и обратной пропорциональных зависимостях; способствовать развитию умения решать задачи; подготовить учащихся к контрольной работе.
Ход урока
I. Повторение и обобщение ранее изученного материала.
1. Решить № 795 (б; г) устно.
2. Укажите верную пропорцию:
а) 2 : 3 = 5 : 10; б) 5 : 10 = 8 : 4; в) 2 : 3 = 10 : 15;
г) 3 : 5 = 10 : 12; д) 16 : 6 = 8 : 3.
3. Найдите неизвестный член пропорции:
а) 18 : х = 6 : 0,1; б) у : 2,5 = 40 : 0,2.
4. Решить устно № 1499 и 1500 на с. 269 учебника.
II. Решение задач и уравнений.
1. Решить задачу № 787 на доске и в тетрадях.
Решение.
![]()
![]() .
.
Ответ: 85% всхожести.
2. Решить задачу № 788.
Решение.
![]()
![]()
Ответ: 60 лип посадили.
3. Решить задачу № 789 с комментированием на месте.
Решение.
![]()
![]()
40% составляют девочки, 60% – мальчики.
Ответ: 40%, 60%.
4. Решить задачу № 790 на доске и в тетрадях.
Решение.
![]()
![]()
Ответ: 1127 т.
5. Решить задачу 1.
Для отопления здания заготовлено угля на 180 дней при норме расхода 0,6 т угля в день. На сколько дней хватит этого запаса, если его расходовать ежедневно по 0,5 т?
Решение.
![]()
![]()
Ответ: на 216 дней.
6. Решить задачу 2.
На участке дороги бетонные плиты длиной 6 м заменили новыми длиной 8 м. Сколько нужно новых плит для замены 240 старых?
Решение.
![]()
![]()
Ответ: 180 плит.
7. Решить задачу № 793 с комментированием.
Решение.
![]()
![]()
Ответ: 31,5 т.
8. Решить задачу № 794 самостоятельно.
Решение.
![]()
![]()
Ответ: 390 г.
III. Итог урока.
Ответить на вопросы к пункту 22 (с. 130 учебника).
Домашнее задание: повторить правила п. 20–22; решить № 815, 816, 817, 1575.
МАСШТАБ
Урок 1
Цели: ввести понятие масштаба карты; показать решение задач с помощью пропорции при заданном масштабе; закрепить навык решения уравнений, записанных в виде пропорции.
Ход урока
I. Устные упражнения.
1. Решить устно № 829 (а; в).
2. Решить № 831 (а; в), вызывая поочередно учащихся к доске для записи пропорций.
Решение.
а) 18 : 2 = 54 : 6; 18 : 54 = 2 : 6; 6 : 2 = 54 : 18; 6 : 54 = 2 : 18.
3. Решить задачу № 835 с помощью пропорции и без пропорции (по действиям).
Двое учащихся решают на доске, остальные на черновиках, затем проверяется решение.
I способ.
![]()
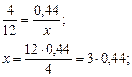
х = 1,32.
Ответ: 1,32 кг картофеля.
II способ.
1) 0,44 : 4 = 0,11 (кг) картофеля на одну порцию запеканки.
2) 0,11 · 12 = 1,32 (кг) потребуется картофеля для 12 порций запеканки.
Ответ: 1,32 кг картофеля.
II. Объяснение нового материала.
1. Участки земной поверхности изображают на бумаге в уменьшенном виде (рис. 35 учебника на с. 134).
2. Определение масштаба карты:
М 1 : 1 00 000 = ![]() Говорят, что
карта сделана в масштабе одна стотысячная. Это означает, что 1 см на карте
соответствует 1 00 000 см = 1000 м = 1 км на местности.
Говорят, что
карта сделана в масштабе одна стотысячная. Это означает, что 1 см на карте
соответствует 1 00 000 см = 1000 м = 1 км на местности.
3. Рассмотреть решение задачи 1.
Длина отрезка на карте 3 см. Масштаб карты М 1 : 1 000 000. Найти длину на местности.
Решение.
![]()
![]()
х = 3 · 1 000 000 = 3 000 000 см = 30 000 м = 30 км на местности.
Ответ: 30 км.
4. Рассмотреть решение задачи 2.
Длина отрезка на местности 4,5 км.
М 1 : 100 000. Найти длину отрезка на карте.
Решение.
Обозначим длину (в километрах) отрезка на карте буквой х и составим пропорцию:
х : 4,5 = 1 : 100 000.
х = 4,5 · 1 : 100000 = 0,000045.
Но 0,000045 км = 0,045 м = 4,5 см длина отрезка на карте.
Ответ: 4,5 см.
III. Закрепление изученного материала.
1. Решить задачу № 820, используя рисунок 36 учебника.
2. Решить задачу № 825 на доске и в тетрадях.
Решение.
![]()
![]() .
.
Ответ: 252 км.
3. Решить задачу № 821 самостоятельно с проверкой.
4. Решить уравнение № 839 (1) на доске и в тетрадях.
Решение.
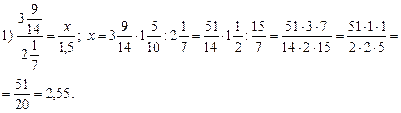
Ответ х = 2,55.
5. Решить задачу № 792 (повторение ранее изученного материала).
Решение.
![]()
![]()
Ответ: 11 дней.
IV. Итог урока.
1. Что называют масштабом карты?
2. Чему равен масштаб чертежа, если на нем детали увеличены в 5 раз? уменьшены в 50 раз?
3. Решить задачу:
Длина детали 10 см. Найти длину детали на чертеже, если масштаб:
1) 1 : 10; 2) 1 : 5; 3) 2 : 1; 4) 5 : 1.
Домашнее задание: изучить п. 23; решить № 840, 843, 846 (б), 873 (а; б).
Урок 2
Цели: способствовать выработке навыков и умений решения задач, связанных с масштабом; подготовить учащихся к выполнению контрольной работы; развивать логическое мышление учащихся.
Ход урока
I. Повторение изученного материала.
1. Решить № 829 (б; г; д) устно.
2. Что называется пропорцией? Сформулировать основное свойство пропорции. Указать верную пропорцию: а) 4 : 5 = 9 : 10; б) 28 : 35 = 4 : 5; в) 5 : 6 =36 : 30; г) 6 : 7 = 42 : 36.
3. Найти неизвестный член пропорции:
а) 3 : 8 = х : 24; б) х : 15 = 2 : 3; в) 18 : х = 9 : 5.
4. Измерить длину и ширину классной комнаты и начертить на доске план этой комнаты в масштабе 1 : 10.
II. Решение задач и уравнений.
1. Решить задачу № 824 по рисунку 37 учебника.
2. Решить задачу № 823.
Решение.
М 1 : 10 000 000; на местности 10 000 000 см = 100 000 м = 100 км; значит, расстояние от Бреста до Владивостока будет соответствовать 100 см на карте, то есть 1 м, поэтому на одной странице тетради это расстояние не уместится.
3. Решить задачу № 827 на доске и в тетрадях с помощью пропорции.
Решение.
![]()
![]()
Ответ: 20 см.
4. Решить задачу № 828 (на доске решают два ученика, остальные в тетрадях).
5. Решить задачу № 826 (б) самостоятельно.
Решение.
М 1 : 2 000 000. Это означает, что 1 см на карте соответствует
2 000 000 см = 20 км на местности.
1) 3140 : 20 = 157 (см) на карте.
Ответ: 157 см.
6. Повторение ранее изученного материала.
а) Решить уравнение 7,8 : 2,6 = 4,5 : х.
б) Решить задачу:
На изготовление 14 деталей расходуется 16,8 кг металла. Сколько потребуется металла на изготовление 27 таких деталей?
Решение.
![]()
![]()
Ответ: 32,4 кг.
в) Решить задачу (самостоятельно с проверкой):
24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью?
Решение.
![]()
![]()
Ответ: 4 дня.
III. Итог урока. Как найти расстояние на местности с помощью карты?
Домашнее задание: повторить материал п. 20–23; решить № 841, 844, 845, 864 (1), 873 (в; г).
КОНТРОЛЬНАЯ РАБОТА № 7 (1 час)
Цели: проверить знания, умения и навыки учащихся при решении задач с помощью пропорций и степень усвоения ими изученного материала.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение контрольной работы по вариантам.
Вариант I.
1. Отведенный участок земли распределили между садом и огородом. Сад занимает 5,6 а, огород 3,2 а. Во сколько раз площадь огорода меньше площади сада? Какую часть всего участка занимает огород?
2. Решите уравнение 1,3 : 3,9 = х : 0,6.
3. Для изготовления 8 одинаковых приборов требуется 12 кг цветных металлов. Сколько килограммов цветных металлов потребуется для изготовления 6 таких приборов?
4. Для перевозки груза автомашине грузоподъемностью 7,5 т пришлось сделать 12 рейсов. Сколько рейсов придется сделать автомашине грузоподъемностью 9 т для перевозки этого же груза?
5. Сколько имеется несократимых правильных дробей со знаменателем 145?
Вариант II.
1. На пошив сорочки ушло 2,6 м купленной ткани, а на пошив пододеяльника – 9,1 м ткани. Во сколько раз больше ткани пошло на пододеяльник, чем на сорочку? Какая часть всей ткани пошла на сорочку?
2. Решите уравнение 7,2 : 2,4 = 0,9 : х.
3. Производительность первого станка-автомата 15 деталей в минуту, а второго станка – 12 деталей в минуту. Чтобы выполнить заказ, первому станку потребовалось 3,6 мин. Сколько минут потребуется второму станку на выполнение этого же заказа?
4. Из 12 кг пластмассы получаются 32 одинаковые трубы. Сколько таких труб получится из 9 кг пластмассы?
5. Сколько имеется несократимых правильных дробей со знаменателем 123?
Вариант III.
1. Сережа прошел 5,6 км пешком и проехал 12,6 км на автобусе. Во сколько раз путь, проделанный пешком, меньше пути на автобусе? Какую часть всего пути Сережа проехал на автобусе?
2. Решить уравнение 2,4 : х = 6 : 4,5.
3. При изготовлении 9 одинаковых приборов потребовалось 300 г серебра. Сколько серебра потребуется для изготовления 6 таких приборов?
4. Для перевозки груза потребовалось 14 автомашин грузоподъемностью 4,5 т. Сколько потребуется автомашин грузоподъемностью 7 т для перевозки этого же груза?
5. Сколько имеется несократимых правильных дробей со знаменателем 115?
Вариант IV.
1. Масса пустого бидона 1,6 кг, а масса подсолнечного масла, находящегося в бидоне, равна 4 кг. Во сколько раз масса масла больше массы пустого бидона? Какую часть общей массы бидона с маслом составляет масса пустого бидона?
2. Решите уравнение у : 4,2 = 3,4 : 5,1.
3. На изготовление некоторого количества одинаковых деталей первый станок тратит 3,5 мин, а второй 5 мин. Сколько деталей в минуту изготовляет второй станок, если первый станок изготовляет 20 деталей в минуту?
4. Для изготовления 18 одинаковых приборов потребовалось 27 г платины. Сколько платины потребуется для изготовления 28 таких приборов?
5. Сколько имеется несократимых правильных дробей со знаменателем 133?
ДЛИНА ОКРУЖ И ПЛОЩАДЬ КРУГА
Урок 1
Цели: ввести понятие окружности и диаметра окружности, изучить формулу длины окружности и научить применять ее при решении задач.
Ход урока
I. Анализ контрольной работы.
1. Сообщить результаты контрольной работы.
2. Решить задания, вызвавшие затруднения у учащихся.
II. Изучение нового материала.
1. Если острие ножки циркуля установить неподвижно в точке О, а другую ножку с грифелем вращать на плоскости листа (или доски), то грифель опишет замкнутую кривую линию, все точки которой будут равноудалены от одной точки О. Эта кривая линия называется окружностью. Точка О называется центром окружности. Отрезок, соединяющий любую точку окружности с ее центром, называется радиусом окружности. Обозначают радиус r. Все радиусы окружности равны между собой.
2. Отрезок, проходящий через центр окружности и соединяющий две ее точки, называется диаметром окружности (d).
Диаметр вдвое больше радиуса (d = 2r). Концы диаметра делят окружность на две равные части.
3. Возьмем круглый стакан, поставим на лист бумаги и обведем его карандашом. На бумаге получится окружность. Если «опоясать» стакан ниткой, а потом распрямить ее, то длина нитки будет приближенно равна длине нарисованной на листе окружности.
4. Длина окружности тем больше, чем больше ее диаметр. Длина окружности прямо пропорциональна длине ее диаметра. Поэтому для всех окружностей отношение длины окружности к длине ее диаметра является одним и тем же числом.
Это отношение обозначают греческой буквой p (читают: «Пи»).
5. Если длину окружности обозначить буквой c, а диаметр – буквой d, то с : d = p, или с = pd .
Так как d = 2r, то с = pd = 2pr формула длины окружности.
6. В практических расчетах часто пользуются приближенным значением числа p с точностью до сотых:
p » 3,14 (или p » ![]() ).
).
7. (Устно). Вычислить длину окружности, радиус которой 1 см; 10 см; 100 см; 1000 см; 1 м; 2 дм.
III. Закрепление изученного материала.
1. Решить № 849 на доске и в тетрадях.
Решение.
d = 50 см; p » 3,1; с = pd » 50 · 3,1 » 135 (см).
Ответ: 135 см.
2. Решить № 847 (три человека решают на доске, остальные самостоятельно в тетрадях, потом проверяется решение).
3. Решить № 850 (выполнить необходимые измерения – изме-рить диаметр окружности).
Решение.
d = 2,8 см; r = 1,4 см; длина половины окружности равна
pr = 1,4 · 3,14 » 4,396 » 4,4 (см).
Ответ: 4,4 см.
4. Решить задачу:
Чтобы определить диаметр ствола дерева, лесник измерил длину окружности ствола дерева. Она равна 3,3 м. Каков диаметр ствола дерева?
Решение.
с = ![]() (м).
(м).
Ответ: 1,05 м.
5. Повторение ранее изученного материала:
1) решить задачу № 862.
Решение.
1 км = 100 000 см; 10: 100 000 = 1 : 10 000.
Ответ: М 1 : 10 000.
2) Самостоятельно решить № 859 (а; б).
IV. Итог урока.
1. Написать формулы для нахождения длины окружности по длине ее диаметра и по длине ее радиуса.
2. Пропорциональна ли длина окружности длине ее радиуса?
Домашнее задание: изучить п. 24; решить № 867, 868, 869, 863.
Урок 2
Цели: ввести формулу площади круга и научить применять ее к решению задач; закрепить полученные знания в ходе выполнения упражнений, развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить № 858 (а; б; в) устно и № 859 (в; г).
2. Решить задачу, повторив формулу длины окружности с = pd: определите диаметры стволов деревьев-гигантов у их оснований: а) эвкалипта, длина окружности которого 25 м; б) мамонтова дерева, длина окружности которого 32 м.
II. Объяснение нового материала.
1. Кругом называется часть плоскости, ограниченная окружностью. Например, дно стакана, поверхность крышки консервной банки.
2. Работа по рисунку 40 учебника на с. 138.
Если площадь круга
обозначить через S, то ее можно вычислить по формуле ![]() .
.
3. Вычислить площадь круга, радиус которого равен 5 см.
Решение.
S = pr2 = 3,14 · 52 = 3,14 · 25 = 78,5 (см2).
Ответ: 78,5 см2.
4. (Устно.) Вычислить площадь круга, диаметр которого равен 2 см; 20 см; 0,2 см.
5. Начертите круг. Измерьте его радиус и вычислите площадь круга.
III. Тренировочные упражнения.
1. Решить задачу № 854 на доске и в тетрадях.
Решение.
с = 40,8 м;![]()
Диаметр арены цирка 13 м, радиус 6,5 м. Площадь арены цирка равна
S = pr2 = 3 · 6,52 » 3 42,25 » 126,75 (м2) » 127 м2.
Ответ: 13 м; »127 м2.
2. Решить задачу № 855 на доске и в тетрадях.
3. Решить задачу № 853 самостоятельно, используя рисунок 42 учебника и выполнив измерения радиуса каждой окружности.
4. Решить задачу (объясняет учитель):
Останкинская
телебашня в Москве опирается на площадку, имеющую форму кольца. Диаметр
наружной окружности 63 м,
а внутренней окружности 44 м. Вычислите площадь фундамента Останкинской
телебашни.
Решение.
Sкольца = pr12 – pr22 = p(r12 – r22); p » 3.
r1 = 63 : 2 = 31,5 (м); · r2 = 44 : 2 = 22 (м);
Sкольца = 3 · (31,52 – 222) = 3 (992,25 – 484) = 3 · 508,25 =
= 1524,75 (м)2 » 1525 м2.
Ответ: 1525 м2.
IV. Итог урока.
1. Повторить все формулы по теме.
2. Что называется кругом?
3. Как разделить круг на две равные части?
4. Найдите площадь
![]() круга, радиус
которого 4,4 дм. Число p
округлите
до десятых.
круга, радиус
которого 4,4 дм. Число p
округлите
до десятых.
Домашнее задание: запомнить формулы п. 24; решить № 856, 870, 871.
ШАР
Урок 1
Цели: ввести представление о шаре, радиусе шара, диаметре шара, о сфере; закрепить знание учащимися формул длины окружности и площади круга; способствовать выработке навыков решения задач.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Решить № 878 (а; в) устно.
2. Решить № 882.
3. Повторить формулы длины окружности, площади круга.
4. Решить задачу:
Диаметр опаленной площади тайги от взрыва Тунгусского метеорита (1908 г.) равен примерно 38 км. Какая площадь тайги пострадала от метеорита?
II. Объяснение нового материала.
1. «Родственником» круга в пространстве является шар. Футбольный мяч, глобус, арбуз дают представление о шаре. Подобно тому как круг ограничен окружностью, так же шар ограничен шаровой поверхностью, которая иначе называется сферой. Все точки шаровой поверхности одинаково удалены от центра шара.
2. Отрезок, соединяющий точку поверхности шара с центром, называют радиусом шара.
3. Отрезок, соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара. Диаметр шара равен двум радиусам.
4. Вы знаете, что наша Земля имеет шарообразную форму, но она несколько сплюснута, поэтому полярный радиус на 21 км меньше экваториального и длина экватора на 67 156 м больше длины меридиана.
5. Представьте себе, что у вас есть деревянный шар и вы распиливаете его.
В плоскости распила получается фигура, она называется сечением шара.
Всякое сечение шара плоскостью есть круг, а сферу плоскость пересекает по окружности.
Чем дальше проходит секущая плоскость от центра сферы, тем меньше радиус сечения. Самые большие окружности получаются при сечении сферы плоскостями, проходящими через центр. В этом случае радиус окружности является и радиусом сферы.
III. Закрепление изученного материала.
1. Назвать предметы, имеющие форму шара.
2. Можно ли поместить в куб с ребром 7 см шар радиусом 4 см?
3. Решить задачу № 874 на доске и в тетрадях.
4. Решить задачу № 877.
Решение.
1) 5000 · 2,48 = 12400 (км) диаметр планеты Венера.
2) 12400 · ![]() = 400 · 17 = 6800
(км) диаметр планеты Марс.
= 400 · 17 = 6800
(км) диаметр планеты Марс.
Ответ: 12400 км; 6800 км.
5. Повторение ранее изученного материала:
а) Решить задачу № 879.
Решение.
М 1 : 1000. Значит, 1 см на плане составляет 1000 см = 10 м на местности. Поэтому радиус бассейна равен 10 м, а диаметр бассейна – 20 м. Площадь бассейна равна
S = pr2 = 3,14 · 102 = 3,14 · 100 = 314 (м2).
Ответ: 20 м; 314 м2.
б) Решить задачу № 883.
Решение.
![]() (см2) площадь первого
круга.
(см2) площадь первого
круга.
![]() (см) радиус
второго круга.
(см) радиус
второго круга.
3) p · 62 = 3,14 · 36 = 113,04 (см2) площадь второго круга.
Ответ: 150,72 см2; 113,04 см2.
в) Решить № 885 (1) самостоятельно.
IV. Итог урока.
1. Что называется радиусом шара? диаметром шара?
2. Что такое сфера?
3. Формулы длины окружности и площади круга.
Домашнее задание: изучить п. 25; решить № 861, 887, 888, 890 (а).
Урок 2
Цели: обобщить и закрепить изученный материал; способствовать развитию навыков и умений решать задачи и примеры; подготовить учащихся к контрольной работе.
Ход урока
I. Устная работа.
1. Решить № 878 (б; г) устно и № 880 (1-й и 2-й столбцы).
2. Решить задачу: Древнегреческий математик Архимед установил, что длина окружности относится к длине диаметра приближенно как 22 : 7. Найдите длину окружности, диаметр которой 4,2 дм.
Решение.
![]() (дм).
(дм).
Ответ: 13,2 дм.
3. Повторить формулу площади круга. Составить задачу (самим учащимся) на вычисление площади круга и решить ее.
II. Тренировочные упражнения.
1. Решить задачу № 875 на доске и в тетрадях.
2. Решить задачу № 876 с комментированием на месте.
Решение.
1) 38 млн км2 : 0,075 = 506,6 » 507 млн км2.
Ответ: » 507 млн км2.
3. Решить задачу:
Около водопада Виктория в Центральной Африке растет баобаб, окружность ствола которого 26,2 м, а окружность ствола кипариса, растущего в Мексике, на 22,6 м больше. Определите диаметры поперечного сечения ствола баобаба и ствола кипариса.
Решение.
1) 26,2 + 22,6 = 48,8 (м) окружность ствола кипариса.
![]() диаметр
поперечного сечения ствола.
диаметр
поперечного сечения ствола.
2) 26,2 : 3,1 » 262 : 31 » 8,45 (м) » 8 м 45 см диаметр поперечного сечения ствола баобаба.
3) 48,8 : 3,1 » 488 : 31 » 15,74 (м) » 15 м 74 см диаметр поперечного сечения ствола кипариса.
Ответ: 8 м 45 см; 15 м 74 см.
4. Повторение ранее изученного материала: Решить задачи:
а) Один отрезок на карте имеет длину 3,2 см, а на местности 1,6 км. Второй отрезок на местности имеет длину 2,8 км. Какую длину он будет иметь на этой карте?
б) Расстояние между городами Луганск и Россошь равно 185 км. Какое расстояние между этими городами на карте, если масштаб карты 1 : 5 000 000?
в) Расстояние между городами Охотск и Якутск на карте 4,3 см. Найдите расстояние между этими городами на местности, если масштаб карты 1 : 20 000 000.
г) Найдите площадь
круга, если длина ![]() окружности этого
круга равна 12,4 см. (Число p
» 3,1.)
окружности этого
круга равна 12,4 см. (Число p
» 3,1.)
5. Найдите значение выражения:
![]()
III. Итог урока.
Повторить правила и формулы п. 23–25.
Домашнее задание: повторить правила и формулы п. 23–25; решить № 886; № 880 (3-й, 4-й, 5-й столбцы); № 949 (а); № 1581; 1583.
КОНТРОЛЬНАЯ РАБОТА № 8 (1 час)
Цели: проверить знания учащихся по изученному материалу; выявить степень усвоения материала.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение контрольной работы по вариантам.
Вариант I.
1. Найдите значение выражения:
![]()
2. Какую длину имеет на карте отрезок, изображающий расстояние 85 км, если масштаб карты 1 : 1 000 000?
3. На чертеже в одном и том же масштабе изображены два стержня. Первый на чертеже имеет длину 5,2 см, а второй 6,4 см. Какова длина первого стержня в действительности, если действительная длина второго стержня 0,96 м?
4. Найдите площадь
круга, если ![]() длины окружности
этого круга равны 24,8 см. (Число p
» 3,1.)
длины окружности
этого круга равны 24,8 см. (Число p
» 3,1.)
5. Найдите длину окружности, если длина ее радиуса 2,25 дм. (Число p » 3,14.)
6. Площадь земельного участка прямоугольной формы 6а. Найдите площадь прямоугольника, изображающего этот участок на плане, масштаб которого 1 : 500.
Вариант II.
1. Найдите значение выражения:
![]()
2. Какую длину имеет на карте отрезок, изображающий расстояние в 45 км, если масштаб карты 1 : 1 000 000?
3. На чертеже изображен напильник с ручкой. Длина напильника на чертеже 4,2 см, а длина ручки 1,5 см. Какова длина ручки напильника в действительности, если длина напильника в действительности равна 25,2 см?
4. Найдите площадь
круга, если длина ![]() окружности этого
круга равна 12,4 см. (Число p
» 3,1.)
окружности этого
круга равна 12,4 см. (Число p
» 3,1.)
5. Найдите длину окружности, если ее радиус равен 3,25 дм. (Число p » 3,14.)
6. На чертеже изображен прямоугольник, площадь которого 216 см2. Найдите площадь этого прямоугольника в действительности, если чертеж выполнен в масштабе 1 : 5.
Вариант III.
1. Найдите значение выражения:
![]()
2. Какому расстоянию на местности соответствует 8,5 см на карте, если масштаб карты 1 : 10 000?
3. На чертеже в одном масштабе изображены две трубы. Первая труба на чертеже имеет длину 24 см, а в действительности 6 м. Какую длину на чертеже имеет вторая труба, если ее действительная длина 4,5 м?
4. Найдите площадь
круга, если ![]() длины окружности
этого круга равны 49,6 см. (Число p
» 3,1.)
длины окружности
этого круга равны 49,6 см. (Число p
» 3,1.)
5. Найдите длину окружности, если ее радиус равен 4,25 дм. (Число p » 3,14.)
6. Площадь земельного участка изображается на плане, масштаб которого 1 : 250, в виде прямоугольника площадью 128 см2. Найдите действительную площадь этого земельного участка.
ПОЛОЖ И ОТРИЦ ЧИСЛА
КООРДИНАТЫ НА ПРЯМОЙ
Урок 1
Цели: познакомить учащихся с отрицательными числами, с координатной прямой, с понятием координаты точки на прямой; научить отмечать точки на координатной прямой.
Ход урока
I. Анализ контрольной работы.
1. Указать ошибки, сделанные учащимися при выполнении заданий.
2. Решить задачи, вызвавшие затруднения у учащихся.
II. Устная работа.
1. Решить № 908 (а; в) и № 909 (а; б) устно.
2. Решить задачу № 911 устно.
III. Объяснение нового материала.
1. На уроках математики до сих пор мы рассматривали натуральные и дробные числа. Однако в жизни вы уже наверняка встречались и с другими числами – отрицательными. В самом деле, из сообщения о погоде вы могли узнать, что температура воздуха была – 12 градусов, а на географической карте увидеть отметку – 1733 (в метрах) для глубины Байкала.
Такие числа, «похожие» на натуральные, но со знаком «минус», нужны в тех случаях, когда величина может изменяться в двух противоположных направлениях, повышаться или понижаться.
2. Покажем расположение положительных и отрицательных чисел на прямой.
3. Работа по учебнику (с. 147, рис. 48 и 49). Числа со знаком «+» перед ними называют положительными. Числа со знаком «–» перед ними называют отрицательными.
Для краткости
записи обычно опускают знак «+» перед положительными числами и вместо +7
пишут 7. Поэтому ![]() + 6,3 = 6,3.
+ 6,3 = 6,3.
Математики в древнем Китае использовали для обозначения отрицательных чисел другой цвет, чем для положительных чисел. Однако в настоящее время обозначение отрицательных чисел с помощью знака «минус» принято во всем мире.
4. Начало отсчета (или начало координат) – точка 0 изображает 0 (нуль). Само число 0 не является ни положительным, ни отрицательным. Оно отделяет положительные числа от отрицательных.
5. Определение координатной прямой (рис. 49 и 50). Определение координаты точки на прямой.
Пишут: А (–2![]() В (–3; 6); С (8;
4).
В (–3; 6); С (8;
4).
6. На координатной прямой можно найти точку, соответствующую любому числу – положительному или отрицательному. В то же время с помощью положительных, отрицательных чисел и числа нуль можно указать положение любой точки на прямой.
7. С координатной прямой мы встречаемся на уроках истории («линия времени»). Шкалу с положительными и отрицательными числами и нулем имеют термометры. Начало отсчета соответствует температуре таяния льда 0 °С. При 100 °С закипает вода.
IV. Закрепление изученного материала.
1. Решить № 891, 892 и 893 устно.
2. Решить № 895, 897, 898 на доске и в тетрадях.
3. Решить № 917 (1; 2) самостоятельно на два варианта, затем проверить решение.
V. Итог урока.
1. Вопросы к п. 26 на с. 148 учебника.
2. Задания по демонстрационному термометру.
Домашнее задание: изучить п. 26; решить № 918, 919, 920, 917 (3)
Урок 2
Цели: учить учащихся изображать на координатной прямой точки по их координатам; способствовать развитию навыков и умений учащихся при решении задач и выполнении упражнений; развивать логическое мышление учащихся.
Ход урока
I. Проверка изученного материала.
1. Ответить на вопросы:
Что такое координатная прямая?
Что называют координатой точки на прямой?
Какими числами являются координаты точек на горизонтальной прямой, расположенных:
а) справа от начала координат;
б) слева от начала координат?
Какую координату имеет начало координат?
2. Записать (на доске) с помощью знаков «+» и «–» сообщения службы погоды:
а) 20 градусов тепла; г) 20 градусов мороза;
б) 5 градусов тепла; д) 12 градусов тепла;
в) 3 градуса мороза; е) 7 градусов мороза.
3. Устно решить № 908 (б; г; д) и № 910.
II. Выполнение упражнений.
1. Решить № 894 (по рис. 53) устно.
2. Решить № 896 (рис. 54) самостоятельно.
3. Решить № 900, изобразив координатную прямую на доске и в тетрадях.
4. Решить № 902 (по рис. 57) устно.
5. Самостоятельно решить № 901 (а) и № 907.
Решение.
Отрицательные
числа: ![]()
Положительные
числа: ![]()
6. Решить № 906 (устно) по рисунку 58 учебника.
7. Практическое задание: Начертите шкалу термометра и отметьте на этой шкале показания термометра: –5°; + 3,5°; –4°; –2,5°; +4°; +1,5°; –3°; –1°; + 7°; 0°.
8. Повторение ранее изученного материала:
1) Решить № 914 (а; б) на доске и в тетрадях.
Решение.
![]()
= 0,3 · 1,39 = 0,417 или же можно решить так:
0,3 + 0,09 + 0,027 = 0,39 + 0,027 = 0,417.
б) 0,5 – (0,5)2 – (0,5)3 =0,5 – 0,25 – 0,125 = 0,250 – 0,125 = 0,125.
2) Решить задачу № 912 самостоятельно с последующей проверкой.
Решение.
1) 75 млн км2 : ![]() млн ·
млн · ![]() млн км2 площадь
поверхности планеты Венера.
млн км2 площадь
поверхности планеты Венера.
Ответ: 460 млн км2.
3) Решить № 915. Повторить признак делимости чисел на 3.
Решение.
Можно составить числа: 57; 87; 357; 537; 387; 837. Эти числа кратны 3.
III. Итог урока. 1. Назвать
координаты точек В, А, М, К и Р, изображенных на координатной
прямой (заранее начертить на
доске):

2. Может ли число жильцов в доме выражаться отрицательным числом?
3. Может ли длина комнаты выражаться отрицательным числом?
4. Есть ли различие между числами:
+ 9 и 9; –13 и 13; +0; 0 и –0?
5. Привести свои примеры величин, которые можно записать положительными или отрицательными числами.
Домашнее задание: решить № 914 (в; г), № 922, 923, 917 (4).
Урок 3
Цели: закрепить изученный материал в ходе выполнения упражнений; проверить степень усвоения учащимися материала в ходе проведения самостоятельной работы.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Двое учащихся работают на доске, выполняя домашнее задание № 923 и № 917 (4).
2. С остальными учащимися устная работа:
а) решить № 909 (в; г) и № 913;
б) повторить определение координатной прямой и определение координаты точки на прямой; устно решить № 904.
3. Используя демонстрационный термометр, решить № 905.
II. Тренировочные упражнения.
1. Решить № 899 и № 903, используя координатную прямую.
2. Начертить координатную прямую и на ней изобразить точки задания № 901 (б).
3. Начертите
координатную прямую, приняв за единичный отрезок пять клеток тетради. Отметьте
на этой прямой точки А(2); В(–3); С(–1); Д(1,2); Е![]() F
F![]() М(–2,6);
Д(4,8); Н
М(–2,6);
Д(4,8); Н![]() .
.
4. Начертите горизонтальную прямую и отметьте на ней точку А. Правее точки А на расстоянии 3 см отметьте точку В. Отметьте точку О – начало отсчета, если А(–6), а В(–3).
5. Решить задачу № 916, используя рисунок 59 учебника.
III. Самостоятельная работа (10 мин).
Вариант I.
1. Запишите координаты точек М, N, К, А и Д, изображенных на рисунке.

2. Начертите
координатную прямую, приняв за единичный отрезок длину четырех клеток тетради.
Отметьте на этой прямой точки Е(3); К(–2); Д(2,5); F(–1,5);
S![]() ; Р(4,25); В(–2,75).
; Р(4,25); В(–2,75).
3. Начертите горизонтальную прямую. Отметьте на прямой точки С и Д так, чтобы точка Д была правее точки С и СД = 5 см. Отметьте на прямой начало отсчета 0, если С(–2), а Д(3).
Вариант II.
1. Запишите координаты точек Е, F, К, В и Р, изображенных на рисунке.

2. Начертите
координатную прямую, приняв за единичный отрезок длину пяти клеток тетради.
Отметьте на этой прямой точки А(2); М(–3); Д(–2,6); Р(–2,4);
N![]() T
T![]() К(–1,8).
К(–1,8).
2. Начертите горизонтальную прямую и отметьте на этой прямой точки Е и F так, чтобы точка F была правее точки Е и EF = 6 см. Отметьте точку 0 – начало отсчета, если Е(–4), а F(2).
Домашнее задание: изучить п. 26; решить № 921, 924, 925.
ПРОТИВОПОЛОЖНЫЕ ЧИСЛА
Урок 1
Цели: ввести определение противоположных чисел, определение целых чисел; научить находить числа, противоположные данным числам.
Ход урока
I. Анализ самостоятельной работы.
1. Выполнить работу над ошибками.
2. Решить задачи, вызвавшие затруднения у учащихся.
II. Устная работа.
1. Решить № 935, 939 и 936 (а; б) устно.
2. Проверить решение задачи № 925.
Решение.
1) 560 · 0,35 = 196 (кг) семян собрано в первый день.
2) 196 : ![]() (кг) семян собрано
во второй день.
(кг) семян собрано
во второй день.
3) 560 – (196 + 224) = 560 – 420 = 140 (кг) семян собрано в третий день.
Ответ: 140 кг.
III. Объяснение нового материала.
1. Рассмотреть рисунок 61 учебника и ввести понятие противоположных чисел: 5 противоположно – 5, а –5 противоположно 5.
2. Определение. Два числа, отличающиеся друг от друга только знаками, называют противоположными числами.
Например,
противоположными будут числа 7 и –7; –2,7 и 2,7; ![]()
3. Для каждого
числа есть только одно противоположное ему число: число –![]() противоположно
числу 4
противоположно
числу 4![]() а
а ![]() противоположно –
противоположно –![]() .
.
4. Число нуль противоположно самому себе.
5. Условимся считать, что знак «–», поставленный перед каким-нибудь числом, изменяет его на число, ему противоположное. Например, –(+3) = –3; –(–3) = + 3. Условимся также, что знак «+», поставленный перед каким-нибудь числом, оставляет это число без изменения.
Например, +(+8) = +8; +(–8) = –8.
Число, противоположное числу а, обозначают – а. Если а = 4, то –а = –4; если а = –5, то –а = +5, если –а = 10, то а = –10. Запись –2,8 можно читать двумя способами: «Минус 2,8» и «Число, противоположное числу 2,8».
Вообще, –(–а) = а.
6. Определение. Натуральные числа, противоположные им числа и нуль называют целыми числами.
IV. Закрепление изученного материала.
1. Решить № 926 устно.
2. Решить № 927 (а; б; г) на доске и в тетрадях.
Решение.
а) –(–80) = 80; б) 3,5 = –(–3,5); г) 3,2 = –(–3,2).
3. Решить № 931 на доске и в тетрадях.
Заполнить таблицу, а затем отметить точки на координатной прямой.
4. Решить № 933 (а; б; в; г), используя координатную прямую.
Решение.
а) Целые числа: а) –7; –6; б) –2; –1; в) –1; 0; 1; г) –3; –2; –1; 0; 1; 2; 3; 4.
5. Решить задачу № 941 (1) (повторение материала).
Решение.
1) 270 · ![]() = 120 тыс. штук
кирпича изготовлено за первую неделю.
= 120 тыс. штук
кирпича изготовлено за первую неделю.
2) 120 · 0,1 = 12 тыс. штук больше изготовлено во вторую неделю.
3) 120 + 12 = 132 тыс. штук кирпича изготовил завод во вторую неделю.
4) 270 – (120 + 132) = 270 – 252 = 18 тыс. штук кирпича осталось изготовить заводу.
Ответ: 18 тыс. штук.
V. Итог урока.
1. Какие числа называют противоположными?
2. Какое число противоположно нулю?
3. Существует ли число, имеющее два противоположных ему числа?
4. Какие числа называют целыми?
5. Назовите числа,
противоположные 23; –8; –1,5; 4,2; –3![]()
Домашнее задание: изучить п. 27; решить № 943, 945 (а, б), 947, 948 (а).
Урок 2
Цели: закрепить знания учащихся при нахождении чисел, противоположных данным и изображении их на координатной прямой; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить № 934, № 936 (в; г) устно.
2. Найдите значение выражения (устно):
а) –(–31); б)
–(+9); в) –(18,9); г) –0; д) –(–1); е) –![]() .
.
II. Выполнение упражнений.
1. Решить № 927 (в; д; е) на доске и в тетрадях.
2. Решить № 929 (по рис. 62).
3. Решить № 928 на доске и в тетрадях.
4. Решить уравнения (объясняет учитель):
а) –х = 123; х = –123;
б) –у = –49; у = 49;
в) –а = ![]() а = –
а = –![]()
г) –х = –4![]()
д) +3,4 = –k; k = –3,4.
5. Решить уравнения № 932 самостоятельно.
Решение.
а) –х = 607; х = –607;
б) –а = 30,4; а = –30,4;
в) –у = ![]() .
.
6. Повторение ранее изученного материала:
а) Решить задачу № 941 (2).
Решение.
1) 434 · ![]() =140 (т)
обмолотили в первый день.
=140 (т)
обмолотили в первый день.
2) 140 · 0,1 = 14 (т) меньше во второй день.
3) 140 – 14 = 126 (т) обмолотили во второй день.
4) 434 – (140 + 126) = 434 –266 = 168 (т) зерна обмолотили в третий день.
Ответ: 168 т.
б) Решить № 937 самостоятельно.
III. Самостоятельная работа (10 мин).
Вариант I.
1. Отметьте на координатной прямой точки, координаты которых 5; –3; –4,5; 1,5, и точки, координаты которых противоположны этим числам.
2. Запишите число, противоположное числу:
а) 2,48; б) –9;
в) 4; г) –5![]() д)
д) ![]() е) –0,029.
е) –0,029.
3. Найдите значение k, если
а) –k = 4,6; б) –k = –3,5.
4. Найдите
значение –m, если m = 6; m = –12![]()
5. Отметьте на
координатной прямой точки А (–2, 5), В (–4),
С (3, 5), Д ![]() . За единичный
отрезок примите длину четырех клеток тетради.
. За единичный
отрезок примите длину четырех клеток тетради.
6. Докажите, что 6 % от х равны х % от 6.
Вариант II.
1. Отметьте на
координатной прямой точки, координаты которых 4; –2; –3,5; 1![]() , и точки,
координаты которых противоположны этим числам.
, и точки,
координаты которых противоположны этим числам.
2. Запишите число, противоположное числу:
а) –3,18; б) 11;
в) –5; г) 2![]() д)
д) ![]() е) –0,417.
е) –0,417.
3. Найдите значение m, если
а) –m = 9,7; б) –m = –2,1.
4. Найдите
значение –k, если k = 3; k = –6![]()
5. Отметьте на
координатной прямой точки А (–1, 2), В (–0, 8),
С (2, 2), Д![]() . За единичный
отрезок примите длину пяти клеток тетради.
. За единичный
отрезок примите длину пяти клеток тетради.
6. Докажите, что у % от 8 равны 8% от у.
Домашнее задание: изучить п. 27; решить № 944, 946, 948 (б), 949 (б).
МОДУЛЬ ЧИСЛА
Урок 1
Цели: ввести понятие модуля числа; научить находить модули чисел; способствовать развитию навыков и умений учащихся при решении задач и упражнений.
Ход урока
I. Устная работа.
1. Решить устно № 959 (повторить определения противоположных и обратных чисел).
2. Решить устно задачу № 965 (а, в, г, и).
3. Решить устно уравнение № 964.
II. Объяснение нового материала.
1. Работа по учебнику: по рисунку 63 на с. 159 найти расстояние от точек М (–6) и В (5) до начала отсчета 0 на координатной прямой.
2. Определение. Модулем рационального числа называют расстояние от начала отсчета до точки координатной прямой, соответствующей этому числу.
Записывают: |–6| = 6; |5| = 5.
3. Мы знаем, что числа 3 и –3 противоположные. Точки на координатной прямой, соответствующие противоположным числам, одинаково удалены от начала отсчета, поэтому модули противоположных чисел равны:
|3| = |–3| = 3; |–а| = |а|.
4. Модуль числа 0 равен 0, так как точка координатной прямой, соответствующая числу 0, совпадает с началом отсчета, то есть удалена от нее на 0 единичных отрезков. Пишут: |0| = 0.
5. Расстояние между двумя точками не может выражаться отрицательным числом, поэтому модуль числа не может быть отрицательным.
Для положительного числа и нуля он равен самому числу, а для отрицательного числа – противоположному числу.
6. Примеры. |9| = 9; |2,6| = 2,6; |0| = 0;
|–9| = –(–9) =
9; |–12,6| = –(–12,6) = 12,6; ![]()
III. Закрепление изученного материала.
1. Решить № 950 на доске и в тетрадях.
2. Решить устно № 952.
3. Решить № 956 (а; б) с комментированием на месте.
Решение.
а) |26| = 26 и |–26| = 26;
б) ![]() .
.
4. Решить № 953 (а – е) на доске и в тетрадях.
Решение.
а) |–8| – |–5| = 8 – 5 = 3; б) |–10| · |–15| = 10 · 15 = 150;
в) |240| : |–80| = 240 : 80 = 3; г) |–710| + |–290|= 710 + 290 = 1000;
д) |–2,3| + |3,7| = 2,3 + 3,7 = 6; е) |–4,7| – |–1,9| = 4,7 – 1,9 = 2,8.
5. Решить устно:
1) Укажите наименьшее по модулю число:
а) –19,37; б)
6,3; в) 53,8; г) –2![]() .
.
2) Укажите наибольшее по модулю число:
а) –91,3; б)
10,8; в) –3![]() г)
г) ![]()
6. Решить самостоятельно: найдите значение выражения:
а) |–7| + |–9|; б) |–12| – |–7|; в) |–10| · |–17|; г) |–180| : |60|; д) |–13| – |0|.
7. Повторение материала: решить задачу № 971.
Решение.
Пусть скорость
легковой машины х км/ч, тогда скорость грузовика ![]() км/ч. По условию
задачи известно, что скорость грузовика на 22 км/ч меньше скорости легковой
автомашины.
км/ч. По условию
задачи известно, что скорость грузовика на 22 км/ч меньше скорости легковой
автомашины.
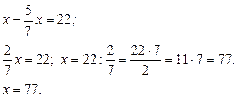
Скорость легковой машины 77 км/ч.
IV. Итог урока.
Ответить на вопросы к п. 28 на с. 160 учебника.
Домашнее задание: изучить п. 28; решить № 967, 968 (а – г), 970, 969.
Урок 2
Цели: закрепить определение модуля и нахождения модуля чисел в ходе выполнения упражнений; проверить усвоение изученного материала при выполнении самостоятельной работы.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Решить на доске задачу № 970 домашнего задания.
2. Решить устно № 960, № 963 и № 961.
3. Решить устно:
а) Найдите модуль
числа: –8; 1,3; –6,5; ![]()
б) Модуль каких
чисел равен: 3; 0,16; ![]()
в) Найдите значение выражения:
1) |–2,3| + |1,7|; 2) |–5,5| · |–0,2|; 3) |7,2| : |–0,6|;
4) ![]() |–2,9| –
|–0,9|; 6) |–10| : |–0,2|.
|–2,9| –
|–0,9|; 6) |–10| : |–0,2|.
II. Выполнение упражнений.
1. Решить № 951 самостоятельно.
2. Решить № 954 устно.
3. Решить № 956 (в; г; д) самостоятельно с последующей проверкой.
4. Решить № 953 (ж–м) на доске и в тетрадях.
Решение.
ж) |28,52| : |–2,3| = 28,52 : 2,3 = 285,2 : 23 = 12,4;
з) |0,1| · |–10| = 0,1 · 10 = 1;
и) ![]()
k) ![]()
л) ![]()
м) ![]()
5. Решить № 958 с комментированием на месте.
III. Самостоятельная работа.
Вариант I.
1. Найдите модуль числа:
а) 3; б) –2,8;
в) 7,2; г) –2![]()
2. Запишите числа, модули которых равны:
а) 5; б) 2,4;
в) ![]()
3. Запишите числа 11,75; –11,85; –11,76; –10,89 и 10,98 в порядке возрастания их модулей.
4. Найдите значение выражения:
а) |–8,3| + |–2,9|; г) |–2,73| : |1,3|;
б) |–5,75| –
|2,38|; д) ![]()
в) |–8,4| ·
|–1,5|; е) ![]()
Вариант II.
1. Найдите модуль
числа: а) 8; б) –2,8; в) 9,2; г) ![]()
2. Запишите числа 14,38; –14,49; –14,39; 14, 47; –13,67 и 13, 84 в порядке убывания их модулей.
4. Найдите значение выражения:
а) |–7,6| + |–4,7|; г) 7,14| : |–2,1|;
б) |–3,84| –
|1,97|; д) ![]()
в) |–7,5| ·
|–4,6|; е) ![]()
Домашнее задание: повторить определение модуля числа и правила п. 28; решить № 968 (д–з), № 972, 973; индивидуальное задание – упражнение 962.
СРАВНЕНИЕ ЧИСЕЛ
Урок 1
Цели: повторить сравнение положительных чисел и рассмотреть сравнение отрицательных чисел, используя термометр и координатную прямую; развивать логическое мышление.
Ход урока
I. Анализ самостоятельной работы.
1. Сообщить результаты самостоятельной работы и ошибки, допущенные учащимися при выполнении работы.
2. Решить задания, вызвавшие затруднения у учащихся.
3. Решить устно № 984 и № 982.
II. Изучение нового материала.
1. Используя демонстрационный термометр, сравнить температуру воздуха:
а) 18° и 21°; б) 9° и 0°; в) 20° и 14,5°.
г) 2° и –15°; д) –10° и 5 °; е) 0° и –8°;
ж) –18° и –6°; з) –1,5° и 0°.
Результаты записать в виде неравенств.
2. Записать в тетрадях выводы:
1) Любое положительное число больше нуля и больше любого отрицательного числа.
Например, 1 > 0; 12 > –2,5.
2) Любое отрицательное число больше нуля и больше любого отрицательного числа.
Например, –56 < 0; –9 < 0,0024.
3) Из двух отрицательных чисел больше то, модуль которого меньше.
Например, –4 < –1; так как |–4| > |–1|; –75 < –9, так как |–75| > |–9|; –45 > –126, так как |–45| < |–126|.
Эти правила позволяют сравнивать рациональные числа, не обращаясь к координатной прямой.
3. Если надо отметить, что число а положительное, то записывают: а > 0.
Если надо отметить, что число а отрицательное, то записывают: а < 0.
4. Сравнить числа, используя координатную прямую (рис. 65 учебника).
Сделать вывод: из двух отрицательных чисел больше то, которое на прямой расположено ближе к 0.
III. Закрепление изученного материала.
1. Решить устно № 975.
2. Решить № 974 (а – е) на доске и в тетрадях.
3. Решить № 976 (а; б; г; ж) на месте с комментированием.
4. Решить № 981 (объясняет учитель).
Решение.
а) –4,3 < 0 (отрицательное число);
б) 27,1 > 0 (положительное число);
в) а < 0; г) в > 0.
5. Решить № 979, используя координатную прямую.
Решение.
а) –3 < –2,73 < –2; б) –10 < – 9,5 < –9;
в) –1 < –0,63 < 0; г) 0 < 0,87 < 1;
д) –2 < –1![]() < –1;
е) –7 < –6
< –1;
е) –7 < –6![]() < –6.
< –6.
6. Повторение изученного материала:
1) Решить № 990 самостоятельно.
2) Вычислите: а)![]() ; б)
; б) ![]()
Решение.

3) Решить № 992 (1; 2) самостоятельно. Двое учащихся решают на доске, а затем проверяется решение.
Решение.
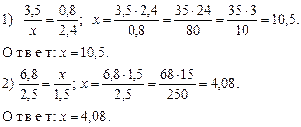
IV. Итог урока.
Ответить на вопросы на странице 163 учебника.
домашнее задание: изучить п. 29; решить № 995 (а; б; в), 998, 999.
Урок 2
Цели: упражнять учащихся в сравнении чисел, закрепить полученные знания и умения в ходе выполнения упражнений; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить устно № 983 (а) и № 987.
2. По тетрадям проверить выполнение учащимися домашней работы.
3. Расположите в порядке убывания следующие числа: –12; 17; –10; –23; 13; 0; –3,5; 7,2; 1,6.
4. Назвать три числа, меньше:
а) –23; б) –0,4; в) 11,3.
5. Назовите три решения неравенства:
а) х < 0; б) у > 5; в) а < –4.
II. Выполнение упражнений.
1. решить № 974 (ж – м) на доске и в тетрадях.
2. Решить № 976 (в; з; д; е) самостоятельно с проверкой.
3. Решить № 980 (а; б; д; е) на доске и в тетрадях, № 980 (в; ж) самостоятельно.
4. Между какими соседними целыми числами заключено число:
а) –4,5; б) 3,8;
в) ![]() г)
г) ![]() д) –7
д) –7![]() е) 1,012?
е) 1,012?
Ответ запишите в виде двойного неравенства.
5. Решить самостоятельно:
Расположите числа в порядке возрастания:
а) –2![]()
б) ![]()
6. Сравните (на доске и в тетрадях):
а) |3| + |7| и |3 + 7|. Ответ: равны.
б) |–1| + |10| и |(–1) + 10|. Ответ: 11 > 9.
в) |–6| + |5| и |(–6) + 5|. Ответ: 11 > 1.
г) |–5| + |–8| и |(–5) + (–8) |. Ответ: равны.
7. Повторение материала:
1) Решить устно № 988.
2) Решить самостоятельно № 989.
Решение.
а) |х| – |у| = |–64,1| – |–7,6| = 64,1 –7,6 = 56,5;
б) |х| + |у| = |–54,5| + |52,8| = 54,5 + 52,8 = 107,3.
3) Решить задачу № 993 (1) на доске и в тетрадях.
Решение.
1) 2,5 + 2 + 0,5 = 5 (кг) взяли фруктов для компота;
2) 2,5 : 5 · 100% = 0,5 · 100% = 50% составляют яблоки;
3) 2 : 5 · 100% = 0,4 · 100% = 40% составляют груши;
4) 0,5 : 5 · 100% = 0,1 · 100% = 10% взяли вишен.
Ответ: 50%; 40; и 10%.
4) Решить задачу № 993(2) самостоятельно.
III. Итог урока.
1. Повторить правила сравнения чисел.
2. Какое из чисел меньше:
а) –3 или –0,3;
б) –8 или –7; в) –2![]() или –3
или –3![]()
г) –0,17 или
0,173; д) –![]() е) –0,1 или
0,001?
е) –0,1 или
0,001?
3. Решить уравнение (устно):
а) |х| =
1; б) |у| = 7,3; в) |х| = 0; г) |у| = ![]()
Домашнее задание: выучить правила п. 29, решить № 995 (г; д; е), 996, 997 (а).
Урок 3
Цели: вырабатывать навыки сравнения чисел и нахождения модуля числа; развивать навыки решения задач и упражнений; развивать навыки самостоятельного решения заданий.
Ход урока
I. Проверка домашнего задания.
1. Двое учащихся работают на доске:
а) решить № 996 и 1031;
б) решить № 997 (а) и 1032.
2. Решить № 983 (б) и 985.
3. Число а – положительное число, число в – отрицательное. Какое из неравенств верно:
а > в или а < в?
4. Числа а и в – отрицательные, |а| > |в|. Какое из неравенств верно: а > в или а < в?
II. Выполнение упражнений.
1. Решить № 977 устно по таблице учебника.
2. Решить № 978 (а; б; г; ж) самостоятельно с последующей проверкой.
3. Решение № 978 (в; д; е; з) объясняет учитель.
Решение.
в) ![]() Приведем дроби к
общему знаменателю 20:
Приведем дроби к
общему знаменателю 20:
![]() ;
;
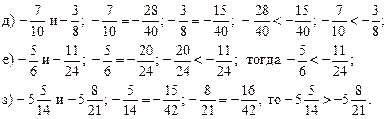
4. Решить № 980 (г; з; л) на доске и в тетрадях; № 980 (и; k; м) с комментированием на месте.
5. Расположите
числа ![]() в порядке
возрастания.
в порядке
возрастания.
6. Запишите все целые числа, которые заключены между:
а) –8,2 и 1; б) –7,8 и –5,4.
Решение:
а) –8,2 < х < 1; х = –8; –7; –6; –5; –4; –3; –2; –1; 0.
б) –7,8 < х < –5,4; х = –7; – 6.
III. Самостоятельная работа.
Вариант I.
1. Сравните: а) –547 и 546; б) –3,8 и –3,9;
в) –0,005 и
–0,05; г) ![]()
2. Расположите числа 7,6; –8,9; 8,2; –7,7; 0,3; –0,1 в порядке возрастания.
3. Между какими соседними целыми числами заключено:
а) –4![]()
4. Запишите все целые числа, которые заключены между
а) –6,6 и 2; б) –8,9 и –3,7.
Вариант II.
1. Сравните: а)
506 и –509; б) –6,2 и –6,8; в) –0,001 и –0,0001; г) –![]() д)
д) ![]() е)
е) ![]()
2. расположите числа –6,7; –3,8; 0,9; –4,2; 1,5 и –1,1 в порядке убывания.
3. Между какими
соседними целыми числами заключено: а) –0,915; б) –8![]() ?
?
4. Запишите все целые числа, которые заключены между:
а) –5,1 и –1,7; б) –1,2 и 4,6.
IV. Итог урока. Повторить правила сравнения чисел и нахождения модуля чисел.
Домашнее задание: решить № 997 (б), 1000, 991.
ИЗМЕНЕНИЕ ВЕЛИЧИН
Урок 1
Цели: рассмотреть примеры, связанные с изменением величин; закрепить знания учащихся по сравнению чисел; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Решить устно № 1008 по рисунку 70 учебника.
2. Решить устно № 1010 (а–г) и № 1011 (а; б; в).
3. Какие целые числа можно подставить вместо буквы а, чтобы неравенство стало верным:
а) –1 < а < 3; б) –7 < а < 7; в) –105 < a < –96?
4. Сравните сначала данные числа, а затем – противоположные им:
а) 10 и 15; б) –6 и –8; в) –12 и –1; г) 4 и –5.
II. Объяснение нового материала.
1. Температура может как повышаться, так и понижаться. Повышение температуры выражают положительными числами, а понижение – отрицательными (привести различные примеры).
2. Длина пружины может как увеличиваться, так и уменьшаться. Увеличение длины пружины будем выражать положительными числами, а уменьшение – отрицательными.
3. Точка на координатной прямой может перемещаться влево или вправо по этой прямой. Перемещение точки вправо обозначают положительными числами, а перемещение влево – отрицательными числами (рисунок 68 учебника).
4. Вывод: увеличение любой величины можно выразить положительными числами, а уменьшение – отрицательными.
III. Закрепление изученного материала.
1. Решить устно № 1001 (а).
2. Решить № 1002 на доске и в тетрадях.
Решение.
а) m = –6; б) m = 3,6; в) m = 60; г) m = –3,4.
3. Решить устно № 1004, используя рисунок 69 на странице 169 учебника.
4. Решить № 1005, используя координатную прямую.
5. Повторение изученного материала:
1) Решить № 1012.
Решение.
а) ![]() приведем обе дроби
к знаменателю 30, тогда
приведем обе дроби
к знаменателю 30, тогда ![]() ; тогда
; тогда![]()
в) 0,16 < х < 0,17; например, х = 0,162; 0,165; х = 0,167; 0,169.
2) Решить № 1014 самостоятельно.
3) Найдите значение выражения:
а) |–4,8| +
|5,2|; в) |–6,5| : |3,9|; д) ![]()
б) |–5,21| –
|–4,8|; г) |26,5| · |–8,3|; е) ![]()
IV. Итог урока.
1. Ответить на вопросы на странице 168 учебника.
2. Точка х при перемещении на – 4 перешла в точку А(–1), а точка у при перемещении на 2,5 перешла в В (0,5). Найдите координаты точек х и у.
3. При перемещении точка Р(–2) перешла в точку К(1,5). Чему равно перемещение точки Р?
4. Сравните
(устно): а) –298 и –196; б) –673 и –637; в) –6,4 и –18,9; г) –2,0003 и
–2,03; д) ![]()
5. Найдите модуль числа (устно):
а) 47; б)
–2,9; в) 0,75; г) ![]()
Домашнее задание: изучить п. 30; решить № 1015, 1017, 1019 (а).
Урок 2
Цели: закрепить изученный материал, упражнять учащихся в сравнении чисел и нахождении модуля чисел, подготовить к контрольной работе.
Ход урока
I. Устная работа.
1. Решить устно № 1007 и № 1010 (д – з).
2. Решить № 1011 (б; г; д; е), используя координатную прямую.
3. Решить устно № 1009 по рисунку 71 учебника.
II. Тренировочные упражнения.
1. Решить устно № 1001 (б).
2. Решить № 1003 самостоятельно с последующей проверкой.
3. Решить № 1006 с комментированием на месте.
4. Отметьте на координатной прямой точку А(–4). Найдите координату точки, в которую перейдет точка А при перемещении:
а) на 2; б) на 6; в) на –3; г) на –4.
5. Точка А при перемещении на 5 перешла в точку В(–1), а точка С при перемещении на –3 перешла в точку Д(–1). Найдите координаты точек А и С.
6. При перемещении точка А(4) перешла в точку В(–1). Чему равно перемещение точки А?
7. Отметьте на координатной прямой точки Д(–6), Р(2), М(–1, 5), К(6) и в(4,5). Какие из этих точек имеют противоположные координаты?
8. Сравните числа:
а) –249 и
248; г) ![]()
б) –10,3 и
–10,5; д) ![]()
в) –0,07 и
–0,007; е) ![]()
9. Найдите значение выражения:
а) |–6,8| :
|–17|; б) ![]() в)
в) ![]()
г) ![]() д) |–5,2|
: |–13|; е)
д) |–5,2|
: |–13|; е) ![]()
Решение.
а) 6,8 : 17 =
0,4; г) ![]()
б) ![]()
в) 11,8 – ![]()
10. Отметьте на координатной прямой точку С(–4), приняв за единичный отрезок длину двух клеток тетради. Отметьте на этой прямой точки А, В, М и К, если М правее точки С на 7 клеток, В правее точки М на 11 клеток, А – середина отрезка СВ, К – середина отрезка АС.
11. Решить № 1029, используя координатную прямую.
III. Итог урока.
Повторить правила пунктов 26–30.
Домашнее задание: повторить материал п. 26–30; прочитать исторический материал к п. 30 на с. 171 учебника; решить № 1016, 1018, 1019 (б).
КОНТРОЛЬНАЯ РАБОТА № 9 (1 час)
Цели: выявить степень усвоения учащимися изученного материала.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение работы по вариантам.
Вариант I.
1. Отметьте на координатной прямой точки А(3), В(–4), С(–4,5), Д(5,5), Е(–3). Какие из отмеченных точек имеют противоположные координаты?
2. Отметьте на координатной прямой точку А(–6), приняв за единичный отрезок длину двух клеток тетради. Отметьте на этой прямой точки В, С, д и Е, если В правее А на 20 клеток, С – середина отрезка АВ, точка Д левее точки С на 5 клеток и Е правее точки Д на 10 клеток. Найдите координаты точек В, С, Д и Е.
3. Сравните числа:
а) –1,5 и
–1,05; б) –2,8 и 2,7; в) ![]()
4. Найдите значение выражения:
а) |–3,8| :
|–19|; б) ![]() в)
в) ![]()
5. Сколько целых чисел расположено между числами –20 и 105?
Вариант II.
1. Отметьте на координатной прямой точки М(–7), N(4), К(3,5), Р(–3,5) и S(–1). Какие из отмеченных точек имеют противоположные координаты?
2. Отметьте на координатной прямой точку А(3), приняв за единичный отрезок длину двух клеток тетради. Отметьте на этой прямой точки M, N, К и Р, если М левее точки А на 18 клеток, N – середина отрезка АМ, точка К левее точки N на 6 клеток, а Р правее точки N на 7 клеток. Найдите координаты точек M, N, К и Р.
3. Сравните числа:
а) 3,6 и –3,7;
б) –8,3 и –8,03; в) ![]()
4. Найдите значение выражения:
а) |5,4| :
|–27|; б) ![]() в)
в) ![]()
5. Сколько целых чисел расположено между числами –157 и 44?
Вариант III.
1. Отметьте на координатной прямой точки Д(5), Е(–3), М(4,5), N(–4,5) и С(–1). Какие из отмеченных точек имеют противоположные координаты?
2. Отметьте на координатной прямой точку А(–8), приняв за единичный отрезок длину двух клеток тетради. Отметьте на этой прямой точки В, С, М и N, если М правее точки А на 5 клеток, N правее точки А на 11 клеток, С – середина отрезка MN и точка В правее точки С на 10 клеток. Найдите координаты точек В, С, М и N.
3. Сравните числа:
а) –7,6 и –7,06; б) –5,3 и 5,2; в) –![]()
4. Найдите
значение выражения: а) |–3,6| : |–18|; б) ![]() в)
в) ![]()
5. Сколько целых чисел расположено между числами –74 и 131?
Вариант IV.
1. Отметьте на координатной прямой точки М(–5), N(3), В(2,5), А(–1,5), С(–2,5). Какие из этих точек имеют противоположные координаты?
2. Отметьте на координатной прямой точку В(6), приняв за единичный отрезок длину двух клеток тетради. Отметьте на этой прямой точки М, С, N и К, если К левее точки В на 20 клеток, С – середина отрезка КВ, точка М – середина отрезка КС, а N правее точки С на 7 клеток.
3. Сравните числа:
а) –9,8 и 9,7;
б) –1,08 и –1,1; в) ![]()
4. Найдите значение выражения:
а) |–4,8| :
|16|; б) ![]() в)
в) ![]()
5. Сколько целых чисел расположено между числами –199 и 38?
СЛОЖЕНИЕ ЧИСЕЛ С ПОМ КООРДИН ПРЯМОЙ…..
Урок 1
Цели: показать учащимся, как складывают числа с помощью координатной прямой; развивать логическое мышление учащихся.
Ход урока
I. Анализ контрольной работы.
1. Сообщить результаты контрольной работы.
2. Решить задачи, вызвавшие затруднения у учащихся.
3. Решить устно № 1027, 1028.
II. Работа по учебнику.
1. Рассмотреть показания термометра на рисунках 72 и 73 учебника (с. 172) и записать результаты:
8 + 3 = 11; 8 + (–3) = 5.
2. Рассмотреть сложение чисел с помощью координатной прямой по рисунку 74 учебника на с. 172.
3. Сделать вывод:
а) Прибавить к числу а число в – значит, изменить число а на в единиц.
б) Любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного числа уменьшается.
4. Рассмотреть решение примеров 1, 2 и 3 на страницах 172–173 учебника, используя рисунки 75, 76 и 77.
Записать в тетрадях:
(–7) + 4 = 3; (–2) + (–4) = –6; 4 + (–4) = 0.
5. Записать в тетрадях вывод: сумма двух противоположных чисел равна нулю: а + (–а) = 0.
6. Разобрать решение примера 4 учебника. Записать в тетрадях: от прибавления нуля число не изменяется: а + 0 = а.
Примеры. (–5) + 0 = –5; 0 + (–11,3) = –11,3;
![]()
III. Закрепление изученного материала.
1. Решить № 1020 (а; б; в; е), используя координатную прямую.
2. Решить № 1021 с комментированием на месте. Учащиеся проговаривают правила при выполнении действий.
Решение.
4 + 0 = 4; 0 + (–3) = –3; (–5) + 0 = –5; (–3) + 3 = 0; 7 + (–7) = 0.
3. Решить № 1023, используя рисунок 78.
4. Решить № 1025, используя координатную прямую для сложения чисел.
Решение.
–2 + 3 = 1; –2 + 1 = –1; –2 + 2 = 0;
–2 + (–3) = –5; –2 + 5 = 3; –2 + (–4) = –6.
5. Повторение изученного материала:
а) Решить задачу № 1033.
Решение.
78% = 0,78;
1) 156 : 0,78 = 15600 : 78 = 200 (выстрелов) было сделано.
Ответ: 200 выстрелов.
б) Решить задачу № 1035.
Решение.
1) 9 : 15 · 100% = 0,6 · 100% = 60% цветов завяло.
Ответ: 60%.
IV. Итог урока.
1. Ответить на вопросы на с. 173 учебника.
2. С помощью координатной прямой сложите числа:
а) 2 и –5; в) –3 и –2; д) –1,5 + 3;
б) –4 и 6; г) –1 и –4; е) 4 и –5,5.
3. Найдите значение выражения:
а) (–28,6 + 28,6) + (–8); б) (0 + (–4,5)) + 4,5.
Домашнее задание: изучить п. 31; решить № 1039 (а; б; г; е), 1041, 1042 (а).
Урок 2
Цели: вырабатывать навыки сложения чисел с помощью координатной прямой, способствовать развитию умения решать упражнения и задачи, развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Решить устно № 1026 (а; б) и № 1030.
2. Решить устно № 1031, повторив определение модуля числа.
3. Повторить правила сравнения чисел и решить № 1032.
II. Выполнение упражнений.
1. Решить № 1020 (г, д, ж, з).
2. Устно решить № 1021.
3. Решить № 1022 с комментированием на месте. Повторить правила.
4. Решить № 1024, используя рисунок 78.
5. С помощью координатной прямой сложите числа:
а) –7 и 9; б) 4 и –5; в) –3 и 2;
г) 4,5 и –3,5; д) –5 и 2,5; е) –2,5 и –4,5.
6. Найдите значение выражения:
а) –7 + (–15,6 + 15,6); б) 9,7 + (0 + (–9,7)).
7. Повторение изученного материала:
а) решить задачу № 1034.
Решение.
I способ. 30% = 0,3
1) 13 · 0,3 = 3,9 (м) провода отрезали;
2) 13 –3,9 = 9,1 (м) провода осталось.
II способ.
1) 100% –30% = 70% провода осталось;
2) 13 · 0,7 = 9,1 (м) провода осталось.
Ответ: 9,1 м.
б) Решить задачу № 1036.
Решение.
1) 1,8 · 0,3 = 0,54 (м) глубина шкафа.
2) 0,54 · 2,5 = 1,35 (м) ширина шкафа.
3) V = авс; 1,8 · 0,54 · 1,35 = 1,3122 (м3) объем шкафа.
Ответ: 1,3122 м3.
III. Самостоятельная работа.
Вариант I.
1. С помощью координатной прямой сложите числа:
а) 8 и –3; б) –2 и 6; в) –5 и –4;
г) –3,5 и 2,5; д) 4,5 и –3; е) –1,5 и –2,5.
2. Найдите значение выражения:
а) (–37,4 + 37,4) + (–10); б) ((–3,6) + 0) + 3,6.
3. Дополнительно: решить № 1021 (1).
Вариант II.
1. С помощью координатной прямой сложите числа:
а) 5 и –2; б) –3 и 7; в) –4 и –3;
г) –2,5 и 1,5 д) 4,5 и –2; е) –2,5 и –1,5.
2. Найдите значение выражения:
а) (–18,7 + 18,7) + (–7); б) (0 + (–2,4)) + 2,4.
3. Дополнительно: решить № 1037 (2).
IV. Итог урока. Ответить на вопросы:
1. Что значит прибавить к числу а число в?
2. К числу а прибавили число в; как изменится число а, если в положительное, если в отрицательное, если в = 0?
3. Чему равна сумма противоположных чисел? Привести свои примеры.
Домашнее задание: решить № 1039 (в; д; ж; з), № 1040, № 1042 (б), № 1038 (устно).
СЛОЖЕНИЕ ОТРИЦ ЧИСЕЛ
Урок 1
Цели: ввести правило сложения отрицательных чисел и закрепить знание этого правила в ходе выполнения упражнений.
Ход урока
I. Устная работа.
1. Сообщить учащимся результаты самостоятельной работы и выполнить задания, вызвавшие затруднения у учащихся.
2. Решить устно № 1049 (а; б) и 1050.
3. Выполнить задание № 1053, используя заранее начерченную на доске координатную прямую.
II. Объяснение нового материала.
1. Рассмотреть показания термометра на рисунке 80 учебника.
Сначала температура воздуха была –6 °С, а потом она изменилась на –3 °С (то есть понизилась на 3 °С).
Какова стала температура воздуха после понижения?
2. Рассмотреть показания термометра на рисунке 80 учебника.
3. Сделать вывод: –6 + (–3) = –9.
4. Используя рисунок 81 учебника, сложить числа с помощью координатной прямой: А (–6) и В (–9), значит, –6 + (–3) = –9.
Но 9 = 6 + 3, причем, 6 = |–6|, а 3 = |–3|.
5. Сформулировать правило сложения отрицательных чисел.
6. Выполнить сложение (устно):
|
а) 40 + 60 –40 + (–60) 20 + (+15) –20 + (–15) |
б) 0,3 + 0,7 –0,3 + (–0,7) 1,2 + 0,6 –1,2 + (–0,6) |
в)
|
III. Закрепление изученного материала.
1. Решить № 1043, используя координатную прямую на доске.
2. Решить на доске и в тетрадях:
Найдите значение суммы:
а) –12 + (–8); б)
–7 + (–9); в) –5,4 + (–3,5); д) ![]() ;
;
е) ![]() ; ж)
; ж) ![]() .
.
3. Решить № 1045 (а; б; в; г; ж; и) самостоятельно, с последующей проверкой.
4. Решить № 1045 (л; м) (объясняет учитель).
Решение.
л) ![]() ;
;
м) ![]()
5. Найти значение суммы (самостоятельно):
![]() .
.
6. Решить № 1046 (а) на доске; № 1046 (б) самостоятельно с проверкой.
7. Повторение ранее изученного материала:
Решить № 1055 (1). Вызывать к доске по одному ученику для решения одного только действия.
Решение.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) 70,5 + 9,7 = 80,2;
5) 80,2 · 22,5 = 1804,5.
IV. Итог урока.
1. Сформулируйте правило сложения отрицательных чисел. Приведите свои примеры.
2. Может ли при сложении отрицательных чисел получиться нуль? отрицательное число?
Домашнее задание: выучить правило п. 32, решить № 1056 (а – е), № 1055 (2), № 1060 (а). Урок 2
Цели: закрепить в ходе выполнения упражнений правило сложения отрицательных чисел; развивать логическое мышление учащихся.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Решить устно № 1049 (в; г) и 1051 (а – д).
2. Сформулировать правило сложения отрицательных чисел. Привести свои примеры.
3. Решить задачи (устно):
а) Ветки смородины выносили температуру –195°, а после закаливания могли выдержать температуру ниже этой на 58°. Какую температуру выдерживали ветки смородины после закаливания?
б) Мучные жуки выдерживают температуру –19°, а жуки-древоточцы выдерживают температуру ниже этой на 1,4°. Какую температуру выдерживают жуки-древоточцы?
4. С помощью демонстрационного термометра выполните сложение:
а) +5° + (+4°); г) о° + (–7°);
б) –5° + (–4°); д) –3,5° + (–4,5°);
в) 0° + (+7°); е) –1,5° + (–9,5°).
II. Выполнение упражнений.
1. Решить № 1044 (устно).
2. Решить № 1045 (д; е; з; к) с комментированием на месте.
3. Решить № 1047 (в) на доске и в тетрадях; № 1047 (а) самостоятельно.
Решение.
а) х + у + (–16) = –17 + (–29) + (–16) = –62;
в) х + у
+ (–16) = ![]()
![]()
![]() .
.
4. Решить № 1048 на доске и в тетрадях.
а) (–0,251 + (–0,37)) + (–0,2 + (–0,152)) = –0,621 + (–0,352) = – 0,973.
б) ![]()
![]()
III. Самостоятельная работа.
Вариант I.
1. Найдите значение суммы:
а) –0,48 +
(-0,76); б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
2. К сумме чисел: а) –24 и –56 прибавьте –39;
б) ![]() и
и ![]() прибавьте –3,5.
прибавьте –3,5.
3. Разность забитых и пропущенных шайб в первой игре команды равна –5, во второй игре она равна –2, а в третьей игре равна 0 (нулю). Какова разность забитых и пропущенных шайб у этой команды за эти три игры вместе?
Вариант II.
1. Найдите значение суммы:
а) –0,37 +
(–0,84); б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
2. К сумме чисел: а) –37 и 25 прибавьте –49;
б) ![]() и
и ![]() прибавьте –1,4.
прибавьте –1,4.
3. Разность забитых и пропущенных шайб в первом тайме игры команды равна –1, во втором тайме она равна –4, а в третьем тай-ме – 2. Какова разность забитых и пропущенных шайб у команды за всю игру?
Домашнее задание: повторить правила; решить № 1056 (ж – м), № 1057 (б), № 1059, 1060 (б, в).
СЛОЖЕНИЕ ЧИСЕЛ С РАЗНЫМИ ЗНАКАМИ
Урок 1
Цели: ввести правило сложения чисел с разными знаками; упражнять учащихся в сложении чисел с разными знаками и сложении отрицательных чисел.
Ход урока
I. Анализ самостоятельной работы.
Сообщить результаты самостоятельной работы и указать ошибки, сделанные учащимися в ходе работы.
II. Устная работа.
1. Решить устно № 1072 (а – г) и 1074.
2. Повторить определение модуля числа и решить устно задачу № 1060.
3. Сформулировать правило сложения отрицательных чисел. Решить устно задачу:
Вечером температура воздуха была –10,5°, а за ночь температура воздуха понизилась на 2,5°. Какая температура воздуха была утром?
4. Подберите такое число, чтобы получилось верное равенство:
а) –6 + … = –8; г) … + (–3,8) = –4;
б) –6,5 + … = –10,5; д) … + (–9,1) = –10,1;
в) … + (–3,9) = –13,9; е) –0,2 + … = –0,4.
III. Изучение нового материала.
1. Используя демонстрационный термометр, сложить числа:
9 + (–6) = +3; –6 + 2 = –4; –8 + 10 = 2;
7 + (–7) = 0; 9 + (–12) = –3.
2. Разобрать сложение чисел с разными знаками по координатной прямой (рис. 84 и 86 учебника).
3. Сформулировать правило сложения чисел с разными знаками. Обратить внимание учащихся, что обычно сначала определяют и записывают знак суммы, а потом находят разность модулей.
4. Выполнить сложение (устно):
а) –7 + 11; б) 7 + (–11); в) –10 + (–4);
г) –10 + 4; д) 10 + (–4); е) –3 + 8; ж) 3 + (–8).
IV. Закрепление изученного материала.
1. Решить № 1061–1064, используя координатную прямую, заранее начерченную на доске.
2. Решить № 1066 (а; в; д) на доске и в тетрадях, № 1066 (б; г; е; ж) самостоятельно.
Решение.
а) 26 + (–6) = 20; г) 80 + (–120) = –40;
б) –70 + 50 = –20; д) –6,3 + 7,8 = 1,5;
в) –17 + 30 = 13; е) –9 + 10,2 = 1,2;
ж) 1 + (–0,39) = 0,61.
3. Решить № 1065 самостоятельно.
4. Решить № 1069 (а; б).
5. Повторение ранее изученного материала:
а) Решить задачу № 1079 (1) на доске и в тетрадях.
Решение.
1) 140 · 3 = 420 (км) – проехали в третий день.
2) 240 + 140 + 420 = 800 (км) – проехали за три дня.
3) 230 · 5 = 1150 (км) – проехали за пять дней.
4) 1150 – 800 = 350 (км) – проехали в пятый день.
Ответ: 350 км.
б) Решить № 1073 (б).
Решение.
![]()
![]() .
.
Ответ: –9.
V. Итог урока.
1. Ответить на вопросы на с. 181 учебника.
2. Выполнить сложение:
а) 37 + (–56); в) 4,61 + (–2,29);
б) –43 + 75; г) –3,08 + 1,69.
Домашнее задание: выучить правила п. 33, решить № 1081 (а – г), № 1083 (а), № 1085. Урок 2
Цели: способствовать выработке навыков сложения отрицательных чисел и сложения чисел с разными знаками; развивать логическое мышление учащихся.
Ход урока
I. Проверка усвоения материала.
1. Сформулировать правило сложения отрицательных чисел.
Решить устно № 1072 (д – ж).
2. Решить устно № 1075 (а) и № 1076 (в; г).
3. Сформулировать правило сложения чисел с разными знаками.
4. Подберите такое число, чтобы получилось верное равенство:
а) –4,5 + … = –3,5; г) –7,2 + … = 4,2;
б) … + 3 = –2,9; д) … + (–4,9) = –2,9;
в) –13,1 + … = –13,1; е) 0,48 + … = 0.
II. Выполнение упражнений.
1. Решить № 1066 (з – м) (объясняет учитель).
решение.
к) ![]() ;
;
л) ![]() ; м)
; м) ![]() .
.
2. Выполнить сложение (самостоятельно):
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3. Решить № 1069 (в; г).
4. Решить № 1067 (а) на доске и в тетрадях, 1067 (б) самостоятельно.
Решение.
а) (–6 + (–12)) + 20 = –18 + 20 = 2;
б) 2,6 + (–1,8 + 5,2) = 2,6 + 3,4 = 6.
5. Решить № 1070 (а; б) на доске и в тетрадях.
Решение.
а) ![]()
= –1,35;
б) ![]()
![]() .
.
6. Повторение ранее изученного материала:
а) Решить задачу № 1079 (2) самостоятельно.
б) Решить № 1080 (1).
Решение.
1) 2,35 + 4,65 = 7; 2) 40 – 2,9 = 37,1; 3) 7 · 5,3 = 37,1;
4) 37,1 : 37,1 = 1.
в) Решить задачу № 1078 (а – г).
III. Итог урока.
1. Сформулировать правило сложения отрицательных чисел. Привести свои примеры.
2. Сформулировать правило сложения чисел с разными знаками. Привести свои примеры.
3. Выполните сложение:
а) –379 + 948; в)
![]() ;
;
б) –0,81 + 0,66; г)
![]() .
.
Домашнее задание: выучить правила п. 32 и 33; решить № 1081 (д – л), № 1083 (б; в), № 1084.
Урок 3
Цели: способствовать выработке навыков и умений сложения отрицательных чисел и чисел с разными знаками; проверить усвоение материала учащимися в ходе выполнения упражнений.
Ход урока
I. Устная работа.
1. Повторить правило сложения отрицательных чисел. Привести свои примеры.
2. Повторить правило сложения чисел с разными знаками. Привести свои примеры.
3. Решить устно № 1072 (з; и) и 1073 (а).
4. Решить № 1075 (б; в), записывая решение только на доске.
II. Тренировочные упражнения.
1. Решить № 1066 (н – р) на доске и в тетрадях с помощью учителя.
Решение.
н) ![]() ;
;
о) ![]() ;
;
п) ![]() ;
;
р) ![]() = 0.
= 0.
2. Решить № 1067 (в; г) на доске и в тетрадях.
Решение.
в) (–10 + (–1,3)) + (5 + 8,7) = –11,3 + 13,7 = 13,7 – 11,3 = 2,4;
г) (11 + (–6,5)) + (–3,2 + (–6)) = 4,5 + (–9,2) = – (9,2 – 4,5) = –4,7.
3. Решить № 1070 (в; г).
Решение.
в) ![]()
![]() ;
;
г) ![]() .
.
4. Решить № 1068.
5. Повторение ранее изученного материала:
Решить задачу № 1078 (д – з) на доске и в тетрадях.
III. Самостоятельная работа.
Вариант I.
1. Выполните сложение:
а) –543 + 458; г)
![]() ;
;
б) 0,54 + (–0,83); д)
![]() .
.
в) ![]() ;
;
2.
Выполните действия ![]() .
.
3. Найдите значение выражения х + 2,6, если х = –1,47;
![]() ;
х = –18;
;
х = –18; ![]() .
.
4. Сколько решений имеет уравнение |х + 2| = –5?
Вариант II.
1. Выполните сложение:
а) 257 + (–314); б)
–0,28 + (–0,18); в) –6 + ![]() ;
;
г) ![]() ; д)
; д)
![]() .
.
2. Выполните
действия ![]() .
.
3. Найдите значение выражения у + (–4,2), если у = 1,83;
у = ![]() ; у = 16; у
=
; у = 16; у
= ![]() .
.
4. Сколько решений имеет уравнение |у – 9| = –6?
Домашнее задание: решить № 1081 (м – р), № 1082, № 1086.
ВЫЧИТАНИЕ
Урок 3
Цели: способствовать выработке навыков и умений сложения отрицательных чисел и чисел с разными знаками; проверить усвоение материала учащимися в ходе выполнения упражнений.
Ход урока
I. Устная работа.
1. Повторить правило сложения отрицательных чисел. Привести свои примеры.
2. Повторить правило сложения чисел с разными знаками. Привести свои примеры.
3. Решить устно № 1072 (з; и) и 1073 (а).
4. Решить № 1075 (б; в), записывая решение только на доске.
II. Тренировочные упражнения.
1. Решить № 1066 (н – р) на доске и в тетрадях с помощью учителя.
Решение.
н) ![]() ;
;
о) ![]() ;
;
п) ![]() ;
;
р) ![]() = 0.
= 0.
2. Решить № 1067 (в; г) на доске и в тетрадях.
Решение.
в) (–10 + (–1,3)) + (5 + 8,7) = –11,3 + 13,7 = 13,7 – 11,3 = 2,4;
г) (11 + (–6,5)) + (–3,2 + (–6)) = 4,5 + (–9,2) = – (9,2 – 4,5) = –4,7.
3. Решить № 1070 (в; г).
Решение.
в) ![]()
![]() ;
;
г) ![]() .
.
4. Решить № 1068.
5. Повторение ранее изученного материала:
Решить задачу № 1078 (д – з) на доске и в тетрадях.
III. Самостоятельная работа.
Вариант I.
1. Выполните сложение:
а) –543 + 458; г)
![]() ;
;
б) 0,54 + (–0,83); д)
![]() .
.
в) ![]() ;
;
2.
Выполните действия ![]() .
.
3. Найдите значение выражения х + 2,6, если х = –1,47;
![]() ;
х = –18;
;
х = –18; ![]() .
.
4. Сколько решений имеет уравнение |х + 2| = –5?
Вариант II.
1. Выполните сложение:
а) 257 + (–314); б)
–0,28 + (–0,18); в) –6 + ![]() ;
;
г) ![]() ; д)
; д)
![]() .
.
2. Выполните
действия ![]() .
.
3. Найдите значение выражения у + (–4,2), если у = 1,83;
у = ![]() ; у = 16; у
=
; у = 16; у
= ![]() .
.
4. Сколько решений имеет уравнение |у – 9| = –6?
Домашнее задание: решить № 1081 (м – р), № 1082, № 1086.
Урок 2
Цели: упражнять учащихся в вычитании отрицательных чисел; научить находить длину отрезка на координатной прямой; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Повторить правила сложения отрицательных чисел и сложения чисел с разными знаками. Привести примеры.
2. Решить устно № 1098 (а; б; г) и 1101 (в; г).
3. Решить № 1104, записывая на доске приведенные учащимися примеры.
4. Двое учащихся на доске выполняют упражнения из домашнего задания: 1) № 1109 (а – з); 2) № 1116.
Решение.
30 % = 0,3.
Пусть в альбоме было х российских марок, тогда иностранных марок в альбоме было 0,3х. Всего в альбоме 1105 марок.
х + 0,3х = 1105
1,3х = 1105
х = 1105 : 1,3 = 11050 : 13 = 850
х = 850.
В альбоме было 850 российских марок, а иностранных 1105 – 850 = 255 (марок).
Ответ: 255 марок, 850 марок.
II. Выполнение упражнений.
1. Решить № 1091 (к; л; р; н; п) самостоятельно с проверкой; 1091 (о; с; т) решить на доске и в тетрадях.
Решение.
к) –7,62 – (–7,62) = –7,62 +7,62 = 0;
л) –0,21 – 0 = –0,21 + 0 = –0,21;
р) ![]() ;
;
н) ![]() ;
;
п) ![]() ;
;
о) ![]() ;
;
с) ![]() ;
;
т) ![]()
![]() .
.
2. Решить устно № 1094.
3. Решить № 1092 (а; в) на доске и в тетрадях, 1092 (б) – самостоятельно.
Решение.
а) –2 + х = 4,3 б) 8,1 + у = –6 в) 5 – х = 1,7
х = 4,3 – (–2) у = –6 – 8,1 х = 5 – 1,7
х = 4,3 + 2 у = –6 + (–8,1) х = 3,3.
х = 6,3. у = –14,1.
Ответ: х = 6,3. Ответ: у = –14,1. Ответ: х = 3,3.
4. Решить № 1088, используя демонстрационный термометр.
5. Решить № 1096 (а; в; д) на доске и в тетрадях, № 1096 (б; г; е) – самостоятельно.
а) (62 – 28) – 40 = 34 – 40 = 34 + (–40) = –6;
б) –50 + (37 + 30) = –50 + 67 = 17;
в) –6 – (–8 –20) = –6 – (–28) =–6 + 28 = 22;
г) –7 –(–12 + 13) = –7 –1 = –7 + (–1) = –8;
д) 4,1 – (–1,8 + 2,5) = 4,1 – 0,7 = 3,4;
е) (–3,2 + 60) – 0,8 = 56,8 – 0,8 = 56.
III. Изучение нового материала.
1. Разобрать решение задачи на с. 185 учебника.
2. Правило: Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.
3. Решить задачу № 1097 (а; в; д).
а) 8 – 2 = 6; в) 6 – (-1) = 6 + 1 =7; д) 3,2 – (–4,7) = 3,2 + 4,7 = 7,9.
IV. Повторение ранее изученного материала.
1. Решить задачу № 1107 (2) самостоятельно.
2. Решить № 1103.
V. Итог урока.
1. Ответить на вопросы на с. 185 учебника.
2. Найти расстояние между точками:
а) А (–5,2) и В (–1,8);
б) С ![]() и Д
и Д ![]() .
.
3. Решить уравнение:
а) 2,4 + х = –2,8;
б) 18,24 – у = 20.
Домашнее задание: выучить правила п. 34; решить № 1109 (ж – к), 1111, 1113 (в; г), 1115.
Прочитать исторический материал на с. 190.
Урок 3
Цели: закрепить изученный материал, вырабатывать навыки сложения чисел; проверить степень усвоения учащимися материала; подготовиться к контрольной работе.
Ход урока
I. Устная работа.
1. Решить устно № 1098 (в; д; е) и 1104.
2. Решить уравнения № 1103 (д; е) на доске.
3. Двое учащихся работают у доски:
1) один ученик решает задачу № 1106;
2) второй ученик решает задачу № 1115.
II. Выполнение упражнений.
1. Решить № 1090 (г; д; е) устно.
2. Решить № 1095 с комментированием на месте.
3. Решить № 1092 (д; г; е) на доске и в тетрадях.
Решение.
г) ![]() д)
д) ![]() е)
е) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
. ![]()
![]()
Ответ: ![]()
![]() .
. ![]()
Ответ:
![]()
![]() .
.
Ответ:
![]() .
.
4. Решить № 1089 (устно).
5. Решить задачу № 1097 (г; е) на доске и в тетрадях, № 1097 (б) – самостоятельно.
6. Решить № 1096 (ж; и) самостоятельно, № 1096 (к; л; м) – на доске и в тетрадях.
Решение.
ж) ![]() ;
;
и) ![]() ;
;
к) ![]() ;
;
л) ![]() ;
;
м) ![]()
![]() .
.
III. Самостоятельная работа.
Вариант I.
1. Выполните вычитание:
а)7,5 – (–3,7); в)
![]() ;
;
б) –2,3 – 6,2; г)
![]() .
.
2. Решите уравнение:
а)7,8 – х =
9,3; б) у – (–17,85) = 12; в) ![]() .
.
3. Найдите расстояние между точками:
а) С (–6,1)
и Д (3,4); б) Е ![]() и F
и F ![]() .
.
4. Решите уравнение |х – 2| = 4.
5. Дополнительно: решить № 1108 (1).
Вариант II.
1. Выполните вычитание:
а) –25,7 – 4,6; в)
![]() ;
;
б) 6,3 – (–8,1); г)
![]() .
.
2. Решите уравнение:
а) х –
(–2,7) = 3,8; б) 16,37 + у = –30; в) ![]() .
.
3. Найдите расстояние между точками:
а) Е (–8,2)
и F (6,6); б) М ![]() и N
и N ![]() .
.
4. Решите уравнение |х – 3| = 6.
5. Дополнительно: решить № 1108 (2).
Домашнее задание: подготовиться к контрольной работе, выучить правила п. 31–34; решить № 1109 (л – р), № 1112, 1113 (д; е), 1110.
Контрольная работа № 10 (1 час)
Цели: проверить знания, умения и навыки учащихся по изученному материалу; узнать степень усвоения ими сложения и вычитания положительных и отрицательных чисел.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение работы по вариантам.
Вариант I.
1. Выполните действия:
а) –3,8 – 5,7; в)
3,9 – 8,4; д) ![]() ;
;
б) –8,4 + 3,7; г)
–2,9 + 7,3; е) ![]() .
.
2. Найдите значение выражения:
![]() .
.
3. Решите уравнение:
а) х + 3,12
= –5,43; б) ![]() .
.
4. Найдите расстояние между точками А (–2,8) и В (3,7) на координатной прямой.
5. Напишите все целые значения п, если 4 < |п| < 7.
Вариант II.
1. Выполните действия:
а) –3,5 + 8,1; в)
–7,5 + 2,8; д) ![]() ;
;
б) –2,9 – 3,6; г)
4,5 – 8,3; е) ![]() .
.
2. Найдите значение выражения:
![]()
3. Решите уравнение:
а) 5,23 + х
= –7,24; б) ![]() .
.
4. Найдите расстояние между точками С (–4,7) и Д (–0,8) на координатной прямой.
5. Напишите все целые значения у, если 2 < |у| < 7.
Вариант III.
1. Выполните действия:
а)
–7,5 + 4,2; в) –4,7 + 2,9; д) ![]() ;
;
б) –3,7 – 5,8; г)
3,7 – 5,6; е) ![]() .
.
2. Найдите значение выражения:
![]() .
.
3. Решите уравнение:
а)
4,31 – х = 5,18; б) ![]() .
.
4. Найдите расстояние между точками М (–7,1) и N (4,2) на координатной прямой.
5. Напишите все целые значения m, если 4 < |m| < 8.
Вариант IV.
1. Выполните действия:
а) –7,4 – 2,9; в)
8,7 – 9,4; д) ![]() ;
;
б) –4,1 + 2,8; г)
–3,7 + 5,6; е) ![]() .
.
2. Найдите значение выражения:
![]() .
.
3. Решите уравнение:
а) х – 3,22
= –8,19; б) ![]() .
.
4. Найдите расстояние между точками К (–0,2) и Р (–3,1) на координатной прямой.
5. Напишите все целые значения z, если 5 < |z| < 9.
Домашнее задание: повторить изученный материал.
УМНОЖЕНИЕ
Урок 1
Цели: ввести правило умножения положительных и отрицательных чисел и научить применять это правило при выполнении упражнений; развивать логическое мышление учащихся.
Ход урока
I. Анализ контрольной работы.
1. Сообщить результаты контрольной работы и указать ошибки учащихся.
2. Выполнить задания, вызвавшие затруднения у учащихся.
II. Устная работа.
1. Решить устно № 1134 (а) и 1135.
2. Решить устно № 1137. Привести свои примеры.
III. Объяснение нового материала.
1. Разобрать решение задачи 1 на странице 190 учебника.
0,4 · 200 = 80 (м2). Расход ткани изменился на 80 м2.
2. Разобрать решение задачи 2 (с. 190–191).
Вывод: расход ткани на костюмы за день изменился на –80 м2.
Значит, –0,4 · 200 = – (0,4 · 200) = –80. Считают, что и
200 · (–0,4) = – (200 · 0,4) = –80.
3. Правило умножения двух чисел с разными знаками.
Примеры. –2 · 6 = – (2 · 6) = –12;
–6 · 2 = – (6 · 2) = –12;
–1,5 · 0,3 = – (1,5 · 0,3) = –0,45;
7,8 · (–0,1) = – (7,8 · 0,1) = –0,78.
4. Вывод: при изменении знака любого множителя знак произведения меняется, а его модуль остается тем же.
5. Если же меняются знаки обоих множителей, то произведение меняет знак дважды и в результате знак произведения не меняется:
8 · 1,1 = 8,8; –8 · 1,1 = –8,8; (–8) · (–1,1) = – (–8,8) = 8,8.
Видим, что произведение отрицательных чисел есть число положительное.
6. Правило умножения двух отрицательных чисел.
Примеры. –7,5 · (–0,2) = 1,50 = 1,5; –19 · (–0,3) = 5,7;
–5,8 · (–6) = 34,8.
IV. Закрепление изученного материала.
1. Решить № 1118 и 1119 устно.
2. Решить № 1121 (а; б; в; г; е; ж; з; и; м) устно, № 1121 ( д; к; л; н; о) – на доске и в тетрадях.
3. Решить № 1123 (а; б; в) на доске и в тетрадях.
Решение.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
4. Решить № 1129 (а; б) самостоятельно, № 1129 (в; г) – на доске и в тетрадях.
Решение.
а) ![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
5. Самостоятельно решить № 1140 (а; б).
V. Итог урока.
1. Повторить правила, привести свои примеры.
2. Выполнить умножение:
а) 64 · (–10); б) –2,8 · 3; в) –4,7 · (–5);
г) 6,9 · (–0,1);
д) ![]() ; е)
; е) ![]() .
.
Домашнее задание: выучить правила п. 35; решить № 1143 (а – г), № 1144 (а; б; в), № 1148.
Урок 2
Цели: способствовать выработке навыков умножения чисел с разными знаками и умножения отрицательных чисел; закрепить правила умножения десятичных и обыкновенных дробей.
Ход урока
I. Устная работа.
1. Повторить правила умножения чисел с разными знаками и умножения отрицательных чисел. Привести свои примеры.
2. Проверить по тетрадям выполнение учащимися домашнего задания.
3. Решить № 1134 (б) и № 1138 устно.
II. Выполнение упражнений.
1. Решить задачу № 1120, используя рисунок 89 учебника.
2. Решить устно № 1124.
3. Решить № 1121 (п; р; с; т) на доске и в тетрадях.
4. Решить № 1128 (а; б) устно. Учащиеся формулируют правила умножения чисел.
5. Решить № 1123 (г; д; е) на доске и в тетрадях.
Решение.
г) ![]() ; д)
; д) ![]() ;
;
е) ![]() .
.
6. Решить № 1126 на доске и в тетрадях.
7. Объяснить решение № 1127 (а).
Решение.
а) х + 4 + х + 4 + х + 4 = 3х + 12 = 3 · 9,1 + 12 = 27,3 + 12 = 39,3.
8. Решить № 1129 (д) на доске; № 1129 (ж) самостоятельно.
Решение.
д) ![]()
![]() ;
;
ж) ![]() .
.
9. Решить № 1130 (а; б) на доске и в тетрадях.
Решение.
а) ![]() ;
;
б) ![]() .
.
10. Повторение материала:
1) Решить задачу № 1141 (а; б).
2) Решить уравнения № 1140 (в; г) самостоятельно с проверкой.
III. Итог урока.
1. Повторить правила умножения чисел.
2. Решить № 1128 (в; г) устно.
3. Решить № 1125 письменно и сделать вывод.
Домашнее задание: выучить правила п. 35; решить № 1143 (д – з), № 1144 (г; д; е), № 1145 (а – в), № 1147.
Урок 3
Цели: обобщить и закрепить изученный материал в ходе выполнения упражнений; проверить знания и умения учащихся; развивать навыки самостоятельной работы.
Ход урока
I. Повторение изученного материала.
1. Повторить правила сложения, вычитания и умножения чисел с разными знаками и отрицательных чисел. Привести свои примеры.
2. Решить № 1132 (а – г) устно.
3. Повторить определение модуля числа и решить № 1133.
4. Решить № 1136 устно. Привести свои примеры.
II. Тренировочные упражнения.
1. Решить № 1122 с комментированием на месте.
2. Решить № 1127 (б) на доске и в тетрадях.
Решение.
б) ![]()
![]() .
.
3. Решить № 1124 (устно), формулируя правила.
4. Решить № 1123 (ж; з; и) на доске и в тетрадях.
Решение.
ж) ![]() ;
;
з) ![]() ;
;
и) ![]() .
.
5. Решить № 1131 (а) устно.
6. Решить № 1130 (г; д; е) на доске и в тетрадях.
Решение.
г) ![]()
![]() ;
;
д) ![]()
![]() ;
;
е) ![]()
![]() .
.
7. Повторение ранее изученного материала.
Решить № 1141 (г; д) на доске и в тетрадях.
Решение.
г) Пусть высота сосны равна х м, тогда высота ели 0,4х м.
х – 0,4х = 1,2
0,6 х = 1,2
х = 1,2 : 0,6 = 12 : 6
х = 2.
Высота сосны 2 м, высота ели 2 · 0,4 = 0,8 (м).
Ответ: 2 м; 0,8 м.
III. Самостоятельная работа.
Вариант I.
1. Выполните умножение:
а) –59 · (–11);
б) –5,4 · 0,9; в) ![]() .
.
2. Выполните действия:
![]() .
.
3. Найдите
значение выражения ![]() , если а =
–1;
, если а =
–1; ![]() ; а = –
0,45.
; а = –
0,45.
4. Дополнительно: решить № 1142 (1).
Вариант II.
1. Выполните умножение:
а)
49 · (–14); б) –4,2 · (–0,7); в) ![]() .
.
2. Выполните действия:
![]()
3.
Найдите значение выражения ![]() ,
если п = –1;
,
если п = –1; ![]() ; п = –0,84.
; п = –0,84.
4. Дополнительно: решить № 1142 (2).
Домашнее задание: № 1143 (и – м), № 1145 (г – е), № 1146.
ДЕЛЕНИЕ
Урок 1
Цели: ввести правила деления отрицательных чисел и деления чисел с разными знаками; научить применять эти правила при выполнении упражнений.
Ход урока
I. Анализ самостоятельной работы.
1. Указать ошибки, сделанные учащимися при выполнении работы.
2. Решить на доске упражнения, вызвавшие затруднения у учащихся.
II. Устная работа.
1. Решить № 1164 (а; б; в; д) устно; повторить правила умножения чисел.
2. Решить № 1162 устно.
III. Коллективная поисковая работа по изучению материала.
1. Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел: по данному произведению и одному из множителей находят второй множитель.
Привести свои примеры.
Пишут: –12 : (–4) = 12 : 4 = 3; –4,5 : (–1,5) = 45 : 15 = 3;
![]() .
.
2. Сформулировать правило деления отрицательного числа на отрицательное число. Привести свои примеры.
3. В ходе рассуждений и поисковой работы подвести учащихся к правилу деления чисел с разными знаками:
–24 : 4 = –6; 24 : (–4) = –6.
4. Сформулировать правило деления чисел с разными знаками. Привести свои примеры. Важно подчеркнуть, что обычно вначале определяют и записывают знак частного, а потом уже находят модуль частного.
Примеры. 3,6 : (–3) = – (3,6 : 3) = –1,2;
![]() .
.
5. При делении нуля на любое число, не равное нулю, получается нуль.
0 : (–17) = 0; ![]() ; 0 : (–5,8) = 0.
; 0 : (–5,8) = 0.
6. Делить на нуль нельзя!
IV. Закрепление изученного материала.
1. Решить № 1149 устно.
2. Решить № 1150 (а – в) на доске и в тетрадях; № 1150 (г; д) – самостоятельно.
3. Решить № 1158 (а; б) на доске и в тетрадях, № 1158 (в; г) – с комментированием на месте.
Решение.
а) ![]() ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г) ![]() .
.
4. Решить № 1152 (б; в) на доске и в тетрадях, № 1152 (а; д; е) –самостоятельно с проверкой.
Решение.
а) –4 · (–5) – (–30) : 6 = 20 – (–5) = 20 + 5 = 25;
б) 15 : (–15) – (–24) : 8 = –1 – (–3) = –1 + 3 = 2;
в) –8 · (–3 + 12) : 36 + 2 = –8 · 9 : 36 + 2 = –72 : 36 + 2= –2 + 2 = 0;
д) (–8 + 32) : (–6) – 7 = 24 : (–6) – 7 = –4 + (–7) = –11;
е) –21 + (–3 – 4 + 5) : (–2) = –21 + (–2) : (–2) = –21 + 1 = –20.
5. Решить № 1154 (объясняет решение учитель).
6. Повторение ранее изученного материала. Решить № 1166 (б) самостоятельно с проверкой.
V. Итог урока.
1. Сформулируйте правило деления отрицательного числа на отрицательное. Привести свои примеры.
2. Сформулируйте правило деления чисел, имеющих разные знаки. Привести свои примеры.
3. Чему равно частное 0 : а, где а ? 0?
4. Выполните деление (устно):
а) –55 : 5; в) –10 : (–2,5);
б) 3,6 : (–9); г)
![]() .
.
Домашнее задание: выучить правила п. 36; решить № 1172 (а – г), № 1174 (а; б), № 1176.
Урок 2
Цели: научить учащихся применять правила деления и умножения чисел при решении примеров и задач; закрепить правила деления и умножения обыкновенных дробей и десятичных дробей; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
1. Повторить правила умножения и деления отрицательных чисел и чисел с разными знаками. Привести свои примеры.
2. Повторить правило деления обыкновенных дробей. Решить № 1160 (б) устно.
3. Повторить правило умножения десятичных дробей. Решить № 1164 (г; е; ж) устно.
4. Решить № 1165 устно.
Решение.
9 = 3 · 3 = (–3) · (–3); 16 = 4 · 4 = (–4) · (–4);
25 = 5 · 5 = (–5) · (–5).
II. Выполнение упражнений.
1. Решить № 1150 (е; ж; и) самостоятельно, № 1150 (к; л; м) – на доске и в тетрадях.
2. Решить № 1158 (и; к) на доске и в тетрадях.
и) 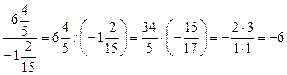 ;
;
к) 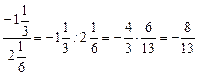 .
.
3. Решить № 1151 (а; б; д; е) (объясняет учитель), № 1151 (в; г; ж) – с комментированием на месте.
Решение.
а) ![]() ; г)
; г)
![]() ;
;
б) ![]() ; д)
; д)
![]() ;
;
в) ![]() ; е)
; е) ![]() ;
;
ж) ![]() .
.
4. Решить уравнения № 1156 (а; б) на доске и в тетрадях.
Решение.
а) ![]() ;
; ![]() ;
; ![]() ; х = –1,5;
; х = –1,5;
б) ![]() ;
; ![]() ;
; ![]() .
.
5. Найти неизвестный член пропорции, решить № 1159 (а; б). Повторить определение пропорции и основное свойство пропорции.
Решение.
а) ![]() ;
; ![]() ;
; ![]()
![]() . Ответ: х
= –2,9.
. Ответ: х
= –2,9.
б) ![]() ;
; ![]()
![]() ; х = 52,5.
Ответ: х = 52,5.
; х = 52,5.
Ответ: х = 52,5.
6. Решить № 1152 (г; ж; з) самостоятельно. Три ученика самостоятельно решают на доске, остальные в тетрадях, а затем проверяется решение.
Решение.
г) 2,3 · (–6 – 4) : 5 = 2,3 · (–10) : 5 = –23 : 5 = –4,6;
ж) –6 · 4 – 64 : (–3,3 + 1,7) = –24 – 64 : (–1,6) = –24 + 40 = 16;
з) (–6 + 6,4 –10) : (–8) · (–3) = –9,6 : (–8) · (–3) = 1,2 · (–3) = –3,6.
7. Повторение ранее изученного материала.
Решить № 1168 (а; б).
III. Итог урока.
1. Повторить правила умножения и деления чисел, правила знаков.
2. Решить № 1155 (а; б) устно.
Домашнее задание: повторить правила п. 35 и 36; решить № 1172 (д – з), № 1174 (в; г), № 1173 (а; б), № 1177 (а).
Урок 3
Цели: повторить и закрепить изученный материал, способствовать выработке навыков и умений решения примеров и задач и применения при этом изученных правил; проверить знания учащихся в ходе самостоятельной работы.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Двое учащихся на доске выполняют номера из домашнего задания № 1174 (в; г) и № 1177 (а).
2. Повторить правила сложения, вычитания, умножения и деления отрицательных чисел и чисел с разными знаками. Приводить свои примеры (учитель записывает их на доске).
3. Решить устно № 1161 и № 1164 (з; и).
4. Решить № 1170 устно, используя координатную прямую.
II. Тренировочные упражнения.
1. Решить № 1151 (к – р). Учащиеся по одному вызываются к доске для решения примеров, остальные самостоятельно решают и потом сверяют свое решение с решением на доске.
Решение.
к) ![]() ;
;
л) ![]() ;
;
м) ![]() ;
;
н) ![]() ;
;
о) ![]() ;
;
п) ![]() ;
;
р) ![]()
2. Решить № 1154 устно.
3. Решить № 1153 на доске и в тетрадях.
Решение.
а) (3m + 6m) : 9, если m = –12; –5,96;
9m : 9 = m.
Ответ: –12; –5,96.
б) (5,2а – 5,2 в) : 5,2 = 5,2 (а – в) : 5,2 = а – в = –27 – (–3,64) =
= –27 + 3,64 = –23,36.
4. Решить № 1158 (д).
Решение.
д)
![]() .
.
5. Решить уравнение № 1159 (в) на доске и в тетрадях, № 1159 (г) самостоятельно.
Решение.
в) 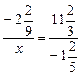 ;
; ![]()
![]() ;
; ![]() .
.
г) 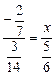 ;
; ![]() ;
;
![]() .
.
6. Решить уравнения № 1155 (в; г) с комментированием на месте.
Решение.
в) –0,1у =
33 г) ![]()
у = 33 : (–0,1)
![]()
у = –330. х = –3.
Ответ: у = –330. Ответ: х = –3.
III. Самостоятельная работа.
Вариант I.
1. Выполните деление:
а) –29,682 : 9,7;
б) ![]() ; в)
; в) ![]() .
.
2. Решите уравнение:
а) –4,3х =
14,62; б) ![]() .
.
3. Найдите значение выражения:
![]() .
.
4. Сколько целых решений имеет неравенство |х| < 50?
Вариант II.
1. Выполните деление:
а) 23,316 :
(–5,8); б) –0,6 : ![]() ; в)
; в) ![]() .
.
2. Решить уравнение:
а) 1,7у =
–14,11; б) ![]() .
.
3. Найдите значение выражения:
![]() .
.
4. Сколько целых решений имеет неравенство |х| < 30?
Домашнее задание: решить № 1172 (и – м), № 1174 (д; е), № 1173 (в; г; д; е), № 1175, № 1177 (б).
РАЦИОНАЛЬНЫЕ ЧИСЛА
Урок 1
Цели: ввести понятие рациональных чисел, показать запись рациональных чисел либо в виде десятичной дроби, либо в виде периодической дроби.
Ход урока
I. Анализ самостоятельной работы.
II. Устная работа.
1. Вспомнить правило деления числа на обыкновенную дробь и решить № 1185 (б) устно.
2. Решить устно № 1187 (а – г), № 1191 и № 1192.
III. Объяснение нового материала.
1. Определение рационального числа.
2. Любое целое
число а является рациональным числом, так как его можно записать в виде ![]() .
.
Например, ![]() ;
; ![]() ;
; ![]() .
.
3. Запись любого рационального числа.
4. Сумма, разность и произведение рациональных чисел тоже рациональные числа.
5. Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.
6. Выражение обыкновенных дробей в виде десятичных дробей. Не все обыкновенные дроби можно представить в виде десятичной дроби. Привести примеры.
7. Понятие периодической дроби; запись периодической дроби: 0,(3); 0,(45).
8. Любое рациональное число можно записать либо в виде десятичной дроби (в частности, целого числа), либо в виде периодической дроби.
IV. Закрепление изученного материала.
1. Решить № 1178 на доске и в тетрадях.
2. Решить № 1179 (а) на доске и в тетрадях.
Решение.
![]() ;
;
![]() ;
;
![]() ;
;
0,5 – 3,1 = –2,6.
3. Решить № 1181 устно.
4. Решить № 1180 (взять первые четыре числа) на доске и в тетрадях.
5. Решить № 1182 (а; в; д) на доске и в тетрадях.
6. Повторение изученного материала. Решить № 1195 (1; 2) самостоятельно с проверкой решения.
V. Итог урока.
1. Ответить на вопросы к п. 37 на с. 203 учебника.
2. Покажите, что
числа 0,85; –3,4; ![]() ;
; ![]() ; 12 являются
рациональными.
; 12 являются
рациональными.
Домашнее задание: изучить п. 37; решить № 1196 (а), № 1197 (а), № 1199, № 1200 (а).
Урок 2
Цели: закрепить изученный материал, способствовать развитию навыков и умений в представлении обыкновенных дробей в виде приближенного значения десятичной дроби; повторить правила округления десятичных дробей.
Ход урока
I. Устная работа.
1. Решить № 1185 (а) и № 1186 (устно).
2. Решить № 1190 с записью действий на доске. Повторить правила деления отрицательных чисел и деления чисел с разными знаками.
3. Как узнать, какой десятичной дробью может быть выражено рациональное число? Полезно запомнить такое правило:
Если в знаменателе обыкновенной дроби нет простых множителей, кроме 2 и 5, то она записывается конечной десятичной дробью.
Если в знаменателе несократимой обыкновенной дроби имеются простые множители, отличные от 2 и 5, то эту дробь можно выразить только бесконечной десятичной дробью.
4. Решить № 1193 устно, используя предыдущее правило.
II. Выполнение упражнений.
1. Решить № 1179 (б; в) на доске и в тетрадях, вызывая к доске по одному ученику для решения задания.
Решение.
б) ![]() ;
; ![]() ;
;
![]() ;
;
![]() .
.
в) ![]() ; 0,27 : 0,9 = 2,7
: 9 =0,3 =
; 0,27 : 0,9 = 2,7
: 9 =0,3 = ![]() ;
;
–0,26 : (–0,13) =
26 : 13 = ![]() ;
; ![]() .
.
2. Решить № 1180 (5-е – 8-е числа). Вызвать к доске сразу четырех учеников, остальные учащиеся решают самостоятельно, а потом проверяется решение.
3. Решить № 1181 устно.
4. Повторить правило округления десятичных дробей и решить № 1184.
5. Решить № 1182 (б; г; е) на доске и в тетрадях.
6. Выразить числа ![]() ;
; ![]() и
и ![]() в виде
приближенного значения десятичной дроби до тысячных. (Учащиеся решают
самостоятельно.)
в виде
приближенного значения десятичной дроби до тысячных. (Учащиеся решают
самостоятельно.)
7. Повторение ранее изученного материала. Решить № 1195 самостоятельно по вариантам:
Вариант I Вариант II
№ 1195 (3; 5). № 1195 (4; 6).
Учитель просматривает и оценивает решения учеников.
Решение.
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() .
.
III. Итог урока.
1. Ответить на вопросы п. 37 на с. 203 учебника.
2. Когда обыкновенная дробь записывается конечной десятичной дробью?
3. Когда несократимую обыкновенную дробь нельзя записать конечной десятичной дробью? Какой десятичной дробью можно выразить данную обыкновенную дробь?
4. Не выполняя деления, скажите, конечной или бесконечной десятичной дробью можно выразить данную обыкновенную дробь:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() ; и)
; и) ![]() ; к)
; к) ![]() ; м)
; м) ![]() .
.
Домашнее задание: решить № 1196 (б; в), № 1198, № 1197 (б), № 1200 (б).
СВОЙСТВА ДЕЙСТВИЙ С РАЦ ЧИСЛАМИ
Урок 1
Цели: повторить переместительный и сочетательный законы сложения и показать на примерах их применение для рациональных чисел; развивать логическое мышление учащихся.
Ход урока
I. Повторение ранее изученного материала.
1. Решить № 1215 (а) устно, повторяя правила.
2. Повторить понятие модуля числа и решить № 1217 устно.
3. Решить № 1218 (а; б; в) устно.
4. Повторить свойства сложения – переместительный и сочетательный. Привести свои примеры.
II. Изучение нового материала.
1. Сложение рациональных чисел обладает переместительным и сочетательным свойствами:
а + в = в + а; а + (в + с) = (а + в) + с.
2. Переместительный и сочетательный законы сложения часто облегчают вычисление суммы.
Например, 3,5 + (–2,7) + 4,6 + (–5,8) = (3,5 + 4,6) + (–2,7 + (–5,8)) =
= 8,1 + (–8,5) = –0,4.
Здесь мы сначала отдельно сложили положительные слагаемые и отрицательные слагаемые.
3. Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю:
а + 0 = а; а + (–а) = 0.
Пример.
2,9 + 3,7 + (–4,2) + (–2,9) + 4,2 = (2,9 + (–2,9)) + 3,7 + (–4,2 + 4,2) = = 0 + 3,7 + 0 = 3,7.
Здесь мы сначала сгруппировали противоположные слагаемые, сумма которых равна 0.
III. Закрепление изученного материала.
1. Решить № 1201 (а) устно.
2. Решить № 1204 (а; б) с комментированием на месте.
3. Решить № 1203 (а; б) на доске и в тетрадях.
Решение.
а) –17 + 83 + 49 – 27 – 36 + 28 = (–17 – 27 – 36) + (83 + 49 + 28) =
= –80 + 160 = 80;
б) 2,15 + (–3,81) – 5,76 + 3,27 + 5,48 – 4,33 = (2,15 + 3,27 + 5,48) +
+ (–3,81 – 5,76 – 4,33) = 10,9 + (–13,9) = –3.
4. Решить № 1205 (а; б) с комментированием на месте.
5. Решить № 1206 (а; в).
Решение.
а) ![]() ;
;
в) ![]()
![]()
6. Повторение материала:
а) Решить № 1221 (а; г) самостоятельно; б) решить № 1223 (устно).
7. Вычислите наиболее простым способом (самостоятельно):
а) 6,3 + (–3,7) + 2,6; г) 1,7 + (–2,6) + (–1,7) + 2,6;
б) (–9,2) + 5,4 + (–3,2); д) (–4,9) + 5,5 + 4,9 + (–5,5);
в) 8,2 + (–2,9) + 1,2; е) 1,8 + (–6,2) + (–4,1) + (–1,8) + 6,2.
IV. Итог урока.
1. Перечислите свойства сложения рациональных чисел. Приведите свои примеры.
2. Вычислите:
а) – 6,8 + 4,23 + (– 17,21) + (– 4,23) + 6,8;
б) 36 + (– 52) + (– 173) + 79 + 185 + (– 85).
Домашнее задание: изучить п. 38 (с. 207–208); решить № 1226 (а; б; в), № 1230, № 1233 (а).
Урок 2
Цели: повторить свойства умножения и научить применять их к рациональным числам; закреплять знания и умения учащихся при выполнении действий с рациональными числами.
Ход урока
I. Устная работа.
1. Решить № 1215 (б) и 1216 (а) устно.
2. Решить задачу № 1220 (а) по рисунку 91 (а) учебника.
3. Решить устно № 1219 (а; б).
4. Повторить переместительное, сочетательное свойства умножения чисел. Привести свои примеры.
II. Изучение нового материала.
1. Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами:
а·в = в·а; а (вс) = (ав) с.
2. Умножение на 1 не изменяет рационального числа, а произведение числа на обратное ему число равно 1:
а·1 = а; а·![]() = 1, если а
= 1, если а
![]() 0.
0.
III. Закрепление изученного материала.
1. Решить № 1207 (а) устно.
2. Решить № 1208 (а) самостоятельно.
3. Решить № 1209 (а; б; г) на доске и в тетрадях.
Решение.
а) ![]() ;
;
б) ![]()
![]() ;
;
г) ![]()
![]() .
.
4. Решить № 1210 и № 1211 устно.
5. Решить № 1204 (в; г) самостоятельно, проверить ответы.
6. Решить № 1203 (в; г) на доске и в тетрадях.
Решение.
в) ![]()
![]() ;
;
г) ![]()
![]() .
.
7. Решить № 1205 (а; б) (объясняет учитель):
Решение.
а) х + 8 – х – 22 = (х – х) + (8 – 22) = – 14;
б) – х – а + 12 + а – 12 = – х + (– а + а) + (12 – 12) = – х.
8. Повторение изученного материала:
1) Решить № 1221 (д – з) самостоятельно с проверкой.
2) Решить № 1222 с комментированием на месте.
IV. Итог урока.
1. Перечислите свойства сложения и умножения рациональных чисел.
2. Выполните умножение, выбрав удобный порядок вычислений:
а) ![]() ;
;
б) ![]() .
.
Домашнее задание: выучить правила п. 38; решить № 1226 (г; д), № 1227 (а; б; в), № 1228 (а; б), № 1231; прочитать исторический материал на с. 213–214 учебника.
Урок 3
Цели: повторить распределительное свойство умножения относительно сложения и вычитания и научить применять это свойство при действиях с рациональными числами; повторить весь изученный материал и подготовить учащихся к контрольной работе.
Ход урока
I. Актуализация опорных знаний учащихся.
1. Проверить по тетрадям выполнение учащимися домашнего задания.
2. Повторить свойства действий с рациональными числами. Привести свои примеры.
3. Решить устно № 1250 (а; б; в; г) и № 1251 (а).
4. Решить № 1218 (г; д; е) устно.
II. Объяснение нового материала.
1. Умножение числа на нуль дает в произведении нуль:
а · 0 = 0.
2. Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю:
если а·в =
0, то либо а = 0, либо в = 0 (может случиться, что и
а = 0, и в = 0).
3. Использовав это свойство, решить уравнение:
а) 2,3 (58 – х) = 0; так как 2,3 не равно 0, то 58 – х = 0; х = 58.
Ответ: х = 58.
б) (11,7 + 3х) · (– 6) = 0; так как – 6 не равно 0, то
11,7 + 3х = 0;
3х = 0 – 11,7
3х = – 11,7
х = – 11,7 : 3
х = – 3,9.
Ответ: х = – 3,9.
в) (8х + 4) · (5х – 10) = 0.
8х + 4 = 0 или 5х – 10 = 0
8х = – 4 или 5х = 10
х = – 4 : 8 х = 10 : 5
х = – 0,5 х = 2.
Ответ: х = – 0,5; х = 2.
4. Умножение рациональных чисел обладает и распределительным свойством относительно сложения и относительно вычитания:
(а + в) · с = ас + вс; (а – в) · с = са – вс.
5. Решить № 1213 (а).
III. Закрепление изученного материала.
1. Решить № 1212 на доске и в тетрадях.
2. Решить № 1214 на доске и в тетрадях.
Решение.
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]() .
.
3. Решить № 1210 (устно), повторив еще раз сделанный ранее вывод.
4. Решить № 1206 (б; г) на доске и в тетрадях.
5. Решить № 1205 (в; г) с комментированием на месте.
6. Повторение ранее изученного материала. Решить задачу № 1224 (1).
Домашнее задание: повторить правила п. 35–38; подготовиться к контрольной работе; решить № 1226 (е), № 1228 (в; г), № 1229 (а – г), № 1294, 1298.
Контрольная работа № 11 (1 час)
Цели: выявить степень усвоения учащимися изученного материала; проверить знания, умения и навыки учащихся по изученному материалу.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение работы по вариантам.
Вариант I.
1. Выполните действие:
а) 1,6 · (– 4,5); в)
![]() ;
;
б) – 135,2 :
(–6,5); г) ![]() .
.
2. Выполните действия:
(– 9,18 : 3,4 – 3,7) · 2,1 + 2,04.
3. Выразите числа ![]() и
и ![]() в виде
приближенного значения десятичной дроби до сотых.
в виде
приближенного значения десятичной дроби до сотых.
4. Найдите значение выражения:
![]() .
.
5. Найдите корни уравнения (6х – 9) (4х + 0,4) = 0.
Вариант II.
1. Выполните действие:
а) – 3,8 · 1,5; в)
![]() ;
;
б) – 433,62 : (–
5,4); г) ![]() .
.
2. Выполните действия:
(– 3,9 · 2,8 + 26,6) : (– 3,2) – 2,1.
3.
Выразите числа ![]() и
и ![]() в
виде приближенного значения десятичной дроби до сотых.
в
виде приближенного значения десятичной дроби до сотых.
4.
Найдите значение выражения: ![]() .
.
5. Найдите корни уравнения (– 4х – 3) (3х + 0,6) = 0.
Вариант III.
1. Выполните действие:
а) 4,6 · (– 2,5); в)
![]() ;
;
б) – 25,344 : (–
3,6); г) ![]() .
.
2. Выполните действия:
(15,54 : (– 4,2) – 2,5) · 1,4 + 1,08.
3.
Выразите числа ![]() и
и ![]() в
виде приближенного значения десятичной дроби до сотых.
в
виде приближенного значения десятичной дроби до сотых.
4. Найдите значение выражения:
![]() .
.
5. Найдите корни уравнения (5у – 7) (2у – 0,4) = 0.
Вариант IV.
1. Выполните действие:
а)
– 5,8 · (– 6,5); в) ![]() ;
;
б)
37,26 : (– 9,2); г) ![]() .
.
2. Выполните действия:
(36,67 + 2,9 · (– 3,8)) : (– 5,7) + 2,5.
3.
Выразите числа ![]() и
и ![]() в
виде приближенного значения десятичной дроби до сотых.
в
виде приближенного значения десятичной дроби до сотых.
4. Найдите значение выражения:
![]() .
.
5. Найдите корни уравнения (15у – 24) (3у – 0,9) = 0.
Домашнее задание: повторить правила сложения, вычитания, умножения и деления чисел с разными знаками и отрицательных чисел.
РЕШЕНИЕ УРАВНЕНИЙ
РАСКРЫТИЕ СКОБОК
Урок 1
Цели: ввести правила раскрытия скобок на примерах и учить применять их при выполнении упражнений; развивать логическое мышление учащихся.
Ход урока
I. Анализ контрольной работы.
1. Указать ошибки, сделанные учащимися при выполнении работы.
2. Решить задания, вызвавшие затруднения у учащихся.
II. Объяснение нового материала.
1. Выражение а + (в + с) можно записать без скобок:
а + (в + с) = а + в + с. Эту операцию называют раскрытием скобок.
2. Разобрать решение примера 1 на с. 214 учебника. Сформулировать правило раскрытия скобок, перед которыми стоит знак «+» (плюс).
3. Решить пример 2 на с. 215.
4. Рассматривая решение выражения – (–9 + 5) = 9 + (–5) = 4, вывести правило: – (а + в) = – а – в.
5. Разобрать решение примера 3 и вывести правило раскрытия скобок, перед которыми стоит знак «–» (минус).
6. Раскрытие скобок и применение переместительного и сочетательного свойств сложения позволяют упрощать вычисления. Разобрать решение примеров 4 и 5 по учебнику на с. 215–216.
III. Закрепление изученного материала.
1. Решить № 1234 (а; б) на доске и в тетрадях.
2. Решить № 1235 на доске и в тетрадях, проговаривая правила раскрытия скобок и правила сложения рациональных чисел.
Решение.
а) – (– 5,75 + 3,24) = 5,75 – 3,24 = 2,51;
б) – (6,38 – 2,47) = – 6,38 + 2,47 = – 3,91;
в) ![]() .
.
3. Решить № 1236 (а – г) с комментированием на месте.
Решение.
а) 85 + (7,8 + 98) = 85 + 7,8 + 98 = 190,8;
б) (4,7 – 17) + 7,5 = 4,7 + 7,5 –17 = 12,2 – 17 = – 4,8;
в) 64 – (90 + 100) = 64 – 90 – 100 = 64 – 190 = –126;
г) – (80 – 16) + 84 = – 80 + 16 + 84 = – 80 +100 = 20.
4. Решить № 1237 (а; б; г) устно, № 1237 (в; д; е) – самостоятельно. Повторить правило сложения противоположных чисел:
а + (– а) = 0 или – а + а = 0.
Решение.
а) 5,4 + (3,7 – 5,4) = 5,4 + 3,7 – 5,4 = 3,7;
б) – 8,79 + (– 1,76 + 8,79) = – 8,79 – 1,76 + 8,79 = – 1,76;
в) 3,4 + (2,9 – 3,4 + 4,1) = 3,4 + 2,9 – 3,4 + 4,1 = 2,9 + 4,1 = 7;
г) (4,67 – 3,94) + (3,94 – 3,67) = 4,67 – 3,94 + 3,94 – 3,67 = 1;
д) 7,2 – (3,2 – 5,9) = 7,2 – 3,2 + 5,9 = 4 + 5,9 = 9,9;
е) (4,8 + 2,75) – (4,8 – 3,25) = 4,8 + 2,75 – 4,8 + 3,25 = 6.
5. Решить № 1238 (а; б; в; г; з; к) (объясняет решение учитель); № 1238 (д; е; ж; и; л) решить самостоятельно с проверкой.
6. Повторение ранее изученного материала:
1) Решить № 1252 (вызвать два человека к доске, остальные учащиеся решают самостоятельно в тетрадях).
Решение.
а) ![]() ;
; ![]() .
.
Ответ: х = 8.
б) ![]() ;
; ![]() .
.
Ответ: х = 3,9.
2) Решить № 1250 (а; б) устно; № 1250 (в; г) – самостоятельно с проверкой.
IV. Итог урока.
1. Ответить на вопросы на с. 216 учебника.
2. Раскройте скобки и найдите значение выражения:
а) 8,3 + (4,5 –
6,3); б) 4,1 – (5,6 – 6,9); в) ![]() .
.
Домашнее задание: выучить правила п. 39; решить № 1254 (а – в), № 1255 (а; б), № 1258 (а; б), № 1259 (а).
Урок 2
Цели: способствовать выработке навыков и умений раскрытия скобок; закрепить правила раскрытия скобок в ходе выполнения упражнений и правила сложения рациональных чисел.
Ход урока
I. Устная работа.
1. Решить № 1244 (а), № 1246 (а; б), № 1247 (а; б) и № 1248 (а – г) устно.
2. Повторить правила раскрытия скобок, привести свои примеры.
3. Повторить правила сложения рациональных чисел. Привести свои примеры.
II. Выполнение упражнений.
1. Решить № 1234 (в; г) на доске и в тетрадях.
2. Решить № 1236 (ж; з) на доске и в тетрадях.
Решение.
ж) а – (в – к – п) = а – в + к + п;
з) – (а – в + с) = – а + в – с.
3. Решить № 1239 (а – в) с комментированием на месте. Найти сумму и разность двух выражений.
Решение.
а) (–4 – m) + (m + 6,4) = – 4 – m + m + 6,4 = – 4 + 6,4 = 2,4;
(–4 – m) – (m + 6,4) = – 4 – m – m – 6,4 = – 10,4 – 2 m;
б) (1,1 + а) + (– 26 – а) = 1,1 + а – 26 – а = – 24,9;
(1,1 + а) – (– 26 – а) = 1,1 + а + 26 + а= 27,1 + 2а;
в) (а + 13) + (– 13 + в) = а + 13 – 13 + в = а + в;
(а + 13) – (– 13 + в) = а + 13 + 13 – в = 26 + а – в.
4. Решить № 1240 (а; б; г) самостоятельно с проверкой.
5. Решить № 1237 (ж; з; н; п) на доске и в тетрадях; № 1237 (и; м) – самостоятельно.
Решение.
ж) – 6,9 – (4,21 – 10,9) = – 6,9 – 4,21 + 10,9 = 4 – 4,21 = – 0,21;
з) (3,72 – 5,43) – (4,57 + 3,22) = 3,72 – 5,43 – 4,57 – 3,22 =
= 0,5 – 10 = – 9,5;
и) ![]() ;
;
м) ![]() ;
;
н) ![]() ;
;
п) ![]()
6. Решить № 1238 (м; н; о) с комментированием на месте.
Решение.
м) – а – (m – а + р) = – а – m + а – р = – m – р;
н) – (m – а) – (к + а) = – m + а – к – а = – m – к;
о) m + (к – а – m) = m + к – а – m = к – а.
7. Решить уравнение № 1241 (а; б; е) на доске и в тетрадях.
Решение.
а) 7,2 – (6,2 – х) = 2,2 б) – 5 + (а – 25) = – 4
7,2 – 6,2 + х = 2,2 – 5 + а – 25 = – 4
1 + х = 2,2 а – 30 = – 4
х = 2,2 – 1 а = – 4 + 30
х = 1,2. а = 26.
Ответ: х = 1,2. Ответ: а = 26.
е) ![]()
![]()
![]()
![]()
m = 0,8 – 0,4
m = 0,4.
Ответ: m = 0,4.
8. Решить № 1243 (а; б; в) самостоятельно. Вызывать по одному ученику к доске для решения примеров самостоятельно, потом проверяется решение.
Решение.
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
9. Повторение ранее изученного материала.
1) Решить № 1250 (д; е), повторив распределительный закон умножения.
Решение.
д) ![]() ;
;
е) ![]() .
.
2) Решить № 1245 (а; б) самостоятельно с проверкой.
III. Итог урока.
1. В выражении – 1,2 + а + 2,3 – 4,7 заключите в скобки три последних слагаемых, поставив перед скобками:
а) знак «+»; б) знак «–».
2. Решите уравнение 7,7 – (3,8 + х) = – 1,1.
Домашнее задание: изучить п. 39; решить № 1254 (г – е), № 1255 (в; д), № 1256 (а; б), № 1258 (в).
Урок 3
Цели: упражнять в раскрытии скобок, закреплять правила действий с рациональными числами при упрощении выражений и нахождении значений выражений; проверить знания учащихся в ходе самостоятельной работы.
Ход урока
I. Устная работа.
1. Решить устно № 1247 (в), № 1246 (г), № 1248 (г – е).
2. Решить № 1251 (б) с записью в тетрадях.
3. Повторить правила действий с рациональными числами и правила раскрытия скобок.
4. Раскройте скобки и найдите значение выражения:
а) – 0,23 + (5,3 – 6,77); б) –15,29 – (– 40,7 – 15,29);
в) ![]() .
.
5. Разобрать решение примера 6 на с. 216 учебника.
II. Тренировочные упражнения.
1. Решить № 1236 (д; е; и) с комментированием на месте.
2. Решить № 1238 (п; р) на доске и в тетрадях.
3. Решить № 1237 (к; л; о; р). Вызывать по одному ученику к доске для решения, остальные учащиеся решают самостоятельно, потом проверяют решение.
Решение.
к) ![]() ;
;
л) ![]() ;
;
о) ![]() ;
;
р) ![]() .
.
4. Решить № 1243 (е; ж; з) на доске и в тетрадях.
Решение.
е) ![]()
![]() ;
;
ж) ![]()
![]() ;
;
з) ![]()
![]() .
.
5. Решить уравнения № 1241 (в; г; д).
Решение.
в) ![]() г) (х
+ 3) – 17 = – 20
г) (х
+ 3) – 17 = – 20
![]() х
+ 3 – 17 = – 20
х
+ 3 – 17 = – 20
![]() х
– 14 = –20
х
– 14 = –20
![]() х
= –20 + 14
х
= –20 + 14
![]() . х
= – 6.
. х
= – 6.
Ответ: ![]() . Ответ:
х = – 6.
. Ответ:
х = – 6.
д) – (10 – в) + 23,5 = – 40,4
–10 + в + 23,5 = – 40,4
в + 13,5 = – 40,4
в = – 40,4 –13,5
в = – 53,9.
Ответ: в = – 53,9.
III. Самостоятельная работа.
Вариант I.
1. Раскройте скобки и найдите значение выражения:
а) – 0,56 + (3,8 – 2,44); б) – 3,24 – (– 4,76 – 2,9);
в) ![]() .
.
2. Упростите выражение (с + 5,4) – (4,9 + с).
3. Решите уравнение – 5,4 – (х – 7,2) = 1,9.
Вариант II.
1. Раскройте скобки и найдите значение выражения:
а) – 0,37 + (4,2 – 4,63); б) – 13,96 – (– 15,87 – 2,51);
в) ![]() .
.
2. Упростите выражение (п – 5,8) – (4,9 + п).
3. Решите уравнение – 8,9 – (3,7 – х) = –13,6.
Домашнее задание: повторить все правила, решить № 1255 (г; е), № 1256 (в – д), № 1257 (а; б), № 1259 (б).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.