Развитие логического мышления

   «Развитие логического мышления на уроках математики».

подготовила

учитель начальных классов

I квалификационной категории

Т.А.Ледовских

«Предмет математики настолько серьёзен,

что полезно не упускать  случая  делать

его немного занимательным».

Паскаль

  Актуальность моей работы обусловлена требованиями времени, которое постоянно диктует нам свои перемены, а развитие логических суждений способствует повышению мотивации к учебной деятельности. Практическая значимость выбранной темы заключается в том, что развитие логики в младшем возрасте – фундамент дальнейшего успешного обучения.            

    Что такое мышление и логика? Мышление – это познавательный процесс, который позволяет получать знания об окружающем мире на основе суждений, выводов и умозаключений. Логика – наука о формах и способах мышления. Основы логики заложил Аристотель. Он исследовал терминологию логики, подробно разобрал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления. Ну, а что же такое логическое мышление? Это мыслительный процесс, в котором человек пользуется чёткими и конкретными понятиями. Логическое мышление необходимо при принятии решения, когда требуется применить и анализировать полученные ранее знания. Лучше всего привычку логически думать прививать ребёнку с дошкольного возраста, но не предлагая ему готовый ответ на заданный вопрос, а давая возможность найти решение самому. В этом поможет дидактическая игра. Дидактическая игра делает процесс обучения более лёгким, занимательным. Та или иная умственная задача, заключенная в игру, решается в ходе доступной и привлекательной для детей деятельности.

Уже в начальной школе дети должны овладеть элементами логических действий (сравнения, классификации, обобщения, анализа и др.). Поэтому одной из важнейших задач, стоящих перед учителем начальных классов, является развитие самостоятельной логики мышления, которая позволила бы детям строить умозаключения, приводить доказательства, высказывания, логически связанные между собой, делать выводы, обосновывая свои суждения, и, в конечном итоге, самостоятельно приобретать знания. Математика именно тот предмет, где можно в большой степени это реализовывать. Многие исследователи Е.В. Веселовская, Е.Е. Останина, А.А. Столяр, Л.М. Фридман отмечают, что целенаправленная работа по развитию логического мышления младших школьников должна носить системный характер. При этом исследования психологов позволяют сделать вывод о том, что результативность процесса развития логического мышления младших школьников зависит от способа организации специальной развивающей работы. В работах данных авторов доказывается, что в результате правильно организованного обучения младшие школьники весьма быстро приобретают навыки логического мышления, в частности, умение обобщать, классифицировать  и  аргументировано обосновывать свои выводы. Значительное место вопросу развития у младших школьников логического мышления уделял в своих работах известнейший отечественный педагог В. Сухомлинский. Суть его размышлений сводится к изучению и анализу процесса решения детьми логических задач, при этом он опытным путем выявлял особенности мышления детей. О работе в этом направлении он писал в своей книге «Сердце отдаю детям»: «В окружающем мире — тысячи задач. Их придумал народ, они живут в народном творчестве как рассказы-загадки». Опыт показывает, что именно на уроках математики может происходить целенаправленное, систематическое формирование логических понятий и действий, т. к. именно в ней, в силу ее специфических особенностей, содержатся большие потенциальные возможности для развития логического мышления младших школьников. Развивая своё логическое мышление, мы способствуем работе интеллекта, а интеллект — это гарантия личной свободы человека и самодостаточности его индивидуальной судьбы. Чем в большей мере человек использует свой интеллект в анализе и оценке происходящего, тем в меньшей мере он податлив к любым попыткам манипулирования им извне. Развитие мышления, совершенствование умственных операций, способности рассуждать прямым образом зависят от методов обучения. Умение мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять суждения по определенным правилам — это необходимое условие успешного усвоения учебного материала младшими школьниками.              Мы, учителя, берясь за какое- то дело, ставим перед собой конкретные задачи для его выполнения. Я считаю, что главными задачами для успешного развития логического мышления у младших школьников являются:

- формирование интереса к математике, как к науке;

- развитие творческой инициативы;

- повышение качества обучения;

- раскрепощение мышления  обучающихся.

Одним из важнейших условий построения обучения, которое способствует развитию мыслительной деятельности школьников на уроках математики, является пробуждение их к самостоятельной мысли. Развитие у школьников теоретического сознания и мышления есть следствие того, что соответствующими знаниями, умениями и навыками обучающиеся овладевают в форме учебной деятельности. Это овладение теоретическими знаниями происходит в диалоге, дискуссии; в их сознании постоянно функционирует анализ, обобщение, планирование, рефлексия.

В развитии мышления младших школьников психологи выделяют две основные стадии:

На первой стадии (1-2 классы) их мышление во многом похоже на мышление дошкольников: анализ учебного материала производится по преимуществу в наглядно- действенном и наглядно- образном плане. Обобщения и понятия этой стадии сильно зависят от внешних характеристик предметов и фиксируют те свойства, которые лежат на поверхности. Например, один и тот же предлог «на» выделяется второклассниками успешнее в тех случаях, когда его значение конкретно, чем когда его значение более абстрактно («на днях», «на память»). Именно поэтому так важен в начальной школе принцип наглядности.

На второй стадии (3-4 классы) качественно новая ступень. К третьему классу дети овладевают родовидовыми отношениями между отдельными признаками понятий, формируется аналитико–синтетический тип деятельности, осваивается действие моделирования. Начинает формироваться формально- логическое мышление. В начальной школе уделяется большое внимание формированию научных понятий.

Какие же причины способствуют необходимости развития логического мышления у детей младшего школьного возраста?

Во- первых, появилось много новых учебников, которые требуют от учителя активной мыслительной деятельности для усвоения их содержания;

во – вторых, обучающиеся начальных классов принимают участие в различного уровня интеллектуальных конкурсах, в основе которых необходимо не только знание предмета, но и умение нестандартно мыслить. Значит, необходимо усилить логическую подготовку учеников младших классов;

в- третьих, изменения в системе образования, связанные с достижением нового образовательного стандарта: всестороннее развитие личности обеспечивается единством нравственного, умственного, эстетического и физического воспитания. Умственное воспитание выступает как формирование у детей интеллектуальных умений, в состав которых входят логические приёмы мышления.

Роль математики в развитии логического мышления младших школьников очень велика. Причина этого состоит в том, что математика – это самая теоретическая наука из всех изучаемых в школе. В ней высокий уровень абстракции и в ней наиболее естественным способом изложения знаний является способ восхождения от абстрактного к конкретному.  Все задания по формированию логического мышления у младших школьников на уроках математики должны носить развивающий характер, располагаться в определённой последовательности и должны быть связаны между собой; должно прослеживаться постепенное усложнение заданий и повышение уровня самостоятельности детей в процессе их выполнения; задания должны быть во взаимосвязи с ранее усвоенными знаниями, умениями и навыками; вопросы в заданиях должны быть нацелены на развитие мыслительных операций обучающихся, включать их в творческую деятельность, содействовать их развитию. Давно известны приёмы, которые также помогают в развитии логического мышления детей и используются не только на уроках математики.

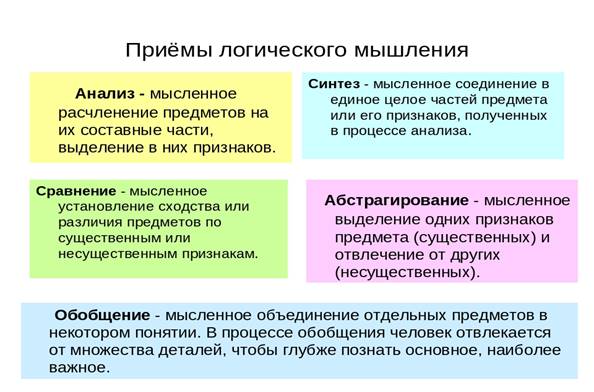
Применяю на уроках занимательные задачи и задачи-шутки, числовые, геометрические головоломки, магические квадраты, математические ребусы, кроссворды, различные интерактивные упражнения. Всё это способствует более высокому уровню усвоения материала младшими школьниками. Во время проведения таких уроков математики наблюдается большая заинтересованность учащихся, они активны, работают с удовольствием. Поэтому, моя задача — создать все условия, при которых склонность детей к новому, нестандартному, желание самостоятельно решать поставленные задачи могли иметь дальнейшее развитие. В качестве заданий, развивающих логическое мышление, на уроках математики использую следующие упражнения:

Например, задание на сравнение. – Сравни каждый ряд и объясни.

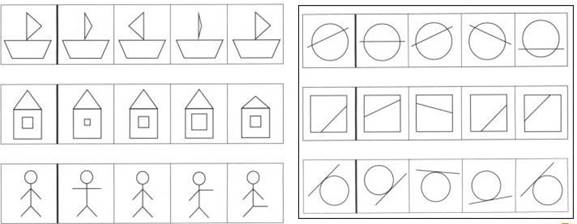
Логический приём – обобщение. – Посмотри и скажи, что должно быть нарисовано в левом углу?

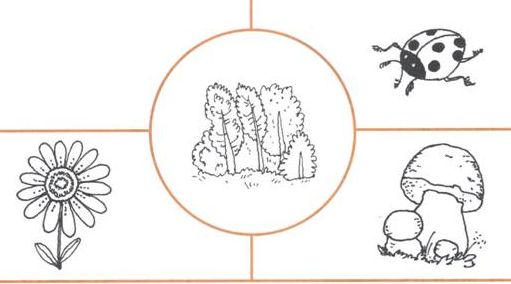
Ну, а теперь приведу примеры заданий, которые также направлены на развитие логического мышления:

- числовые фигуры;

- задачи- шутки;

- задачи на смекалку;

- математические игры;

- задачи с геометрическим содержанием;

- логические упражнения со словами;

- кроссворды и ребусы и т. д.

Логические задачи позволяют продолжить занятия с детьми по овладению такими понятиями, как слева, справа, выше, ниже, больше, меньше, шире, уже, ближе, дальше и др.

1.Алеша на дорогу в школу тратит 5 минут. Сколько минут он потратит, если пойдет вдвоем с сестрой?

2. Коля ростом выше Андрея, но ниже Сережи. Кто выше Андрей или Сережа?

3.В прямоугольной комнате следует расставить 8 стульев так. Чтобы у каждой стены стояло по 3 стула.

4.Чтобы распилить доску на несколько частей, ученик сделал на ней шесть отметок. На сколько частей ученик распилит доску?

5. По улице идут два сына и два отца. Всего три человека. Может ли так быть?

6.Какое число лишнее? 9,7,4,1,3,7.

7.Из 5 палочек нужно построить 2 треугольника.       И другие:

·         -Запиши число, которое получится при сложении самого большого двузначного числа и самого маленького трехзначного.

·         -Три брата живут в одном доме, но в разных подъездах. Кто в каком подъезде живет, если     известно, что старший брат живет не во втором подъезде, а средний не во втором и не в третьем?

·         -Два мальчика и две девочки нашли 10 грибов, причем каждый нашел разное количество грибов. Сколько грибов нашли мальчики, если вместе они нашли столько же грибов, сколько и девочки?

·         -Табло электронных часов показывает 17:13. Какое время будут показывать электронные                 часы в следующий раз, когда сумма часов и минут будет такой же. 

·         -Таня, Вера и Лена - сестры. Тане и Вере вместе 5 лет, а сумма лет Веры и Лены составляет 7 лет. Вера самая маленькая. Кто старше: Таня или Лена?

·         -У Валеры есть попугайчики и хомячки. У всех  -  5 голов и 16 ног. Сколько у Валеры           попугайчиков и сколько хомячков? (5 баллов)

·         -Вместо* поставь знаки + или - так, чтобы равенства были верными.

o   17*3=15*1

o   16*2=10*4

o   15*3=2*16 (2 балла)

·         -Одна мышка- норушка и 2 лягушки- квакушки весят столько же, сколько 2 мышки - норушки и одна лягушка-квакушка. Кто тяжелее: мышка или лягушка?

-Запиши двухзначные числа, используя цифры 7, 0, 4 ,2  так, чтобы число десятков было больше числа единиц.

- Числа 7, 8, 6, 5 поставь в окошки так, чтобы записи были верными:

        + 20 > 20 +                -           <              +            

1. Саша ел яблоко – большое и кислое. Коля ел яблоко – большое и сладкое. Что в этих яблоках одинаковое? Разное?

2. Маша и Нина рассматривали картинки. Одна девочка рассматривала картинки в журнале, а другая девочка – в книжке. Где рассматривала картинки Нина, если Маша не рассматривала картинки в журнале?

3. Толя и Игорь рисовали. Один мальчик рисовал дом, а другой - ветку с листьями. Что рисовал Толя, если Игорь не рисовал дом?

4.Внимательно рассмотри рисунок и найди правильную подпись для него.

- Геометрические фигуры объединены по форме: треугольники, квадраты, круги.

- Геометрические фигуры объединены по цвету: красные, синие, зелёные.

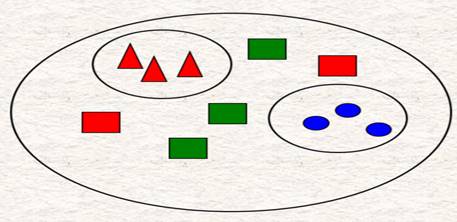
Комбинаторная задача (метод перебора)

В магазине продают воздушные шары: красные, желтые, зелёные, синие. Какие наборы можно составить из двух разных шаров? Сколько наборов у тебя получилось?

Представленные задания, игры, упражнения вызывают у детей большой интерес. А ведь именно он должен лежать в основе обучения младшего школьника. Интерес поддерживает высокий уровень познавательной активности, что в свою очередь способствует развитию интеллектуальных способностей ребенка.

  Для активизации обучающихся и поддержания интереса к изучаемому материалу применяются активные методы учения: деловые и сюжетно-ролевые и дидактические игры, компьютерные и настольные игры, дискуссии, уроки-конкурсы, уроки-презентации с использованием возможностей компьютерных технологий. Все это носит познавательный и праздничный характер. Положительная эмоциональная окраска усиливает мотивационный аспект. Активность учеников в процессе обучения тесно связана с его интересом к предмету.

Заключение.

Систематическое использование на уроках математики специальных задач и заданий, направленных на развитие логического мышления, расширяет математический кругозор младших школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни; такие задания стимулируют творческую мыслительную деятельность в процессе обучения, помогают обеспечить то деятельное состояние мозга, которое является необходимым условием для образования новых связей. Все виды работы, представленные в заданиях, направлены на развитие логического мышления, и поэтому предлагаю детям на каждом уроке математики. На определённом этапе работы ввожу дифференциацию, заменяю фронтальную форму работы групповой, парной или индивидуальной. Данные задания не только развивают умения анализировать, рассуждать, комбинировать, обобщать, но и активно формируют весь процесс мышления. Используя на уроках такие виды заданий, я заметила, что учащиеся с интересом выполняют предложенные задания, составляют аналогичные задания, лучше усваивают учебный материал.

Список использованной литературы

1.     Бакина Т. И учеба, и игра; математик. Издательство: Академия, 2014.

2.     Богун И. Развитие творческого мышления детей. Издательство: Академия, 2011.

3.     Практическое приложение: «Играем в числа». Издательство: Эксмо, 2014.

4.     Светлова И.Логика. Издательство: Эксмо, 2004.

5.     Смирнов С. Педагогические теории, системы, технологии. Издательство: Эксмо, 2000.

6.     Шведова Л. Открой в себе гения. Развитие логического мышления и интеллекта. Издательство: БАО, 2007.

7.     3. Яндекс. Картинки.