"Развитие пространственного мышления младших школьников"

Педагогический опыт

учителя начальных классов Муниципального Бюджетного Общеобразовательного Учреждения Прохоровской основной

общеобразовательной школы Красносулинского района

Ростовской области

Нихаевой Татьяны Николаевны

по теме:

«Развитие пространственного мышления младших школьников на уроках математики»

Мышление - это естественная

потребность человека, и

главная движущая сила – это

чувство радости от

преодоления трудностей.

Возрастной период младших школьников – 6-10 лет. В работах Р.С.Немова говорится о том, что младший школьный возраст содержит в себе значительный потенциал умственного развития детей, но точно определить его не представляется возможным. Известный психолог Л.В.Выготский справедливо утверждал, что умственное развитие ребёнка состоит не столько в развитии отдельных процессов, сколько в развитии взаимосвязей между ними. Все исследователи младшего школьного возраста сходятся на том, что основная особенность ребёнка этой ступени обучения заключается не в том, что он в состоянии выполнять и достичь сегодня, а в потенциальных возможностях, которыми располагают дети этого возраста, в возможностях, которые лежат в зоне ближайшего развития младшего школьника. Поэтому Л.С.Выготский и подчёркивал, что педагогика должна опираться не на вчерашний, а на завтрашний день детского развития. В своей педагогической работе учитель должен учитывать и слабость в развитии логической памяти младшего школьника и трудности, которые дети этого возраста испытывают в усвоении отвлечённого материала. Строить свою работу он должен с ориентацией не на эти слабые стороны психики ребёнка, а на то, что младший школьник обладает гораздо большими интеллектуальными возможностями, чем те, которые он обычно обнаруживает.

При обучении математике по учебникам современных развивающих систем (система "Гармония", «Перспективная начальная школа» - это программы, по которым мне довелось работать.) умения ребенка писать, считать, складывать и вычитать (на деле это обычно выливается в попытку выучить наизусть результаты сложения и вычитания в пределах 10) очень недолго выручают ребенка на уроках математики. Запас заученных знаний кончается очень быстро (через месяц-два), и несформированность собственного умения продуктивно мыслить очень быстро приводит к появлению "проблем с математикой".

Учебники математики современных, развивающих систем построены таким образом, что уже на первых уроках ребенок должен использовать умения сравнивать, классифицировать, анализировать и обобщать результаты своей деятельности.

Однако не следует думать, что развитое логическое мышление - это природный дар, с наличием или отсутствием которого следует смириться. Существует большое количество исследований, подтверждающих, что развитием логического мышления можно и нужно заниматься (даже в тех случаях, когда природные задатки ребенка в этой области весьма скромны). Прежде всего разберемся в том, из чего складывается логическое мышление.

Логические приемы умственных действий - сравнение, обобщение, анализ, синтез, классификация, сериация, аналогия, систематизация, абстрагирование - в литературе также называют логическими приемами мышления. При организации специальной развивающей работы над формированием и развитием логических приемов мышления наблюдается значительное повышение результативности этого процесса независимо от исходного уровня развития ребенка.

Интерес к теме "Формирование пространственного мышления у детей младшего школьного возраста на уроках математики" вызван её актуальностью и недостаточной разработанностью. Её актуальность обусловлена тем, что в период младшего школьного возраста происходят существенные изменения в психике ребенка и период младшего школьного возраста является сенситивным доля развития пространственного мышления. Математика способствует развитию у детей мышления, памяти, внимания, творческого воображения, наблюдательности, строгой последовательности рассуждения и его доказательности; дает реальные предпосылки для развития пространственного мышления учеников. Такому развитию способствует изучение геометрического материала, связанного с алгебраическим и арифметическим материалом. Изучение геометрического материала обеспечивает числовую грамотность учащихся, дает им начальные геометрические представления, развивает пространственное мышление и пространственное воображение детей, формирует у них элементы конструкторского мышления и конструктивных умений.

В младшем школьном возрасте, особенно на начальном этапе обучения, основным показателем сформированности пространственных представлений является узнавание и дифференцирование пространственных признаков на основе перцептивной деятельности (деятельности по восприятию объекта). Оперативной единицей пространственного восприятия объекта является образ, который характеризуется не только и не столько пространственными признаками (форма и размер), но в большей степени пространственными отношениями, определяющими направление (вперед – назад, вверх – вниз), расстояние (далеко – близко), местоположение (высокий – низкий, короткий – длинный) и так далее.

Одна из психологических особенностей детей младшего школьного возраста - преобладание наглядно-образного мышления и именно на первых этапах обучения математике используется образ, как основная оперативная единица пространственных представлений младших школьников. Однако большие возможности для дальнейшего развития этого вида мышления, а также для наглядно-действенного мышления дает такая работа с геометрическим материалом на уроках математики, когда образ, в котором представлены пространственные признаки объекта, и слово соотносятся ребенком взаимно однозначно. В этом случае сформированность пространственных представлений дает ребенку возможность оперировать ими не только на уровне узнавания и дифференциации объекта по пространственным признакам, но главное – на уровне мысленного воспроизведения образа объекта и изменения его положения в пространстве размещать и ориентировать объект в какой-либо системе отсчета, то есть понимать его положение среди совокупности других объектов.

"Именно такой подход к изучению геометрического материала делает его эффективным для развития детей", - считает Л. В. Занков. Формирование пространственных представлений у младших школьников способствует развитию восприятия, памяти, внимания, выработке у младших школьников математических понятий на основе содержательного обобщения, которое означает, что ребенок движется в учебном материале от частного к общему, от конкретного к абстрактному. Переход от наглядно-образного к наглядно-действенному мышлению требует сложной аналитико-синтетической работы, выделения деталей, сопоставления их друг с другом, что немыслимо без наличия у ребенка развитых пространственных представлений и пространственного воображения. В этом процессе большое значение принадлежит и речи, которая помогает назвать признак, сопоставить признаки. Только на основе развития наглядно-действенного и наглядно-образного мышления начинает формироваться в этом возрасте формально-логическое мышление, которое в совокупности с наглядно-образным и наглядно-действенным мышлением является основой умственного развития младшего школьника. При этом, с помощью каждого из них, у ребенка лучше формируются те или иные качества ума.

Исходя из собственного опыта, я сделала вывод, что уже в начальной школе большинство обучающихся занимают в учебном процессе пассивную роль и начинают терять интерес к учебе. Поэтому важно развивать способности и поддерживать стремление ученика, не учить его, а помогать ему учиться и развиваться. Способность к саморазвитию должна стать результатом познавательной деятельности. Наиболее конструктивным решением проблемы является создание таких условий в обучении, в которых обучаемый может занять активную личностную позицию и в полной мере выразить себя. Таким образом, у меня возникла идея по развитию пространственного мышления у детей в процессе изучения геометрического материала.

Приемы развития пространственных представлений младших школьников.

Изучая методические разработки и рекомендации о путях и способах формирования пространственных представлений у учащихся, я заметила, что подавляющее большинство из них (и теоретически, и исходя из опыта работы) приходят к выводу о необходимости:

используя способность детей шестилетнего возраста к восприятию формы начинать формирование пространственных представлений с первых уроков математики в 1-м классе. При знакомстве учеников с геометрическими фигурами следует опираться не только на зрительное восприятие образа ребенком, но и на все другие анализаторы, учитывая мнение психолога Е. Г. Ананьева о том, что связующая роль между всеми анализаторами принадлежит двигательно-кинестетическому анализатору;

придерживаясь последовательности изучения геометрического материала в начальной школе, предусмотренного учебными программами по математике, в первую очередь моей задачей было помочь детям осмыслить основные пространственные отношения, какие, как: быть впереди, находиться между, находиться на противоположной стороне, быть внутри, следовать за, и так далее. Среди них особым видом выделяются такие отношения, как: справа - слева, ближе – дальше, вверху – внизу, над – под, оперирование которыми, в силу их относительности, вызывает значительные трудности.

Решая проблему развития пространственного мышления в русле методической концепции развивающего обучения младших школьников математике, мой опыт ориентировался на общекультурные цели обучения геометрии и стремится развивать у учащихся интуицию, образное (пространственное) и логическое мышление (приемы умственной деятельности: анализ и синтез, сравнение, классификация, аналогия, обобщение), формировать у них конструктивно-геометрические умения и навыки, способность читать и понимать графическую информацию, а также комментировать ее на доступном детям данного возраста языке.

При разработке заданий руководствовалась:

1. Данными психологических исследований об особенностях пространственного мышления как вида умственной деятельности (И.С. Якиманская);

2. Логикой построения начального курса математики, в состав которого входит геометрический материал (Н.Б.Истоминой);

3. Богатейшим опытом начального обучения геометрии, отраженным в методической литературе;

4. Результатами исследований, связанных с изучением материала в начальных классах и 5-6 классах среднего звена;

Задачи:

· Отрабатывать геометрический навык.

· Подготовить ум к более серьезной работе. Для успешного освоения программы обучения ребенку необходимо не только много знать, но и последовательно мыслить, догадываться, проявлять умственное напряжение.

Интеллектуальная деятельность, основанная на активном думании, поиске способов действий, при соответствующих условиях может стать привычной для детей. Так, головоломки целесообразны при закреплении представлений ребят о геометрических фигурах. Загадки, задачи-шутки уместны в ходе обучения решения арифметических задач, действий над числами, формирование временных представлений и т.д. формы организации учеников разнообразны: игры проводятся со всеми, с подгруппами и индивидуально. Дети могут, не отвлекаясь, подолгу упражняться в преобразовании фигур, перекладывании палочки или другие предметы по заданному образцу, по собственному замыслу.

Умственная задача: составить фигуру, видоизменить, найти путь решения, отгадать число - реализуется средствами игры, в игровых действиях. Развитие смекалки, находчивости, инициативы осуществляется в активной умственной деятельности, основанной на непосредственном интересе. Занимательность математическому материалу придают игровые элементы, содержащиеся в каждой задаче, логическом упражнении, развлечении, будь то шашки или самая элементарная головоломка. Например, в вопросе: «Как из двух палочек сложить на столе квадрат?» - необычность его постановки заставляет ребенка задуматься в поисках ответа, втянуться в игру воображения. Многообразие занимательного материала - игр, задач, головоломок, дает основание для классификации, хотя довольно трудно разбить на группы столь разнообразный материал, созданный математиками, методистами и нами учителями. Классифицировать его можно по разным признакам: по содержанию и значению, характеру мыслительных операций, а также по признаку общности, направленности на развитие тех или иных умений. Исходя из логики действий, осуществляемых решающим, разнообразный элементарный занимательный материал можно классифицировать, выделив в нем условно 3 основные группы: развлечения, математические игры и задачи, развивающие (дидактические) игры и упражнения. Характер и назначение материала того или иного вида.

Геометрические упражнения и задачи по развитию пространственного мышления младших школьников.

Целью формирующего этапа была разработка системы геометрических упражнений и задач по развитию пространственного мышления у детей в процессе изучения геометрического материала. В процессе реализации цели формирующего этапа была проведена работа по исследованию серии заданий по геометрии, направленных на развитие пространственного мышления младших школьников, которая включалась в уроки математики. Разработанная система заданий была апробирована в такой последовательности:

1. Задания, связанные с составлением и преобразованием геометрических фигур при помощи счетных палочек.

2. Задания, направленные на работу с симметричными фигурами.

3. Задания на установление соответствия образа фигуры и ее изображения с учетом переориентации на плоскости и в пространстве.

4. Задания, связанные с мысленным оперированием кубика в пространстве, состоящие из трех последовательно усложняющихся групп.

5. Задания на построение геометрических тел по их развертке.

6. Система игр «Танграм», «Пифагор», «Волшебный круг» на воссоздание из геометрических фигур образных и сюжетных изображений.

7. Практические работы на построение фигур на листе бумаги и на местности.

Сначала я давала простые задания всех семи видов, которые являлись своеобразной подготовкой для выполнения заданий более сложного характера. Повторно давала задания среднего уровня трудности, а затем самые сложные. При выполнении таких заданий использовался дифференцированный и индивидуальный подход к учащимся.

Большое внимание уделяла выполнению заданий, связанных с составлением и преобразованием геометрических фигур при помощи счетных палочек. Такие задания предлагала в определенной последовательности, в зависимости от степени сложности.

1. На составление фигур из определенного количества палочек:

Из 9 палочек составить 2 квадрата - 1 маленький и 1 большой.

Такого рода задания не вызывали затруднений у учащихся.

2. На преобразование фигур:

В фигуре, состоящей из 4 квадратов, убрать 2 палочки так, чтобы осталось 2 неравных квадрата (рис.1).

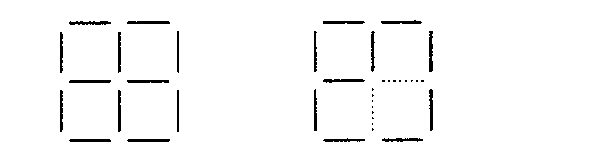
Рис. 1

Особое место в работе с геометрическим материалом занимают упражнения, связанные с преобразованиями симметрии, которые способствуют развитию пространственного мышления учащихся. В основном я использовала задания, связанные с геометрическими преобразованиями - осевой симметрией на плоскости.

3. Начерти треугольник, симметричный данному, если прямая - ось симметрии (рис.2).

4. Догадайся! Как можно построить окружность, симметричную данной, если прямая - ось симметрии (рис.3).

Рис. 2 Рис. 3

Выполнение таких заданий вызывает большой интерес у учащихся, причем они не испытывают затруднений при решении.

С целью организации работы по ориентации плоских и объемных геометрических фигур использовалась серия упражнений на соответствие образа (модели) и его изображения с учетом переориентации на плоскости и в пространстве.

5. «Раскрась фигуру справа». Из столбика трех квадратов следует выбрать квадрат, имеющий такой же рисунок, как и исходный, но изменивший свое положение при повороте против часовой стрелки на четверть оборота. Это квадрат 2, изображенный на рис.4.

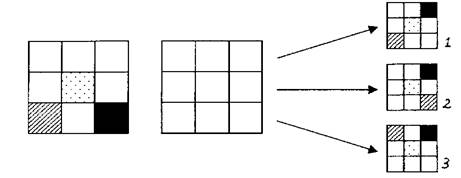
Рис. 4

6. Чем похожи квадраты? Чем они отличаются? (Рис.5а, б)

Важную роль в развитии пространственного мышления учащихся играют задания на построение геометрических фигур при помощи развертки. У учащихся при этом формируются представления о развертке геометрического тела, умение соотносить модель геометрического тела с ее изображением и разверткой.

Сначала третьеклассникам я предлагаю несложные задания, правильность которых можно проверить практически: изготовить развертку, непосредственно оперируя ею, прийти к нужному варианту ответа. Затем учащимся даю задания более сложные, решить которые надо мысленно, не прибегая к практическим действиям.

11. Подумай, какие из фигур, изображенных на рисунке, могут быть разверткой куба? (Рис.11)

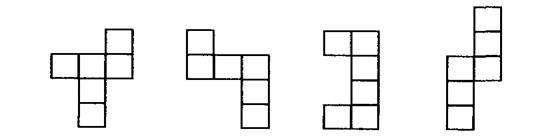
Рис. 11

Особый интерес у учащихся вызывают упражнения в составлении изображений по собственному замыслу. Дети вспоминают, какие плоские фигуры составляли ранее, воспроизводят их по памяти; при передаче формы некоторых фигур-силуэтов дети воспроизводят общие очертания формы, а составные элементы отдельных частей располагают несколько иначе, чем делали ранее по образцу. Хотя данный вид заданий является наиболее сложным для учащихся, он вызывает большой интерес, способствует активизации познавательной деятельности.

С целью развития пространственного мышления, воображения детей на внеклассных занятиях по математике я использовала аналогичные игры «Пифагор», «Монгольская игра», «Колумбово яйцо», «Вьетнамская игра», «Волшебный круг», «Пентамино». Кроме того, в каждый урок математики включались задания по геометрии, которые имели практический характер. При этом важно отметить, что в результате выполнения практических упражнений учащиеся лучше усваивают геометрические понятия.

Практическая работа по развитию пространственных представлений младших школьников при изучении геометрического материала

Целью формирующего этапа являлась разработка упражнений, направленных на развитие воображения и пространственного мышления у детей в процессе изучения геометрического материала. В уроки я старалась активно включать задания геометрического характера, проводила работу по исследованию серии заданий по геометрии, направленных на развитие воображения и мышления младших школьников.

Задания, направленные на развитие воображения, достаточно сложны для детей, так как в процессе решения требуется представить фигуры; осмыслить характер их преобразования и получаемый результат (какие фигуры должны получиться и сколько), а также соотнести его с предлагаемыми или уже осуществленными изменениями, проконтролировать себя. В процессе решения задачи или выполнения задания необходим не только зрительный, но и мысленный анализ объекта, умение представить возможные изменения в объекте и их результат. Постепенно вводятся новые задания по формированию у детей системы различных способов действий по созданию моделей и преобразованию геометрических фигур:

· изменение формы фигуры при сохранении размера и цвета, цвета при сохранении формы и размера и, наконец, размера при сохранении формы и цвета (задания со счетными палочками);

· выбор фигуры нужной формы для восстановления целого (игра «Танграм», игра «Каких фигур не хватает?»);

· определение на глаз размеров плоских фигур («Какая фигура лишняя?»);

· выбор пары идентичных фигур сложной конфигурации;

· распознавание и выделение заданных фигур;

· составление фигур из частей, выбор которого осуществляется из множества.

Большое внимание я уделяю выполнению заданий, связанных с составлением и преобразование геометрических фигур при помощи счетных палочек. Такие задания предлагаю в определенной последовательности, в зависимости от степени сложности.

Сначала дети выполняют задания первой группы, на составление фигур из определенного количества палочек, например:

Из 9 палочек составить 2 квадрата?1 маленький и 1 большой.

Такого рода задания не вызывают затруднения у учащихся.

Процесс поисков решения заданий второй группы был гораздо сложнее, так как они предполагают преобразование фигур:

В фигуре, состоящей из 4 квадратов, убрать 2 палочки так, чтобы осталось 2 неравных квадрата.

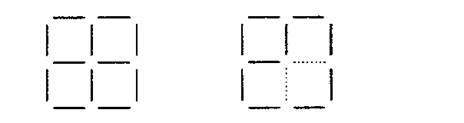
Рис.1.

Особое место в работе с геометрическим материалом занимают упражнения, связанные в преобразованиями симметрии, которые способствуют развитию воображения учащихся. В основном использую задания, связанные с геометрическими преобразованиями — осевой симметрией на плоскости.

Это раскрашенные яйца. Покажите, на каких симметричные рожицы?

Рис.3.

На уроках математики, а также на внеклассных занятиях стараюсь использовать задания по развитию воображения, которые предлагают воссоздание из геометрических фигур образных и сюжетных изображений.

Пример такого вида заданий является игра «Танграм». Используя части игры — плоскостные геометрические фигуры, плотно присоединяя, их друг к другу, учащиеся составляют различные изображения по образцам и по собственному замыслу. В процессе выполнения этого задания у учащихся закрепляются знания названий геометрических фигур, их свойств, отличительных признаков, формируются умения владеть способами обследования форм зрительным и осязательно-двигательным путем.

На первом этапе освоения игры были проведены подготовительные упражнения, направленные на развитие у детей пространственных представлений, элементов геометрического воображения, на выработку практических умений в составлении новых фигур. Детям предлагаю выполнить задание в плане представления, а потом практически.

Кто быстрее составит фигуры?

Цель игры — развитие воображения.

Рис.4.

Оборудование. 1) Набор моделей плоских геометрических фигур, например, равносторонние треугольники, разрезанные на два равных прямоугольных треугольника, или прямоугольник и два равных прямоугольных треугольника с катетами, равными сторонам прямоугольника.

2) На каждую пару игроков — лист бумаги и карандаш.

Правила игры. Участники игры распределяются на пары. Каждая пара получает одинаковый набор фигур. У них одна и та же задача: составить из имеющихся фигур как можно быстрее и больше различных геометрических фигур и зарисовать их. При этом один игрок складывает фигуры, а другой их зарисовывает.

Получив фигуры, игроки по сигналу руководителя приступают к выполнению задания. Когда отдельные пары заканчивают работу, руководитель дает команду «Стоп! Положить карандаши!» и оценивает успехи каждой пары, быстро просматривая сделанные чертежи.

Упражнения были подготовительными ко второму этапу освоения игры — составлению фигур-силуэтов по расчлененным образцам на основе танграма из 7 частей.

Рис. 5

Особый интерес у учащихся вызывают упражнения в составлении изображений по собственному замыслу. Дети вспоминают, какие плоские фигуры составляли ранее, воспроизводят их по памяти; при передаче формы некоторых фигур-силуэтов дети воспроизводят общие очертания формы, а составные элементы отдельных частей располагают несколько иначе, чем делали ранее по образцу. Хотя данный вид заданий является наиболее сложным для учащихся, он вызывает больший интерес, способствует активизации познавательной деятельности.

Очень похожа на «Танграм» «Вьетнамская игра», которая также предполагает воссоздание из изображений. Цель игры та же, что и у «Танграма». А суть игры заключается в следующем.

Круг разделен на части, как показано на рисунке. Ориентиром при разрезании служит центр круга. Получается 7 частей. Из них равны между собой 2 части, похожие на овал, и 2 части, имеющие сходство с треугольником, остальные 3 части разные по форме и размеру.

Попробуй из полученных в результате разреза частей составить фигурки:

1.Индюшонка. 3.Бабочки.

2.Тюленя. 4.Собачки.

Рис.7.

Также большое внимание с целью развития воображения я старалась уделять заданиям на выбор фигуры нужной формы для восстановления целого. Такие упражнения включаю как в урочную деятельность, так и во внеклассную.

1. Каких фигур не хватает? Начерти.

Рис.8. Рис.9

2. Разрежьте кораблик на 2 части так, чтобы из него можно было сложить квадрат.

Рис.10.

3. Начерти и вырежи данные фигуры и выложи из них квадрат.

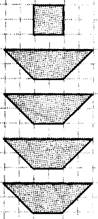
Рис.11.

Формирование пространственных представлений не является прерогативой исключительно курса математики, поскольку образы, в которых фиксируется форма, величина, пространственное соотношение фигур в целом или их частей, выстраиваются в сознании ребёнка уже с самого раннего детства. Однако задачу формирования этого вида мышления традиционно относят к математическому образованию. Столь же традиционно она связывается с геометрическим материалом, как в начальной, так и в средней школах.

Формирование пространственного мышления ребёнка является важнейшей частью его интеллектуального развития в целом. Хорошее пространственное воображение необходимо и инженеру, и дизайнеру, и компьютерщику, и экономисту, и математику. Задача формировать определённый уровень пространственного мышления ребёнка до начала изучения стабильного курса математических дисциплин курсом математики начальных классов трудная, а порой не выполнимая. В дальнейшем же невысокий уровень пространственного мышления и пространственного воображения ученика обычно является для него практически непреодолимым препятствием для постижения курса стереометрии. Нельзя рассчитывать на то, что можно будет сформировать пространственное мышление у 15-летнего школьника, да ещё сделать это быстро. В то же время и жизненный опыт, и исследования психологов показывают, что эффективно формировать элементы пространственного мышления можно уже у младших школьников. А возраст младшего школьника является в принципе наиболее благоприятным для развития пространственного мышления, поскольку наглядно-образный стиль мыслительной деятельности является в этот период ведущим, а, следовательно, этот возраст наиболее благоприятен для формирования как базовой, так и операционной стороны пространственного мышления.

Пространственные понятие и пространственное воображение ребенка являются предпосылками для формирования его пространственного мышления и обеспечиваются различными психическими процессами, такими как восприятие (первоосновой которого являются ощущения), внимание, память, воображение при обязательном участии речи. Базой для развития пространственного мышления являются пространственные представления, которые отражают соотношения и свойства реальных предметов, то есть свойства трехмерного видимого или воспринимаемого пространства.

Геометрический материал в высокой степени соответствует ведущему в младшем школьном возрасте виду мышления - образному. Уроки математики в начальной школе играют в процессе обучения, ориентированного на индивидуальные интересы обучающихся, очень существенную роль. Формирование пространственных представлений не является прерогативой исключительно курса математики, поскольку образы, в которых фиксируется форма, величина, пространственное соотношение фигур в целом или их частей, выстраиваются в сознании ребёнка уже с самого раннего детства. Однако задачу формирования этого вида мышления традиционно относят к математическому образованию. Столь же традиционно она связывается с геометрическим материалом, как в начальной, так и в средней школах.

Содержанием пространственного мышления является оперирование пространственными образами на основе их создания с использованием наглядной опоры (предметной или графической, разной меры общности и условности). Оперирование пространственными образами определяется их исходным содержанием (отражение в образе геометрической формы, величины, пространственной размещенности объектов); типом оперирования (изменение в ходе оперирования положения объекта, его структуры); полнотой, динамичностью образа (наличием в нем различных характеристик, их системности, подвижности и т. п.). Все эти особенности пространственного мышления отражают процесс работы с образом, позволяют выявлять его качественное своеобразие, фиксировать возрастные и индивидуальные особенности проявления этого процесса, что весьма существенно в диагностических целях.

Важно подчеркнуть, что особенности пространственного мышления нельзя выявить в полной мере, используя для этого различные головоломки, пространственно-комбинаторные игры и т. п. В реальной практике пространственное мышление всегда включено в решение различных задач, опирается на систему знаний, которые не могут (и не должны) нивелироваться.

Конечно, содержание, структуру, условия формирования и другие особенности пространственного мышления можно исследовать в индивидуальных (лабораторных) экспериментах. Однако разнообразные практические задачи, которые приходится решать психологам в современных условиях, требуют проведения массовых исследований, получения оперативной информации об особенностях умственной деятельности учащихся, которая должна дополняться сведениями об их школьной успешности, клиническими наблюдениями за учебным поведением, педагогическими характеристиками и др.

Используемая литература

1. Истомина Н.Б. «Активизация учащихся на уроках математики в начальных классах: Пособие для учителей». М. Просвещение. 1985 г.

2. Истомина Н.Б. «Методика обучения математике в начальной школе». М. Просвещение. 1992 г.

3. Болотина Л. Р. Развитие мышления учащихся. /Л. Р. Болотина Начальная школа - 1994 - №11 Венгер Л.А., Мухина В.С. Психология: Учеб. Пособие для уч-ся пед. уч-щ по спец./ Л.А. Венгер, В.С. Мухина М.: Просвещение, 1988.

4. Волкова С. Н. Задания развивающего характера в новом едином учебнике «Математика». /С.Н. Волкова //Начальная школа. - 1997 - №9 - с. 68

5. Гаркавцева Т.Ю. Геометрический материал в 1 классе как средство развития пространственного мышления учащихся. // Журнал «Начальная школа». 2006 г. № 10,.

6. Долбилин Н.П., Шарыгин И.Ф. О курсе наглядной геометрии в младших классах. // Журнал «Математика в школе». 1990 г. № 6,.

7. Коннова В. А. Задания творческого характера на уроках математики. / В.А. Коннова. //Начальная школа. 1995 - №12 - с. 55.

8. Методика начального обучения математике. /Под общ. ред. А.А.Столяра, В.Л.Дроздова - Минск: Высш. школа, 1988.

9. Михайлова З.А. Игровые занимательные задачи для дошкольников». М., «Просвещение», 1990 г.

10. Обухова Л.Ф. Детская психология: теории, факты, проблемы. /Л.Ф.Обухова //М.: Тривола, 1996.

11. Пичугин С.С. Организация творческой работы с геометрическим материалом. //Журнал «Начальная школа». № 4, 2007.

12. Якиманская И.С. Развитие пространственного мышления школьников. /И.С. Якиманская М. 1980.

13. ФГОС.

14. Интернет ресурсы.

Приложение

Материал, используемый мной в работе

Раскрась кольца пирамидки, если желтое кольцо находится между красным и синим кольцами, а синее между желтым и зеленым (рис 1).

Рис 1.

2. По щучьему велению ведра с водой ходят в избу сами так, что озеро всегда остается от Емели справа. Нарисуй дорожку, по которой ходит Емеля (рис. 2).

Рис. 2

3. Мартышка, попугай, слоненок и удав отправляются в путешествие. «Все садятся в вагоны, следующие за моим», - приказала мартышка. «Я поеду между слоненком и удавом», - сказал попугай. «А я поеду за попугаем», - промолвил слоненок. Обозначьте нужной буквой вагон, в котором поедет каждый из друзей (рис. 3).

Рис. 3

Формирование пространственных представлений учеников начальных классов может осуществляться путем использования некоторых топологических свойств поверхностей (в частности отсутствия связи между формой и размером). Для этого можно применять такие задания, как раскрашивание многоугольных областей, построение плоских графов, поиск путей в графе. Различные способы вложения в пространство можно увидеть, экспериментируя с узлами и зацеплениями, и так далее.

Три кольца сцеплены так, как показано на рисунке.

Рис. 4

Вырежи кольца и, разрезав только одно из них, сделай зацепление, показанное на рисунке 4.

4. Закончи раскраску фигуры так, чтобы соседние области были одного цвета. Используй только те цвета, которые есть на рисунке 5.

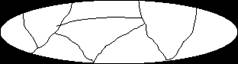
Рис. 5.

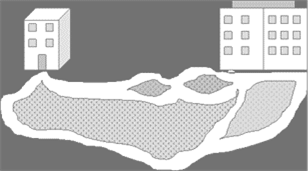
3. Два дома соединены пешеходными дорожками. Нарисуй линией путь, по которому можно обойти все дорожки только по одному разу, если прогулку надо начать и закончить у дома, изображенного слева (рис. 6).

Рис. 6.

4. Катя, Маша и Петя нарисовали пейзажи, которые они видят. Найди и обозначь нужной буквой тот пейзаж, который нарисовал каждый из детей (рис. 7).

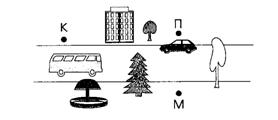
рис. 7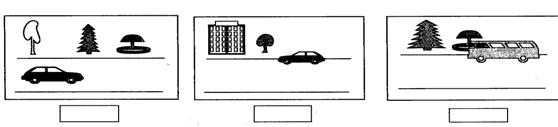

5. Задания на подборку фигуры заданной формы и размера, типа «Подбери заплатку». Задания выполняются путем логического мышления; предположения тетей проверяются практически, так как все детали съёмные.

Фрагмент урока в 1-м классе.

Тема: Размер.

Этап урока: повторение изученного.

На классной доске и на столе у каждого ученика разноцветные геометрические фигуры, изученные на предыдущем уроке (разного размера).

- в какой руке мы держим ручку, карандаш когда пишем, рисуем? (В правой).

Уточнение направлений налево, направо и взаимного расположения предметов в пространстве (вверху, низу):

- покажите правую руку, левую руку.

- кто сидит слева от Коли?

- какие предметы находятся справа от Кати?

- что в классе находится вверху классной доски? (таблица)- что находится внизу доски? (прикреплены геометрические фигуры.)

Ребята! Внимательно посмотрите на рисунок в задаче № 1 и расположите эти фигуры так, как показано на рисунке.

Один из учеников выполняет задание на доске, а остальные - на рабочих местах.

- Какая фигура расположена слева? Как называется фигура, расположенная справа?

- Какие фигуры расположены слева от круга? А какие – справа от квадрата?

- Какая фигура находится между кругом и прямоугольником? Между треугольником и кругом?

- Переложите прямоугольник так, чтобы он оказался справа от треугольника и слева от овала? Как это можно сделать?

- Куда можно переложить треугольник, чтобы он был справа от круга? и т.д.

(последние задания дети выполняют задание на доске и на рабочих местах)

Фрагмент урока в 1 классе.

Тема: Замкнутые и незамкнутые кривые.

Этап урока: Повторение изученного материала.

(вначале проводится проверка знаний по материалу урока № 11, а перед переходом к новой теме с целью повторения основных геометрических фигур и формирования пространственных представлений предлагаю провести игру)

Игра «Составь узор» - работа с математическим набором:

Положи зеленый кружок так, чтобы он был выше красного квадрата, но ниже красного треугольника. Справа от зеленого кружка положи желтый треугольник, а слева -желтый квадрат. За желтым треугольником положи красный кружок так, чтобы между ним и желтым треугольником находился зеленый квадрат. (ответ проверяется по заранее подготовленному узору на доске, закрытому шторкой или листом ватмана).

У детей на столах должен получиться рисунок (узор):

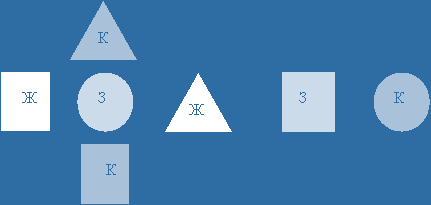
После показа узора на доске задаю дополнительные вопросы:

- Какая фигура следует за зеленым квадратом?

- Какая фигура предшествует желтому треугольнику?

- Какая фигура находится между двумя желтыми фигурами?

-Какие фигуры находятся ниже красного треугольника?

Этап урока: изучение нового материала.

При выполнении задачи № 3 задаю дополнительные вопросы:

- какие фигуры находятся над замкнутой кривой?

- какие фигуры расположены под кривой?

- какая фигура расположена справа от кривой линии? и т.п.

"Развитие пространственного мышления младших школьников"

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

21.01.2020