«Решение геометрических задач ЕГЭ по математике из части С»

 «Решение геометрических задач ЕГЭ по математике из части С»

Преподавая много лет в старших классах, я увидела, что учащиеся имеют очень большие затруднения в изучении геометрии. На экзаменах по математике задача по геометрии является самым трудным заданием. Окончив 9 классов и изучив планиметрию, ученик должен, казалось бы, уметь решать любую задачу в данном курсе. Однако учащиеся не только не умеют решать задачи, даже боятся за них браться. Я не могла согласиться с таким положением дел. Мне было бы очень обидно терять баллы на этих задачах.Помочь учащимся можно было бы, заинтересовав их изучением геометрии и организовав их деятельность таким образом, чтобы был результат.Необходимо постоянно повторять, контролировать, организовывать взаимопроверку и самопроверку на уроках и во внеурочное время, чтобы вызывать постоянный интерес к решению задач.

Рассмотрим некоторые задачи:

Расстояние между прямыми и плоскостями

1. Задание 14 

В правильной четырёхугольной пирамиде SABCD сторона AB основания равна а высота SH пирамиды равна 3. Точки M и N — середины рёбер CD и AB, соответственно, а NT — высота пирамиды NSCD с вершиной N и основанием SCD.

а) Докажите, что точка T является серединой SM.

б) Найдите расстояние между NT и SC.

Решение.

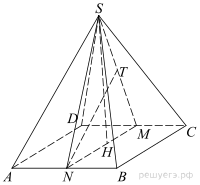
а) Точка H лежит на отрезке MN. Так как NC = ND, то TC = TD. Это означает, что точка T лежит на SM. Таким образом, точки T и H лежат в плоскости SNM, перпендикулярной плоскости ABC.

Значит, треугольник SNM равносторонний, а NT — его высота. Следовательно, T — середина SM.

б) Пусть E — основание перпендикуляра, опущенного из точки T на прямую SC. 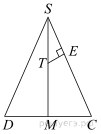Прямые NT и TE перпендикулярны, так как NT — высота пирамиды NSCD. Поскольку отрезок TE перпендикулярен как прямой SC, так и прямой NT, его длина и есть искомое расстояние.

Прямоугольные треугольники SET и SMC подобны, следовательно, откуда

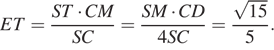
Ответ: б)

2. Задание 14 

Основанием прямой треугольной призмы ABCA₁B₁C₁ является прямоугольный треугольник ABC с прямым углом C. Грань ACC₁A₁ является квадратом.

а) Докажите, что прямые CA₁ и AB₁ перпендикулярны.

б) Найдите расстояние между прямыми CA₁ и AB₁, если AC = 4, BC = 7.

Решение.

а) Заметим, что как катеты прямоугольного треугольника, и , поскольку призма прямая. Тогда по признаку перпендикулярности прямой и плоскости . Кроме того, как диагонали квадрата.

Имеем: − наклонная, − проекция на плоскость , − прямая в плоскости , перпендикулярная проекции. Тогда по теореме о трёх перпендикулярах что и требовалось доказать.

б) Пусть M − середина AC₁. Тогда искомое расстояние равно расстоянию от точки M до прямой AB₁, поскольку прямая A₁C перпендикулярна AB₁C₁. Это расстояние равно половине высоты прямоугольного треугольника AB₁C₁, проведённой к гипотенузе:

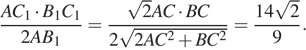
Ответ:б)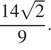

Сечения многогранников

1. Задание 14 

В основании правильной треугольной призмы ABCA₁B₁C₁ лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A₁C₁.

а) Постройте сечение призмы плоскостью BAN.

б) Найдите периметр этого сечения.

Решение.

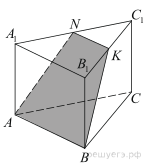
а) Проведём через точку N прямую, параллельную прямой AB, до пересечения с прямой B₁C₁ в точке K. Трапеция ABKN — искомое сечение.

б) Имеем A₁N= 3, так как точка N — середина ребра A₁C₁. Значит, Аналогично BK = 5.

Далее NK = 3, как средняя линия треугольника A₁B₁C₁. Следовательно, искомый периметр сечения равен 6 + 5 + 5 + 3 = 19.

Ответ: 19.

2. Задание 14 

В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.

а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.

б) Найдите площадь сечения.

Решение.

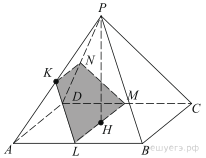
а) В плоскости ABP через точку K проведем прямую, параллельную прямой PB до пересечения ее с прямой AB в точке L — середине AB. В основании ABCD через точку L проведем прямую, параллельную прямой BC до пересечения ее с ребром СD в точке M — его середине. По признаку параллельности прямой и плоскости плоскость KLM параллельна прямым PB и BC. Прямая LM параллельна прямой AD, следовательно, она параллельна плоскости APD, а, значит, плоскость KLM пересекает плоскость APD по прямой, параллельной LM и пересекает ребро PD в его середине N.

Таким образом, искомое сечение ― трапеция KLMN.

б) Отрезки KL и MN равны, как средние линии равных правильных треугольников ABP и DCP, а отрезок LM ― средняя линия квадрата ABCD, следовательно, построенное сечение ― равнобедренная трапеция, в которой LM = 4, 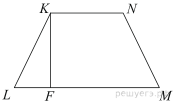KL = KN = MN = 2. Проведем высоту KF этой трапеции. Тогда и из прямоугольного треугольника KLF находим

Окончательно получаем

Ответ: