Решение линейных неравенств

Тема урока «Неравенства и система неравенств с одной переменной»

Тип урока: урок повторения знаний и умений.

Цели урока.

Образовательные:

а) Обобщение и систематизация знаний учащихся по теме “Неравенства и система неравенств”.

б) Проверка знаний учащихся в ходе самостоятельной работы.

Развивающие:

а) Развивать навыки реализации теоретических знаний в практической деятельности.

Воспитывающие:

а) Воспитание умения работать самостоятельно.

б) Воспитание умения выдерживать регламент времени, отведенного на решение каждого задания.

Знания, умения, навыки и качества, закрепят ученики в ходе урока.

1. Знать и понимать алгебраическую трактовку отношений “больше” и “меньше” между числами; знать и применять свойства числовых неравенств;
2. Знать и понимать термины “решение неравенства с одной переменной”, “решение системы неравенств с одной переменной”;
3. Решать линейные неравенства с одной переменной и их системы;
4. Находить множество решений квадратного неравенства с одной переменной, опираясь на графическое изображение.

Необходимое оборудование и материалы: компьютер, видеопроектор.

Ход урока

1. Мотивация учащихся

а)  Приветствие учащихся, проверка их готовности к уроку.

Здравствуйте, ребята. Сегодня у нас на уроке гости. Улыбнёмся гостям, друг другу, мне и начнём урок с хорошим настроением.

Сегодня на уроке мы закрепим свои знания, умения  по теме «Неравенства и система неравенств с одной переменной», вы должны:

1. Знать и понимать алгебраическую трактовку отношений “больше” и “меньше” между числами; знать и применять свойства числовых неравенств;
2. Знать и понимать термины “решение неравенства с одной переменной”, “решение системы неравенств с одной переменной”;
3. Решать линейные неравенства с одной переменной и их системы;
4. Находить множество решений квадратного неравенства с одной переменной, опираясь на графическое изображение.

Результаты вашего плодотворного труда- на экзаменах покажет хорошая оценка.

И эпиграф к уроку у нас следующий : «Дорогу осилит идущий,  а математику – мыслящий!»

Я уверена, что мы осилим математику и сдадим экзамены с первого раза.

Урок у нас поделен на несколько блоков.

И первый блок – это повторение теоретического материала по теме. Ребята, я вам раздаю вопросы, а вы в парах обсудите, вспомните.  И если кто готов, поднимаем руки и отвечаем. Чем смелее и быстрее вы будете работать, вы сможете набрать себе больше баллов и получить высокую оценку за урок.

Листы самооценки у вас на столах. Это для вас не новое.

На это задание я вам даю 2 минуты. Пожалуйста, приступайте к обсуждению. Можете подглядывать в учебники глава 2, стр. 83.

НУ ЧТО ГОТОВЫ ?– 2 МИНУТЫ

- Что такое числовое неравенство?  (Запись, в которой знаком неравенства соединены два числа или два числовых выражения, называют числовым  неравенством).

- Что такое неравенство с одной переменной?  (Неравенство, как и уравнение содержит одну букву (Переменную)). Вместо знака равно, содержат знаки меньше , больше…

- Какие неравенства называются строгими, а какие нестрогими? (Неравенства, которые содержат знаки < или >  называют строгими, а неравенства которые содержат знаки  ≤ или ≥ называют нестрогими.)

- Что значит решить неравенство с одной переменной?  (найти множество решений  исходного неравенства или установить, что их нет. )

-Какие неравенства называются равносильными? (Неравенства, которые имеют одни и те же решения, называются равносильными неравенствами).

А как вы думаете неравенства, которые не имеют решений равносильные? ( неравенства, не имеющие решений, также называют равносильными)

- Какие неравенства называются квадратными?  ( неравенства следующих  видов…)

ПРОВЕРИМ ПО ЭКРАНУ -ВСЁ ЛИ ВЫ ПРАВИЛЬНО ВСПОМНИЛИ?

Поставили себе за каждый правильный ответ 1 балл.

Следующий блок урока:

Тест по проверке усвоения теоретического материала: (обратите внимание вопросы начинаются с линейных неравенств и плавно переходят в квадратные неравенства. Поэтому будьте внимательны. На это задание 10 минут

1.    A ) Число 4 является решением неравенства 2x– 11≥0
а) да   б) нет  в) нельзя ответить на поставленный вопрос

B)  Являются ли равносильными неравенства 3,2 + 0,9x<4x – 4,6 и 0,9x – 4x< - 3,2 – 4,6?
а) да   б) нет  в) нельзя ответить на поставленный вопрос

C)  Являются ли равносильными неравенства 11x – 3x + 9x>7 +2 – 21 и 17x> - 12?
а) да   б) нет  в) нельзя ответить на поставленный вопрос

D)    Являются ли равносильными неравенства 2 +9x<11 и 10 + 45x>55?

а) да   б) нет  в) нельзя ответить на поставленный вопрос

            E)  Являются ли равносильными неравенства – 2x>24 и x< - 12?
            а) да   б) нет  в) нельзя ответить на поставленный вопрос

   
          2.     Является ли число 3 решением системы уравнений:

А)                      B )-

С-                      Д-

3.  На каком из рисунков дано правильное изображение числового множества, являющегося решением соответствующего неравенства:

4.  Запишите с помощью числового промежутка:

A  а) ( 2; 11)   б) ( 2; + ∞)  в) ( - ∞; 11)

Bа) ( 3; 7)   б) ( 7; + ∞)  в) ( - ∞; 3 )

Cа) ( - 12; 11)    б) ( -∞; - 12 )   в) ( 11 ; + ∞)

D а) ( - 2; 0)   б) ( 0 ; + ∞)  в) ( - ∞; - 2)

5.       Какому промежутку соответствует данное неравенство:

A       x< - 3   а) (- 3; +∞)  б) ( 0; - 3) в) (- ∞; - 3)
B      11 <x< 15  а) ( 15; +∞)  б) ( 11;   в) (11; 15)
C      - 2,9 <x<0,3   а)  ( - ∞; 0,3)  б) ( 0,3; +∞)   в) ( - 2,9; 0,3)
D      x> 7,1   а)  ( - ∞; 7,1 )   б) ( 7,1; + ∞ )   в)  ( 1; 7 )

6.      Какие из неравенств вы бы назвали квадратными неравенствами

1) 6х²– 13х>0;                          2) x²– 3x – 14>0;                      3) (5 + x)(x – 4)>7;

4) 8x²>0;                                    5) (x – 5)² – 25>0;                    6) x(x – 9) – x²>0?

УЧИТЕЛЬ: Следующий блок, ребята практический  он поделён на 2 части. Первая часть «Решение квадратных неравенств» и 2 часть «Решение системы неравенств»

Ребята работа эта проводится не для того чтобы кому-то поставить плохую оценку, а для того чтобы выяснить, кто как понял и кому надо еще потренироваться над данной темой.

Учитель: И так нам предстоит  решить квадратные неравенства. Кто ребята помнит алгоритм решения квадратных неравенств?

Посмотрим на экран и проверим правильно ли сказали?

ВКЛЮЧАЮ ЭКРАН

Алгоритм решения квадратных неравенств.

1. Подготавливаем неравенство к решению путём тождественных преобразований. Если неравенство уже готово, этот пункт пропускаем.

2. Делаем из неравенства уравнение. Решаем его, находим корни.

3. Рисуем ось Х, отмечаем точками корни уравнения. Если исходное неравенство нестрогое, точки - черные (закрашенные). Если строгое - белые (пустые внутри).

4. Схематично рисуем параболу по исходному выражению. Парабола будет  вниз ветвями, если  в исходном выражении перед x² стоит минус. Запомните! Минус перед одночленом с квадратом икса всегда переворачивает параболу.

5. Определяем области +/- на рисунке. Выбираем нужные области по исходному неравенству и записываем ответ.

- Допустим, корней уравнения нет. Тогда и множество решений исходного неравенства пустое.

- Пусть квадратное уравнение имеет единственный корень . Тогда решение неравенства сводится к выбору промежутка значений, как в линейных неравенствах.

Вспомнили. Тогда приступаем:  Вас 5 человек, и пять уравнений. Поэтому здесь все смогут заработать баллы. За каждое правильное уравнение у доски 3 балла.  Я думаю 15 минут на эту работу нам достаточно.

Кто первый желает?

Задание: 1) – х² + 8х – 12 > 0.

Решение: Пусть у =  – х² + 8х – 12.

а =  – 1, а<0. Ветви параболы направлены вниз.

– х² + 8х – 12 = 0; D =  82 – 4(– 1)(– 12) = 16 = 42, D > 0

x1 = 6; x2 = 2.

Схематически строим график функции.

Ответ:  х Є (2; 6).

2.  х²+ 2х – 48 < 0
3.  – 2х² – 5х +18 ≤ 0

4.  25х²+ 30х +9 > 0
5.   – 2х²+7х > 0

Следующая часть практического блока «Решение систем неравенств».

Давайте сначала вспомним алгоритм решения системы линейного неравенства.

Может кто из вас помнит и сразу у доски будет решать с пояснением?

Решите систему неравенств:

Ход решения б) группируем(с неизв. в левую, числа в правую)  в) подобные слагаемые  г) решаем каждое нер-во   д) изображаем решение каждого неравенства на одной числовой оси   е) ищем общие решения(пересечение)  ж) записываем ответ(два вида – промежуток, неравенство).Ответ: ( 2; 3 )  или 2 <x< 3

 А теперь вспомним алгоритм решения системы квадратного неравенства.

Рассмотрим систему квадратных неравенств из двух уравнений с одним неизвестным:

.

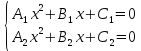Алгоритм решения этой системы абсолютно аналогичен алгоритму при решении системы линейных неравенств:

1.      Решить первое неравенство, найти его промежутки значений.

2.      Решить второе неравенство, найти промежутки значений второго неравенства.

Найти пересечение двух множеств значений Х.

Решим самостоятельно. На эту работу 10 минут.

1. 

Ответ: ( ;  ) или <x<

2.Сборник заданий стр. 124. № 4.21 (№1)

ПОДВЕДЕНИЕ ИТОГОВ. Рефлексия. ПРОДОЛЖИ ПРЕДЛОЖЕНИЯ

Подведём итоги. Кто сколько набрал баллов.

6.Домашнее задание. Сборник заданий. Стр. 124-125

4.21 (2), 4.20; 4.22.

Повторить теорию. На следующем уроке продолжим повторять систему неравенства квадратных уравнений.

Скачано с www.znanio.ru