Решение практико - ориентированных задач для 9 класса

 Элективная программа по теме:

 «Решение практико - ориентированных задач»

9 класс

всего 30 часов

Составила:

Хулап Е.А.

Владивосток, 2020 г.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Социальной адаптации наших выпускников во многом способствует качественная базовая математическая подготовка. Без нее невозможна постановка образования современного человека. В школе математика служит опорным предметом для изучения смежных дисциплин. В после школьной жизни реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной общеобразовательной подготовки, в том числе и математической.

Все больше специальностей, требующих высокого уровня образования, связано с непосредственным применением математики. Таким образом, расширяется круг школьников, для которых математика становится профессионально значимым предметом.

В отдельных случаях преподавание математики может рассматриваться как связующая дисциплина общеобразовательных и профессиональных знаний. Особенно это верно при формировании с помощью математики профессионального мышления. Такое профессиональное мышление можно условно обозначить как социально-экономическое мышление в зависимости профессиональной направленности студентов. Само формирование мышления может происходить как непосредственно через прикладной характер курса математики.

 Они показывают прикладной характер математических знаний, Практико-ориентированная деятельность - это деятельность, направленная на осуществление связи школьного курса с практикой, что предполагает формирование у учащихся умений, необходимых для решения средствами математики практических задач.

Для реализации целей практико-ориентированного обучения необходимо включать  в учебный процесс задачи с практическим содержанием.  активизируют мыслительную деятельность, развивают интерес к математике как к предмету. Именно поэтому при изучении данного элективного курса у девятиклассников повысится возможность намного полнее удовлетворить свои интересы и запросы в математическом образовании. Элективный курс «решение практико-ориентированных задач» займёт значимое место в образовании старшеклассников, так как может научить их применять свои умения в нестандартных ситуациях. С другой стороны, курс позволяет выпускнику основной школы приобрести необходимый и достаточный набор умений по решению задач и лучше подготовиться к обучению в старшем классе, где математика является профилирующим предметом.

Предлагаемый элективный курс «Решение практико-ориентированных задач" позволяет решать задачи на предпрофильной подготовке учащихся 9 классов.

Курс рассчитан на 30 часов.

Как показывает практика, одним из эффективных способов развития предметной грамотности являются практико-ориентированные задачи.

Задачи, которые раскрывают приложения математики в окружающей нас действительности, в смежных дисциплинах, знакомят  с ее использованием в  технологии и экономике современного производства, в сфере обслуживания, в быту, при выполнении трудовых операций. Способы представления статистических данных. Работа с  таблицами, диаграммами.

Кроме того, решение задач практического содержания способно привить интерес ученика к изучению математики. Они базируются на знаниях и умениях, и требуют умения применять накопленные знания в практической деятельности.

Целесообразность введения данного элективного курса состоит и в том, что содержание курса, форма его организации помогут школьнику через практические занятия оценить свой потенциал с точки зрения образовательной перспективы и предоставят ему возможность работать на уровне повышенных возможностей. Элективный курс «решение практико-ориентированных задач» способствует развитию у выпускника функциональной грамотности. Такой подход к обучению позволяет в дальнейшем выпускнику школы решать проблемы, возникающие в жизни и в профессиональной деятельности

Цель курса: углубление знаний учащихся о различных методах решения задач и базовых математических понятий, используемых при обосновании того или иного метода решения; формирование у школьников компетенций, направленных на выработку навыков самостоятельной и групповой исследовательской деятельности.

Задачи курса:

1.       Разобрать задачи практико-ориентированного блока из открытого банка ОГЭ.

2. Классификация способов решения нестандартных задач, углубление теоретических основ школьной математики для решения каждого вида задач.
3.Интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для полноценной жизни в обществе.

4. Воспитание личности в процессе освоения математики и математической деятельности, развитие у учащихся самостоятельности и способности к самоорганизации.

ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ СОДЕРЖАНИЯ КУРСА:

В результате изучения курса учащиеся овладевают следующими способами деятельности:

·       умеют анализировать, сопоставлять, сравнивать, систематизировать и обобщать;

·       умеют самостоятельно работать с математической литературой;

·       имеют представление о математике как форме описания и методе познания действительности;

·       знают основные приемы решения нестандартных задач, понимают теоретические основы способов решения задач;

·       умеют решать задачи различными методами;

·       умеют проводить самоанализ деятельности и самооценку ее результата.

ФОРМЫ КОНТРОЛЯ

Смысл предпрофильного курса заключается в предоставлении каждому ученику «индивидуальной зоны потенциального развития», поэтому – нельзя требовать от каждого ученика твердого усвоения каждого «нестандартного приема». Специальный зачет или экзамен по курсу не предусмотрен, но предлагаются некоторые варианты выполнения учениками зачетных заданий:

1. Решение учеником в качестве индивидуального домашнего задания предложенных учителем задач из того списка, что завершает каждый модуль и называется «Упражнения для самостоятельной работы», т.к. осознание и присвоение учащимися достигаемых результатов происходит с помощью рефлексивных заданий. Подбор индивидуальных заданий осуществляется с учетом уровневой дифференциации, причем выбор делают сами ученики, оценивая свои возможности и планируя перспективу развития.
2. Решение группой учащихся в качестве домашнего задания предложенных учителем задач из того же раздела. Работа в группе способствует проявлению интереса к учению как деятельности.

Учащимся, ориентированным на выполнение заданий более высокого уровня сложности, предлагается:

• Самостоятельное изучение некоторых вопросов курса с последующей презентацией.

• Самостоятельное решение предложенных задач с последующим разбором вариантов решений.

• Самостоятельное построение метода, позволяющего решить предложенную задачу.

• Самостоятельный подбор задач на изучаемую тему курса из дополнительной математической литературы.

Для реализации целей и задач данного элективного курса предполагается использовать следующие формы учебных занятий: лекции, семинары, практикумы. Также на протяжении всего курса учащимся можно предложить выполнение проекта по одной из тем программы, результаты которых будут представлены на итоговых занятиях курса.

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

Список литературы:

1. Республиканский журнал «12-летнее образование» №6, №8 2010г,2011г;

2.  Перминова Л.М. Минимальное поле функциональной грамотности (из опыта С.-Петербургской школы)//Педагогика. - 1999. - №2. - С.26-29; 
 3. «Национальный план действий на 2012-2016 годы по развитию функциональной грамотности школьников»;

4. Нарикбаева Л.М., Калиева С.И. Подготовка будущего учителя к работе с одаренными детьми: Методическое пособие. – Алматы: Изд-во АГУ им. Абая, 2001. – 45 с;

5. Лебедев О.Е. Компетентностный подход в образовании // 

Школьные технологии. –2004 г. – №5;

6. Иванов Д.А. Компетенции и компетентностный подход в современном образовании//Завуч.-2008.-№1;

7.Печёнкина Е.Н. Практико-ориентированные задачи на уроках математики в основной школе // Электронный ресурс [http://rudocs.exdat.com/docs/index-100680.html]

9.Колягин Ю.М. и Пикан В.В. О прикладной и практической направленности обучения математике : Математика в школе. 1985. © 6.

10.  Ященко: ОГЭ-2020. Математика. 20 тренировочных вариантов ОГЭ

ПРАКТИКО - ОРИЕНТИРОВАННЫЕ ЗАДАНИЯ 1-5 ОГЭ-2020.

Вариант -  1.

Прочитайте внимательно текст и выполните задания 1—5.

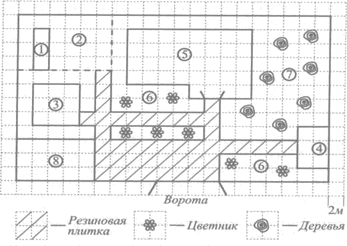
 На плане изображён загородный дачный участок садовод­ства «Садовод», улица Абрикосовая, 65. (Сторона каждой клетки на плане равна 2 м.) Участок имеет прямоугольную форму. Въезд и выезд осуществляются через единственные ворота. При въезде на участок слева от ворот находится баня, а справа = гараж , отмеченный цифрой 4.

Площадь, занятая гаражом, равна 50 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеются квадратный бассейн, расположенный рядом с баней, и теп­лица, построенная на территории огорода (огород отмечен цифрой 2). Справа от жилого дома имеются посадки фруктовых деревьев: яблоневых, вишнёвых, абрикосовых, грушевых.

Перед жилым домом и рядом с гаражом разбиты клумбы с цветами. Перед домом растут розы, а рядом с баней — гладиолусы. Перед баней имеется площадка, вымощенная резиновой плиткой размером 2 м х 2 м. Все дорожки внутри участка имеют ширину 2 м и вымощены такой же плиткой.

К домохозяйству подведены электричество и вода. Имеется магистральное газоснабжение.

1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

2. Резиновая плитка продаётся в упаковках по 6 штуки. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки и площадку перед гаражом?

3. Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.

4. Найдите наименьшее расстояние (в метрах) от жилого дома до входных ворот.

5. Хозяин планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: газовое или электрическое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электро-энергии и их стоимость даны в таблице.

Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?

Вариант -  2.

Прочитайте внимательно текст и выполните задания 1—5.

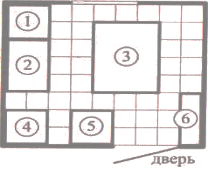Владелец собирается провести ремонт своей квартиры, расположен­ной по адресу: г. Близкий, ул. 5-я Смородиновая, д. 14, кв. 6. На плане изображена будущая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,4 м. Кухня име­ет прямоугольную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно.

Справа от двери будут поставлены полки для посуды, слева от двери будет холодильник. Слева от холодильника, в углу кухни, предполагается смонтировать раковину. Между раковиной и газовой плитой будет собран буфет, отмеченный на плане цифрой 2. Площадь, занятая буфетом, по плану будет равна 0,96 кв. м. В центре кухни планируется поставить обеденный стол.

Пол кухни (в том числе там, где будет стоять мебель и бытовая тех­ника) планируется покрыть плиткой размером 40 см х 40 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический по­догрев пола. Чтобы сэкономить, владелец не станет подводить, обогрев под холодильник, газовую плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,32 кв. м между буфетом и раковиной.

1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите по­следовательность четырёх цифр.

2. Плитка для пола продаётся в упаковках по 5 штук. Сколько упаковок плитки нужно купить, чтобы покрыть пол кухни?

3.  Найдите площадь той части кухни, на которой будет смонтирован электрический подогрев пола. Ответ дайте в квадратных метрах.

4.  Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах.

5.  Владелец квартиры выбирает холодильник из двух моделей А и Б. Цена холодильников и их среднее суточное потребление электроэнергии указаны в таблице.

 Цена электроэнергии составляет 4 рубля за кВт • ч.

Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электро­энергии окупит разницу в цене этих холодильников? Ответ округлите до целого числа.

Вариант -  3.

Прочитайте внимательно текст и выполните задания 1—5.

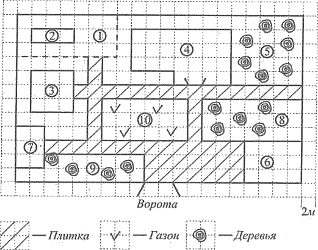
На плане изображён загородный дачный участок садо­водства «Дружба», улица Медовая, 32. (Сторона каждой клетки на плане равна 2 м.)

Участок имеет прямоугольную форму. Въезд и выезд осуществляются через единственные ворота.

При въезде на участок справа от ворот находится гараж, а слева — баня, отмеченная цифрой 7.

Площадь, занятая гаражом, равна 48 кв. м. Жилой дом находится в глубине территории. Справа от жилого дома расположен вишнёвый сад (отмечен цифрой 5). Перед жилым домом имеются посадки фруктовых деревьев: абрикосовых, яблоневых, грушевых (отмечены цифрой 8). Все дорожки внутри участка имеют ширину 2 м и вымощены тротуарной плит­кой размером 1 м х 1 м. Помимо жилого дома, гаража и бани, на участке имеется беседка квадратной формы.  Позади беседки, слева от дома, расположены огород (отмечен цифрой 1) и теплица. Перед домом находится газон, отмеченный на плане числом 10. К домохозяйству подведено электричество и имеется магистральное газоснабжение.

1. Для объектов, указанных в таблице, определите, какими числами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

2.  Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.

3.  Найдите расстояние (в метрах) от жилого дома до теплицы. Расстояние измеряйте между двумя ближайшими точками по прямой.

4.  Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки и площадку перед гаражом?

5.  Хозяин планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: газовое или электрическое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимость даны в таблице.

Обдумав оба варианта, хозяин решил установить газовое оборудова­ние. Через сколько полных часов непрерывной работы отопления эконо­мия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?

Вариант -  4.

Прочитайте внимательно текст и выполните задания 1—5.

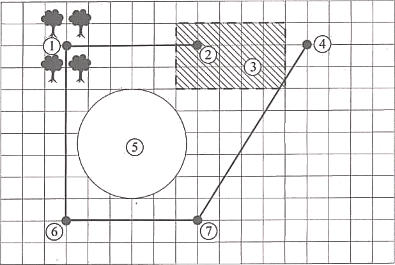
На плане изображена местность, прилегающая к озе­ру Круглому. Для удобства план нанесён на квадратную сетку, сторона квадрата равна 500 м. Населённые пункты обозначены на плане жирными точками.

Рядом с озером Круглое находится болото, обозначенное на плане штриховкой. На болоте расположен хутор Камышино. От хутора Камышино проложена дорога к деревне Дубки, вокруг которой имеются дубо­вые рощи. Далее дорога идёт к селу Большое, расположенному по другую сторону озера от хутора Камышино. Село Большое соединено также до­рогой с деревней Малая, обозначенной на плане цифрой 7. Деревня Ма­лая, в свою очередь, соединена дорогой с деревней Дальней (отмечена цифрой 4). Большая часть изображённой на плане местности — это по­ля, используемые для выращивания злаков.

1.   Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

2.  Автомобиль расходует 9 л топлива на 100 км пути. Сколько литров топлива израсходует автомобиль при поездке из хутора Камышино в деревню Малая по имеющимся дорогам?

3.  Найдите площадь болота, отмеченного на плане. Ответ дайте в квадратных километрах.

4.  Найдите расстояние по прямой от хутора Камышино до села Большое. Ответ дайте в метрах.

5.  Для улучшения сообщения между населёнными пунктами планируется построить ещё одну дорогу: из хутора Камышино в деревню Малая либо из хутора Камышино в деревню Дальняя. Дорога должна соединить населённые пункты по прямой. Цена прокладки дороги по полю равна 10 млн рублей за 1 км, по болоту — 20 млн рублей за 1 км. Из указанных двух вариантов дороги выберите тот, стоимость которого будет ниже. В ответе укажите стоимость (в млн рублей) выбранного варианта дороги.

Вариант -  5.

Прочитайте внимательно текст и выполните задания 1—5.

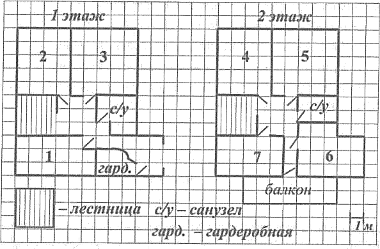
Сергей Васильевич — крупный учёный, его исследования востребова­ны в промышленности. На рисунке изображён план двухэтажного дома (сторона клетки соответствует 1 м), в котором он проживает с женой Ва­лентиной Петровной и двумя детьми: Костей и Викой. На первом этаже гостиная — самая большая по площади комната. Кухня имеет вытянутую форму, её длина в два раза больше ширины, она тоже находится на первом этаже. Рядом с гостиной расположена столовая. Комната Кости располо­жена на втором этаже над кухней, его комната — соседняя с комнатой сестры Вики. Комната родителей расположена над столовой, рядом с ней просторный кабинет Сергея Васильевича.

1.   Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

2.   На втором этаже расположен открытый балкон. На его бортике закреплены деревянные поручни. Определите их общую протяжённость (в метрах)

3.   Найдите площадь комнаты Вики. Ответ дайте в квадратных метрах.

4.   В каждой из пронумерованных комнат, кроме Костиной, два окна, а в Костиной — всего одно. Других окон нет. Площадь стекла для каждого окна составляет 3 кв. м. Стоимость окон при установке складывалась из стоимости стекла (3000 рублей за квадратный метр окна) и стоимости монтажа и фурнитуры (7000 рублей за каждое окно). Определите общую стоимость всех окон и их установки. Ответ дайте в рублях.

5.   После постройки дома денег на внутреннюю отделку осталось меньше, чем планировалось первоначально, поэтому пришлось экономить. В гостиной и столовой предполагалось класть паркетную доску, но обошлись ламинатом, а на сэкономленные деньги приобрели туристические путёвки в Крым. Ламинат и паркетная доска продаются только в упаковках. Каждая упаковка содержит одинаковое число квадратных метров материала.

Сколько рублей в результате удалось сэкономить на путёвки?

Вариант -  6.

Прочитайте внимательно текст и выполните задания 1—5.

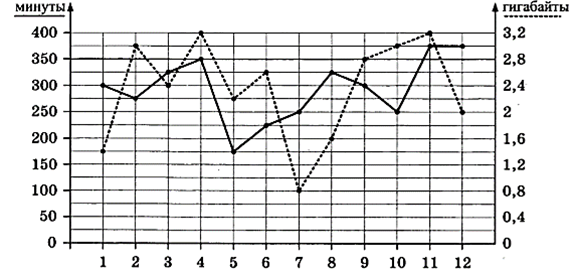На графике точками изображено количество минут, потраченных на исходящие вызовы, и количество гигабайтов мобильного интернета, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2018 года. Для удобства точки, соответст­вующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответ­ственно.

В течение года абонент пользовался тарифом «Стандартный», абонентская плата по кото­рому составляет 400 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:

•          пакет минут, включающий 350 минут исходящих вызовов на номера, зарегистри­рованные на территории РФ;

•          пакет интернета, включающий 2,8 гигабайта мобильного интернета;

•          пакет SMS, включающий 150 SMS в месяц;

•          безлимитные бесплатные входящие вызовы.

Стоимость минут, интернета и SMS сверх пакета указана в таблице.

Абонент не пользовался услугами связи в роуминге и не звонил на номера, зарегистриро­ванные за рубежом. За весь год абонент отправил 140 SMS.

1. Определите, какие месяцы соответствуют указанному в таблице количеству израсходованных минут.

Заполните таблицу, в ответ запишите подряд числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответ нужно записать число 51118).

2.    Сколько рублей потратил абонент на услуги связи в ноябре?

3.    Сколько месяцев в 2018 году абонент превышал лимит по пакету мобильного интернета?

4.    Сколько месяцев в 2018 году абонент превышал лимит либо по пакету минут, либо по пакету мобильного интернета?

5. В конце 2018 года оператор связи предложил абоненту перейти на новый тариф. Его условия приведены в таблице.

*исходящие вызовы на номера, зарегистрированные на территории РФ.

Абонент решает, перейти ли ему на новый тариф, посчитав, сколько бы он потратил на ус­луги связи за 2018 г., если бы пользовался им. Если получится меньше, чем он потратил фактически за 2018 г., то абонент примет решение сменить тариф.

Перейдёт ли абонент на новый тариф? В ответе запишите ежемесячную абонентскую плату по тарифу, который выберет абонент на 2019 год.

Решение задач на проценты.

Задача 1.

 На сколько процентов увеличится площадь квадрата, если его сторону увеличить на 30%?

Решение. Если сторона квадрата равна а, то площадь квадрата S=а². После увеличения стороны на 30% ее длина составит 130% от а. Это 1,3а. Новая площадь S₁=(1,3a)²=1,69a². Разница составила 0,69а². Обращаем десятичную дробь 0,69 в проценты и получаем 69%.

Ответ: Если сторону квадрата увеличить на 30%, то площадь квадрата увеличится на 69%.

Задача 2

 Яблоки, содержащие 70% воды, потеряли при сушке 60% своей массы. Сколько процентов воды содержат сушеные яблоки?

Решение. Пусть было х яблок по массе. В них содержится 70% воды, значит, 30% сухого концентрата. 30% от х – это 0,3х. После сушки яблок это количество 0,3х сухого вещества так и остается. Известно, что при сушке яблоки потеряли 60% своей массы. Следовательно, осталось 40% от х, Это 0,4х. То, что осталось, примем за 100%. В этой массе 0,3х сухого вещества. Узнаем, сколько это процентов.

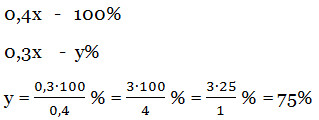
В сушеных яблоках 75% сухого вещества, значит, воды в сушеных яблоках 100%-75%=25%.

 Ответ: в сушеных яблоках 25% воды.

Задача 3.

 Свежие грибы содержат 90% влаги, сушеные – 12%. Сколько сушеных грибов получится из 13,2 кг свежих?

Решение. Пусть из 13,2 кг свежих грибов получится х кг сушеных грибов. Тогда сухого вещества в х кг будет содержаться 100%-12%=88%. Получается 0,88х кг. В 13,2 кг свежих грибов сухого вещества содержится 100%-90%=10%. В килограммах получается 0,1∙13,2=1,32 кг. Имеем равенство: 0,88х=1,32, отсюда х=1,32 : 0,88;

х=1,5 кг.

Ответ: из 13,2 кг свежих грибов получается 1,5 кг сушеных грибов.

Задача 4.

Сколько литров воды нужно разбавить с 300 г соли для получения раствора с концентрацией 15%?

Решение. Пусть нужно х граммов воды разбавить с 300 г соли для получения раствора с концентрацией 15%. Выразим количество соли в х г воды 15%-го раствора. Это 15% от х. Получаем 0,15х г. По условию соли 300 г. Получаем равенство:

0,15х=300, отсюда х=300:0,15=30000:15=2000 г = 2 л воды.

Ответ: нужно разбавить 2 л воды.

Задача 5.

 В раствор соленой воды массой 600 г с концентрацией 15% добавили раствор соленой воды массой 240 г с концентрацией 50%. Сколько процентов соли в полученной смеси?

Решение. В 600 г соленой воды с концентрацией 15% содержится 15% от 600 г соли. Это 0,15∙600=90 г соли. В 240 г соленой воды с концентрацией 50% содержится 50% от 240 г соли. Это 0,5∙240=120 г соли. Масса полученной смеси равна 600+240=840 г. Соли в этой массе 90+120=210 г. Найдем процент соли в полученной смеси.

Ответ: в полученной смеси содержится 25% соли.

Задача 6.

Цену товара сначала снизили на 20%, затем новую цену снизили еще на 25%. На сколько процентов снизили первоначальную цену товара?

Решение. Обозначив первоначальную стоимость товара через х, выразим окончательную стоимость товара и найдем, сколько процентов последняя цена товара будет составлять от первоначальной. После первого снижения на 20%  товар стал стоить 80% от первоначальной цены. Это 80% от х или 0,8х Эту цену снизили еще на 25%, стоимость стала составлять 75% от последней цены, равной 0,8х. Тогда последняя цена составит 75% от 0,8х или 0,75∙0,8х=0,6х. Находим, сколько процентов 0,6х (последняя цена товара) составляет от х (первоначальной цены товара).

Получается, что новая цена составляет 60% от первоначальной цены. Это означает, что цена товара после двух снижений уменьшилась на 40%.

 Ответ: цену товара снизили на 40%.

Задача 7

 Вода составляет 76% картофеля. Сколько килограммов воды в 35 кг картофеля?

Решение. Вода составляет 76% от 35 кг. По правилу нахождения процентов от данного числа (чтобы найти проценты от данного числа нужно обратить проценты в десятичную или обыкновенную дробь, а затем умножить данное число на эту дробь) получаем  0,76∙35=26,6 кг.

Ответ: в 35 кг картофеля содержится 26,6 кг воды.

Задача8.

В классе 20 человек. Контрольную работу по математике 25% учащихся написали на «5», 35 % написали на «4», 10% всех учащихся получили «2». Сколько пятерок, четверок, троек и двоек получил класс?

Решение. Количество пятерок составляет 25% от 20. По правилу нахождения процентов от данного числа это 0,25∙20=5 учащихся. Четверки получили 35% от 20. Это 0,35∙20=7 учащихся. Двоек 10%. Это  1/10 часть от 20 учащихся, т.е. 2 человека. Остальные учащиеся получили оценку «3». Их 20-5-7-2=6 человек.

Ответ: оценку «5» получило 5 учащихся; оценку «4» получили 7 учащихся; оценку «3» получило 6 учащихся и оценку «2» получили 2 ученика.

Задача 9.

 Токарю нужно было сделать 120 деталей, но он перевыполнил план на 10%. Сколько деталей изготовил токарь?

Решение. 10% от 120 деталей – это одна десятая часть от 120, т.е. это 12 деталей. Токарь изготовил 120+12=132 детали.

Ответ: 132 детали изготовил токарь.

Задача10.

 После уценки на 10% цена холодильника стала 11430 рублей. Какова была цена холодильника  до уценки?

Решение. Имеем: 11430 рублей – это 90% от начальной цены холодильника. Находим число по его процентам. 1) 90%=0,9; 2) 11430:0,9=114300:9=12700 рублей.

Ответ: до уценки холодильник стоил 12700 рублей.

Решение задач на движение.

Задача 1. Дорога между пунктами А и В состоит из подъема и спуска, а ее длина равна 19 км. Турист прошёл путь из А в В за 5 часов, из которых подъём занял  1час. С какой скоростью турист шёл на спуске, если его скорость на спуске больше его скорости на подъёме на 1 км/ч?
Решение:

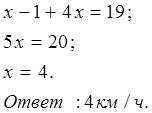
Задача 2.  Два автомобиля отправляются в 340-километровый пробег. Первый едет со скоростью на 17 км/ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найдите скорость первого автомобиля.

Решение:

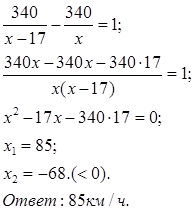
Задача 3.   Из двух городов одновременно навстречу друг другу отправляются два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 6 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 162 км, скорость первого велосипедиста равна 15 км/ч, скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

Решение:

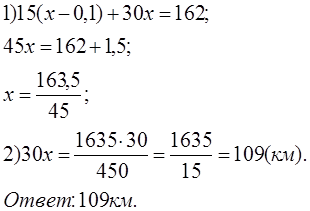
Задача 4.       Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 3,5 км от места отправления. Один идет со скоростью 2,7 км/ч, а другой – со скоростью 3,6 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдет их встреча?

Решение:

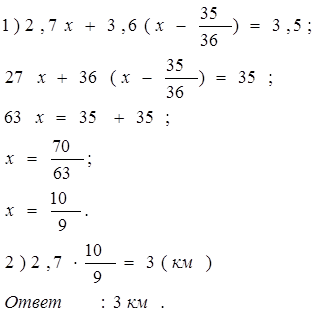
Задача 5.   Катер рыбнадзора патрулирует участок реки длиной 240 км. Скорость течения реки 2 км/ч. Найдите скорость катера в стоячей воде, если по течению катер проходит патрулируемый участок на 2 часа быстрее, чем против течения.

     Решение: х- собственная скорость катера

240/(х – 2) - 240/(х + 2) = 2;

120(x + 2) - 120(x - 2) = (x + 2)(x - 2);

120x + 240 - 120x + 240 = х² – 4;

х²  -  484 = 0;

(x - 22)(x + 22) = 0;

х = 22 или x = - 22 (не удовлетворяет условию задачи);

22 км/ч – скорость  катера в стоячей воде.

Ответ: 22 км/ч.

Задача 6.  Велосипедист отправился с некоторой скоростью из города А в город В, расстояние между которыми равно 88 км. Возвращаясь из В в А, он ехал поначалу с той же скоростью, но через один час пути вынужден был сделать остановку на 15 мин. После этого он продолжил путь в А, увеличив скорость на 2 км/ч, и в результате затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

 Решение:

По условию задачи: 88/х = 1 + (88 – х)/(х + 2) + 0,25

88(x + 2) -  1,25x(x+2) - x(88 - x) = 0

88 ∙ 2 – 0,25х² – 2,5х = 0

х² + 10х – 4 ∙ 8 ∙ 11 ∙ 2 = 0

х  = - 32 (не удовлетворяет условию задачи);

х = 22, значит, 22 км/ч скорость велосипедиста на пути из А в В.

Ответ: 22 км/ч.

Решение задач на переливания.

Задача 1 Для разведения картофельного пюре быстрого приготовления "Зеленый великан" требуется 1 л воды. Как, имея два сосуда емкостью 5 и 9 литров, налить 1 литр воды из водопроводного крана?

 Задача 2 Как с помощью 2-литровой и 5-литровой банок отмерить ровно 1 литр?

Задача 3  Для марш-броска по пустыне путешественнику необходимо иметь 4 литра воды. Больше он взять не может. На базе, где имеется источник воды, выдают только 5-литровые фляги, а также имеются 3-литровые банки. Как с помощью одной фляги и одной банки набрать 4 литра во флягу?

Задача 4 Есть два кувшина емкостью 5 л и 9 л. Нужно набрать из источника 7 л воды, если можно пользоваться только кувшинами.

Задача 5 Отмерить 3 л, имея сосуд 5 л. Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды? 

Задача 6 Деление 10 л поровну, имея сосуды 3, 6 и 7 л. Разделить на 2 равные части воду, находящуюся в 6-литровом сосуде (4 л) и в 7-литровом (6 л), пользуясь этими и 3-литровым сосудами. Какое наименьшее количество переливаний потребуется? 

 Задача 7 Деление 16 л поровну, имея сосуды 6, 11 и 16 л. Разделить на две равные части воду, находящуюся в полном 16 литровом сосуде, пользуясь этим и пустыми 11- и 6-литровыми сосудами. Какое наименьшее количество переливаний потребуется? 

Задача 8 Два сосуда и кран с водой. Какое наименьшее число переливаний необходимо для того, чтобы с помощью 7- и 11-литровых сосудов и крана с водой отмерить 2 л? 

Решение задач на применение дробно –рациональных уравнений.

Задача 1.   Одна мастерская должна была изготовить 420 деталей, другая, за тот же срок 500 деталей. Первая выполнила свою работу на 4 дня раньше срока, а вторая на 7. Сколько деталей в день изготовляла вторая мастерская, если известно, что ежедневно она изготовляла на 5 деталей больше, чем первая?

Решение:

Разница в выполнении: 7 – 4 =3,то

Д=4225 +30000=34225=185

Х ₁ =                   

Х₂= (не удовлетворяет условию задачи)

Ответ: 20 деталей.